Achieving Metabolic Flux Analysis for S. cerevisiae at a Genome-Scale: Challenges, Requirements, and Considerations
Abstract
:1. Introduction
2. Requirements for Genome-Scale MFA
3. Scale-up Considerations and Loss of Resolution
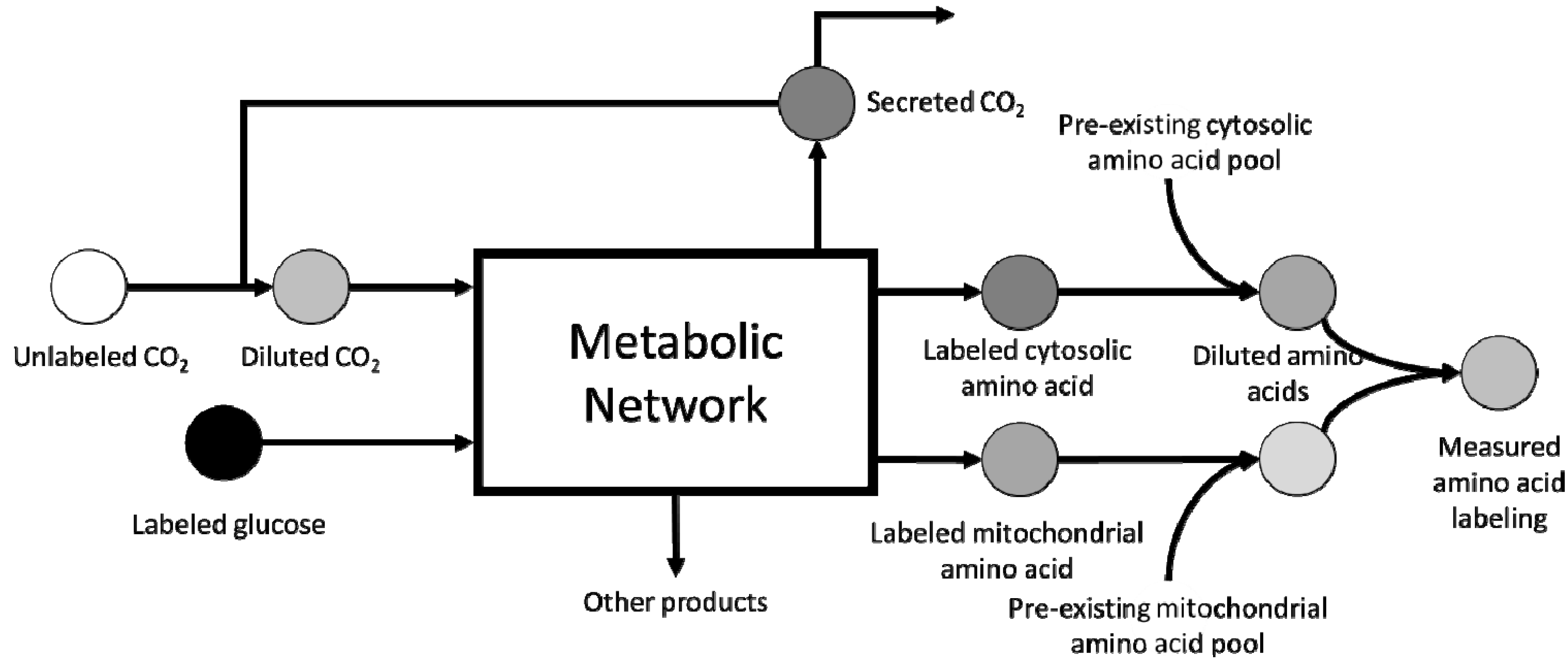
4. Computational Challenges Associated with Model Scale-up
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Brauer, M.J.; Saldanha, A.J.; Dolinski, K.; Botstein, D. Homeostatic adjustment and metabolic remodeling in glucose-limited yeast cultures. Mol. Biol. Cell 2005, 16, 2503–2517. [Google Scholar] [CrossRef] [PubMed]
- Broach, J.R. Nutritional control of growth and development in yeast. Genetics 2012, 192, 73–105. [Google Scholar] [CrossRef] [PubMed]
- Lodolo, E.J.; Kock, J.L.; Axcell, B.C.; Brooks, M. The yeast Saccharomyces cerevisiae- the main character in beer brewing. FEMS Yeast Res. 2008, 8, 1018–1036. [Google Scholar] [CrossRef] [PubMed]
- Mattanovich, D.; Branduardi, P.; Dato, L.; Gasser, B.; Sauer, M.; Porro, D. Recombinant protein production in yeasts. Methods Mol. Biol. 2012, 824, 329–358. [Google Scholar] [PubMed]
- Porro, D.; Sauer, M.; Branduardi, P.; Mattanovich, D. Recombinant protein production in yeasts. Mol. Biotechnol. 2005, 31, 245–259. [Google Scholar] [CrossRef]
- Buijs, N.A.; Siewers, V.; Nielsen, J. Advanced biofuel production by the yeast Saccharomyces cerevisiae. Curr. Opin. Chem. Biol. 2013, 17, 480–488. [Google Scholar] [CrossRef] [PubMed]
- Tippmann, S.; Chen, Y.; Siewers, V.; Nielsen, J. From flavors and pharmaceuticals to advanced biofuels: Production of isoprenoids in Saccharomyces cerevisiae. Biotechnol. J. 2013, 8, 1435–1444. [Google Scholar] [CrossRef] [PubMed]
- Bankar, A.V.; Kumar, A.R.; Zinjarde, S.S. Removal of chromium (vi) ions from aqueous solution by adsorption onto two marine isolates of Yarrowia lipolytica. J. Hazard. Mater. 2009, 170, 487–494. [Google Scholar] [CrossRef] [PubMed]
- Fickers, P.; Benetti, P.H.; Wache, Y.; Marty, A.; Mauersberger, S.; Smit, M.S.; Nicaud, J.M. Hydrophobic substrate utilisation by the yeast Yarrowia lipolytica, and its potential applications. FEMS Yeast Res. 2005, 5, 527–543. [Google Scholar] [CrossRef] [PubMed]
- Oswal, N.; Sarma, P.M.; Zinjarde, S.S.; Pant, A. Palm oil mill effluent treatment by a tropical marine yeast. Bioresour. Technol. 2002, 85, 35–37. [Google Scholar] [CrossRef]
- Antoniewicz, M.R. Methods and advances in metabolic flux analysis: A mini-review. J. Ind. Microbiol. Biotechnol. 2015, 42, 317–325. [Google Scholar] [CrossRef] [PubMed]
- Vera, J.; de Atauri, P.; Cascante, M.; Torres, N.V. Multicriteria optimization of biochemical systems by linear programming: Application to production of ethanol by Saccharomyces cerevisiae. Biotechnol. Bioeng. 2003, 83, 335–343. [Google Scholar] [CrossRef] [PubMed]
- Famili, I.; Forster, J.; Nielsen, J.; Palsson, B.O. Saccharomyces cerevisiae phenotypes can be predicted by using constraint-based analysis of a genome-scale reconstructed metabolic network. Proc. Natl. Acad. Sci. USA 2003, 100, 13134–13139. [Google Scholar] [CrossRef] [PubMed]
- Zomorrodi, A.R.; Suthers, P.F.; Ranganathan, S.; Maranas, C.D. Mathematical optimization applications in metabolic networks. Metab. Eng. 2012, 14, 672–686. [Google Scholar] [CrossRef] [PubMed]
- Mahadevan, R.; Schilling, C.H. The effects of alternate optimal solutions in constraint-based genome-scale metabolic models. Metab. Eng. 2003, 5, 264–276. [Google Scholar] [CrossRef] [PubMed]
- Varma, A.; Palsson, B.O. Stoichiometric flux balance models quantitatively predict growth and metabolic by-product secretion in wild-type Escherichia coli w3110. Appl. Environ. Microbiol. 1994, 60, 3724–3731. [Google Scholar] [PubMed]
- Bro, C.; Regenberg, B.; Forster, J.; Nielsen, J. In silico aided metabolic engineering of Saccharomyces cerevisiae for improved bioethanol production. Metab. Eng. 2006, 8, 102–111. [Google Scholar] [CrossRef] [PubMed]
- Burgard, A.P.; Pharkya, P.; Maranas, C.D. Optknock: A bilevel programming framework for identifying gene knockout strategies for microbial strain optimization. Biotechnol. Bioeng. 2003, 84, 647–657. [Google Scholar] [CrossRef] [PubMed]
- Agren, R.; Otero, J.M.; Nielsen, J. Genome-scale modeling enables metabolic engineering of Saccharomyces cerevisiae for succinic acid production. J. Ind. Microbiol. Biotechnol. 2013, 40, 735–747. [Google Scholar] [CrossRef] [PubMed]
- Brochado, A.R.; Matos, C.; Moller, B.L.; Hansen, J.; Mortensen, U.H.; Patil, K.R. Improved vanillin production in baker’s yeast through in silico design. Microb. Cell Fact. 2010, 9, 84. [Google Scholar] [CrossRef] [PubMed]
- Asadollahi, M.A.; Maury, J.; Patil, K.R.; Schalk, M.; Clark, A.; Nielsen, J. Enhancing sesquiterpene production in Saccharomyces cerevisiae through in silico driven metabolic engineering. Metab. Eng. 2009, 11, 328–334. [Google Scholar] [CrossRef] [PubMed]
- Chowdhury, R.; Chowdhury, A.; Maranas, C.D. Using gene essentiality and synthetic lethality information to correct yeast and cho cell genome-scale models. Metabolites 2015, in press. [Google Scholar]
- Zomorrodi, A.R.; Maranas, C.D. Improving the imm904 S. cerevisiae metabolic model using essentiality and synthetic lethality data. BMC Syst. Biol. 2010, 4, 178. [Google Scholar] [CrossRef] [PubMed]
- Cakir, T.; Patil, K.R.; Onsan, Z.; Ulgen, K.O.; Kirdar, B.; Nielsen, J. Integration of metabolome data with metabolic networks reveals reporter reactions. Mol. Syst. Biol. 2006, 2, 50. [Google Scholar] [CrossRef] [PubMed]
- Mo, M.L.; Palsson, B.O.; Herrgard, M.J. Connecting extracellular metabolomic measurements to intracellular flux states in yeast. BMC Syst. Biol. 2009, 3, 37. [Google Scholar] [CrossRef] [PubMed]
- Patil, K.R.; Nielsen, J. Uncovering transcriptional regulation of metabolism by using metabolic network topology. Proc. Natl. Acad. Sci. USA 2005, 102, 2685–2689. [Google Scholar] [CrossRef] [PubMed]
- Crown, S.B.; Antoniewicz, M.R. Publishing 13c metabolic flux analysis studies: A review and future perspectives. Metab. Engineering 2013, 20, 42–48. [Google Scholar] [CrossRef] [PubMed]
- Van Winden, W.A.; van Dam, J.C.; Ras, C.; Kleijn, R.J.; Vinke, J.L.; van Gulik, W.M.; Heijnen, J.J. Metabolic-flux analysis of Saccharomyces cerevisiae cen.Pk113–7d based on mass isotopomer measurements of (13)c-labeled primary metabolites. FEMS Yeast Res. 2005, 5, 559–568. [Google Scholar] [CrossRef] [PubMed]
- Frick, O.; Wittmann, C. Characterization of the metabolic shift between oxidative and fermentative growth in Saccharomyces cerevisiae by comparative 13c flux analysis. Microb. Cell Fact. 2005, 4, 30. [Google Scholar] [CrossRef] [PubMed]
- Gopalakrishnan, S.; Maranas, C.D. 13C metabolic flux analysis at the genome-scale. Metab. Eng. 2015, in press. [Google Scholar] [CrossRef] [PubMed]
- Jouhten, P.; Rintala, E.; Huuskonen, A.; Tamminen, A.; Toivari, M.; Wiebe, M.; Ruohonen, L.; Penttila, M.; Maaheimo, H. Oxygen dependence of metabolic fluxes and energy generation of Saccharomyces cerevisiae cen.Pk113-1a. BMC Syst. Biol. 2008, 2, 60. [Google Scholar] [CrossRef] [PubMed]
- Costenoble, R.; Muller, D.; Barl, T.; van Gulik, W.M.; van Winden, W.A.; Reuss, M.; Heijnen, J.J. 13c-labeled metabolic flux analysis of a fed-batch culture of elutriated Saccharomyces cerevisiae. FEMS Yeast Res. 2007, 7, 511–526. [Google Scholar] [CrossRef] [PubMed]
- Niklas, J.; Schneider, K.; Heinzle, E. Metabolic flux analysis in eukaryotes. Curr. Opin. Biotechnol. 2010, 21, 63–69. [Google Scholar] [CrossRef] [PubMed]
- Blank, L.M.; Sauer, U. Tca cycle activity in saccharomyces cerevisiae is a function of the environmentally determined specific growth and glucose uptake rates. Microbiology 2004, 150, 1085–1093. [Google Scholar] [CrossRef] [PubMed]
- Velagapudi, V.R.; Wittmann, C.; Schneider, K.; Heinzle, E. Metabolic flux screening of Saccharomyces cerevisiae single knockout strains on glucose and galactose supports elucidation of gene function. J. Biotechnol. 2007, 132, 395–404. [Google Scholar] [CrossRef] [PubMed]
- Kleijn, R.J.; Geertman, J.M.; Nfor, B.K.; Ras, C.; Schipper, D.; Pronk, J.T.; Heijnen, J.J.; van Maris, A.J.; van Winden, W.A. Metabolic flux analysis of a glycerol-overproducing Saccharomyces cerevisiae strain based on GC-MS, LC-MS and NMR-derived c-labelling data. FEMS Yeast Res. 2007, 7, 216–231. [Google Scholar] [CrossRef] [PubMed]
- Feng, X.; Zhao, H. Investigating xylose metabolism in recombinant Saccharomyces cerevisiae via 13c metabolic flux analysis. Microb. Cell Fact. 2013, 12. [Google Scholar] [CrossRef] [PubMed]
- Wasylenko, T.M.; Stephanopoulos, G. Metabolomic and (13)c-metabolic flux analysis of a xylose-consuming Saccharomyces cerevisiae strain expressing xylose isomerase. Biotechnol. Bioeng. 2015, 112, 470–483. [Google Scholar] [CrossRef] [PubMed]
- Kajihata, S.; Matsuda, F.; Yoshimi, M.; Hayakawa, K.; Furusawa, C.; Kanda, A.; Shimizu, H. (13)c-based metabolic flux analysis of Saccharomyces cerevisiae with a reduced crabtree effect. J. Biosci. Bioeng. 2015, 120, 140–144. [Google Scholar] [CrossRef] [PubMed]
- Gombert, A.K.; Moreira dos Santos, M.; Christensen, B.; Nielsen, J. Network identification and flux quantification in the central metabolism of Saccharomyces cerevisiae under different conditions of glucose repression. J. Bacteriol. 2001, 183, 1441–1451. [Google Scholar] [CrossRef] [PubMed]
- Monschau, N.; Stahmann, K.P.; Sahm, H.; McNeil, J.B.; Bognar, A.L. Identification of Saccharomyces cerevisiae gly1 as a threonine aldolase: A key enzyme in glycine biosynthesis. FEMS Microbiol. Lett. 1997, 150, 55–60. [Google Scholar] [CrossRef]
- Tu, B.P.; Kudlicki, A.; Rowicka, M.; McKnight, S.L. Logic of the yeast metabolic cycle: Temporal compartmentalization of cellular processes. Science 2005, 310, 1152–1158. [Google Scholar] [CrossRef] [PubMed]
- Bonarius, H.P.; Timmerarends, B.; de Gooijer, C.D.; Tramper, J. Metabolite-balancing techniques vs. 13c tracer experiments to determine metabolic fluxes in hybridoma cells. Biotechnol. Bioeng. 1998, 58, 258–262. [Google Scholar] [CrossRef]
- Ahn, W.S.; Antoniewicz, M.R. Metabolic flux analysis of cho cells at growth and non-growth phases using isotopic tracers and mass spectrometry. Metab. Eng. 2011, 13, 598–609. [Google Scholar] [CrossRef] [PubMed]
- Murphy, T.A.; Dang, C.V.; Young, J.D. Isotopically nonstationary 13c flux analysis of myc-induced metabolic reprogramming in b-cells. Metab. Eng. 2013, 15, 206–217. [Google Scholar] [CrossRef] [PubMed]
- Miyagi, H.; Kawai, S.; Murata, K. Two sources of mitochondrial NADPH in the yeast Saccharomyces cerevisiae. J. Biol. Chem. 2009, 284, 7553–7560. [Google Scholar] [CrossRef] [PubMed]
- Outten, C.E.; Culotta, V.C. A novel nadh kinase is the mitochondrial source of NADPH in Saccharomyces cerevisiae. EMBO J. 2003, 22, 2015–2024. [Google Scholar] [CrossRef] [PubMed]
- Jin, L.; Bhuiya, M.W.; Li, M.; Liu, X.; Han, J.; Deng, W.; Wang, M.; Yu, O.; Zhang, Z. Metabolic engineering of Saccharomyces cerevisiae for caffeine and theobromine production. PLoS ONE 2014, 9, e105368. [Google Scholar] [CrossRef] [PubMed]
- Aung, H.W.; Henry, S.A.; Walker, L.P. Revising the representation of fatty acid, glycerolipid, and glycerophospholipid metabolism in the consensus model of yeast metabolism. Ind. Biotechnol. 2013, 9, 215–228. [Google Scholar] [CrossRef] [PubMed]
- Duarte, N.C.; Herrgard, M.J.; Palsson, B.O. Reconstruction and validation of Saccharomyces cerevisiae ind750, a fully compartmentalized genome-scale metabolic model. Genome Res. 2004, 14, 1298–1309. [Google Scholar] [CrossRef]
- Forster, J.; Famili, I.; Fu, P.; Palsson, B.O.; Nielsen, J. Genome-scale reconstruction of the Saccharomyces cerevisiae metabolic network. Genome Res. 2003, 13, 244–253. [Google Scholar] [CrossRef] [PubMed]
- Heavner, B.D.; Smallbone, K.; Barker, B.; Mendes, P.; Walker, L.P. Yeast 5—An expanded reconstruction of the Saccharomyces cerevisiae metabolic network. BMC Systems Biology 2012, 6, 55. [Google Scholar] [CrossRef] [PubMed]
- Heavner, B.D.; Smallbone, K.; Price, N.D.; Walker, L.P. Version 6 of the consensus yeast metabolic network refines biochemical coverage and improves model performance. Database (Oxford) 2013, 2013. [Google Scholar] [CrossRef] [PubMed]
- Vieira, E.D.; Andrietta Mda, G.; Andrietta, S.R. Yeast biomass production: A new approach in glucose-limited feeding strategy. Braz. J. Microbiol. 2013, 44, 551–558. [Google Scholar] [CrossRef] [PubMed]
- Feist, A.M.; Henry, C.S.; Reed, J.L.; Krummenacker, M.; Joyce, A.R.; Karp, P.D.; Broadbelt, L.J.; Hatzimanikatis, V.; Palsson, B.O. A genome-scale metabolic reconstruction for Escherichia coli k-12 mg1655 that accounts for 1260 orfs and thermodynamic information. Mol. Syst. Biol. 2007, 3, 121. [Google Scholar] [CrossRef] [PubMed]
- Leighty, R.W.; Antoniewicz, M.R. Parallel labeling experiments with [u-13c]glucose validate E. coli metabolic network model for 13c metabolic flux analysis. Metab. Eng. 2012, 14, 533–541. [Google Scholar] [CrossRef] [PubMed]
- Covert, M.W.; Knight, E.M.; Reed, J.L.; Herrgard, M.J.; Palsson, B.O. Integrating high-throughput and computational data elucidates bacterial networks. Nature 2004, 429, 92–96. [Google Scholar] [CrossRef] [PubMed]
- Nazem-Bokaee, H.; Gopalakrishnan, S.; Ferry, J.G.; Wood, T.K.; Maranas, C.D. Assessing methanotrophy and carbon fixation for biofuel production by Methanosarcina acetivorans. Microb. Cell Fact. 2015, in press. [Google Scholar]
- Satish Kumar, V.; Ferry, J.G.; Maranas, C.D. Metabolic reconstruction of the archaeon methanogen Methanosarcina acetivorans. BMC Syst. Biol. 2011, 5. [Google Scholar] [CrossRef] [PubMed]
- Aslankoohi, E.; Zhu, B.; Rezaei, M.N.; Voordeckers, K.; de Maeyer, D.; Marchal, K.; Dornez, E.; Courtin, C.M.; Verstrepen, K.J. Dynamics of the Saccharomyces cerevisiae transcriptome during bread dough fermentation. Appl. Environ. Microbiol. 2013, 79, 7325–7333. [Google Scholar] [CrossRef] [PubMed]
- Rintala, E.; Jouhten, P.; Toivari, M.; Wiebe, M.G.; Maaheimo, H.; Penttila, M.; Ruohonen, L. Transcriptional responses of Saccharomyces cerevisiae to shift from respiratory and respirofermentative to fully fermentative metabolism. OMICS 2011, 15, 461–476. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.; Chen, J.; Liu, J.; Han, B. Transcriptome analysis reveals the oxidative stress response in Saccharomyces cerevisiae. RSC Adv. 2015, 5, 22923–22934. [Google Scholar] [CrossRef]
- Caspi, R.; Altman, T.; Billington, R.; Dreher, K.; Foerster, H.; Fulcher, C.A.; Holland, T.A.; Keseler, I.M.; Kothari, A.; Kubo, A.; et al. The metacyc database of metabolic pathways and enzymes and the biocyc collection of pathway/genome databases. Nucleic Acids Res. 2014, 42, D459–D471. [Google Scholar] [CrossRef] [PubMed]
- Tanabe, M.; Kanehisa, M. Using the kegg database resource. Curr. Protoc. Bioinform. 2012. [Google Scholar] [CrossRef]
- Kumar, A.; Suthers, P.F.; Maranas, C.D. Metrxn: A knowledgebase of metabolites and reactions spanning metabolic models and databases. BMC Bioinform. 2012, 13. [Google Scholar] [CrossRef] [PubMed]
- Xu, H.; Andi, B.; Qian, J.; West, A.H.; Cook, P.F. The alpha-aminoadipate pathway for lysine biosynthesis in fungi. Cell Biochem. Biophys. 2006, 46, 43–64. [Google Scholar] [CrossRef]
- Clasquin, M.F.; Melamud, E.; Singer, A.; Gooding, J.R.; Xu, X.; Dong, A.; Cui, H.; Campagna, S.R.; Savchenko, A.; Yakunin, A.F.; et al. Riboneogenesis in yeast. Cell 2011, 145, 969–980. [Google Scholar] [CrossRef] [PubMed]
- Latendresse, M.; Malerich, J.P.; Travers, M.; Karp, P.D. Accurate atom-mapping computation for biochemical reactions. J. Chem. Inf. Model. 2012, 52, 2970–2982. [Google Scholar] [CrossRef] [PubMed]
- Kumar, A.; Maranas, C.D. Clca: Maximum common molecular substructure queries within the metrxn database. J. Chem. Inf. Model. 2014, 54, 3417–3438. [Google Scholar] [CrossRef] [PubMed]
- Weininger, D.; Weininger, A.; Weininger, J.L. Smiles. 2. Algorithm for generation of unique smiles notation. J. Chem. Inf. Comput. Sci. 1989, 29, 97–101. [Google Scholar] [CrossRef]
- Zamboni, N.; Fendt, S.M.; Ruhl, M.; Sauer, U. (13)c-based metabolic flux analysis. Nat. Protoc. 2009, 4, 878–892. [Google Scholar] [CrossRef] [PubMed]
- Antoniewicz, M.R.; Kelleher, J.K.; Stephanopoulos, G. Accurate assessment of amino acid mass isotopomer distributions for metabolic flux analysis. Anal. Chem. 2007, 79, 7554–7559. [Google Scholar] [CrossRef] [PubMed]
- Szyperski, T. Biosynthetically directed fractional 13c-labeling of proteinogenic amino acids. An efficient analytical tool to investigate intermediary metabolism. Eur. J. Biochem. 1995, 232, 433–448. [Google Scholar] [CrossRef] [PubMed]
- Aboka, F.O.; Heijnen, J.J.; van Winden, W.A. Dynamic 13c-tracer study of storage carbohydrate pools in aerobic glucose-limited Saccharomyces cerevisiae confirms a rapid steady-state turnover and fast mobilization during a modest stepup in the glucose uptake rate. FEMS Yeast Res. 2009, 9, 191–201. [Google Scholar] [CrossRef] [PubMed]
- Wahrheit, J.; Nicolae, A.; Heinzle, E. Eukaryotic metabolism: Measuring compartment fluxes. Biotechnol. J. 2011, 6, 1071–1085. [Google Scholar] [CrossRef] [PubMed]
- Wurm, M.; Schopke, B.; Lutz, D.; Muller, J.; Zeng, A.P. Microtechnology meets systems biology: The small molecules of metabolome as next big targets. J. Biotechnol. 2010, 149, 33–51. [Google Scholar] [CrossRef] [PubMed]
- Ratcliffe, R.G.; Shachar-Hill, Y. Probing plant metabolism with NMR. Annu. Rev. Plant Physiol. Plant Mol. Biol. 2001, 52, 499–526. [Google Scholar] [CrossRef] [PubMed]
- Allen, D.K.; Evans, B.S.; Libourel, I.G. Analysis of isotopic labeling in peptide fragments by tandem mass spectrometry. PLoS ONE 2014, 9, e91537. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Allen, D.K.; Goldford, J.; Gierse, J.K.; Mandy, D.; Diepenbrock, C.; Libourel, I.G. Quantification of peptide m/z distributions from 13c-labeled cultures with high-resolution mass spectrometry. Anal. Chem. 2014, 86, 1894–1901. [Google Scholar] [CrossRef] [PubMed]
- Mandy, D.E.; Goldford, J.E.; Yang, H.; Allen, D.K.; Libourel, I.G. Metabolic flux analysis using (1)(3)c peptide label measurements. Plant J. 2014, 77, 476–486. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, A.; Nilmeier, J.; Weaver, D.; Adams, P.D.; Keasling, J.D.; Mukhopadhyay, A.; Petzold, C.J.; Martin, H.G. A peptide-based method for 13c metabolic flux analysis in microbial communities. PLoS Comput. Biol. 2014, 10, e1003827. [Google Scholar] [CrossRef] [PubMed]
- Dobson, G.; Christie, W.W. Mass spectrometry of fatty acid derivatives. Eur. J. Lipid Sci. Technol. 2002, 104, 36–43. [Google Scholar] [CrossRef]
- Dudley, E.; Bond, L. Mass spectrometry analysis of nucleosides and nucleotides. Mass Spectrom. Rev. 2014, 33, 302–331. [Google Scholar] [CrossRef] [PubMed]
- Crown, S.B.; Long, C.P.; Antoniewicz, M.R. Integrated 13c-metabolic flux analysis of 14 parallel labeling experiments in Escherichia coli. Metab. Eng. 2015, 28, 151–158. [Google Scholar] [CrossRef] [PubMed]
- Chang, Y.; Suthers, P.F.; Maranas, C.D. Identification of optimal measurement sets for complete flux elucidation in metabolic flux analysis experiments. Biotechnol. Bioeng. 2008, 100, 1039–1049. [Google Scholar] [CrossRef] [PubMed]
- Antoniewicz, M.R.; Kelleher, J.K.; Stephanopoulos, G. Determination of confidence intervals of metabolic fluxes estimated from stable isotope measurements. Metab. Eng. 2006, 8, 324–337. [Google Scholar] [CrossRef] [PubMed]
- Easlon, E.; Tsang, F.; Skinner, C.; Wang, C.; Lin, S.J. The malate-aspartate NADH shuttle components are novel metabolic longevity regulators required for calorie restriction-mediated life span extension in yeast. Genes Dev. 2008, 22, 931–944. [Google Scholar] [CrossRef] [PubMed]
- Leighty, R.W.; Antoniewicz, M.R. Complete-mfa: Complementary parallel labeling experiments technique for metabolic flux analysis. Metab. Eng. 2013, 20, 49–55. [Google Scholar] [CrossRef] [PubMed]
- Dauner, M. From fluxes and isotope labeling patterns towards in silico cells. Curr. Opin. Biotechnol. 2010, 21, 55–62. [Google Scholar] [CrossRef] [PubMed]
- Futcher, B. Cell cycle synchronization. Methods Cell Sci. 1999, 21, 79–86. [Google Scholar] [CrossRef] [PubMed]
- Antoniewicz, M.R.; Kelleher, J.K.; Stephanopoulos, G. Elementary metabolite units (emu): A novel framework for modeling isotopic distributions. Metab. Eng. 2007, 9, 68–86. [Google Scholar] [CrossRef] [PubMed]
- Wiechert, W.; Siefke, C.; de Graaf, A.A.; Marx, A. Bidirectional reaction steps in metabolic networks: Ii. Flux estimation and statistical analysis. Biotechnol. Bioeng. 1997, 55, 118–135. [Google Scholar] [CrossRef]
- Foster, L.V. Rank and null space calculations using matrix decomposition without column interchanges. Linear Algebra Appl. 1986, 74, 47–71. [Google Scholar] [CrossRef]
- Schmidt, K.; Marx, A.; de Graaf, A.A.; Wiechert, W.; Sahm, H.; Nielsen, J.; Villadsen, J. 13c tracer experiments and metabolite balancing for metabolic flux analysis: Comparing two approaches. Biotechnol. Bioeng. 1998, 58, 254–257. [Google Scholar] [CrossRef]
- Isermann, N.; Wiechert, W. Metabolic isotopomer labeling systems. Part ii: Structural flux identifiability analysis. Math. Biosci. 2003, 183, 175–214. [Google Scholar] [CrossRef]
- Lewis, N.E.; Hixson, K.K.; Conrad, T.M.; Lerman, J.A.; Charusanti, P.; Polpitiya, A.D.; Adkins, J.N.; Schramm, G.; Purvine, S.O.; Lopez-Ferrer, D.; et al. Omic data from evolved E. coli are consistent with computed optimal growth from genome-scale models. Mol. Syst. Biol. 2010, 6. [Google Scholar] [CrossRef] [PubMed]
- Gebreselassie, N.A.; Antoniewicz, M.R. 13c-metabolic flux analysis of co-cultures: A novel approach. Metab. Eng. 2015, 31, 132–139. [Google Scholar] [CrossRef] [PubMed]
- Young, J.D.; Shastri, A.A.; Stephanopoulos, G.; Morgan, J.A. Mapping photoautotrophic metabolism with isotopically nonstationary (13)c flux analysis. Metab. Eng. 2011, 13, 656–665. [Google Scholar] [CrossRef] [PubMed]
- Kayser, A.; Weber, J.; Hecht, V.; Rinas, U. Metabolic flux analysis of Escherichia coli in glucose-limited continuous culture. I. Growth-rate-dependent metabolic efficiency at steady state. Microbiology 2005, 151, 693–706. [Google Scholar] [CrossRef] [PubMed]
- Albers, E.; Larsson, C.; Andlid, T.; Walsh, M.C.; Gustafsson, L. Effect of nutrient starvation on the cellular composition and metabolic capacity of Saccharomyces cerevisiae. Appl. Environ. Microbiol. 2007, 73, 4839–4848. [Google Scholar] [CrossRef] [PubMed]
- Larsson, C.; von Stockar, U.; Marison, I.; Gustafsson, L. Growth and metabolism of Saccharomyces cerevisiae in chemostat cultures under carbon-, nitrogen-, or carbon- and nitrogen-limiting conditions. J. Bacteriol. 1993, 175, 4809–4816. [Google Scholar] [PubMed]
- Schulze, U.; Liden, G.; Nielsen, J.; Villadsen, J. Physiological effects of nitrogen starvation in an anaerobic batch culture of Saccharomyces cerevisiae. Microbiology 1996, 142, 2299–2310. [Google Scholar] [CrossRef] [PubMed]
- Long, C.P.; Antoniewicz, M.R. Quantifying biomass composition by gas chromatography/mass spectrometry. Anal. Chem. 2014, 86, 9423–9427. [Google Scholar] [CrossRef] [PubMed]
- Maaheimo, H.; Fiaux, J.; Cakar, Z.P.; Bailey, J.E.; Sauer, U.; Szyperski, T. Central carbon metabolism of Saccharomyces cerevisiae explored by biosynthetic fractional (13)c labeling of common amino acids. Eur. J. Biochem. 2001, 268, 2464–2479. [Google Scholar] [CrossRef] [PubMed]
- Lanza, I.R.; Zhang, S.; Ward, L.E.; Karakelides, H.; Raftery, D.; Nair, K.S. Quantitative metabolomics by H-NMR and LC-MS/MS confirms altered metabolic pathways in diabetes. PLoS ONE 2010, 5. [Google Scholar] [CrossRef] [PubMed]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gopalakrishnan, S.; Maranas, C.D. Achieving Metabolic Flux Analysis for S. cerevisiae at a Genome-Scale: Challenges, Requirements, and Considerations. Metabolites 2015, 5, 521-535. https://doi.org/10.3390/metabo5030521
Gopalakrishnan S, Maranas CD. Achieving Metabolic Flux Analysis for S. cerevisiae at a Genome-Scale: Challenges, Requirements, and Considerations. Metabolites. 2015; 5(3):521-535. https://doi.org/10.3390/metabo5030521
Chicago/Turabian StyleGopalakrishnan, Saratram, and Costas D. Maranas. 2015. "Achieving Metabolic Flux Analysis for S. cerevisiae at a Genome-Scale: Challenges, Requirements, and Considerations" Metabolites 5, no. 3: 521-535. https://doi.org/10.3390/metabo5030521
APA StyleGopalakrishnan, S., & Maranas, C. D. (2015). Achieving Metabolic Flux Analysis for S. cerevisiae at a Genome-Scale: Challenges, Requirements, and Considerations. Metabolites, 5(3), 521-535. https://doi.org/10.3390/metabo5030521




