Wind Turbine Anomaly Detection Based on SCADA Data Mining
Abstract
1. Introduction
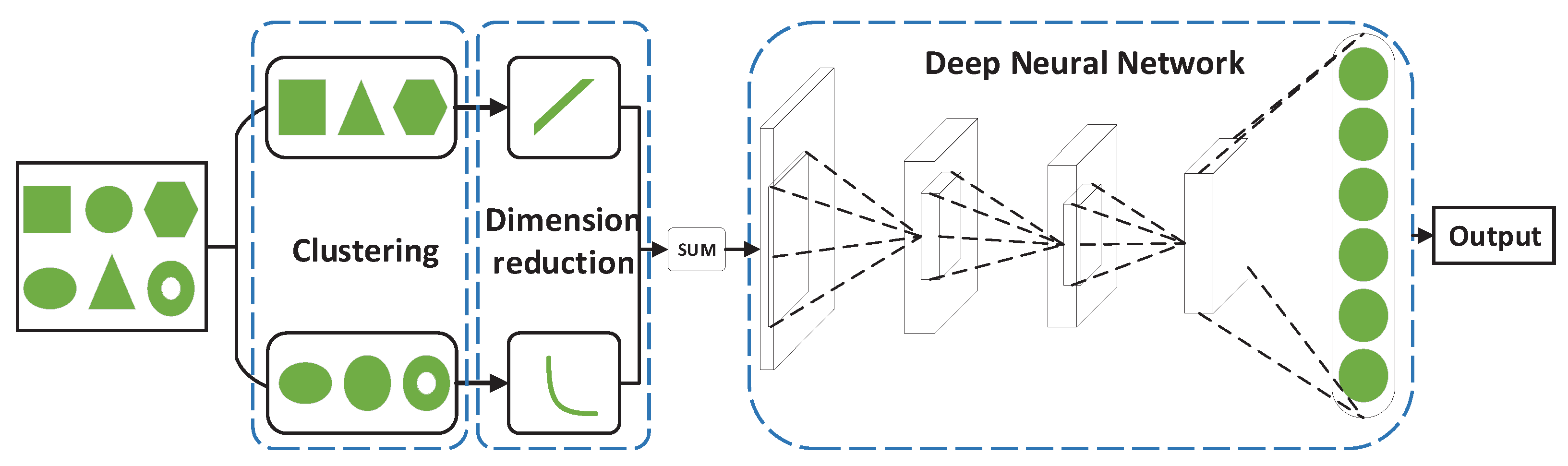
2. Architecture of the Proposed Method
3. Data Feature Extraction
3.1. K-Means Clustering
3.1.1. Clarify the Maximum Number of Clusters
3.1.2. 0-1 Normalization Processing
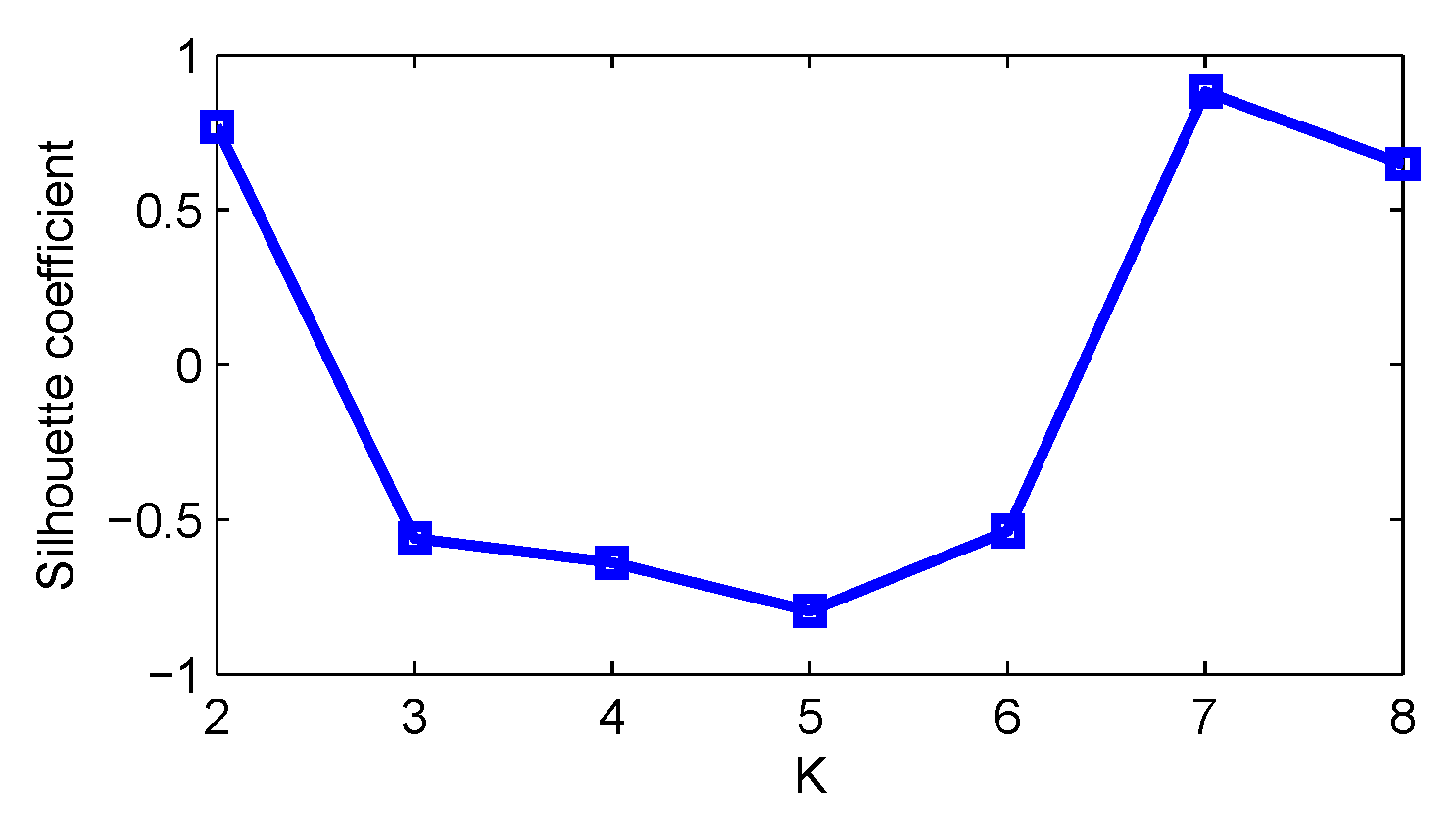
3.1.3. Determine the Number of Clusters
3.2. T-SNE Dimensionality Reduction
4. Architecture of Detection Model
4.1. Deep Neural Network
4.2. Description of Each Layer
4.3. Training Process of the Model
5. Experimental and Discussion
5.1. Data Description
5.2. Model Parameters Setting
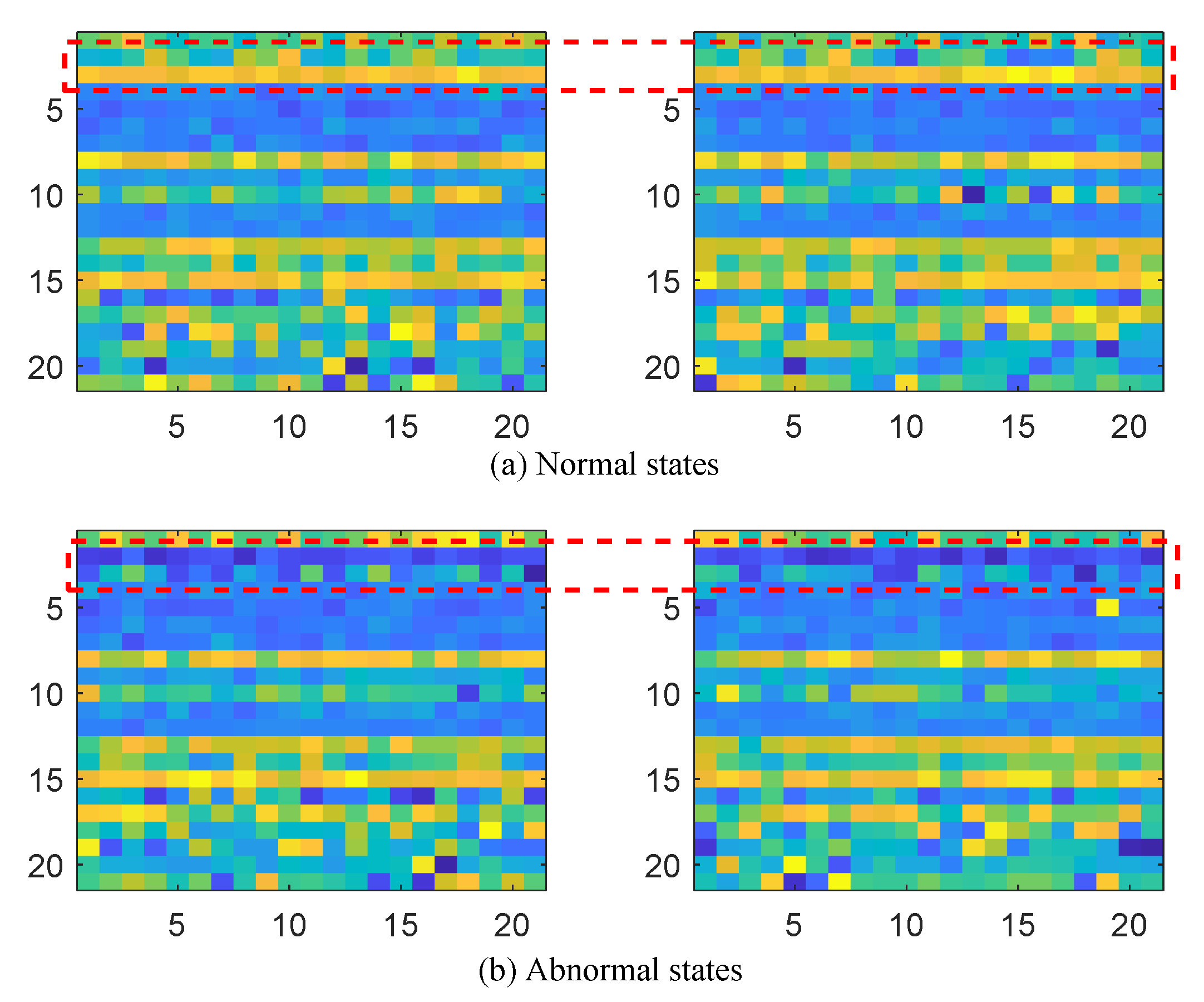
5.3. Cases Analysis
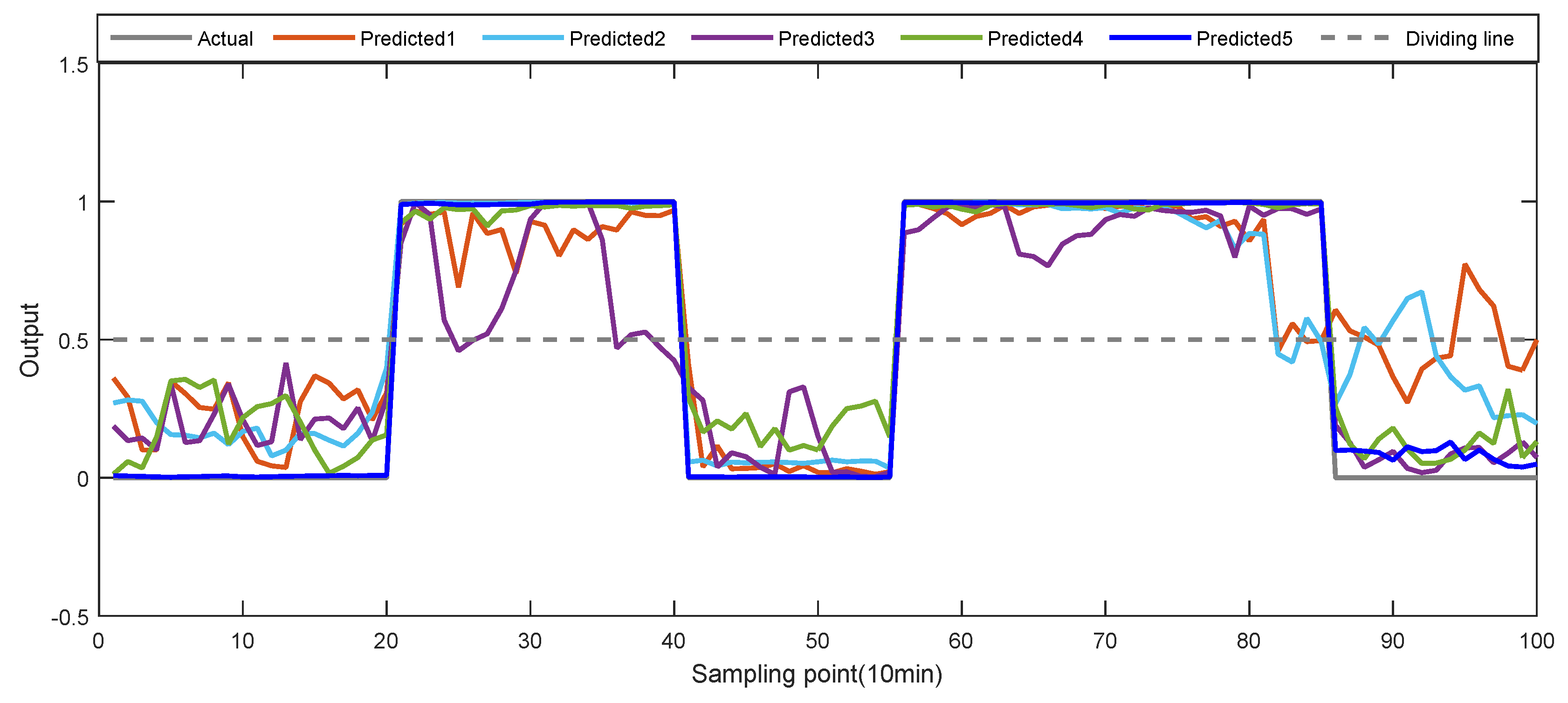
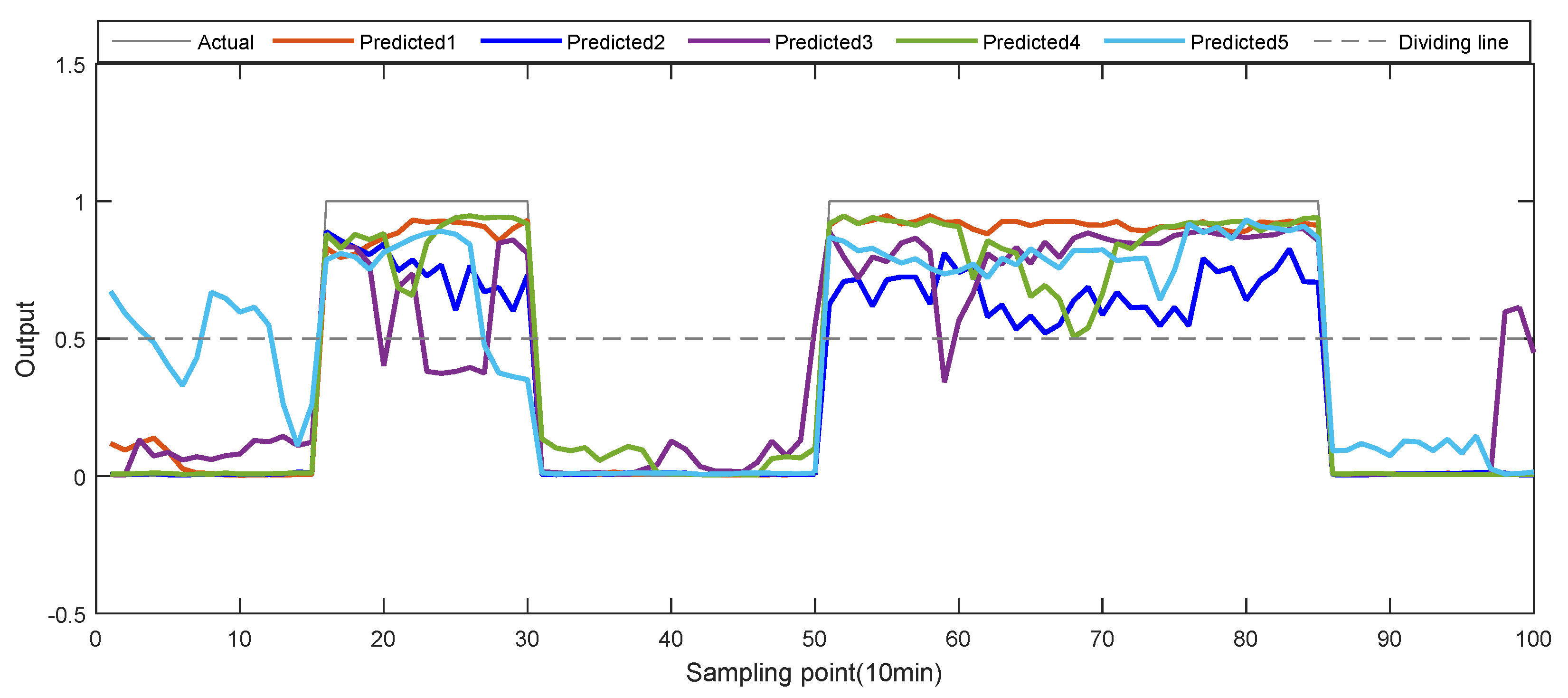
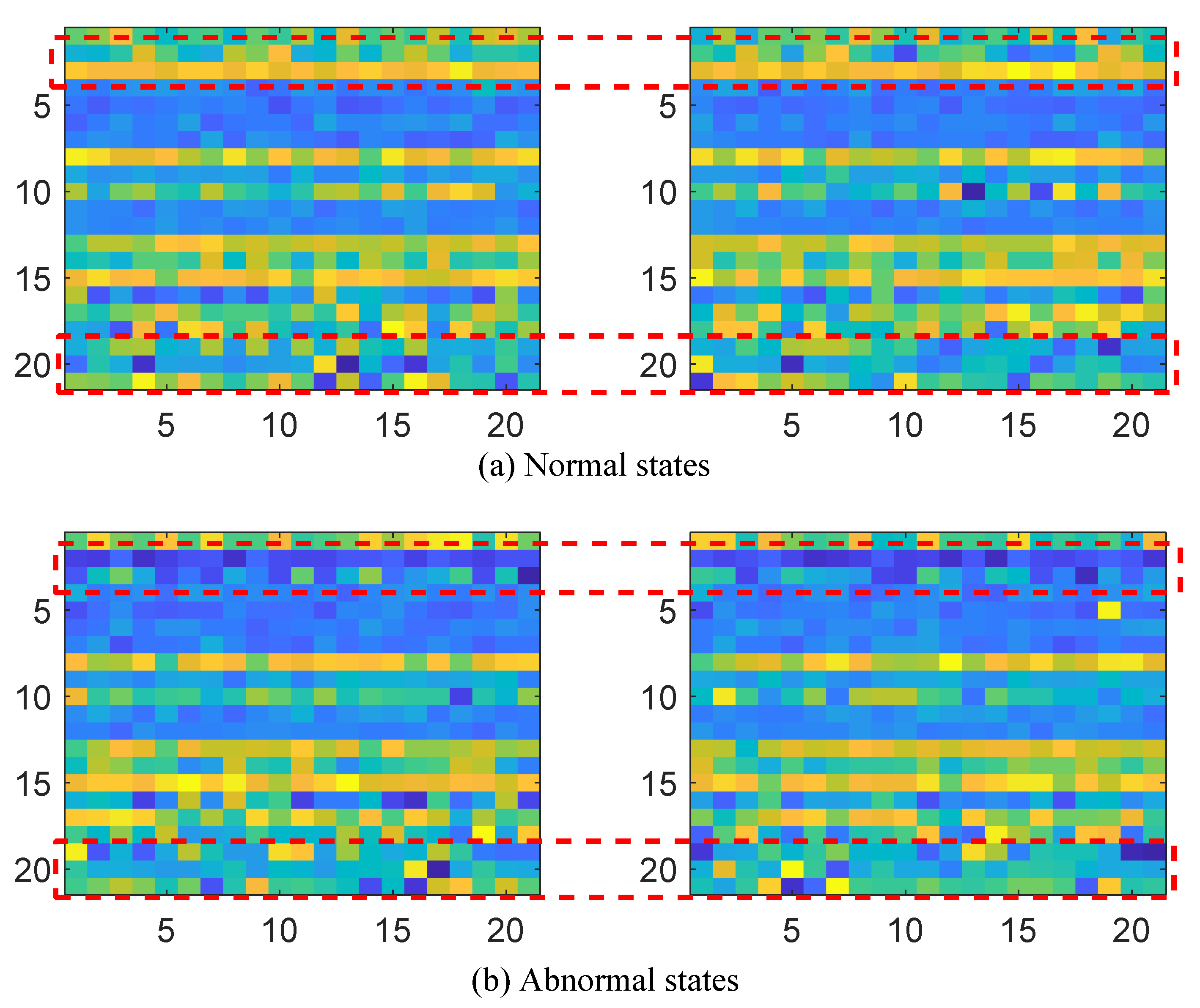
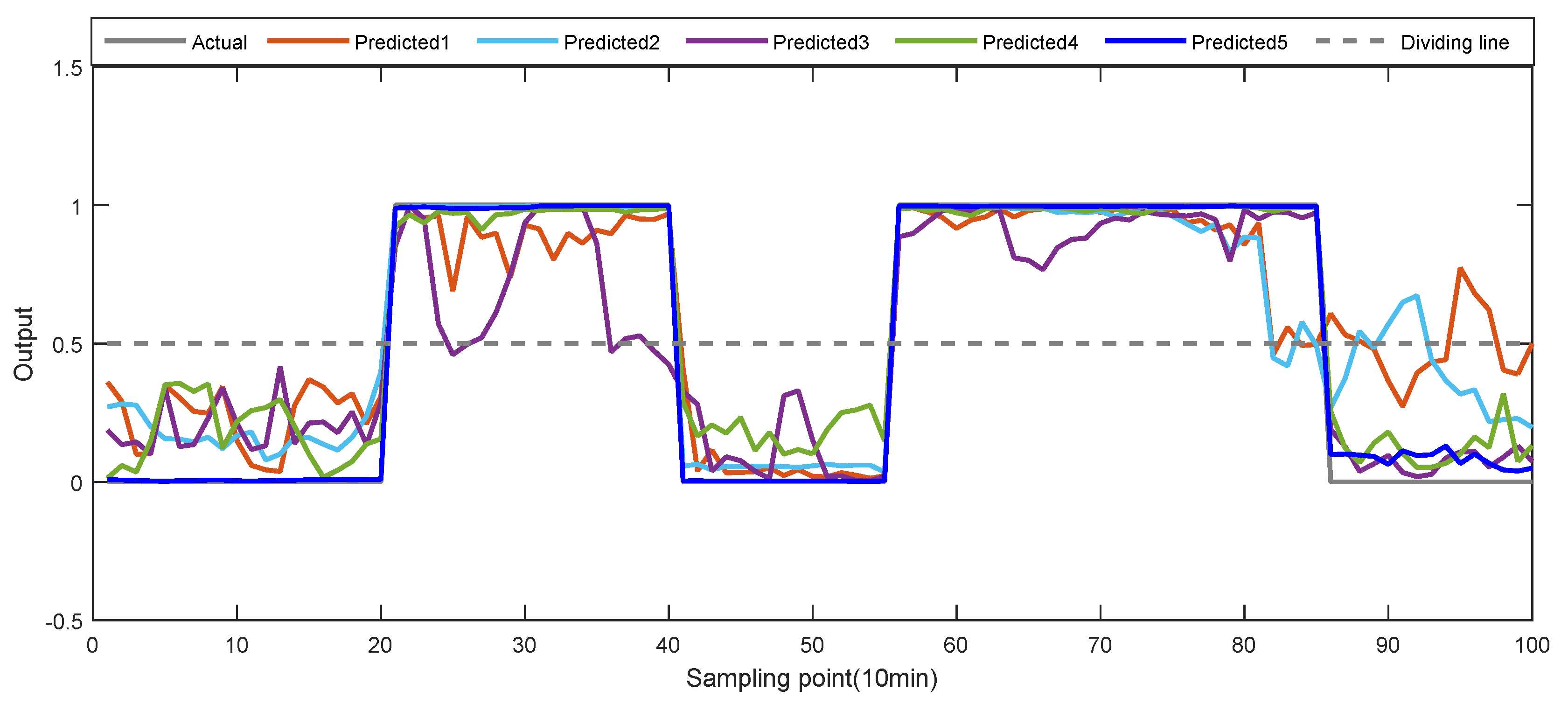
5.3.1. Cases 1: Single Anomaly Detection of 1st Attribute
5.3.2. Cases 2: Multi-Anomalies Detection of 6th Attribute
5.3.3. Cases 3: Multi-Anomalies Detection of Multi-Attributes
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Amirat, Y.; Benbouzid, M.E.H.; Al-Ahmar, E.; Bensa, B.; Turri, S. A brief status on condition monitoring and fault diagnosis in wind energy conversion systems. Renew. Sustain. Energy Rev. 2009, 13, 2629–2636. [Google Scholar] [CrossRef]
- Márquez, F.P.G.; Tobias, A.M.; Pérez, J.M.P.; Papaelias, M. Condition monitoring of wind turbines: Techniques and methods. Renew. Energy 2012, 46, 169–178. [Google Scholar] [CrossRef]
- Qian, P.; Zhang, D.; Tian, X.; Si, Y.; Li, L. A novel wind turbine condition monitoring method based on cloud computing. Renew. Energy 2019, 135, 390–398. [Google Scholar] [CrossRef]
- Zhang, F.; Wen, Z.; Liu, D.; Jiao, J.; Wan, H.; Zeng, B. Calculation and Analysis of Wind Turbine Health Monitoring Indicators Based on the Relationships with SCADA Data. Appl. Sci. 2020, 10, 407. [Google Scholar] [CrossRef]
- Lutz, M.A.; Vogt, S.; Berkhout, V.; Faulstich, S.; Dienst, S.; Steinmetz, U.; Gück, C.; Ortega, A. Evaluation of Anomaly Detection of an Autoencoder Based on Maintenace Information and Scada-Data. Energies 2020, 13, 1063. [Google Scholar] [CrossRef]
- Davide, A.; Francesco, C.; Francesco, N. Wind Turbine Generator Slip Ring Damage Detection through Temperature Data Analysis. Diagnostyka 2019, 20, 3–9. [Google Scholar]
- Tang, M.; Chen, W.; Zhao, Q.; Wu, H.; Long, W.; Huang, B.; Liao, L.; Zhang, K. Development of an SVR Model for the Fault Diagnosis of Large-Scale Doubly-Fed Wind Turbines Using SCADA Data. Energies 2019, 12, 3396. [Google Scholar] [CrossRef]
- Shao, H.; Gao, Z.; Liu, X.; Busawon, K. Parameter-varying modelling and fault reconstruction for wind turbine systems. Renew. Energy 2018, 116, 145–152. [Google Scholar]
- Hwang, I.; Kim, S.; Kim, Y.; Seah, C.E. A survey of fault detection, isolation, and reconfiguration methods. IEEE Trans. Control Syst. Technol. 2009, 18, 636–653. [Google Scholar] [CrossRef]
- Hameed, Z.; Hong, Y.S.; Cho, Y.M.; Ahn, S.H.; Song, C.K. Condition monitoring and fault detection of wind turbines and related algorithms: A review. Renew. Sustain. Energy Rev. 2009, 13, 1–39. [Google Scholar] [CrossRef]
- Simani, S.; Alvisi, S.; Venturini, M. Data-Driven Control Techniques for Renewable Energy Conversion Systems: Wind Turbine and Hydroelectric Plants. Electronics 2019, 8, 237. [Google Scholar] [CrossRef]
- Schlechtingen, M.; Santos, I.F. Wind turbine condition monitoring based on SCADA data using normal behavior models. Part 2: Application examples. Appl. Soft Comput. 2014, 14, 447–460. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, M.; Dong, Z.Y.; Meng, K. A probabilistic anomaly detection approach for data-driven wind turbine condition monitoring. Int. J. Electr. Power Energy Syst. 2019, 5, 149–158. [Google Scholar] [CrossRef]
- Cui, Y.; Bangalore, P.; Tjernberg, L.B. An Anomaly Detection Approach Based on Machine Learning and SCADA Data for Condition Monitoring of Wind Turbines. In Proceedings of the 2018 IEEE International Conference on Probabilistic Methods Applied to Power Systems (PMAPS), Boise, ID, USA, 24–28 June 2018. [Google Scholar]
- Kusiak, A.; Verma, A. A data-mining approach to monitoring wind turbines. IEEE Trans. Sustain. Energy 2011, 3, 150–157. [Google Scholar] [CrossRef]
- Kusiak, A.; Verma, A. A data-driven approach for monitoring blade pitch faults in wind turbines. IEEE Trans. Sustain. Energy 2010, 2, 87–96. [Google Scholar] [CrossRef]
- Aghenta, L.; Iqbal, T. Low-Cost, Open Source IoT-Based SCADA System Design Using Thinger. IO and ESP32 Thing. Electronics 2019, 8, 822. [Google Scholar] [CrossRef]
- González, I.; Calderón, A.J. Integration of open source hardware Arduino platform in automation systems applied to Smart Grids/Micro-Grids. Sustain. Energy Technol. Assess. 2019, 36, 100557. [Google Scholar] [CrossRef]
- Vargas-Salgado, C.; Aguila-Leon, J.; Chiñas-Palacios, C.; Hurtado-Perez, P. Low-cost web-based Supervisory Control and Data Acquisition system for a microgrid testbed: A case study in design and implementation for academic and research applications. Heliyon 2019, 5, e02474. [Google Scholar] [CrossRef]
- Salgado-Plasencia, E.; Carrillo-Serrano, R.V.; Rivas-Araiza, E.A.; Toledano-Ayala, M. SCADA-Based Heliostat Control System with a Fuzzy Logic Controller for the Heliostat Orientation. Appl. Sci. 2019, 9, 2966. [Google Scholar] [CrossRef]
- Tautz-Weinert, J.; Watson, S.J. Using SCADA data for wind turbine condition monitoring—A review. IET Renew. Power Gener. 2016, 11, 382–394. [Google Scholar] [CrossRef]
- Larios, D.F.; Personal, E.; Parejo, A.; García, S.; García, A.; Leon, C. Operational Simulation Environment for SCADA Integration of Renewable Resources. Energies 2020, 13, 1333. [Google Scholar] [CrossRef]
- Sun, P.; Li, J.; Wang, C.; Lei, X. A generalized model for wind turbine anomaly identification based on SCADA data. Appl. Energy 2016, 168, 550–567. [Google Scholar] [CrossRef]
- Santos, P.; Villa, L.F.; Reñones, A.; Bustillo, A.; Maudes, J. An SVM-based solution for fault detection in wind turbines. Sensors 2015, 15, 5627–5648. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Zhang, Z.; Long, H.; Xu, J.; Liu, R. Wind turbine gearbox failure identification with deep neural networks. IEEE Trans. Ind. Inf. 2016, 13, 1360–1368. [Google Scholar] [CrossRef]
- Shanlin, Y.; Yongsen, L.; Xiaoxuan, H. Study on the value optimization of k-means algorithm. Syst. Eng. Theory Pract. 2006, 2, 97–101. [Google Scholar]
- Fukushima, K. Neocognitron: A self-organizing neural network model for a mechanism of pattern recognition unaffected by shift in position. Biol. Cybern. 1980, 36, 193–202. [Google Scholar] [CrossRef]
- Lawrence, S.; Giles, C.L.; Tsoi, A.C.; Back, A.D. Face recognition: A convolutional neural-network approach. IEEE Trans. Neural Netw. 1997, 8, 98–113. [Google Scholar] [CrossRef]
- Chen, Y.; Jiang, H.; Li, C.; Jia, X.; Ghamisi, P. Deep feature extraction and classification of hyperspectral images based on convolutional neural networks. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6232–6251. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Spatial pyramid pooling in deep convolutional networks for visual recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 1904–1916. [Google Scholar] [CrossRef]
- Cun, Y.L.; Bengio, Y. Word-level training of a handwritten word recognizer based on convolutional neural networks. In Proceedings of the 12th IAPR International Conference on Pattern Recognition, Jerusalem, Israel, 9–13 October 1994; pp. 88–92. [Google Scholar]
- Nair, V.; Hinton, G. Rectified linear units improve restricted boltzmann Machines. In Proceedings of the 27th International Conference on International Conference on Machine Learning, Haifa, Israel, 21–24 June 2010; pp. 807–814. [Google Scholar]
- LeCun, Y.; Ranzato, M. Deep learning tutorial. In Proceedings of the International Conference on Machine Learning (ICML13), Atlanta, GA, USA, 16–21 June 2013. [Google Scholar]
- Glorot, X.; Bordes, A.; Bengio, Y. Deep sparse rectiler neural networks. In Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics, Fort Lauderdale, FL, USA, 11–13 April 2011; pp. 315–323. [Google Scholar]





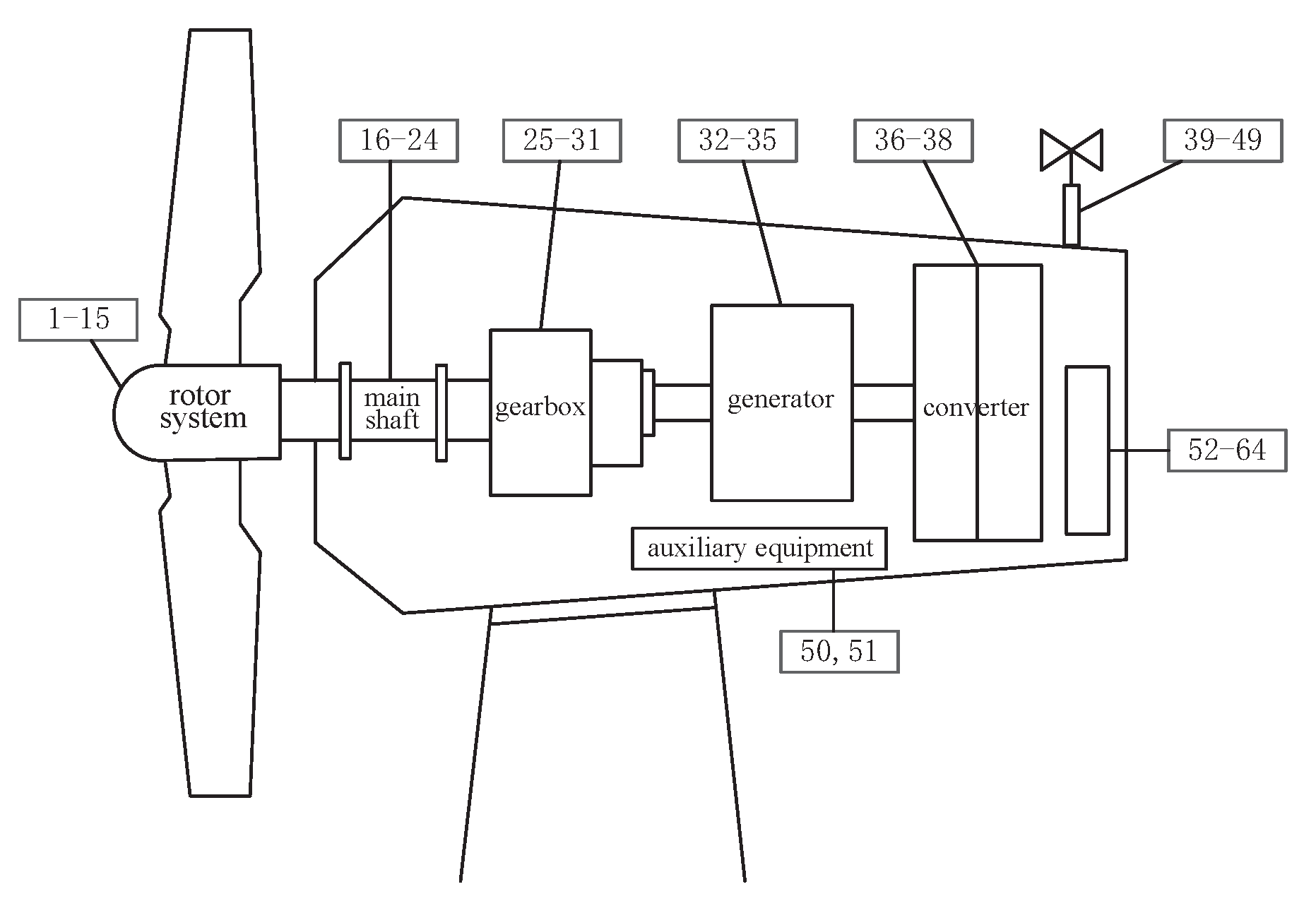



| No. | Parameter | Unit | No. | Parameter | Unit |
|---|---|---|---|---|---|
| 1 | Temp. of hub | C | 33 | Temp. of generator output shaft | C |
| 2 | Temp. of generator of blade 1 | C | 34 | Temp. of generator stator winding | C |
| 3 | Temp. of generator of blade 2 | C | 35 | Speed of the generator | rpm |
| 4 | Temp. of generator of blade 3 | C | 36 | Ambient temperature of the converter | C |
| 5 | Current of generator of blade 1 | A | 37 | Measured torque of the converter | Nm |
| 6 | Current of generator of blade 2 | A | 38 | Measured speed of the converter | rpm |
| 7 | Current of generator of blade 3 | A | 39 | Wind direction | |
| 8 | Function code | 40 | Absolute wind direction | ||
| 9 | Value of the encoder of blade 1A | 41 | Average wind direction of 1 s | ||
| 10 | Value of the encoder of blade 2A | 42 | Average wind direction of 1 min | ||
| 11 | Value of the encoder of blade 3A | 43 | Average wind direction of 10 min | ||
| 12 | Value of the encoder of blade 1B | 44 | Average wind velocity | m/s | |
| 13 | Value of the encoder of blade 2B | 45 | Maximum wind velocity | m/s | |
| 14 | Value of the encoder of blade 3B | 46 | Minimum wind speed | m/s | |
| 15 | Angle of the cable | 47 | Average wind speed of 1 s | m/s | |
| 16 | Temp. of the main bearing | C | 48 | Average wind speed of 1 min | m/s |
| 17 | Pressure of the hydraulic system | bar | 49 | Average wind speed of 10 min | m/s |
| 18 | Speed of variable pitch for shaft 1 | rpm | 50 | Ambient temperature | C |
| 19 | Speed of variable pitch for shaft 2 | rpm | 51 | Temp. of the cabin | C |
| 20 | Speed of variable pitch for shaft 3 | rpm | 52 | Frequency of power system | HZ |
| 21 | Vibration on x direction of node 100 | g | 53 | Active power | kW |
| 22 | Vibration on y direction of node 100 | g | 54 | Reactive power | kW |
| 23 | Vibration on x direction of node 101 | g | 55 | Voltage of phase A | V |
| 24 | Vibration on y direction of node 101 | g | 56 | Voltage of phase B | V |
| 25 | Speed of the gearbox | rpm | 57 | Voltage of phase C | V |
| 26 | Temp. of gearbox oil | C | 58 | Current of phase A | A |
| 27 | Temp. of gearbox input shaft | C | 59 | Current of phase B | A |
| 28 | Inlet temperature of the gearbox oil | C | 60 | Current of phase C | A |
| 29 | Temp. of gearbox output shaft | C | 61 | Average power of 1 s | kW |
| 30 | Pressure of gearbox oil pump | bar | 62 | Average power of 1 min | kW |
| 31 | Inlet pressure of the gearbox oil | bar | 63 | Average power of 10 min | kW |
| 32 | Temp. of generator input shaft | C | 64 | Power factor |
| K | SC |
|---|---|
| 2 | 0.7699 |
| 3 | −0.5612 |
| 4 | −0.6385 |
| 5 | 0.7954 |
| 6 | −0.5370 |
| 7 | 0.8814 |
| 8 | 0.6953 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
|---|---|---|---|---|---|---|---|
| Perp | 100 | 50 | 40 | 30 | 25 | 40 | 40 |
| T | 3000 | 2000 | 500 | 1000 | 1000 | 1200 | 1500 |
| The first convolution layer | 6 kernels of size 6 × 6 |
| Output the feature map | 6 maps of size 16 × 16 |
| The first pool layer | 2 × 2 |
| Output the feature map | 6 maps of size 8 × 8 |
| The second convolution layer | 12 kernels of size 3 × 3 |
| The second pool layer | 2 × 2 |
| Output the feature map | 12 maps of size 3 × 3 |
| learning rate:alpha | 1 |
| The number of samples in batch training:batchsize | 10 |
| Iteration number:numepochs | 2 |
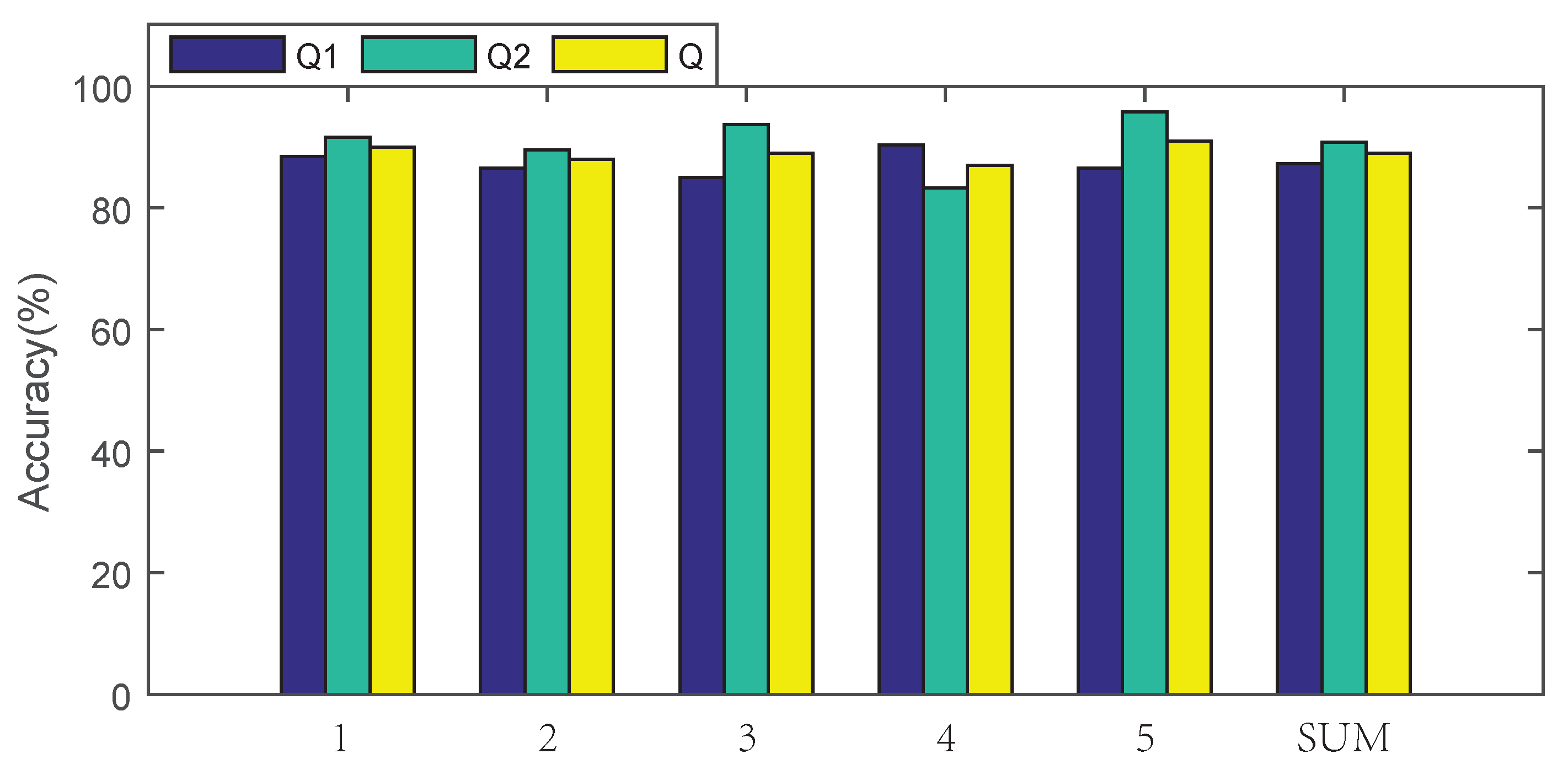
| 1 | 2 | 3 | 4 | 5 | SUM | |
|---|---|---|---|---|---|---|
| TA | 46 | 45 | 44 | 47 | 45 | 227 |
| FA | 6 | 7 | 8 | 5 | 7 | 33 |
| TH | 44 | 43 | 45 | 40 | 46 | 218 |
| FH | 4 | 5 | 3 | 8 | 2 | 22 |
| 1 | 2 | 3 | 4 | 5 | Average | |
|---|---|---|---|---|---|---|
| Q1 | 88% | 87% | 85% | 90% | 87% | 87.4% |
| Q2 | 92% | 90% | 94% | 83% | 96% | 91% |
| Q | 90% | 88% | 89% | 87% | 91% | 89% |
| 1 | 2 | 3 | 4 | 5 | SUM | |
|---|---|---|---|---|---|---|
| TA | 50 | 50 | 47 | 50 | 42 | 239 |
| FA | 0 | 0 | 3 | 0 | 8 | 11 |
| TH | 50 | 50 | 42 | 50 | 46 | 238 |
| FH | 0 | 0 | 8 | 0 | 4 | 12 |
| 1 | 2 | 3 | 4 | 5 | Average | |
|---|---|---|---|---|---|---|
| Q1 | 100% | 100% | 94% | 100% | 84% | 95.6% |
| Q2 | 100% | 100% | 84% | 100% | 92% | 95.2% |
| Q | 100% | 100% | 89% | 100% | 88% | 95.4% |
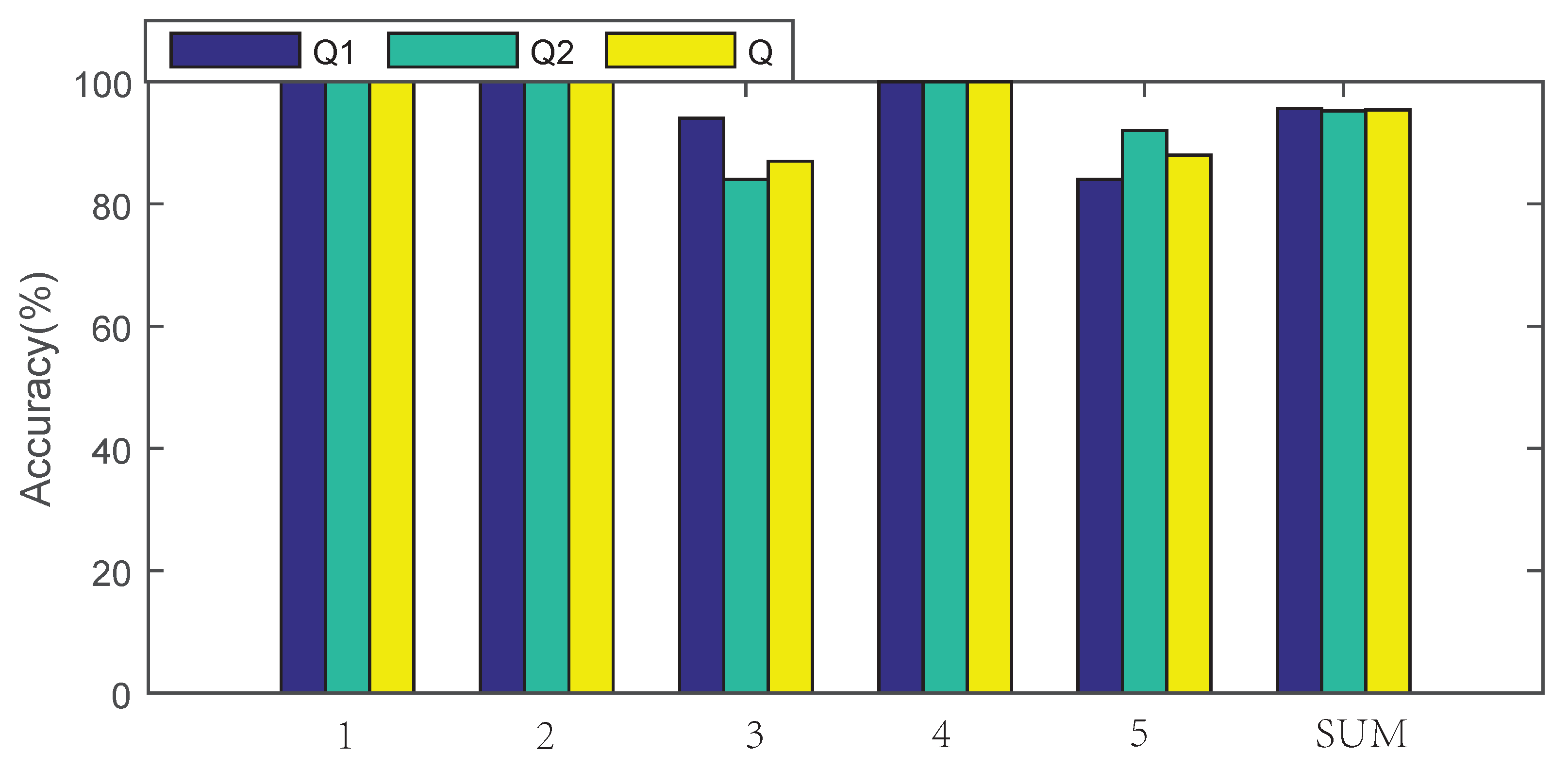
| 1 | 2 | 3 | 4 | 5 | Average | |
|---|---|---|---|---|---|---|
| Q1 | 88% | 92% | 100% | 100% | 100% | 96% |
| Q2 | 94% | 94% | 90% | 100% | 100% | 95.6% |
| Q | 91% | 93% | 90% | 100% | 100% | 95.8% |
| Method | Q1 | Q2 | Q |
|---|---|---|---|
| BPNN | 81.2% | 84.8% | 83% |
| SVM | 80.4% | 83.6% | 82% |
| The proposed method | 96% | 95.6% | 95.8% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Lu, S.; Ren, Y.; Wu, Z. Wind Turbine Anomaly Detection Based on SCADA Data Mining. Electronics 2020, 9, 751. https://doi.org/10.3390/electronics9050751
Liu X, Lu S, Ren Y, Wu Z. Wind Turbine Anomaly Detection Based on SCADA Data Mining. Electronics. 2020; 9(5):751. https://doi.org/10.3390/electronics9050751
Chicago/Turabian StyleLiu, Xiaoyuan, Senxiang Lu, Yan Ren, and Zhenning Wu. 2020. "Wind Turbine Anomaly Detection Based on SCADA Data Mining" Electronics 9, no. 5: 751. https://doi.org/10.3390/electronics9050751
APA StyleLiu, X., Lu, S., Ren, Y., & Wu, Z. (2020). Wind Turbine Anomaly Detection Based on SCADA Data Mining. Electronics, 9(5), 751. https://doi.org/10.3390/electronics9050751





