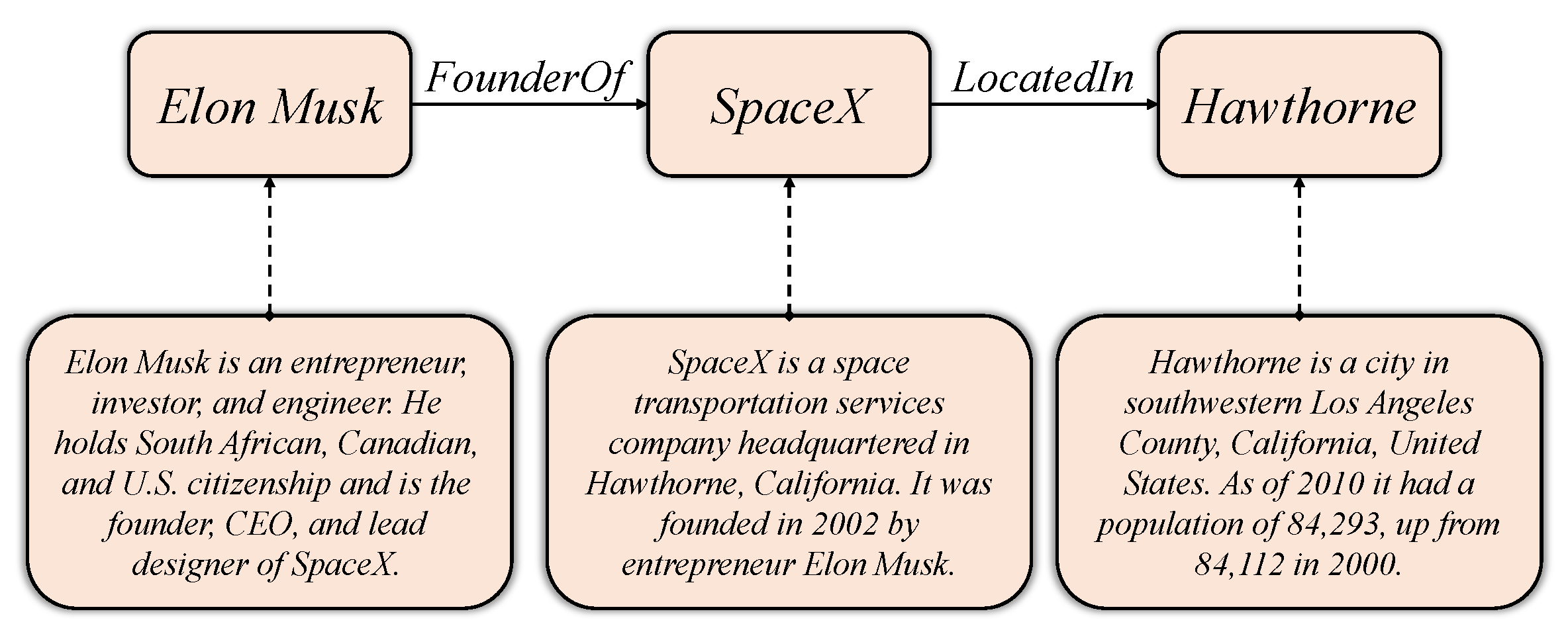
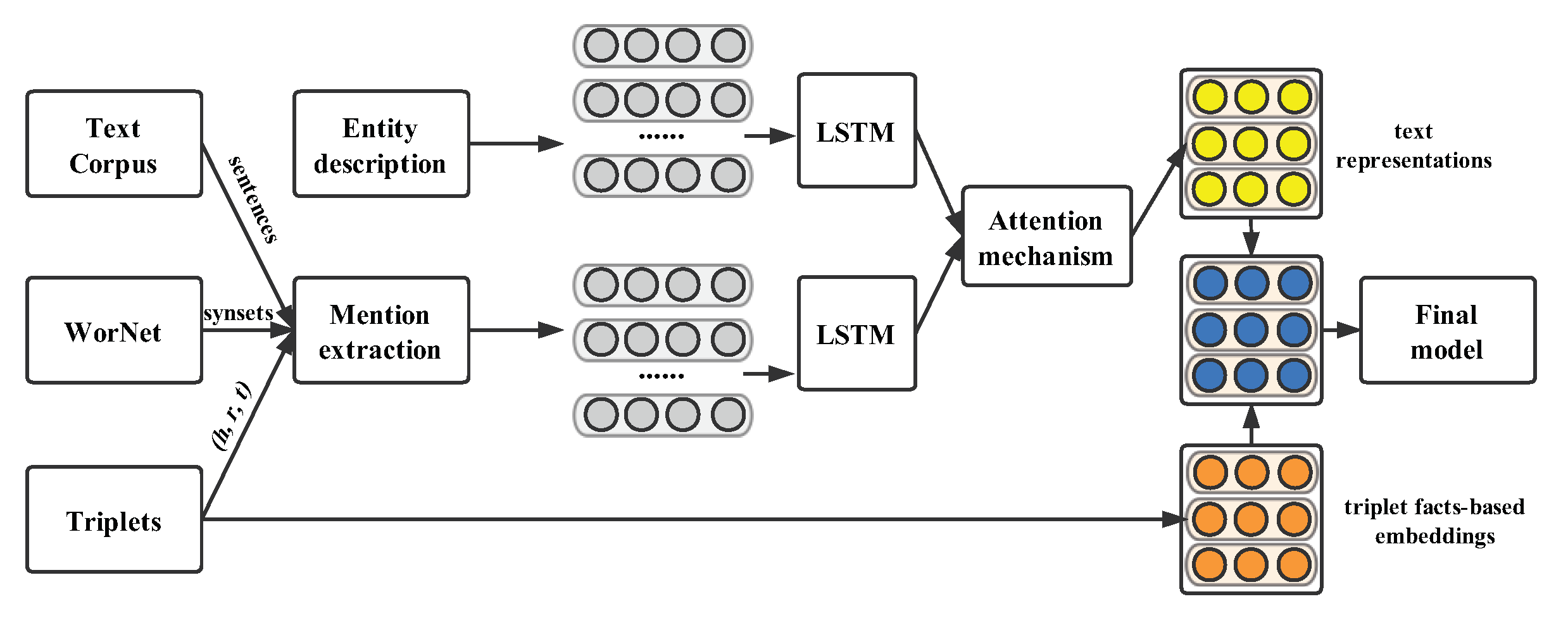
Triplet fact-based embedding model treats the knowledge graph as a set of triplets containing all observed facts. In this section, we will introduce three groups of embedding models: translation-based models, tensor factorization-based models, and neural network-based models.
2.2.1. Translation-Based Models
Since Mikolov et al. [
49,
50] proposed a word embedding algorithm and its toolkit
word2vec, the distributed representations learning has attracted more and more attention. Using that model, the authors found that there are interesting translation invariance phenomena in the word vector space. For example:
where
is the vector of word
w transformed by the
word2vec model. This result means that the word representation model can capture some of the same implicit semantic relationship between the words “
” (“
”) and “
” (“
”). Mikolov et al. proved experimentally that the property of translation invariance exists widely in the semantic and syntactic relations of vocabulary.
Inspired by the
word2vec, Bordes et al. [
19] introduced the idea of translation invariance into the knowledge graph embedding field, and proposed the TransE embedding model. TransE represents all entities and relations to the uniform continuous, low-, feature space
, and the relations can be regarded as connection vectors between entities. Let
E and
R indicate the set of entity and relation, respectively. For each triplet (
), the head and tail entity
h,
t, and the relation
r are embedded to the embedding vectors
,
, and
. As illustrated in
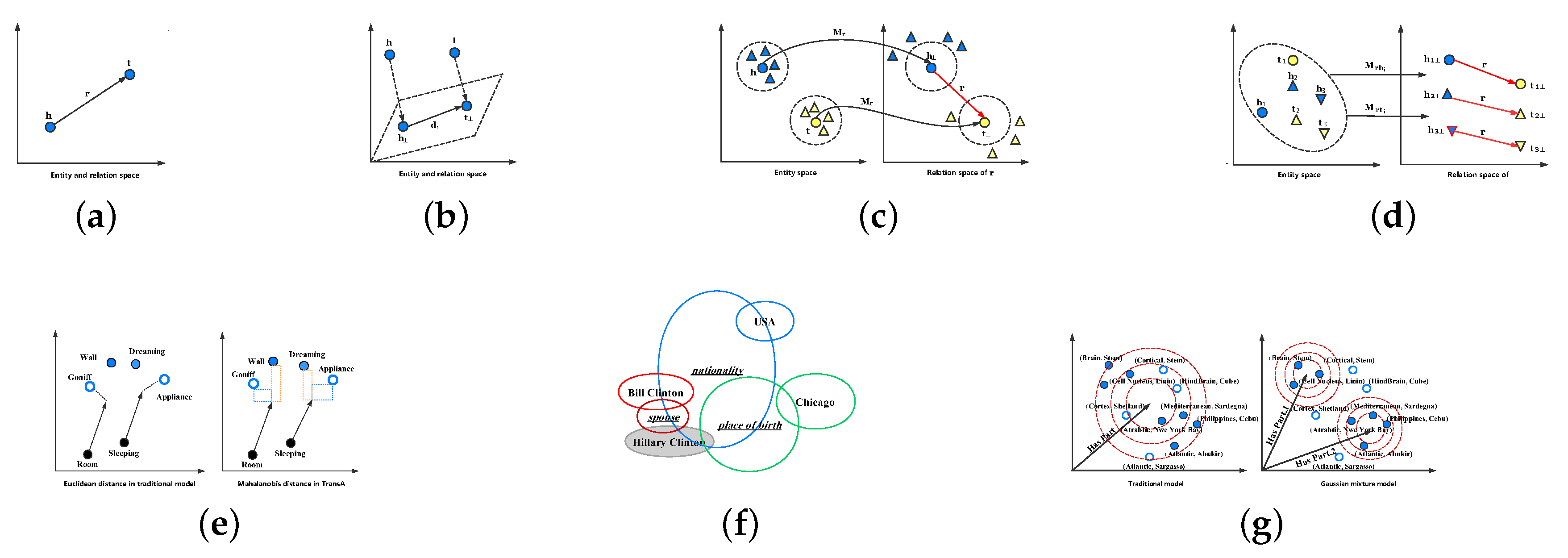
Figure 2a, for each triplet (
), TransE follows a geometric principle:
The authenticity of the given triplet (
) is computed via a score function. This score function is defined as a distant between
and
under
-norm or
-norm constraints. In mathematical expressions, it is shown as follows:
In order to learn an effective embedding model which has the ability to discriminate the authenticity of triplets, TransE minimizes a margin-based hinge ranking loss function over the training process.
where
S and
denote the set consisting of correct triplets and corrupted triplets, respectively, and
indicates the margin hyperparameter. In training, TransE stochastically replaces the head or tail entity in each triplet with other candidate entities to generate corrupted triplet set
. The construction formula is shown in Equation (
5).
Although TransE has achieved a great advancement in large-scale knowledge graph embedding, it still has difficulty in dealing with complex relations, such as
,
, and
[
51,
52]. For instance, there is a
relation where the head entity has multiple corresponding tail entities, i.e.,
. According to the guidelines TransE followed
, all embedding vectors of the tail entities should be approximately similar, as
. More visually, there are two triplet facts
and
, in which
is a
relation mentioned above. Following TransE, the embedding vectors of
and
should be very similar in feature space. However, this result is clearly irrational because
and
are two companies in entirely different fields, except
is their founder. In addition, other complex relations such as
and
also raise the same problem.
To handle this issue in complex relations, TransH [
51] extended the original TransE model, it enables each entity to have different embedding representations when the entity is involved in diverse relations. In other words, TransH allows each relation to hold its own relation-specific hyperplane. Therefore, an entity would have different embedding vectors in different relation hyperplanes. As shown in
Figure 2b, for a relation
r, TransH employs the relation-specific translation vector
and the normal vector of hyperplane
to represent it. For each triplet fact
, the embedding vectors of
and
are firstly projected to the relation-specific hyperplane in the direction of the normal vector
.
and
indicate the projections.
Afterwards, the
and
are connected by the relation-specific translation vector
. Similar to TransE, a small score is expected when
holds. The score function is formulated as follows:
Here, is the squared Euclidean distance. By utilizing this relation-specific hyperplane, TransH can project an entity to different feature vectors depending on different relations, and solve the issue of complex relations.
Following this idea, TransR [
52] extended on the original TransH algorithm. Although TransH enables each entity to obtain a different representation corresponding to its different relations, the entities and relations in this model are still represented in the same feature space
. In fact, an entity may contain various semantic meanings and different relations may concentrate on entities’ diverse aspects; therefore, entities and relations in the same semantic space might make the model insufficient for graph embedding.
TransR expands the concept of relation-specific hyperplanes proposed by TransH to relation-specific spaces. In TransR, for each triplet
, entities are embedded as
and
into an entity vector space
, and relations are represented as a translation vector
into a relation-specific space
. As illustrated in
Figure 2c, TransR projects
and
from the entity space into the relation space. This operation can render those entities (denoted as triangles with color) that are similar to head or tail entities (denoted as circles with color) in the entity space as distinctly divided in the relation space.
More specifically, for each relation
r, TransR defines a projection matrix
to transform the entity vectors into the relation-specific space. The projected entity vectors are signified by
and
, and the scoring function is similar to that of TransH:
Compared with TransE and TransH, TransR has made significant progress in performance. However, it also has some deficiencies: (i) For a relation r, the head and tail entities share the same projection matrix , whereas it is intuitive that the types or attributes between head and tail entities may be essentially different. For instance, in the triplet , is a person and is a company; they are two different types of entities. (ii) The projection from the entity space to the relation-specific space is an interactive process between entities and relations; it cannot capture integrated information when the projection matrix is generated only related to relations. (iii) Owing to the application of the projection matrix, TransR requires a large amount of computing resources, the memory complexity of which is , compared to TransE and TransH with .
To eliminate the above drawback, an improved method TransD [
22] was proposed. It optimizes TransR by using two vectors for each entity-relation pair to construct a dynamic mapping matrix that could be a substitute for the projection matrix in TransR. Its illustration is in
Figure 2d. Specifically, given a triplet
, each entity and relation is represented to two embedding vectors. The first vector represents meanings of the entity/relation, denoted as
,
and
, and the second vector (defined as
,
and
) is used to form two dynamic projection matrices
. These two matrices are calculated as:
where
is an identity matrix. Therefore, the projection matrix involve both entity and relation, and the embedding vectors of
and
are defined as:
Finally, the score function is the same as that of TransR in Equation (
9). TransD refined this model, it constructs a dynamic mapping matrix with two projection vectors, that effectually reduces the computation complexity to
.
All the methods described above including Trans (E, H, R, and D) ignore two properties of existing KGs: heterogeneity (some relations have many connections with entities and others do not), which causes underfitting on complex relations or overfitting on simple relations, and the imbalance (there is a great difference between head and tail entities for a relation in quantities), which indicates that the model should treat head and tail entities differently. TranSparse [
24] overcomes the heterogeneity and imbalance by applying two model versions: TranSparse(share) and TranSparse(separate).
TranSparse (share) leverages adaptive sparse matrices
to replace dense projection matrices for each relation
r. The sparse degree
is linked to the number of entities connected with relation
r; it is defined as follows:
where
(
) is a hyperparameter,
denotes the number of entity pairs connected with the relation, and
represents the maximum of them. Therefore, the projected vectors are formed by:
TranSparse (separate) employs two separate sparse mapping matrices,
and
, for each relation, where
projects the head entities and the other projects the tail entities. The sparse degree and the projected vectors are extended as follows:
A simpler version of this method was proposed by Nguyen et al. [
53], called sTransE. In that approach, the sparse projection matrices
and
are replaced by mapping matrices
and
, such that the projected vectors are transformed to:
The methods introduced so far merely modify the definition of the projection vectors or matrices, but they do not consider other aspects to optimize TransE. TransA [
54] also boosted the performance of the embedding model from another view point by modifying the distance measure of the score function. It introduces adaptive Mahalanobis distance as a better indicator to replace the traditional Euclidean distance because Mahalanobis distance shows better adaptability and flexibility [
55]. Given a triplet
,
is defined as a symmetric non-negative weight matrix with the relation
r; the score function of
TransA is formulated as:
As shown in
Figure 2e, the two arrows represent the same relation
, and
and
are true facts. If we use the isotropic Euclidean distance, which is utilized in traditional models to distinguish the authenticity of a triplet, it could yield erroneous triplets such as
. Fortunately, TransA has the capability of discovering the true triplet via introducing the adaptive Mahalanobis distance because the true one has shorter distances in the
x or
y directions.
The above methods embedded the entity and relation to a real number space, KG2E [
56] proposed a novel approach that introduces the uncertainty to construct a probabilistic knowledge graph embedding model. KG2E takes advantage of multi, Gaussian distributions to embed entities and relations; each entity and relation is represented to a Gaussian distribution, in which the mean of this Gaussian distribution is the position of the entity or relation in a semantic feature space, and the covariance signifies the uncertainty of the entity or relation, i.e.,
Here,
are the mean vectors of
,
, and
, respectively, and
indicate the covariance matrices corresponding to entities and relations. KG2E also utilizes the distance between
and
as metric to distinguish the authenticity of triplets, where the traditional
is transformed to the distribution formula of
. This model employs two categories of approaches to estimate the similarity between two probability distributions: Kullback–Leibler divergence [
57] and expected likelihood [
58].
Figure 2f displays an illustration of KG2E. Each entity is represented as a circle without underline and the relations are the circles with underline. These circles with the same color indicate an observed triplet, where the head entity of all triplets is
. The area of a circle denotes the uncertainty of the entity or relation. As we can see in
Figure 2e that there are three triplets, and the uncertainty of the relation “
” is lower than the others.
TransG [
59] discusses the new situation of multiple relationship semantics, that is, when a relationship is associated with different entity pairs, it may contain multiple semantics. It also uses a Gaussian distribution to embed entities, but it is significantly different from KG2E because it leverages a Gaussian mixture model to represent relations:
where
is the weight of distinct semantics and
indicates an identity matrix. As shown in
Figure 2g, dots are correct entities related to the relation “
” and the triangles represent corrupted entities. In the traditional models (left), the corrupted entities do not have the ability to distinguish from the entire set of entities because all semantics are confused in the relation “
.” In contrast, TransG (right) can find the incorrect entities by utilizing multiple semantic components.
TransE only has the ability to handle simple relations, and it is incompetent for complex relations. The extensions of TransE, including TransH, TransR, TransD, TransA, TransG, and so forth, proposed many thoughtful and insightful models to address the issue of complex relations. Extensive experiments in public benchmark datasets, which are generated from WordNet [
60] and Freebase, show that these modified models achieve significant improvements with respect to the baseline, and verify the feasibility and validity of these methods. A comparison of these models in terms of their scoring functions and space size is shown in
Table 2.
2.2.2. Tensor Factorization-Based Models
Tensor factorization is another category of effective methods for KG representation learning. The core idea of these methods is described as follows. First, the triplet facts in the KG are transformed into a 3D binary tensor
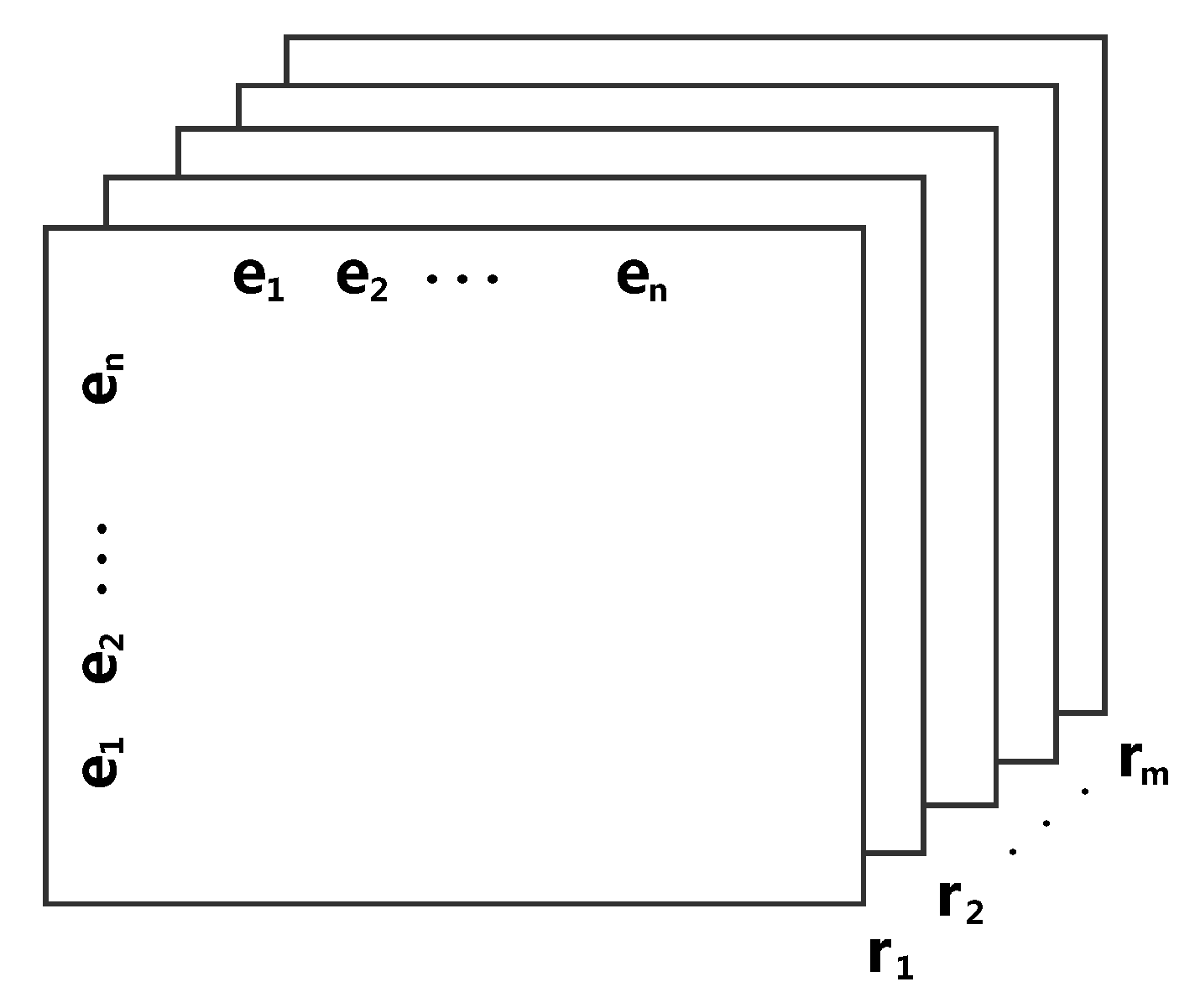
. As illustrated in
Figure 3, given a tensor
, where
n and
m denote the number of entities and relations, respectively, each slice
(
) corresponds to a relation type
, and
refers to the fact that the triplet (
i-th entity,
k-th relation,
j-th entity) exists in the graph; otherwise,
indicates a non-existent or unknown triplet. After that, the embedding matrices associated with the embedding vectors of the entities and relations are calculated to represent
as some factors of a tensor. Finally, the low-, representation for each entity and relation is generated along with these embedding matrices.
RESCAL [
61] applies a tensor to express the inherent structure of a KG and uses the rank-
d factorization to obtain its latent semantics. The principle that this method follows is formulated as:
where
is a matrix that captures the latent semantic representation of entities and
is a matrix that models the pairwise interactions in the
k-th relation. According to this principle, the scoring function
for a triplet
is defined as:
Here,
,
are the embedding vectors of entities in the graph and the matrix
represents the latent semantic meanings in the relation. It is worth noting that
and
, which represent the embedding vectors of the
i-th and
j-th entity, are actually assigned by the values of the
i-th and
j-th row of matrix A in Equation (
21). A more complex version of
was proposed by García-Durán et al. [
62], which extends RESCAL by introducing well-controlled two-way interactions into the scoring function.
However, this method requires
parameters. To simplify the computational complexity of RESCAL, DistMult [
63] restricts
to be diagonal matrices, i.e.,
. The scoring function is transformed to:
DistMult not only reduces the algorithm complexity into , but the experimental results also indicate that this simple formulation achieves a remarkable improvement over the others.
Hole [
64] introduced a circular correlation operation [
65], denoted as
, between head and tail entities to capture the compositional representations of pairwise entities. The formulation of this operation is shown as follows:
The circular correlation operation has the significant advantage that it can reduce the complexity of the composite representation compared to the tensor product. Moreover, its computational process can be accelerated via:
Here,
indicates the fast Fourier transform (FFT) [
66],
denotes its inverse, and
denotes the complex conjugate of
. Thus, the scoring function corresponding to Hole is defined as:
It is noteworthy that circular correlation is not commutative, i.e., ; therefore, this property is indispensable for modeling asymmetric relations to semantic representation space.
The original DistMult model is symmetric in head and tail entities for every relation; Complex [
67] leverages complex-valued embeddings to extend DistMult in asymmetric relations. The embeddings of entities and relations exist in the complex space
, instead of the real space
in which DistMult embedded. The scoring function is modified to:
where
denotes the real part of a complex value, and
represents the complex conjugate of
. By using this scoring function, triplets that have asymmetric relations can obtain different scores depending on the sequences of entities.
In order to settle the independence issue of entity embedding vectors in Canonical Polyadic (CP) decomposition, SimplE [
68] proposes a simple enhancement of CP which introduces the reverse of relations and computes the average CP score of
and
:
where ∘ is the element-wise multiplication and
indicates the embedding vector of reverse relation. Inspired by Euler’s identity
, RotatE [
69] introduces the rotational Hadmard product, it regards the relation as a rotation between the head and tail entity in complex space. The score function is defined as follows:
QuatE [
70] extends complex space into four-dimensional, hypercomplex space
, it utilizes the Hamilton product to obtain latent inter-dependency between entities and relations in this complex space:
where ⊗ denotes the Hamilton product.
Table 3 summarizes the scoring function and memory complexity for all tensor factorization-based models.
2.2.3. Neural Network-Based Models
Deep learning is a very popular and extensively used tool in many different fields [
71,
72,
73,
74]. They are also models with strong representation and generalization capabilities that can express complicated nonlinear projections. In recent years, it has become a hot topic to embed a knowledge graph into a continuous feature space by a neural network.
SME [
21] defines an energy function for semantic matching, which can be used to measure the confidence of each observed fact
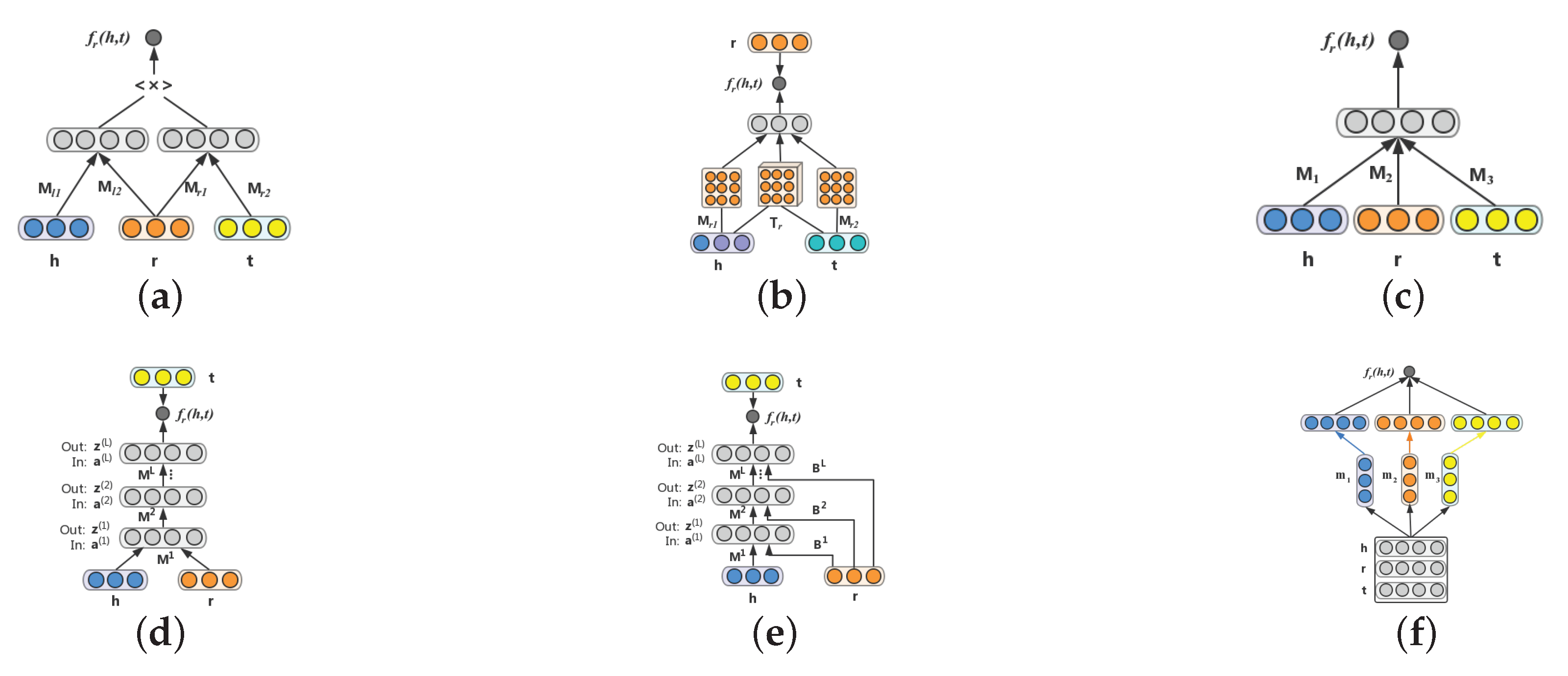
by utilizing neural networks. As shown in
Figure 4a, in SME, each entity and relation is firstly embedded to its embedding feature space. Then, to capture intrinsic connections between entities and relations, two projection matrices are applied. Finally, the semantic matching energy associated with each triplet is computed by a fully connected layer. More specifically, given a triplet
in
Figure 4a, SME represents entities and relations to the semantic feature space by the input layer. The head entity vector
is then combined with the relation vector
to acquire latent connections (i.e.,
). Likewise,
is generated from the tail entity and the relation vectors
and
. Bordes et al. provided two types of
functions, so there are two versions for SME. SME is formulated by Equation (
31):
SME (bilinear) is formulated in Equation (
32):
where
is the weight matrix and
denotes the bias vector. Finally, the
and
are concatenated to obtain the energy score
via a fully connected layer.
NTN [
20] proposes a neural tensor network to calculate the energy score
. It replaces the standard linear layer, which is in the traditional neural network, by employing a bilinear tensor layer. As shown in
Figure 4b, given an observed triplet
, the first layer firstly embeds entities to their embedding feature space. There are three inputs in the second nonlinear hidden layer including the head entity vector
, the tail entity vector
and a relation-specific tensor
. The entity vectors
,
are embedded to a high-level representation via projection matrices
respectively. These three elements are then fed to the nonlinear layer to combine semantic information. Finally, the energy score is obtained by providing a relation-specific linear layer as the output layer. The score function is defined as follows:
where
indicates an activation function and
denotes a bias, which belongs to a standard neural network layer. Meanwhile, a simpler version of this model is proposed in this paper, called a single layer model (SLM), as shown in
Figure 4c. This is a special case of NTN, in which
. The scoring function is simplified to the following form:
NTN requires a relation-specific tensor
for each relation, such that the number of parameters in this model is huge and it would be impossible to apply to large-scale KGs. MLP [
75] provides a lightweight architecture in which all relations share the same parameters. The entities and relation in a triplet fact
are synchronously projected into the embedding space in the input layer, and they are involved in higher representation to score the plausibility by applying a nonlinear hidden layer. The scoring function
is formulated as follows:
Here, is an activation function, and represent the mapping matrices that project the embedding vectors , and to the second layer; are the second layer parameters.
Since the emergence of deep learning technology, more and more studies have been proposed for deep neural networks (DNNs) [
71,
76,
77]. NAM [
78] establishes a deep neural network structure to represent a knowledge graph. As illustrated in
Figure 4d, given a triplet
, NAM firstly embeds each element in the triplet to embedding feature space. Then, the head entity vector
and the relation vector
are concatenated to a single vector
as the input to feed to the
layer where it consists of
L rectified linear (ReLU) [
79] hidden layers as follows:
where
is the weight matrix and
is the bias for layer
ℓ. Finally, a score is calculated by applying the output pf the last hidden layer with the tail entity vector
:
where
is a sigmoid activation function. A more complicated model is proposed in this paper, called relation-modulated neural networks (RMNN).
Figure 4e shows an illustration of this model. Compared with NAM, it generates a knowledge-specific connection (i.e., relation embedding
) to all hidden layers in the neural network. The layers are defined as follows:
where
and
denote the weight and bias matrices for layer
ℓ, respectively. After the feed-forward process, RMNN can yield a final score using the last hidden layer’s output and the concatenation between the tail entity vector
and relation vector
:
ConvKB [
80] captures latent semantic information in the triplets by introducing a convolutional neural network (CNN) for knowledge graph embedding. In the model, each triplet fact
is represented to a three-row matrix, in which each element is transformed as a row vector. The matrix is fed to a convolution layer to yield multiple feature maps. These feature maps are then concatenated and projected to a score that is used to estimate the authenticity of the triplet via the dot product operation with the weight vector.
More specifically, as illustrated in
Figure 4f,
. First, the embedding vectors
,
, and
are viewed as a matrix
, and
indicates the
i-th column of matrix
. After that, the filter
is slid over the input matrix to explore the local features and obtain a feature map
, such that:
where
signifies the ReLU activation function and
b indicates the bias. For this instance, there are three feature maps corresponding to three filters. Finally, these feature maps are concatenated as a representation vector
, and calculated with a weight vector
by a dot product operation. The scoring function is defined as follows:
Here, is the set of filters, and denotes that a convolution operation is applied to matrix via the filters in the set . is the concatenation operator. It is worth mentioning that and are shared parameters; they are generalized for all entities and relations.
In recent years, graph neural networks (GNNs) have captured more attention due to their great ability in representation of graph structure. R-GCN [
81] is an improved model, which provides relation-specific transformation to represent knowledge graphs. The forward propagation is formulated as follows:
where
signifies the hidden state of the entity
i in
l-th layer,
indicates a neighbor collection where it connects to entity
i with relation
,
and
are the weight matrices, and
denotes the normalization process such as
.
Inspired by burgeoning generative adversarial networks (GANs), Cai et al. [
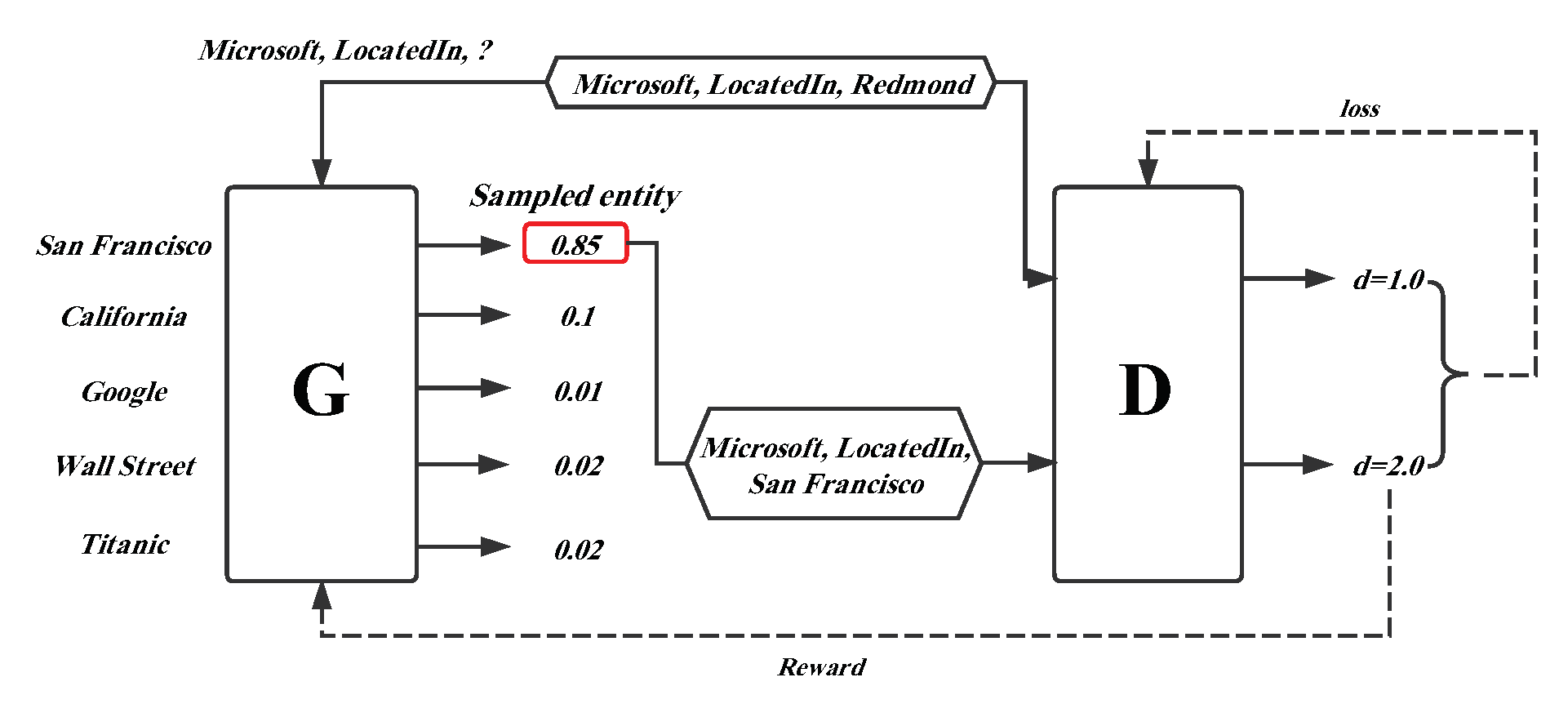
82] proposed a generative adversarial learning framework to improve the performance of the existing knowledge graph representation models and named it KBGAN. KBGAN’s innovative idea is to apply a KG embedding model as the generator to obtain plausible negative samples, and leverage the positive samples and generated negative samples to train the discriminator, which is the embedding model we desire.
A simple overview introducing the framework is shown in
Figure 5. There is a ground truth triplet
, which is corrupted by disposing of its tail entity, such as
. The corrupted triplet is fed as an input into a generator (G) that can receive a probability distribution over the candidate negative triplets. Afterwards, the triplet with the highest probability
is sampled as the output of the generator. The discriminator (D) utilizes the generated negative triplet and original truth triplet as input to train the model, and computes their score
d, which indicates the plausibility of the triplet. The two dotted lines in the figure denote the error feedback in the generator and discriminator. One more point to note is that each triplet fact-based representation learning model mentioned above can be employed as the generator or discriminator in the KBGAN framework to improve the embedding performance.
Table 4 illustrates the scoring function and memory complexity of each neural network-based model.
The above three types of triplet fact-based models focus on modifying the calculation formula of the scoring function , and their other routine training procedures are roughly uniform. The detailed optimization process is illustrated in Algorithm 1. First, all entity and relation embedding vectors are randomly initialized. In each iteration, a subset of triplets is constructed by sampling from the training set S, and it is fed into the model as inputs of the minibatch. For each triplet in , a corrupted triplet is generated by replacing the head or tail entity with other ones. After that, the original triplet set S and all generated corrupted triplets are incorporated as a batch training set . Finally, the parameters are updated by utilizing certain optimization methods.
Here, the set of corrupted triplets
is generated according to
, and there are two alternative versions of the loss function. The margin-based loss function is defined as follows:
and the logistic loss function is:
where
is a margin hyperparameter and
is a label that indicates the category (negative or positive) to which a given training triplet
belongs. These two functions can both be calculated by the stochastic gradient descent (SGD) [
83] or Adam [
84] methods.
| Algorithm 1 Learning triplet fact-based models. |
Input: The training set , entity set E, relation set R, embedding dimension k
Output: Entity and relation embeddings
- 1:
initialize the entity embeddings and relation embeddings - 2:
loop - 3:
// sample a subset from S with minibatch size b - 4:
// initialize the set of pairs of triplets - 5:
for do - 6:
// sample a corrupted triplet - 7:
- 8:
end for - 9:
Update embeddings by minimizing the loss function - 10:
end loop
|