Framework Integrating Lossy Compression and Perturbation for the Case of Smart Meter Privacy
Abstract
1. Introduction
2. State of the Art
2.1. Data Compression in General
2.2. Protection of Privacy Power Usage
2.3. Compression Approaches for Privacy Power Usage
2.4. Perturbation with Gaussian Distribution Encoding
3. Approach 1: Compression and Classification Based Smart Meter Privacy
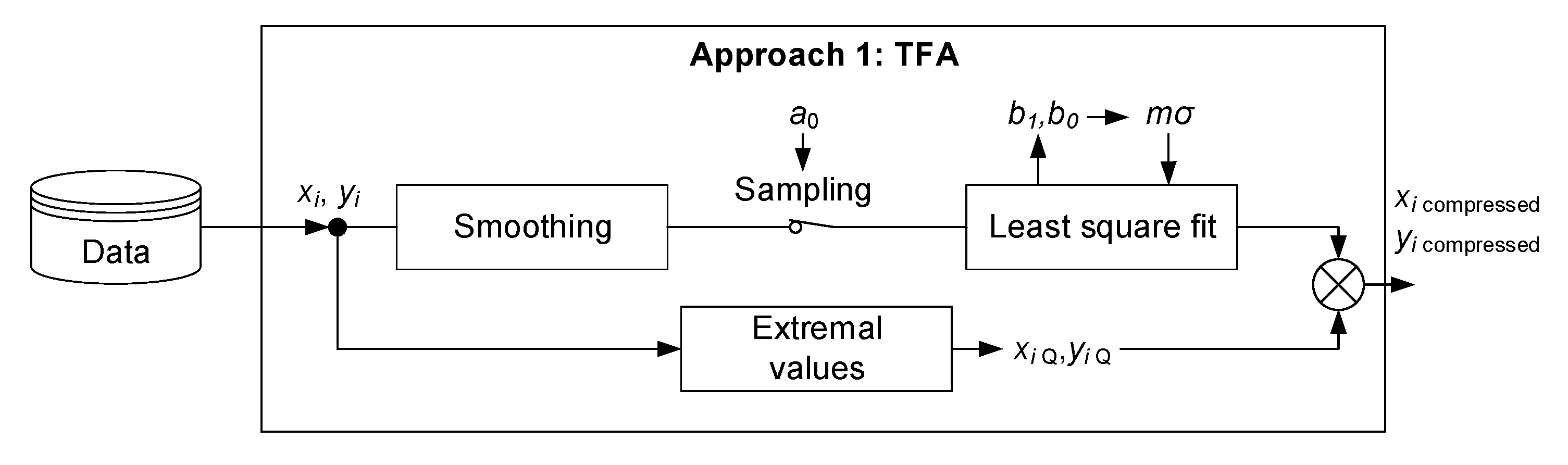
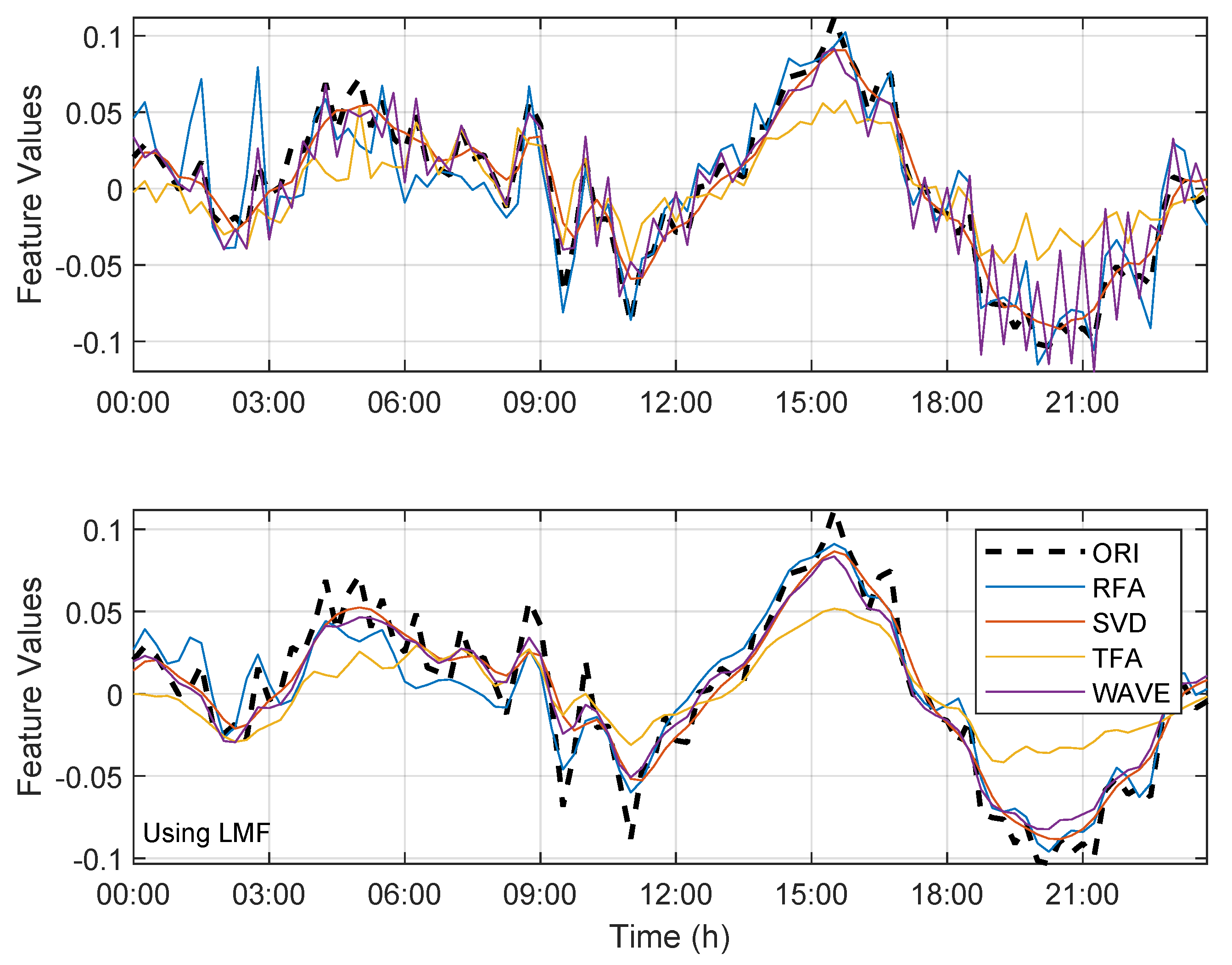
3.1. Lossy Compression Methodologies
3.1.1. Triangular Function Algorithm (TFA)
3.1.2. Rectangular Function Algorithm (RFA)
3.1.3. Singular Value Decomposition (SVD)
3.1.4. Wavelet Transform (WT)
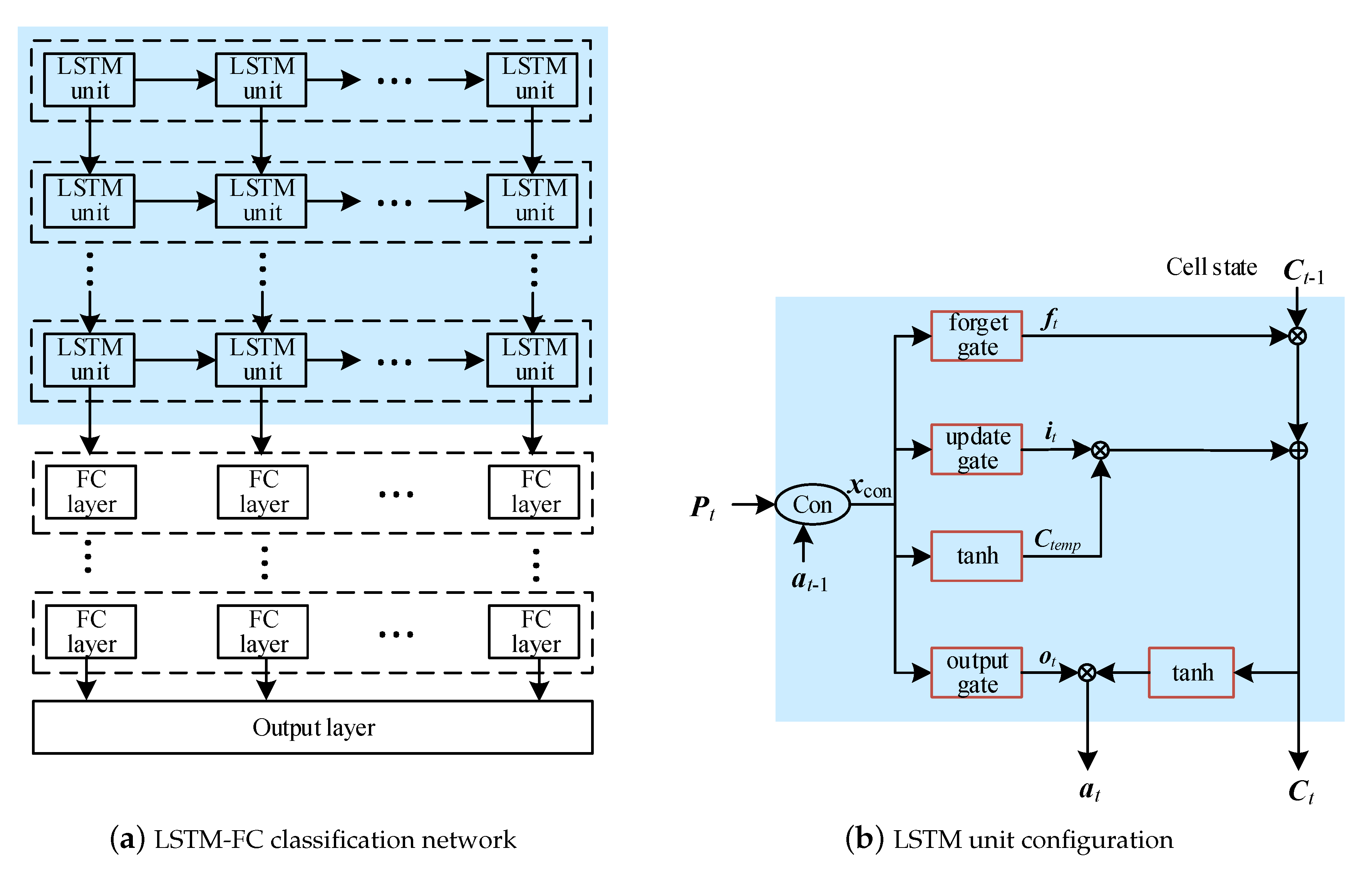
3.2. Classification of the Compressed Dataset
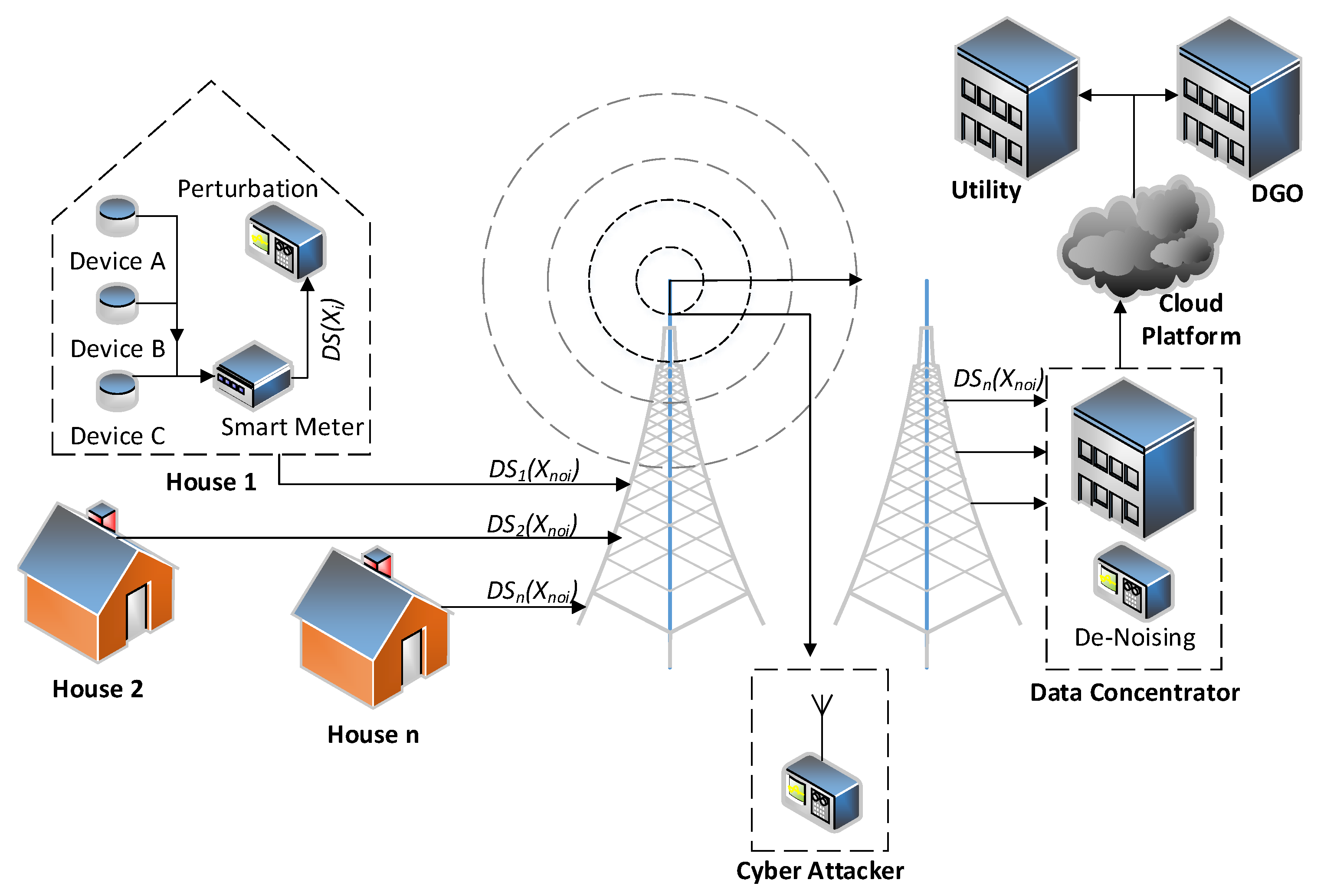
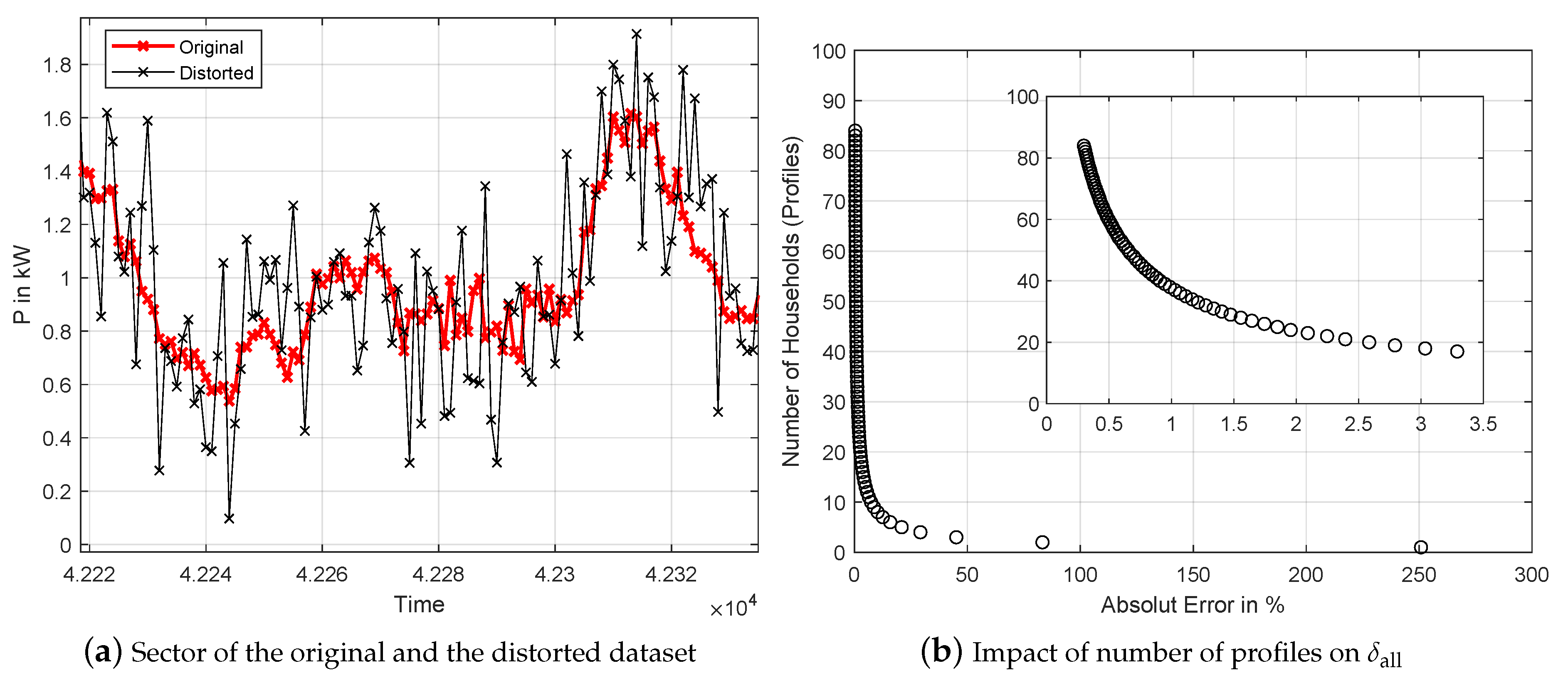
4. Approach 2: Perturbation with Gaussian Distribution Based Smart Meter Privacy
4.1. General Approach
4.2. Comparison to Approach 1
5. Evaluation
5.1. Description of Evaluation and Key Metrics
5.2. Dataset
6. Results and Discussion
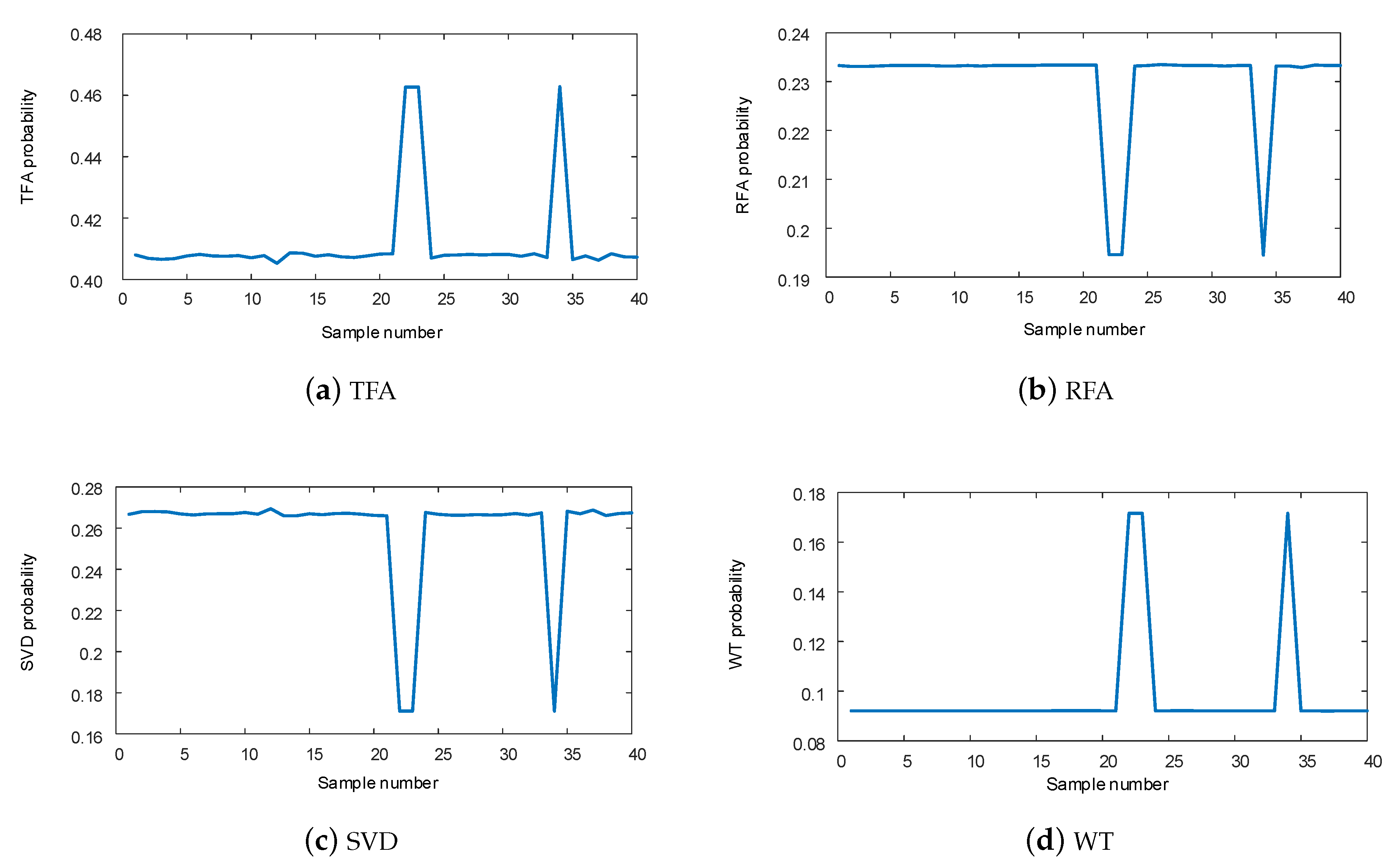
6.1. Approach 1: Compression and Classification Approach
6.2. Approach 2: Gaussian Distribution Approach
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| AF | All Features |
| DF | Distorted Features |
| DGO | Distribution Grid Operator |
| FC | Fully Connected |
| GDA | Gaussian Distribution Approach |
| LSTM | Long Short-Term Memory |
| NILM | Non-Intrusive Load Monitoring |
| OTF | Optimal-Transmission-Factor |
| RFA | Rectangular Function Algorithm |
| SVD | Singular Value Decomposition |
| TFA | Triangular Function Algorithm |
| WT | Wavelet Transform |
References
- Rajagopalan, S.; Sankar, L.; Mohajer, S.; Poor, V. Smart meter privacy: A utility-privacy framework. In Proceedings of the 2nd IEEE International Conference on Smart Grid Communications, Brussels, Belgium, 17–20 October 2011. [Google Scholar]
- Unterweger, A.; Engel, D. Resumable load data compression in smart grids. IEEE Trans. Smart Grid. 2015, 6, 919–929. [Google Scholar] [CrossRef]
- Wen, L.; Zhou, K.; Yang, S.; Li, L. Compression of smart meter big data: A survey. Renew. Sustain. Energy Rev. 2018, 91, 59–69. [Google Scholar] [CrossRef]
- Hart, G. Nonintrusive appliance load monitoring. Proc. IEEE 1992, 80, 1870–1891. [Google Scholar] [CrossRef]
- Lisovich, M.; Mulligan, D.; Wicker, S. Inferring personal information from demand-response systems. IEEE Secur. Priv. 2010, 8, 11–20. [Google Scholar] [CrossRef]
- Storer, J. Data Compression: Methods and Theory; Computer Science Press, Inc.: New York, NY, USA, 1988. [Google Scholar]
- Salomon, D.; Motta, G. Handbook of Data Compression, 5th ed.; Springer Science & Business Media: London, UK, 2010. [Google Scholar]
- Blelloch, E. Introduction to Data Compression; Computer Science Department, Carnegie Mellon University: Pittsburgh, PA, USA, 2010. [Google Scholar]
- Pu, I. Fundamental Data Compression; Butterworth-Heinemann: Oxford, UK, 2005. [Google Scholar]
- Tate, J. Preprocessing and Golomb–Rice Encoding for Lossless Compression of Phasor Angle Data. IEEE Trans. Smart Grid. 2016, 7, 718–729. [Google Scholar] [CrossRef]
- Kraus, J.; Pavel, S.; Kukačka, L. Optimal data compression techniques for smart grid and power quality trend data. In Proceedings of the 2012 IEEE 15th International Conference on Harmonics and Quality of Power, Hong Kong, China, 17–20 June 2012. [Google Scholar]
- Wang, Y.; Chen, Q.; Kang, C.; Xia, Q.; Luo, M. Sparse and Redundant Representation-Based Smart Meter Data Compression and Pattern Extraction. IEEE Trans. Smart Grid 2017, 32, 2142–2151. [Google Scholar] [CrossRef]
- Unterweger, A.; Engel, D. Lossless compression of high-frequency voltage and current data in smart grids. In Proceedings of the IEEE 2016 International Conference on Big Data, Washington, DC, USA, 5–8 December 2016; IEEE: New York, NY, USA, 2016; pp. 3131–3139. [Google Scholar]
- Ringwelski, M.; Renner, C.; Reinhardt, A.; Weigel, A.; Turau, V. The hitchhiker’s guide to choosing the compression algorithm for your smart meter data. In Proceedings of the 2012 IEEE International Energy Conference and Exhibition (EnergyCon’12), Florence, Italy, 9–12 September 2012; pp. 935–940. [Google Scholar]
- Notaristefano, A.; Chicco, G.; Piglione, F. Data size reduction with symbolic aggregate approximation for electrical load pattern grouping. IET Gener. Transm. Distrib. 2013, 7, 108–117. [Google Scholar] [CrossRef]
- Du Pin Calmon, F.; Fawaz, N. Privacy against statistical inference. In Proceedings of the 2012 50th Annual Allerton Conference on Communication, Control, and Computing (Allerton 2012), Monticello, IL, USA, 1–5 October 2012; pp. 1401–1408. [Google Scholar]
- Sankar, L.; Rajagopalan, S.; Mohajer, S. Smart meter privacy: A theoretical framework. IEEE Trans. Smart Grid 2013, 4, 837–846. [Google Scholar] [CrossRef]
- Erdogdu, M.; Fawaz, N.; Montanari, A. Privacy-utility tradeoff for time-series with application to smart-meter data. In Proceedings of the AAAI 2015 Workshop on Computational Sustainability, Austin, TX, USA, 25–26 January 2015. [Google Scholar]
- McLaughlin, S.; McDaniel, P.; Aiello, W. Protecting consumer privacy from electric load monitoring. In Proceedings of the 18th ACM Conference on Computer and Communications Security, Chicago, IL, USA, 7–21 October 2011; pp. 87–98. [Google Scholar]
- Kalogridis, G.; Efthymiou, C.; Denic, S.; Lewis, T.; Cepeda, R. Privacy for smart meters: Towards undetectable appliance load signatures. In Proceeding of the 2010 First IEEE International Conference on Smart Grid Communications (SmartGridComm), Gaithersburg, MD, USA, 4–6 October 2010; pp. 232–237. [Google Scholar]
- Garcia, F.; Jacobs, B. Privacy-friendly energy-metering via homomorphic encryption. In International Workshop on Security and Trust Management; Springer: Berlin/Heidelberg, Germany, 2010; pp. 226–238. [Google Scholar]
- Erkin, Z.; Tsudik, G. Private computation of spatial and temporal power consumption with smart meters. In Applied Cryptography and Network Security, Proceedings of the International Conference on Applied Cryptography and Network Security, Singapore, 6–9 June 2006; Springer: Berlin/Heidelberg, Germany, 2012; pp. 561–577. [Google Scholar]
- Im, J.; Kwon, H.; Jeon, S.; Lee, M. Privacy-Preserving Electricity Billing System Using Functional Encryption. Energies 2019, 12, 1237. [Google Scholar] [CrossRef]
- Eibl, G.; Engel, D. Influence of data granularity on smart meter privacy. IEEE Trans. Smart Grid 2015, 6, 930–939. [Google Scholar] [CrossRef]
- Engel, D.; Eibl, G. Multi-Resolution Load Curve Representation with Privacy-preserving Aggregation. In Proceedings of the IEEE Innovative Smart Grid Technologies (ISGT), Lyngby, Denmark, 6–9 October 2013; pp. 1–5. [Google Scholar]
- Engel, D. Wavelet-based Load Profile Representation for Smart Meter Privacy. In Proceedings of the IEEE PES Innovative Smart Grid Technologies (ISGT’13), Washington, DC, USA, 24–27 February 2013; pp. 1–6. [Google Scholar]
- Engel, D.; Eibl, G. Wavelet-Based Multiresolution Smart Meter Privacy. IEEE Trans. Smart Grid 2016, 99, 1–12. [Google Scholar] [CrossRef]
- Evfimievski, S. Randomization techniques for privacy preserving association rule mining. SIGKDD Explor. 2002, 4, 43–48. [Google Scholar] [CrossRef]
- Agrawal, R.; Srikant, R. Privacy-preserving data mining. In Proceedings of the ACM SIGMOD Conference on Management of Data, Dallas, TX, USA, 16–18 May 2000; pp. 439–450. [Google Scholar]
- Chen, K.; Liu, L. A random rotation perturbation approach to privacy data classification. In Proceedings of the IEEE International Conference on Data Mining (ICDM), Houston, TX, USA, 27–30 November 2005; pp. 589–592. [Google Scholar]
- Kargupta, H.; Datta, S.; Wang, Q.; Sivakumar, K. Random data perturbation techniques and privacy preserving data mining. Knowl. Inf. Syst. 2005, 7, 387–414. [Google Scholar] [CrossRef]
- Huang, Z.; Du, W.; Chen, B. Deriving private information from randomized data. In Proceedings of the ACM SIGMOD Conference, Baltimore, MD, USA, 14–16 June 2005; pp. 37–48. [Google Scholar]
- Kim, J.J.; Winkler, W.E. Multiplicative Noise for Masking Continuous Data; Technical Report Statistics 2003-01; Statistical Research Division, US Bureau of the Census: Washington, DC, USA, 2003. [Google Scholar]
- Clements, A.; McCulloch, M.; Nixon, K. Low-loss, high-compression of energy profiles. In Proceedings of the International Conference IEEE Renewable Energy Research and Applications (ICRERA), Palermo, Italy, 22–25 November 2015. [Google Scholar]
- Ning, J.; Wang, J.; Gao, W.; Liu, C. A wavelet-based data compression technique for smart grid. IEEE Trans. Smart Grid 2010, 2, 212–218. [Google Scholar] [CrossRef]
- Aprillia, H.; Yang, H.; Huang, C. Optimal Decomposition and Reconstruction of Discrete Wavelet Transformation for Short-Term Load Forecasting. Energies 2019, 12, 4654. [Google Scholar] [CrossRef]
- Rand, W. Objective criteria for the evaluation of clustering methods. J. Am. Stat. Assoc. 1971, 66, 846–850. [Google Scholar] [CrossRef]
- Makonin, S.; Wang, Z.J.; Tumpach, C. The Rainforest Automation Energy Dataset for Smart Grid Meter Data Analysis. Data 2018, 3, 8. [Google Scholar] [CrossRef]
- He, X.; Xinwen, Z.; Jay Kuo, C.-C. A distortion-based approach to privacy-preserving metering in smart grids. IEEE Access 2013, 1, 67–78. [Google Scholar]


| Properties Smart Meter | |
|---|---|
| Smart meter, read out from remote location | 109 |
| Time series resolution | 15-min |
| Transferred accounting data | Active energy |
| Transferred energy network data | |
| Transmission technique | GSM, GPRS |
| Transmitted data (daily) | 157,248 data points |
| TFA | RFA | SVD | WT | |
|---|---|---|---|---|
| 20.1 | 20.4 | 20.5 | 20.4 | |
| time () | 35.6 s | 1.7 s | 38.1 s | 4.3 s |
| 0.68 | 0.70 | 0.69 | 0.70 | |
| 13.67 | 14.28 | 14.15 | 14.28 |
| DF/AF | DF/AF after LMF | |
|---|---|---|
| Original | 100.00% | - |
| Approach 1: Attack during transmission | ||
| TFA, RFA, SVD, WT | <0.01% | <0.05% |
| Approach 1: Attack after decompression | ||
| TFA | 80.29% | 79.88% |
| RFA | 78.74% | 79.29% |
| SVD | 79.27% | 79.65% |
| WT | 80.97% | 79.45% |
| Approach 2: Attack during transmission | ||
| DSF = 5 | 4.10% | 14.84% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Plenz, M.; Dong, C.; Grumm, F.; Meyer, M.F.; Schumann, M.; McCulloch, M.; Jia, H.; Schulz, D. Framework Integrating Lossy Compression and Perturbation for the Case of Smart Meter Privacy. Electronics 2020, 9, 465. https://doi.org/10.3390/electronics9030465
Plenz M, Dong C, Grumm F, Meyer MF, Schumann M, McCulloch M, Jia H, Schulz D. Framework Integrating Lossy Compression and Perturbation for the Case of Smart Meter Privacy. Electronics. 2020; 9(3):465. https://doi.org/10.3390/electronics9030465
Chicago/Turabian StylePlenz, Maik, Chaoyu Dong, Florian Grumm, Marc Florian Meyer, Marc Schumann, Malcom McCulloch, Hongjie Jia, and Detlef Schulz. 2020. "Framework Integrating Lossy Compression and Perturbation for the Case of Smart Meter Privacy" Electronics 9, no. 3: 465. https://doi.org/10.3390/electronics9030465
APA StylePlenz, M., Dong, C., Grumm, F., Meyer, M. F., Schumann, M., McCulloch, M., Jia, H., & Schulz, D. (2020). Framework Integrating Lossy Compression and Perturbation for the Case of Smart Meter Privacy. Electronics, 9(3), 465. https://doi.org/10.3390/electronics9030465








