Improving Deep Learning-Based UWB LOS/NLOS Identification with Transfer Learning: An Empirical Approach
Abstract
1. Introduction
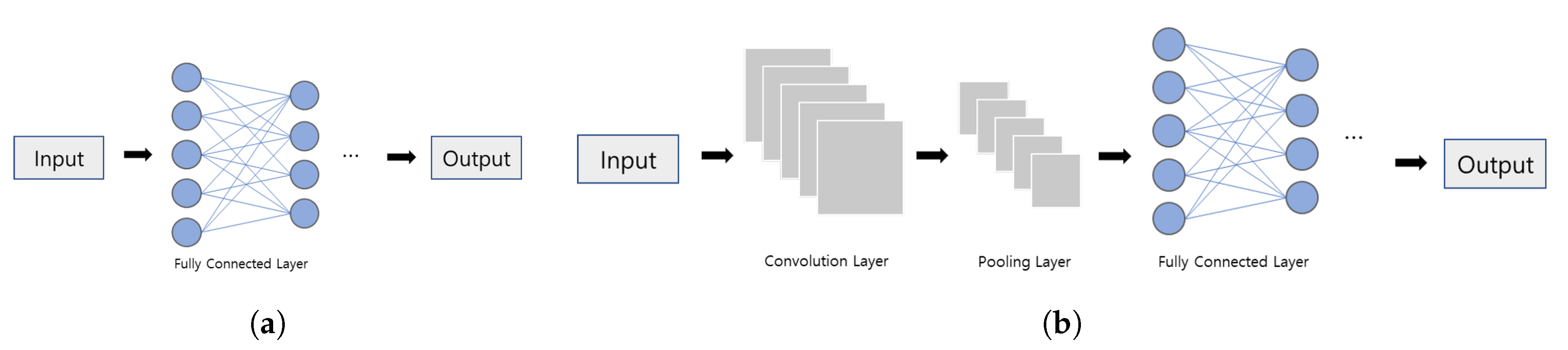
- We introduce two UWB channel classification schemes based on multilayer perceptron (MLP) and convolutional neural network (CNN).
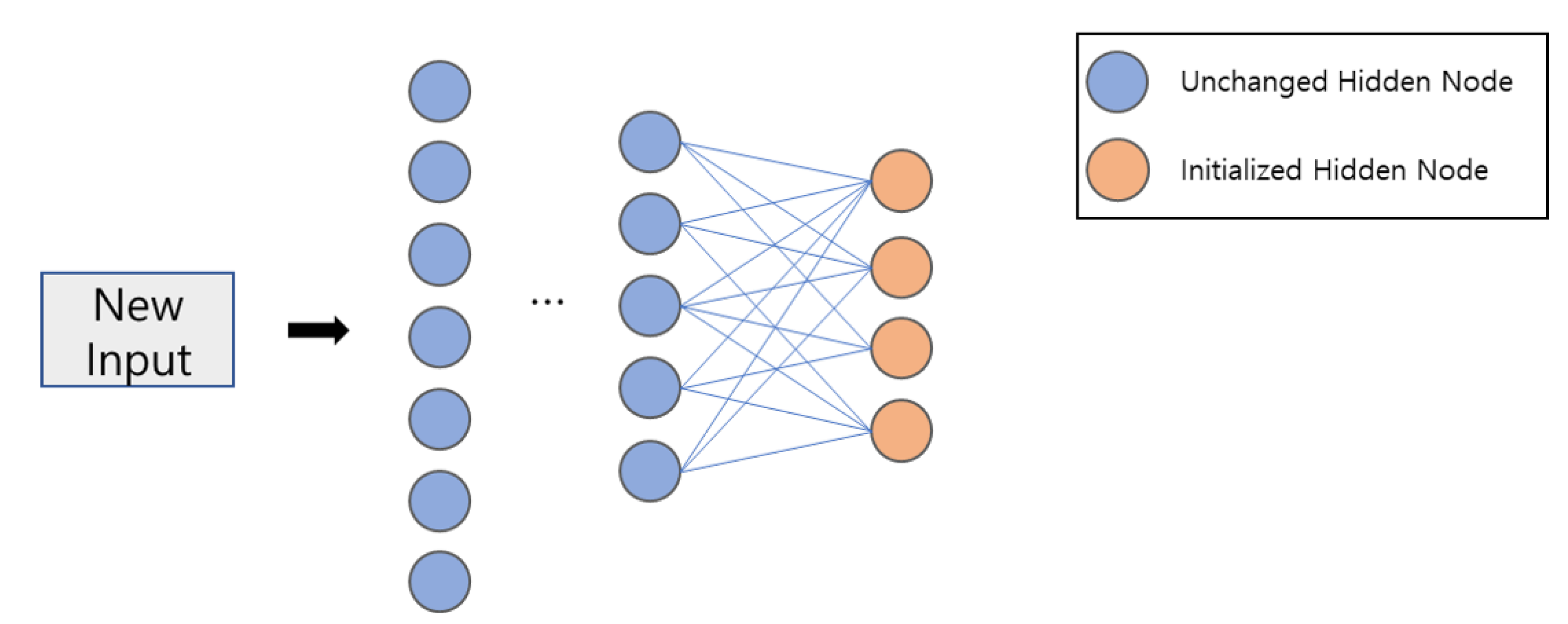
- We propose a transfer learning algorithm for accurate NLOS classification in an unmeasured place.
- We conduct extensive experiments using commercial UWB devices to examine the performance of a deep neural network (DNN) model in an unmeasured environment.
- By comparing the performance, we propose a model for optimizing the neural network structure according to the surrounding environment. In this model, we implement a transfer learning-based NLOS condition classification method for an unmeasured environment.
2. Related Work
2.1. Algorithm-Based NLOS Identification
2.2. Machine Learning-Based NLOS Identification
3. UWB NLOS Identification
3.1. Problem Statement
3.2. Proposed Scheme
4. Experimental Setup
5. Experimental Analysis and Performance Evaluation
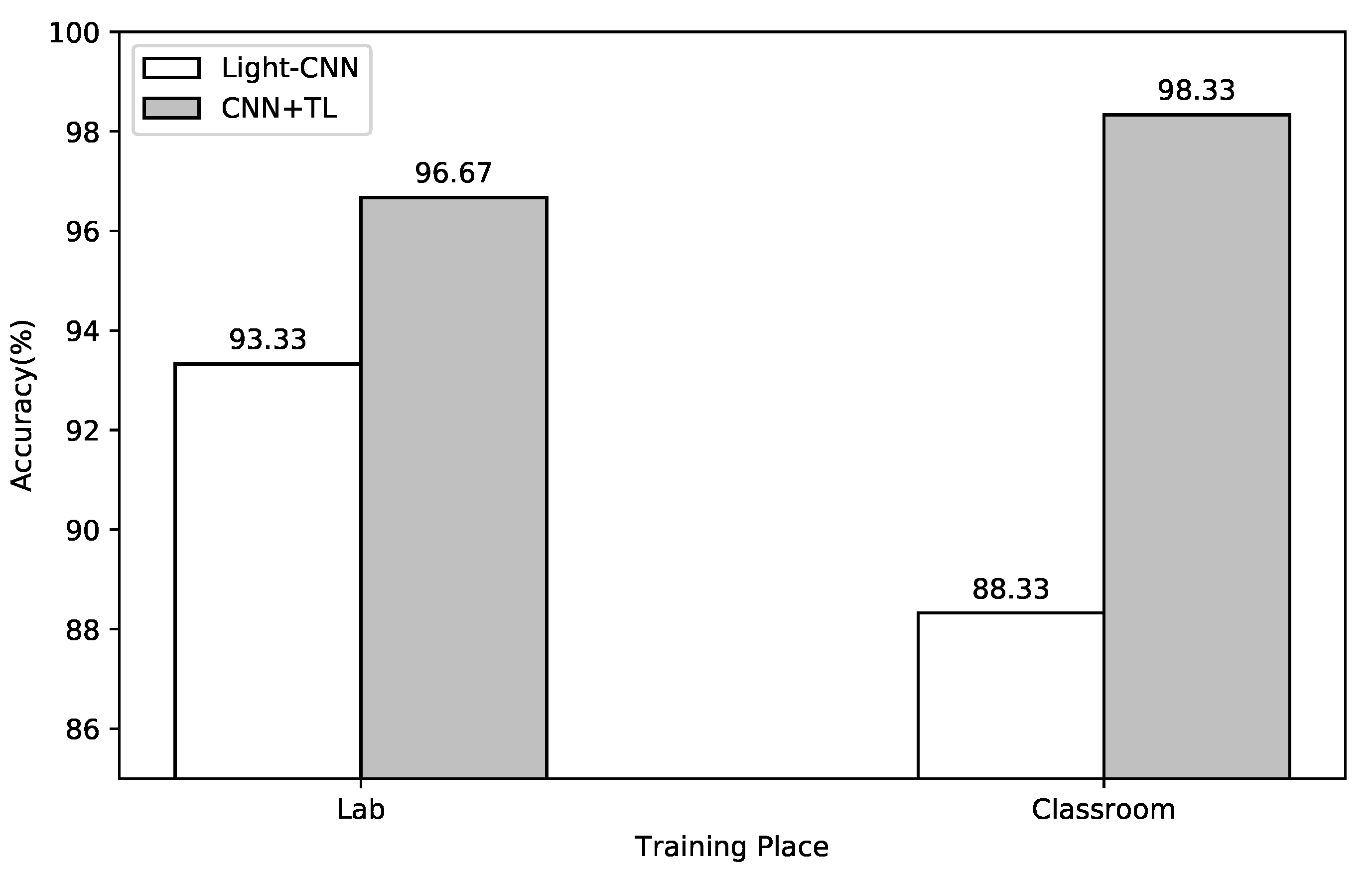
5.1. UWB Channel Classification Performance
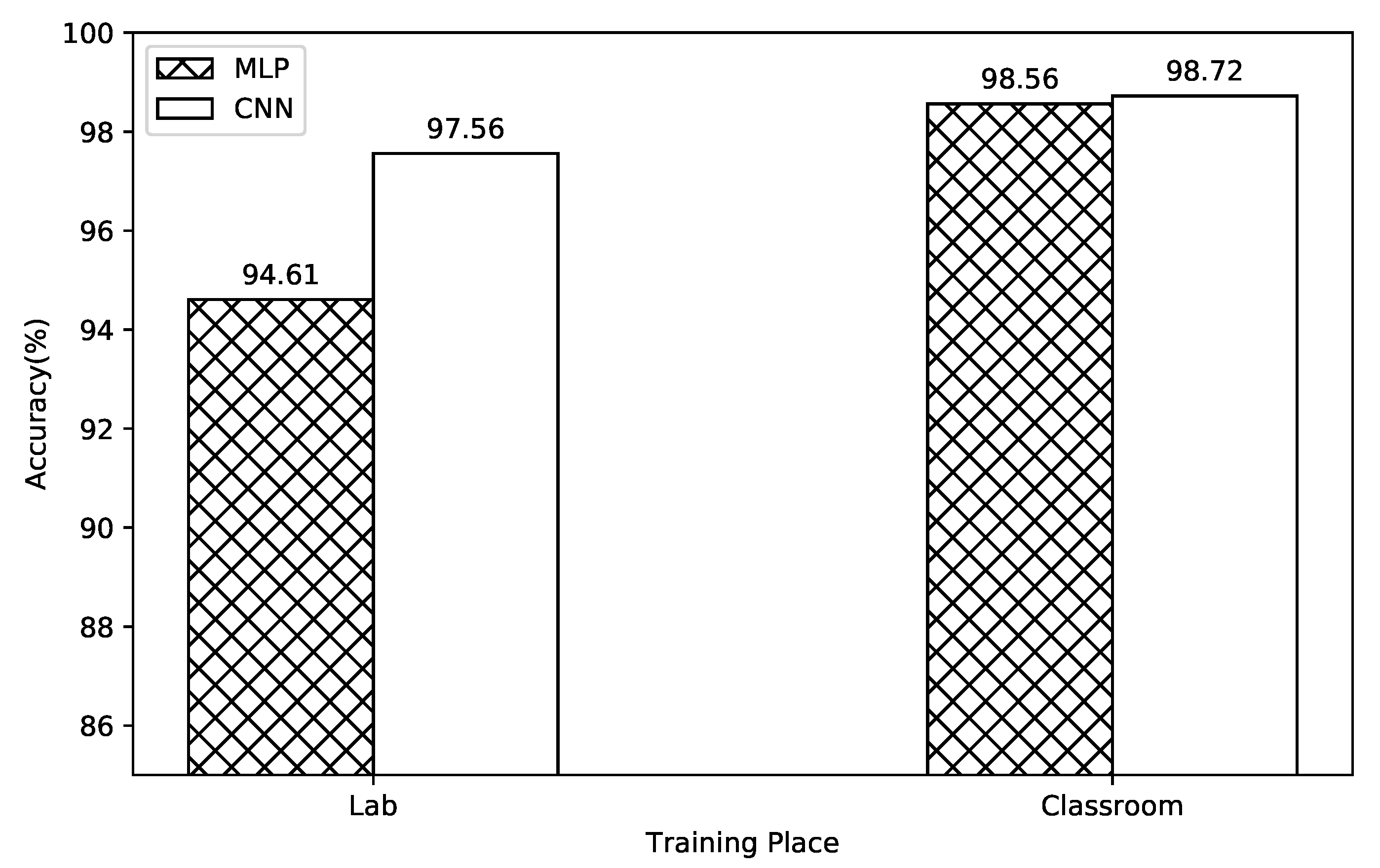
5.1.1. Classification Performance in the Measured Environment
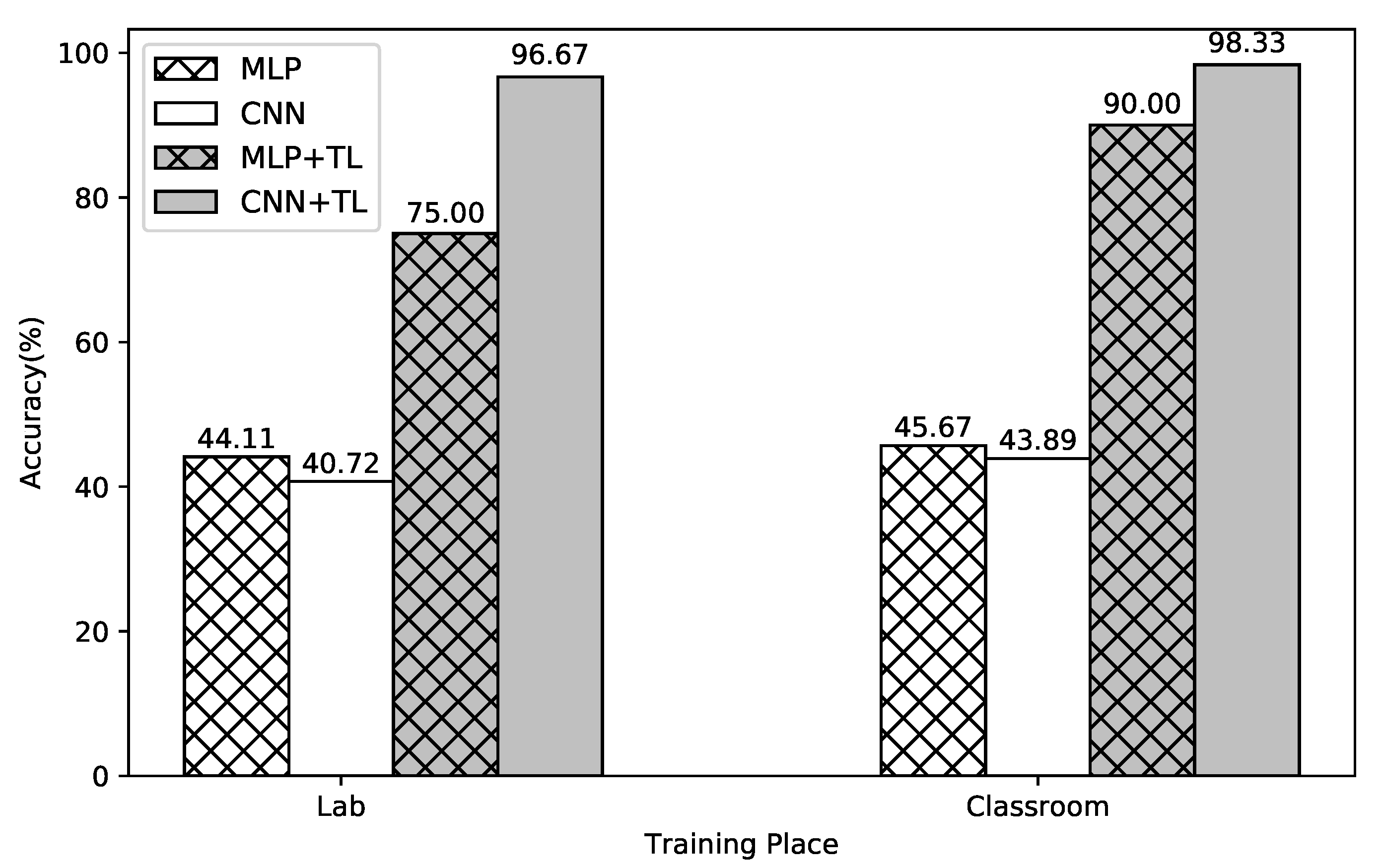
5.1.2. Classification Performance in the Unmeasured Environment
5.2. Computational Overhead
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Desk, E.D. Continental smartphone-based car key to be introduced in 2021 models of three more car manufacturers. The Financial Express. 24 January 2020. Available online: https://www.financialexpress.com/auto/car-news/continental-smartphone-based-car-key-cosma-2021-models-digital-car-key-apple/2002031 (accessed on 2 September 2020).
- Eadicicco, L. Apple and Samsung newest phones use a little-known technology that lets your phone understand exactly where it is—And could mean you never misplace anything again. Business Insider. 20 August 2020. Available online: https://www.businessinsider.com/uwb-explained-samsung-galaxy-note-ultra-apple-iphone-features-airdrop-2020-8 (accessed on 2 September 2020).
- Sedlacek, P.; Slanina, M.; Masek, P. An overview of the IEEE 802.15.4z standard its comparison and to the existing UWB standards. In Proceedings of the 2019 29th International Conference Radioelektronika (RADIOELEKTRONIKA), Pardubice, Czech Republic, 16–18 April 2019; pp. 1–6. [Google Scholar]
- Gezici, S.; Tian, Z.; Giannakis, G.B.; Kobayashi, H.; Molisch, A.F.; Poor, H.V.; Sahinoglu, Z. Localization via ultra-wideband radios: A look at positioning aspects for future sensor networks. IEEE Signal Process. Mag. 2005, 22, 70–84. [Google Scholar] [CrossRef]
- Connell, C. What’s the difference between measuring location by UWB Wi-Fi and bluetooth? Electron. Des. Febr. 2015, 6, 2015. Available online: https://www.electronicdesign.com/technologies/communications/article/21800581/whats-the-difference-between-measuring-location-by-uwb-wifi-and-bluetooth (accessed on 7 October 2020).
- Monica, S.; Ferrari, G. Improving UWB-based localization in IoT scenarios with statistical models of distance error. Sensors 2018, 18, 1592. [Google Scholar] [CrossRef] [PubMed]
- Aileni, R.M.; Suciu, G.; Sukuyama, C.A.V.; Pasca, S.; Maheswar, R. Internet of wearable low-power wide-area network devices for health self-monitoring. In LPWAN Technologies for IoT and M2M Applications; Elsevier: London, UK, 2020; pp. 307–325. [Google Scholar]
- Choi, H.B.; Lim, K.W.; Ko, Y.B. Sensor Localization System for AR-assisted Disaster Relief Applications (poster). In Proceedings of the 17th Annual International Conference on Mobile Systems, Applications, and Services, Seoul, Korea, 12–21 June 2019; pp. 526–527. [Google Scholar]
- Ridolfi, M.; Vandermeeren, S.; Defraye, J.; Steendam, H.; Gerlo, J.; De Clercq, D.; Hoebeke, J.; De Poorter, E. Experimental evaluation of UWB indoor positioning for sport postures. Sensors 2018, 18, 168. [Google Scholar] [CrossRef] [PubMed]
- Huo, Y.; Dong, X.; Beatty, S. Cellular Communications in Ocean Waves for Maritime Internet of Things. IEEE Internet Things J. 2020, 7, 9965–9979. [Google Scholar] [CrossRef]
- Li, L.; Ren, H.; Cheng, Q.; Xue, K.; Chen, W.; Debbah, M.; Han, Z. Millimeter-wave networking in sky: A machine learning and mean field game approach for joint beamforming and beam-steering. IEEE Trans. Wirel. Commun. 2020, 19, 6393–6408. [Google Scholar] [CrossRef]
- He, Y.; Chen, Y.; Hu, Y.; Zeng, B. WiFi Vision: Sensing, Recognition, and Detection with Commodity MIMO-OFDM WiFi. IEEE Internet Things J. 2020, 7, 8296–8317. [Google Scholar] [CrossRef]
- Huo, Y.; Dong, X.; Lu, T.; Xu, W.; Yuen, M. Distributed and multilayer UAV networks for next-generation wireless communication and power transfer: A feasibility study. IEEE Internet Things J. 2019, 6, 7103–7115. [Google Scholar] [CrossRef]
- Khodjaev, J.; Park, Y.; Malik, A.S. Survey of NLOS identification and error mitigation problems in UWB-based positioning algorithms for dense environments. Ann. Telecommun./Annales des Télécommunications 2010, 65, 301–311. [Google Scholar] [CrossRef]
- Yu, K.; Wen, K.; Li, Y.; Zhang, S.; Zhang, K. A novel NLOS mitigation algorithm for UWB localization in harsh indoor environments. IEEE Trans. Veh. Technol. 2018, 68, 686–699. [Google Scholar] [CrossRef]
- Kim, D.H.; Kwon, G.R.; Pyun, J.Y.; Kim, J.W. NLOS Identification in UWB channel for Indoor Positioning. In Proceedings of the 2018 15th IEEE Annual Consumer Communications & Networking Conference (CCNC), Las Vegas, NV, USA, 12–15 January 2018; pp. 1–4. [Google Scholar]
- Zeng, Z.; Bai, R.; Wang, L.; Liu, S. NLOS identification and mitigation based on CIR with particle filter. In Proceedings of the 2019 IEEE Wireless Communications and Networking Conference (WCNC), Marrakesh, Morocco, 15–18 April 2019; pp. 1–6. [Google Scholar]
- Gururaj, K.; Rajendra, A.K.; Song, Y.; Law, C.L.; Cai, G. Real-time identification of NLOS range measurements for enhanced UWB localization. In Proceedings of the 2017 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Sapporo, Japan, 18–21 September 2017; pp. 1–7. [Google Scholar]
- Zeng, Z.; Liu, S.; Wang, L. UWB NLOS identification with feature combination selection based on genetic algorithm. In Proceedings of the 2019 IEEE International Conference on Consumer Electronics (ICCE), Las Vegas, NV, USA, 11–13 January 2019; pp. 1–5. [Google Scholar]
- Kristensen, J.B.; Ginard, M.M.; Jensen, O.K.; Shen, M. Non-Line-of-Sight Identification for UWB Indoor Positioning Systems using Support Vector Machines. In Proceedings of the 2019 IEEE MTT-S International Wireless Symposium (IWS), Guangzhou, China, 19–22 May 2019; pp. 1–3. [Google Scholar]
- Barral, V.; Escudero, C.J.; García-Naya, J.A. NLOS Classification Based on RSS and Ranging Statistics Obtained from Low-Cost UWB Devices. In Proceedings of the 2019 27th European Signal Processing Conference (EUSIPCO), Coruna, Spain, 2–6 September 2019; pp. 1–5. [Google Scholar]
- Zeng, H.; Xie, R.; Xu, R.; Dai, W.; Tian, S. A Novel Approach to NLOS Identification for UWB Positioning Based on Kernel Learning. In Proceedings of the 2019 IEEE 19th International Conference on Communication Technology (ICCT), Xi’an, China, 16–19 October 2019; pp. 451–455. [Google Scholar]
- Fan, J.; Awan, A.S. Non-line-of-sight identification based on unsupervised machine learning in ultra wideband systems. IEEE Access 2019, 7, 32464–32471. [Google Scholar] [CrossRef]
- Wang, F.; Xu, Z.; Zhi, R.; Chen, J.; Zhang, P. Los/nlos channel identification technology based on cnn. In Proceedings of the 2019 6th NAFOSTED Conference on Information and Computer Science (NICS), Hanoi, Vietnam, 12–13 December 2019; pp. 200–203. [Google Scholar]
- Stahlke, M.; Kram, S.; Mutschler, C.; Mahr, T. NLOS Detection using UWB Channel Impulse Responses and Convolutional Neural Networks. In Proceedings of the 2020 International Conference on Localization and GNSS (ICL-GNSS), Tampere, Finland, 2–4 June 2020; pp. 1–6. [Google Scholar]
- ShirinAbadi, P.A.; Abbasi, A. Uwb channel classification using convolutional neural networks. In Proceedings of the 2019 IEEE 10th Annual Ubiquitous Computing, Electronics & Mobile Communication Conference (UEMCON), New York, NY, USA, 10–12 October 2019; pp. 1064–1068. [Google Scholar]
- Jiang, C.; Shen, J.; Chen, S.; Chen, Y.; Liu, D.; Bo, Y. UWB NLOS/LOS Classification Using Deep Learning Method. IEEE Commun. Lett. 2020, 24, 2226–2230. [Google Scholar] [CrossRef]
- Molisch, A.F.; Balakrishnan, K.; Chong, C.C.; Emami, S.; Fort, A.; Karedal, J.; Kunisch, J.; Schantz, H.; Schuster, U.; Siwiak, K. IEEE 802.15.4a channel model-final report. IEEE P802 2004, 15, 0662. [Google Scholar]
- Decawave. EVK1000 User Manual. 2016. Available online: https://www.decawave.com/product/evk1000-evaluation-kit/ (accessed on 7 October 2020).


| Layer (Type) | Shape | Parameters |
|---|---|---|
| input (InputLayer) | 2032 | 0 |
| dense (Dense) | 128 | 260,224 |
| dense_1 (Dense) | 128 | 16,512 |
| dense_2 (Dense) | 128 | 16,512 |
| dense_3 (Dense) | 3 | 387 |
| Layer (Type) | Shape | Parameters |
|---|---|---|
| input (InputLayer) | 2032 | 0 |
| reshape (Reshape) | (2032, 1) | 0 |
| conv1d_1 (Conv1D) | (2025, 128) | 1152 |
| conv1d_2 (Conv1D) | (2018, 128) | 131,200 |
| max_pooling1d_1 (MaxPooling1D) | (1009, 128) | 0 |
| conv1d_3 (Conv1D) | (1002, 128) | 131,200 |
| conv1d_4 (Conv1D) | (995, 128) | 131,200 |
| max_pooling1d_2 (MaxPooling1D) | (497, 128) | 0 |
| flatten (Flatten) | 63,616 | 0 |
| dense (Dense) | 128 | 8,142,976 |
| dense_1 (Dense) | 128 | 16,512 |
| dense_2 (Dense) | 3 | 387 |
| Train: Lab, Test: Lab | Train: Classroom, Test: Classroom | |||||||
|---|---|---|---|---|---|---|---|---|
| MLP | CNN | MLP | CNN | |||||
| Precision | Recall | Precision | Recall | Precision | Recall | Precision | Recall | |
| LOS | 94.54 | 95.33 | 98.32 | 97.66 | 99.33 | 98.50 | 97.24 | 100.0 |
| Weak NLOS | 95.94 | 90.67 | 98.31 | 97.00 | 98.66 | 98.33 | 99.16 | 98.33 |
| NLOS | 93.47 | 97.84 | 96.08 | 98.00 | 97.69 | 98.33 | 99.83 | 97.83 |
| Train: Lab, Test: Classroom | Train: Classroom, Test: Lab | |||||||
|---|---|---|---|---|---|---|---|---|
| MLP | CNN | MLP | CNN | |||||
| Precision | Recall | Precision | Recall | Precision | Recall | Precision | Recall | |
| LOS | 50.40 | 63.67 | 44.52 | 44.67 | 71.52 | 54.83 | 52.99 | 69.50 |
| Weak NLOS | 40.15 | 62.84 | 41.77 | 76.17 | 36.07 | 74.60 | 40.09 | 56.67 |
| NLOS | 33.98 | 5.83 | 7.69 | 1.33 | 45.92 | 7.50 | 20.00 | 5.50 |
| train: Lab, Test: Classroom | Train: Classroom, Test: Lab | |||||||
|---|---|---|---|---|---|---|---|---|
| MLP+TL | CNN+TL | MLP+TL | CNN+TL | |||||
| Precision | Recall | Precision | Recall | Precision | Recall | Precision | Recall | |
| LOS | 100.0 | 70.00 | 95.24 | 100.0 | 100.0 | 80.00 | 100.0 | 95.00 |
| Weak NLOS | 77.78 | 70.00 | 95.24 | 100.0 | 85.71 | 90.00 | 100.0 | 100.0 |
| NLOS | 60.71 | 85.00 | 100.0 | 90.00 | 86.96 | 100.0 | 95.24 | 100.0 |
| MLP | CNN | MLP+TL | CNN+TL | Light-CNN | |
|---|---|---|---|---|---|
| Lab | 3 s | 14 m 26 s | 3 s | 7 s | 1 m 6 s |
| Classroom | 4 s | 14 m 28 s | 3 s | 18 s | 1 m 22 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, J.; Nam, S.; Choi, H.; Ko, Y.; Ko, Y.-B. Improving Deep Learning-Based UWB LOS/NLOS Identification with Transfer Learning: An Empirical Approach. Electronics 2020, 9, 1714. https://doi.org/10.3390/electronics9101714
Park J, Nam S, Choi H, Ko Y, Ko Y-B. Improving Deep Learning-Based UWB LOS/NLOS Identification with Transfer Learning: An Empirical Approach. Electronics. 2020; 9(10):1714. https://doi.org/10.3390/electronics9101714
Chicago/Turabian StylePark, JiWoong, SungChan Nam, HongBeom Choi, YoungEun Ko, and Young-Bae Ko. 2020. "Improving Deep Learning-Based UWB LOS/NLOS Identification with Transfer Learning: An Empirical Approach" Electronics 9, no. 10: 1714. https://doi.org/10.3390/electronics9101714
APA StylePark, J., Nam, S., Choi, H., Ko, Y., & Ko, Y.-B. (2020). Improving Deep Learning-Based UWB LOS/NLOS Identification with Transfer Learning: An Empirical Approach. Electronics, 9(10), 1714. https://doi.org/10.3390/electronics9101714







