Abstract
Physical unclonable functions (PUF) are emerging as a promising alternative to traditional cryptographic protocols for IoT authentication. XOR Arbiter PUFs (XPUFs), a group of well-studied PUFs, are found to be secure against machine learning (ML) attacks if the XOR gate is large enough, as both the number of CRPs and the computational time required for modeling n-XPUF increases fast with respect to n, the number of component arbiter PUFs. In this paper, we present a neural network-based method that can successfully attack XPUFs with significantly fewer CRPs and shorter learning time when compared with existing ML attack methods. Specifically, the experimental study in this paper shows that our new method can break the 64-bit 9-XPUF within ten minutes of learning time for all of the tested samples and runs, with magnitudes faster than the fastest existing ML attack method, which takes over 1.5 days of parallel computing time on 16 cores.
1. Introduction
The Internet of Things (IoTs) are rapidly expanding into all realms of business activities and people’s daily lives. As reported in [1], 20.4 billion connected IoTs will be in service by 2020. Unfortunately, low-cost resource-constrained IoTs face security challenges, since the conventional cryptographic protocols are not adequately lightweight [2] and need to store secret keys in non-volatile memories. Studies reveal that any data stored in non-volatile memories can be exposed by invasive or side-channel attacks [3,4,5,6,7,8,9].
Physical unclonable functions (PUFs) [8,10] were proposed as a possible lightweight alternative to traditional cryptographic techniques. PUFs exploit circuits’ variations, such as gate delays, SRAM turn-on state, etc., in order generate responses that are unique for individual PUF circuits, which can be used as the chips’ fingerprints. Thus, PUFs can be employed to produce unique keys [11,12] for authentication. However, some PUFs can be compromised by Machine Learning (ML) attacks. An attacker can create a mathematical clone of the targeted PUF by building an ML model of the PUF, which can be trained to reach high predictive power after obtaining adequate Challenge-Response pairs (CRPs) through eavesdropping or other means.
Arbiter PUFs (APUFs) are simplistic delay-based PUF and one of the most widely studied PUFs. Based on a linear classification model that was developed from the additive delay model (ADM) [13], multiple ML methods can reverse engineer the gate delays so that the responses of APUFs can be accurately predicted [14,15]. ML methods that have successfully cracked APUFs [15] include Support Vector Machine (SVM), Evolution Strategies (ES), and Logistic Regression (LR). Thus, the researchers of [11,16,17,18] have investigated the APUFs’ vulnerability to modeling attacks, and the XOR Arbiter PUF (XPUF) is one of the results out of such efforts.
An n-XPUF consists of n APUFs with n responses that are XORed to produce the final response of the XPUF. An n-XPUF is also said to have n streams or n components. It was reported that XPUFs with a smaller number of streams are weak against ML attacks [15,19,20]. However, XPUFs with eight or nine streams were found to be fairly secure against all existing model building attacks, as they require larger numbers of CRPs and longer model training times for the attacks, as reported in [15,19,20]. Thus, large XPUFs were considered as a secured entity to be used in resource-constrained IoT applications [21].
To the best of our knowledge, none of the studies were able to break the 64-bit 9-XPUF with sequential training time below one day. In this paper, we report a neural network method that is able to crack large XPUFs magnitudes faster than all existing attack methods. Experimental results, while using both simulated and silicon CRPs, show a substantial reduction in neural network training time and the required number of CRPs as compared to all prior attacking models. Additionally, in particular, our method was able to crack 64-stage 9-XPUFs with a training time of about 10 min, while the fastest existing method [20] took about 1.6 days of 16-core parallel computing time, approximately 25 days of single-core processing time.
The rest of the paper is organized, as follows: Section 2 presents the background information and preliminaries of XPUFs with previously reported attacks. Section 3 presents our proposed deep learning attacking method. In Section 4, we discuss the experimental setup for our experiments. In Section 5, we discuss the experimental results obtained. Section 6 concludes the paper.
2. Preliminaries
2.1. The XOR Arbiter PUF
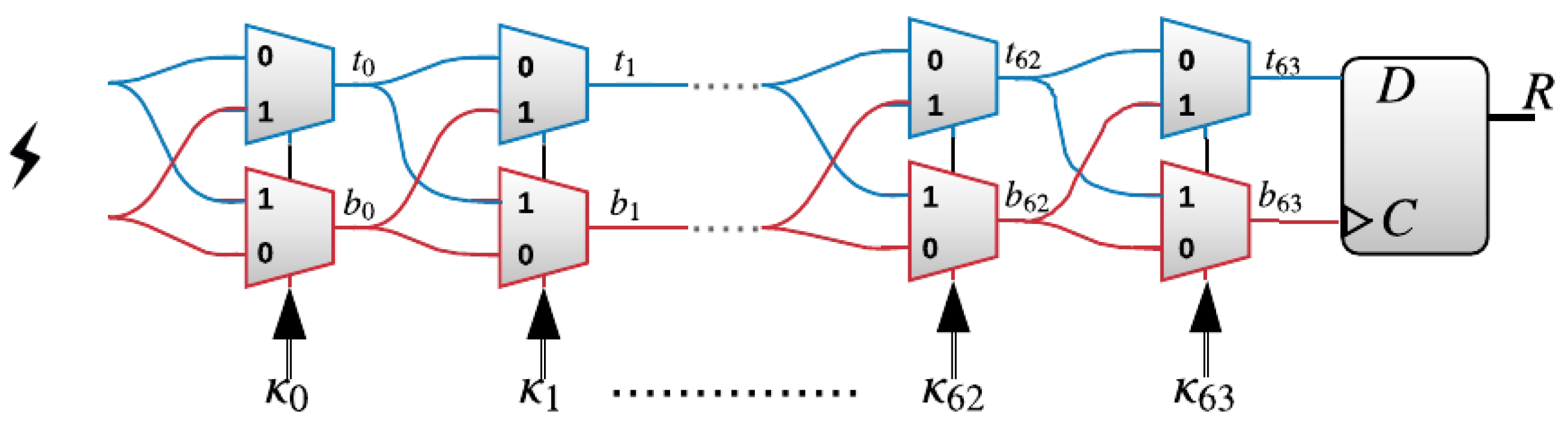
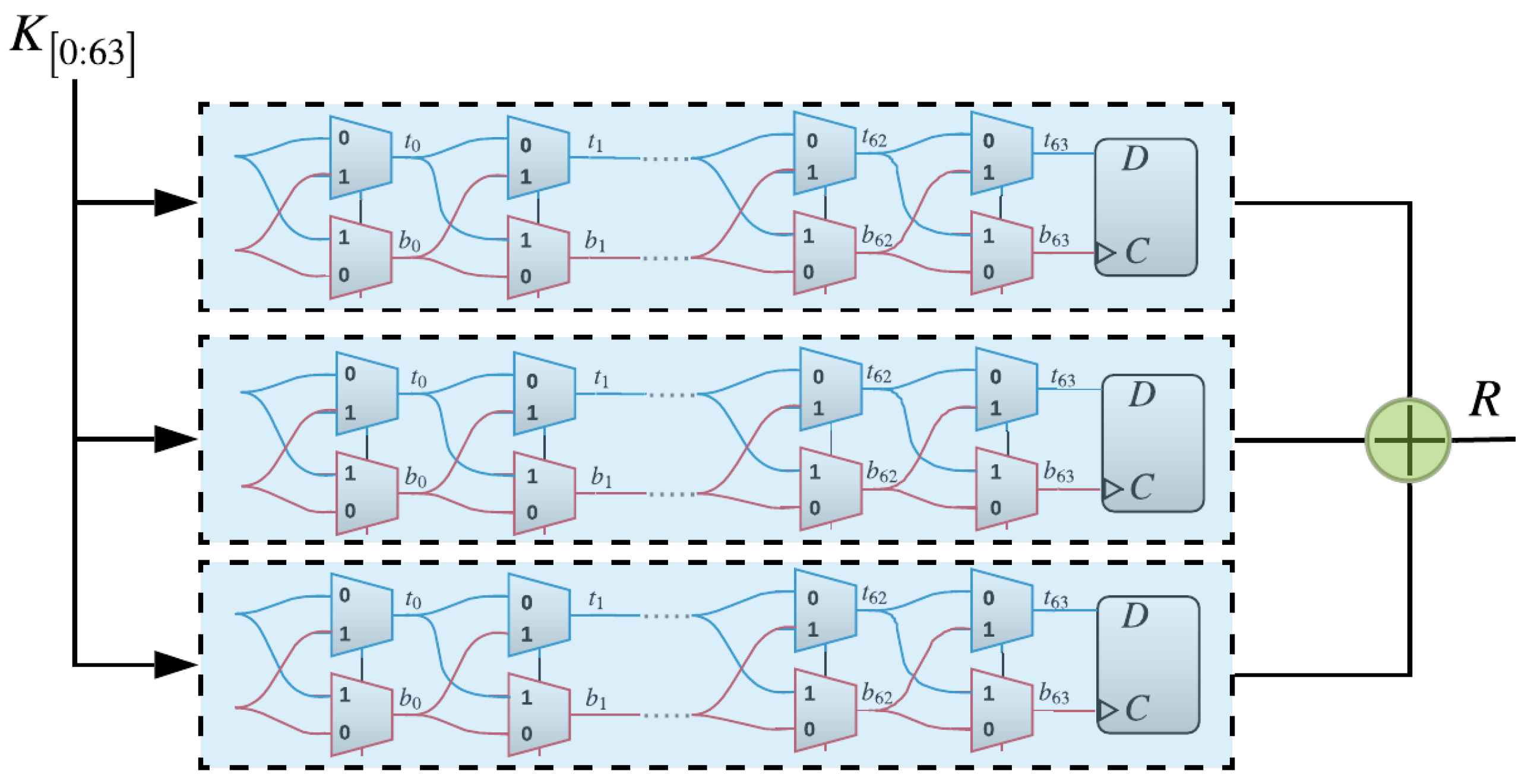
The XPUF, as introduced in [11], comprises of multiple APUFs (also known as components or streams). APUFs are delay-based silicon PUFs introduced in [8]. An APUF’s response is determined by the delay difference between the signals through two symmetric paths, as shown in Figure 1. The two signals race through a sequence of K stages, each consisting of two multiplexers (MUXes) [6,22]. At each stage, the paths traveled by the two signals, straight or crossing, depends on the value of the challenge bit. The delays that are introduced by different gates are different and, hence, different paths traveled by the signals lead to different arrival times at the arbiter. The arbiter determines the final output to be either 0 or 1. That is, if the signal on the top path arrives first, then the arbiter output would be 1; otherwise, the output is 0. The delay differences of the two signals were studied in order to satisfy the so-called Additive Delay Model (ADM) [13], which stipulates that the delay of a signal at the arbiter is the summation of delays at all gates traveled by this signal. An n-XPUF consists of n APUFs or streams, as shown in Figure 2, which illustrates a 64-bit 3-XPUF. The outputs of all APUFs are XORed in order to produce the response of the XPUF.
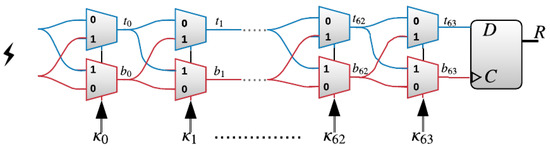
Figure 1.
A 64-stage arbiter physical unclonable functions (PUF), consisting of two multiplexers at each stage, where the number of stages refers to the number of bits of the challenge .
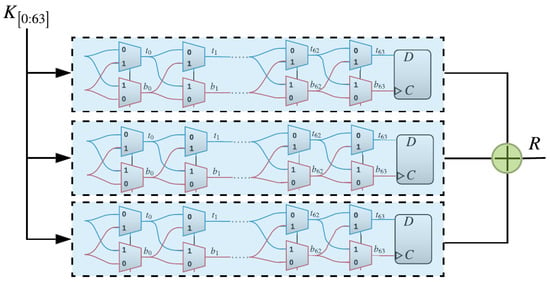
Figure 2.
A 3-XOR PUF, which consists of three arbiter PUFs whose outputs are XORed to generate the final response of the XOR Arbiter PUFs (XOR PUF).
2.2. XOR Arbiter PUF Attack Methods
Many studies have examined XPUFs’ resistance against ML attacks with different attacking methods. In [15], Ruhrmair et al. (2010) attacked several XPUFs up to 6-XPUF 128-bit and succeeded in predicting the responses by 98% while using LR. However, their attacking model consumes a very long training time, up to 31.01 h for breaking the 6-XPUF 64-bit. On the other hand, Tobisch and Becker (2015) [20] succeeded in decreasing the training time of the attacking model by parallelizing the LR method introduced in [15]. Their best prediction accuracy after optimizing the performance of the attacking method was 98% for 8-XPUF 64-bit, and the training time was over 6 h using 16 cores, which equals 4.2 days in serial execution. Even though the 8-XPUF was found to be vulnerable by their method, their training process requires a very large input, up to 150 million CRPs. Moreover, their success rate for breaking the 8-XPUF was only 50%, that is, the method can crack the XPUF only for about half of the tested sets of CRPs. Their method was also applied to 9-XPUFs while using 350 million CRPs, taking 37 h of parallel computing time on 16 cores, which is approximately 25 days of single-core execution. Out of the runs they performed for the experiment, only two out of eight was successful, leading to a success rate of 25%.
The first attempt to model the XPUFs using Feed-Forward neural network or Multilayer Perceptron (MLP) was done by Hospodar, Maes, and Verbauwhede [23] in 2012. They employed a one-layered MLP with four neurons. With this architecture, they achieved approximately 90% prediction accuracy for attacking the 2-XPUF with 64-bit of challenges. In the next attempt in 2017, Alkatheiri et al. proposed a new MLP architecture model for the Feed-Forward Arbiter PUFs (FF) with a different number of loops ranging from one to six, using a more complex MLP architecture comprising of three hidden layers, each with , where k is the number of loops in an FF PUF. Their proposed model is able to break the FF PUFs with 64- and 128-bit of challenges [24]. Following that, Aseeri et al., in [19] (2018), proposed an MLP-based architecture model for the n-XPUF with n ranging from 4 to 8 components for the input of size 64-bits and 128-bits. They succeeded in predicting the testing CRPs of 8-XPUF 64-bit by 99% using only 30 million CRPs while the best existing method used five times this number in prior works. References [19,23,24] showed that applying the MLP in creating ML attacking model is more effective than using the LR in terms of the training time. In the most recent work using MLP, the authors in [17] (2019) targeted different APUF variants such as XPUF, LSPUF, IPUF, and MPUF. In the case of XPUF, they were able to break the 6-XPUF with a moderate number of CRPs, 680K, but with a longer time than [19]. However, they did not report the accuracy of attacking the 7, 8, and 9-XPUF 64-bit.
3. The Proposed MLP-Based Architecture Method
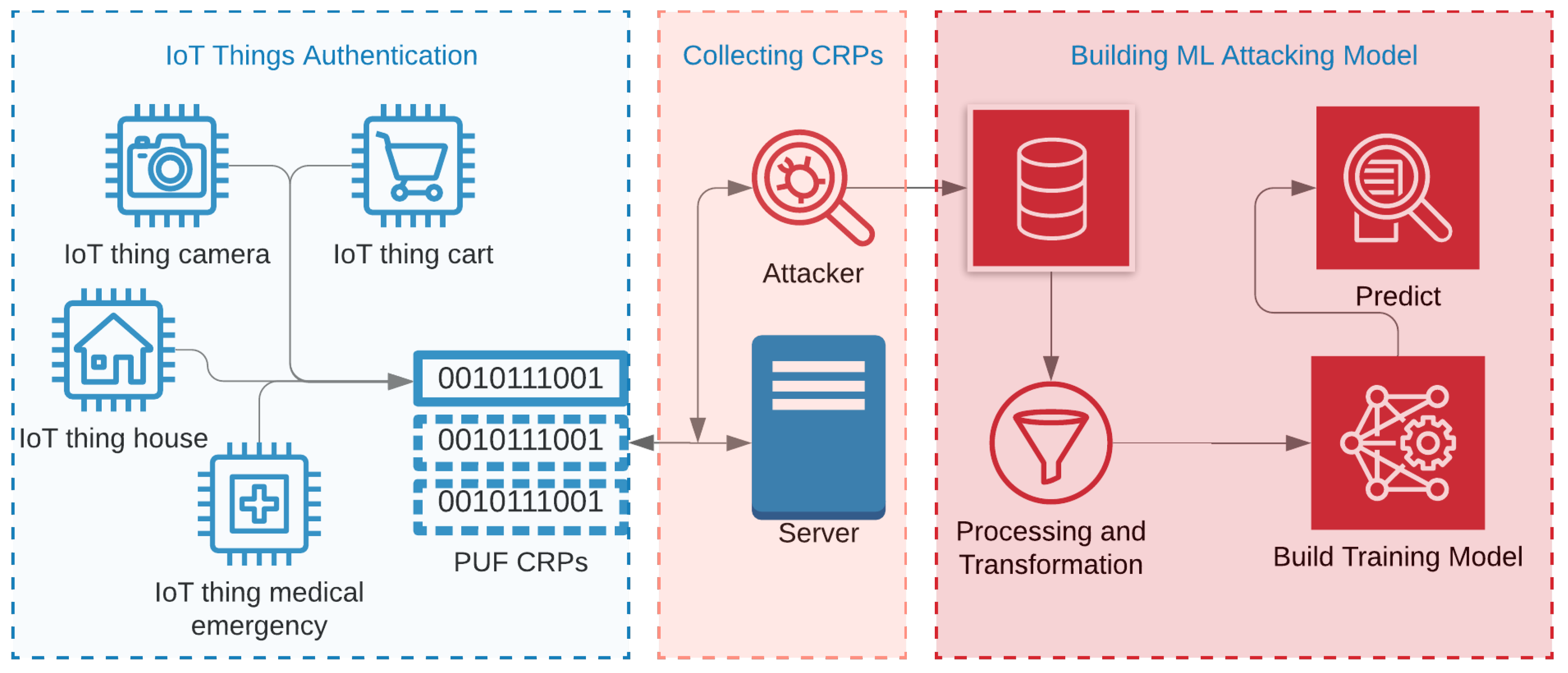
Figure 3 shows a high-level process of breaking the PUFs using ML attacks [2,11]. As shown in the figure, PUFs can be inducted in various IoT devices for authentication purposes. It can be embedded in carts, cameras, medical components, radio-frequency identifications chips, and credit cards. When IoTs communicate with their corresponding servers in order to process a PUF-based authentication, a meddling attacker can collect enough CRPs for malicious purposes. The collected CRPs can then be used as training data in order to build an ML attacking model. The number of CRPs needed by any attacking method depends on the PUFs’ complexity as well as the model being used. For example, the studies showed that APUFs can be broken, even with half the number of CRPs than what is needed for breaking the 3-XPUFs [25,26].
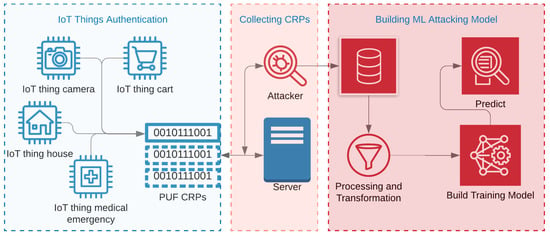
Figure 3.
A high-level process of attacking PUFs, which includes collecting Challenge-Response pairs (CRPs) from ongoing authentication between IoT applications and server, preprocessing the gathered CRPs, and building an attacking model.
Neural network methods, as studies [17,19,23,24,25,27] have shown, are more powerful for attacking PUFs in terms of the performance and training data size when compared with LR and SVM [15,20]. These studies motivated us to develop a deep neural network to attack the large XPUFs. Deep neural networks, networks with larger numbers of processing layers, are found to be particularly effective in complex classification problems [28]. However, choosing a good number of hidden layers and neurons in each hidden-layer is still challenging for many problems.
Coming up with a neural network with good predictive power requires a good understanding of the data of the object to be modeled. As discovered by Lim et al. in [13], an APUF is representable by a linear classification with the transformed challenge space being separated by a hyperplane, where the dimensionality of the challenge space is the same as the number of bits of the PUF, and a transformed challenge is obtained by applying reverse accumulative product transform [15] to a challenge.
An XPUF consists of multiple APUFs. For an n-XPUF, the relationship between the transformed challenge and its response can be modeled by a classification where the space of the transformed challenges is partitioned by n hyperplanes into multiple regions, with the response taking the value 0 on some regions, the value 1 on the other regions, and two neighboring regions (i.e., regions separated by a hyperplane) having different values for the response. Even though an XPUF defines a binary classification, but an n-XPUF with a large n could result in a large number of regions, possibly regions. Thus, an n-XPUF defines a highly oscillating function for large n. It is well known that highly oscillating functions are difficult to approximate, and it is likely that the multi-layer and multi-neuron neural networks are more suitable for n-XPUFs than LR, a method that is viewable as a single-layer single neuron neural network [23].
The MLP in [19] has three hidden layers for different XPUFs that range from four to eight streams with neurons in each hidden layer, where n is the number of component APUFs in an n-XPUF. On the other hand, Reference [17] used a different number of hidden layers for different XPUFs with components ranging from two to six. In [17], their MLP architecture for the 64-bit 6-XPUF has five hidden layers with 230 neurons in each hidden layer, which took about 20 min of training time for 64-bit 6-XPUFs, longer than the 7.4 min reported in [19].
The two most recent machine learning attack studies [17,19] used the Rectified Linear Unit (ReLU) [29] as the activation function for hidden layers. ReLU,
is popular for image learning applications, but it is unknown whether it is better than other activation functions, since there have not been adequate PUF attack studies using neural networks. We surmise that Hyperbolic tangent activation function (tanh),
is more suitable than ReLU for PUF attacks while using neural networks, and our thought behind our surmise is the following. An XPUF actually defines a binary-valued function on its challenge space, and an attack method is to approximate the function by identifying the separating hyperplanes that cut the challenge space into regions with neighboring regions having different values for the PUF response. It is easy to mathematically verify that a single neuron with the activation function tanh, with scaling and rotating of input variables, can highly accurately approximate the binary-valued function representing the linear classification problem that is by an APUF, while a single neuron with the ReLU activation function cannot accurately approximate linear binary classification problems. However, the composition of two shifted-and-rotated ReLU functions, which is a two-layer neural network with a single neuron for each layer, can approximate an APUF.
This observation on the modeling of APUFs by tanh or ReLU has led us to surmise that, for modeling an XPUF, which consists of multiple APUFs, neural networks with tanh as activation functions might need fewer layers than networks using ReLU as activation functions. Following this inference, we constructed a neural network using tanh as the activation function. We tried two and three layers, and we also tried a large combination of different numbers of neurons for different layers, and we finally found an architecture that is the best among those that we tried, and the neural network turned out to have significantly better performance than all of the neural networks used in earlier PUF attack studies. Additionally, as reported in [17], tanh may suffer from the gradient vanishing problem. But based on our experiments, the vanishing gradient problem is not an issue when training the XPUF using our model, since we used a network architecture with a small number of layers, see [30].
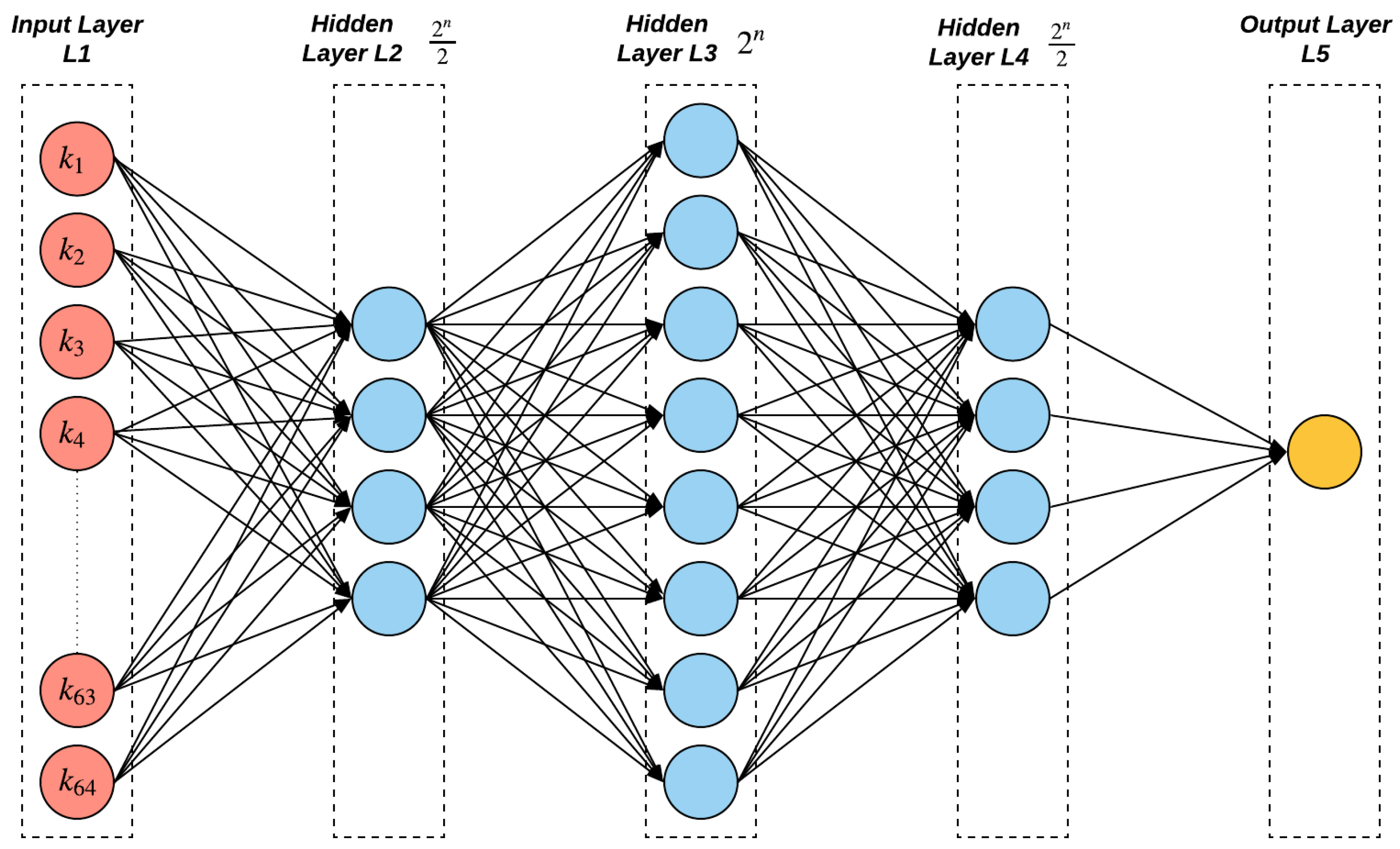
Our MLP comprised of three hidden layers, with () neurons for the first and last layers and () for the middle layer (see Figure 4 for illustration) for modeling the n-XPUFs where . However, for 9-XPUFs, we use the same neural network as for 8-XPUFs, since, otherwise, there would be a large number of neurons whose weights have to be learned and incur much longer training time than the current choice in our trials. Table 1 lists the details of the model parameters of the proposed method as compared to the prior methods in attacking the XPUFs.
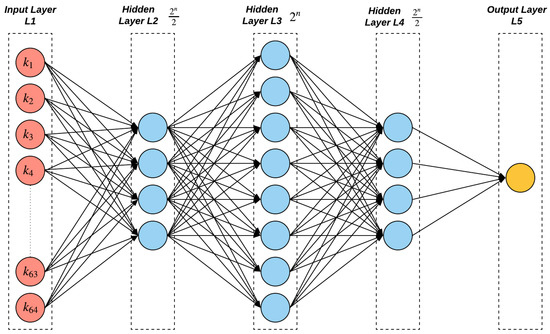
Figure 4.
A deep feed forward neural network architecture for 3-XOR 64-bit. Since n is equal 3, the first and third hidden layers consists of four neurons, while eight for the second hidden layer. The architecture changes based on the number of streams in an n-XPUF.

Table 1.
Parameters of machine learning attack methods.
4. Experimental Setup
4.1. Simulated CRPs
In our experiment, we used two ways to generate the CRPs. The first is a simulator that is based on the ADM, while the second is from PUFs that were implemented on silicon FPGAs. We developed our in-house simulator in C language which is fast for generating a large number of CRPs. The challenges in each simulation were randomly chosen from 0 to for 64-bit XPUFs. Subsequently, the gate delays were chosen following the Gaussian distribution with a mean of and a standard deviation of [15,19,24,27,31]. We generated 20 million CRPs of each simulated 64-bit XPUF instance, with the numbers of components ranging from 5 to 6, to 7, to 8, and 9, leading to a total of 100 million CRPs for the experimental study. For the convenience of the readers and the research community, we have made the dataset available (The silicon CRPs can be found at https://www.kaggle.com/khalidtmursi/attacking-xor-physical-unclonable-function-crps/, and it will be public by the time that this paper is published).
4.2. Silicon CRPs
To see how our attack method works on silicon CRPs, we programmed XPUFs on Artix®-7 FPGAs using the Xilinx Vivado design suite. VHSIC Hardware Description Language (VHDL) was utilized to build XPUFs designs. Each XPUF was placed vertically on the chip while using Tool Command Language (TCL). For example, the first component APUF of the 9-XPUF placement starts from SLICE_X0_Y149 down to SLICE_X0_Y86 for the top MUXes and SLICE_X1_Y149 down to SLICE_X1_Y86 for the bottom MUXes. Subsequently, we increase X location by one until the eighth stream. For the ninth stream, we start the placement from SLICE_X28_Y149, because there are no slices in the middle of Artix®-7 that can fit the vertical placement for the 9-XPUF. After placing the MUXs, each stream output meets at an arbiter, which takes place on SLICE_X[]_Y85 to its corresponding stream. Finally, the XOR gate is placed in the middle between the streams on row number Y84.
AXI Universal Asynchronous Receiver Transmitter (UART), with a baud rate of 230,400 bits/second, was used to speed-up the CRPs transformation between the Tera Term terminal and the FPGAs. As a result of using the UART with the mentioned speed, the estimated time of generating one million CRPs in our experiment is ten minutes. Finally, the Xilinx SDK was utilized in order to program the input/output workflow behavior of the CRPs generation from the chips. The experiments were done on three 28-nm test chips. We generated five million CRPs out of each chip and XPUF type, 90 million CRPs in total (five million × 6 XPUF designs × three devices), so we can have a variety of samples for the training and testing process. We do not need to generate 20 million CRPs from the chips as the ADM CRPs because applying the same five million challenges on different devices would provide different samples.
A PUF needs to be tested under different conditions, voltage, and temperature, in order to be able to choose a reliable set of challenges for practical use, as reported in [32,33]. However, our report in [25,34] shows that XPUFs generates reliable CRPs when tested on different ambient temperature and voltages, more than for correctness and steadiness. Thus, in this work, the silicon CRPs were generated at an ambient temperature of approximately 23 °C, and core voltage set to 1.0V using the built-in chips resistor. Even though the incurred noise during the generation process affects the model training, we were able to break the XPUFs on silicon CRPs with high accuracies when compared to those that were trained using the simulated CRPs, as shown in Section 5.
4.3. Attacking Model
Our attacking code was written using Python 3.7, and the ML library used for building the model was Keras [35] with Tensorflow [36] back-end (tf.keras). The experiments were carried out on a Mackbook Pro with 2.6 GHz 6-Core Intel Core i7 and a memory capacity of 16 GB. Each of the recorded results was calculated based on three different samples and five runs. Each attacking test uses 85% CRPs for training, 5% for validation, and 10% for testing. In order to evaluate the attacking model, we measured the testing CRPs’ prediction accuracy. For each set of PUF parameters (i.e., 64-bit 5-XOR PUF), three sets of CRPs and five runs for each CRPs’ set were carried out. For the simulated data, the three CRPs’ sets were generated by changing the input challenges in the simulator, and for the silicon CRPs, the three CRPs’ sets were generated from three different devices. Additionally, to assure fair training for different classes of XPUF responses, namely the class of 0’s and the class of 1’s, we checked the datasets’ entropies before starting the training. The uniformity [37,38] is a reasonable measure of data entropy that can be calculated while using the Hamming Weights of the dataset’s responses, as follows:
where r is the response bit that is produced when the input challenge is in the s-th CRP set or from the s-th chip, and S is the total number of CRPs in a file. The XPUFs that we used in our experiments, simulated or silicon, produce highly uniform responses, consistent with what was reported in [25]. We believe that it is essential to report our datasets’ entropy before showing the attacking results. Table 2 lists the entropy results. For the convenience of the readers and the research community, we have made the proposed attack model available (The source code can be found at https://github.com/kmursi/ML_Attack_XOR_PUF/, and it will be public by the time this paper is published).

Table 2.
Average uniformity of the training datasets samples. The ideal rate of the uniformity is 50%, where it indicates a 50% of 0’s and 1’s in a dataset.
5. Experimental Results and Discussion
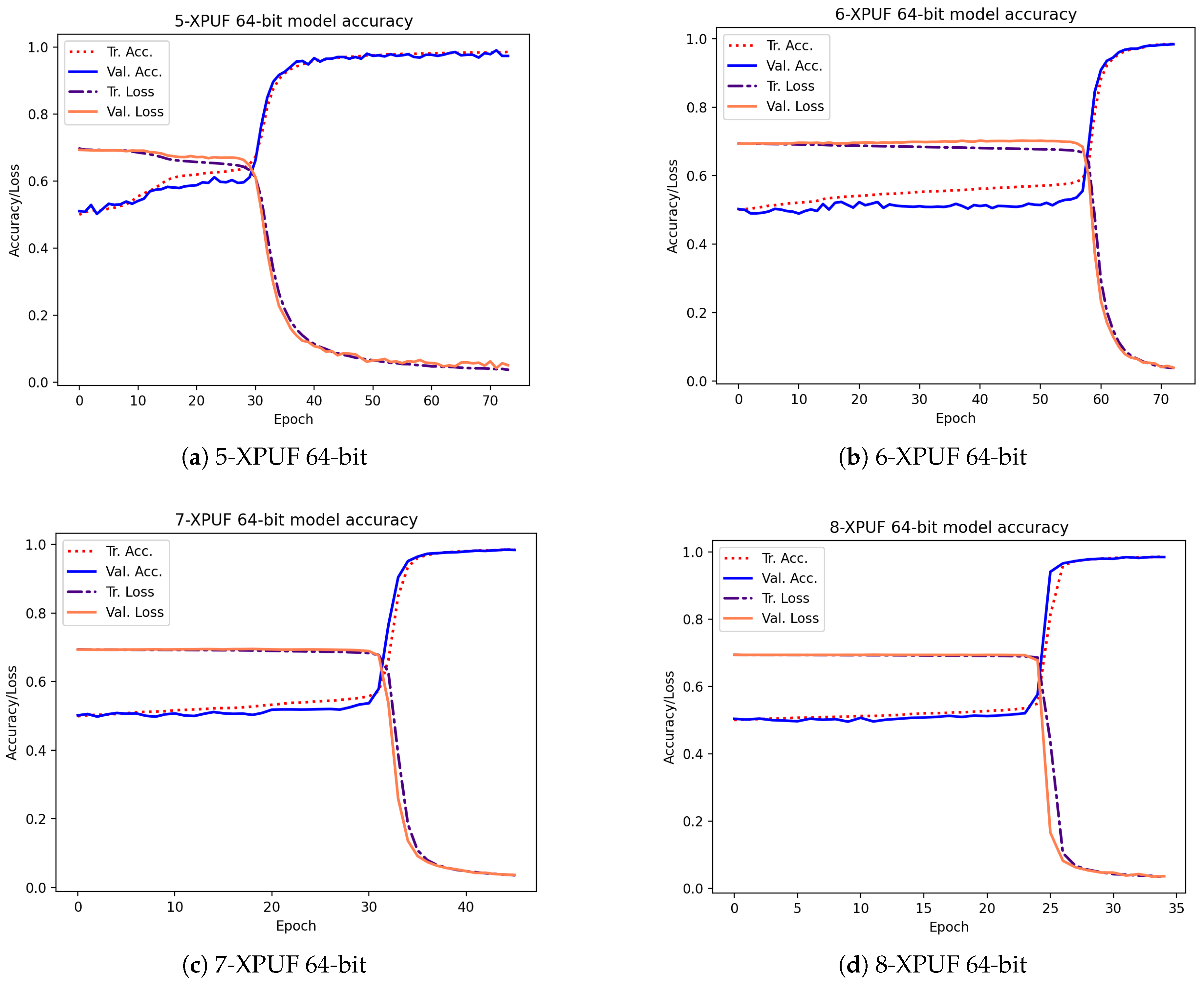
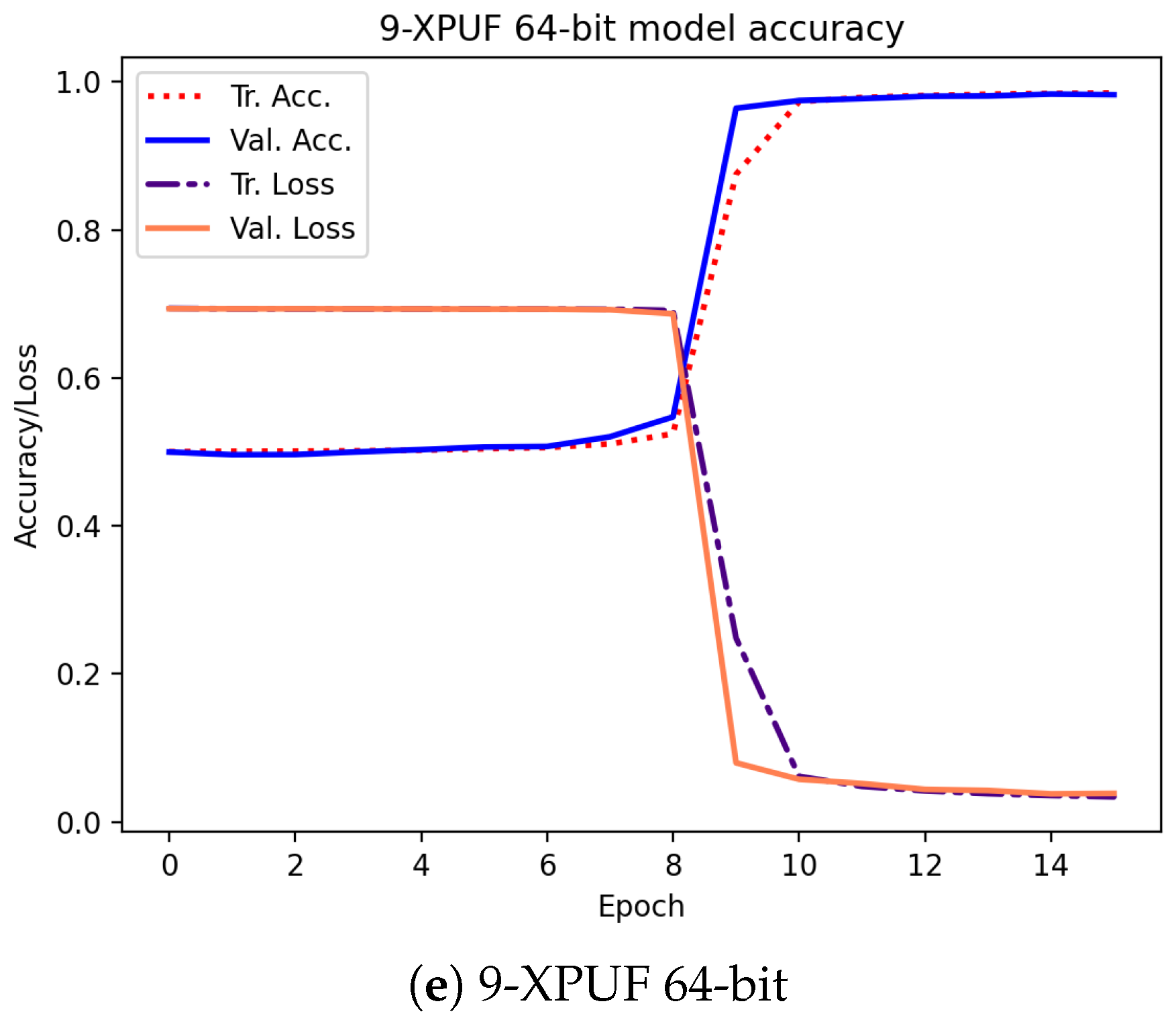
Table 3 shows the attacking results on simulated CRPs for our method (indicated by E) and the results from methods in other studies. The column Tr. CRPs in the table contains the number of CRPs used in training, and the column Tr. Time is the average training time for breaking an XPUF with PUF parameters being given in columns 1 and 2. The other methods we compared our method against include that of Tobisch & Becker [20] (indicated by A), Ruhrmair et al. [15] (indicated by B), Aseeri et al. [19] (indicated by C), and Santikellur et al. [17] (indicated by D). Please note that none of the prior research achieved a high attacking accuracy with a 100% success rate for 9-XPUF (Method A has a success rate of 25%, as shown by Table 2 shown in [20]). Among all the listed methods, Method B reported the smallest size of trained CRPs, but their training time was relatively large. Method A employs parallel computing with 16 cores, and the training times of Method A listed in Table 3 were multiplied by 16 of those in [20] in order to be consistent with the sequential training times by others. We were able to break the 5-XPUFs and 6-XPUFs with CRP sizes that were less than those needed by Methods A, C, and D while being close to those needed by Method B, but our method incurs much shorter training times. Method C was reported to be applied n-XPUF with n up to 8 and the maximum n for Methods B and D was 6. Accordingly, for large n, Method A and E were applied to 8-XPUFs and 9-XPUFs. Our method converges with 680K CRPs for 7-XPUFs, 1.7 million CRPS for 8-XPUFs, and a very low number of 4.2 million CRPs for 9-XPUFs as compared with that needed by Method A. Additionally, it is worth mentioning that, for each CRP set of 4.2 million we tested and for each of the 5 runs, our method successfully broke the 9-XPUF, a 100% success rate, while Method A has a 25% success rate with 250 million CRPs. We also plotted the average loss function values and average accuracies of training and validation in the training process in Figure 5. The losses and accuracies were plotted over the epochs for the XPUFs, with XOR size ranging from 5 to 9.

Table 3.
Prediction rate and timing of our attacking method and other methods using simulated CRPs.
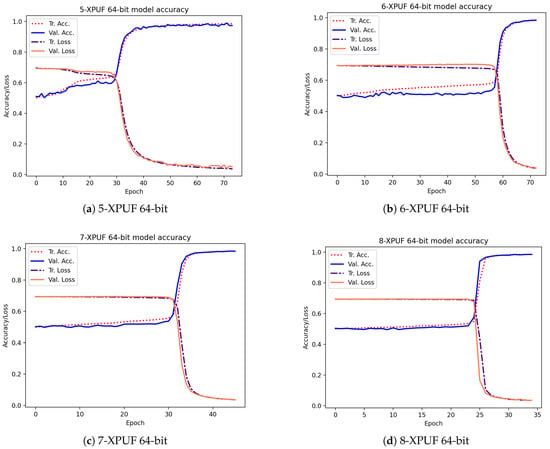
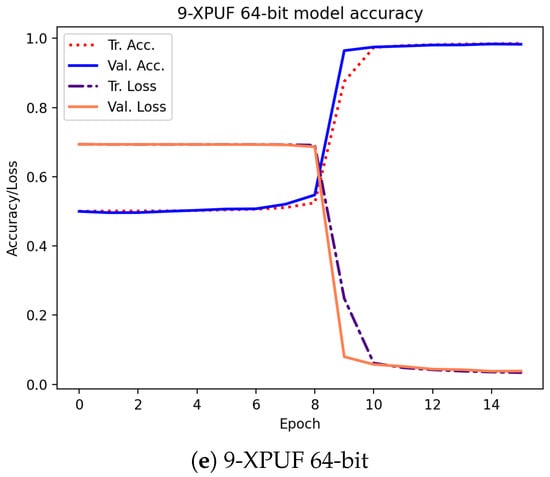
Figure 5.
Training and validation curves over epochs for our attacking model that was captured while attacking the XPUFs, with a different number of components ranging from 5 to 9.
In addition to simulated CRPs, we also applied our method to silicon CRPs, CRPs generated by PUFs implemented on FPGAs. Table 4 lists the results of attacking N-XPUFs with N ranging from five to nine using silicon CRPs. We added two more columns in this table than Table 3. The two additional columns are the training batch size and exit loss. Our experimental trials revealed that the training batch size has a considerable impact on training time and accuracy. We noticed that big batch sizes would boost the overall training, but negatively affect the validation accuracy. Consequently, we chose batch sizes to the way of guaranteeing the accuracy and overall performance with higher priority for the validation accuracy. Regarding the loss value for obtaining an accurate prediction, we found that the loss must be minimized to below 0.05 for training in order to achieve 98% testing accuracy. However, since the silicon data have noise, it was hard to reach a loss value of 0.05 when training FPGA’s data. Nevertheless, we will show in the future works as we succeed, our current research on how to overcome the hardware noise to get better training.

Table 4.
Prediction rate and timing of our attacking method using 28-nm test chips CRPs.
6. Conclusions
In this paper, we have presented a neural network-based method for attacking the XPUFs. When compared to the attack methods reported earlier, our method achieves similar or higher prediction accuracy with fewer CRPs and shorter training times. In particular, the proposed method was able to break the 64-bit 9-XPUFs using around four million CRPs within only 10 min of training time, and with a 100% success rate. This shows that our method is significantly faster and uses much fewer CRPs than the existing attack method for 9-XPUFs. We tested the method using the simulated CRPs as well as silicon CRPs generated from the PUF circuits on Artix®-7 FPGAs, and the test results from these two types of CRPs show the high efficiency of the training while attaining high prediction accuracy, proving itself to be a powerful tool for examining the security vulnerability of XPUFs against ML attacks. On the other side, the proposed attack method has also revealed that 64-bit 9-XPUFs are not secure enough, calling for longer XPUFs with larger XOR gates for higher security. However, it is known that larger XPUFs will lead to lower reliability and, hence, new security enhancement designs for maintaining good reliability are sorely needed.
Author Contributions
Methodology, K.T.M. and Y.Z.; software-attacking model programming, K.T.M.; software-CRPs generator programming, Y.Z., B.T., and K.T.M.; validation, Y.Z.; Hardware-generating silicon CRPs, K.T.M.; Writing—original draft preparation, K.T.M. Writing—review and editing, K.T.M., Y.Z., B.T., A.O.A., M.S.A. All authors have read and agreed to the published version of the manuscript.
Funding
The research was supported in part by the National Science Foundation under Grant No. CNS-1526055, and by the Deputyship for Research & Innovation, Ministry of Education in Saudi Arabia through the project number 383.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| PUF | Physical Unclonable Function |
| CRP | Challenge-Response-Pair |
| XPUF | XOR Arbiter PUFs |
| SVM | Support Vector Machine |
| ML | Machine Learning |
| IoT | Internet of Thing |
| ADM | Additive Delay Model |
| APUF | Arbiter PUF |
| MUX | Multiplexer |
| MLP | Multi-Layered Perceptron |
| DL | Deep Learning |
| ReLU | Rectified Linear Unit |
| tanh | tangent activation function |
| VHDL | VHSIC Hardware Description Language |
References
- van der Meulen, R. Gartner Says 8.4 Billion Connected “Things” Will Be in Use in 2017, up 31 Percent from 2016 Gartner, Newsroom; Press Releases: Brussels, Belgium, 2017. [Google Scholar]
- Yu, M.D.; Hiller, M.; Delvaux, J.; Sowell, R.; Devadas, S.; Verbauwhede, I. A lockdown technique to prevent machine learning on PUFs for lightweight authentication. IEEE Trans. Multi-Scale Comput. Syst. 2016, 2, 146–159. [Google Scholar] [CrossRef]
- Gruss, D.; Maurice, C.; Wagner, K.; Mangard, S. Flush+ Flush: A fast and stealthy cache attack. In International Conference on Detection of Intrusions and Malware, and Vulnerability Assessment; Springer: Berlin/Heidelberg, Germany, 2016; pp. 279–299. [Google Scholar]
- Kömmerling, O.; Kuhn, M.G. Design Principles for Tamper-Resistant Smartcard Processors. Smartcard 1999, 99, 9–20. [Google Scholar]
- Osvik, D.A.; Shamir, A.; Tromer, E. Cache attacks and countermeasures: The case of AES. In Cryptographers’ Track at the RSA Conference; Springer: Berlin/Heidelberg, Germany, 2006; pp. 1–20. [Google Scholar]
- Rührmair, U.; Holcomb, D.E. PUFs at a glance. In Proceedings of the Conference on Design, Automation & Test in Europe, European Design and Automation Association, Grenoble, France, 28 March 2014; p. 347. [Google Scholar]
- Skorobogatov, S.P. Semi-Invasive Attacks: A New Approach to Hardware Security Analysis; Technical Report; Computer Laboratory, University of Cambridge: Cambridge, UK, 2005. [Google Scholar]
- Gassend, B.; Clarke, D.; Van Dijk, M.; Devadas, S. Silicon physical random functions. In Proceedings of the 9th ACM Conference on Computer and Communications Security. ACM, Washington, DC, USA, 18–22 November 2002; pp. 148–160. [Google Scholar]
- Yarom, Y.; Falkner, K. FLUSH+ RELOAD: A high resolution, low noise, L3 cache side-channel attack. In Proceedings of the 23rd {USENIX} Security Symposium ({USENIX} Security 14), San Diego, CA, USA, 20–22 August 2014; pp. 719–732. [Google Scholar]
- Gassend, B.; Clarke, D.; Van Dijk, M.; Devadas, S. Controlled physical random functions. In Proceedings of the 18th IEEE Annual Computer Security Applications Conference, Las Vegas, NV, USA, 9–13 December 2002; pp. 149–160. [Google Scholar]
- Suh, G.E.; Devadas, S. Physical unclonable functions for device authentication and secret key generation. In Proceedings of the 44th ACM/IEEE Design Automation Conference 2007 (DAC’07), San Diego, CA, USA, 4–8 June 2007; pp. 9–14. [Google Scholar]
- Majzoobi, M.; Rostami, M.; Koushanfar, F.; Wallach, D.S.; Devadas, S. Slender PUF protocol: A lightweight, robust, and secure authentication by substring matching. In Proceedings of the 2012 IEEE Symposium on Security and Privacy Workshops, San Francisco, CA, USA, 24–25 May 2012; pp. 33–44. [Google Scholar]
- Lim, D.; Lee, J.W.; Gassend, B.; Suh, G.E.; Van Dijk, M.; Devadas, S. Extracting secret keys from integrated circuits. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2005, 13, 1200–1205. [Google Scholar]
- Majzoobi, M.; Koushanfar, F.; Potkonjak, M. Testing techniques for hardware security. In Proceedings of the 2008 IEEE International Test Conference, Santa Clara, CA, USA, 28–30 October 2008; pp. 1–10. [Google Scholar]
- Rührmair, U.; Sehnke, F.; Sölter, J.; Dror, G.; Devadas, S.; Schmidhuber, J. Modeling attacks on physical unclonable functions. In Proceedings of the 17th ACM Conference on Computer and Communications Security, Chicago, IL, USA, 4–8 October 2010; pp. 237–249. [Google Scholar]
- Majzoobi, M.; Koushanfar, F.; Potkonjak, M. Lightweight secure pufs. In Proceedings of the 2008 IEEE/ACM International Conference on Computer-Aided Design, San Jose, CA, USA, 10–13 November 2008; pp. 670–673. [Google Scholar]
- Santikellur, P.; Bhattacharyay, A.; Chakraborty, R.S. Deep Learning Based Model Building Attacks on Arbiter PUF Compositions. Technical Report, Cryptology ePrint Archive, Report 2019/566. 2019. Available online: https://eprint.iacr.org/2019/566.pdf (accessed on 2 February 2020).
- Nguyen, P.H.; Sahoo, D.P.; Jin, C.; Mahmood, K.; Rührmair, U.; van Dijk, M. The interpose puf: Secure puf design against state-of-the-art machine learning attacks. Iacr Trans. Cryptogr. Hardw. Embed. Syst. 2019, 243–290. [Google Scholar] [CrossRef]
- Aseeri, A.O.; Zhuang, Y.; Alkatheiri, M.S. A Machine Learning-based Security Vulnerability Study on XOR PUFs for Resource-Constraint Internet of Things. In Proceedings of the IEEE International Congress on Internet of Things (ICIOT 2018), San Francisco, CA, USA, 2–7 July 2018. [Google Scholar]
- Tobisch, J.; Becker, G.T. On the scaling of machine learning attacks on PUFs with application to noise bifurcation. In International Workshop on Radio Frequency Identification: Security and Privacy Issues; Springer: Berlin/Heidelberg, Germany, 2015; pp. 17–31. [Google Scholar]
- Zhou, C.; Parhi, K.K.; Kim, C.H. Secure and reliable XOR arbiter PUF design: An experimental study based on 1 trillion challenge response pair measurements. In Proceedings of the 54th Annual Design Automation Conference 2017, Austin, TX, USA, 18–22 June 2017; p. 10. [Google Scholar]
- Herder, C.; Yu, M.D.; Koushanfar, F.; Devadas, S. Physical unclonable functions and applications: A tutorial. Proc. IEEE 2014, 102, 1126–1141. [Google Scholar] [CrossRef]
- Hospodar, G.; Maes, R.; Verbauwhede, I. Machine Learning Attacks on 65nm Arbiter Pufs: Accurate Modeling Poses Strict Bounds on Usability; WIFS: Halifax, NS, Canada, 2012; pp. 37–42.
- Alkatheiri, M.S.; Zhuang, Y. Towards fast and accurate machine learning attacks of feed-forward arbiter PUFs. In Proceedings of the 2017 IEEE Conference on Dependable and Secure Computing, Taipei, Taiwan, 7–10 August 2017; pp. 181–187. [Google Scholar]
- Mursi, K.T.; Zhuang, Y.; Alkatheiri, M.S.; Aseeri, A.O. Extensive Examination of XOR Arbiter PUFs as Security Primitives for Resource-Constrained IoT Devices. In Proceedings of the 2019 17th IEEE International Conference on Privacy, Security and Trust (PST), Fredericton, NB, Canada, 26–28 August 2019; pp. 1–9. [Google Scholar]
- Zhang, J.; Wan, L.; Wu, Q.; Qu, G. DMOS-PUF: Dynamic multi-key-selection obfuscation for strong PUFs against machine learning attacks. arXiv 2018, arXiv:1806.02011. [Google Scholar]
- Alamro, M.A.; Zhuang, Y.; Aseeri, A.O.; Alkatheiri, M.S. Examination of Double Arbiter PUFs on Security against Machine Learning Attacks. In Proceedings of the 2019 IEEE International Conference on Big Data (Big Data), Los Angeles, CA, USA, 9–12 December 2019; pp. 3165–3171. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Alamro, M.A.; Mursi, K.T.; Zhuang, Y.; Aseeri, A.O.; Alkatheiri, M.S. Robustness and Unpredictability for Double Arbiter PUFs on Silicon Data: Performance Evaluation and Modeling Accuracy. Electronics 2020, 9, 870. [Google Scholar] [CrossRef]
- Zhang, J.L.; Wu, Q.; Ding, Y.P.; Lv, Y.Q.; Zhou, Q.; Xia, Z.H.; Sun, X.M.; Wang, X.W. Techniques for design and implementation of an FPGA-specific physical unclonable function. J. Comput. Sci. Technol. 2016, 31, 124–136. [Google Scholar] [CrossRef]
- Alkatheiri, M.S.; Zhuang, Y.; Korobkov, M.; Sangi, A.R. An experimental study of the state-of-the-art PUFs implemented on FPGAs. In Proceedings of the 2017 IEEE Conference on Dependable and Secure Computing, Taipei, Taiwan, 7 August 2017; pp. 174–180. [Google Scholar]
- Mursi, K.T.; Zhuang, Y. Experimental Study of Component-Differentially-Challenged XOR PUFs as Security Primitives for Internet-of-Things. J. Commun. 2020, 714–721. [Google Scholar]
- Chollet, F. Keras. Available online: https://github.com/fchollet/keras (accessed on 22 September 2020).
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems. 2015. Available online: https://www.tensorflow.org/ (accessed on 18 February 2020).
- Maiti, A.; Casarona, J.; McHale, L.; Schaumont, P. A large scale characterization of RO-PUF. In Proceedings of the 2010 IEEE International Symposium on Hardware-Oriented Security and Trust (HOST), Anaheim, CA, USA, 13–14 June 2010; pp. 94–99. [Google Scholar]
- Maiti, A.; Gunreddy, V.; Schaumont, P. A systematic method to evaluate and compare the performance of physical unclonable functions. In Embedded Systems Design with FPGAs; Springer: Berlin/Heidelberg, Germany, 2013; pp. 245–267. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).