Abstract
This paper proposes an energy-efficient cluster head selection method in the wireless ad hoc network by using a hybrid quantum-classical approach. The wireless ad hoc network is divided into several clusters via cluster head selection, and the performance of the network topology depends on the distribution of these clusters. For an energy-efficient network topology, none of the selected cluster heads should be neighbors. In addition, all the selected cluster heads should have high energy-consumption efficiency. Accordingly, an energy-efficient cluster head selection policy can be defined as a maximum weight independent set (MWIS) formulation. The cluster head selection policy formulated with MWIS is solved by using the quantum approximate optimization algorithm (QAOA), which is a hybrid quantum-classical algorithm. The accuracy of the proposed energy-efficient cluster head selection via QAOA is verified via simulations.
1. Introduction
The present era is a turbulent period of technological advancement towards the noisy intermediate-scale quantum (NISQ) era and the 6G era [1,2]. With the development of NISQ devices, various fields, such as quantum communication, quantum machine learning, and quantum optimization, are evolving as components of 6G. In the field of quantum optimization, in particular, various studies have been conducted, based on technologies such as quantum adiabatic algorithm (QAA), variational quantum eigensolver (VQE), and quantum approximate optimization algorithm (QAOA) [3,4,5]. Among them, the QAOA, a special case of bounded-error quantum polynomial time (BQP) algorithm, can be applied to various fields because of its simple structure [6,7]. The structure of QAOA is divided into a parameterized quantum circuit part and a classical optimization part that determines the optimal parameters. Heuristic methods are mainly used in the classical optimization part, and control of hyperparameters is necessary to find the optimal parameter. Therefore, QAOA does not always guarantee quantum supremacy; however, it has the flexibility to adapt to variations of the target problem [8,9]. The main target problem of QAOA research is the maximum cut problem, and various studies have been conducted to empirically optimize this problem [10,11,12,13,14,15]. In addition, QAOA application studies have also been actively conducted [16,17]. Along with these various research attempts, QAOA is expected to be useful as a quantum heuristic optimizer in the near future.
The wireless ad hoc network is an important research topic, even in the 6G era, because of its relevance to the internet of things (IoT) and autonomous driving [18,19,20,21,22]. In a wireless ad hoc network using limited resources, it is advantageous to construct a hierarchical network topology through clustering [23]. In the hierarchical network topology, the cluster heads are located at the centers of the clusters and play pivotal roles in communication between nodes. Therefore, considering both communication quality and network lifetime, the cluster heads are preferably nodes with high energy-consumption efficiency. In various types of real-world wireless ad hoc networks, energy-consumption considerations are essential.
Although energy-efficient clustering is an old problem, various researches are still being actively conducted due to its importance. Various clustering methods have been proposed, and clustering mechanisms based especially on game theory are very practical and efficient [24,25]. However, more simple and flexible clustering methods should be required in wireless ad hoc networks. Thus, this paper proposes an energy-efficient cluster head selection method via QAOA, which has a more intuitive and flexible structure than these existing methods. First, the weight of the node is assigned according to the energy-consumption efficiency of each node constituting the network. The cluster head selection policy is modeled using the maximum weight independent set (MWIS) formulation, as MWIS-based clustering has various advantages over minimum ID clustering and maximum degree clustering and is preferable in terms of energy efficiency [26]. The policy modeled as an MWIS formulation is mapped to the problem Hamiltonian via Boolean functions. The QAOA circuit is designed based on the problem Hamiltonian. The optimal parameter of the designed QAOA circuit is determined using the stochastic gradient descent method. By obtaining the expectation value of the problem Hamiltonian in the optimal parameterized state, an approximate solution of the policy modeled by the MWIS formulation is obtained. The cluster heads are selected based on the approximate solution.
This MWIS-based clustering via QAOA has several characteristics compared to related works such as game theory-based clustering. In terms of purpose, the game theory-based clustering proposed by Soorki et al. [24] focuses on both reduction of the system-fail ratio and energy-consumption by considering energy-consumption and queue length of access requests as the payoffs. However, MWIS-based clustering via QAOA focuses only primarily on energy-consumption efficiency. Thus, game theory-based clustering prefers the completely separated clusters (nonoverlapping clusters), but the MWIS-based clustering via QAOA does not. Structurally, game theory-based clustering does not need to search all partitions or send information to a centralized controller about the changes. On the other hand, MWIS-based clustering via QAOA is better to search all partitions and to send information about the changes to a centralized controller or an arbitrary node. This is because the rapid quantum computations in one quantum circuit can update the information of all nodes simultaneously by the principles of superposition and entanglement.
The remainder of this paper is organized as follows. Section 2 describes the QAOA and MWIS as background materials. Section 3 describes the details of energy-efficient cluster head selection via QAOA. In particular, Section 3.3 describes the intuitive design method of the problem Hamiltonian and the implementation of the QAOA circuit. Section 4 presents the simulation and analyzes the results of for the 3-regular weighted and 5-regular weighted graphs. Section 5 concludes the paper.
2. Background
For many decades, quantum computing researchers have aimed to find quantum algorithms that can surpass classical algorithms. Various attempts have been made, and a few quantum algorithms with quantum supremacy over classical algorithms in certain cases have been identified [5,27,28]. In the NISQ era, the discovery of potential quantum algorithms has been accelerated because of the evolved quantum processors and interactions with machine learning techniques [1]. In particular, QAOA is one of the lightest and most flexible hybrid quantum-classical optimization algorithms in the NISQ era and is suitable for application to various graph-based systems [5,29]. QAOA can control the resource (quantum operations and times) usage-performance trade-off by adjusting the circuit depth, so it can be used in various environments. If the proper quantum hardware is supported, QAOA is also suitable in sensor networks or embedded systems with limited resources and capabilities. Therefore, before discussing a hybrid quantum-classical approach to energy-efficient cluster head selection in limited systems, this section describes the QAOA and a graph-based MWIS formulation.
2.1. Quantum Approximate Optimization Algorithm (QAOA)
QAOA is a hybrid quantum-classical optimization algorithm that uses a parameterized quantum circuit composed of unitary operators [5,30,31]. In addition, the QAOA is a type of quantum heuristic algorithm which is known to perform well in some combinatorial optimization problems.
The first step in QAOA is to map the objective function of the problem consisting of binary bit strings to the Hamiltonian , as follows:
where is a problem Hamiltonian. The problem Hamiltonian can be divided into the objective Hamiltonian and constraint Hamiltonian , as follows:
where is a constant coefficient. The Hamiltonians and represent the objective and constraint, respectively, of the problem.
The mixing Hamiltonian , a transverse-field Hamiltonian, is defined as follows:
where is a Pauli-X operator applied on the jth qubit. The Pauli-X operator acts similar to the classical NOT operator, that is, it acts as a bit-flip.
To construct a quantum circuit, and are converted into unitary operators, as follows:
where and are parameters and where and are usually called the problem operator and mixing operator, respectively. In the QAOA circuit, the initial state can be a uniform superposition state, as follows:
where . If the depth of a quantum circuit is defined as , the parameters are represented as follows:
Therefore, the parameterized state , which is generated in a quantum circuit, is as follows:
The expectation value of for the solution samples obtained via repeated measurements on is as follows:
The optimal parameters and can be obtained from the classical optimization loop; therefore, the optimal solution can be computed from (9) via and .
A schematic of the QAOA is shown in Figure 1. The green part represents the classical optimization loop, for example, the stochastic gradient descent (SGD). Indeed, the optimization of parameters in the classical optimization loop part has a significant impact on the performance of the QAOA. The p value also has a significant impact on the performance of QAOA, and the proper p value is different depending on the problem. When the p value increases, the number of unitary operators increases and, thus, the number of quantum gates in the circuit increases. In other words, the accuracy of the computation can be increased but the gate noise increases as well. Therefore, in QAOA, proper design of the problem Hamiltonian, proper optimization of parameters, and proper setting of the p value are all important.
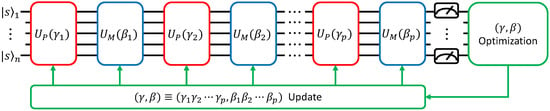
Figure 1.
Quantum approximate optimization algorithm (QAOA) circuit with the classical optimization loop part.
2.2. Maximum Weight Independent Set (MWIS)
Let us consider a weighted graph with nodes and edges. Assume that the weight is at node , where . The independent set can be constructed by selecting only nonadjacent nodes. Among the possible independent sets, the MWIS has the largest sum of weights.
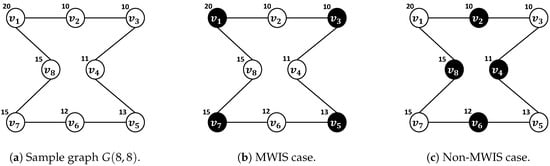
Figure 2.
Examples of the maximum weight independent set (MWIS) and non-MWIS of sample graph .
The sums of the weights of each set are as follows:
There is no independent set having a sum of weights greater than 58; thus, is MWIS. Expanding from the example, the generalized formulation of the MWIS is as follows:
The MWIS formulation has been applied to various research fields, such as communication, machine learning, and computer vision [32,33,34,35,36]. Although the MWIS is non-deterministic polynomial-time (NP) hard, which requires an approximate solution, it is useful for modeling complex and large-scale structures.
3. Energy-Efficient Cluster Head Selection
Clustering is an essential technique for organizing networks more efficiently. In particular, the communication between clusters in a wireless ad hoc network which has a distributed control structure is performed by the cluster heads [26]. Therefore, it is very important to set the cluster head selection policy according to the purpose of the wireless ad hoc network. This section describes the clustering method via cluster head selection for an energy-efficient wireless ad hoc network.
3.1. Clustering Wireless Ad Hoc Network
The wireless ad hoc network is a multi-hop system of self-organizing wireless nodes that can communicate with each other without additional infrastructure [37,38].
Let us consider a wireless ad hoc network, as shown in Figure 3. Figure 3a,b represents the flat ad hoc network topology before clustering and the hierarchical ad hoc network topology after clustering, respectively. The numbers on the nodes indicate the weight of each node. In real-world applications, the weight can be a numerical representation of the feature; for example, the efficiency of energy-consumption, level of security, or robustness [26]. In the graphs covered in this paper, the weight of each node represents the efficiency of energy-consumption. When transmitting the same data, less energy is used and more stable transmission is possible on a node that has high efficiency of energy-consumption. Therefore, it is good to use nodes that have high efficiency of energy-consumption in wireless ad hoc network communication.
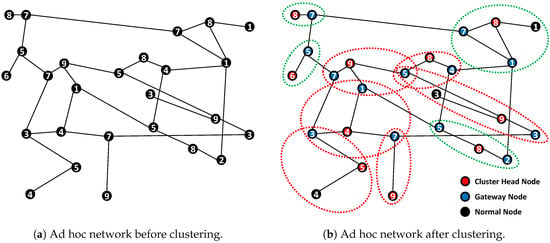
Figure 3.
Examples of wireless ad hoc network topology.
In the wireless ad hoc network, a hierarchical structure such as that shown in Figure 3b has more advantages than a nonhierarchical structure such as that in Figure 3a for limited resource utilization [23,37]. In the hierarchical structure, all nodes are classified into cluster head, gateway, and normal nodes. The general clustering process in which the roles of the nodes are determined as follows:
- (i)
- The cluster head nodes are determined sequentially according to the policy.
- (ii)
- The clusters are created by grouping the cluster head nodes and adjacent nodes.
- (iii)
- Except for the cluster head node in each cluster, the nodes required for communication with other clusters are determined as gateway nodes.
- (iv)
- The remaining nodes that are not required for communication with other clusters are determined as normal nodes.
Through this process, 10 clusters are identified in Figure 3b, marked with dotted lines. The completely separated clusters are marked with green dotted lines, and the others are marked with red dotted lines. The network topology can be completely changed according to the cluster head selection policy. In other words, the numbers and distributions of clusters depend on the cluster head selection policy. Therefore, the stability and performance of the network also depend on the cluster head selection.
3.2. Cluster Head Selection Policy using MWIS
As mentioned in Section 3.1, it is recommended to select nodes with high energy-consumption efficiency as cluster heads, for stable data transmission. In order to construct an energy-efficient network topology, the cluster heads should not be neighbors. Therefore, for an energy-efficient and stable network, the cluster head selection policy can be formulated with MWIS. The proposed cluster head selection policy is as follows:
Note that is a binary decision variable of the jth node, is the set of binary decision variables of all nodes in the network topology, is the energy-consumption efficiency of the jth node, and is the adjacency matrix.
The cluster head selection policy formulated with MWIS can be implemented using heuristic approaches, such as the greedy algorithm [39]. For example, the clusters in Figure 3b are the implementation results of the cluster head selection policy using MWIS. Clustering via the MWIS-based cluster head selection policy has several advantages over minimum ID clustering and maximum degree clustering [26]. One of the advantages of clustering via MWIS-based cluster head selection policy is that it produces fewer completely separated clusters. This can reduce the communication time and energy consumption when transmitting data between cluster heads.
3.3. Energy-Efficient Cluster Head Selection via QAOA
The cluster head selection policy proposed in Section 3.2 can be implemented via QAOA, a hybrid quantum-classical optimization algorithm, by proper Hamiltonian design [5,12]. In other words, the problem Hamiltonian, which represents the proposed policy, can be designed, and based on this, a QAOA circuit can be implemented. This approach with the QAOA circuit can have an advantage in speed over the classical MWIS-based clustering algorithm by rapid quantum computation by the principles of superposition and entanglement. In addition, the performance benefits can be also expected if advanced quantum hardware is supported in the future. Theoretically, QAOA increases the approximation quality corresponding to performance by increasing the circuit depth [5]. In the advanced quantum hardware that is free from the effects of gate noise, the circuit depth can be increased to a greater extent; thus, it can be possible to obtain a more accurate solution for the MWIS-formulated cluster head selection policy.
3.3.1. Hamiltonian Design
By (2), the problem Hamiltonian is designed by dividing into the objective Hamiltonian and constraint Hamiltonian. To match the optimization directions of the objective Hamiltonian and constraint Hamiltonian, both Hamiltonians are designed to be minimized rather than maximized. The mixing Hamiltonian is redefined with the symbols of (18).
The objective Hamiltonian. Suppose that there is a Boolean function, , as follows:
To obtain a Boolean Hamiltonian mapped from , the following equation can be constructed for a single qubit:
where I is the identity operator, is the Pauli-Z operator, and A and B are constant coefficients. For the same input, the expectation value of should be adjusted to the same value as the output of .
Therefore, the system of equations for obtaining the values of A and B, according to Table 1, is as follows:

Table 1.
Single-qubit mapping table to obtain mapped from .
The values of the constant coefficients A and B are obtained from (23) as and , respectively. Therefore, mapped from can be defined as follows, from (22):
According to (24), the objective function (18) of the energy-efficient cluster head selection policy is mapped to the following Hamiltonian :
where is the Pauli-Z operator applied on the jth node. Because should be maximized, the objective Hamiltonian that should be minimized is as follows:
The constraint Hamiltonian. According to the constraint (19), all cases between two nodes are shown in Figure 4. The black nodes represent the cluster heads, and in the energy-efficient cluster head selection policy, it is a prohibition condition that two cluster heads are directly connected via an edge. The constraint function that extends this prohibition condition to the entire network topology can be defined as follows:
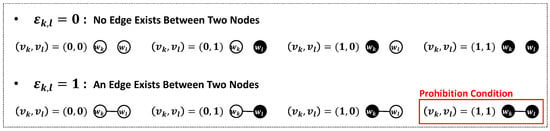
Figure 4.
Number of all possible cases between 2 nodes.
Note that ∧ represents a Boolean AND operator and that is a condition to avoid duplication of and , indicating the same edge.
The definition of a Boolean AND function is as follows:
To obtain a Boolean Hamiltonian mapped from , the following equation can be constructed:
where C, D, E, and F are constant coefficients and and are Pauli-Z operators applied on the first and second nodes, respectively.
According to Table 2, configured to obtain the Hamiltonian that has the same expectation value as the output of , the following system of equations can be constructed:

Table 2.
2-qubit mapping table to obtain mapped from .
The values of the constant coefficients C, D, E, and F are obtained from (30) as , , , and , respectively. Therefore, mapped from can be defined as follows, from (29):
According to (31), the constraint function (27) of the energy-efficient cluster head selection policy is mapped to the following Hamiltonian that should be minimized:
In (32), and are the Pauli-Z operators applied on the kth and lth nodes, respectively. By removing the constant term of (32), the simplified version of the constraint Hamiltonian that should be minimized is obtained as follows:
The problem Hamiltonian. From the definition of in (26) and in (33), the problem Hamiltonian that should be minimized is defined as follows:
Note that is a constant coefficient called the penalty rate. determines the proportion of compared to , which determines the optimal value of .
3.3.2. Circuit Implementation
From the problem Hamiltonian in (34), which defines the energy-efficient cluster head selection policy, and the mixing Hamiltonian in (35), which provides various states via bit-flip, the unitary operators for constructing the quantum circuit are defined as follows:
Note that , , , and are called the problem operator, objective operator, constraint operator, and mixing operator, respectively. In addition, and are the parameters of the QAOA circuit defined in (7). Note that the forms of Equations (37)–(39) are in consideration of the rotation-z (RZ) and rotation-x (RX) gates.
The RZ gate , representing a single-qubit rotation about the z-axis, and the RX gate , representing a single-qubit rotation about the x-axis, are defined as follows:
According to Equation (37), can be implemented using the RZ gates. Moreover, can be implemented as a combination of the RZ gates and controlled-not (CNOT) gates, according to Equation (38). Therefore, can be implemented with and , according to Equation (36). Subsequently, can be implemented using the RX gates by (39).
The proposed QAOA circuit for energy-efficient cluster head selection is shown in Figure 5. This circuit is an example applied to a simple network topology with 5 nodes and the following adjacency matrix .
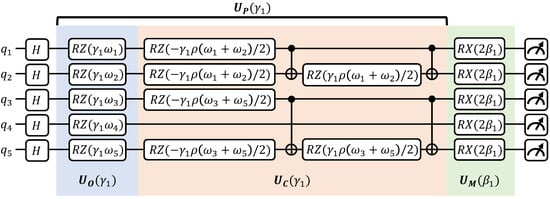
Figure 5.
Proposed circuit for MWIS with 5 qubits: The qubit corresponds to jth node. and are circuit parameters, and is the weight of jth node. Each qubit is initialized to the uniform superposition state via the Hadamard gate. The objective operator is implemented using the gates. The constraint operator is implemented as a combination of the gates, CNOT gates, and gates, where . In (42), only () and () are 1, so is implemented only between and and between and . The mixing operator is implemented using the gates. At the end of the circuit, measurements are performed.
Each node corresponds to each qubit, and the initial state is set to a uniform superposition state by the Hadamard gates. After passing the quantum gates that represent the unitary operators from the initial state, the measurement is performed on the created parameterized state. This sample circuit represents QAOA with depth ; the parameters of unitary operators are expressed as and . As p increases, the number of parameters increases, as in (7).
As shown in Figure 5, requires as many RZ gates as the number of nodes. requires as many RZ gates and CNOT gates as 3 times and 2 times the number of edges, respectively. requires as many RX gates as the number of nodes. The total number of RZ gates, CNOT gates, and RX gates required for the circuit, which has a circuit depth of p, is p times greater than that of the circuit.
4. Simulation Results
This section discusses the QAOA simulation results for the energy-efficient cluster head selection policy formulated using MWIS. The simulation is performed on the regular graphs that are suitable for wireless ad hoc networks. QAOA is one of the simple quantum algorithms that intuitively express the state with qubit rotation via the quantum gate [16,40]. This intuitive and simple process has something in common with the classical greedy algorithm. Therefore, the greedy algorithm, which is also useful for MWIS-based cluster head selection, is used as a comparison algorithm [26].
4.1. Simulation Method
A set of 10-node 3-regular weighted graphs and a set of 10-node 5-regular weighted graphs were randomly generated with 1000 instances each. The range of the node weight representing the energy-consumption efficiency was from 1 to 10. The optimal solution of each graph was found by the brute-force search so that the following approximation ratio could be computed for each graph [41].
where is the solution obtained via the approximation algorithm, is the optimal solution obtained via brute-force search, is the problem Hamiltonian in (34), and and are the parameters of the QAOA circuit. For each instance, the greedy algorithm and QAOA with depth were evaluated in terms of the obtained from 1000 measurements. The simulation was performed using TensorFlow Quantum, and the Adam optimizer was used to optimize the parameters of the QAOA circuit [42,43].
4.2. Simulation Analysis
The simulation aimed to find a valid circuit depth p for which the QAOA could outperform the greedy algorithm in MWIS-based clustering.
4.2.1. Simulation on 3-Regular Weighted Graphs
As shown in Figure 6a and Table A1, when focusing on the mean of on the 3-regular weighted graphs, it is observed that defeats the greedy algorithm when . Moreover, has a larger minimum of than the greedy algorithm, except for , , and . Based on the mean and minimum of , it is confirmed that outperforms the greedy algorithm at .
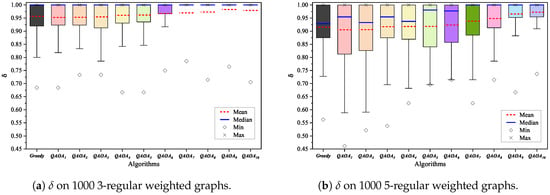
Figure 6.
Approximation ratio of each algorithm: the performance of MWIS-based clustering depends on the of each algorithm. As the circuit depth p increases, the mean of tends to increase.
In Figure 7a, most of shows a better distribution than that of the greedy algorithm expressed in dark gray. In particular, shows an overwhelming performance over the greedy algorithm at expressed in blue and dark blue, respectively. In Table A1, it can be numerically confirmed that the optimal solution ratio of is at , which outperforms of the greedy algorithm.
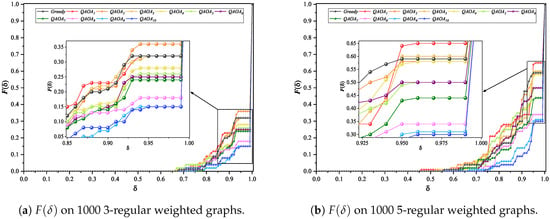
Figure 7.
Cumulative distribution function : the accuracy of MWIS-based clustering heavily depends on the ratio of . In general, the ratio of tends to increase as the circuit depth p increases.
4.2.2. Simulation on 5-Regular Weighted Graphs
As shown in Figure 6b and Table A2, when focusing on the mean of on the 5-regular weighted graphs, it is observed that defeats the greedy algorithm when . Moreover, has a larger minimum than the greedy algorithm, except for , , and . Based on the mean and minimum of , it is confirmed that outperforms the greedy algorithm at .
In Figure 7b, most of shows a better distribution than the greedy algorithm expressed in dark gray. Similar to the 3-regular graphs case, shows an overwhelming performance over the greedy algorithm at expressed in blue and dark blue, respectively. In Table A2, and show the optimal solution ratios of and , respectively. These are overwhelming accuracies when compared to that of the greedy algorithm with an optimal solution ratio of .
4.3. Summary and Further Discussion
On the 3-regular weighted graphs and 5-regular weighted graphs, performance analysis was performed for () and the greedy algorithm.
As p increases, the mean of tends to increase, the standard deviation of tends to decrease, and the optimal solution ratio tends to increase. In other words, it is experimentally proven that the MWIS-based clustering accuracy via increases as p increases. In particular, and show overwhelming accuracies over the greedy algorithm. However, it is not a good choice to increase p recklessly. Because each time p increases by 1, the number of parameters in the circuit increases by 2, increasing the time spent on parameter optimization and increasing the risk of falling into a local optimum. Therefore, finding the appropriate p, which depends on the graph type of the network, is the key to clustering via .
As a topic of further discussion, there is an interesting point about the measurement of . The best solution for each instance can be defined as the value closest to or the same as the optimal solution, from among the outputs of the measurements. Therefore, the minimum number of measurements required to obtain the best solution for each instance can be computed by dividing the number of total measurements by the number of best solutions. , which is the mean of the minimum number of measurements required to obtain the best solution for all instances at the circuit depth p, is as shown in Figure 8. On both 3-regular weighted and 5-regular weighted graphs, shows a tendency to decrease as p increases. Considering that the optimal solution ratio tends to increase as the circuit depth p increases, at large p, the possibility that the best solution and optimal solution are the same is high. Therefore, at large p, the optimal solution can be obtained even with a small number of measurements. This shows the potential for an efficient design of by reducing the number of measurements at large p.
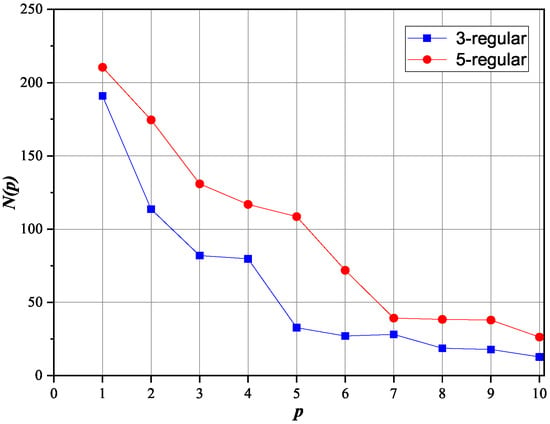
Figure 8.
is the mean of the minimum number of measurements required to obtain one best solution for all instances at the circuit depth p. tends to decrease as p increases.
5. Conclusions and Future Work
This paper proposed an energy-efficient clustering method with a hybrid quantum-classical approach. First, the cluster head selection policy was modeled via an MWIS formulation. Subsequently, the objective and constraint of the modeled policy were mapped to a designed objective Hamiltonian and constraint Hamiltonian, respectively. Based on the designed Hamiltonians, the circuit that implemented an energy-efficient cluster head selection policy was proposed. According to the simulation results, the proposed outperformed the greedy algorithm at on the 3-regular weighted graphs and on the 5-regular weighted graphs. In particular, and showed the highest performance. Finally, it was experimentally proven that the accuracy of the cluster head selection via tended to increase as p increased.
One of the future research directions will focus on improving the performance and efficiency by optimizing the gate configuration of the constraint operator part. A larger number of nodes with a large degree would lengthen the circuit of the constraint operator part. As a solution, a parallel gate configuration of the circuit was considered. By separating the set of nodes into subsets via graph preprocessing, the circuit of the constraint operator part could be divided into sub-circuits. Subsequently, a parallel gate configuration could be created in which the CNOT gates on the sub-circuits ran at the maximum simultaneously. This optimization of the gate configuration could certainly shorten the circuit. Therefore, one of our next works would be a concrete implementation of the parallel gate configuration.
Another future research direction will focus on data-intensive performance evaluation with various types of real quantum computers or better testbeds. Using a superconducting quantum computer, a photonic quantum computer, a trapped ion quantum computer, or a better testbed, various clustering algorithms will be compared with our MWIS-based clustering via QAOA. Considering the scalability, the experiment will be performed with more nodes. An analysis of the energy-consumption according to the number of gates and qubits for each type of quantum computer will also be performed to quantify the required energy. In other words, another of our next works would be to conduct more realistic performance evaluations for real-world implementation.
Author Contributions
J.C. was the main researcher who initiated and organized the research reported in the paper, and all authors including S.O. and J.K. were responsible for analyzing the simulation results and writing the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by NRF-Korea (2019M3E4A1080391 and 2019M3E3A1084054).
Acknowledgments
J. Kim is the corresponding author of this paper.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Details on Simulation Results
Here, there are supplementary data tables of the simulation results in Section 4.

Table A1.
Simulation data for the 3-regular weighted graphs.
Table A1.
Simulation data for the 3-regular weighted graphs.
| Algorithm | Standard Deviation of | Mean of | Median of | Minimum of | Maximum of | Ratio of |
|---|---|---|---|---|---|---|
| Greedy | 0.071 | 0.957 | 1.000 | 0.684 | 1.000 | 0.680 |
| 0.078 | 0.952 | 1.000 | 0.684 | 1.000 | 0.681 | |
| 0.073 | 0.953 | 1.000 | 0.733 | 1.000 | 0.640 | |
| 0.074 | 0.955 | 1.000 | 0.733 | 1.000 | 0.680 | |
| 0.074 | 0.961 | 1.000 | 0.667 | 1.000 | 0.720 | |
| 0.077 | 0.962 | 1.000 | 0.667 | 1.000 | 0.741 | |
| 0.063 | 0.967 | 1.000 | 0.750 | 1.000 | 0.750 | |
| 0.059 | 0.970 | 1.000 | 0.786 | 1.000 | 0.761 | |
| 0.062 | 0.973 | 1.000 | 0.714 | 1.000 | 0.820 | |
| 0.045 | 0.983 | 1.000 | 0.765 | 1.000 | 0.850 | |
| 0.057 | 0.979 | 1.000 | 0.706 | 1.000 | 0.850 |

Table A2.
Simulation data for the 5-regular weighted graphs.
Table A2.
Simulation data for the 5-regular weighted graphs.
| Algorithm | Standard Deviation of | Mean of | Median of | Minimum of | Maximum of | Ratio of |
|---|---|---|---|---|---|---|
| Greedy | 0.097 | 0.915 | 0.929 | 0.563 | 1.000 | 0.410 |
| 0.112 | 0.905 | 0.955 | 0.462 | 1.000 | 0.351 | |
| 0.111 | 0.906 | 0.933 | 0.522 | 1.000 | 0.419 | |
| 0.105 | 0.917 | 0.955 | 0.538 | 1.000 | 0.400 | |
| 0.097 | 0.918 | 0.938 | 0.625 | 1.000 | 0.422 | |
| 0.100 | 0.918 | 0.981 | 0.696 | 1.000 | 0.500 | |
| 0.092 | 0.924 | 0.977 | 0.714 | 1.000 | 0.499 | |
| 0.091 | 0.938 | 1.000 | 0.625 | 1.000 | 0.561 | |
| 0.083 | 0.948 | 1.000 | 0.714 | 1.000 | 0.659 | |
| 0.065 | 0.966 | 1.000 | 0.667 | 1.000 | 0.690 | |
| 0.054 | 0.973 | 1.000 | 0.737 | 1.000 | 0.699 |
References
- Preskill, J. Quantum Computing in the NISQ Era and Beyond. Quantum 2018, 2, 79. [Google Scholar]
- Viswanathan, H.; Mogensen, P.E. Communications in the 6G Era. IEEE Access 2020, 8, 57063–57074. [Google Scholar] [CrossRef]
- Farhi, E.; Goldstone, J.; Gutmann, S.; Lapan, J.; Lundgren, A.; Preda, D. A Quantum Adiabatic Evolution Algorithm Applied to Random Instances of an NP-Complete Problem. Science 2001, 292, 472–475. [Google Scholar] [CrossRef] [PubMed]
- Kandala, A.; Mezzacapo, A.; Temme, K.; Takita, M.; Brink, M.; Chow, J.M.; Gambetta, J.M. Hardware-Efficient Variational Quantum Eigensolver for Small Molecules and Quantum Magnets. Nature 2017, 549, 242–246. [Google Scholar] [PubMed]
- Farhi, E.; Goldstone, J.; Gutmann, S. A Quantum Approximate Optimization Algorithm. arXiv 2014, arXiv:1411.4028. [Google Scholar]
- Jordan, S.P.; Krovi, H.; Lee, K.S.; Preskill, J. BQP-Completeness of Scattering in Scalar Quantum Field Theory. Quantum 2018, 2, 44. [Google Scholar] [CrossRef]
- Farhi, E.; Harrow, A.W. Quantum Supremacy through the Quantum Approximate Optimization Algorithm. arXiv 2016, arXiv:1602.07674. [Google Scholar]
- Harrow, A.W.; Montanaro, A. Quantum Computational Supremacy. Nature 2017, 549, 203–209. [Google Scholar] [CrossRef]
- Arute, F.; Arya, K.; Babbush, R.; Bacon, D.; Bardin, J.C.; Barends, R.; Biswas, R.; Boixo, S.; Brandao, F.G.; Buell, D.A.; et al. Quantum Supremacy using a Programmable Superconducting Processor. Nature 2019, 574, 505–510. [Google Scholar] [CrossRef]
- Wang, Z.; Hadfield, S.; Jiang, Z.; Rieffel, E.G. Quantum Approximate Optimization Algorithm for MaxCut: A Fermionic View. Phys. Rev. A 2018, 97, 022304. [Google Scholar]
- Mitarai, K.; Negoro, M.; Kitagawa, M.; Fujii, K. Quantum Circuit Learning. Phys. Rev. A 2018, 98, 032309. [Google Scholar] [CrossRef]
- Zhou, L.; Wang, S.T.; Choi, S.; Pichler, H.; Lukin, M.D. Quantum Approximate Optimization Algorithm: Performance, Mechanism, and Implementation on Near-Term Devices. Phys. Rev. X 2020, 10, 021067. [Google Scholar] [CrossRef]
- Wecker, D.; Hastings, M.B.; Troyer, M. Training a Quantum Optimizer. Phys. Rev. A 2016, 94, 022309. [Google Scholar] [CrossRef]
- Streif, M.; Leib, M. Training the Quantum Approximate Optimization Algorithm without Access to a Quantum Processing Unit. Quantum Sci. Technol. 2020, 5, 034008. [Google Scholar] [CrossRef]
- Alam, M.; Saki, A.A.; Ghosh, S. Accelerating Quantum Approximate Optimization Algorithm using Machine Learning. In Proceedings of the 23rd IEEE DATE, Grenoble, France, 9–13 March 2020; pp. 686–689. [Google Scholar]
- Matsumine, T.; Koikeakino, T.; Wang, Y. Channel Decoding with Quantum Approximate Optimization Algorithm. In Proceedings of the 2019 IEEE ISIT, Paris, France, 7–12 July 2019; pp. 2574–2578. [Google Scholar]
- Li, J.; Alam, M.; Saki, A.A.; Ghosh, S. Hierarchical Improvement of Quantum Approximate Optimization Algorithm for Object Detection. In Proceedings of the 21st IEEE ISQED, Santa Clara, CA, USA, 25–26 March 2020; pp. 335–340. [Google Scholar]
- Adavoudi-Jolfaei, A.; Ashouri-Talouki, M.; Aghili, S.F. Lightweight and Anonymous Three-Factor Authentication and Access Control Scheme for Real-Time Applications in Wireless Sensor Networks. Peer-to-Peer Netw. Appl. 2019, 12, 43–59. [Google Scholar] [CrossRef]
- Aghili, S.F.; Mala, H.; Shojafar, M.; Peris-Lopez, P. LACO: Lightweight Three-Factor Authentication, Access Control and Ownership Transfer Scheme for E-Health Systems in IoT. Future Gener. Comput. Syst. 2019, 96, 410–424. [Google Scholar] [CrossRef]
- Talavera, E.; Álvarez, A.D.; Naranjo, J.E. A Review of Security Aspects in Vehicular Ad-Hoc Networks. IEEE Access 2019, 7, 41981–41988. [Google Scholar]
- Tang, F.; Kawamoto, Y.; Kato, N.; Liu, J. Future Intelligent and Secure Vehicular Network Toward 6G: Machine-Learning Approaches. Proc. IEEE 2020, 108, 292–307. [Google Scholar] [CrossRef]
- Awan, K.A.; Din, I.U.; Almogren, A.; Guizani, M.; Khan, S. StabTrust-A Stable and Centralized Trust-Based Clustering Mechanism for IoT Enabled Vehicular Ad-Hoc Networks. IEEE Access 2020, 8, 21159–21177. [Google Scholar] [CrossRef]
- Ozger, M.; Alagoz, F.; Akan, O.B. Clustering in Multi-Channel Cognitive Radio Ad Hoc and Sensor Networks. IEEE Commun. Mag. 2018, 56, 156–162. [Google Scholar] [CrossRef]
- Soorki, M.N.; Saad, W.; Manshaei, M.H.; Saidi, H. Stochastic Coalitional Games for Cooperative Random Access in M2M Communications. IEEE Trans. Wirel. Commun. 2017, 16, 6179–6192. [Google Scholar] [CrossRef]
- Lin, D.; Wang, Q. An Energy-Efficient Clustering Algorithm Combined Game Theory and Dual-Cluster-Head Mechanism for WSNs. IEEE Access 2019, 7, 49894–49905. [Google Scholar] [CrossRef]
- Zhu, G.; Jiang, X.; Wu, C.; He, Z. A Cluster Head Selection Algorithms in Wireless Network Based on Maximal Weighted Independent Set. In Proceedings of the 5th IEEE CUTE, Sanya, China, 16–18 December 2010; pp. 1–6. [Google Scholar]
- Shor, P.W. Algorithms for Quantum Computation: Discrete Logarithms and Factoring. In Proceedings of the 35th IEEE FOCS, Santa Fe, NM, USA, 20–22 November 1994; pp. 124–134. [Google Scholar]
- Grover, L.K. A Fast Quantum Mechanical Algorithm for Database Search. In Proceedings of the 28th ACM STOC, Philadelphia, PA, USA, 22–24 May 1996; pp. 212–219. [Google Scholar]
- Bravyi, S.; Gosset, D.; König, R. Quantum Advantage with Shallow Circuits. Science 2018, 362, 308–311. [Google Scholar] [CrossRef] [PubMed]
- Hadfield, S.; Wang, Z.; O’Gorman, B.; Rieffel, E.G.; Venturelli, D.; Biswas, R. From the Quantum Approximate Optimization Algorithm to a Quantum Alternating Operator Ansatz. Algorithms 2019, 12, 34. [Google Scholar] [CrossRef]
- Choi, J.; Kim, J. A Tutorial on Quantum Approximate Optimization Algorithm (QAOA): Fundamentals and Applications. In Proceedings of the 10th IEEE ICTC, Jeju Island, Korea, 16–18 October 2019; pp. 138–142. [Google Scholar]
- Kim, J.; Caire, G.; Molisch, A.F. Quality-Aware Streaming and Scheduling for Device-to-Device Video Delivery. IEEE/ACM Trans. Netw. 2016, 24, 2319–2331. [Google Scholar] [CrossRef]
- Sanghavi, S.; Shah, D.; Willsky, A.S. Message Passing for Maximum Weight Independent Set. IEEE Trans. Inf. Theory 2009, 55, 4822–4834. [Google Scholar] [CrossRef]
- Ma, X.; Sun, H.; Hu, R.Q. Scheduling Policy and Power Allocation for Federated Learning in NOMA Based MEC. arXiv 2020, arXiv:2006.13044. [Google Scholar]
- Brendel, W.; Todorovic, S. Segmentation as Maximum-Weight Independent Set. In Proceedings of the 24th NIPS, Vancouver, BC, Canada, 6–9 December 2010; pp. 307–315. [Google Scholar]
- Brendel, W.; Amer, M.; Todorovic, S. Multiobject Tracking as Maximum Weight Independent Set. In Proceedings of the 24th IEEE CVPR, Providence, RI, USA, 20–25 June 2011; pp. 1273–1280. [Google Scholar]
- Wei, D.; Chan, H.A. Clustering Ad Hoc Networks: Schemes and Classifications. In Proceedings of the 3rd IEEE SECON, Reston, VA, USA, 28–28 September 2006; pp. 920–926. [Google Scholar]
- Demarchou, E.; Psomas, C.; Krikidis, I. Asynchronous Ad Hoc Networks With Wireless Powered Cognitive Communications. IEEE Trans. Cogn. Commun. Netw. 2019, 5, 440–451. [Google Scholar] [CrossRef]
- Feo, T.A.; Resende, M.G. Greedy Randomized Adaptive Search Procedures. J. Glob. Optim. 1995, 6, 109–133. [Google Scholar]
- Guerreschi, G.G.; Matsuura, A.Y. QAOA for Max-Cut Requires Hundreds of Qubits for Quantum Speed-Up. Sci. Rep. 2019, 9, 6903. [Google Scholar] [CrossRef]
- Shaydulin, R.; Alexeev, Y. Evaluating Quantum Approximate Optimization Algorithm: A Case Study. In Proceedings of the 10th IEEE IGSC, Alexandria, VA, USA, 21–24 October 2019; pp. 1–6. [Google Scholar]
- Broughton, M.; Verdon, G.; McCourt, T.; Martinez, A.J.; Yoo, J.H.; Isakov, S.V.; Massey, P.; Niu, M.Y.; Halavati, R.; Peters, E.; et al. TensorFlow Quantum: A Software Framework for Quantum Machine Learning. arXiv 2020, arXiv:2003.02989. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).