HIL-Assessed Fast and Accurate Single-Phase Power Calculation Algorithm for Voltage Source Inverters Supplying to High Total Demand Distortion Nonlinear Loads
Abstract
1. Introduction
- Improving the velocity of the transient response of the averaged power calculation.
- Improving the steady-state accuracy of the averaged power calculation.
2. Droop-Based Local Control Techniques against Nonlinear Loads
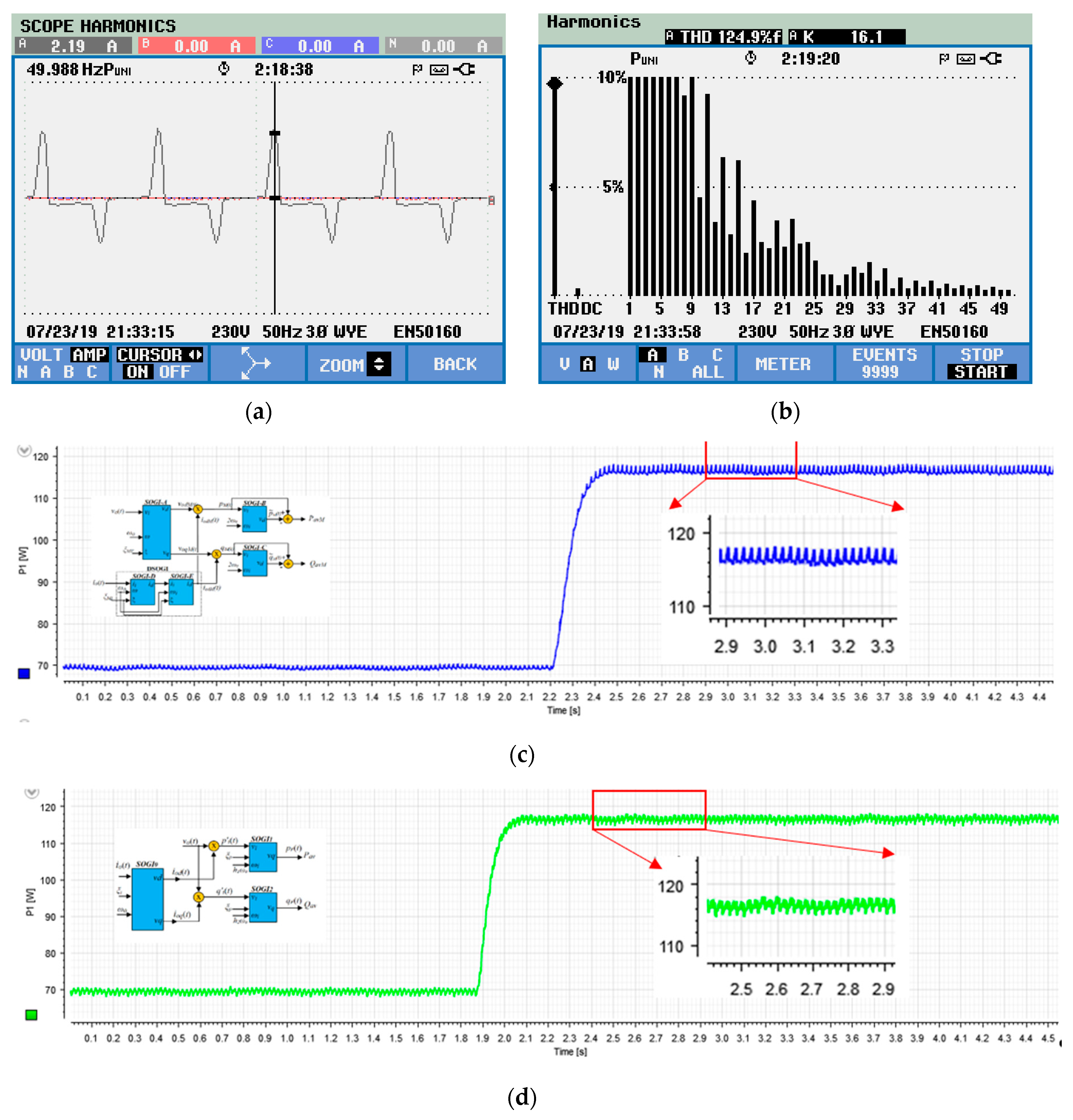
3. Description of the System under Test: VSI Supplying to a Nonlinear Load
4. P–Q Calculation Algorithms
5. Proposed P–Q Calculation Algorithm
6. Simulation Results
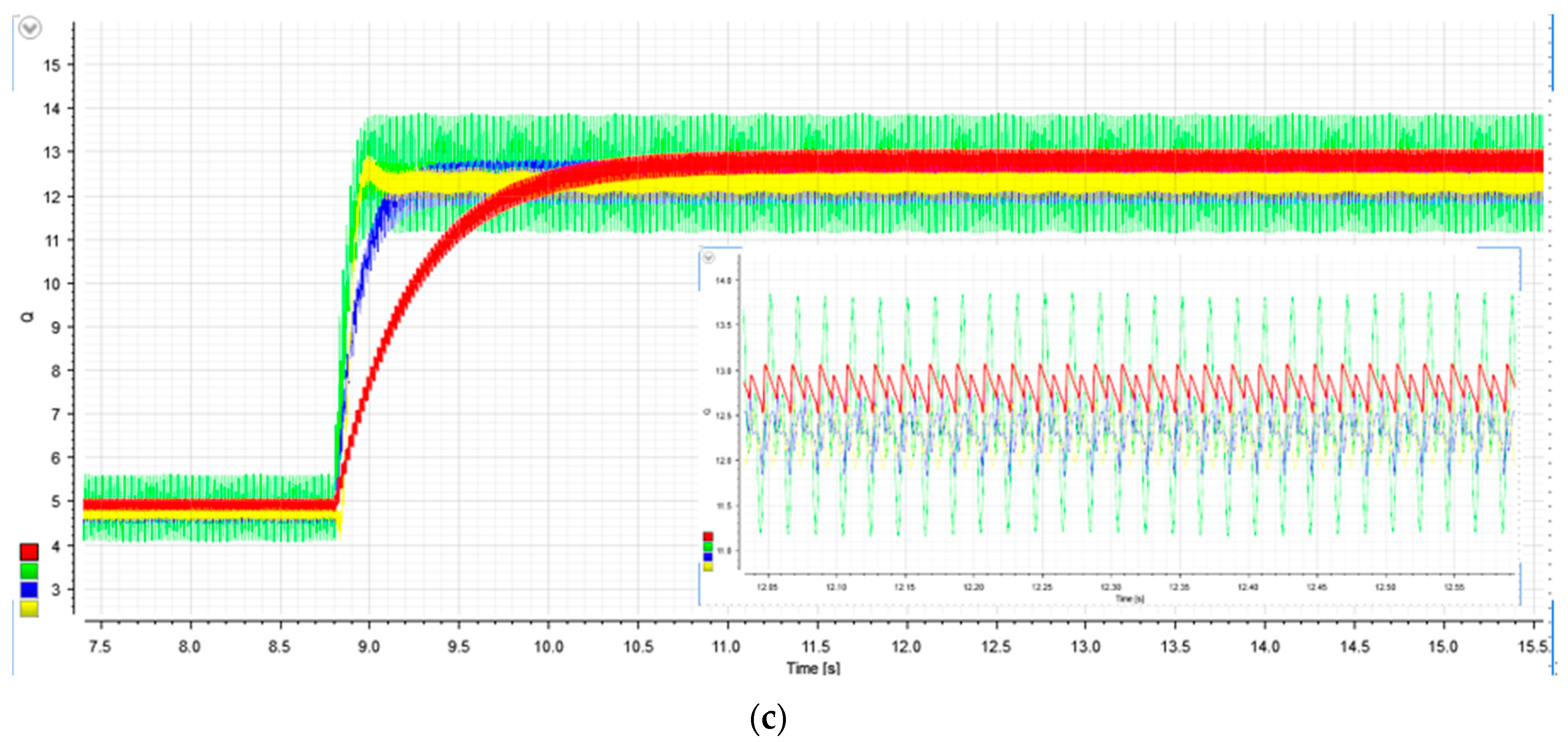
7. Hardware in the Loop Assessment
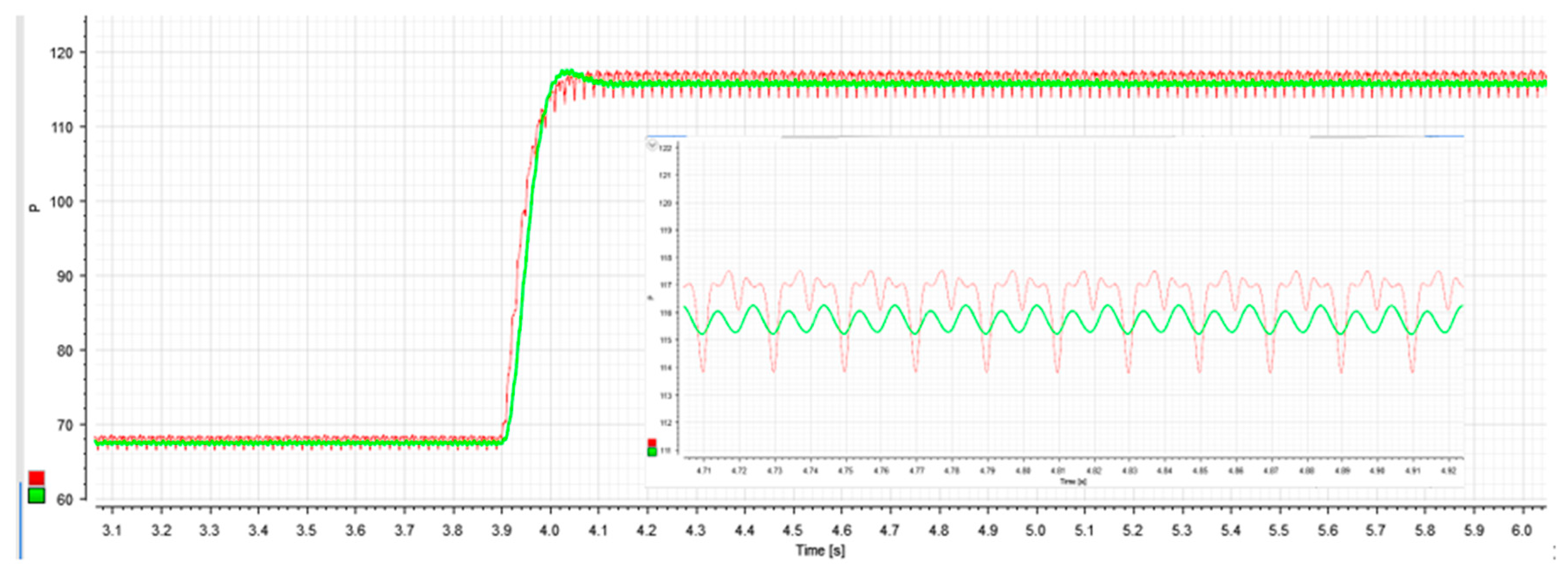
8. Experimental Results
9. Conclusions
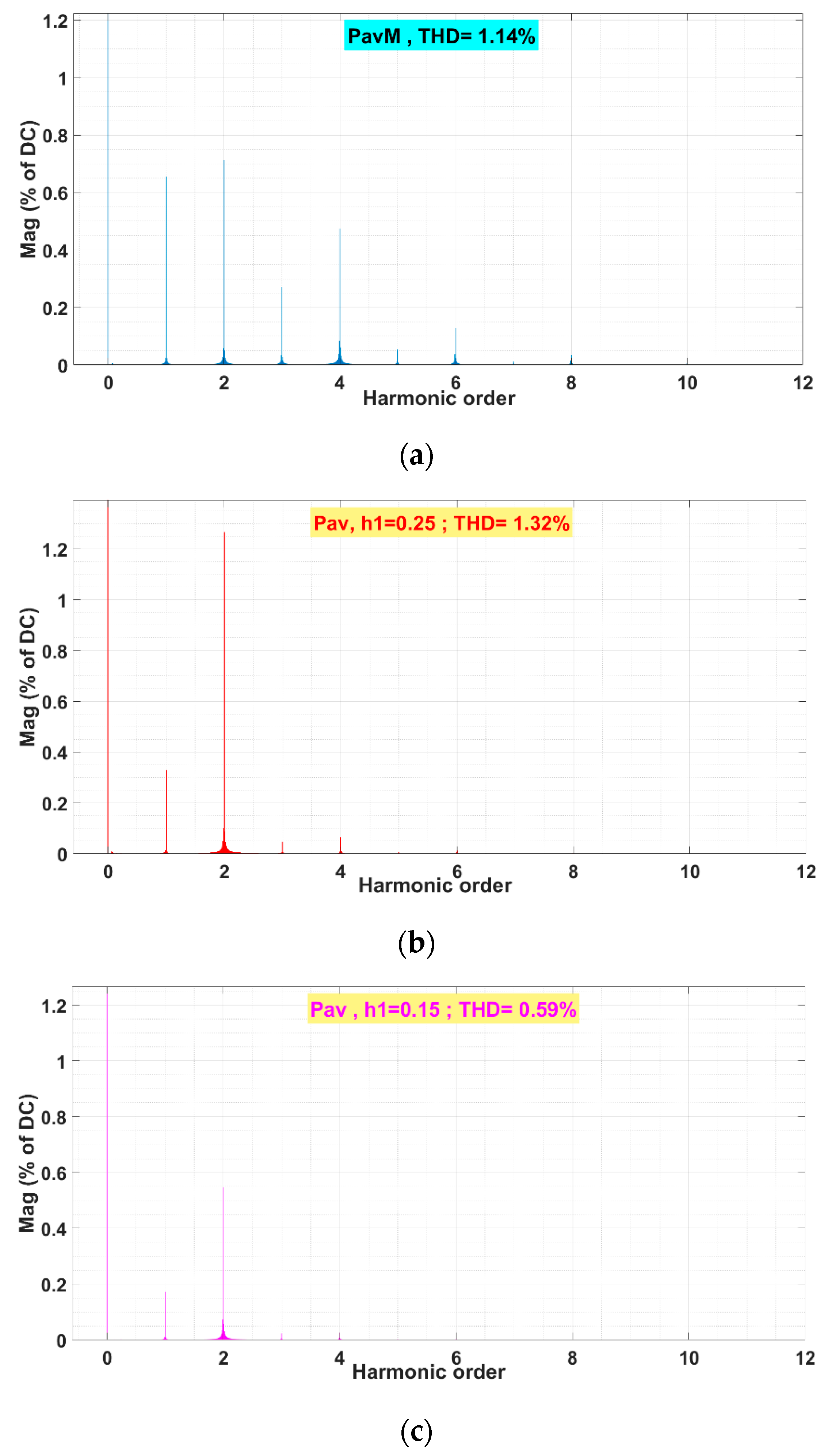
- Active Power: Reduction in 47.78% of the steady-state calculated THD with respect to DC in the simulations for Pav, when the settling-time is similar (Table 4).
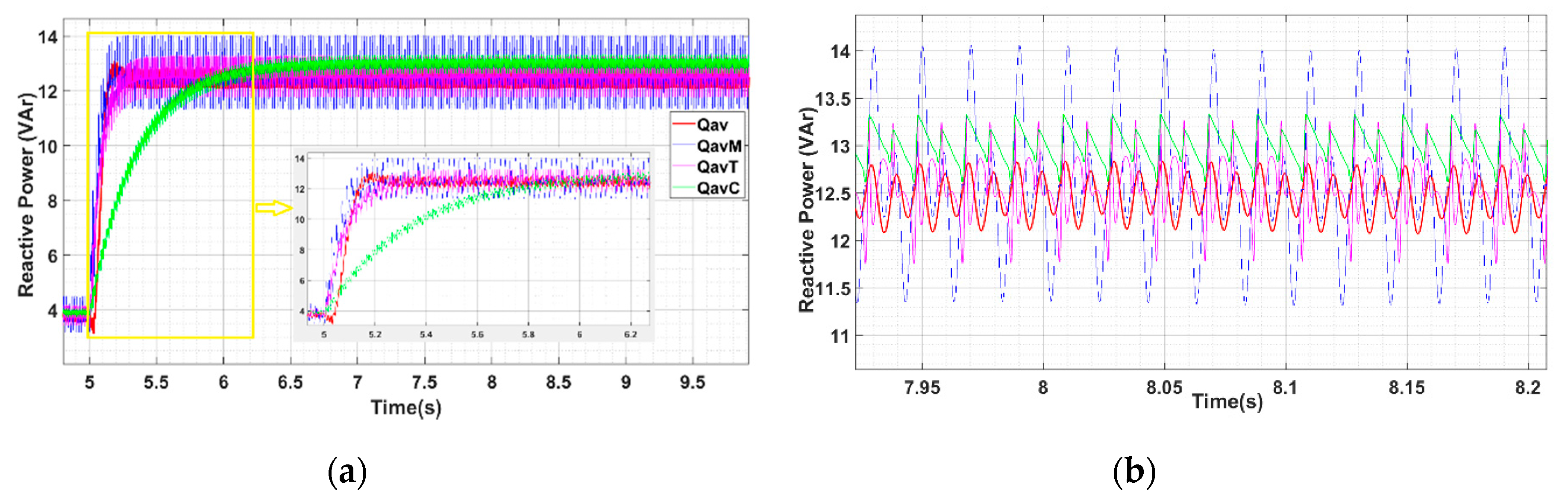
- Reactive Power: Reduction in 68.66% of the steady-state calculated THD with respect to DC in the simulations for Qav, when the settling-time is similar (Table 5).
Author Contributions
Funding
Conflicts of Interest
References
- U.S. Department of Energy. The Smart Grid: An Introduction; DOE: Washington, DC, USA, 2003. [Google Scholar]
- European Commission; Directorate-General for Research. European Technology Platform SmartGrids: Vision and Strategy for Europe’s Electricity Networks of the Future; Office for Official Publications of the European Communities: Luxembourg, 2006. [Google Scholar]
- Sustainable Development Goal 7 (SDG). Available online: https://sustainabledevelopment.un.org/sdg7 (accessed on 4 September 2020).
- Kumar, N.M.; Chopra, S.S.; Chand, A.A.; Elavarasan, R.M.; Shafiullah, G. Hybrid Renewable Energy Microgrid for a Residential Community: A Techno-Economic and Environmental Perspective in the Context of the SDG7. Sustainability 2020, 12, 3944. [Google Scholar] [CrossRef]
- Manoj Kumar, N.; Ghosh, A.; Chopra, S.S. Power Resilience Enhancement of a Residential Electricity User Using Photovoltaics and a Battery Energy Storage System under Uncertainty Conditions. Energies 2020, 13, 4193. [Google Scholar] [CrossRef]
- Kumar, S.A.; Subathra, M.S.P.; Kumar, N.M.; Malvoni, M.; Sairamya, N.J.; George, S.T.; Suviseshamuthu, E.S.; Chopra, S.S. A Novel Islanding Detection Technique for a Resilient Photovoltaic-Based Distributed Power Generation System Using a Tunable-Q Wavelet Transform and an Artificial Neural Network. Energies 2020, 13, 4238. [Google Scholar] [CrossRef]
- Ton, D.T.; Smith, M.A. The U.S. Department of Energy’s Microgrid Initiative. Electr J. 2012, 25, 84–94. [Google Scholar] [CrossRef]
- Lasseter, R.H. Microgrids. In Proceedings of the 2002 IEEE Power Engineering Society Winter Meeting, New York, NY, USA, 27–31 January 2002; pp. 305–308. [Google Scholar]
- Ali, A.; Li, W.; Hussain, R.; He, X.; Williams, B.W.; Memon, A.H. Overview of Current Microgrid Policies, Incentives and Barriers in the European Union, United States and China. Sustainability 2017, 9, 1146. [Google Scholar] [CrossRef]
- IEEE Power and Energy Society. IEEE Power and Energy Society. IEEE Standard for the Specification of Microgrid Controllers. In IEEE Std 2030.7; IEEE: Piscataway, NJ, USA, 2017; pp. 1–43. [Google Scholar]
- Cigré. Microgrids 1 Engineering, Economics, & Experience; WG C6.22; Cigré: Paris, France, 2015; ISBN 9782858733385. [Google Scholar]
- Carpintero-Rentería, M.; Santos-Martín, D.; Guerrero, J.M. Microgrids Literature Review through a Layers Structure. Energies 2019, 12, 4381. [Google Scholar] [CrossRef]
- De Oliveira Costa Souza Rosa, C.; Costa, K.A.; Christo, E.D.S.; Bertahone, P.B. Complementarity of Hydro, Photovoltaic, and Wind Power in Rio de Janeiro State. Sustainability 2017, 9, 1130. [Google Scholar] [CrossRef]
- Kanase-Patil, A.B.; Saini, R.; Sharma, M. Integrated renewable energy systems for off grid rural electrification of remote area. Renew. Energy 2010, 35, 1342–1349. [Google Scholar] [CrossRef]
- Shan, Y.; Hu, J.; Liu, M.; Zhu, J.; Guerrero, J.M. Model Predictive Voltage and Power Control of Islanded PV-Battery Microgrids With Washout-Filter-Based Power Sharing Strategy. IEEE Trans. Power Electron. 2020, 35, 1227–1238. [Google Scholar] [CrossRef]
- Angelopoulos, A.; Ktena, A.; Manasis, C.; Voliotis, S. Impact of a Periodic Power Source on a RES Microgrid. Energies 2019, 12, 1900. [Google Scholar] [CrossRef]
- Rocabert, J.; Luna, A.; Blaabjerg, F.; Rodriguez, P. Control of Power Converters in AC Microgrids. IEEE Trans. Power Electron. 2012, 27, 4734–4749. [Google Scholar] [CrossRef]
- Guerrero, J.M.; Vasquez, J.C.; Matas, J.; De Vicuna, L.G.; Castilla, M. Hierarchical Control of Droop-Controlled AC and DC Microgrids—A General Approach Toward Standardization. IEEE Trans. Ind. Electron. 2011, 58, 158–172. [Google Scholar] [CrossRef]
- De Brabandere, K.; Vanthournout, K.; Driesen, J.; Deconinck, G.; Belmans, R. Control of microgrids. In Proceedings of the 2007 IEEE Power Engineering Society General Meeting, Tampa, FL, USA, 24–28 June 2007; pp. 1–7. [Google Scholar]
- Aghaee, F.; Dehkordi, N.M.; Bayati, N.; Hajizadeh, A.; Dehkordi, M. Distributed Control Methods and Impact of Communication Failure in AC Microgrids: A Comparative Review. Electronics 2019, 8, 1265. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, K.; Chi, S.; Lyu, L.; Cai, G. The Hierarchical Control Algorithm for DC Microgrid Based on the Improved Droop Control of Fuzzy Logic. Energies 2019, 12, 2995. [Google Scholar] [CrossRef]
- Ranjbaran, A.; Ebadian, M. A power sharing scheme for voltage unbalance and harmonics compensation in an islanded microgrid. Electr. Power Syst. Res. 2018, 155, 153–163. [Google Scholar] [CrossRef]
- Tavakoli, A.; Sanjari, M.J.; Kohansal, M.; Gharehpetian, G.B. An innovative power calculation method to improve power sharing in VSI based micro grid. In Proceedings of the Iranian Conference on Smart Grids, Tehran, Iran, 24–25 May 2012; pp. 3–7. [Google Scholar]
- Golestan, S.; Joorabian, M.; Rastegar, H.; Roshan, A.; Guerrero, J.M. Droop based control of parallel-connected single-phase inverters in D-Q rotating frame. In Proceedings of the 2009 IEEE International Conference on Industrial Technology, Gippsland, Australia, 10–13 February 2009; pp. 1–6. [Google Scholar]
- Arbab-Zavar, B.; Palacios-Garcia, E.J.; Vasquez, J.C.; Guerrero, J.M. Smart Inverters for Microgrid Applications: A Review. Energies 2019, 12, 840. [Google Scholar] [CrossRef]
- Wang, X.; Qing, H.; Huang, P.; Zhang, C. Modeling and Stability Analysis of Parallel Inverters in Island Microgrid. Electronics 2020, 9, 463. [Google Scholar] [CrossRef]
- Kim, J.-H.; Lee, Y.-S.; Kim, H.-J.; Han, B.-M. A New Reactive-Power Sharing Scheme for Two Inverter-Based Distributed Generations with Unequal Line Impedances in Islanded Microgrids. Energies 2017, 10, 1800. [Google Scholar] [CrossRef]
- Toub, M.; Bijaieh, M.M.; Weaver, W.W.; Robinett, R.D.; Maaroufi, M.; Aniba, G. Droop Control in DQ Coordinates for Fixed Frequency Inverter-Based AC Microgrids. Electronics 2019, 8, 1168. [Google Scholar] [CrossRef]
- Ren, B.; Sun, X.; Chen, S.; Liu, H. A Compensation Control Scheme of Voltage Unbalance Using a Combined Three-Phase Inverter in an Islanded Microgrid. Energies 2018, 11, 2486. [Google Scholar] [CrossRef]
- Ma, J.; Wang, X.; Liu, J.; Gao, H. An Improved Droop Control Method for Voltage-Source Inverter Parallel Systems Considering Line Impedance Differences. Energies 2019, 12, 1158. [Google Scholar] [CrossRef]
- Yang, N.; Paire, D.; Gao, F.; Miraoui, A.; Liu, W. Compensation of droop control using common load condition in DC microgrids to improve voltage regulation and load sharing. Int. J. Electr. Power Energy Syst. 2015, 64, 752–760. [Google Scholar] [CrossRef]
- Guerrero, J.; Matas, J.; Vicuna, L.G.; Castilla, M.; Miret, J. Decentralized Control for Parallel Operation of Distributed Generation Inverters Using Resistive Output Impedance. IEEE Trans. Ind. Electron. 2007, 54, 994–1004. [Google Scholar] [CrossRef]
- Yao, W.; Chen, M.; Matas, J.; Guerrero, J.M.; Qian, Z. Design and Analysis of the Droop Control Method for Parallel Inverters Considering the Impact of the Complex Impedance on the Power Sharing. IEEE Trans. Ind. Electron. 2011, 58, 576–588. [Google Scholar] [CrossRef]
- El Mariachet, J.; Matas, J.; de la Hoz, J.; Al-Turki, Y.; Abdalgader, H. Power Calculation Algorithm for Single-Phase Droop-Operated Inverters Considering Nonlinear Loads. Renew. Energy Power Qual. J. 2018, 1, 710–715. [Google Scholar] [CrossRef]
- El Mariachet, J.; Matas, J.; Martin, H.; Li, M.; Guan, Y.; Guerrero, J.M. A Power Calculation Algorithm for Single-Phase Droop-Operated-Inverters Considering Linear and Nonlinear Loads HIL-Assessed. Electronics 2019, 8, 1366. [Google Scholar] [CrossRef]
- Wang, H.; Yue, X.; Pei, X.; Kang, Y. A new method of power calculation based on parallel inverters. In Proceedings of the IEEE EPE-PEMC, Novi Sad, Serbia, 28–30 October 2009; pp. 1573–1576. [Google Scholar]
- Yu, W.; Xu, D.; Ma, K.A. Novel Accurate Active and Reactive Power Calculation Method for Paralleled UPS System. In Proceedings of the APEC, Singapore, 15–16 November 2009; pp. 1269–1275. [Google Scholar]
- Akagi, H.; Watanabe, E.; Aredes, M. Instantaneous Power Theory and Application to Power Conditioning; Wiley-IEEE Press: Piscataway, NJ, USA, 2007; pp. 5–28. [Google Scholar]
- Gao, M.; Yang, S.; Jin, C.; Ren, Z.; Chen, M.; Qian, Z. Analysis and experimental validation for power calculation based on p-q theory in single-phase wireless-parallel inverters. In Proceedings of the 2011 Twenty-Sixth Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Fort Worth, TX, USA, 6–11 March 2011; pp. 620–624. [Google Scholar]
- Matas, J.; Castilla, M.; De Vicuna, L.G.; Miret, J.; Vasquez, J.C. Virtual Impedance Loop for Droop-Controlled Single-Phase Parallel Inverters Using a Second-Order General-Integrator Scheme. IEEE Trans. Power Electron. 2010, 25, 2993–3002. [Google Scholar] [CrossRef]
- Tolani, S.; Sensarma, P. An improved droop controller for parallel operation of single-phase inverters using R-C output impedance. In Proceedings of the 2012 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Bengaluru, India, 16–19 December 2012; pp. 1–6. [Google Scholar]
- Cardoso, T.D.; Azevedo, G.M.S.; Cavalcanti, M.C.; Neves, F.A.S.; Limongi, L.R. Implementation of droop control with enhanced power calculator for power sharing on a single-phase microgrid. In Proceedings of the 2017 Brazilian Power Electronics Conference (COBEP), Juiz de Fora, Brazil, 19–22 November 2017; pp. 1–6. [Google Scholar]
- Yang, Y.; Blaabjerg, F. A new power calculation method for single-phase grid-connected systems. In Proceedings of the 2013 IEEE International Symposium on Industrial Electronics, Taipei, Taiwan, 28–31 May 2013; pp. 1–6. [Google Scholar]
- IEEE Power and Energy Society. IEEE Recommended Practice and Requirements for Harmonic Control in Electric Power Systems. In IEEE Std. 519-2014 (Revision of IEEE Std. 519-1992); IEEE: Piscataway, NJ, USA, 2014; pp. 1–29. [Google Scholar]
- Guan, Y.; Guerrero, J.M.; Zhao, X.; Vasquez, J.C.; Guo, X. A New Way of Controlling Parallel-Connected Inverters by Using Synchronous-Reference-Frame Virtual Impedance Loop—Part I: Control Principle. IEEE Trans. Power Electron. 2015, 31, 4576–4593. [Google Scholar] [CrossRef]
- Kullarkar, V.T.; Chandrakar, V.K. Power Quality Analysis in Power System with Non Linear Load. Int. J. Electr. Eng. 2017, 10, 33–45. [Google Scholar]
- Stošović, M.A.; Stevanović, D.; Dimitrijević, M. Classification of nonlinear loads based on artificial neural networks. In Proceedings of the 2017 IEEE 30th International Conference on Microelectronics (MIEL), Nis, Serbia, 9–11 October 2017; pp. 221–224. [Google Scholar]
- Salam, S.M.; Uddin, M.J.; Hannan, S. A new approach to develop a template based load model that can dynamically adopt different types of non-linear loads. In Proceedings of the 2017 International Conference on Electrical, Computer and Communication Engineering (ECCE), Cox’s Bazar, Bangladesh, 16–18 February 2017; pp. 708–712. [Google Scholar]
- Kneschke, T.A. Distortion and power factor of nonlinear loads. In Proceedings of the 1999 ASME/IEEE Joint Railroad Conference (Cat. No.99CH36340), Dallas, TX, USA, 15 April 1999; pp. 47–54. [Google Scholar]
- Shabbir, H.; Rehman, M.U.; Rehman, S.A.; Sheikh, S.K.; Zaffar, N. Assessment of harmonic pollution by LED lamps in power systems. In Proceedings of the 2014 Clemson University Power Systems Conference, Clemson, SC, USA, 11–14 March 2014; pp. 1–7. [Google Scholar]
- Normanyo, E. Mitigation of Harmonics in a Three-Phase, Four-Wire Distribution System using a System of Shunt Passive Filters. Int. J. Eng. Tech. 2012, 2, 761–774. [Google Scholar]
- Shahl, S.I. Simulation and Analysis Effects of Nonlinear Loads in the Distribution Systems. Int. J. Sci. Eng. Res. 2019, 10, 888–892. [Google Scholar]
- Micallef, A.; Apap, M.; Cyril, S.S.; Guerrero, J.M.; Vasquez, J.C. Reactive Power Sharing and Voltage Harmonic Distortion Compensation of Droop Controlled Single Phase Islanded Microgrids. IEEE Trans. Smart Grid 2014, 5, 1149–1158. [Google Scholar] [CrossRef]

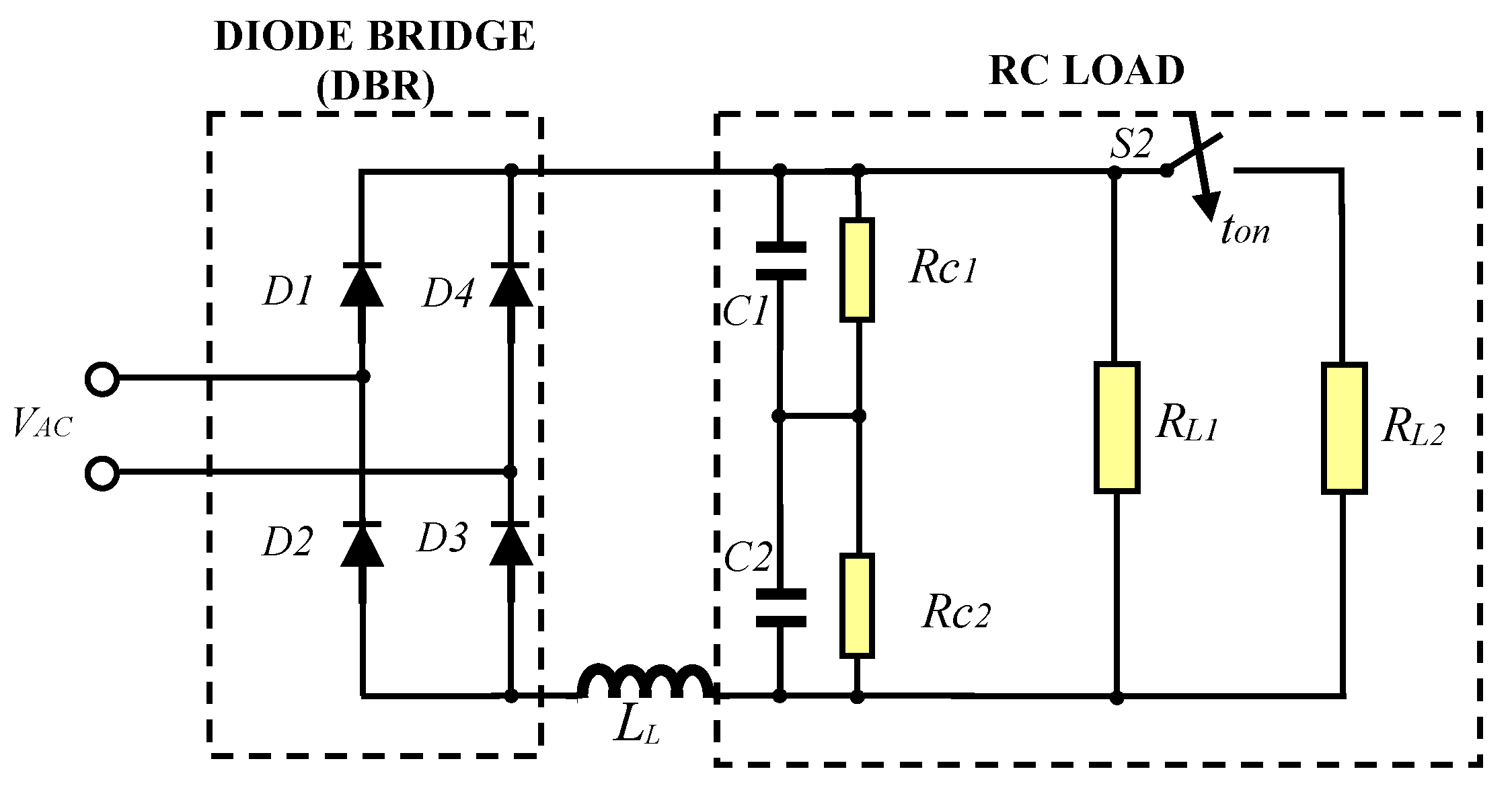
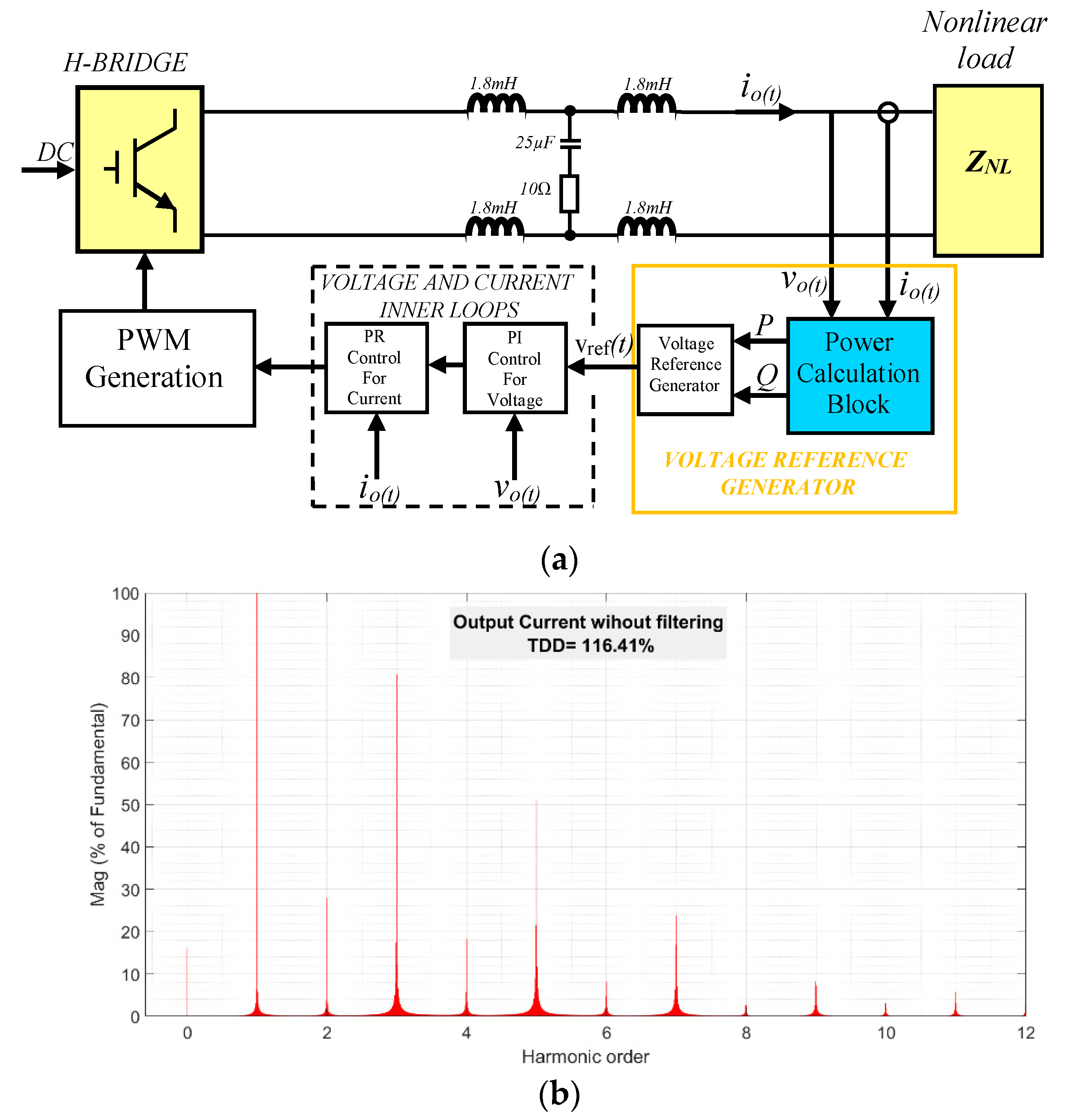
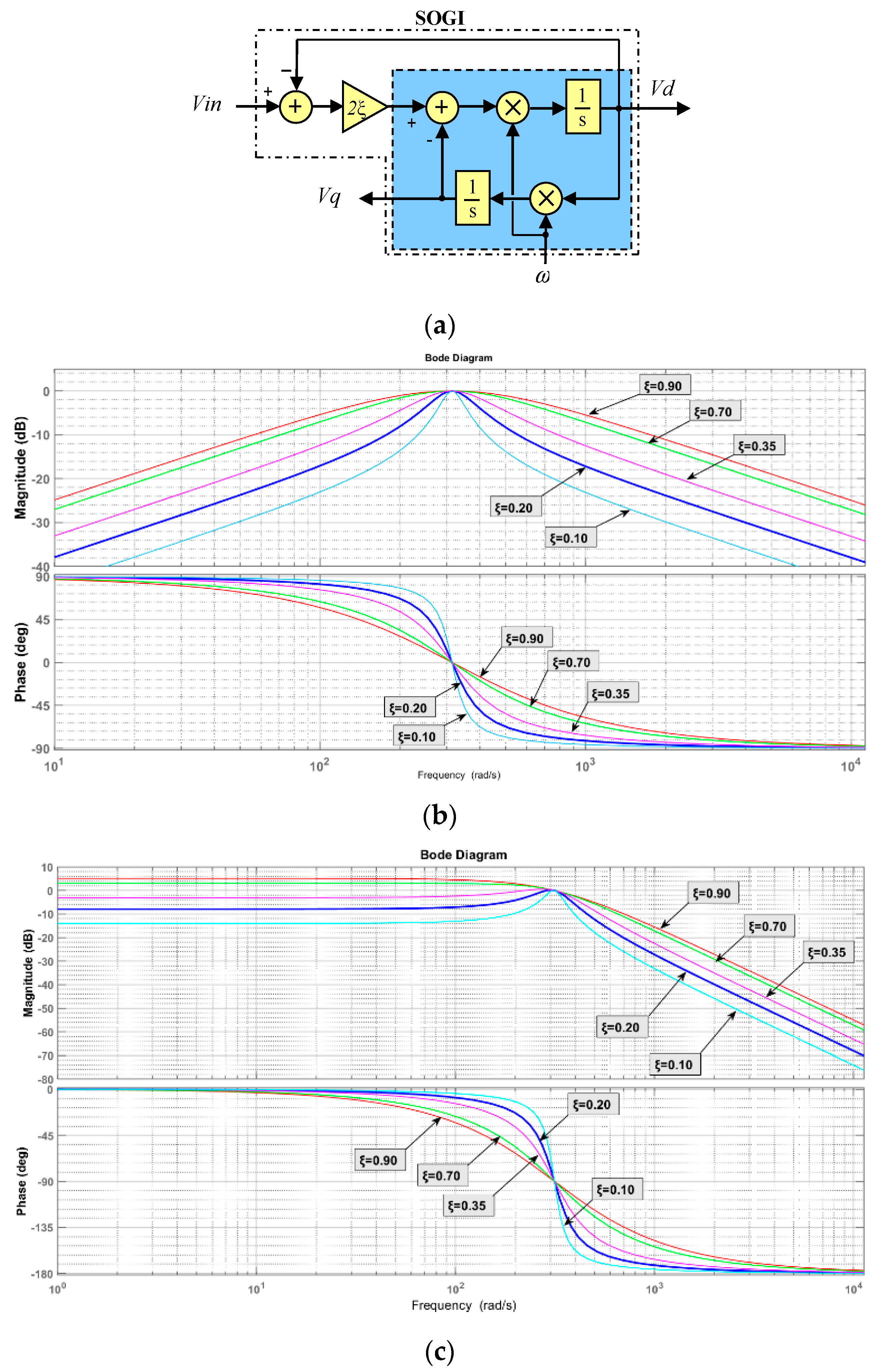
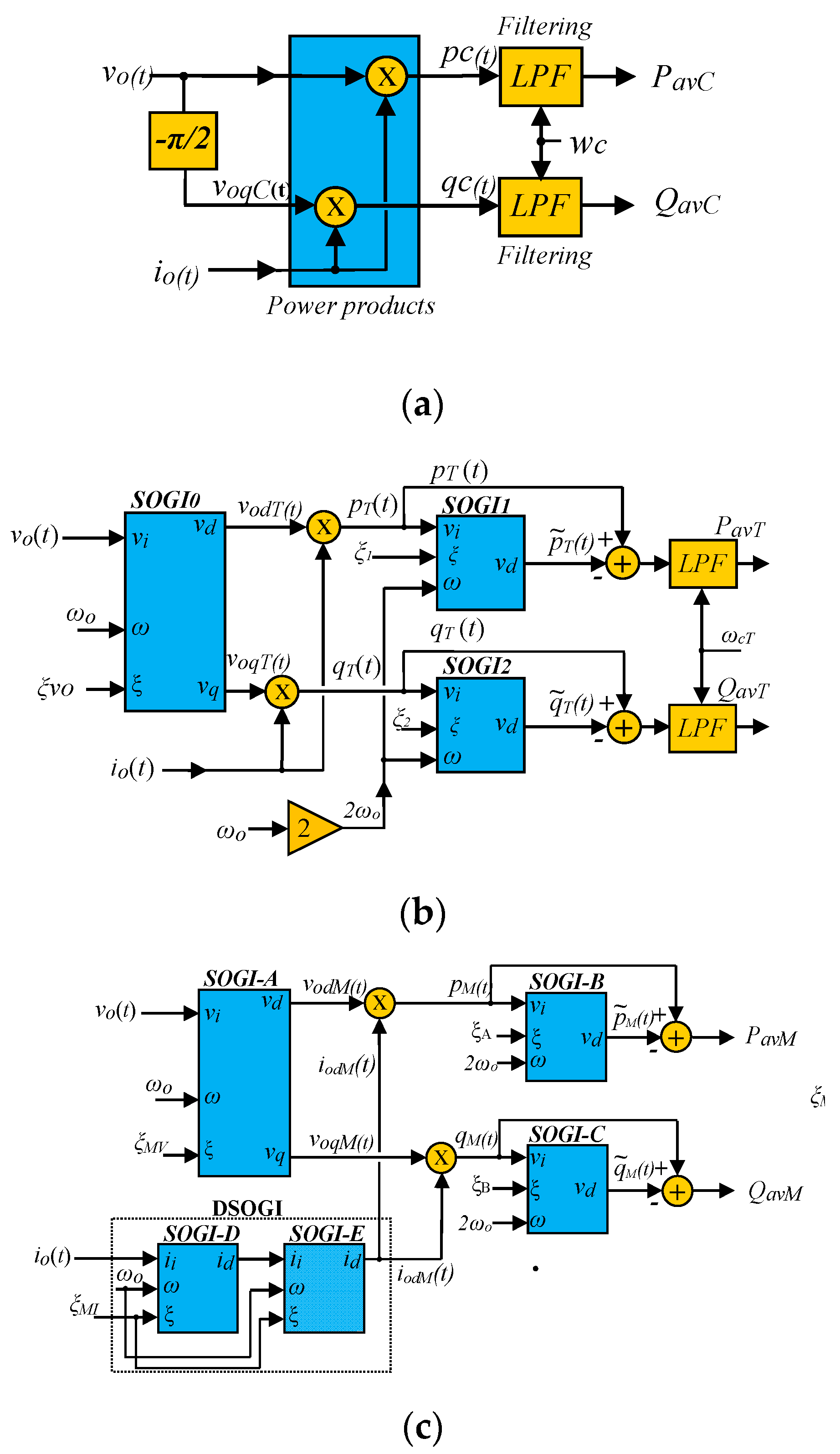
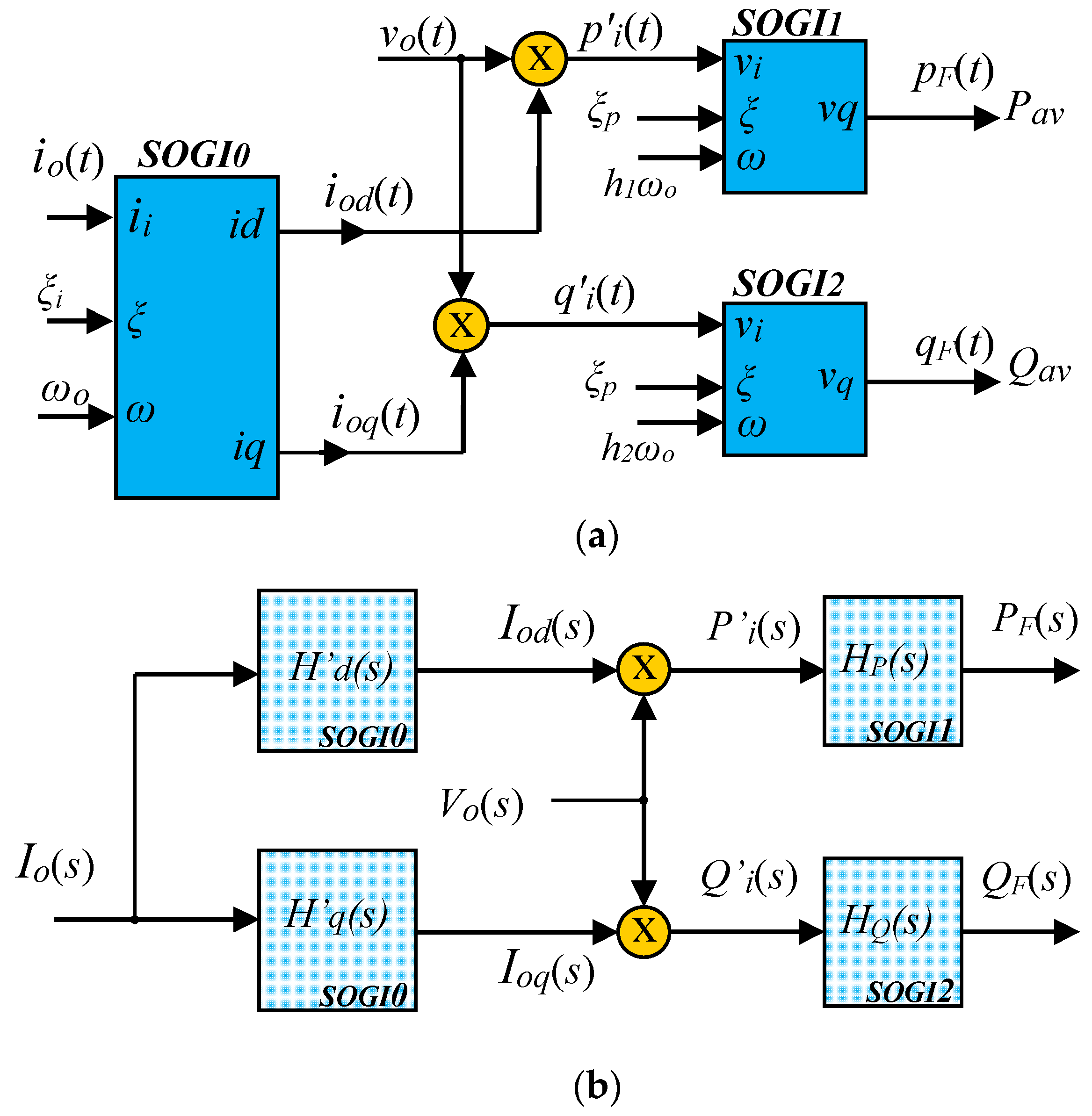
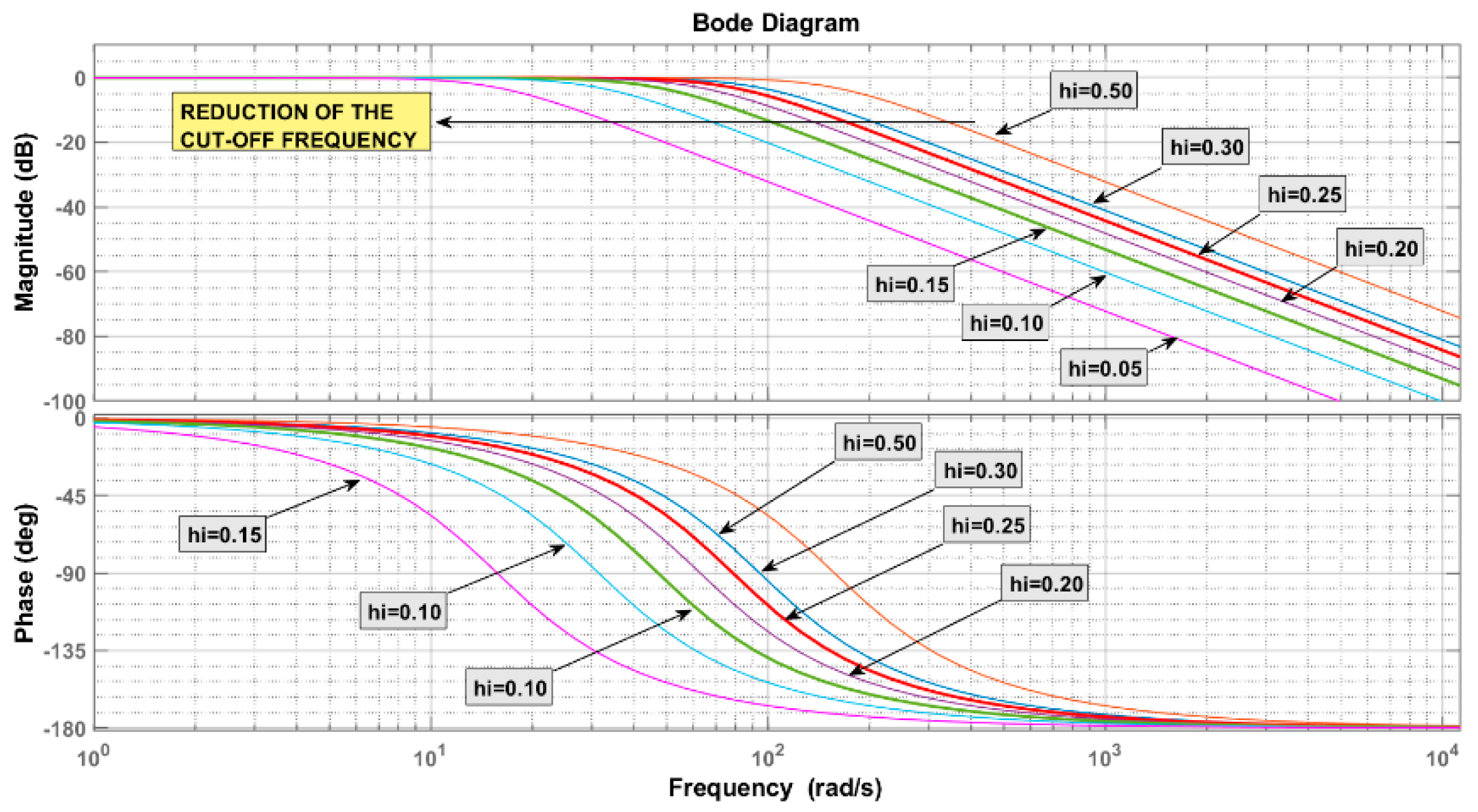

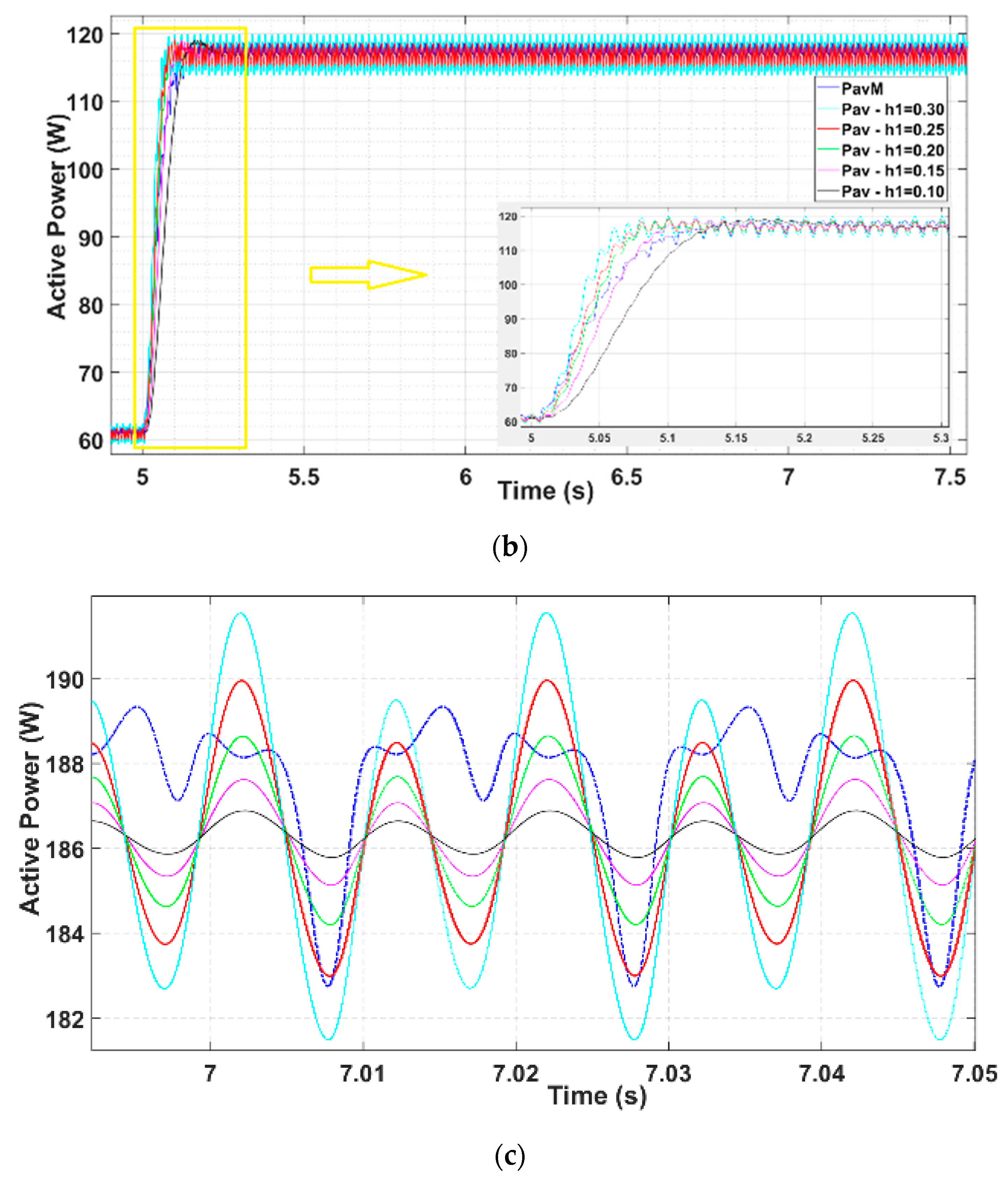
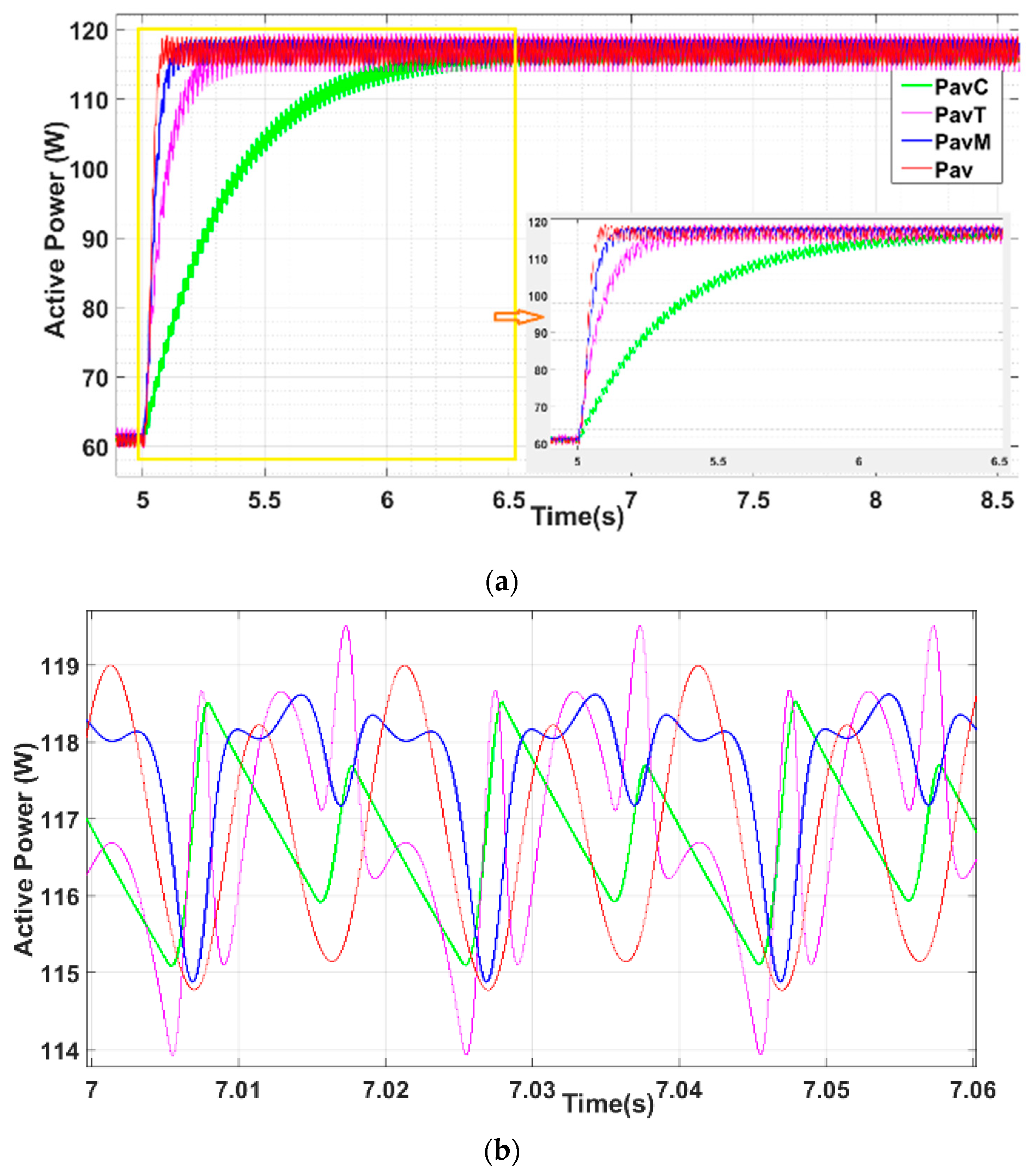


| Parameter | Value |
|---|---|
| RonD1-D3/RonD2-D4 | 0.01 Ω/1 Ω |
| LL/C1 = C2 | 84 µH/470 µF |
| RC1 = RC2/RL1 = RL2 | 37 kΩ/1560 Ω |
| Parameter | Value |
|---|---|
| Individual THDv; Total THD | <5%; <8% |
| Individual THDi | >4% for 3 < odd harmonic < 11 >1% for even harmonics |
| Total TDD in current | >5% |
| Parameter | Value |
|---|---|
| 311 V | |
| 100 π rad/s | |
| TDD for io(t) | 116.41% |
| 0.1 to 0.7075/0.7075 | |
| 0.10 to 0.30 (in steps of 0.05) | |
| 0.10 | |
| ; | 0.74 π rad/s; 2.20 π rad/s |
| 0.7/1 | |
| 0.7/0.14/1 | |
| C1 = C2/ RC1 = RC2 | 470 µF/37 kΩ |
| RL1 = RL2 = RL3 = RL4 | 1.8 mH; 0.01 Ω |
| RC BRANCH | 25 µF; 1 Ω |
| SWITCHING FREQUENCY, fs | 10 kHz |
| Calculated THD | Settling-Time (ms)/% Reduction with Respect to PAVM | Time-Delay (ms)/% Increasing with Respect to PAVM | |
|---|---|---|---|
| 1.13% | 120 | 38 | |
| 1.32% | 75/32% | 40/5% | |
| 0.59% | 90/18% | 50/20% |
| Reactive Power Calculation Algorithm | Calculated THD | Settling-Time (ms) | Reduction of THD with Respect to QavM |
|---|---|---|---|
| 7.85% | 140 | Not applicable | |
| 2.46% | 150 | 68.66% | |
| 3.49% | 250 | 55.64% | |
| 1.87% | 780 | 76.18% |
| Test | ; | ||
|---|---|---|---|
| HIL TEST-1 | 0.2 | 0.7075 | 0.25; 0.10 |
| HIL TEST-2 | 0.2 | 0.7075 | 0.15; 0.10 |
| HIL Calculation Algorithm | Settling-Time (ms) | Time-Delay (ms) |
|---|---|---|
| 90 | 38 | |
| 140 | 40 | |
| 130 | 50 | |
| 140 | 45 |
| Algorithm | Settling-Time Matlab (ms)/(%Reduction) | Settling-Time HIL (ms)/(%Reduction) | Settling-Time Experimental (ms)/(%Reduction) |
|---|---|---|---|
| Pav | 75/37.5% | 90/(35.7%) | 125/(30%) |
| PavM | 120 | 140 | 180 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
El Mariachet, J.; Guan, Y.; Matas, J.; Martín, H.; Li, M.; Guerrero, J.M. HIL-Assessed Fast and Accurate Single-Phase Power Calculation Algorithm for Voltage Source Inverters Supplying to High Total Demand Distortion Nonlinear Loads. Electronics 2020, 9, 1643. https://doi.org/10.3390/electronics9101643
El Mariachet J, Guan Y, Matas J, Martín H, Li M, Guerrero JM. HIL-Assessed Fast and Accurate Single-Phase Power Calculation Algorithm for Voltage Source Inverters Supplying to High Total Demand Distortion Nonlinear Loads. Electronics. 2020; 9(10):1643. https://doi.org/10.3390/electronics9101643
Chicago/Turabian StyleEl Mariachet, Jorge, Yajuan Guan, Jose Matas, Helena Martín, Mingshen Li, and Josep M. Guerrero. 2020. "HIL-Assessed Fast and Accurate Single-Phase Power Calculation Algorithm for Voltage Source Inverters Supplying to High Total Demand Distortion Nonlinear Loads" Electronics 9, no. 10: 1643. https://doi.org/10.3390/electronics9101643
APA StyleEl Mariachet, J., Guan, Y., Matas, J., Martín, H., Li, M., & Guerrero, J. M. (2020). HIL-Assessed Fast and Accurate Single-Phase Power Calculation Algorithm for Voltage Source Inverters Supplying to High Total Demand Distortion Nonlinear Loads. Electronics, 9(10), 1643. https://doi.org/10.3390/electronics9101643









