Distance-Based Resource Allocation for Vehicle-to-Pedestrian Safety Communication
Abstract
1. Introduction
- Optimum power allocation using Q-learning based reinforcement learning with different discount factors.
- A one-to-many weighted bipartite matching scheme (with maximum flow) to create connections between users for frequency assignment.
2. Related Work
3. Network and System Model
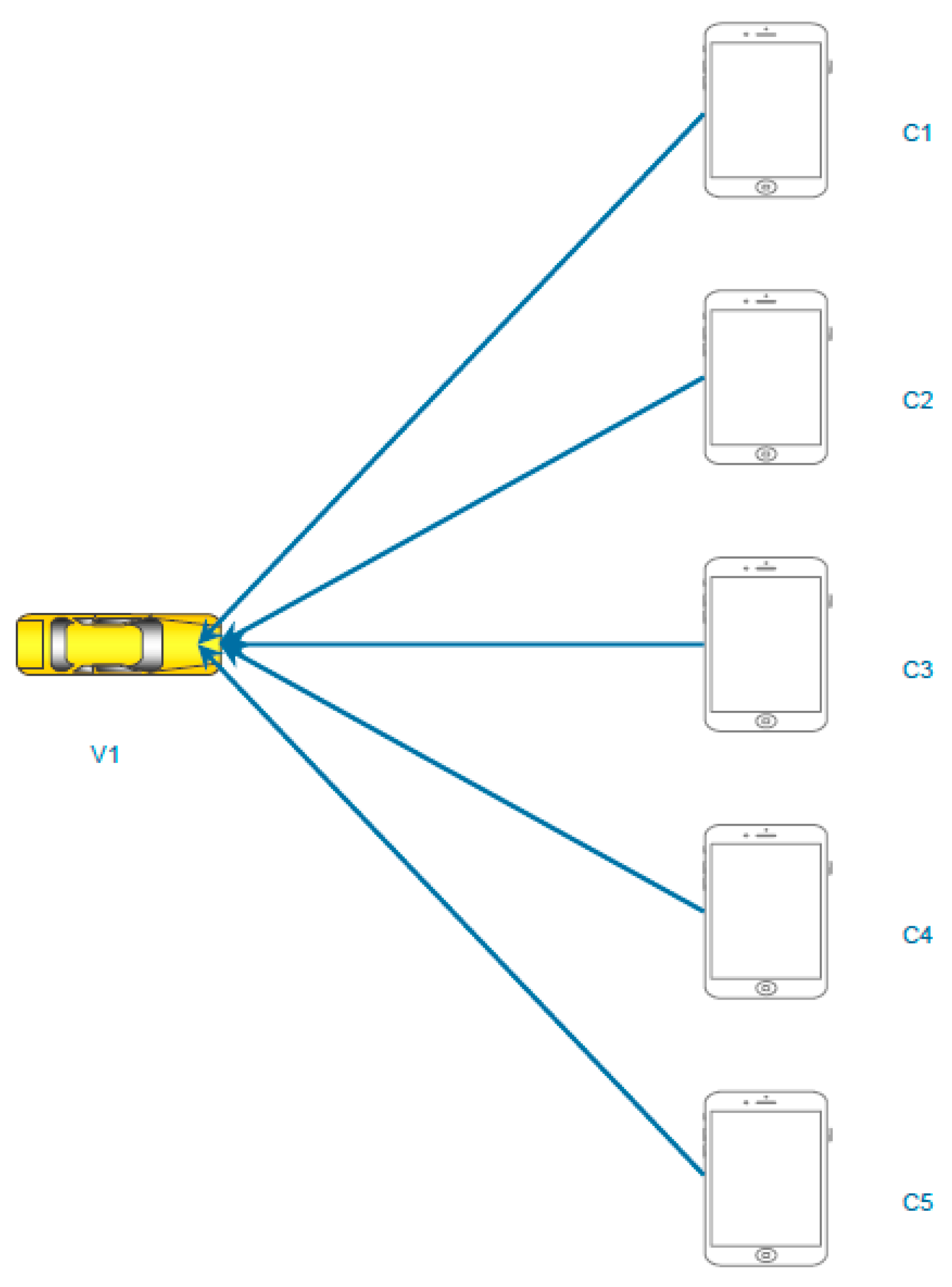
3.1. Network Architecture
3.2. System & Channel Model
3.3. Problem Formulation
4. Classification of Vulnerable Road Users
5. Reinforcement Learning Based Power Allocation
5.1. Learning Process
5.2. Proposed Methodology
6. One-to-Many Bipartite Matching
6.1. Graph Structure
6.2. Algorithm
| Algorithm 1. One-to-Many Bipartite Matching |
| Procedure: createConnections |
| Inputs: W(C,V): distance relation between all V and C |
| for each C unit do |
| CALL “assignVeh(C)” to connect C with optimum V unit |
| Procedure: assignVeh(C) |
| for each V do |
| if W(C,V) > 0 AND (NOT previously visited) |
| Vavailable ← V |
| for each Vavailable do |
| ConnV ← Number of C connected to Vavailable |
| if ConnV < min_connection |
| Vgroup(1) ← Vavailable |
| elseif ConnV ≥ min_connection AND ConnV < max_connection |
| Vgroup(2) ← Vavailable |
| else ConnV ≥ max_connection |
| Vgroup(3) ← Vavailable |
| if Vgroup(1) is NOT empty |
| Voptimum ← Vgroup(1) with max weight (lowest distance from current C) |
| Connect C and Voptimum |
| RETURN TRUE |
| if Vgroup(2) is NOT empty |
| Voptimum ← Vgroup(2) with max weight (lowest distance from current C) |
| Connect C and Voptimum |
| RETURN TRUE |
| if Vgroup(3) is NOT empty |
| Sort Vgroup(3) according to their distance cluster in ascending order |
| for each Vgroup(3) do |
| if ConnV(group_3) ≤ replacement weight AND assignVeh(C’) == TRUE |
| Voptimum ← Vgroup(3) |
| Connect C and Voptimum |
| RETURN TRUE |
| RETURN FALSE |
6.3. Complexity Analysis
7. Simulations and Results
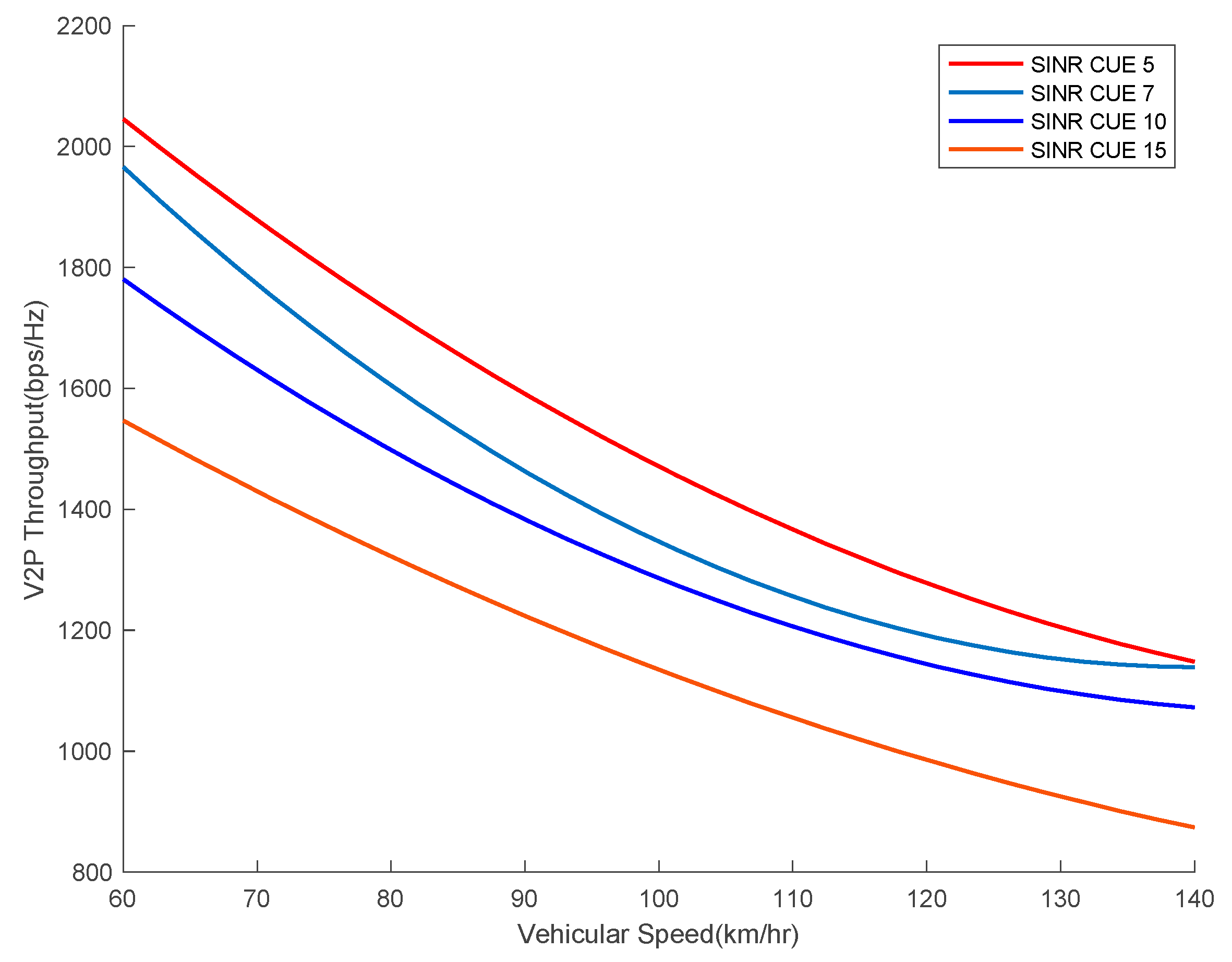
7.1. Vehicular Speed vs. V2P Capacity
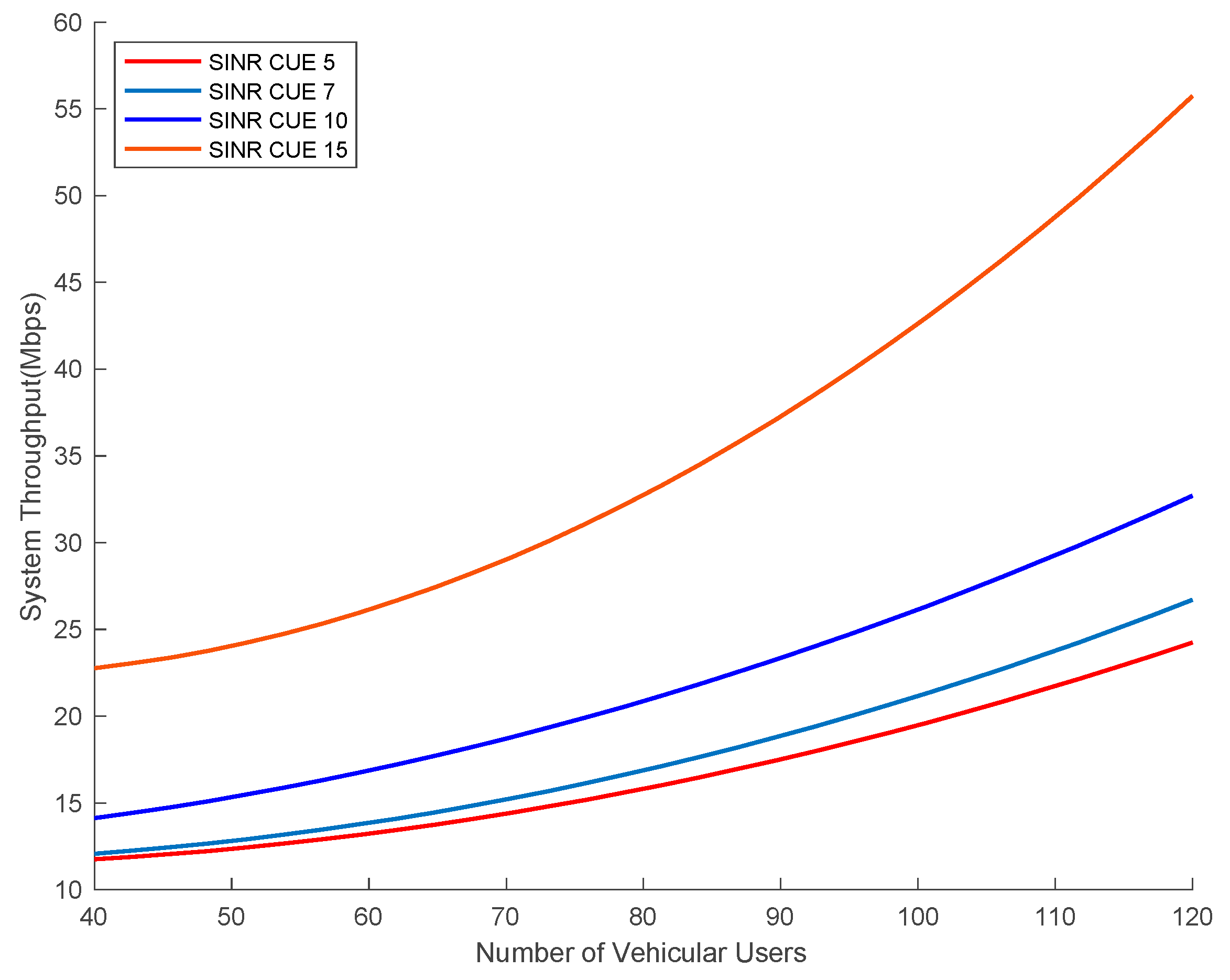
7.2. Number of Vehicles vs. System Throughput under Variable SINR
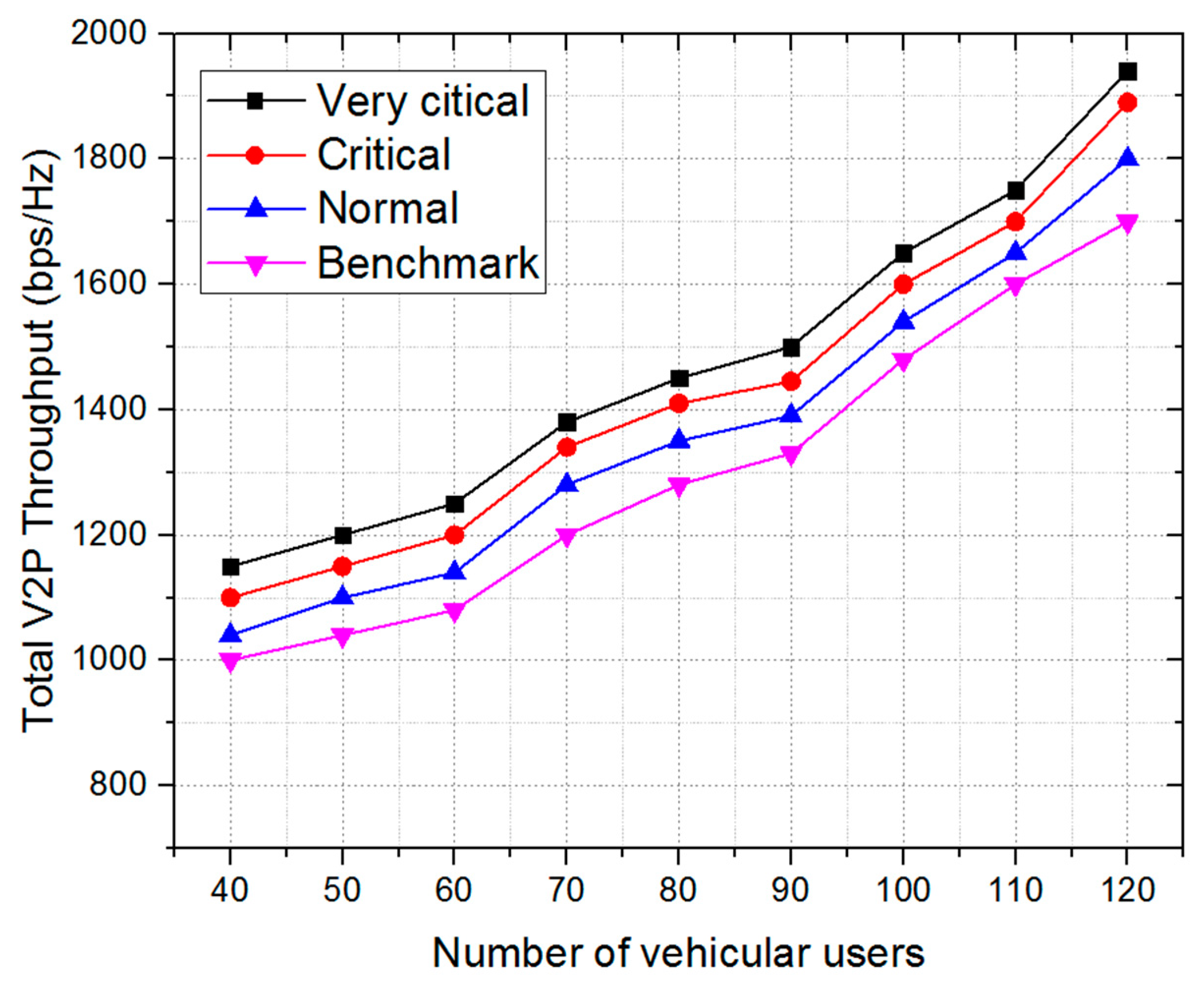
7.3. Number of Vehicles vs. V2P Throughput
7.4. Variable Threshold SINRs of CUEs
7.5. Number of VUEs and Reliability
8. Discussion and Future Work
9. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Höyhtyä, M.; Apilo, O.; Lasanen, M. Review of Latest Advances in 3GPP Standardization: D2D Communication in 5G Systems and Its Energy Consumption Models. Future Internet 2018, 10, 3. [Google Scholar] [CrossRef]
- Singh, P.K.; Nandi, S.K.; Nandi, S. A tutorial survey on vehicular communication state of the art, and future research directions. Veh. Commun. 2019, 18, 100164. [Google Scholar] [CrossRef]
- Loussaief, F.; Marouane, H.; Koubaa, H.; Zarai, F. Radio resource management for vehicular communication via cellular device to device links: Review and challenges. Telecommun. Syst. 2020, 73, 607–635. [Google Scholar] [CrossRef]
- Lozano Domínguez, J.M.; Mateo Sanguino, T.J. Review on V2X, I2X, and PSX Communications and Their Applications: A Comprehensive Analysis over Time. Sensors 2019, 19, 2756. [Google Scholar]
- Sewalkar, P.; Seitz, J. Vehicle-to-Pedestrian Communication for Vulnerable Road Users: Survey, Design Considerations, and Challenges. Sensors 2019, 19, 358. [Google Scholar] [CrossRef]
- Ding, H.; Ma, S.; Xing, C. Feasible D2D communication distance in D2D-enabled cellular networks. In Proceedings of the 2014 IEEE International Conference on Communication Systems, Macau, China, 19–21 November 2014; pp. 1–5. [Google Scholar]
- Masmoudi, A.; Mnif, K.; Zarai, F. A Survey on Radio Resource Allocation for V2X Communication. Wirel.Commun. Mob. Comput. 2019, 2019, 2430656. [Google Scholar] [CrossRef]
- Yu, N.; Mei, J.; Zhao, L.; Zheng, K.; Zhao, H. Radio resource allocation for D2D-based V2V communications with Lyapunov optimization. In Proceedings of the 2017 IEEE/CIC International Conference on Communications in China (ICCC), Qingdao, China, 22–24 October 2017; pp. 1–6. [Google Scholar]
- Liang, L.; Li, G.Y.; Xu, W. Resource Allocation for D2D-Enabled Vehicular Communications. IEEE Trans. Commun. 2017, 65, 3186–3197. [Google Scholar] [CrossRef]
- Liang, L.; Xie, S.; Li, G.Y.; Ding, Z.; Yu, X. Graph-Based Resource Sharing in Vehicular Communication. IEEE Trans. Wirel. Commun. 2018, 17, 4579–4592. [Google Scholar] [CrossRef]
- Souhir, F.E.; Belghith, A.; Zarai, F. A Reinforcement Learning-based Radio Resource Management Algorithm for D2D-based V2V Communication. In Proceedings of the 2019 15th International Wireless Communications & Mobile Computing Conference (IWCMC), Tangier, Morocco, 24–28 June 2019; pp. 1367–1372. [Google Scholar]
- Li, X.; Sun, Y.; Zhou, L.; Qi, A.; Zhou, S. A Resource Allocation Scheme Based on Immune Algorithm for D2D-Based Vehicular Communication Networks. IEEE Access 2019, 7, 122536–122543. [Google Scholar] [CrossRef]
- Nguyen, K.K.; Duong, T.Q.; Vien, N.A.; Le-Khac, N.; Nguyen, L.D. Distributed Deep Deterministic Policy Gradient for Power Allocation Control in D2D-Based V2V Communications. IEEE Access 2019, 7, 164533–164543. [Google Scholar] [CrossRef]
- Guo, C.; Liang, L.; Li, G.Y. Resource Allocation for High-Reliability Low-Latency Vehicular Communications With Packet Retransmission. IEEE Trans. Veh. Technol. 2019, 68, 6219–6230. [Google Scholar] [CrossRef]
- Yang, H.; Zheng, K.; Zhao, L.; Hanzo, L. Twin-Timescale Radio Resource Management for Ultra-Reliable and Low-Latency Vehicular Networks. IEEE Trans. Veh. Technol. 2020, 69, 1023–1036. [Google Scholar] [CrossRef]
- Abbas, F.; Fan, P.; Khan, Z. A Novel Low-Latency V2V Resource Allocation Scheme Based on Cellular V2X Communications. IEEE Trans. Intell. Transp. Syst. 2019, 20, 2185–2197. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, R.; Chen, C.; Cheng, X.; Yang, L.; Jin, Y. Interference Hypergraph-Based 3D Matching Resource Allocation Protocol for NOMA-V2X Networks. IEEE Access 2019, 7, 90789–90800. [Google Scholar] [CrossRef]
- Ashraf, M.I.; Bennis, M.; Perfecto, C.; Saad, W. Dynamic Proximity-Aware Resource Allocation in Vehicle-to-Vehicle (V2V) Communications. In Proceedings of the 2016 IEEE Globecom Workshops (GC Wkshps), Washington, DC, USA, 4–8 December 2016; pp. 1–6. [Google Scholar]
- Abdallah, A.; Mansour, M.M.; Chehab, A. A Distance-Based Power Control Scheme for D2D Communications Using Stochastic Geometry. In Proceedings of the 2017 IEEE 86th Vehicular Technology Conference (VTC-Fall), Toronto, ON, Canada, 24–27 September 2017; pp. 1–6. [Google Scholar]
- Lucas-Estan, M.C.; Gozalvez, J. Distance-Based Radio Resource Allocation for Device to Device Communications. In Proceedings of the 2017 IEEE 85th Vehicular Technology Conference (VTC Spring), Sydney, Australia, 4–7 June 2017; pp. 1–5. [Google Scholar]
- 3GPP. Evolved Universal Terrestrial Radio Access (E-UTRA); Further Advancements for E-UTRA Physical Layer Aspects. V9.0.0, TR 36.814. 2010. Available online: http://www.3gpp.org/ftp/Specs/html-info/36814.htm (accessed on 28 September 2020).
- Yokoyama, R.S.; Kimura, B.Y.L.; Villas, L.A.; Moreira, E.D.S. Measuring Distances with RSSI from Vehicular Short-Range Communications. In Proceedings of the 2015 IEEE International Conference on Computer and Information Technology; Ubiquitous Computing and Communications; Dependable, Autonomic and Secure Computing; Pervasive Intelligence and Computing, Liverpool, UK, 26–28 October 2015; pp. 100–107. [Google Scholar]
- 3GPP. Technical Specification Group Services and System Aspects; Proximity-Based Services (ProSe); Stage 2. TS 23.303, Version 13.3.0. 2016. Available online: https://portal.3gpp.org/desktopmodules/Specifications/SpecificationDetails.aspx?specificationId=840 (accessed on 28 September 2020).
- Ye, H.; Li, G.Y.; Juang, B.F. Deep Reinforcement Learning Based Resource Allocation for V2V Communications. IEEE Trans. Veh. Technol. 2019, 68, 3163–3173. [Google Scholar] [CrossRef]
- Nie, S.; Fan, Z.; Zhao, M.; Gu, X.; Zhang, L. Q-learning based power control algorithm for D2D communication. In Proceedings of the 2016 IEEE 27th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications (PIMRC), Valencia, Spain, 4–8 September 2016; pp. 1–6. [Google Scholar]
- Otterlo, M.V.; Wiering, M. Reinforcement Learning: State-of-the-Art; Springer: Berlin/Heidelberg, Germany, 2012; Volume 12. [Google Scholar]
- Gu, Y.; Saad, W.; Bennis, M.; Debbah, M.; Han, Z. Matching theory for future wireless networks: Fundamentals and applications. IEEE Commun. Mag. 2015, 53, 52–59. [Google Scholar] [CrossRef]
- Wei, Q.; Sun, W.; Bai, B.; Wang, L.; Ström, E.G.; Song, M. Resource allocation for V2X communications: A local search based 3D matching approach. In Proceedings of the 2017 IEEE International Conference on Communications (ICC), Paris, France, 21–25 May 2017; pp. 1–6. [Google Scholar]
- Khan, U.A.; Lee, S.S. Three-Dimensional Resource Allocation in D2D-based V2V Communication. Electronics 2019, 8, 962. [Google Scholar] [CrossRef]
- Dutta, A.; Asaithambi, A. One-to-many bipartite matching based coalition formation for multi-robot task allocation. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 2181–2187. [Google Scholar]
- Heineman, G.T.; Pollice, G.; Selkow, S. Algorithms in a Nutshell; Oreilly Media: Sebastopol, CA, USA, 2008; pp. 226–250. [Google Scholar]
- Chen, S.; Hu, J.; Shi, Y.; Zhao, L.; Li, W. A Vision of C-V2X: Technologies, Field Testing, and Challenges With Chinese Development. IEEE Internet Things J. 2020, 7, 3872–3881. [Google Scholar] [CrossRef]
- Ye, H.; Liang, L.; Li, G.Y.; Kim, J.; Lu, L.; Wu, M. Machine Learning for Vehicular Networks: Recent Advances and Application Examples. IEEE Veh. Technol. Mag. 2018, 13, 94–101. [Google Scholar] [CrossRef]
- Li, Z.; Guo, C. Multi-Agent Deep Reinforcement Learning Based Spectrum Allocation for D2D Underlay Communications. IEEE Trans. Veh. Technol. 2020, 69, 1828–1840. [Google Scholar] [CrossRef]
- Huang, W.; Chen, M.; Yang, Z.; Huang, N.; Pei, L. Resource Allocation for Relay-Assisted D2D Communications with Network Coding. In Proceedings of the 2018 IEEE 88th Vehicular Technology Conference (VTC-Fall), Chicago, IL, USA, 27–30 August 2018; pp. 1–5. [Google Scholar]
- Wang, J.; Rouil, R.A.; Cintron, F.J. Distributed Resource Allocation Schemes for Out-of-Coverage D2D Communications. In Proceedings of the 2019 IEEE Global Communications Conference (GLOBECOM), Waikoloa, HI, USA, 9–13 December 2019; pp. 1–7. [Google Scholar]
- Xiao, H.; Zhu, D.; Chronopoulos, A.T. Power Allocation With Energy Efficiency Optimization in Cellular D2D-Based V2X Communication Network. IEEE Trans. Intell. Transp. Syst. 2019, 1–11. [Google Scholar] [CrossRef]
- Deng, L.; Wu, G.; Fu, J.; Zhang, Y.; Yang, Y. Joint Resource Allocation and Trajectory Control for UAV-Enabled Vehicular Communications. IEEE Access 2019, 7, 132806–132815. [Google Scholar] [CrossRef]
- Yang, Y.; Feng, L.; Zhang, C.; Ou, Q.; Li, W. Resource allocation for virtual reality content sharing based on 5G D2D multicast communication. EURASIP J. Wirel. Commun. Netw. 2020, 2020, 112. [Google Scholar] [CrossRef]
- Abbas, F.; Fan, P. A Hybrid Low-Latency D2D Resource Allocation Scheme Based on Cellular V2X Networks. In Proceedings of the 2018 IEEE International Conference on Communications Workshops (ICC Workshops), Kansas City, MO, USA, 20–24 May 2018; pp. 1–6. [Google Scholar]




| Parameter | V2P Link | CUE Link |
|---|---|---|
| Path loss model | 127 + 30 log10(ℓ) | 128.1 + 37.6 log10(ℓ) [21] |
| Symbol | Definition |
|---|---|
| Desired channel Gain between CUE and BS | |
| Interference channel gain from V2P to CUE | |
| Desired channel gain between V2P | |
| Interference channel gain from CUE to V2P | |
| CUE transmit power | |
| V2P transmit power | |
| Channel gain between two users | |
| Path loss | |
| Log normal shadowing | |
| is the distance between two users and γ is the decay exponent | |
| Small scale fading component | |
| Maximum allowable transmit power for CUE | |
| Maximum allowable transmit power for V2P | |
| Probability of outage | |
| Threshold SINR for CUE |
| Very Critical | Critical | Normal | |
|---|---|---|---|
| V2P Distance | <20 m | 20–35 m | 35–50 m |
| Parameters | Value |
|---|---|
| Operating Frequency | 2 GHz |
| Bandwidth | 10 MHz |
| Cell Radius | 500 m |
| Vehicular Speed | 60–140 km/h |
| Discount Factor (η) | v.c = 0.8, c = 0.5, n =0.3 |
| Maximum Transmit Power | 23 dBm |
| AWGN Noise | –114 dBm |
| SINR Thresholds (γ0) | 5, 7, 10, 15 dBs |
| Number of Vehicular User Equipment (VUEs) | Variable |
| Number of Cellular User Equipment (CUEs) | Variable |
| Learning Rate (α) | 0.5 |
| D2D Communication Radius | 50 m |
| Highway Length | 1 km |
| Number of Lanes | 1 |
| Number of Resource Blocks | 50 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, U.A.; Lee, S.S. Distance-Based Resource Allocation for Vehicle-to-Pedestrian Safety Communication. Electronics 2020, 9, 1640. https://doi.org/10.3390/electronics9101640
Khan UA, Lee SS. Distance-Based Resource Allocation for Vehicle-to-Pedestrian Safety Communication. Electronics. 2020; 9(10):1640. https://doi.org/10.3390/electronics9101640
Chicago/Turabian StyleKhan, Usman Ali, and Sang Sun Lee. 2020. "Distance-Based Resource Allocation for Vehicle-to-Pedestrian Safety Communication" Electronics 9, no. 10: 1640. https://doi.org/10.3390/electronics9101640
APA StyleKhan, U. A., & Lee, S. S. (2020). Distance-Based Resource Allocation for Vehicle-to-Pedestrian Safety Communication. Electronics, 9(10), 1640. https://doi.org/10.3390/electronics9101640





