Abstract
This paper presents a new control approach for the trajectory tracking of a quadrotor in the presence of external disturbances. Unlike in previous studies using hierarchical control strategies, a nonlinear controller is designed by introducing new state transformations that can use Euler angles as virtual control inputs. Thus, the proposed method can eliminate the timescale separation assumption of hierarchical control strategies. To estimate the external disturbances involved in the translational and rotational dynamics of the quadrotor, disturbance observers are developed. Using state transformations and estimates of external disturbances, we design a robust nonlinear controller based on the dynamic surface control method. The stability of the closed-loop system is analyzed without separation into two subsystems. From the Lyapunov stability theory, it is proven that all error signals in the closed-loop system are uniformly ultimately bounded and can be made arbitrarily small. Finally, simulation results are presented to demonstrate the performance of the proposed controller.
1. Introduction
Quadrotors are widely used for military and commercial purposes because of their capabilities of vertical take-off and landing (VTOL) and free mobility [1]. A quadrotor requires position and attitude control for autonomous flight. However, it is difficult to design an appropriate controller because the quadrotor model is underactuated and has strong nonlinear couplings between its dynamic states [2]. Furthermore, robustness against disturbances such as wind gusts during the operation of the quadrotor is essential for control performance [3]. Therefore, various control methods have been proposed to solve these problems.
To address the nonlinear coupling problem, linear control methods such as PID [4,5,6], LQR [7,8], and [9,10] based on linearized models were proposed. To obtain a linearized model, the assumption that the quadrotor is moving around a hovering position is required, which causes the performance of linear control methods to degrade when aggressive maneuvers and external disturbances are applied [11]. Therefore, as an alternative, nonlinear control methods have received considerable attention recently. The main difficulty in designing nonlinear controllers is that a quadrotor is an underactuated system with six DOFs and four control inputs. For such an underactuated system, methods of designing controllers in accordance with particular flight modes were proposed in [12,13]. However, it is difficult to prove the overall stability and/or different flight control modes cannot be used at the same time. To overcome this drawback, a hierarchical control strategy based on inner- and outer-loop subsystems is generally used [14,15,16,17,18,19,20,21,22,23]. Using this strategy, it is possible to prove the stability of the closed-loop system and control the position and attitude of the quadrotor simultaneously. Therefore, nonlinear controllers such as backstepping [16], adaptive [17,18], sliding mode [19,20,21], and neural-network-based controllers [22,23] have all been proposed using hierarchical control strategies. In a hierarchical control strategy, the control system is divided into two subsystems. First, a position controller is designed to track the desired position. Then, the thrust force and desired Euler angles are derived by the position controller under the assumption that the Euler angles track the desired angles instantaneously. Furthermore, the desired Euler angles are derived without considering the disturbances involved in the translational dynamics of the quadrotor, which can degrade the tracking performance. Thus, the control performance of the position controller is directly affected by the convergence rate and accuracy of the attitude controller. For a fast response of the attitude controller, sufficiently large gains are required, but this can lead to a large overshoot of the control inputs [24]. It is well known that physical systems have limited control inputs and that a large overshoot of the control inputs is impractical. Although command filter [24,25], finite-time control [26,27], and invariant dynamic surface [28] methods were proposed to enable fast convergence of the attitude controller, the final control systems are still designed using hierarchical strategies. Moreover, the stability analysis is performed separately for the two subsystems due to the nature of hierarchical control.
Motivated by these observations, we propose a new theoretical control approach different from hierarchical control for the trajectory tracking of a quadrotor in the presence of disturbances. In the proposed approach, the controller is designed using new state transformations to handle the properties of underactuation, nonlinearity, and strong coupling, and a fast attitude control response is not required. Furthermore, disturbances in the translational dynamics of the quadrotor are considered to obtain the desired Euler angles. This implies that unlike a hierarchical strategy, the proposed method can achieve the desired tracking performance even if we choose low gains and disturbances exist in the translational dynamics. To address disturbances including wind and unstructured uncertainty, a disturbance-observer-based nonlinear controller is designed. From the Lyapunov stability theory, the stability of the proposed method is established without separation into two subsystems. The main contributions of this paper are twofold.
- (1)
- A new control approach different from a hierarchical strategy is presented based on state transformations. Since the proposed method does not require the instantaneous convergence of attitude control and obtains the desired Euler angles while considering disturbances, the desired tracking performance can be achieved with low gains.
- (2)
- The stability of the proposed method is analyzed without separation into two subsystems. Thus, the controller is designed without the restrictive assumption known as timescale separation (see details in [29]).
2. Problem Formulation
Consider the quadrotor configuration shown in Figure 1. A rigid-body model of the quadrotor can be given as follows [30]:
where is the position vector of the center of mass in the inertial frame, is the Euler angle vector that describes the orientation of the body-fixed frame with respect to the inertial frame, is the gravitational acceleration vector, is the inertia matrix with respect to the body-fixed frame, is the disturbance vector for the translational dynamics, is the disturbance vector for the rotational dynamics, m is the total mass of the quadrotor, F is the total thrust force exerted by the rotors, and is the torque vector in the body-fixed frame. The vectors and are given below:
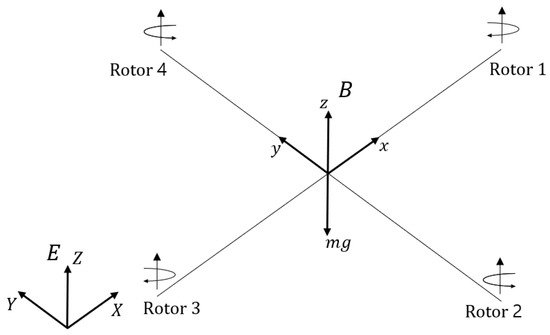
Figure 1.
Quadrotor configuration frame system with body fixed frame B and inertial frame E.
The angular velocity of each rotor for can be calculated from the control inputs F and . The relationship is given by
where b is the lift coefficient, c is the anti-torque coefficient, and l is the distance from the rotor to the center of mass. In this paper, we will focus on designing the control inputs F and .
Assumption 1.
The time derivatives of and are bounded such that and , where and are unknown positive constants.
The control objective is to design the control inputs F and to track the reference trajectory given by a reference position vector and a reference yaw angle . That is, we will design the control inputs to guarantee that
where is a positive constant.
Assumption 2.
The reference signals and are chosen to be three times differentiable, and for any positive constant .
Remark 1.
(i) Assumption 1 is commonly found in some works of the disturbance observer (DOB)-based control for mechanical systems [31,32,33]. This assumption is reasonable when taking into account the finite available energy of the disturbance [34]. (ii) Assumption 2 ensures that we can use the dynamic surface control method for controller design and stability analysis for continuous systems. This assumption is valid because the reference signals can be chosen arbitrarily by the operator.
3. Main Result
The translational dynamics described by (1) are underactuated and involve strong nonlinear couplings between the dynamic states. To address these problems, previously proposed controllers have been designed using a linearized version of (1) under the assumption that the quadrotor is operating very near a hovering position. However, this assumption restricts the quadrotor’s ability to execute complex flight maneuvers [12]. Although nonlinear control using a hierarchical control strategy can solve this problem, it requires the timescale separation assumption. To overcome these limitations, we introduce the following state transformations:
where and are new state variables.
Remark 2.
From (5), we obtain
To design the controller, let us define the following errors:
where , , and are virtual controls and for is the signal passed through a first-order filter, i.e., and . In these expressions, , , and are positive-definite symmetric matrices, and the matrix is given below:
Step 1: Using (7), (8), (9), and (11), we can write the error dynamics of as
where , , and . To design the control laws F and , we take the Lyapunov function
where , with being the estimate of the disturbance vector . Differentiating both sides of (13) along the solution of (12) yields
From (14), we choose F and to be
where ; , , , and are positive design constants; is the signum function; and is obtained from the following disturbance observer:
with a positive-definite symmetric matrix . Using (1) and (16), we have
Note that the positive design constant is used to prevent the singularity of the virtual control in (15).
Remark 3.
The filtered signal of the virtual control will be used as the desired Euler angles to be tracked in the next step. Unlike in hierarchical control, the Euler angles do not need to be the same as the desired angles, and disturbances are considered when deriving the virtual control . Therefore, the proposed method does not require instantaneous convergence of the attitude errors and can achieve improved tracking performance.
Remark 4.
If we use the backstepping technique, the time derivative of the virtual control is required to design the actual torque in the next step; however, we can see from (15) that the time derivative of includes the second time derivative of with an unknown disturbance . The dynamic surface control (DSC) method [35] can be used to address this problem because it does not require the time derivative of the virtual control. Thus, the DSC method is applied to design the virtual control .
Step 2: Using (5), (9), (10), and (11), we can write the error dynamics of as
where . To design the virtual control , we take the Lyapunov function
To design the actual control , we take the Lyapunov function
where , with being the estimate of the disturbance vector . Differentiating both sides of (25) along the solution of (24) results in
From (26), we choose the actual control to be
where is a positive gain and is obtained from the following disturbance observer:
with a positive-definite symmetric matrix .
Let . We now present the main result of our paper in the following theorem.
Theorem 1.
Consider the quadrotor model given in (1) and (2), controlled by the control inputs F and given in (15) and (27) together with the disturbance observers given in (16) and (28) under Assumptions 1 and 2. For any initial conditions satisfying , where is a positive constant, it is ensured that for all and , where is a positive constant that can be made arbitrarily small.
Proof.
From (15) and (22), one can show that and for some continuous functions and . By Assumption 2, there exists a set . Consider the set . Since and are compact, there exist positive constants and such that and on . Then, by Assumption 1 and Young’s inequality, (31) can be written as
where and are identity matrices, is a positive constant, and . Choosing , , , , , and results in
where and . Integrating both sides of (33) yields
One can design the control gains to ensure that . Therefore, from (34), for all . Additionally, where and thus, . By properly choosing , we can make arbitrarily small. This completes the proof. □
Remark 5.
As shown in the proof of Theorem 1, the overall stability of the proposed method is proven without separation into the inner- and outer-loop subsystems commonly used in hierarchical control strategies. Therefore, the timescale separation assumption is not required. Furthermore, unlike [26,27,28], there is no need to prove in advance that the attitude errors are bounded.
4. Simulations
In this section, we present simulations conducted to demonstrate the performance of the proposed method. For comparison, simulation results for the robust backstepping sliding mode control (RB-SMC) method [36] using a hierarchical control strategy are also given. To reduce chattering, we modified the RB-SMC algorithm to use the hyperbolic tangent function instead of the signum function in the simulations. The physical parameters of the quadrotor taken from [37] are summarized as follows: kg, kg·m, kg· m, kg·m, and m/s. To verify the robustness of the proposed controller, external disturbances and were considered in the simulations. The initial position of the quadrotor and the reference trajectory were chosen to be and , respectively. The reference yaw angle was set to . The design parameters of the proposed method were selected to be , , , , , and . To show the efficiency of the proposed method, we selected the control gains of the RB-SMC method necessary to achieve the same position tracking results as our method through trial and error.
The tracking results are provided in Figure 2 and Figure 3. These figures show that both methods can track the desired trajectory successfully and that there are no constraints on the Euler angles. The steady-state root mean square errors are and , with the proposed method being slightly more accurate. The main difference can be seen from Figure 2d and Figure 3d, namely, the settling time of the RB-SMC method is more than two times as fast as that of our method. This observation indicates that the proposed method can achieve results similar to those achieved through hierarchical control without requiring fast convergence of the attitude errors. Thus, we can obtain a smaller overshoot of the control inputs that can be achieved with the hierarchical control strategy because it is possible to design the controller with low gains. This is verified by Figure 4. In Figure 2e,f, the disturbance errors and converge to the bounds of and , respectively. Figure 5 shows the linear and angular velocities of the quadrotor. It is demonstrated that both constant and time-varying disturbances can be effectively estimated by the disturbance observers.
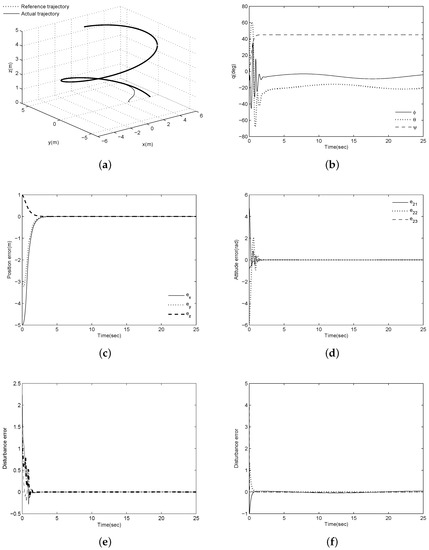
Figure 2.
Tracking results of the proposed method: (a) Three-dimensional trajectory; (b) Euler angles ; (c) Position tracking errors; (d) Attitude tracking errors; (e) (solid: , dashed: , dotted: ); (f) (solid: , dashed: , dotted: ).
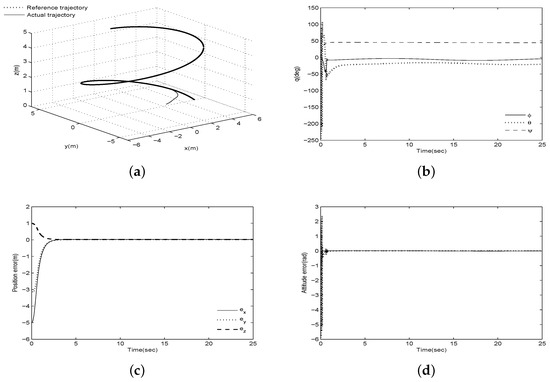
Figure 3.
Tracking results of the robust backstepping sliding mode control (RB-SMC) method: (a) Three-dimensional trajectory; (b) Euler angles ; (c) Position tracking errors; (d) Attitude tracking errors.
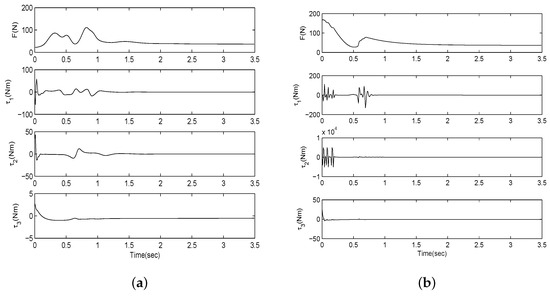
Figure 4.
Control inputs: (a) Proposed method; (b) RBS-SMC method.
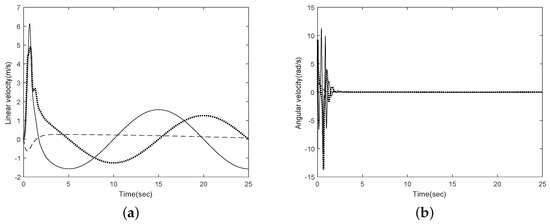
Figure 5.
Velocities: (a) Linear velocities (solid: , dotted: , dashed: ); (b) angular velocities (solid: , dotted: , dashed: ).
To make the simulation results more realistic, we added normally distributed random noise with mean 0 and covariance to the measurements of the Euler angle vector and the angular velocity vector . The tracking results in a noisy environment are depicted in Figure 6. These figures show that even if there is noise, good tracking performance can be achieved with the proposed method. Therefore, we can conclude that the proposed controller is effective for the trajectory tracking of a quadrotor in the presence of external disturbances.
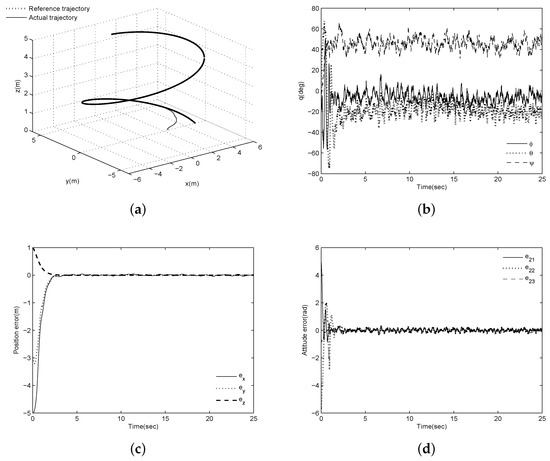
Figure 6.
Tracking results in noise environment: (a) Three-dimensional trajectory; (b) Euler angles ; (c) position tracking errors; (d) attitude tracking errors.
5. Conclusions
A disturbance observer-based nonlinear controller has been presented for the trajectory tracking of a quadrotor in the presence of external disturbances. New state transformations are introduced to design the controller without using a hierarchical control strategy, and disturbance observers are developed to estimate external disturbances. Since the instantaneous convergence of attitude control is not required, the desired tracking performance is achieved with low gains. The stability of the proposed method is analyzed without separation into the inner- and outer-loop subsystems. Thus, the controller is designed without the restrictive assumption known as timescale separation. From the Lyapunov stability theorem, it is proven that all error signals in the closed-loop system are uniformly ultimately bounded. Simulation results, including a comparison, demonstrate that the proposed controller is effective for the trajectory tracking of the quadrotor in the presence of external disturbances. In future work, we will validate the performance of the proposed method based on experimental results.
Author Contributions
The authors contributed to this work as follows. S.W.H. and B.S.P. contributed to writing—original draft; formal analysis; investigation; software and methodology. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (NRF-2019R1A2C1087552).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Altug, E.; Ostrowski, J.P.; Mahony, R. Control of a quadrotor helicopter using visual feedback. In Proceedings of the IEEE International Conference Robotics and Automation, Washington, DC, USA, 11–15 May 2002; pp. 72–77. [Google Scholar]
- Shao, X.; Liu, N.; Liu, J.; Wang, H. Model-assisted extended state observer and dynamic surface control-based trajectory tracking for quadrotors via output-feedback mechanism. Int. J. Robust Nonlinear Control 2018, 28, 2404–2423. [Google Scholar] [CrossRef]
- Xiao, B.; Yin, S. A new disturbance attenuation control scheme for quadrotor unmanned aerial vehicles. IEEE Trans. Ind. Inform. 2017, 13, 2922–2932. [Google Scholar] [CrossRef]
- Tayebi, A.; McGilvray, S. Attitude stabilization of a VTOL quadrotor aircraft. IEEE Trans. Control Syst. Technol. 2006, 14, 562–571. [Google Scholar] [CrossRef]
- Grzonka, S.; Grisetti, G.; Burgard, W. A fully autonomous indoor quadrotor. IEEE Trans. Robot. 2012, 28, 90–100. [Google Scholar] [CrossRef]
- Mahony, R.; Kumar, V.; Corke, P. Modeling, estimation, and control of quadrotor. IEEE Trans. Robot. Autom. Mag. 2012, 19, 20–32. [Google Scholar] [CrossRef]
- Bouabdallah, S.; Noth, A.; Siegwart, R. PID vs LQ control techniques applied to an indoor micro quadrotor. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots, Sendai, Japan, 28 September–2 October 2004; pp. 2451–2456. [Google Scholar]
- Liu, H.; Lu, G.; Zhong, Y. Robust LQR attitude control of a 3-DOF laboratory helicopter for aggressive maneuvers. IEEE Trans. Ind. Electron. 2013, 60, 4627–4636. [Google Scholar] [CrossRef]
- Raffo, G.V.; Ortega, M.G.; Rubio, F.R. An underactuated H∞ control strategy for a quadrotor helicopter. In Proceedings of the European Control Conference, Budapest, Hungary, 23–26 August 2009; pp. 3845–3850. [Google Scholar]
- Gadewadikar, J.; Lewis, F.L.; Subbarao, K.; Peng, K.; Chen, B.M. H-infinity static output-feedback control for rotorcraft. J. Int. Robot. Syst. 2009, 54, 629–646. [Google Scholar] [CrossRef]
- Mellinger, D.; Kumar, V. Minimum snap trajectory generation and control for quadrotors. In Proceedings of the IEEE International Conference on Robotics Automation, Shanghai, China, 9–13 May 2011; pp. 2520–2525. [Google Scholar]
- Lee, T.; Leok, M.; McClamroch, N.H. Nonlinear robust tracking control of a quadrotor UAV on SE(3). Asian J. Control 2013, 15, 391–408. [Google Scholar] [CrossRef]
- Hua, M.D.; Hamel, T.; Morin, P.; Samson, C. A control approach for thrust-propelled underactuated vehicles and its application to VTOL drones. IEEE Trans. Autom. Control 2009, 54, 1837–1853. [Google Scholar]
- Hua, M.D.; Hamel, T.; Morin, P.; Samson, C. Introduction to feedback control of underactuated VTOL vehicles: A review of basic control design ideas and principles. IEEE Trans. Control Syst. Technol. 2013, 33, 61–75. [Google Scholar]
- Zou, Y. Nonlinear robust adaptive hierarchical sliding mode control approach for quadrotors. Int. J. Robust Nonlinear Control 2017, 27, 925–941. [Google Scholar] [CrossRef]
- Chen, F.; Lei, W.; Zhang, K.; Tao, G.; Jiang, B. A novel nonlinear resilient control for a quadrotor UAV via back-stepping control and nonlinear disturbance observer. Nonlinear Dyn. 2016, 85, 1281–1295. [Google Scholar] [CrossRef]
- Lee, C.T.; Tsai, C.C. Adaptive backstepping integral control of a small-scale helicopter for airdrop missions. Asian J. Control 2010, 12, 531–541. [Google Scholar] [CrossRef]
- Zhao, B.; Xian, B.; Zhang, Y.; Zhang, X. Nonlinear robust adaptive tracking control of a quadrotor UAV via immersion and invariance methodology. IEEE Trans. Ind. Electron. 2015, 62, 2891–2902. [Google Scholar] [CrossRef]
- Xiong, J.; Zheng, E. Position and attitude tracking control for a quadrotor. ISA Trans. 2014, 53, 725–731. [Google Scholar] [CrossRef]
- Almakhles, D.J. Robust backstepping sliding mode control for a quadrotor trajectory tracking application. IEEE Access 2020, 8, 5515–5525. [Google Scholar] [CrossRef]
- Castan˜eda, H.; Gordillo, J.L. Embedded flight control based on adaptive sliding mode strategy for a quadrotor micro air vehicle. Electronics 2019, 8, 793. [Google Scholar] [CrossRef]
- Dierks, T.; Jagannathan, S. Output feedback control of a quadrotor UAV using neural networks. IEEE Trans. Neural Netw. 2010, 21, 50–66. [Google Scholar] [CrossRef]
- Shin, J.; Kim, H.J.; Kim, Y.; Dixon, W.E. Autonomous flight of the rotorcraft-based UAV using RISE feedback and NN feedforward terms. IEEE Trans. Control Syst. Technol. 2012, 20, 1392–1399. [Google Scholar] [CrossRef]
- Hu, J.; Zhang, H. Immersion and invariance based command-filtered adaptive backstepping control of VTOL vehicles. Automatica 2013, 49, 2160–2167. [Google Scholar] [CrossRef]
- Zou, Z. Trajectory tracking control design with command-filtered compensation for a quadrotor. IET Control Theory Appl. 2010, 4, 2343–2355. [Google Scholar]
- Jiang, T.; Lin, D.; Song, T. Finite-time backstepping control for quadrotors with disturbances and input constraints. IEEE Access 2018, 6, 62037–62049. [Google Scholar] [CrossRef]
- Tian, B.; Lu, H.; Zou, Z.; Zong, Q.; Zhang, Y. Multivariable finite-time output feedback trajectory tracking control of quadrotor helicopters. Int. J. Robust Nonlinear Control 2018, 28, 281–295. [Google Scholar] [CrossRef]
- Kim, S.; Ahn, C.K.; Shi, P. Performance recovery tracking-controller for quadcopters via invariant dynamic surface approach. IEEE Trans. Ind. Inform. 2019, 15, 5235–5243. [Google Scholar] [CrossRef]
- Lee, T.; Kim, Y. Nonlinear adaptive flight control using backstepping and neural networks controller. J. Guid. Control Dyn. 2001, 24, 675–682. [Google Scholar] [CrossRef]
- Bouabdallah, S.; Siegwart, R. Backstepping and sliding-mode techniques applied to an indoor micro quadrotor. In Proceedings of the IEEE International Conference on Robotics Automatic, Barcelona, Spain, 18–22 April 2005; pp. 2247–2252. [Google Scholar]
- Do, K.K. Practical formation control of multiple underactuated ships with limited sensing ranges. Robot. Auton. Syst. 2011, 59, 457–471. [Google Scholar] [CrossRef]
- Mohammadia, A.; Tavakoli, M.; Marquez, H.J.; Hashemzadeh, F. Nonlinear disturbance observer design for robotic manipulators. Control Eng. Pract. 2013, 21, 253267. [Google Scholar] [CrossRef]
- Chen, W.H.; Ballance, D.J.; Gawthrop, P.J.; O’Reilly, J. A nonlinear disturbance observer for robotic manipulators. IEEE Trans. Ind. Electron. 2000, 47, 932–938. [Google Scholar] [CrossRef]
- Chen, M.; Shi, P.; Lim, C. Robust constrained control for MIMO nonlinear systems based on disturbance observer. IEEE Trans. Autom. Control 2015, 60, 3281–3286. [Google Scholar] [CrossRef]
- Swaroop, D.; Hedrick, J.K.; Yip, P.P.; Gerdes, J.C. Dynamic surface control for a class of nonlinear systems. IEEE Trans. Autom. Control 2000, 45, 1893–1899. [Google Scholar] [CrossRef]
- Chen, F.; Jiang, R.; Zhang, K.; Jiang, B.; Tao, G. Robust backstepping sliding mode control and observer-based fault estimation for a quadrotor UAV. IEEE Trans. Ind. Electron. 2016, 63, 5044–5056. [Google Scholar] [CrossRef]
- Pounds, P.; Mahony, R.; Corke, P. Modeling and control of a large quadrotor robot. Control Eng. Pract. 2010, 18, 691–699. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).