Fallen People Detection Capabilities Using Assistive Robot
Abstract
1. Introduction
- several scenarios with variable light conditions,
- different person sizes,
- images with more than one actor,
- persons wearing different clothes,
- several lying-position perspectives and
- resting and fallen persons.
2. Vision-Based System Overview
- high variability of possible body orientations on the floor,
- different person sizes,
- wide range of background structures and scenarios and
- occlusions being frequent cases in the fall detection context.
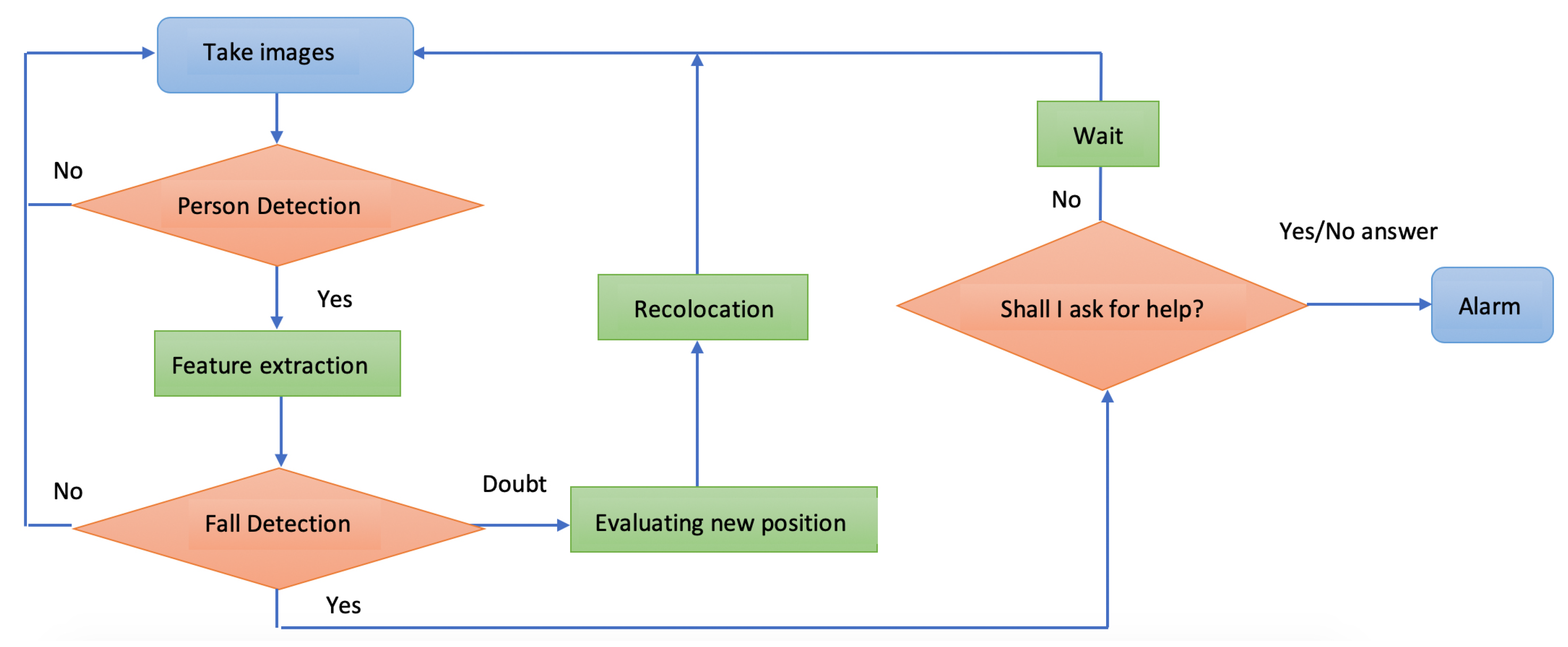
3. Proposed Fall Detection Approach
- Take a single image.
- Person detection. Results are the coordinates of the bounding box of the detected human body.
- Feature extraction from the bounding box coordinates.
- Fall identification.
- –
- Nonfall detection—continue taking new images.
- –
- Fall detection—ask for confirmation of the fall.
- –
- Doubt detection—the bounding box is too small, too big, or is located at the edges of the image. The robot needs to relocate itself to center the possible fall detection with the proper dimensions.
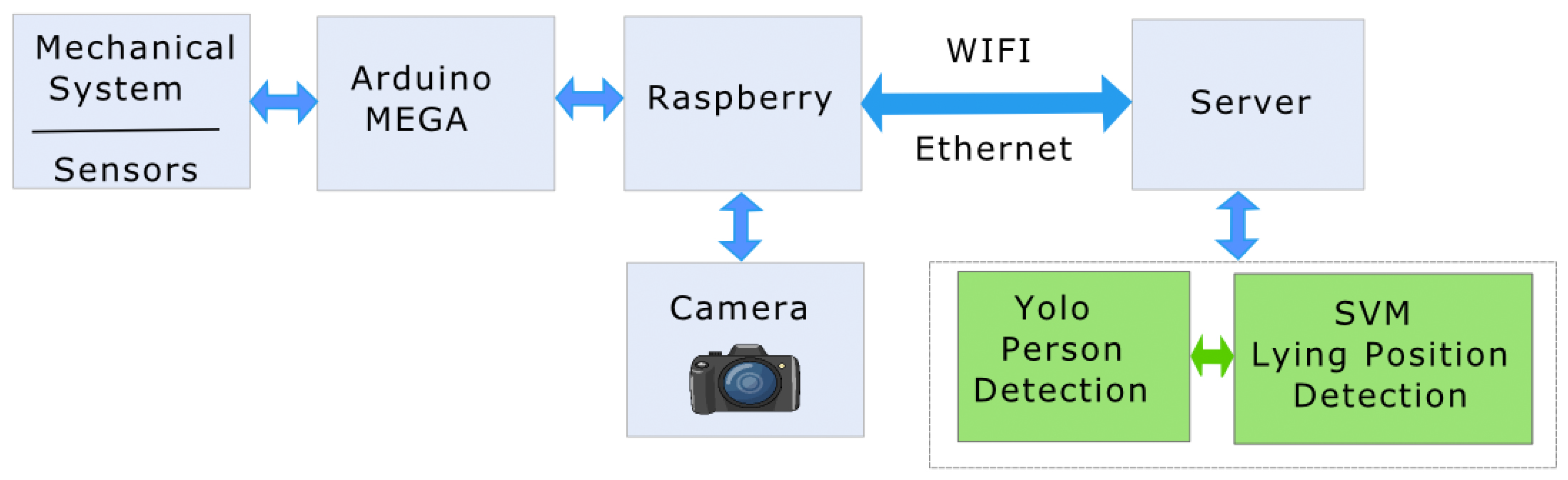
3.1. System Architecture
3.2. Deep Learning-Based Person Detection
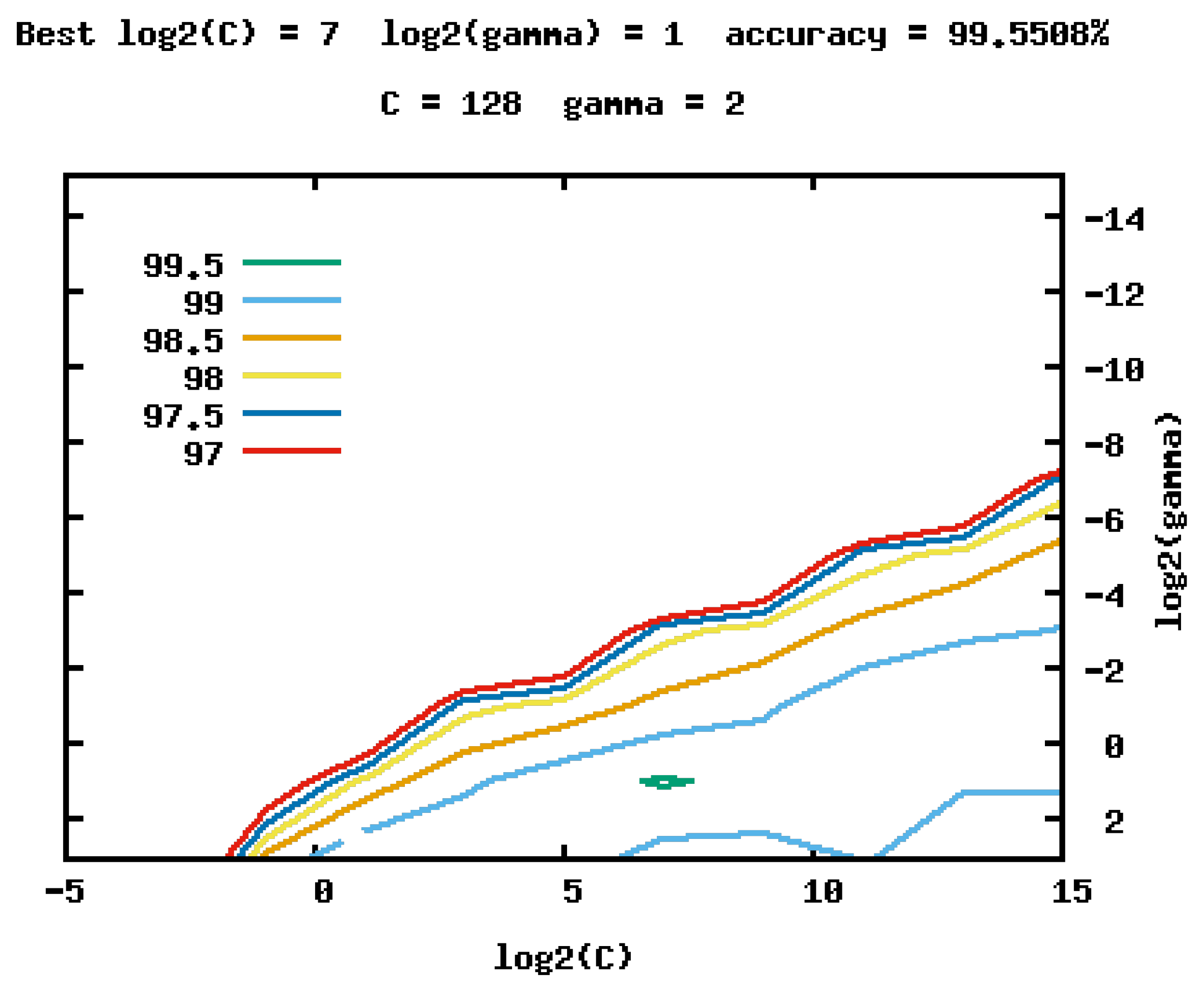
3.3. Learning-Based Fall/Nonfall Classification
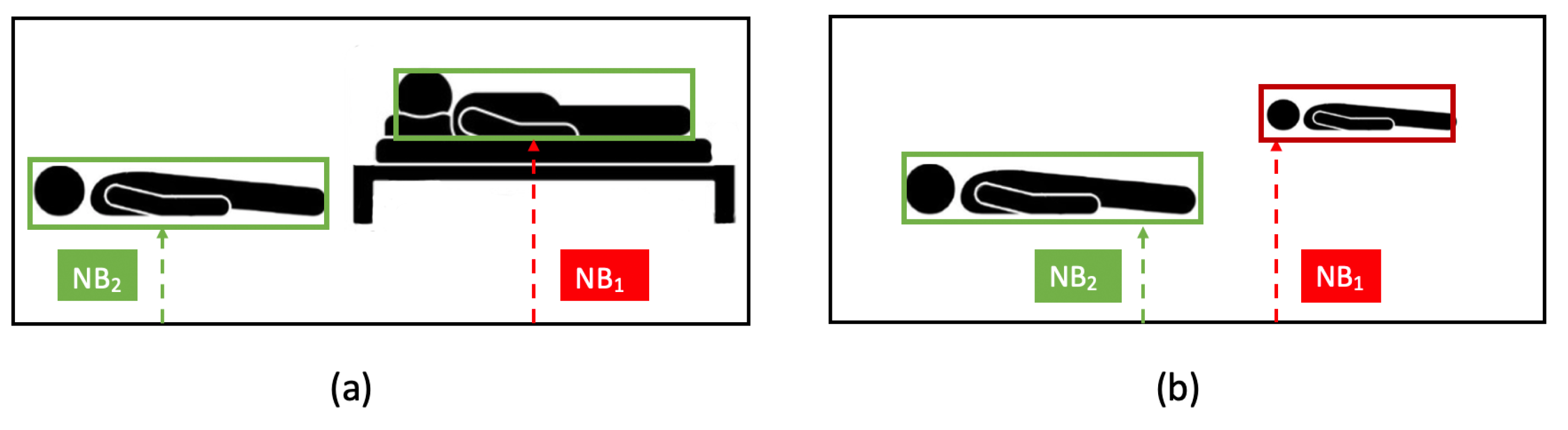
- Aspect ratio of bounding box, :
- Normalized bounding box width, :
- Normalized bounding box bottom coordinate, :
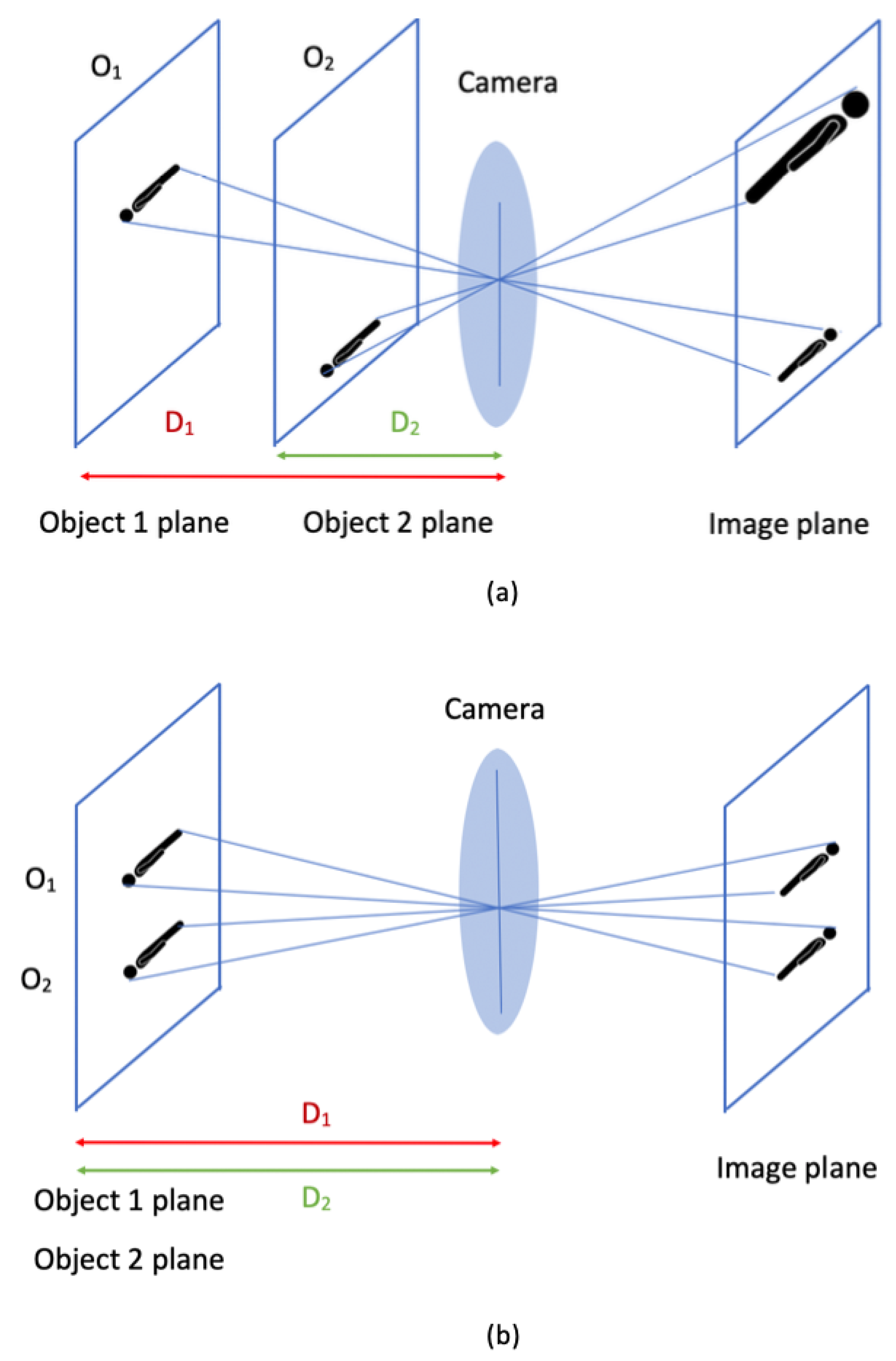
- Objects with the same size at different distances from the camera (object planes) appear with a different size (pixels) in the image plane; the closest one is visible in a larger size (Figure 5a);
- objects with the same size at the same distance to the camera (object planes) appear with the same size (pixels) in the image plane (Figure 5b). If objects are at different heights in the object plane, the same happens in the image plane.
4. Experiment Results
4.1. FPDS Dataset
4.2. Metrics
- True positives ()—number of falls correctly detected,
- false negatives ()—number of falls not detected and
- false positives ()—number of nonfalls detected as falls.
4.3. Experiment 1: Fall Classification
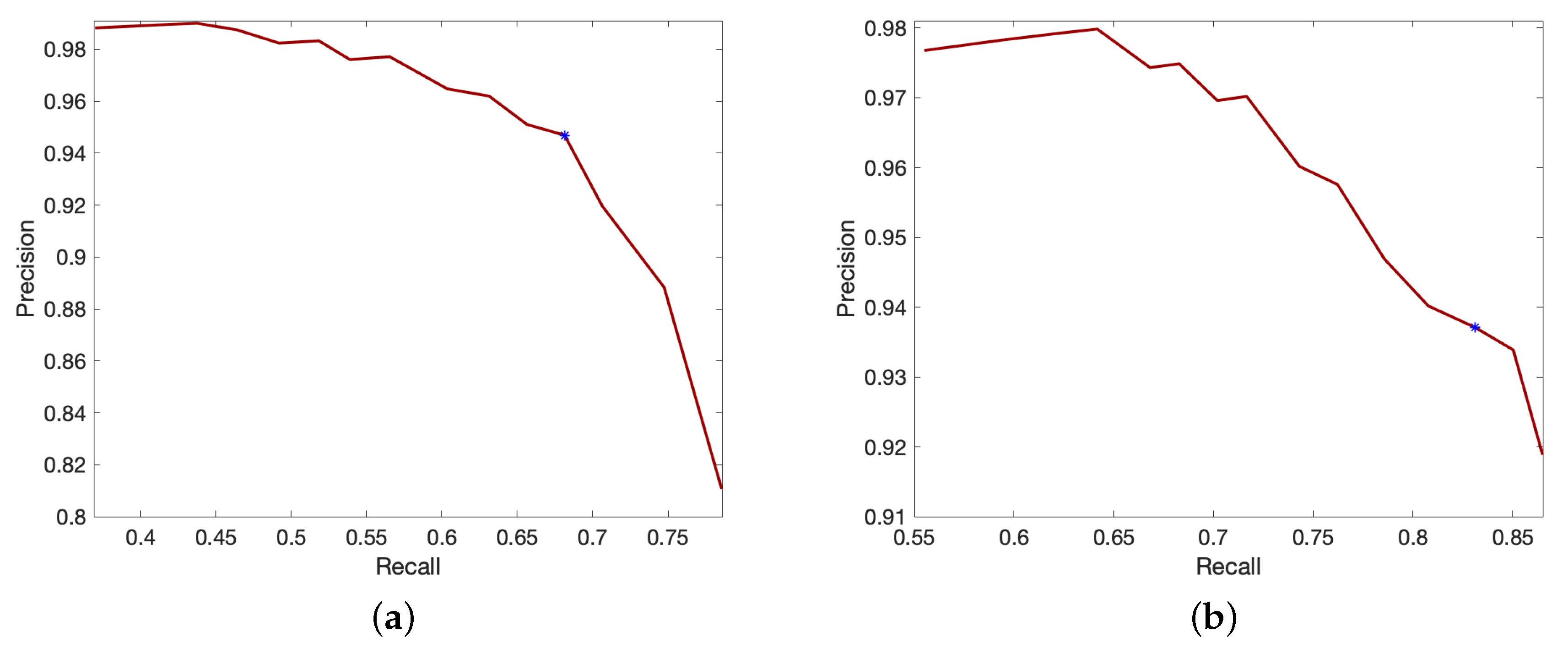
4.4. Experiment 2: Fall Detection Algorithm
4.5. Experiment 3: Fall Detection with Pose Correction
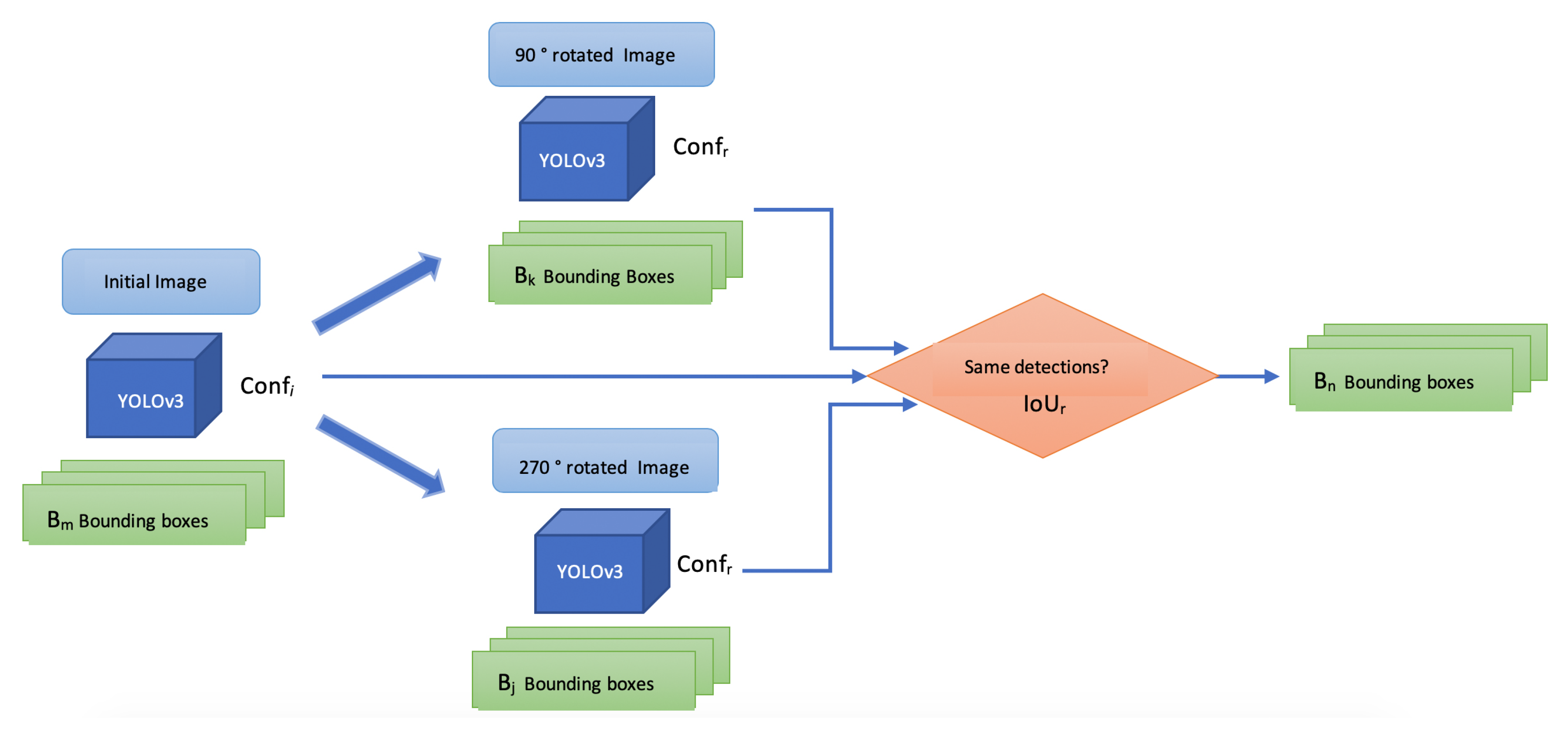
4.6. Evaluation 1: Relocation for Doubtful Cases
4.7. Evaluation 2: Other Datasets
5. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| CNN | Convolutional Neuronal Network |
| RCCN | Region-based Convolutional Neuronal Network |
| YOLO | You Only Look Once |
| SVM | Support Vector Machine |
| RBF | Radial Basis Function |
| FPDS | Fallen Person DataSet |
| TP | True Positive |
| FN | False Negative |
| FP | False Positive |
References
- Ambrose, A.F.; Paul, G.; Hausdorff, J.M. Risk factors for falls among older adults: A review of the literature. Maturitas 2013, 75, 51–61. [Google Scholar] [CrossRef]
- Rubenstein, L.Z. Falls in older people: Epidemiology, risk factors and strategies for prevention. Age Ageing 2006, 35, ii37–ii41. [Google Scholar] [CrossRef] [PubMed]
- World Health Organization. WHO Global Report on Falls Prevention in Older Age. 2007. Available online: https://www.who.int/violence_injury_prevention/publications/other_injury/falls_prevention.pdf?ua=1 (accessed on 18 August 2019).
- Noury, N.; Fleury, A.; Rumeau, P.; Bourke, A.; Laighin, G.; Rialle, V.; Lundy, J. Fall detection-principles and methods. In Proceedings of the 2007 29th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Lyon, France, 22–26 August 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 1663–1666. [Google Scholar]
- Mubashir, M.; Shao, L.; Seed, L. A survey on fall detection: Principles and approaches. Neurocomputing 2013, 100, 144–152. [Google Scholar] [CrossRef]
- Igual, R.; Medrano, C.; Plaza, I. Challenges, issues and trends in fall detection systems. Biomed. Eng. Online 2013, 12, 66. [Google Scholar] [CrossRef]
- Khan, S.S.; Hoey, J. Review of fall detection techniques: A data availability perspective. Med. Eng. Phys. 2017, 39, 12–22. [Google Scholar] [CrossRef]
- Tamura, T.; Yoshimura, T.; Sekine, M.; Uchida, M.; Tanaka, O. A wearable airbag to prevent fall injuries. IEEE Trans. Inf. Technol. Biomed. 2009, 13, 910–914. [Google Scholar] [CrossRef]
- Bianchi, F.; Redmond, S.J.; Narayanan, M.R.; Cerutti, S.; Lovell, N.H. Barometric pressure and triaxial accelerometry-based falls event detection. IEEE Trans. Neural Syst. Rehabil. Eng. 2010, 18, 619–627. [Google Scholar] [CrossRef]
- Tmaura, T.; Zakaria, N.A.; Kuwae, Y.; Sekine, M.; Minato, K.; Yoshida, M. Quantitative analysis of the fall-risk assessment test with wearable inertia sensors. In Proceedings of the 2013 35th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Osaka, Japan, 3–7 July 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 7217–7220. [Google Scholar]
- Rucco, R.; Sorriso, A.; Liparoti, M.; Ferraioli, G.; Sorrentino, P.; Ambrosanio, M.; Baselice, F. Type and location of wearable sensors for monitoring falls during static and dynamic tasks in healthy elderly: A review. Sensors 2018, 18, 1613. [Google Scholar] [CrossRef] [PubMed]
- Mastorakis, G.; Makris, D. Fall detection system using Kinect’s infrared sensor. J. Real-Time Image Process. 2014, 9, 635–646. [Google Scholar] [CrossRef]
- Stone, E.E.; Skubic, M. Fall detection in homes of older adults using the Microsoft Kinect. IEEE J. Biomed. Health Inform. 2015, 19, 290–301. [Google Scholar] [CrossRef]
- Sumiya, T.; Matsubara, Y.; Nakano, M.; Sugaya, M. A mobile robot for fall detection for elderly-care. Procedia Comput. Sci. 2015, 60, 870–880. [Google Scholar] [CrossRef]
- Zigel, Y.; Litvak, D.; Gannot, I. A method for automatic fall detection of elderly people using floor vibrations and sound—Proof of concept on human mimicking doll falls. IEEE Trans. Biomed. Eng. 2009, 56, 2858–2867. [Google Scholar] [CrossRef]
- Martinelli, A.; Tomatis, N.; Siegwart, R. Simultaneous localization and odometry self calibration for mobile robot. Auton. Robot. 2007, 22, 75–85. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, W.; Qi, L.; Zhang, L. Falling detection of lonely elderly people based on NAO humanoid robot. In Proceedings of the 2016 IEEE International Conference on Information and Automation (ICIA), Ningbo, China, 1–3 August 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 31–36. [Google Scholar]
- Máthé, K.; Buşoniu, L. Vision and control for UAVs: A survey of general methods and of inexpensive platforms for infrastructure inspection. Sensors 2015, 15, 14887–14916. [Google Scholar] [CrossRef]
- Iuga, C.; Drăgan, P.; Bușoniu, L. Fall monitoring and detection for at-risk persons using a UAV. IFAC-PapersOnLine 2018, 51, 199–204. [Google Scholar] [CrossRef]
- Zhang, Z.; Conly, C.; Athitsos, V. A survey on vision-based fall detection. In Proceedings of the 8th ACM International Conference on PErvasive Technologies Related to Assistive Environments, Corfu, Greece, 1–3 July 2015; ACM: New York, NY, USA, 2015; p. 46. [Google Scholar]
- Debard, G.; Mertens, M.; Deschodt, M.; Vlaeyen, E.; Devriendt, E.; Dejaeger, E.; Milisen, K.; Tournoy, J.; Croonenborghs, T.; Goedemé, T.; et al. Camera-based fall detection using real-world versus simulated data: How far are we from the solution? J. Ambient. Intell. Smart Environ. 2016, 8, 149–168. [Google Scholar] [CrossRef]
- Kim, K.; Chalidabhongse, T.H.; Harwood, D.; Davis, L. Real-time foreground–background segmentation using codebook model. Real-Time Imaging 2005, 11, 172–185. [Google Scholar] [CrossRef]
- Charfi, I.; Miteran, J.; Dubois, J.; Atri, M.; Tourki, R. Optimized spatio-temporal descriptors for real-time fall detection: comparison of support vector machine and Adaboost-based classification. J. Electron. Imaging 2013, 22, 041106. [Google Scholar] [CrossRef]
- Liu, C.L.; Lee, C.H.; Lin, P.M. A fall detection system using k-nearest neighbor classifier. Expert Syst. Appl. 2010, 37, 7174–7181. [Google Scholar] [CrossRef]
- Wang, S.; Zabir, S.; Leibe, B. Lying pose recognition for elderly fall detection. Robot. Sci. Syst. VII 2012, 29, 345. [Google Scholar]
- Nait-Charif, H.; McKenna, S.J. Activity summarisation and fall detection in a supportive home environment. In Proceedings of the 17th International Conference on Pattern Recognition, ICPR 2004, Cambridge, UK, 26 August 2004; IEEE: Piscataway, NJ, USA, 2004; Volume 4, pp. 323–326. [Google Scholar]
- Rougier, C.; Meunier, J.; St-Arnaud, A.; Rousseau, J. Robust video surveillance for fall detection based on human shape deformation. IEEE Trans. Circuits Syst. Video Technol. 2011, 21, 611–622. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–6 December 2012; pp. 1097–1105. [Google Scholar]
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Rich feature hierarchies for accurate object detection and semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 580–587. [Google Scholar]
- Girshick, R. Fast r-cnn. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 11–18 December 2015; pp. 1440–1448. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster r-cnn: Towards real-time object detection with region proposal networks. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015; pp. 91–99. [Google Scholar]
- Dai, J.; Li, Y.; He, K.; Sun, J. R-fcn: Object detection via region-based fully convolutional networks. In Proceedings of the Advances in Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 379–387. [Google Scholar]
- He, K.; Gkioxari, G.; Dollár, P.; Girshick, R. Mask r-cnn. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2961–2969. [Google Scholar]
- Li, Z.; Peng, C.; Yu, G.; Zhang, X.; Deng, Y.; Sun, J. Light-head r-cnn: In defense of two-stage object detector. arXiv 2017, arXiv:1711.07264. [Google Scholar]
- Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.; Fu, C.Y.; Berg, A.C. Ssd: Single shot multibox detector. In European Conference on Computer Vision; Springer: Cham, Switzerland, 2016; pp. 21–37. [Google Scholar]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You only look once: Unified, real-time object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Redmon, J.; Farhadi, A. YOLO9000: Better, faster, stronger. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Redmon, J.; Farhadi, A. Yolov3: An incremental improvement. arXiv 2018, arXiv:1804.02767. [Google Scholar]
- Laptev, I.; Caputo, B. Recognizing human actions: A local SVM approach. In Null; IEEE: Piscataway, NJ, USA, 2004; pp. 32–36. [Google Scholar]
- Zhang, H.; Berg, A.C.; Maire, M.; Malik, J. SVM-KNN: Discriminative nearest neighbor classification for visual category recognition. In Proceedings of the 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’06), New York, NY, USA, 17–22 June 2006; IEEE: Piscataway, NJ, USA, 2006; Volume 2, pp. 2126–2136. [Google Scholar]
- Ebrahimi, M.; Khoshtaghaza, M.; Minaei, S.; Jamshidi, B. Vision-based pest detection based on SVM classification method. Comput. Electron. Agric. 2017, 137, 52–58. [Google Scholar] [CrossRef]
- Burges, C.J. A tutorial on support vector machines for pattern recognition. Data Min. Knowl. Discov. 1998, 2, 121–167. [Google Scholar] [CrossRef]
- Belousov, A.; Verzakov, S.; Von Frese, J. A flexible classification approach with optimal generalisation performance: Support vector machines. Chemom. Intell. Lab. Syst. 2002, 64, 15–25. [Google Scholar] [CrossRef]
- Rougier, C.; Meunier, J.; St-Arnaud, A.; Rousseau, J. Fall detection from human shape and motion history using video surveillance. In Proceedings of the 21st International Conference on Advanced Information Networking and Applications Workshops (AINAW’07), Niagara Falls, ON, Canada, 21–23 May 2007; IEEE: Piscataway, NJ, USA, 2007; Volume 2, pp. 875–880. [Google Scholar]
- Willems, J.; Debard, G.; Vanrumste, B.; Goedemé, T. A video-based algorithm for elderly fall detection. In Proceedings of the World Congress on Medical Physics and Biomedical Engineering, Munich, Germany, 7–12 September 2009; Springer: Berlin/Heidelberg, Germany, 2009; pp. 312–315. [Google Scholar]
- Svoboda, T.; Pajdla, T.; Hlaváč, V. Epipolar geometry for panoramic cameras. In Proceedings of the European Conference on Computer Vision, Germany, 2–6 June 1998; Springer: Berlin/Heidelberg, Germany, 1998; pp. 218–231. [Google Scholar]
- Igual, R.; Medrano, C.; Plaza, I. A comparison of public datasets for acceleration-based fall detection. Med. Eng. Phys. 2015, 37, 870–878. [Google Scholar] [CrossRef] [PubMed]
- Martínez-Villaseñor, L.; Ponce, H.; Brieva, J.; Moya-Albor, E.; Núñez-Martínez, J.; Peñafort-Asturiano, C. UP-fall detection dataset: A multimodal approach. Sensors 2019, 19, 1988. [Google Scholar] [CrossRef]
- Lin, T.Y.; Maire, M.; Belongie, S.; Hays, J.; Perona, P.; Ramanan, D.; Dollár, P.; Zitnick, C.L. Microsoft coco: Common objects in context. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; Springer: Cham, Switzerland, 2014; pp. 740–755. [Google Scholar]
- Auvinet, E.; Rougier, C.; Meunier, J.; St-Arnaud, A.; Rousseau, J. Multiple Cameras Fall Dataset; DIRO- Université de Montréal, Tech. Rep; Université de Montréal: Montreal, QC, Canada, 2010; Volume 1350. [Google Scholar]
- Kwolek, B.; Kepski, M. Human fall detection on embedded platform using depth maps and wireless accelerometer. Comput. Methods Programs Biomed. 2014, 117, 489–501. [Google Scholar] [CrossRef]
- Antonello, M.; Carraro, M.; Pierobon, M.; Menegatti, E. Fast and robust detection of fallen people from a mobile robot. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 4159–4166. [Google Scholar]









| 1.5 m | 2 m | 3 m | ||||||
|---|---|---|---|---|---|---|---|---|
| 5.33 | 0.85 | 0.014 | 4.54 | 0.61 | 0.11 | 3.47 | 0.39 | 0.22 |
| 4.64 | 0.69 | 0.25 | 4.41 | 0.56 | 0.30 | 3.06 | 0.37 | 0.32 |
| Split 1 | Split 2 | Split 3 | Split 4 | Split 5 | Split 6 | Split 7 | Split 8 | Total | |
|---|---|---|---|---|---|---|---|---|---|
| Number of falls | 278 | 223 | 180 | 104 | 49 | 42 | 15 | 181 | 1072 |
| Number of nonfalls | 175 | 82 | 175 | 3 | 704 | 0 | 39 | 84 | 1262 |
| Number of images | 400 | 323 | 368 | 117 | 553 | 42 | 51 | 210 | 2064 |
| (%) | (%) | ||||
|---|---|---|---|---|---|
| Experiment 1: Fall classification | 390 | 1 | 0 | 100 | 99.74 |
| Experiment 2: Fall detection algorithm | 304 | 87 | 9 | 97.12 | 77.74 |
| Experiment 3: Fall detection with pose correction | 360 | 31 | 17 | 95.49 | 92.07 |
| Initial Image | 90 Rotated Image | 270 Rotated Image |
|---|---|---|
 |  |  |
| (%) | (%) | ||||
|---|---|---|---|---|---|
| Experiment 1: Fall classification | 363 | 0 | 2 | 99.45 | 100 |
| Experiment 2: Fall detection algorithm | 212 | 151 | 43 | 83.13 | 58.40 |
| Experiment 3: Fall detection with pose correction | 271 | 92 | 53 | 83.69 | 74.72 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maldonado-Bascón, S.; Iglesias-Iglesias, C.; Martín-Martín, P.; Lafuente-Arroyo, S. Fallen People Detection Capabilities Using Assistive Robot. Electronics 2019, 8, 915. https://doi.org/10.3390/electronics8090915
Maldonado-Bascón S, Iglesias-Iglesias C, Martín-Martín P, Lafuente-Arroyo S. Fallen People Detection Capabilities Using Assistive Robot. Electronics. 2019; 8(9):915. https://doi.org/10.3390/electronics8090915
Chicago/Turabian StyleMaldonado-Bascón, Saturnino, Cristian Iglesias-Iglesias, Pilar Martín-Martín, and Sergio Lafuente-Arroyo. 2019. "Fallen People Detection Capabilities Using Assistive Robot" Electronics 8, no. 9: 915. https://doi.org/10.3390/electronics8090915
APA StyleMaldonado-Bascón, S., Iglesias-Iglesias, C., Martín-Martín, P., & Lafuente-Arroyo, S. (2019). Fallen People Detection Capabilities Using Assistive Robot. Electronics, 8(9), 915. https://doi.org/10.3390/electronics8090915






