A Fast Algorithm for Multi-Class Learning from Label Proportions
Abstract
1. Introduction
1.1. Related Works
1.2. Motivation
2. Background
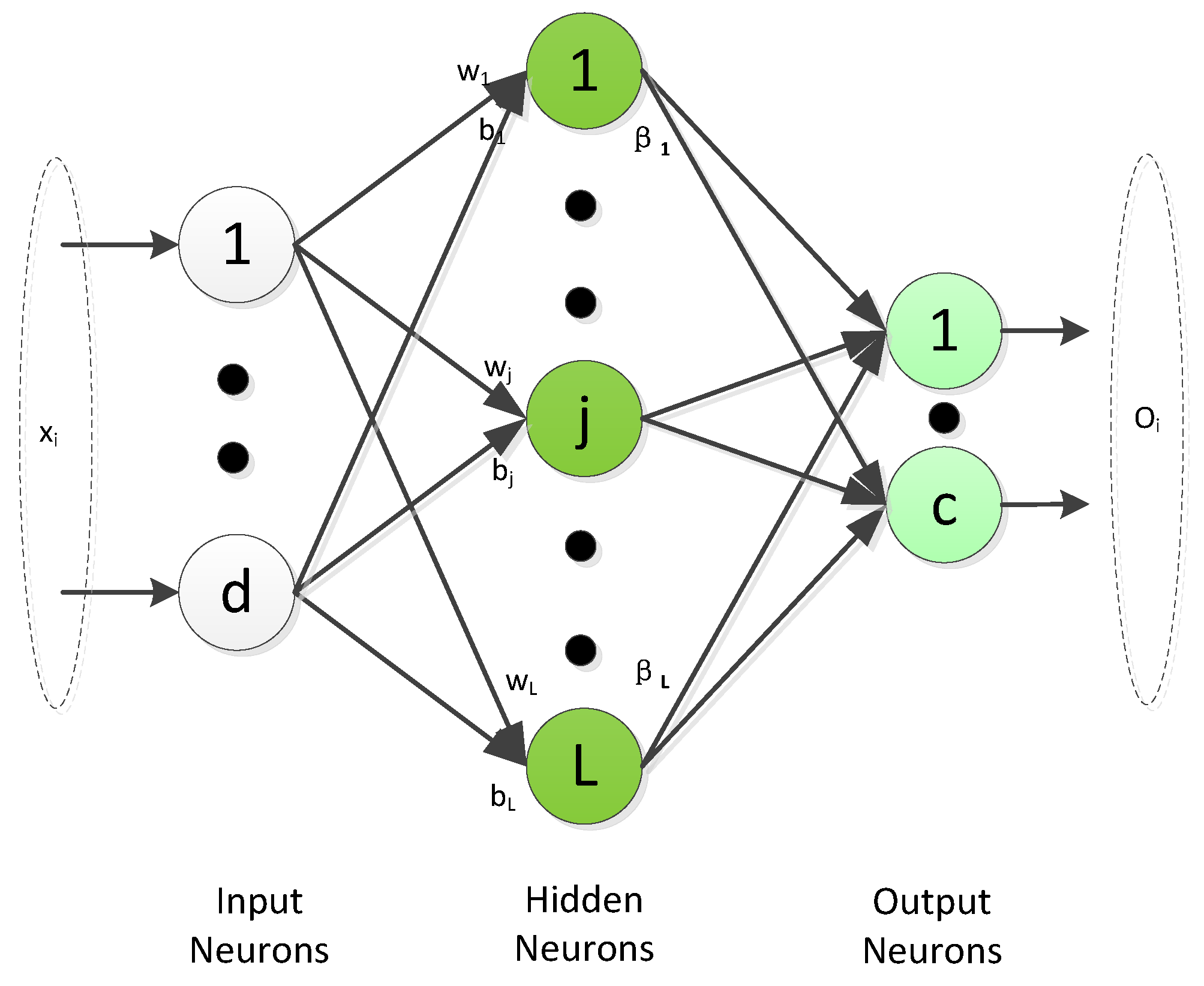
3. The LLP-ELM Algorithm
3.1. Learning Setting
3.2. The LLP-ELM Framework
3.3. How to Solve the LLP-ELM
- has more rows than columns, which means the number of bag is larger than the number of hidden neurons.
- By inverting a L×L matrix directly and multiplying both sides by , we can obtain the following expressionwhich is the optimal solution of (20).
- Compute training data target proportion matrix and the hidden layer output matrix , which is shown in Figure 3.
- Obtain the final optional solution of according to Remark 1 or Remark 2.
| Algorithm 1 LLP-ELM |
| Input: Training datasets in bags; The corresponding proportion of ; Activation function g(x) and the number of hidden nodes N. Output: Classification model f(x,) Begin • Randomly initialize the value and for the jth node, • Compute the training data target proportion matrix by the proportion information of each bag. • Compute the hidden layer output matrix in the bag level . • Obtain the weight vector according to Remark 1 or Remark 2. End |
3.4. Computational Complexity
4. Experiments
4.1. Experiment Setting
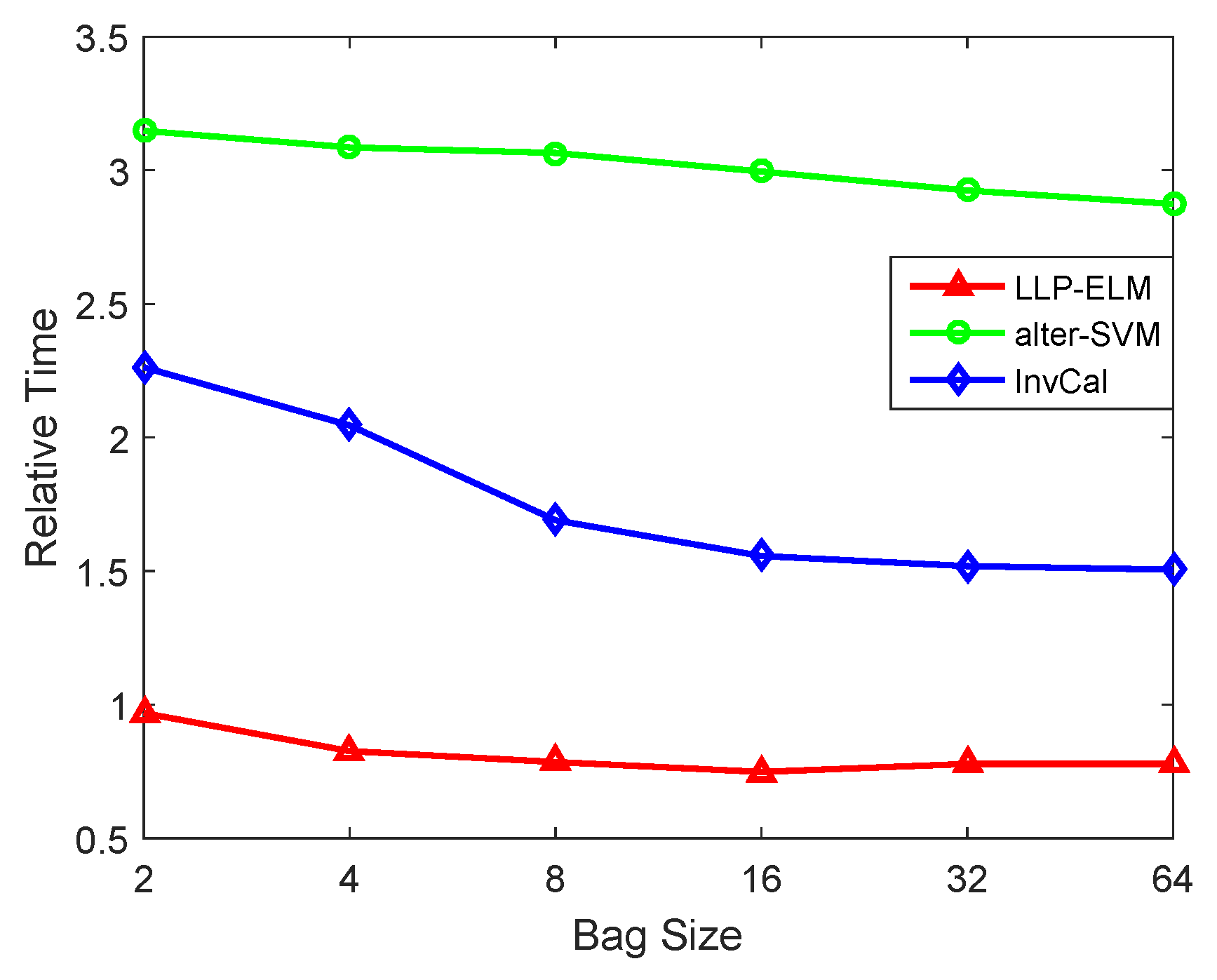
4.2. Binary Datasets
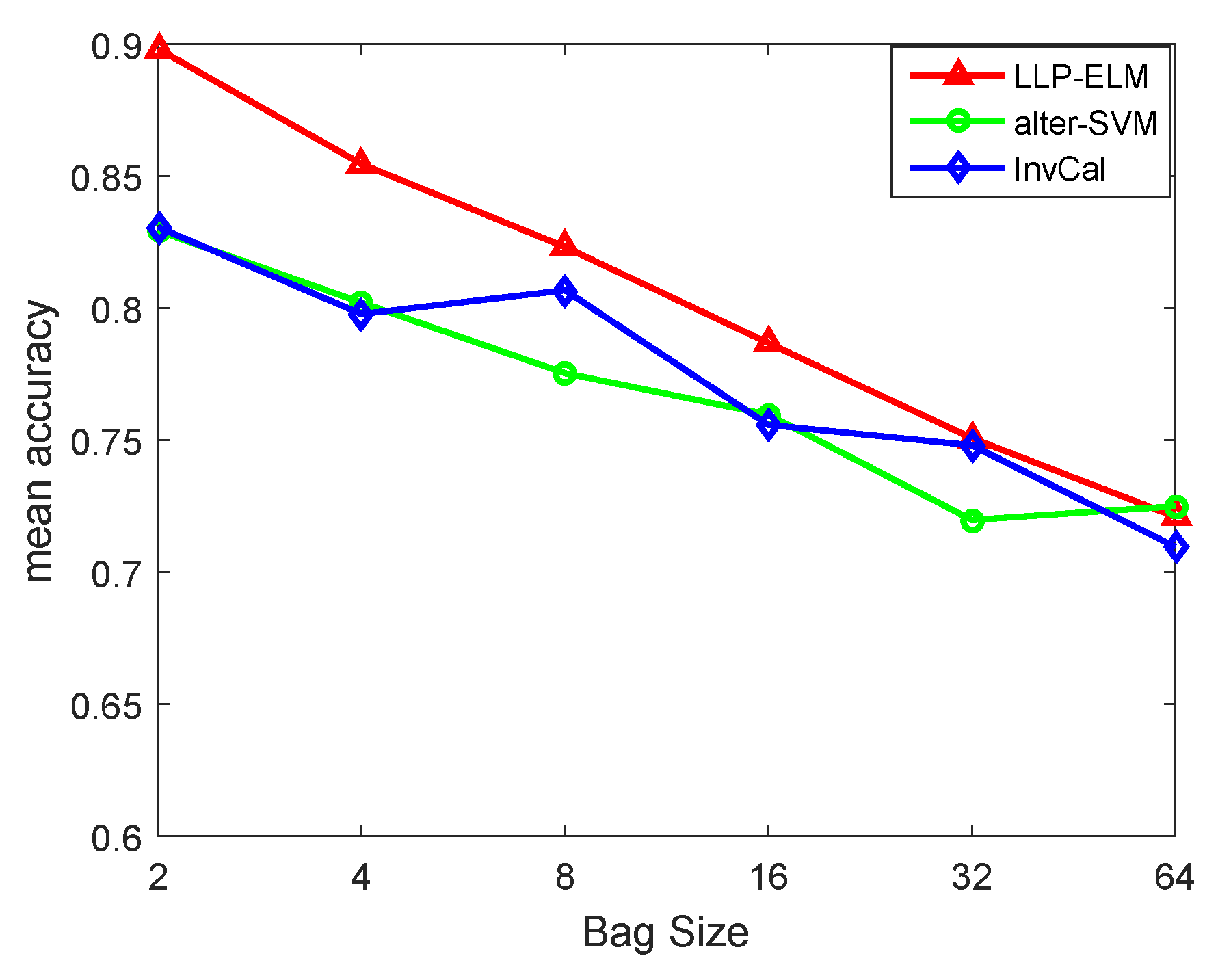
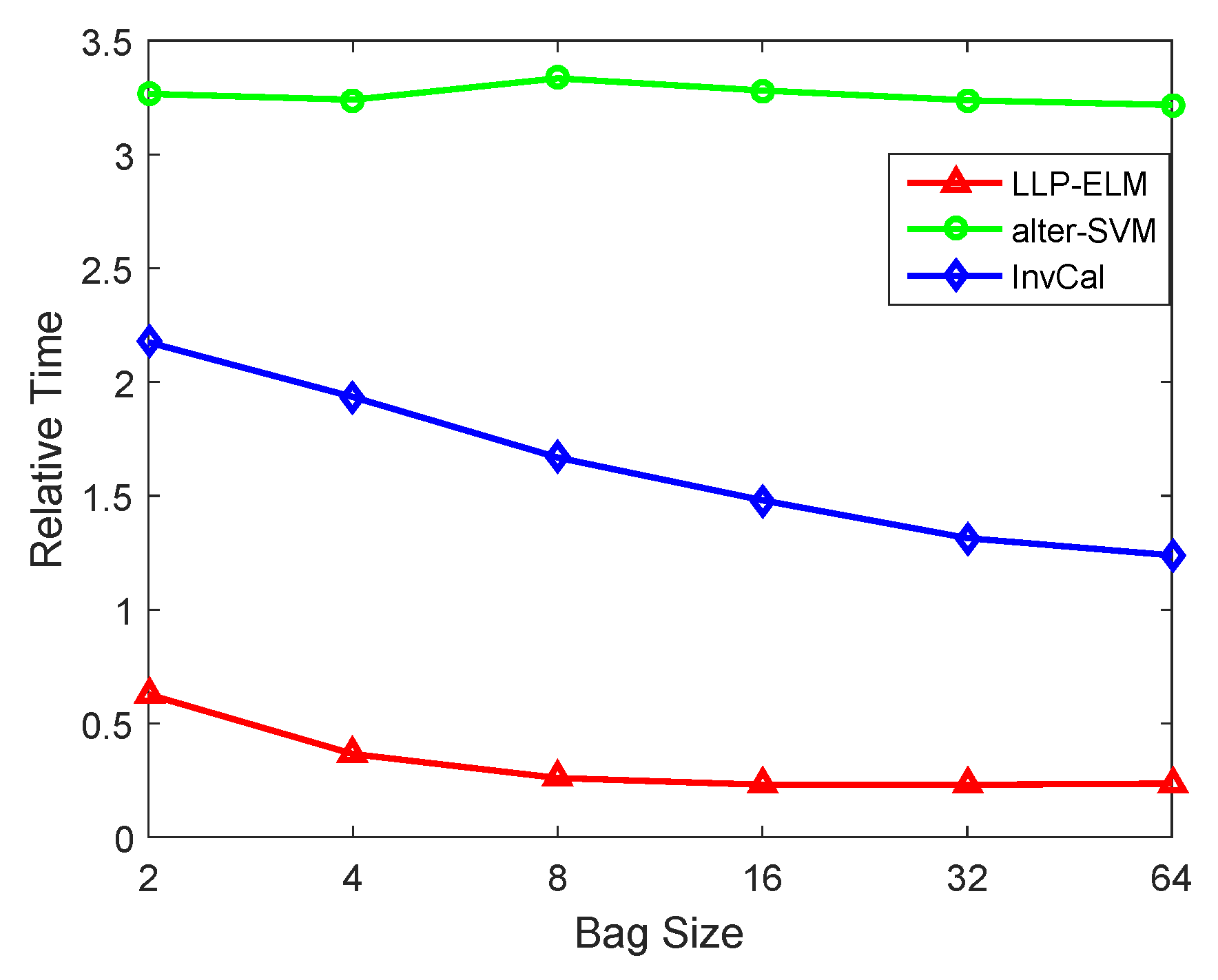
4.3. Multi-Class Datasets
4.4. Caltech-101
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Breiman, L. Random Forest. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Suykens, J.A.K.; Vandewalle, J. Least Squares Support Vector Machine Classifiers; Kluwer Academic Publishers: Norwell, MA, USA, 1999; pp. 293–300. [Google Scholar]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Zhu, J.; Zou, H.; Rosset, S.; Hastie, T. Multi-class AdaBoost. Stat. Interface 2006, 2, 349–360. [Google Scholar]
- Cui, L.; Zhang, J.; Chen, Z.; Shi, Y.; Yu, P.S. Inverse extreme learning machine for learning with label proportions. In Proceedings of the IEEE International Conference on Big Data, Boston, MA, USA, 11–14 December 2017; pp. 576–585. [Google Scholar]
- Yu, F.X.; Cao, L.; Merler, M.; Codella, N.; Chen, T.; Smith, J.R.; Chang, S.F. Modeling Attributes from Category-Attribute Proportions. In Proceedings of the 22nd ACM International Conference on Multimedia, Orlando, FL, USA, 3–7 November 2014; pp. 977–980. [Google Scholar]
- Mann, G.S.; Mccallum, A. Simple, robust, scalable semi-supervised learning via expectation regularization. In Proceedings of the 24th International Conference on Machine Learning, Corvalis, OR, USA, 20–24 June 2007; pp. 593–600. [Google Scholar]
- Ardehaly, E.M.; Culotta, A. Co-training for Demographic Classification Using Deep Learning from Label Proportions. arXiv 2017, arXiv:1709.04108. [Google Scholar]
- Lai, K.T.; Yu, F.X.; Chen, M.S.; Chang, S.F. Video Event Detection by Inferring Temporal Instance Labels. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 2251–2258. [Google Scholar]
- Tao, S.; Dan, S.; Oconnor, B. A Probabilistic Approach for Learning with Label Proportions Applied to the US Presidential Election. In Proceedings of the 2017 IEEE International Conference on Data Mining (ICDM), New Orleans, LA, USA, 18–21 November 2017; pp. 445–454. [Google Scholar]
- Liebig, T.; Stolpe, M.; Morik, K. Distributed traffic flow prediction with label proportions: From in-network towards high performance computation with MPI. In MUD’15 Proceedings of the 2nd International Conference on Mining Urban Data; ACM: Lille, France, 2015; Volume 1392, pp. 36–43. [Google Scholar]
- Hernández-González, J.; Inza, I.; Crisol-Ortíz, L.; Guembe, M.A.; Iñarra, M.J.; Lozano, J.A. Fitting the data from embryo implantation prediction: Learning from label proportions. Stat. Methods Med. Res. 2016, 27, 1056–1066. [Google Scholar] [CrossRef] [PubMed]
- Ding, Y.; Li, Y.; Yu, W. Learning from label proportions for SAR image classification. Eurasip J. Adv. Signal Process. 2017, 2017, 41. [Google Scholar] [CrossRef]
- Kuck, H.; de Freitas, N. Learning about individuals from group statistics. arXiv 2012, arXiv:1207.1393. [Google Scholar]
- Rüping, S. SVM Classifier Estimation from Group Probabilities. In Proceedings of the 27th International Conference on International Conference on Machine Learning, Haifa, Israel, 21–24 June 2010; pp. 911–918. [Google Scholar]
- Yu, F.X.; Liu, D.; Kumar, S.; Jebara, T.; Chang, S.F. ∝SVM for learning with label proportions. In Proceedings of the 30th International Conference on International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013; pp. 504–512. [Google Scholar]
- Wang, Z.; Feng, J. Multi-class learning from class proportions. Neurocomputing 2013, 119, 273–280. [Google Scholar] [CrossRef]
- Fish, B.; Reyzin, L. On the Complexity of Learning from Label Proportions. In Proceedings of the 26th International Joint Conference on Artificial Intelligence, Melbourne, Australia, 19–25 August 2017; pp. 1675–1681. [Google Scholar]
- Fan, K.; Zhang, H.; Yan, S.; Wang, L.; Zhang, W.; Feng, J. Learning a generative classifier from label proportions. Neurocomputing 2014, 139, 47–55. [Google Scholar] [CrossRef]
- Wang, B.; Chen, Z.; Qi, Z. Linear Twin SVM for Learning from Label Proportions. In Proceedings of the 2015 IEEE/WIC/ACM International Conference on Web Intelligence and Intelligent Agent Technology (WI-IAT), Singapore, 6–9 December 2015; pp. 56–59. [Google Scholar]
- Qi, Z.; Wang, B.; Meng, F.; Niu, L. Learning With Label Proportions via NPSVM. IEEE Trans. Cybern. 2017, 47, 3293–3305. [Google Scholar] [CrossRef] [PubMed]
- Qi, Z.; Fan, M.; Tian, Y.; Niu, L.; Yong, S.; Peng, Z. Adaboost-LLP: A Boosting Method for Learning with Label Proportions. IEEE Trans. Neural Netw. Learn. Syst. 2017, 29, 3548–3559. [Google Scholar] [PubMed]
- Shi, Y.; Cui, L.; Chen, Z.; Qi, Z. Learning from label proportions with pinball loss. Int. J. Mach. Learn. Cybern. 2017, 10, 187–205. [Google Scholar] [CrossRef]
- Huang, G.B.; Zhou, H.; Ding, X.; Zhang, R. Extreme learning machine for regression and multiclass classification. IEEE Trans. Syst. Man Cybern. Part B 2012, 42, 513–529. [Google Scholar] [CrossRef] [PubMed]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Li, F.F.; Fergus, R.; Perona, P. Learning generative visual models from few training examples: An incremental Bayesian approach tested on 101 object categories. In Proceedings of the 2004 Conference on Computer Vision and Pattern Recognition Workshop, Washington, DC, USA, 27 June–2 July 2004. [Google Scholar]
- Dalal, N.; Triggs, B. Histograms of oriented gradients for human detection. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005; pp. 886–893. [Google Scholar]


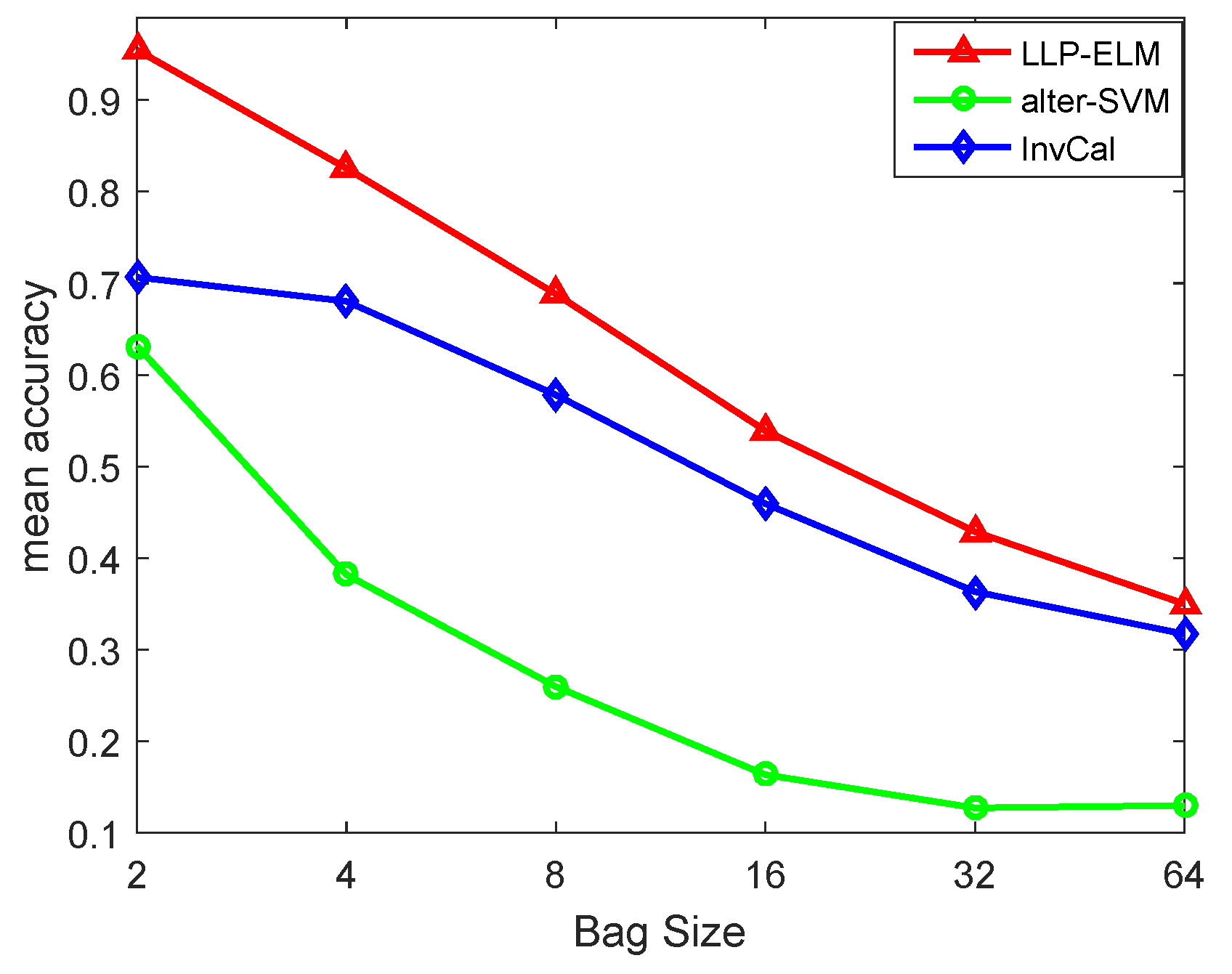
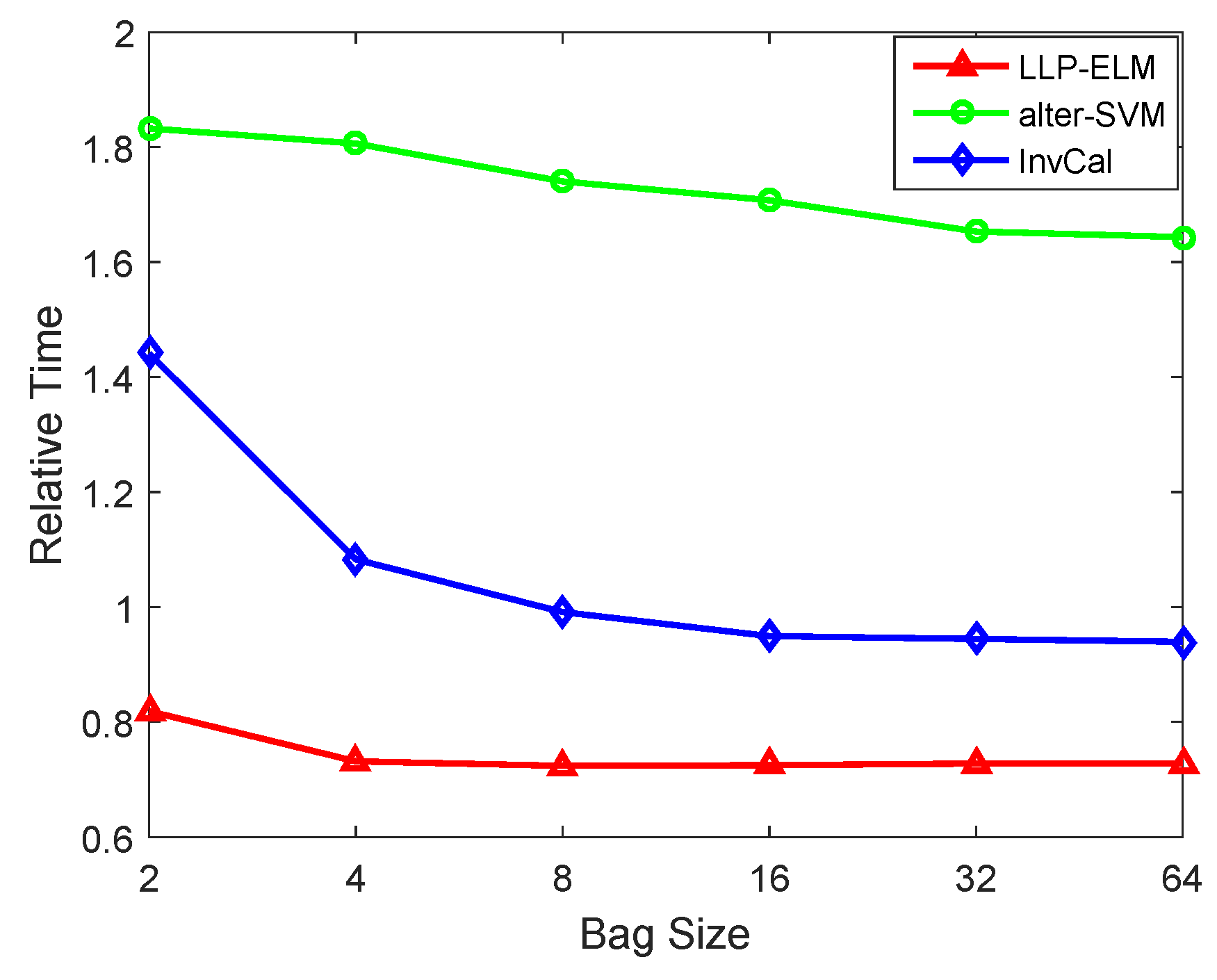
| Dataset | Size | Attributes |
|---|---|---|
| sonar | 208 | 60 |
| heart | 270 | 13 |
| vote | 435 | 16 |
| breast-cancer | 683 | 10 |
| credit-a | 690 | 15 |
| diabetes | 768 | 8 |
| pima-indian | 768 | 8 |
| splice | 1000 | 60 |
| ala | 1065 | 119 |
| Dataset | Method | 2 | 4 | 8 | 16 | 32 | 64 |
|---|---|---|---|---|---|---|---|
| InvCal | 0.76 ± 0.12 | 0.70 ± 0.11 | 0.72 ± 0.11 | 0.65 ± 0.14 | 0.59 ± 0.12 | 0.50 ± 0.13 | |
| sonar | alter-∝SVM | 0.74 ± 0.09 | 0.64 ± 0.09 | 0.51 ± 0.11 | 0.595 ± 0.06 | 0.53 ± 0.10 | 0.49 ± 0.13 |
| LLP-ELM | 0.91 ± 0.02 | 0.78 ± 0.03 | 0.74 ± 0.04 | 0.68 ± 0.09 | 0.58 ± 0.04 | 0.55 ± 0.07 | |
| InvCal | 0.80 ± 0.05 | 0.79 ± 0.04 | 0.81 ± 0.06 | 0.71 ± 0.11 | 0.75 ± 0.07 | 0.73 ± 0.14 | |
| heart | alter-∝SVM | 0.81 ± 0.04 | 0.79 ± 0.03 | 0.80 ± 0.03 | 0.78 ± 0.11 | 0.66 ± 0.20 | 0.77 ± 0.07 |
| LLP-ELM | 0.88 ± 0.02 | 0.84 ± 0.02 | 0.78 ± 0.03 | 0.75 ± 0.11 | 0.76 ± 0.04 | 0.74 ± 0.09 | |
| InvCal | 0.95 ± 0.03 | 0.94 ± 0.03 | 0.94 ± 0.04 | 0.92 ± 0.02 | 0.89 ± 0.04 | 0.84 ± 0.07 | |
| vote | alter-∝SVM | 0.95 ± 0.01 | 0.94 ± 0.03 | 0.94 ± 0.02 | 0.95 ± 0.01 | 0.91 ± 0.06 | 0.89 ± 0.01 |
| LLP-ELM | 0.98 ± 0.01 | 0.97 ± 0.01 | 0.96 ± 0.01 | 0.95 ± 0.01 | 0.91 ± 0.01 | 0.90 ± 0.05 | |
| InvCal | 0.95 ± 0.01 | 0.94 ± 0.01 | 0.95 ± 0.02 | 0.95 ± 0.03 | 0.95 ± 0.01 | 0.90 ± 0.05 | |
| breast-cancer | alter-∝SVM | 0.96 ± 0.02 | 0.96 ± 0.01 | 0.96 ± 0.02 | 0.96 ± 0.02 | 0.96 ± 0.01 | 0.97 ± 0.01 |
| LLP-ELM | 0.97 ± 0.00 | 0.97 ± 0.00 | 0.97 ± 0.00 | 0.96 ± 0.01 | 0.93 ± 0.02 | 0.92 ± 0.04 | |
| InvCal | 0.85 ± 0.02 | 0.85 ± 0.02 | 0.85 ± 0.03 | 0.82 ± 0.02 | 0.82 ± 0.03 | 0.77 ± 0.09 | |
| credit-a | alter-∝SVM | 0.85 ± 0.02 | 0.85 ± 0.02 | 0.81 ± 0.05 | 0.82 ± 0.02 | 0.64 ± 0.14 | 0.76 ± 0.08 |
| LLP-ELM | 0.89 ± 0.01 | 0.88 ± 0.02 | 0.83 ± 0.02 | 0.80 ± 0.03 | 0.74 ± 0.08 | 0.76 ± 0.06 | |
| InvCal | 0.75 ± 0.03 | 0.71 ± 0.05 | 0.73 ± 0.04 | 0.67 ± 0.05 | 0.66 ± 0.05 | 0.64 ± 0.03 | |
| diabetes | alter-∝SVM | 0.76 ± 0.02 | 0.73 ± 0.03 | 0.71 ± 0.04 | 0.67 ± 0.03 | 0.66 ± 0.04 | 0.66 ± 0.05 |
| LLP-ELM | 0.78 ± 0.01 | 0.78 ± 0.02 | 0.75 ± 0.01 | 0.72 ± 0.02 | 0.67 ± 0.02 | 0.68 ± 0.02 | |
| InvCal | 0.76 ± 0.03 | 0.70 ± 0.05 | 0.72 ± 0.04 | 0.70 ± 0.06 | 0.66 ± 0.07 | 0.65 ± 0.03 | |
| pima-indian | alter-∝SVM | 0.75 ± 0.03 | 0.73 ± 0.03 | 0.70 ± 0.03 | 0.67 ± 0.04 | 0.66 ± 0.03 | 0.65 ± 0.02 |
| LLP-ELM | 0.78 ± 0.00 | 0.77 ± 0.01 | 0.75 ± 0.01 | 0.73 ± 0.01 | 0.71 ± 0.03 | 0.56 ± 0.07 | |
| InvCal | 0.79 ± 0.02 | 0.73 ± 0.02 | 0.73 ± 0.06 | 0.65 ± 0.03 | 0.63 ± 0.05 | 0.60 ± 0.04 | |
| splice-scale | alter-∝SVM | 0.78 ± 0.04 | 0.74 ± 0.03 | 0.71 ± 0.04 | 0.65 ± 0.05 | 0.66 ± 0.04 | 0.56 ± 0.17 |
| LLP-ELM | 0.94 ± 0.01 | 0.82 ± 0.03 | 0.78 ± 0.02 | 0.69 ± 0.03 | 0.65 ± 0.03 | 0.60 ± 0.05 | |
| InvCal | 0.82 ± 0.02 | 0.78 ± 0.03 | 0.77 ± 0.02 | 0.71 ± 0.05 | 0.74 ± 0.03 | 0.71 ± 0.05 | |
| ala | alter-∝SVM | 0.82 ± 0.02 | 0.79 ± 0.04 | 0.79 ± 0.03 | 0.72 ± 0.06 | 0.76 ± 0.02 | 0.75 ± 0.02 |
| LLP-ELM | 0.9 ± 0.00 | 0.85 ± 0.01 | 0.81 ± 0.01 | 0.76 ± 0.02 | 0.76 ± 0.02 | 0.75 ± 0.03 |
| Dataset | Method | 2 | 4 | 8 | 16 | 32 | 64 |
|---|---|---|---|---|---|---|---|
| InvCal | 0.83 | 0.38 | 0.35 | 0.33 | 0.32 | 0.31 | |
| sonar | alter-∝SVM | 1.66 | 1.19 | 0.68 | 0.53 | 0.42 | 0.37 |
| LLP-ELM | 0.03 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | |
| InvCal | 0.50 | 0.40 | 0.33 | 0.33 | 0.32 | 0.31 | |
| heart | alter-∝SVM | 2.16 | 1.51 | 1.01 | 0.78 | 0.67 | 0.61 |
| LLP-ELM | 0.03 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | |
| InvCal | 0.61 | 0.46 | 0.35 | 0.33 | 0.32 | 0.31 | |
| vote | alter-∝SVM | 3.83 | 2.82 | 2.88 | 2.14 | 1.73 | 1.54 |
| LLP-ELM | 0.05 | 0.04 | 0.04 | 0.04 | 0.04 | 0.03 | |
| InvCal | 1.46 | 0.58 | 0.41 | 0.35 | 0.32 | 0.31 | |
| breast-cancer | alter-∝SVM | 7.82 | 5.71 | 5.25 | 4.95 | 4.05 | 4.02 |
| LLP-ELM | 0.08 | 0.06 | 0.05 | 0.05 | 0.05 | 0.05 | |
| InvCal | 1.64 | 1.61 | 0.43 | 0.35 | 0.34 | 0.32 | |
| credit-a | alter-∝SVM | 9.39 | 7.35 | 6.84 | 6.07 | 5.32 | 4.95 |
| LLP-ELM | 0.08 | 0.06 | 0.06 | 0.05 | 0.06 | 0.06 | |
| InvCal | 1.90 | 0.63 | 0.43 | 0.35 | 0.33 | 0.31 | |
| diabetes | alter-∝SVM | 13.32 | 11.19 | 9.24 | 8.05 | 6.86 | 6.19 |
| LLP-ELM | 0.1 | 0.07 | 0.06 | 0.06 | 0.06 | 0.06 | |
| InvCal | 1.97 | 0.65 | 0.43 | 0.35 | 0.33 | 0.31 | |
| pima-indian | alter-∝SVM | 14.3 | 10.69 | 9.16 | 7.66 | 6.89 | 6.44 |
| LLP-ELM | 0.09 | 0.07 | 0.06 | 0.06 | 0.06 | 0.06 | |
| InvCal | 4.28 | 1.32 | 0.57 | 0.38 | 0.32 | 0.31 | |
| splice-scale | alter-∝SVM | 25.2 | 25.4 | 22.32 | 18.56 | 15.67 | 13.42 |
| LLP-ELM | 0.13 | 0.10 | 0.09 | 0.08 | 0.09 | 0.09 | |
| InvCal | 3.24 | 3.96 | 1.17 | 0.48 | 0.37 | 0.35 | |
| ala | alter-∝SVM | 48.80 | 43.77 | 47.14 | 40.31 | 33.96 | 29.81 |
| LLP-ELM | 0.25 | 0.17 | 0.15 | 0.13 | 0.14 | 0.15 |
| Dataset | Size | Attributes | Classes |
|---|---|---|---|
| shuttle | 1000 | 9 | 7 |
| connect-4 | 1000 | 126 | 3 |
| protein | 1000 | 375 | 3 |
| dna | 2000 | 180 | 3 |
| satimage | 4435 | 36 | 6 |
| Dataset | Method | 2 | 4 | 8 | 16 | 32 | 64 |
|---|---|---|---|---|---|---|---|
| InvCal | 0.81 ± 0.02 | 0.84 ± 0.02 | 0.86 ± 0.03 | 0.85 ± 0.02 | 0.81 ± 0.02 | 0.81 ± 0.02 | |
| shuttle | alter-∝SVM | 0.88 ± 0.03 | 0.87 ± 0.03 | 0.89 ± 0.03 | 0.85 ± 0.06 | 0.81 ± 0.13 | 0.73 ± 0.08 |
| LLP-ELM | 0.93 ± 0.01 | 0.92 ± 0.01 | 0.92 ± 0.01 | 0.92 ± 0.01 | 0.92 ± 0.02 | 0.92 ± 0.02 | |
| InvCal | 0.78 ± 0.01 | 0.79 ± 0.03 | 0.78 ± 0.03 | 0.70 ± 0.05 | 0.76 ± 0.03 | 0.79 ± 0.03 | |
| connect-4 | alter-∝SVM | 0.79 ± 0.03 | 0.79 ± 0.02 | 0.76 ± 0.03 | 0.74 ± 0.04 | 0.72 ± 0.03 | 0.73 ± 0.03 |
| LLP-ELM | 0.94 ± 0.01 | 0.86 ± 0.01 | 0.81 ± 0.02 | 0.77 ± 0.02 | 0.75 ± 0.04 | 0.77 ± 0.02 | |
| InvCal | 0.53 ± 0.08 | 0.49 ± 0.05 | 0.50 ± 0.03 | 0.48 ± 0.06 | 0.52 ± 0.01 | 0.47 ± 0.03 | |
| protein | alter-∝SVM | 0.54 ± 0.05 | 0.49 ± 0.04 | 0.48 ± 0.05 | 0.43 ± 0.05 | 0.41 ± 0.02 | 0.40 ± 0.02 |
| LLP-ELM | 0.79 ± 0.02 | 0.66 ± 0.01 | 0.59 ± 0.02 | 0.55 ± 0.01 | 0.50 ± 0.02 | 0.50 ± 0.02 | |
| InvCal | 0.92 ± 0.01 | 0.79 ± 0.02 | 0.66 ± 0.02 | 0.73 ± 0.03 | 0.76 ± 0.04 | 0.72 ± 0.03 | |
| dna | alter-∝SVM | 0.92 ± 0.01 | 0.92.85 ± 0.01 | 0.91 ± 0.02 | 0.86 ± 0.05 | 0.77 ± 0.07 | 0.68 ± 0.08 |
| LLP-ELM | 0.98 ± 0.00 | 0.94 ± 0.00 | 0.89 ± 0.01 | 0.81 ± 0.02 | 0.77 ± 0.03 | 0.68 ± 0.04 | |
| InvCal | 0.75 ± 0.01 | 0.76 ± 0.01 | 0.70 ± 0.04 | 0.76 ± 0.03 | 76 ± 0.01 | 0.75 ± 0.02 | |
| satimage | alter-∝SVM | 0.80 ± 0.01 | 0.81 ± 0.01 | 0.81 ± 0.01 | 0.78 ± 0.04 | 0.59 ± 0.05 | 0.61 ± 0.09 |
| LLP-ELM | 0.90 ± 0.00 | 0.89 ± 0.00 | 0.89 ± 0.00 | 0.87 ± 0.00 | 0.84 ± 0.00 | 0.80 ± 0.01 |
| Dataset | Method | 2 | 4 | 8 | 16 | 32 | 64 |
|---|---|---|---|---|---|---|---|
| InvCal | 22.35 | 7.35 | 3.49 | 3.38 | 2.53 | 2.31 | |
| shuttle | alter-∝SVM | 42.12 | 32.53 | 23.71 | 22.36 | 22.15 | 22.21 |
| LLP-ELM | 0.19 | 0.09 | 0.08 | 0.08 | 0.08 | 0.08 | |
| InvCal | 7.80 | 2.93 | 1.56 | 1.21 | 0.99 | 0.96 | |
| connect-4 | alter-∝SVM | 18.88 | 16.54 | 13.58 | 12.12 | 10.75 | 9.54 |
| LLP-ELM | 0.15 | 0.11 | 0.09 | 0.09 | 0.09 | 0.09 | |
| InvCal | 5.65 | 4.30 | 1.47 | 1.35 | 0.97 | 0.91 | |
| protein | alter-∝SVM | 52.74 | 37.93 | 28.55 | 24.00 | 22.27 | 20.99 |
| LLP-ELM | 0.18 | 0.15 | 0.14 | 0.13 | 0.13 | 0.13 | |
| InvCal | 19.43 | 21.98 | 6.03 | 1.47 | 1.05 | 0.91 | |
| dna | alter-∝SVM | 100.54 | 95.54 | 99.67 | 109.08 | 93.19 | 88.06 |
| LLP-ELM | 0.37 | 0.23 | 0.20 | 0.19 | 0.19 | 0.20 | |
| InvCal | 19.55 | 6.41 | 10.73 | 7.70 | 4.77 | 3.57 | |
| satimage | alter-∝SVM | 743 | 710 | 930 | 800 | 730 | 700 |
| LLP-ELM | 1.23 | 0.58 | 0.40 | 0.36 | 0.36 | 0.36 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, F.; Liu, J.; Wang, B.; Qi, Z.; Shi, Y. A Fast Algorithm for Multi-Class Learning from Label Proportions. Electronics 2019, 8, 609. https://doi.org/10.3390/electronics8060609
Zhang F, Liu J, Wang B, Qi Z, Shi Y. A Fast Algorithm for Multi-Class Learning from Label Proportions. Electronics. 2019; 8(6):609. https://doi.org/10.3390/electronics8060609
Chicago/Turabian StyleZhang, Fan, Jiabin Liu, Bo Wang, Zhiquan Qi, and Yong Shi. 2019. "A Fast Algorithm for Multi-Class Learning from Label Proportions" Electronics 8, no. 6: 609. https://doi.org/10.3390/electronics8060609
APA StyleZhang, F., Liu, J., Wang, B., Qi, Z., & Shi, Y. (2019). A Fast Algorithm for Multi-Class Learning from Label Proportions. Electronics, 8(6), 609. https://doi.org/10.3390/electronics8060609





