Enabling Green Wireless Sensor Networks: Energy Efficient T-MAC Using Markov Chain Based Optimization
Abstract
1. Introduction
- We derive an analytical model for T-MAC, applying a discrete-time Markov chain focussing on throughput, energy consumption, power efficiency and service energy under unsaturated traffic conditions.
- A node behaviour model is presented with a transmission probability, which reviews the back-off mechanism in the T-MAC protocol using the Markov chain. Moreover, the probabilities of a successful transmission, collision, and idle state of a node are computed in a cycle probability model, which is also illustrated.
- A system model, based on the M/M/1/∞ queuing model, is presented to analyse the throughput under unsaturated traffic conditions, and a service delay model is illustrated to calculate the average service delay using the adaptive sleep wakeup schedules.
- A comparative performance analysis is done with the aid of a simulation to assess the energy efficiency of the suggested model, as compared to the state-of-the-art S-MAC and X-MAC based techniques, in view of various metrics.
2. Related Works
2.1. MAC Orientated Green Communication
2.2. Routing Orientated Green Communication
3. Analytical Model of T-MAC Protocol
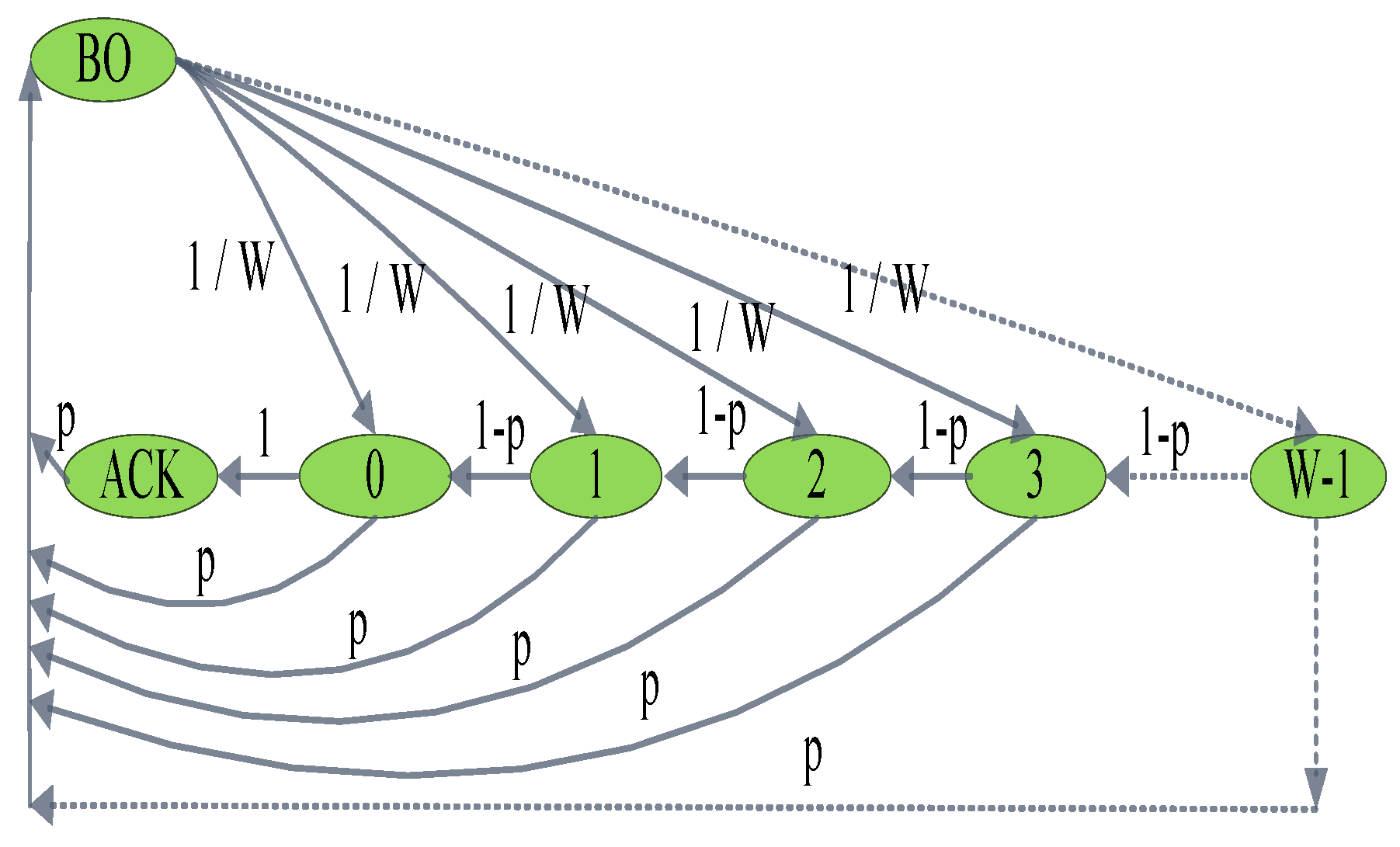
3.1. Node Behaviour Model
3.2. Cycle Probability Model
3.3. Throughput Analysis
3.4. Service Delay Analysis
3.5. Energy Consumption and Power Efficiency
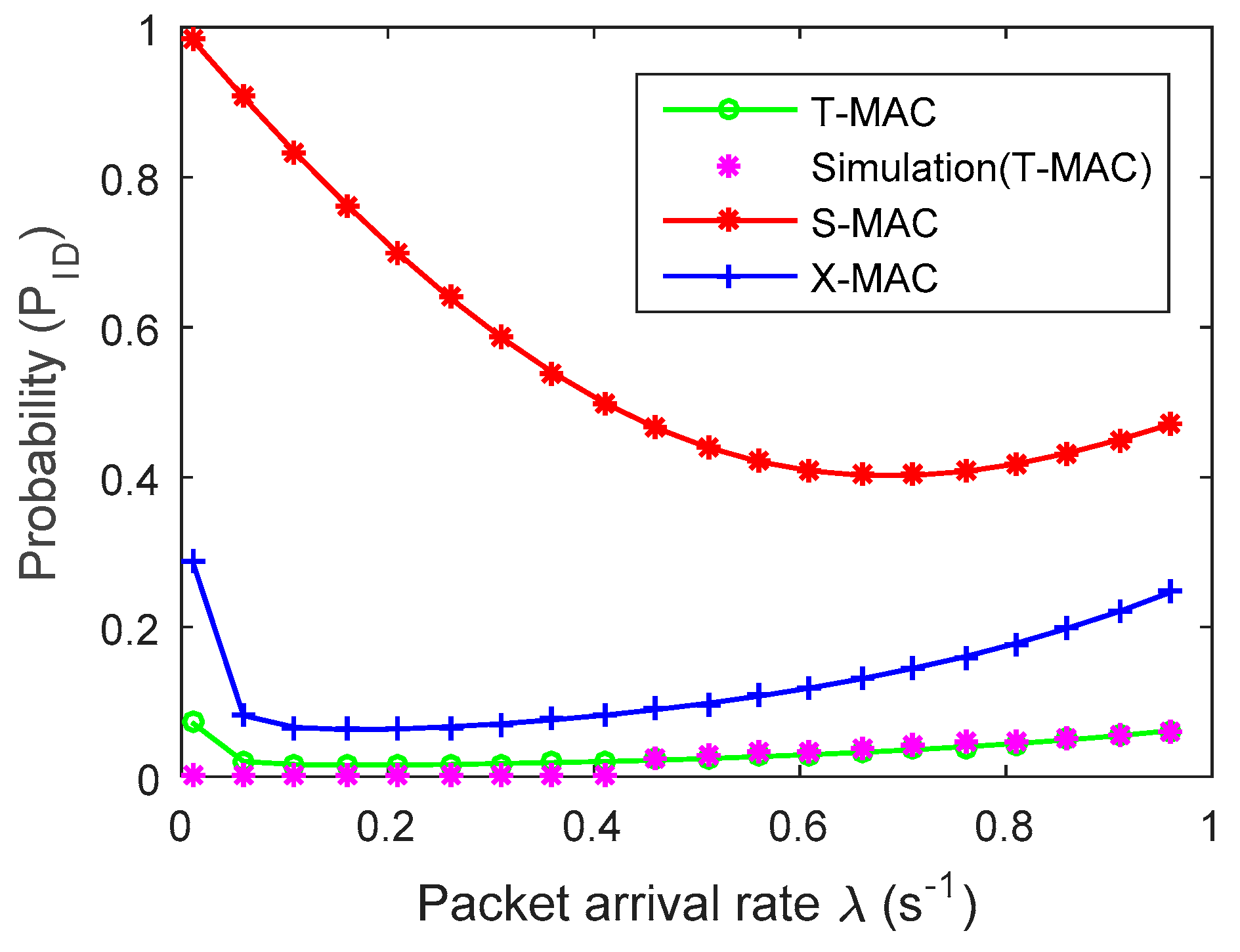
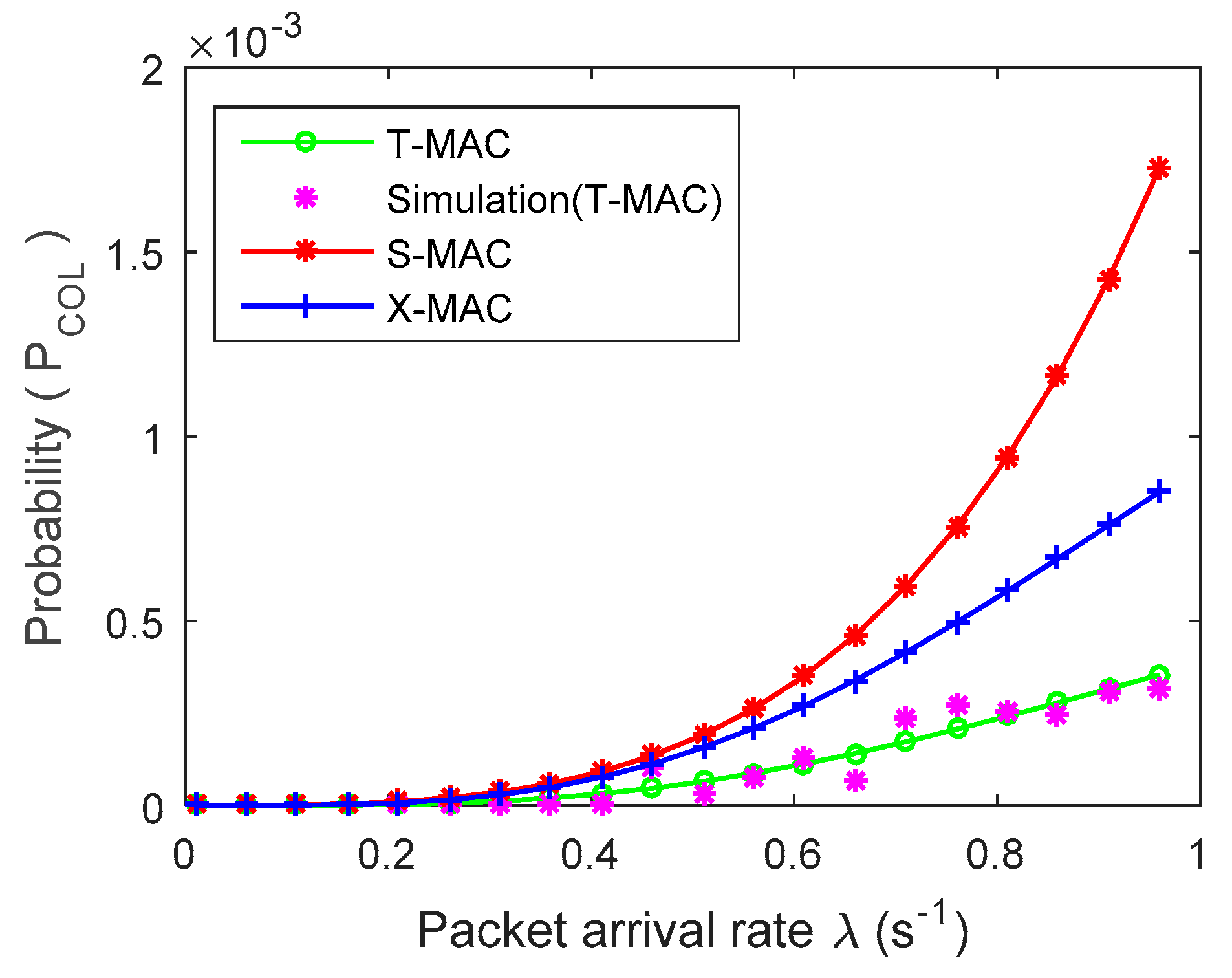
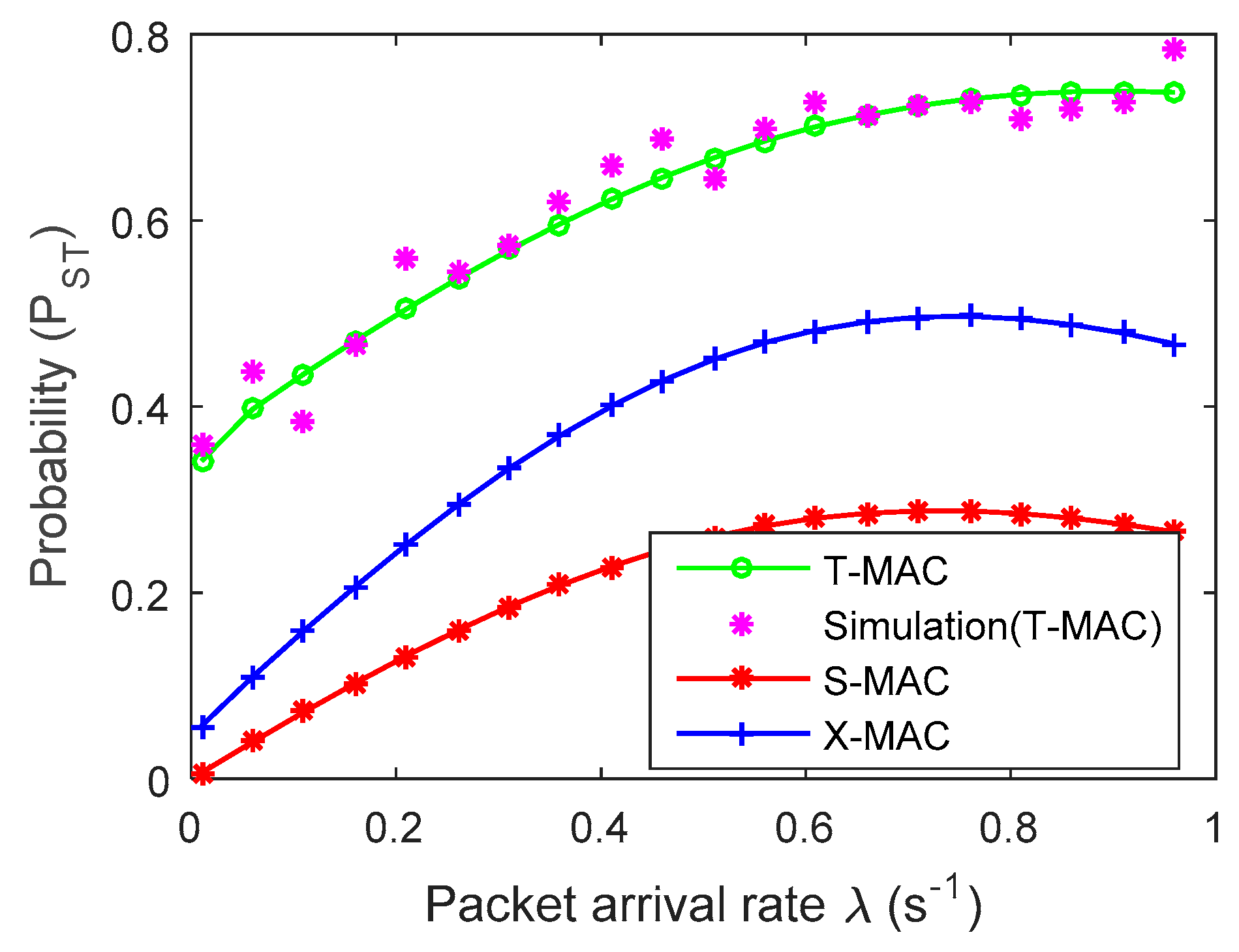
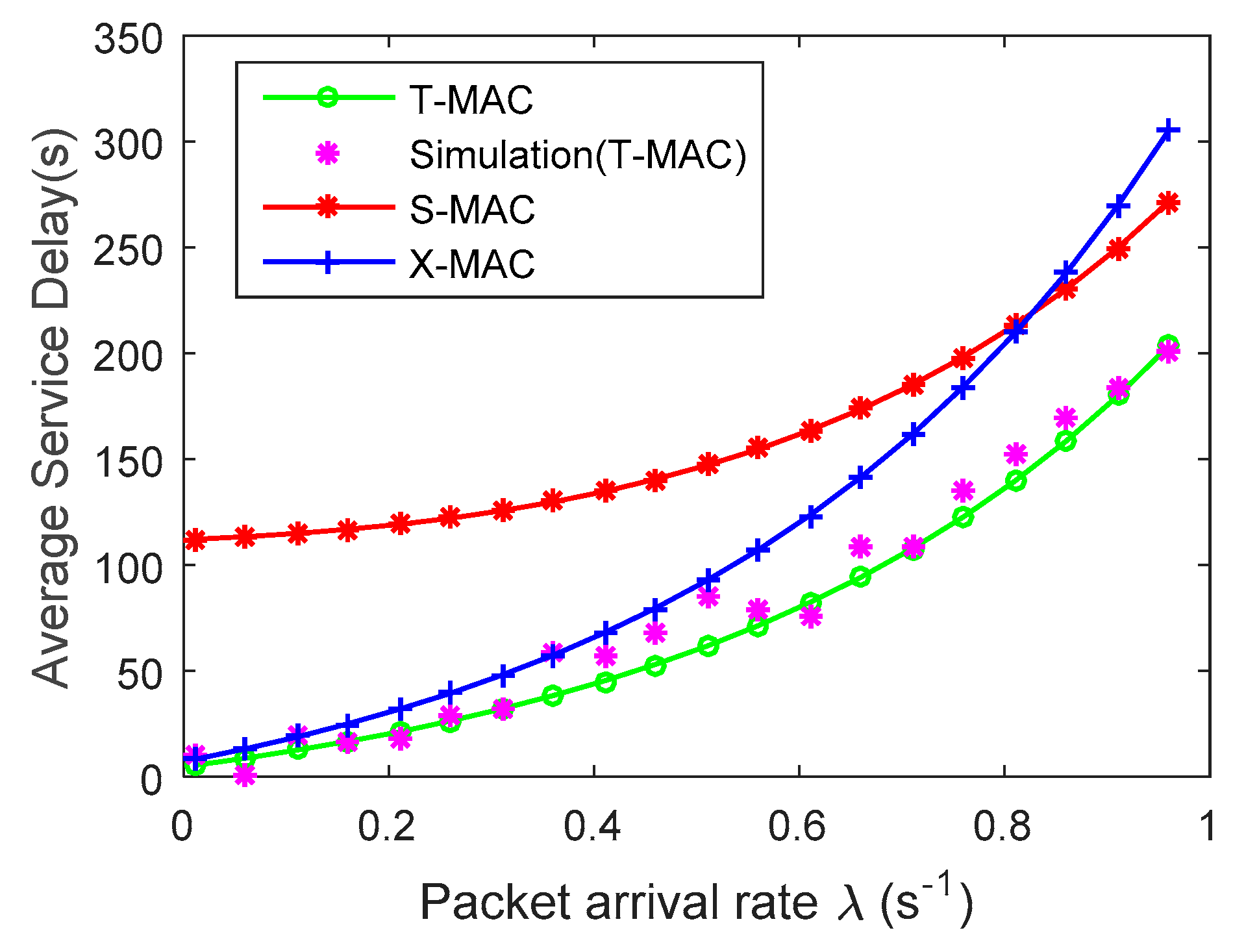
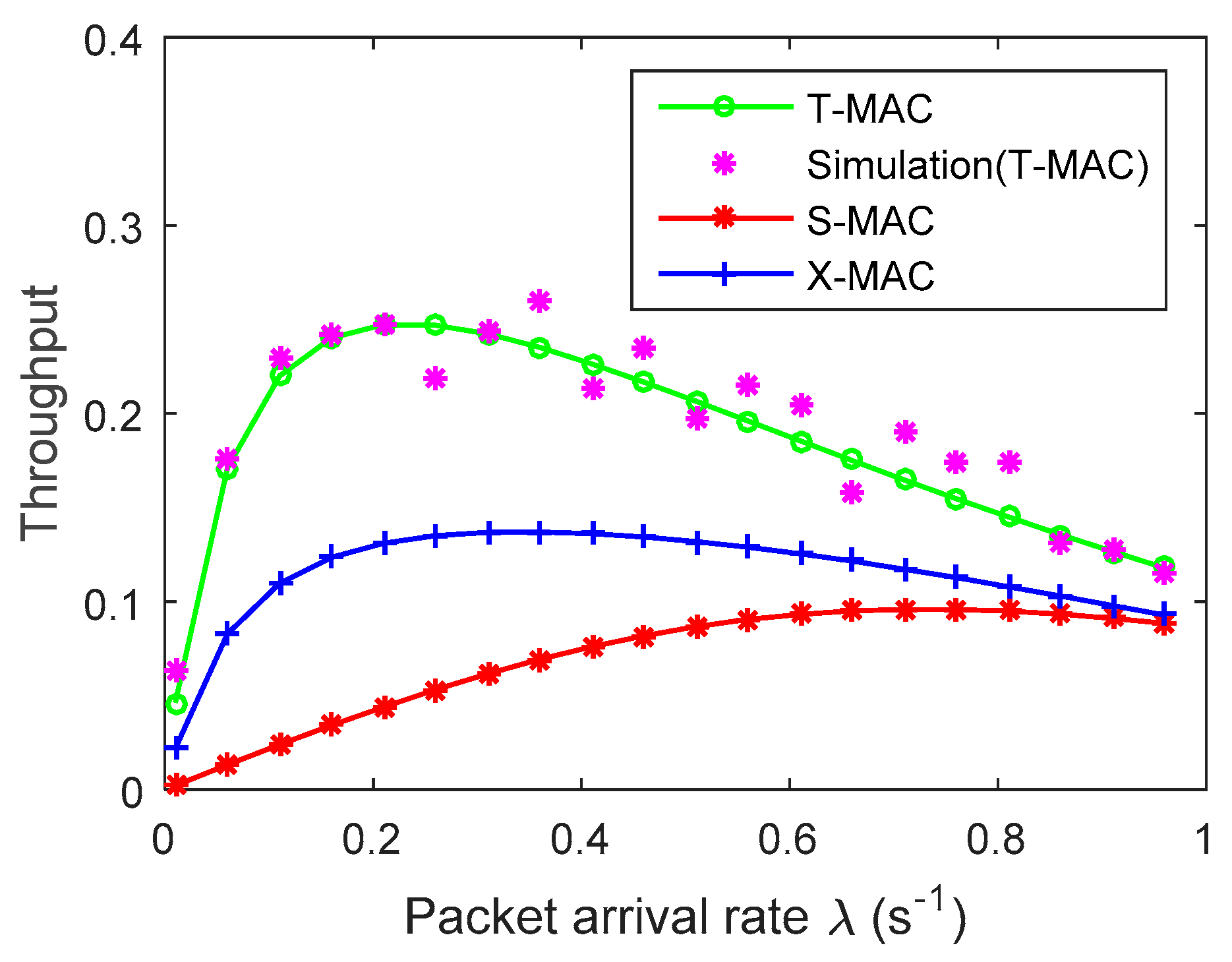
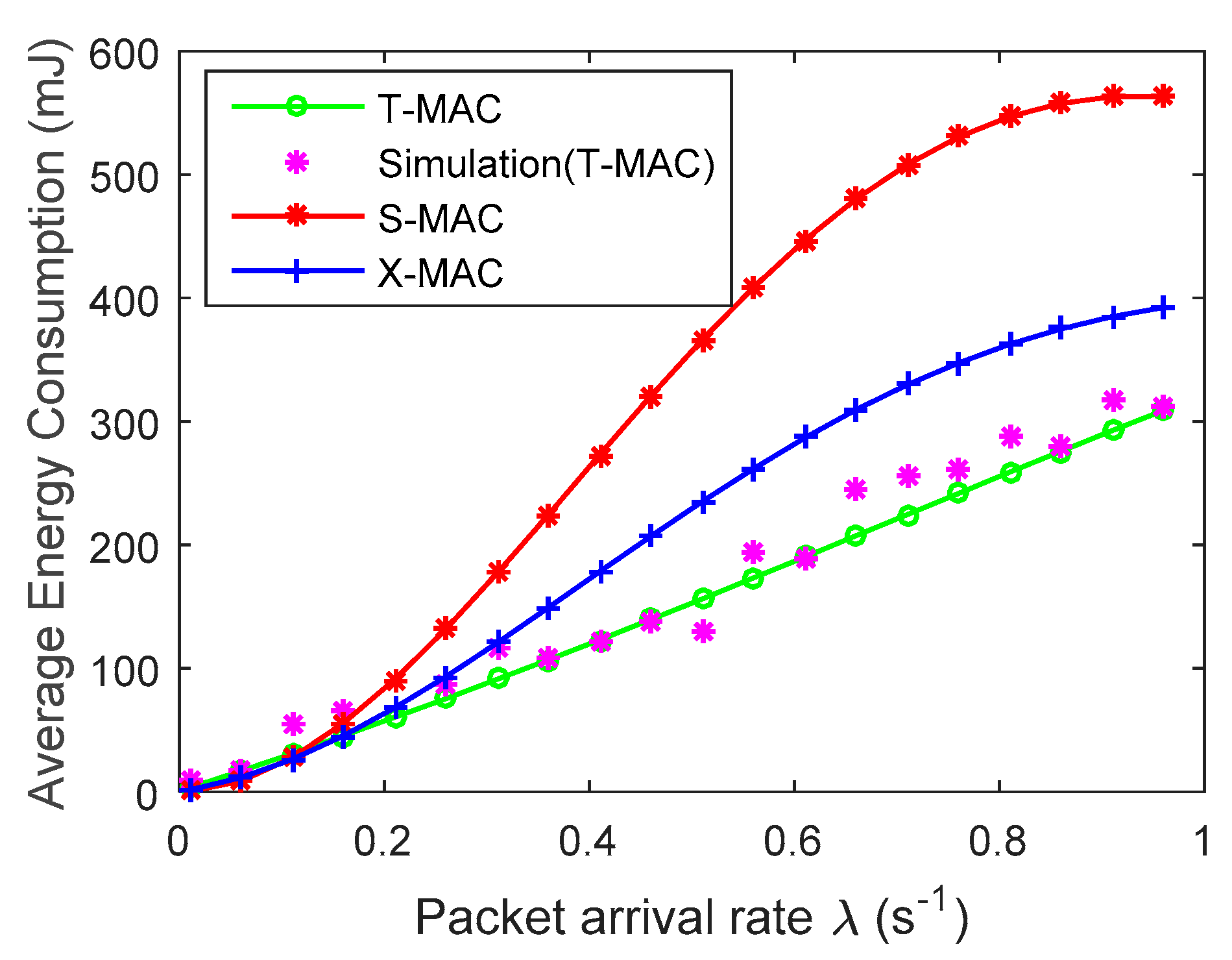
4. Experimental Results and Analysis
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kaiwartya, O.; Abdullah, A.H.; Cao, Y.; Raw, R.S.; Kumar, S.; Lobiyal, D.K.; Isnin, I.F.; Liu, X.; Shah, R.R. T-MQM: Testbed-based multi-metric quality measurement of sensor deployment for precision agriculture—A case study. IEEE Sens. J. 2016, 16, 8649–8664. [Google Scholar] [CrossRef]
- Ullah, F.; Abdullah, A.H.; Kaiwartya, O.; Cao, Y. TraPy-MAC: Traffic priority aware medium access control protocol for wireless body area network. J. Med Syst. 2017, 41, 93. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, M.N.; Abdullah, A.H.; Kaiwartya, O. FSM-F: Finite state machine based framework for denial of service and intrusion detection in MANET. PLoS ONE 2016, 11, e0156885. [Google Scholar] [CrossRef]
- Qureshi, K.N.; Abdullah, A.H.; Kaiwartya, O.; Iqbal, S.; Butt, R.A.; Bashir, F. A Dynamic congestion control scheme for safety applications in vehicular ad hoc networks. Comput. Electr. Eng. 2018, 72, 774–788. [Google Scholar] [CrossRef]
- Hassan, A.N.; Kaiwartya, O.; Abdullah, A.H.; Sheet, D.K.; Raw, R.S. Inter vehicle distance based connectivity aware routing in vehicular adhoc networks. Wirel. Pers. Commun. 2018, 98, 33–54. [Google Scholar] [CrossRef]
- Cao, Y.; Kaiwartya, O.; Zhuang, Y.; Ahmad, N.; Sun, Y.; Lloret, J. A decentralized deadline-driven electric vehicle charging recommendation. IEEE Syst. J. 2018, 99, 1–12. [Google Scholar] [CrossRef]
- Cao, Y.; Wang, T.; Zhang, X.; Kaiwartya, O.; Eiza, M.H.; Putrus, G. Toward anycasting-driven reservation system for electric vehicle battery switch service. IEEE Syst. J. 2019, 13, 906–917. [Google Scholar] [CrossRef]
- Farhan, L.; Kharel, R.; Kaiwartya, O.; Hammoudeh, M.; Adebisi, B. Towards green computing for internet of things: Energy oriented path and message scheduling approach. Sustain. Cities Soc. 2018, 38, 195–204. [Google Scholar] [CrossRef]
- Kaiwartya, O.; Abdullah, A.H.; Cao, Y.; Altameem, A.; Prasad, M.; Lin, C.T.; Liu, X. Internet of vehicles: Motivation, layered architecture, network model, challenges, and future aspects. IEEE Access 2016, 4, 5356–5373. [Google Scholar] [CrossRef]
- Kaiwartya, O.; Kumar, S.; Abdullah, A.H. Analytical model of deployment methods for application of sensors in non-hostile environment. Wirel. Pers. Commun. 2017, 97, 1517–1536. [Google Scholar] [CrossRef]
- Khasawneh, A.; Latiff, M.; Kaiwartya, O.; Chizari, H. Next forwarding node selection in underwater wireless sensor networks (UWSNs): Techniques and challenges. Information 2016, 8, 3. [Google Scholar] [CrossRef]
- Khatri, A.; Kumar, S.; Kaiwartya, O. Optimizing energy consumption and inequality in wireless sensor networks using NSGA-II. In Proceedings of the ICCCS, Boca Raton, FL, USA, 10 September 2016. [Google Scholar]
- Kumar, V.; Kumar, S. Position-based beaconless routing in wireless sensor networks. Wirel. Pers. Commun. 2016, 86, 1061–1085. [Google Scholar] [CrossRef]
- Kumar, K.; Kumar, S.; Kaiwartya, O.; Cao, Y.; Lloret, J.; Aslam, N. Cross-layer energy optimization for IoT environments: Technical advances and opportunities. Energies 2017, 10, 2073. [Google Scholar] [CrossRef]
- .Holland, M.; Wang, T.; Tavli, B.; Seyedi, A.; Heinzelman, W. Optimizing physical-layer parameters for wireless sensor networks. ACM Trans. Sens. Netw. 2011, 7, 28. [Google Scholar] [CrossRef]
- Khasawneh, A.; Latiff, M.S.B.A.; Kaiwartya, O.; Chizari, H. A reliable energy-efficient pressure-based routing protocol for underwater wireless sensor network. Wirel. Netw. 2018, 24, 2061–2075. [Google Scholar] [CrossRef]
- Ullah, F.; Abdullah, A.H.; Kaiwartya, O.; Lloret, J.; Arshad, M.M. EETP-MAC: Energy efficient traffic prioritization for medium access control in wireless body area networks. Telecommun. Syst. 2017, 1–23. [Google Scholar] [CrossRef]
- Ye, W.; Heidemann, J.; Estrin, D. Medium access control with coordinated adaptive sleeping for wireless sensor networks. IEEE Trans. Netw. 2004, 12, 493–506. [Google Scholar] [CrossRef]
- Heinzelman, W.; Chandrakasan, A.; Balakrishnan, H. Energy-efficient communication protocols for wireless microsensor networks. In Proceedings of the 33rd Annual Hawaii International Conference on System Sciences, Maui, HI, USA, 7 January 2000; Volume 1, pp. 3005–3014. [Google Scholar]
- Ye, Z.; He, C.; Ji, L. Performance analysis of S-MAC protocol under unsaturated conditions. IEEE Commun. Lett. 2008, 12, 210–212. [Google Scholar]
- Yang, O.; Heinzelman, W.B. Modeling and performance analysis for duty-cycled MAC protocols with applications to S-MAC and X-MAC. IEEE Trans. Mob. Comput. 2012, 11, 905–921. [Google Scholar] [CrossRef]
- Wijetunge, S.; Gunawardana, U.; Liyanapathirana, R. Performance analysis of IEEE 802.15.4 MAC protocol with ACK frame transmission. Wirel. Pers. Commun. 2013, 69, 509–534. [Google Scholar] [CrossRef]
- Ramachandran, I.; Das, A.K.; Roy, S. Analysis of the contention access period of IEEE 802.15.4 MAC. ACM Trans. Sens. Netw. 2007, 3, 4. [Google Scholar] [CrossRef]
- Pollin, S.; Ergen, M.; Ergen, S.C.; Bougard, B.; van der Perre, L.; Moerman, I.; Bahai, A.; Varaiya, P.; Catthoor, F. Performance analysis of slotted carrier sense IEEE 802.15.4 medium access layer. IEEE Trans. Wirel. Commun. 2008, 7, 3359–3371. [Google Scholar] [CrossRef]
- Park, P.; Marco, P.D.; Soldati, P.; Fischione, C.; Johansson, K.H. A generalized Markov chain model for effective analysis of slotted IEEE 802.15.4. In Proceedings of the 2009 IEEE 6th International Conference on Mobile Adhoc and Sensor Systems, Macau, China, 12–15 October 2009; pp. 130–139. [Google Scholar]
- Vilajosana, X.; Wang, Q.; Chraim, F.; Watteyne, T.; Chang, T.; Pister, K.S.J. A realistic energy consumption model for TSCH networks. IEEE Sens. J. 2014, 14, 482–489. [Google Scholar] [CrossRef]
- Aanchal; Kumar, S.; Kaiwartya, O.; Abdullah, A.H. Green computing for wireless sensor networks: Optimization and Huffman coding approach. Peer Peer Netw. Appl. 2017, 10, 592–609. [Google Scholar] [CrossRef]
- Kumar, V.; Kumar, S. Energy balanced position-based routing for lifetime maximization of wireless sensor networks. Ad Hoc Netw. 2016, 52, 117–129. [Google Scholar] [CrossRef]
- Dohare, U.; Lobiyal, D.K.; Kumar, S. Energy balanced model for lifetime maximization for a randomly distributed sensor networks. Wirel. Pers. Commun. 2014, 78, 407–428. [Google Scholar] [CrossRef]
- Khatri, A.; Kumar, S.; Kaiwartya, O. Towards green computing in wireless sensor networks: Controlled mobility-aided balanced tree approach. Int. J. Commun. Syst. 2018, 31, e3463. [Google Scholar] [CrossRef]
- Kaiwartya, O.; Abdullah, A.H.; Cao, Y.; Lloret, J.; Kumar, S.; Shah, R.R.; Prasad, M.; Prakash, S. Virtualization in wireless sensor networks: Fault tolerant embedding for internet of things. IEEE Internet Things J. 2018, 5, 571–580. [Google Scholar] [CrossRef]
- Ramchand, V.; Lobiyal, D.K. An analytical model for power control T-MAC protocol. Int. J. Comput. Appl. 2010, 12, 13–18. [Google Scholar] [CrossRef]

| Notation | Description | Notation | Description |
|---|---|---|---|
| n | Number of sensor nodes | Sleeping energy | |
| W | Contention window size | Probability of sleeping | |
| p | Probability | Collision time | |
| State probability | Idle time | ||
| Positive integer | Sleep time | ||
| Probability of transmission | Successful transmission time | ||
| Probability of successful transmission | Missing transmission time | ||
| Probability of collision | Time taken by the node for not capturing the channel | ||
| Probability of idle | Time taken due to the back off procedure | ||
| Time slot | Transmission time | ||
| Energy consumption in successful transmission | Duration of a cycle | ||
| Idle energy | Threshold | ||
| Collision energy | Whole network energy | ||
| Sampling time in µs | S | Throughput | |
| Average transmission time | Sampling rate in µs |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ram, M.; Kumar, S.; Kumar, V.; Sikandar, A.; Kharel, R. Enabling Green Wireless Sensor Networks: Energy Efficient T-MAC Using Markov Chain Based Optimization. Electronics 2019, 8, 534. https://doi.org/10.3390/electronics8050534
Ram M, Kumar S, Kumar V, Sikandar A, Kharel R. Enabling Green Wireless Sensor Networks: Energy Efficient T-MAC Using Markov Chain Based Optimization. Electronics. 2019; 8(5):534. https://doi.org/10.3390/electronics8050534
Chicago/Turabian StyleRam, Mahendra, Sushil Kumar, Vinod Kumar, Ajay Sikandar, and Rupak Kharel. 2019. "Enabling Green Wireless Sensor Networks: Energy Efficient T-MAC Using Markov Chain Based Optimization" Electronics 8, no. 5: 534. https://doi.org/10.3390/electronics8050534
APA StyleRam, M., Kumar, S., Kumar, V., Sikandar, A., & Kharel, R. (2019). Enabling Green Wireless Sensor Networks: Energy Efficient T-MAC Using Markov Chain Based Optimization. Electronics, 8(5), 534. https://doi.org/10.3390/electronics8050534






