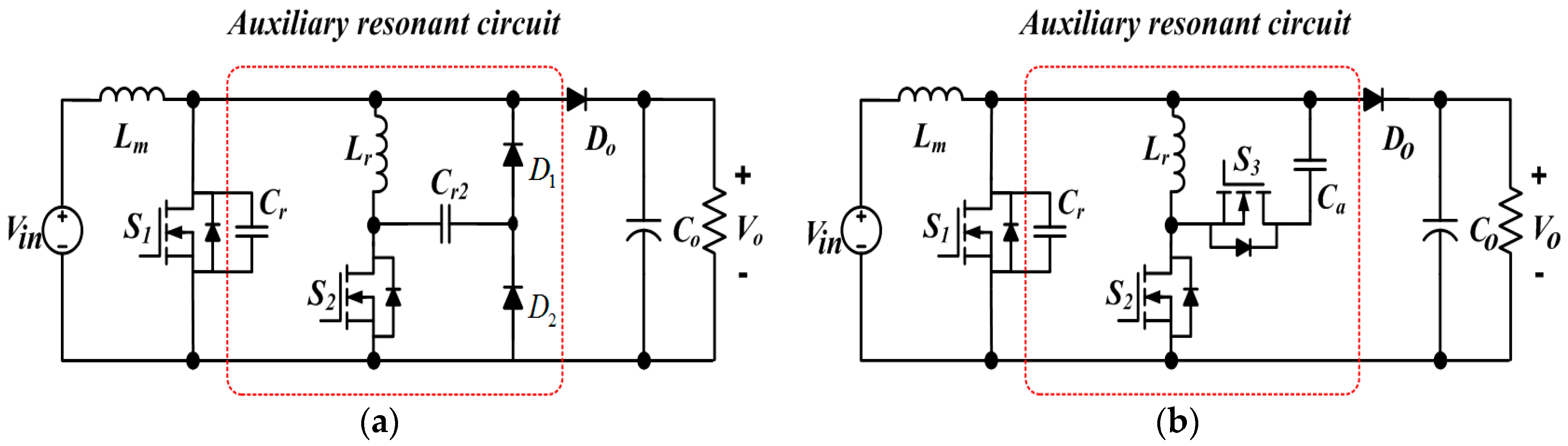
2.2. Analysis of Proposed Converter
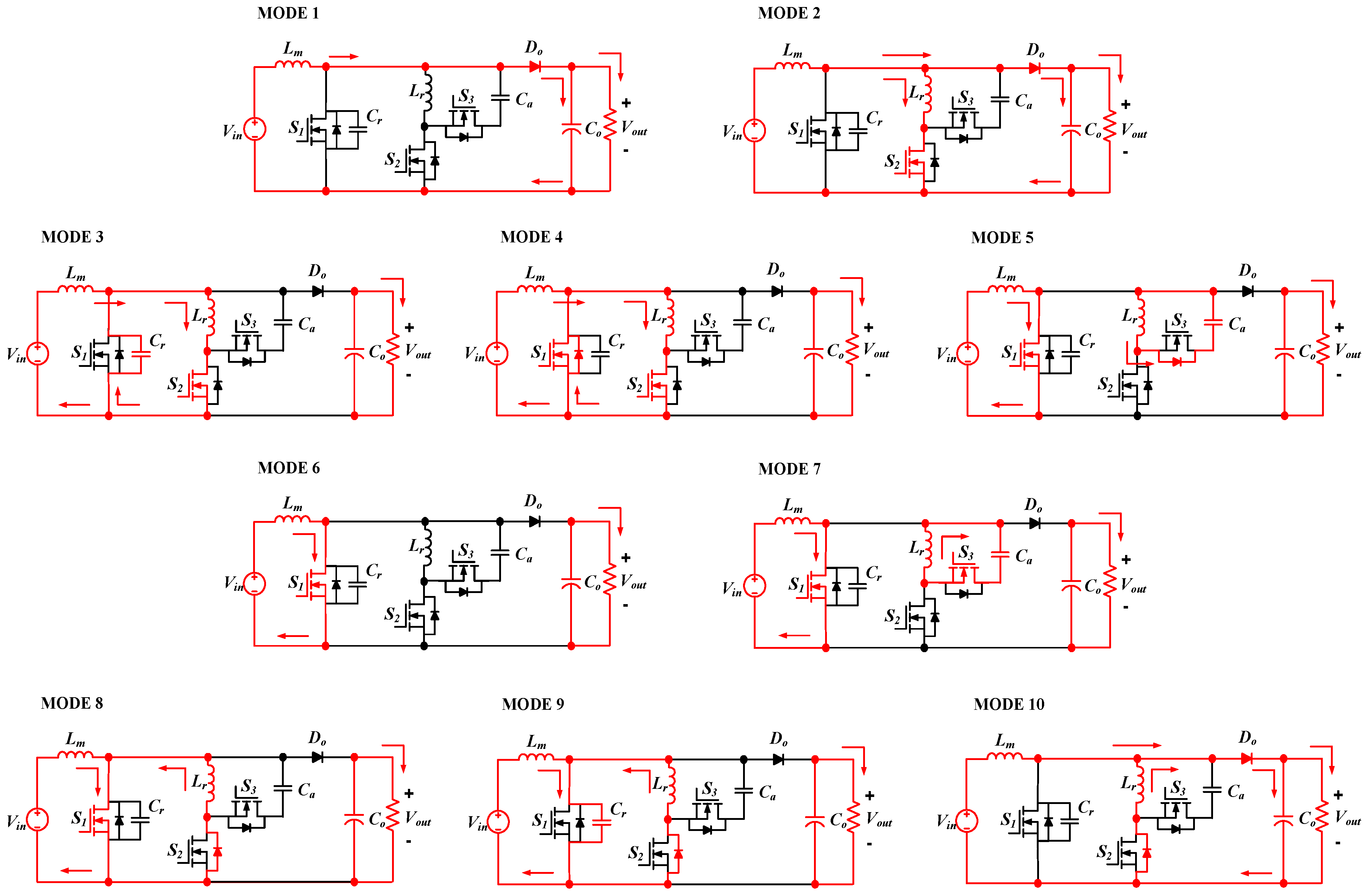
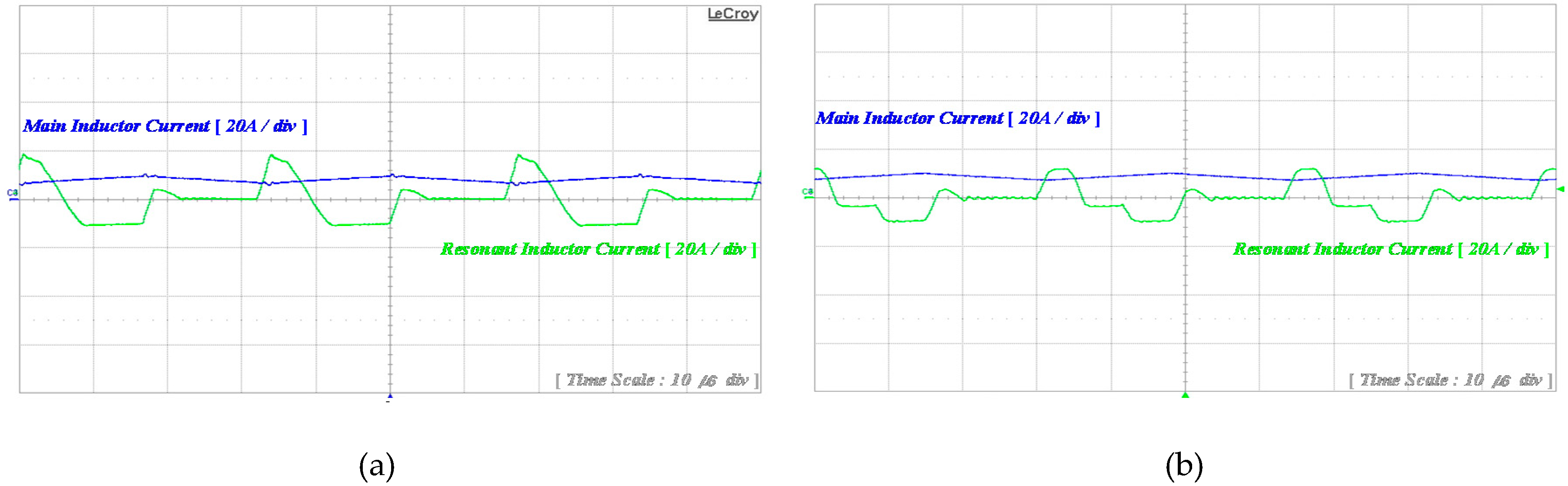
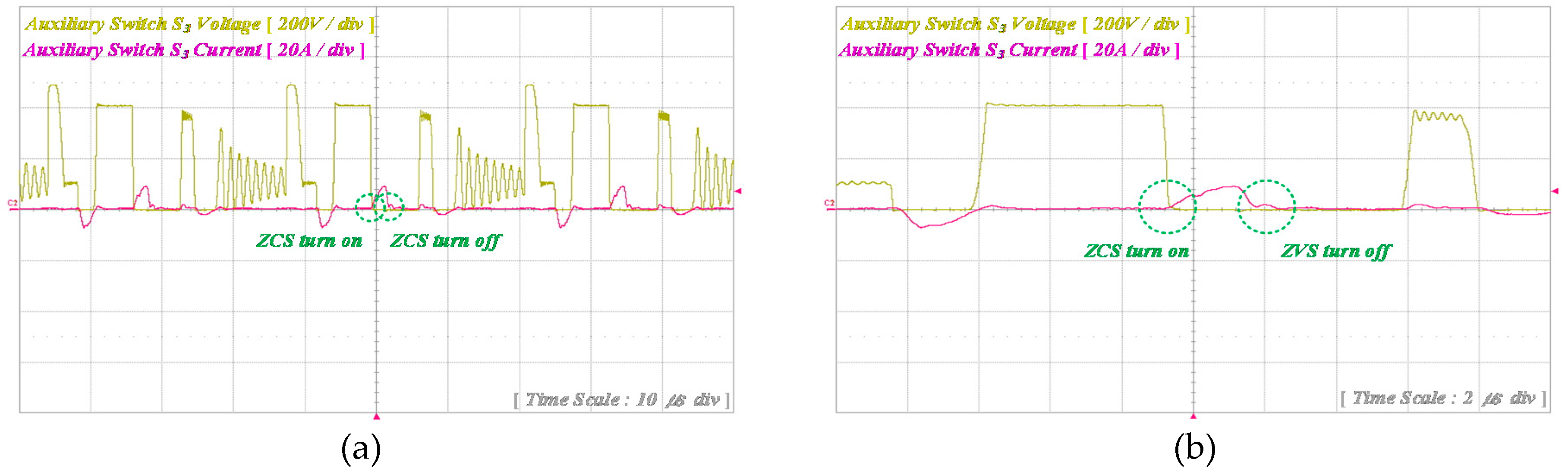
Operation mode of the proposed ZVT resonant boost converter is shown in
Figure 3. The operational principle of the proposed converter is divided into ten modes for simple analysis. The mode 1, mode 2 and mode 10 are discharging mode of the proposed ZVT boost converter. The mode 4 made to satisfy the ZVT condition of the main switch
S1. And next Mode 5 is turned on under the ZVS condition. And the main inductor charges form mode 5 to mode 9. The mode 3, mode 5, mode 7 and mode 9 operate with resonance. The mode 2, mode 5 and mode 7 are turned on the soft switching of the auxiliary switches.
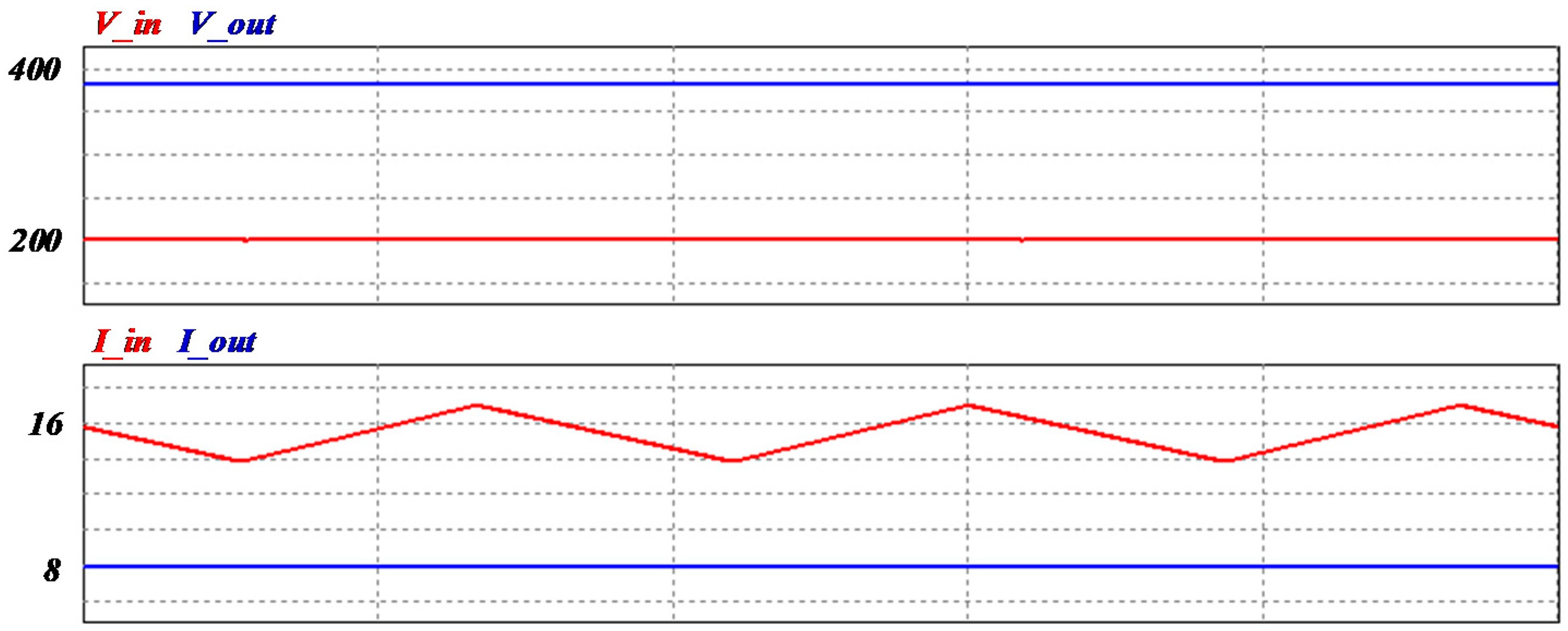
The following statements are assumptions for simple analysis of the proposed converter: First, all switching devices and passive elements (inductor and capacitor) are ideal. Second, the input voltage 200 V and output voltage 380 V are constant. Third, the recovery time of all diodes is ignored. The resonant ZVT boost converters operate in 10 different modes, and the following assumptions were made for a steady-state analysis:
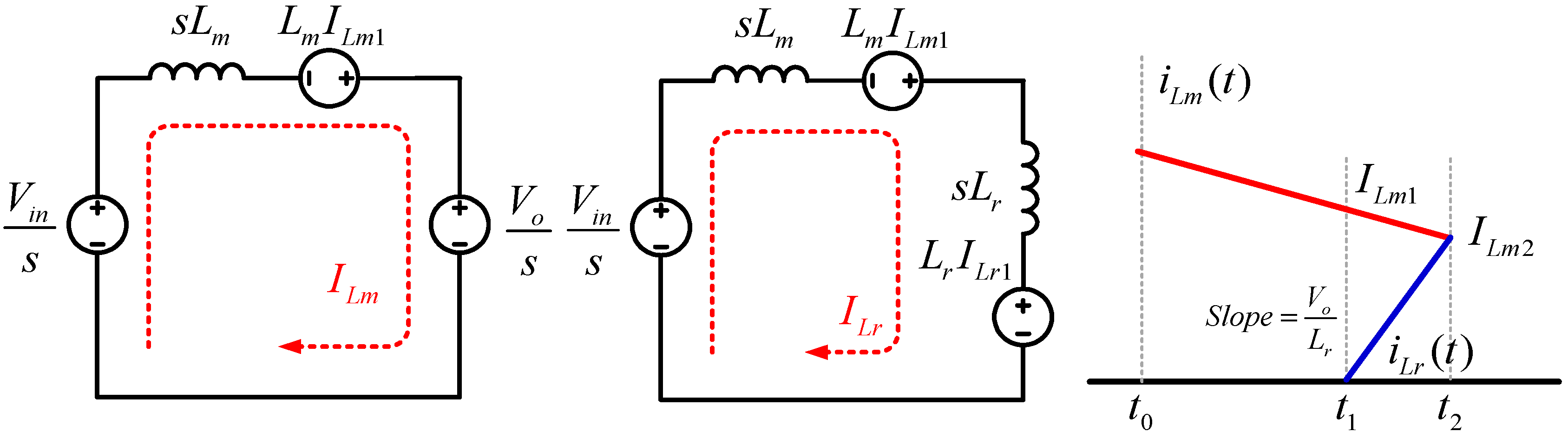
Mode 1 (t0–t1): Main
S1 and auxiliary switches
S2 and
S3 are turned off. The accumulated main inductor current
Lm is flowed through the output diode
Do. Then, output and resonant capacitors
Co Cr are charged the same voltage. Equivalent circuit of mode 1 and key waveform is shown in
Figure 4. The equivalent circuit shows when the main inductor discharges for boost.
In Mode 1, the main inductor current
iLm decreases and the resonant inductor current
iLr and auxiliary capacitor voltage
vCa are zero. This is expressed as the Equations (1) and (2).
Furthermore, the main inductor current
ILm1 is defined for the next mode
t2 analysis.
Mode 2 (t1 < t < t2): In Mode 2, an auxiliary switch
S2 turns on under the ZCS condition. The resonant inductor current
iLr increases linearly from zero. The main inductor current
iLm decreases. When the resonant inductor current
iLr is equal to the main inductor current
iLm, Mode 2 is completed. Also
Figure 5 shows an equivalent circuit and key waveform for analyzing mode 2. And the Equivalent circuit Indicates to calculate the magnitude of the current of main inductor
iLm and resonant inductor
iLr. Thus, the main inductor current is equal to the minimum. The main inductor current
iLm and resonant inductor current
iLr are expressed by Equations (4) and (5).
The resonant capacitor voltage
vCr is equal to output voltage. If parasitic capacitance of resonant switch
S3 is ignored, auxiliary capacitor voltage
vCa is zero.
For Mode 3, the resonant inductor current
ILr2 is defined as Equation (7).
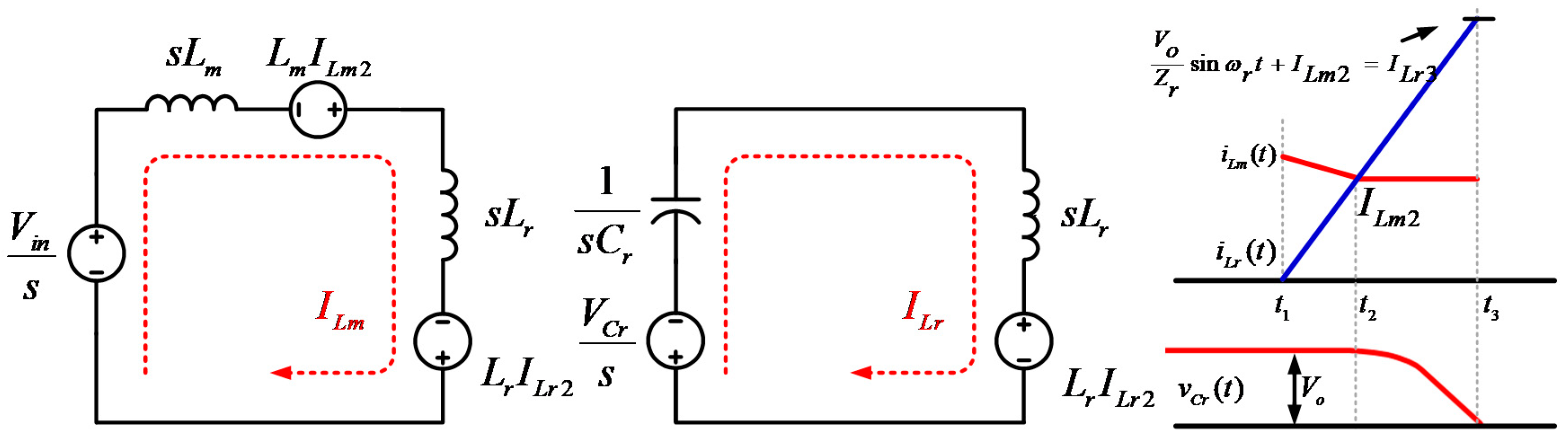
Mode 3 (t2 < t < t3): When the main and resonant inductor currents
iLm and
iLr are equalized, the resonance operation between resonant capacitor
Cr and resonant inductor
Lr is started. Then, output diode
Do is turned off because the resonant capacitor
Cr is discharged. Then, equivalent circuit of resonance operation is shown in
Figure 6. The key waveform of mode 3 indicates main inductor current
iLm, resonant inductor current
iLr and resonant capacitor voltage
vCr.
At the end of Mode 3, the resonant capacitor
Cr is equal to zero. The resonant capacitor voltage
vCr and resonant inductor current
iLr can be obtained by the Laplace transform, following Equations (9), (10), (12), and (13). In addition, the resonant impedance
Zr and angular frequency
ωr are given by Equation (16). Additionally,
iLm,
iLr,
vCa, and
vCr are defined by Equations (8), (11), (14), and (15).
where
The resonant inductor current
ILr3 is defined for the next mode
t4 analysis.
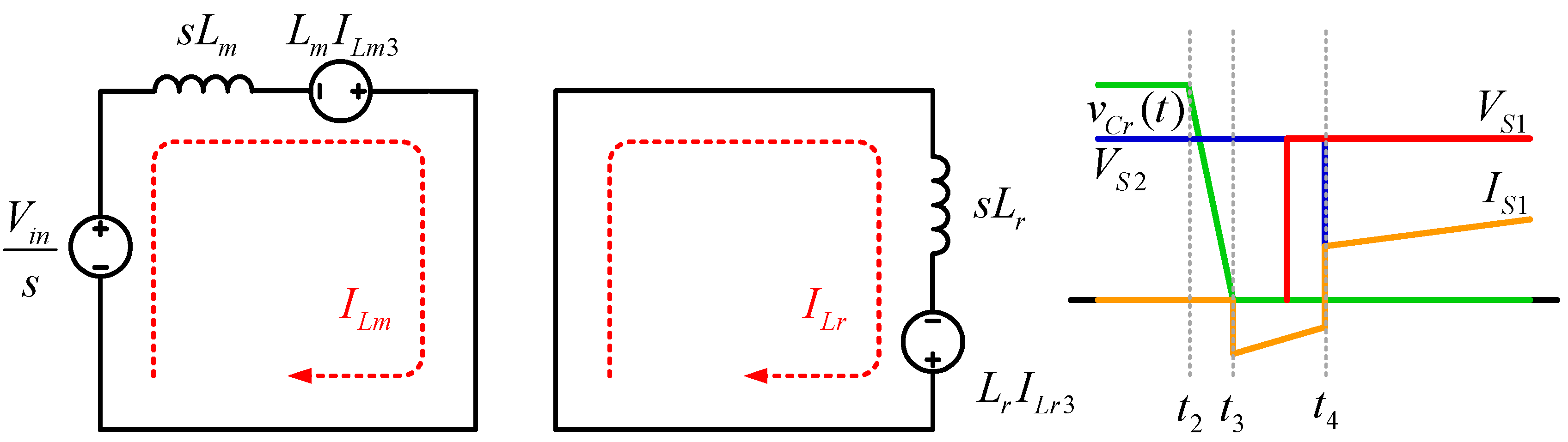
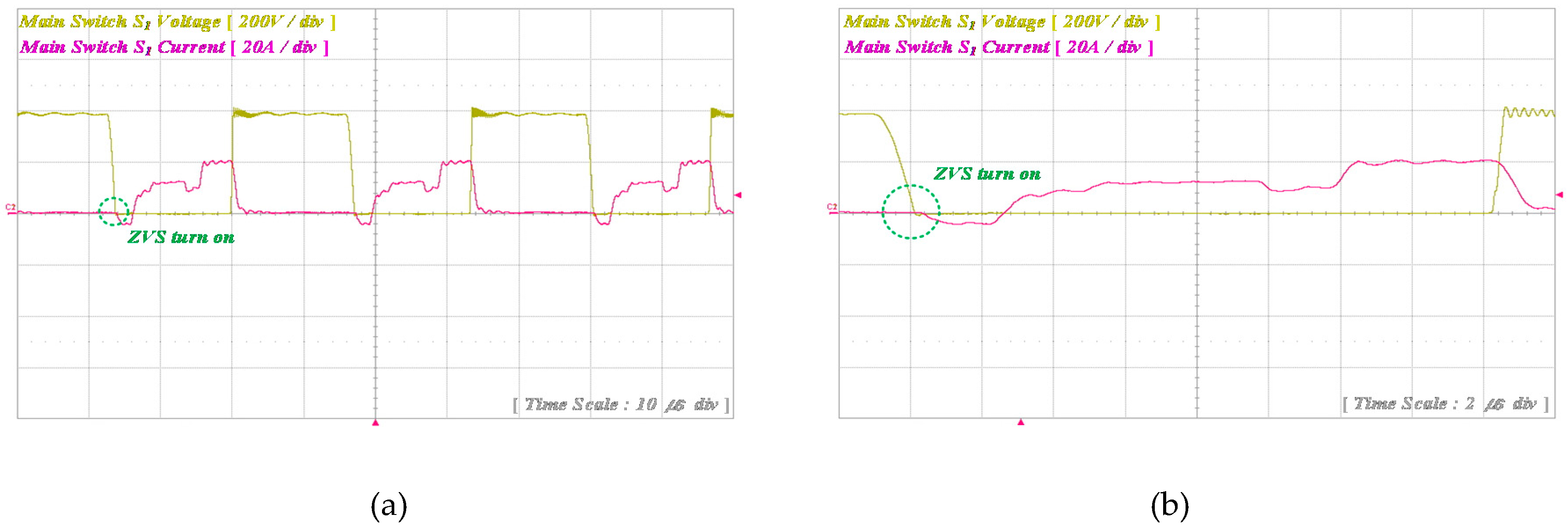
Mode 4 (t3 < t < t4): The body diode of the main switch
S1 is turned on, and the voltage of main switch
S1 is equal to zero. Then, the main switch
S1 is made to satisfy the ZVT condition. Resonant current flows through the anti-parallel diode of the main switch
S1. The main inductor current
iLm and the resonant inductor current
iLr can be derived from Equation (18). Auxiliary and resonant capacitor voltage
vCr are all zero by Equation (19). Thus,
Figure 7 shows for derivation of the equation. And voltage and current of switches is shown in the key waveform. Mode 4 ends when the auxiliary switch
S2 is turned off.
Main inductor current
ILm4 is defined for the next mode
t5 analysis.
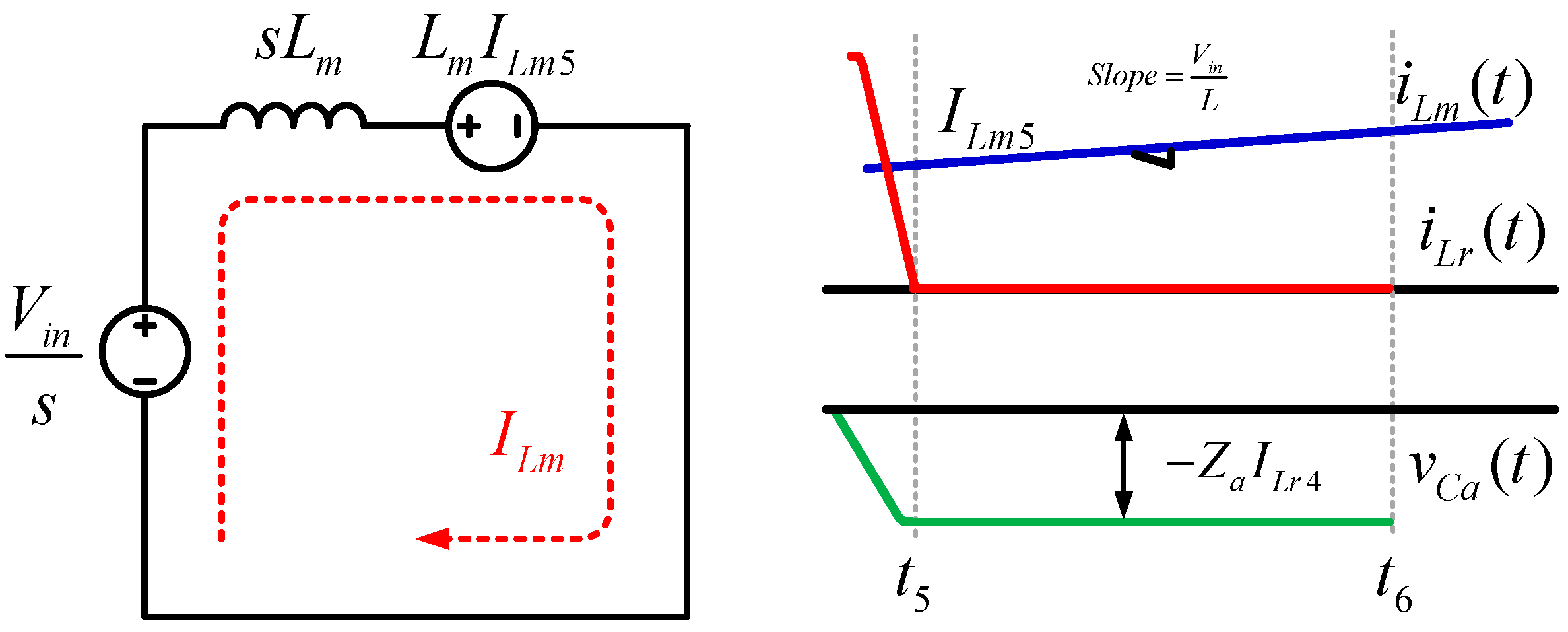
Mode 5 (t4 < t < t5): In Mode 5, the main switch
S1 is turned on under the ZVS condition. Then, the main inductor current
iLm increases linearly. The auxiliary switch
S2 is turned off in the same condition, while the second resonance is begun by the resonant inductor
Lr and auxiliary capacitor
Ca. Thus, the resonant inductor current
iLr decreases. The auxiliary capacitor voltage
vCa and resonant inductor current
iLr can be derived from the Laplace transform, following Equations (22), (24), and (25). At this time, the equivalent circuit of mode 5 is shown in
Figure 8. The equivalent circuit is divided into main inductor current
iLm and resonance circuit. The key waveform indicates resonant inductor current
iLr, main inductor current
iLm and auxiliary capacitor voltage
vCa.
Additionally, the resonant impedance
Za and angular frequency
ωa are given by Equation (27). Then,
iLm,
iLr,
vca, and
vCr are defined by Equations (21), (23), and (26).
where
For Mode 6, the resonant inductor current
iLr and auxiliary capacitor voltage
vCa are defined as Equation (28).
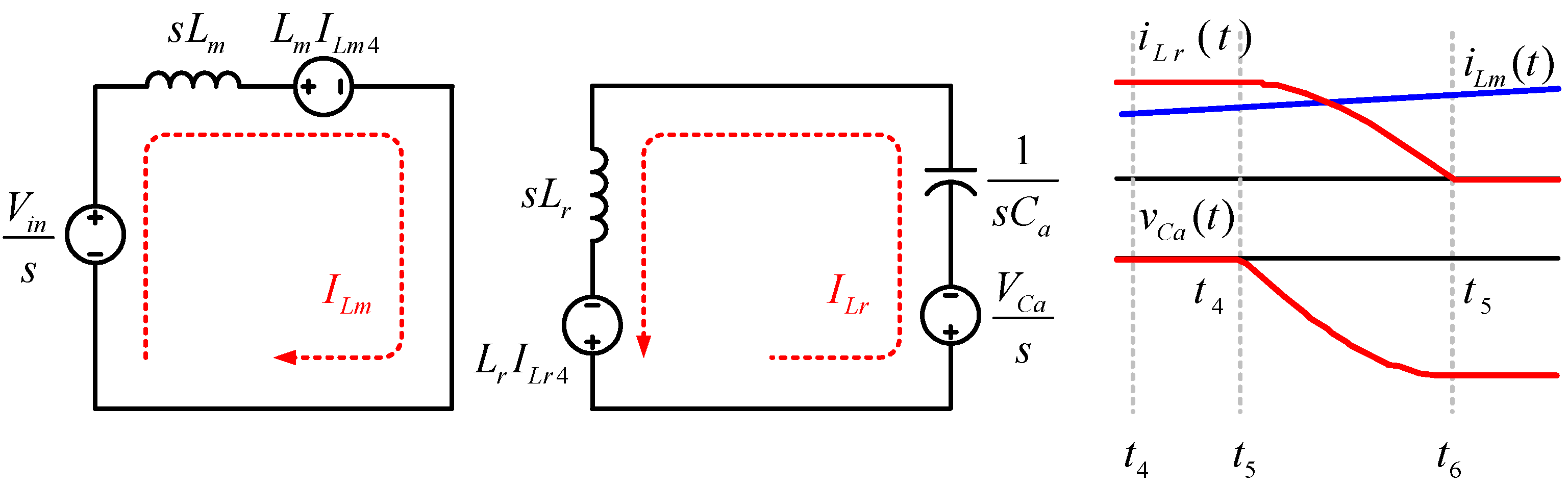
Mode 6 (t5 < t < t6): In Mode 6, resonant inductor
Lr and auxiliary capacitor
Ca end the second resonant operation and the resonant capacitor
Ca is charged. The main inductor current
iLm increases linearly through the main switch
S1. Mode 6 ends when the auxiliary switch
S3 turns on. The equivalent circuit of mode 6 and key waveform is shown in
Figure 9. The main inductor current
iLm can be calculated through the equivalent circuit. The
iLm,
iLr,
vCa, and
vCr values are as follows in Equations (29) and (30):
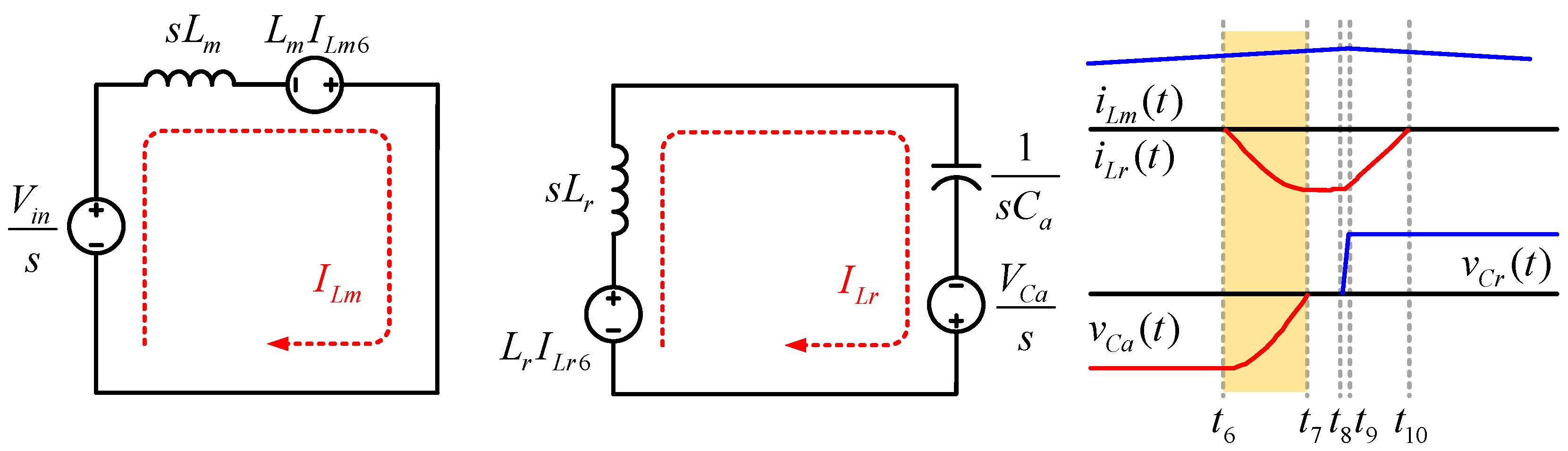
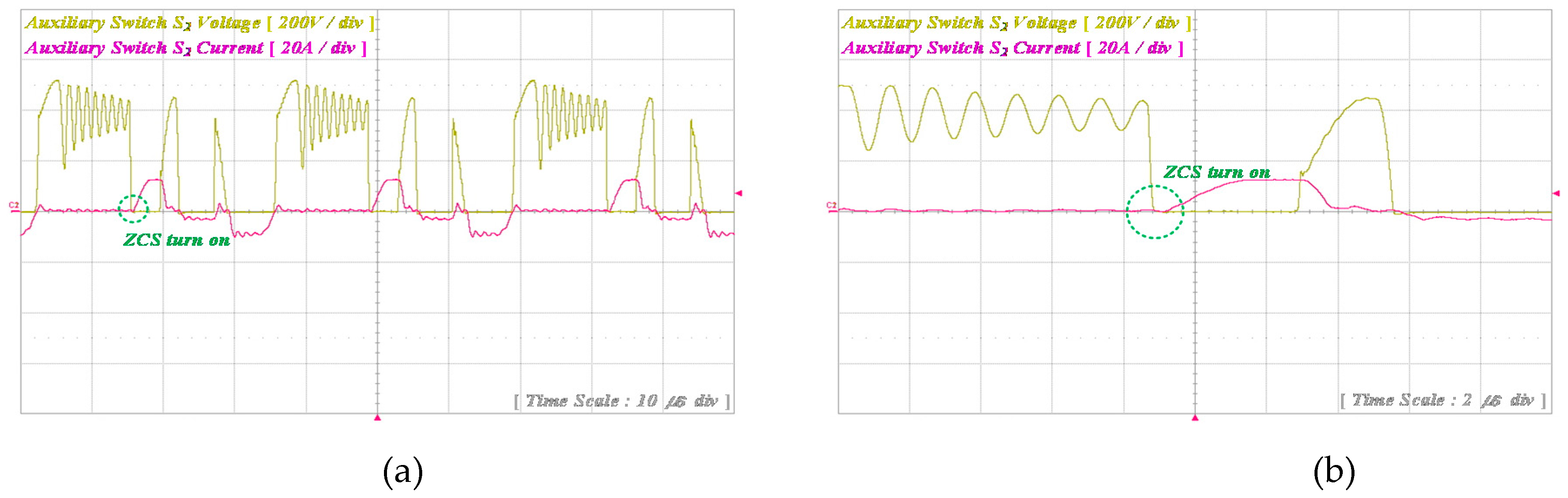
Mode 7 (t6 < t < t7): At the beginning of Mode 7, the third resonance begins. Then, the auxiliary switch
S3 turns on under the ZCS condition. The energy stored in the resonant capacitor
Cr is transferred to the resonant inductor through auxiliary switch
S3. The auxiliary capacitor voltage
vCa and resonant inductor current
iLr can be derived from the Laplace transform, following Equations (32), (33), (35), and (36). Then, the equivalent circuit is shown in
Figure 10. Mode 7 ends when the auxiliary capacitor
Ca voltage reaches 0 V, as in Equation (38). The current that flows through the main inductor
Lm increases linearly, as in Equation (31) and the energy is stored in the resonant inductor
Lr through the auxiliary switch
S3. The
iLr and
vca values were defined by Equations (34) and (37).
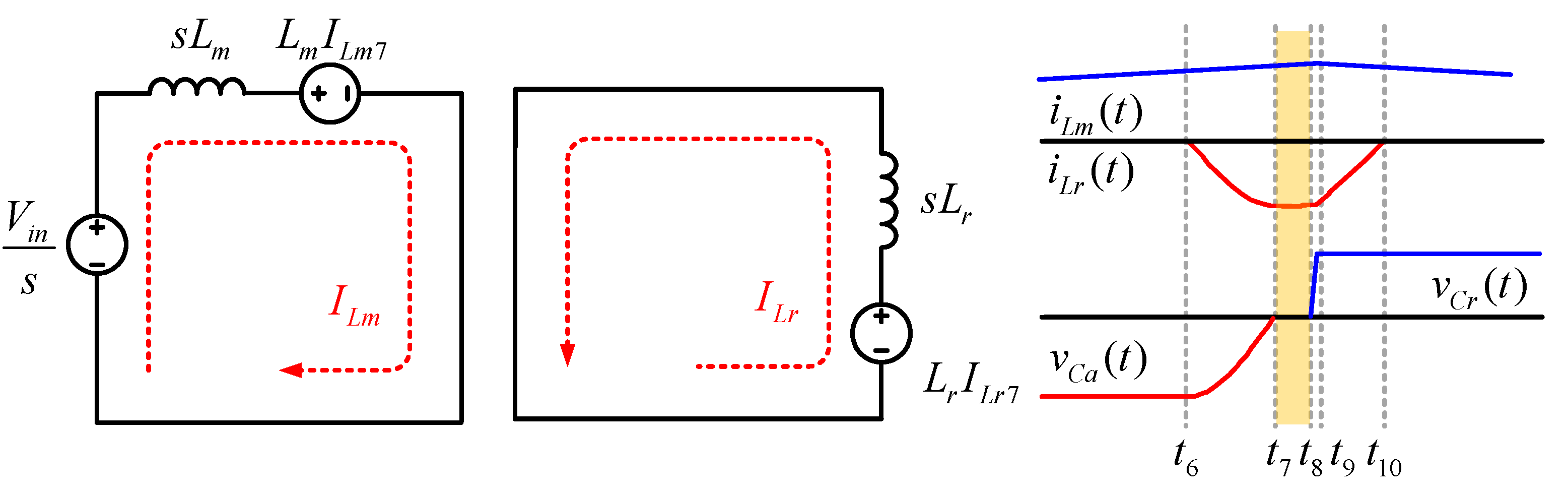
Mode 8 (t7 < t < t8): In Mode 8, the auxiliary capacitor voltage
vCa becomes zero. Then, the main inductor current
iLm increases linearly and the body diode of the auxiliary switch
S2 is turned on. The resonant inductor
Lr current flows through the freewheeling path of the body diode—the main switch
S1. When the main switch
S1 is turned off, Mode 8 is complete. In this interval, the magnitude of the resonant inductor current
iLr is equal to that of Mode 3. However, the current flow is reversed. The
iLm,
iLr,
vCa, and
vCr values are as follows in Equations (39) and (40):
The equivalent circuit of mode 8 and key waveform is shown
Figure 11. The equivalent circuit is divided into main inductor current
iLm and resonant inductor current
iLr. The key waveform indicates
iLm,
iLr,
vCa, and
vCr. For Mode 9, the main and resonant current
ILm8 are defined by Equations (41) and (42).
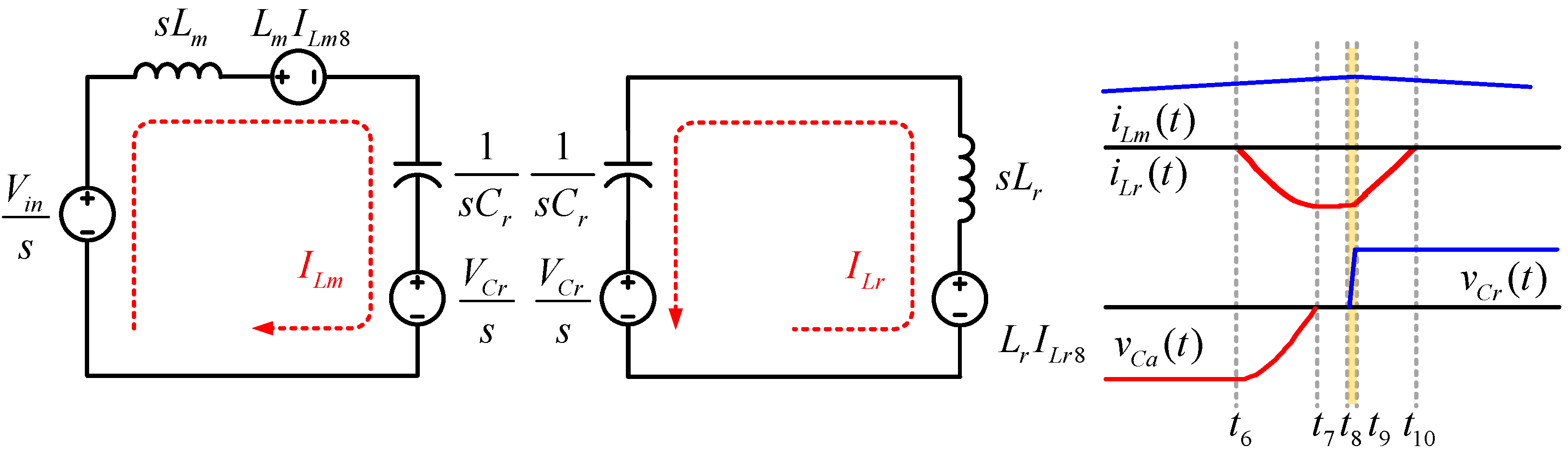
Mode 9 (t8 < t < t9): In this mode, the fourth resonance between the resonant inductor
Lr and the resonant capacitor
Cr begins. The current that flows in the resonance inductor
Lr is reduced from the maximum point and the resonant capacitor
Cr is charged by the total current of the main and resonant inductor. Then, the voltage of the resonant capacitor
vCa is charged to the output voltage
Vo, and Mode 9 ends. The resonant capacitor voltage
vCa and resonant inductor current
iLr can be derived from the Laplace transform, following Equations (44), (45), (47), and (48). The
iLm,
iLr,
vCa, and
vCr values are as follows in Equations (43), (46), (49), and (50):
The Mode 9 is divided into two equivalent circuits in
Figure 12. Then, the equivalent circuit of resonance operation is shown. The key waveform of Mode 9 indicates
iLm,
iLr,
vCa, and
vCr. And the key waveform of
Figure 12 shows the maximum of the main inductor current
iLm.
For Mode 10, the main inductor current
ILm9 is defined:
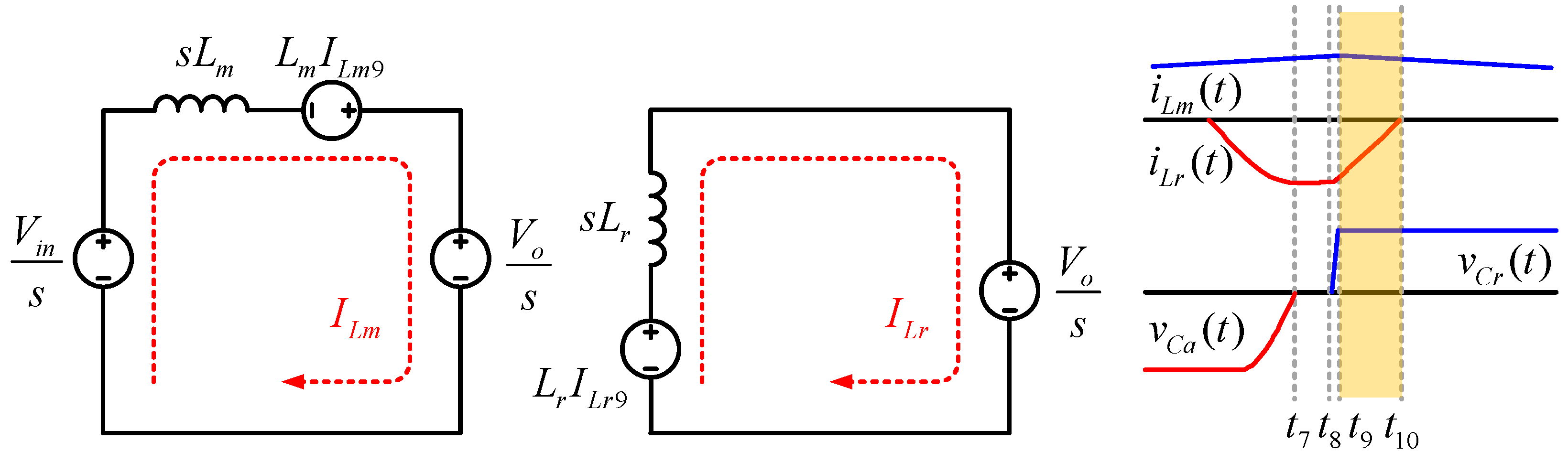
Mode 10 (t9 < t < t10): The resonant inductor current iLr linearly decreases to zero. And if the resonant capacitor voltage vCa is charged with a larger output than output voltage Vo, then the output diode Do is turned on. Mode 10 is completed, and the next switching cycle starts.
The Mode 10 is divided into two equivalent circuits in
Figure 13. Then, the equivalent circuit of main inductor
Lm is shown. Other equivalent circuit indicates resonant inductor
Lr. The key waveform of
Figure 13 shows the maximum of the main inductor current
iLm. And resonant capacitors
Cr are charged the output voltage.
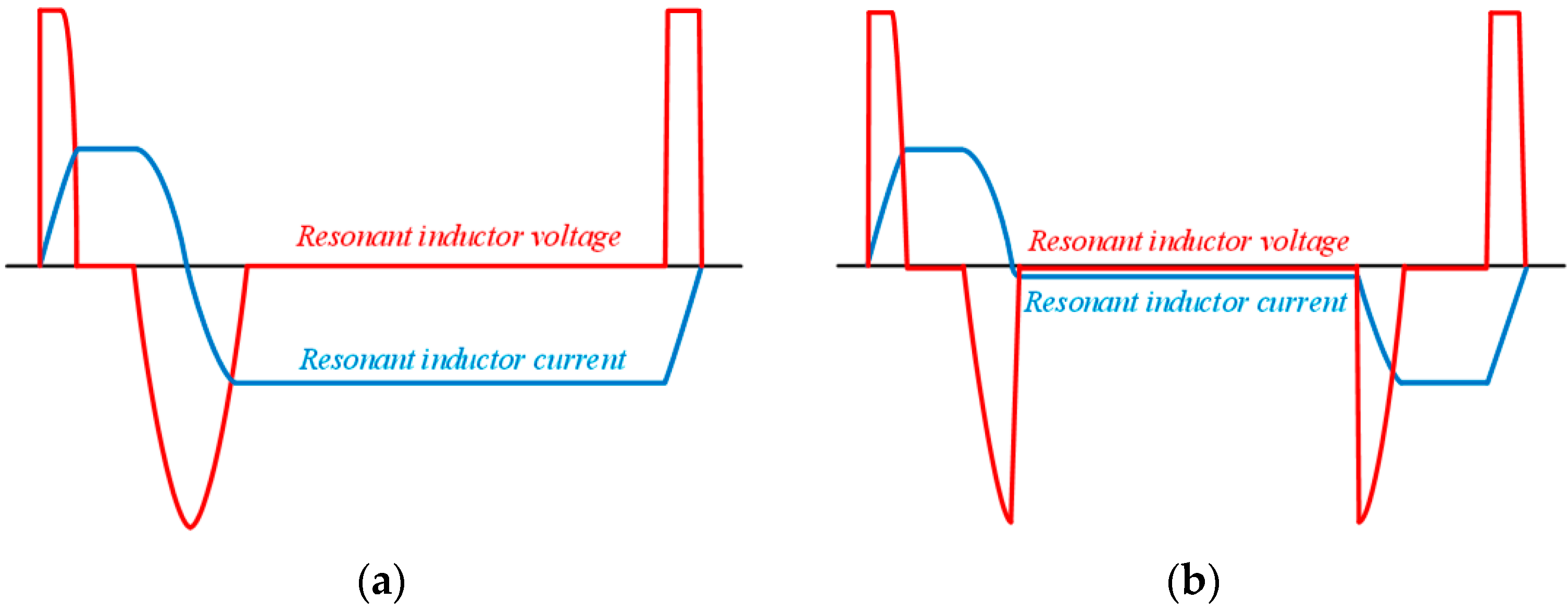
2.3. PWM Signal Analysis
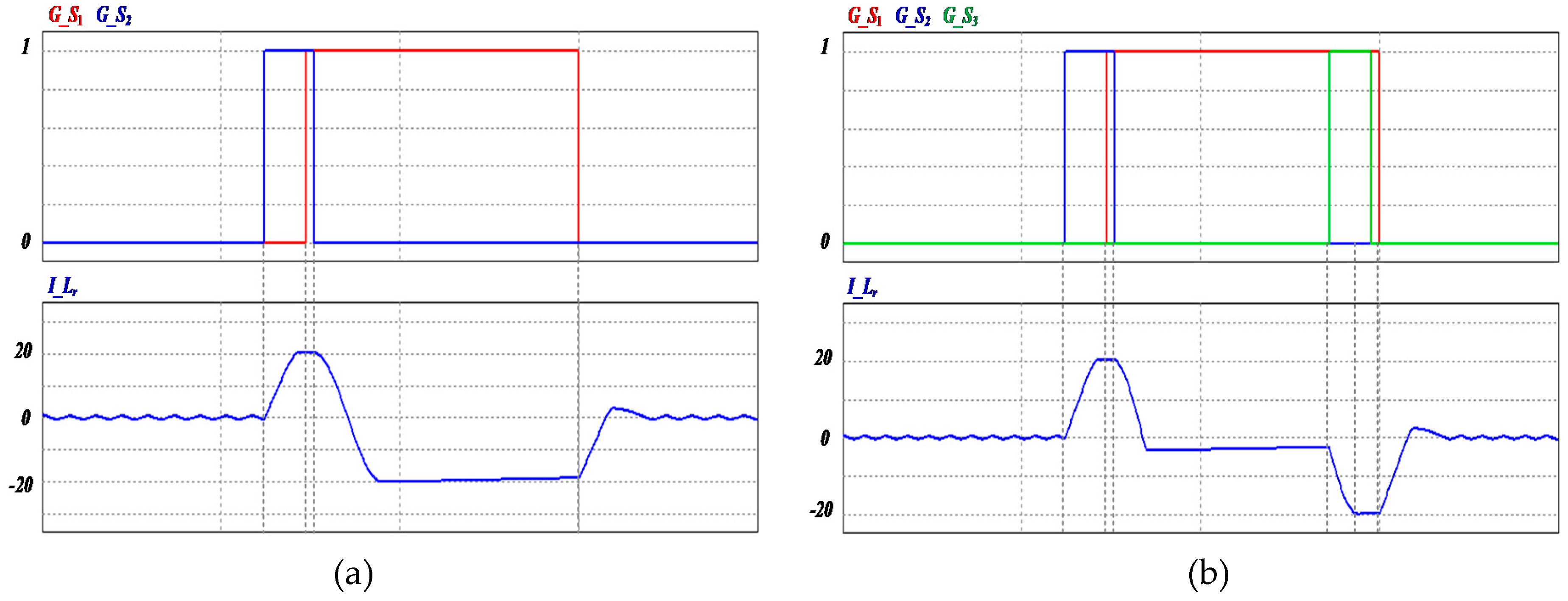
PWM signals of the main and auxiliary switch are shown in
Figure 14. The auxiliary switch
S2 is turned on before the main switch
S1 is turned on. Then turning on interval of the auxiliary switch
S2 can be divided into mode 2, mode 3 and mode 4. The main switch
S1 makes boost at turning on and turning off. The auxiliary switch
S3 operates to reduce conduction loss. And turning on interval of the auxiliary switch
S3 can be shown into mode 7.
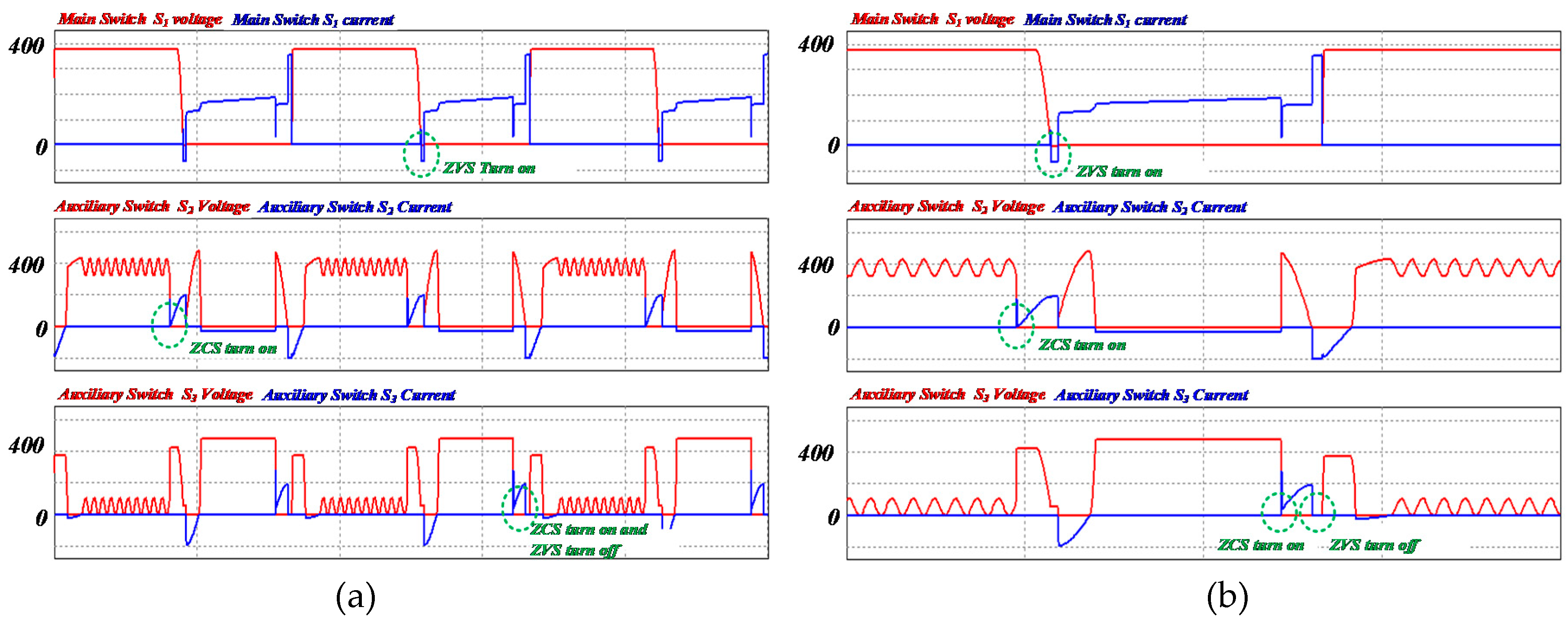
This design for a proposed resonant ZVT boost converter is composed of three switches, and the minimum turn-on and turn-off time should be satisfied in order to achieve ZVS and ZCS. The main switch controls the step-up ratio. Other auxiliary switches enable the main switch to operate with a soft switching. The resonances for the resonant inductor
Lr and the resonant capacitor
Cr are started by turning on the auxiliary switch
S2. When the charged energy completely discharges from the resonant capacitor, the main switch
S1 turns on in the ZVS condition. Before the main switch
S1 turns on, the auxiliary switch
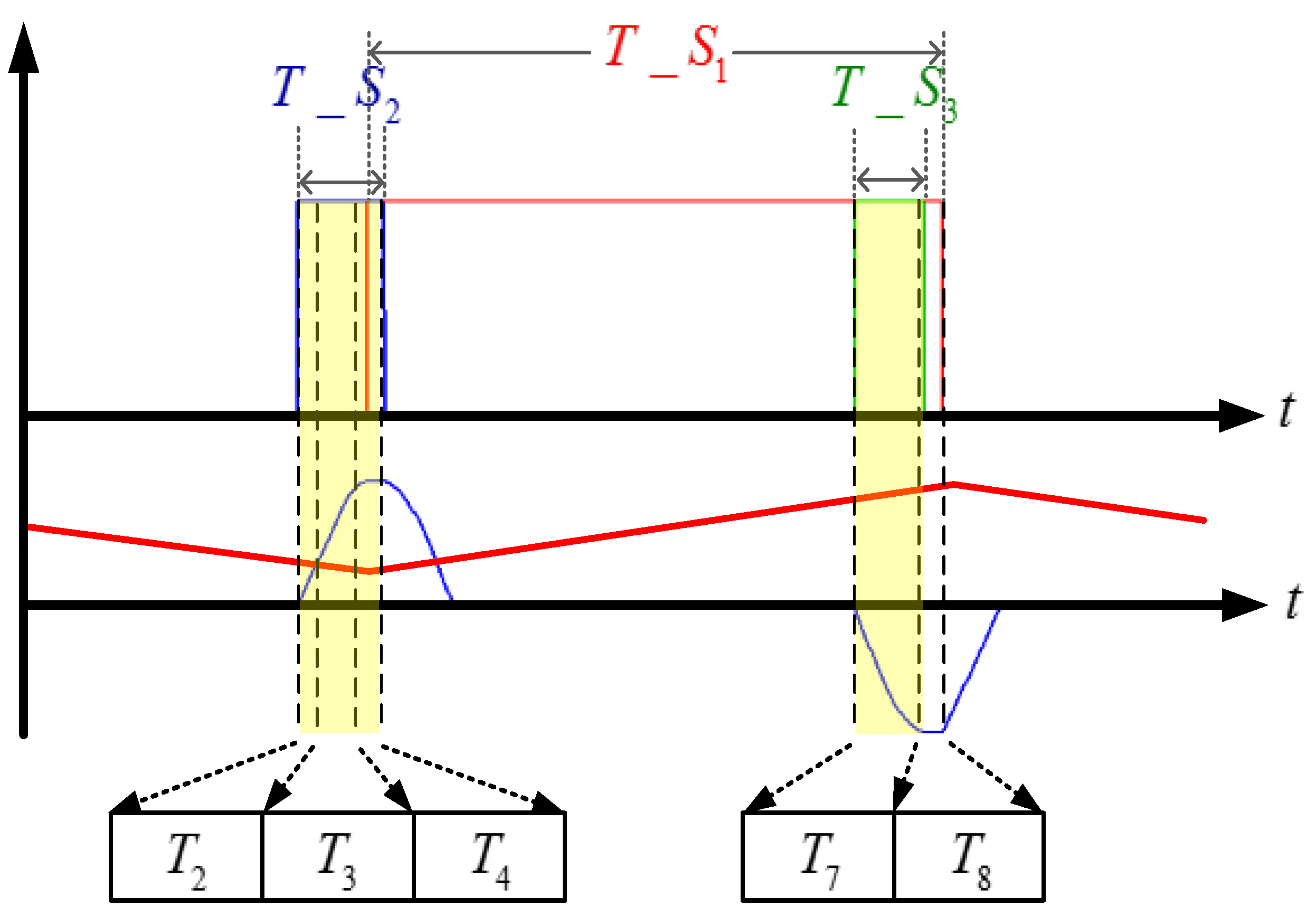
S2 is turned on and turned off. To achieve the ZVS, a minimum time of auxiliary switch pulse width modulation (PWM) is required. The time is determined by Mode 2, Mode 3, and Mode 4. The
T2,
T3, and
T4 time must be satisfied according to the following equation:
T4 is determined by using a factor of
k from the time delay of the switching elements.
The turning on and off times for the auxiliary switch
S2 can be satisfied, as shown in the following Equation (60):
Before the main switch is turned off, the auxiliary switch
S3 is turned on and off. After the energy for the resonant inductor
Lr discharges and reaches zero, the auxiliary switch
S3 turns on. The auxiliary switch
S3 turns on in the ZCS condition. After the auxiliary capacitor
Ca discharges, the auxiliary switch
S3 turns off in the ZVS condition. The turning on and off times for the auxiliary switch
S3 can be calculated by using the equations for Modes 7 and 8.
T7 requires a longer time than half the secondary resonant auxiliary frequency and
T8 requires a longer time than the off-delay time of the elements, which can be obtained from the manufacturer’s data sheet. The shortest time for the auxiliary switch
S3 should be satisfied by using the following Equations (61)–(63).
2.4. Resonant Device Design
Resonant capacitor
Cr influences the ZVS operation of the main switch
S1. The ZVS switching process can be performed when the resonant capacitor
Cr is sufficiently charged [
16]. Thus, the design of resonant capacitors
Cr is important. When the resonant capacitor
Cr is charged and discharged in Mode 3 and Mode 9, the resonant time between the resonant inductor
Lr and resonant capacitor
Cr can be expressed as the following equation:
In Mode 9, resonant capacitor
Cr is charged to output voltage and can be expressed as the following equation:
Assume that the maximum current of the resonant inductor is
Iin_max, and the sum of the two inductor currents is the charging current of the resonant capacitor
Cr. When Mode 9 is longer than Mode 3, the defective duty ratio is lower. Thus, the time is chosen as 0.1
Ts. The sum of Mode 3 and Mode 9 is selected as 1/10 of one cycle. The charging time of the resonant capacitor
Cr must be longer for ZVS of the main switch. For this reason, the value of the resonant capacitor
Cr should be chosen to be 15 times larger than that of the output switch capacitor. According to the output capacitance of main switch
S1, a suitable value of the resonant capacitor is 0.6 nF. The output capacitance of the main switch
S1 is given in the manufacturer’s data sheet. As a result, resonant capacitor
Cr used 10 nF to consider a margin of error.
In addition, the resonant current between the resonant inductor Lr and resonant capacitor Cr charges the auxiliary capacitor Ca. The resonant time between the resonant inductor Lr and auxiliary capacitor Ca in Mode 5 and Mode 7 is set as one-fifth of the total turning on time. If the charging voltage of this resonant capacitor Cr is too large, it may be voltage stress. The auxiliary capacitance was calculated to be 39 nF. The auxiliary capacitor used 40 nF to consider a margin of error.
Resonance between resonant inductor
Lr and capacitor
Cr operates for soft switching of the main switch. Then, the main switch
S1 has satisfied the ZVT condition. Resonance design is very important to satisfy ZVS, ZCS, and ZVT [
17]. But if the resonant inductor current
iLr continues to increase linearly, the magnetic flux of the inductor is saturated [
18]. Thus, the flux of the inductor must be prevented from reaching saturation, using the auxiliary capacitor
Ca. The auxiliary capacitor
Ca is charged from the negative current of the resonant inductor. In this case, energy relation can be defined by auxiliary capacitor
Ca and resonant inductor
Lr. Therefore, stored energy of the inductor is equal to or greater than the stored energy of the capacitor.
The resonant capacitor
Lr must charge below the output voltage
Vo. Obtained values in each mode can be expressed by the following Equations (67) and (68) [
19,
20,
21]: