Active-Model-Based Control for the Quadrotor Carrying a Changed Slung Load
Abstract
1. Introduction
2. Pre-Knowledge: Quadrotor Dynamics
3. Modeling Error and Its Estimation
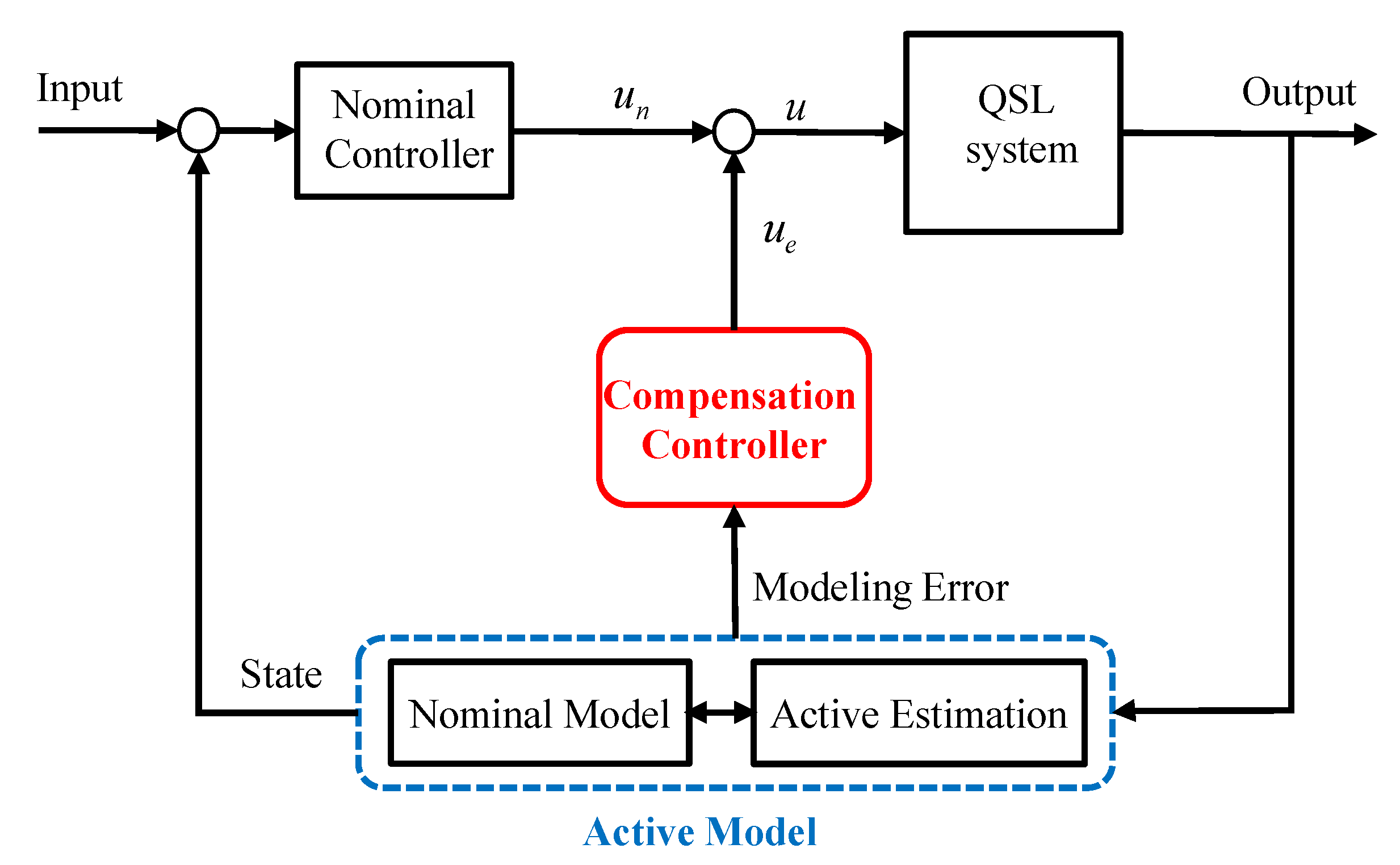
4. Design of Active Model Based Control
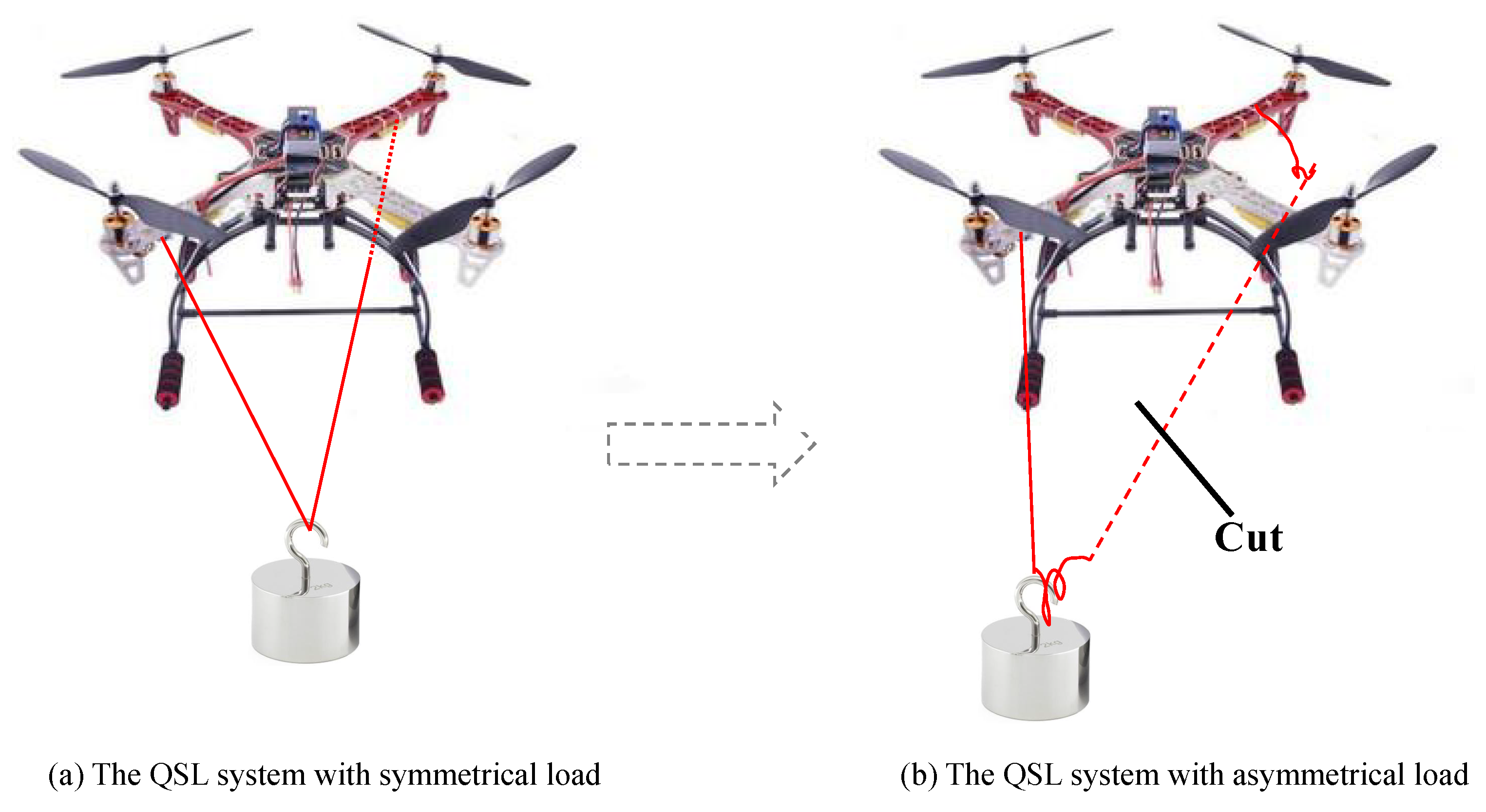
5. Experiments
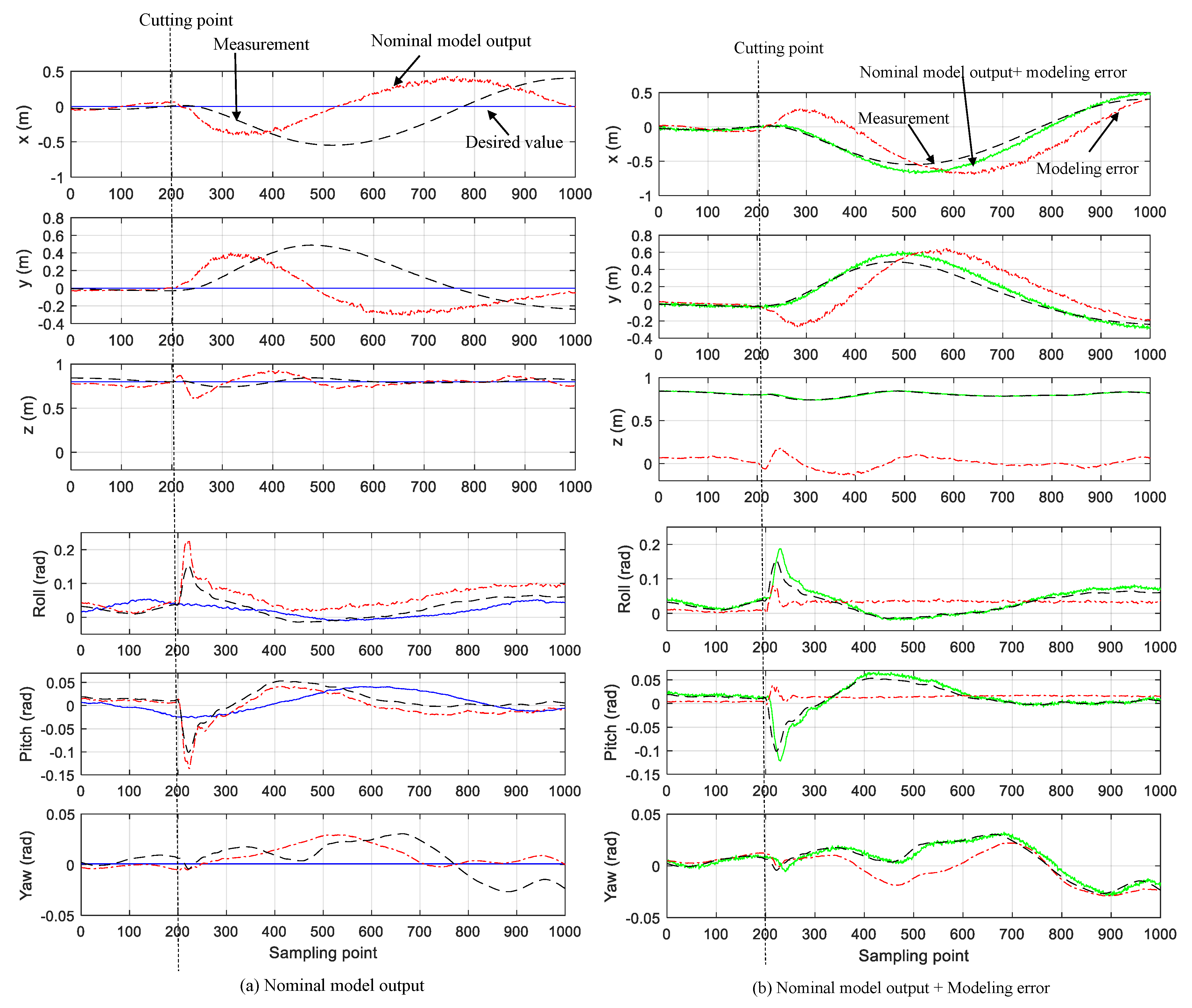
5.1. Experimental Results on Modeling Error Estimation
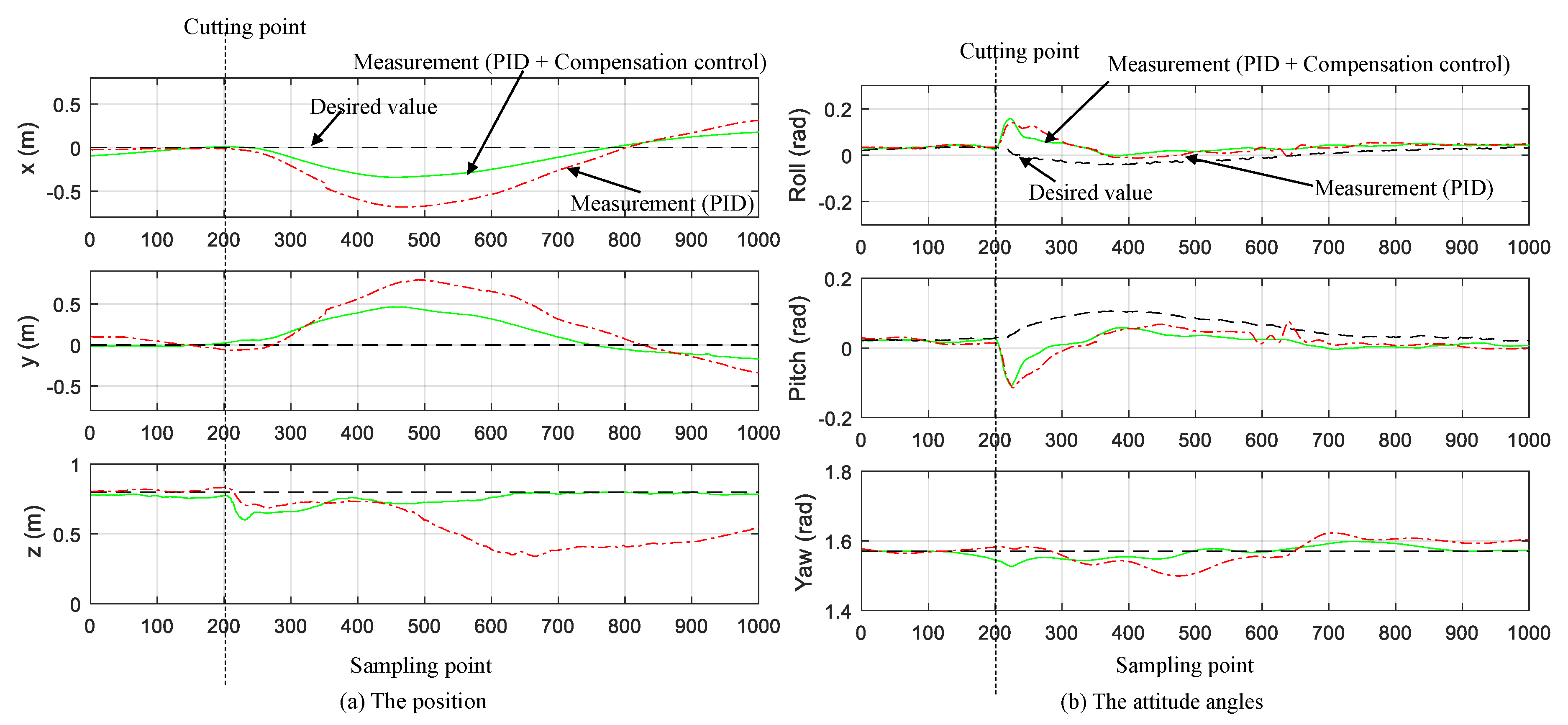
5.2. Experimental Results on the Active-Model-Enhanced Control
6. Conclusions
Supplementary Materials
Supplementary File 1Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yi, K.; Liang, X.; He, Y.; Yang, L.; Han, J. KF-Based Active Modeling for a Quadrotor Slung Load System. In Proceedings of the 2018 IEEE International Conference on Robotics and Biomimetics (ROBIO), Kuala Lumpur, Malaysia, 12–15 December 2018; pp. 2279–2284. [Google Scholar]
- Adams, C.; Potter, J.; Singhose, W. Input-Shaping and Model-Following Control of a Helicopter Carrying a Suspended Load. J. Guid. Control Dyn. 2015, 38, 94–105. [Google Scholar] [CrossRef]
- Yi, K.; Gu, F.; Yang, L.; He, Y.; Han, J. Sliding Mode Control for a Quadrotor Slung Load System. In Proceedings of the 2017 36th Chinese Control Conference (CCC), Dalian, China, 26–28 July 2017; pp. 3697–3703. [Google Scholar]
- Pizetta, I.H.B.; Brandao, A.S.; Sarcinelli-Filho, M. Control and Obstacle Avoidance for an UAV Carrying a Load in Forestal Environments. In Proceedings of the International Conference on Unmanned Aircraft Systems, Dallas, TX, USA, 12–15 June 2018; pp. 62–67. [Google Scholar]
- Liang, X.; Fang, Y.; Sun, N.; Lin, H. Nonlinear Hierarchical Control for Unmanned Quadrotor Transportation Systems. IEEE Trans. Ind. Electron. 2018, 65, 3395–3405. [Google Scholar] [CrossRef]
- Goodarzi, F.A.; Lee, D.; Lee, T. Geometric Stabilization of a Quadrotor UAV with a Payload Connected by Flexible Cable. In Proceedings of the American Control Conference, Portland, OR, USA, 4–6 June 2014; pp. 4925–4930. [Google Scholar]
- Almeida, M.M.D.; Raffo, G.V. Nonlinear Control of a TiltRotor UAV for Load Transportation. IFAC Papersonline 2015, 48, 232–237. [Google Scholar]
- Lee, B.Y.; Hong, S.M.; Yoo, D.W.; Lee, H.I.; Moon, G.H.; Tahk, M.J. Design of a Neural Network Controller for a Slung-Load System Lifted by 1 Quad-Rotor. J. Autom. Control. Eng. 2015, 3, 9–14. [Google Scholar] [CrossRef][Green Version]
- Lee, B.Y.; Lee, H.I.; Yoo, D.W.; Moon, G.H.; Lee, D.Y.; Kim, Y.Y.; Tahk, M.J. Study on Payload Stabilization Method with the Slung-load Transportation System Using a Quad-rotor. In Proceedings of the European Control Conference (ECC), Linz, Austria, 15–17 July 2015; pp. 2097–2102. [Google Scholar]
- Jain, R.P.K. Transportation of Cable Suspended Load Using Unmanned Aerial Vehicles: A Real-Time Model Predictive Control Approach. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2015. [Google Scholar]
- Klausen, K.; Fossen, T.I.; Johansen, T.A. Nonlinear Control of a Multirotor UAV with Suspended Load. In Proceedings of the International Conference on Unmanned Aircraft Systems, Denver, CO, USA, 9–12 June 2015; pp. 176–184. [Google Scholar]
- Nicotra, M.M.; Garone, E.; Naldi, R.; Marconi, L. Nested Saturation Control of an UAV Carrying a Suspended Load. In Proceedings of the American Control Conference, Portland, OR, USA, 4–6 June 2014; pp. 3585–3590. [Google Scholar]
- Zhou, X.; Liu, R.; Zhang, J.; Zhang, X. Stabilization of a Quadrotor with Uncertain Suspended Load Using Sliding Mode Control. In Proceedings of the ASME International Design Engineering Technical Conferences & Computers and Information in Engineering Conference, Charlotte, NC, USA, 21–24 August 2016. [Google Scholar]
- Potter, J.; Singhose, W.; Costelloy, M. Reducing Swing of Model Helicopter Sling Load using Input Shaping. In Proceedings of the IEEE International Conference on Control and Automation, Santiago, Chile, 19–21 December 2011; pp. 348–353. [Google Scholar]
- Adams, C.; Potter, J.; Singhose, W. Modeling and Input Shaping Control of a Micro Coaxial Radio-Controlled Helicopter Carrying a Suspended Load. In Proceedings of the International Conference on Control, Automation and Systems, JeJu Island, Korea, 17–21 October 2012; pp. 645–650. [Google Scholar]
- Ivler, C.M.; Tischler, M.; Powell, J.D. Cable Angle Feedback Control Systems to Improve Handling Qualities for Helicopters with Slung Loads. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Portland, OR, USA, 8–11 August 2011. [Google Scholar]
- Bisgaard, M.; Courharbo, A.L.; Bendtsen, J. Input Shaping for Helicopter Slung Load Swing Reduction. In Proceedings of the AIAA Guidance, Navigation and Control Conference and Exhibit, Keystone, CO, USA, 21–24 August 2006. [Google Scholar]
- Bisgaard, M.; Courharbo, A.L.; Bendtsen, J. Full State Estimation for Helicopter Slung Load System. In Proceedings of the AIAA Guidance, Navigation and Control Conference and Exhibit, Hilton Head Island, SC, USA, 20–23 August 2007. [Google Scholar]
- Bisgaard, M.; Bendtsen, J.; Courharbo, A.L. Modelling of Generic Slung Load System. J. Guidance Control Dyn. 2009, 32, 573–585. [Google Scholar] [CrossRef]
- Bisgaard, M. Modeling, Estimation, and Control of Helicopter Slung Load System. Ph.D. Thesis, Aalborg University, Aalborg, Denmark, 2008. [Google Scholar]
- Bisgaard, M.; Cour-Harbo, A.L.; Bendtsen, J.D. Adaptive Control System for Autonomous Helicopter Slung Load Operations. Control Eng. Pract. 2010, 18, 800–811. [Google Scholar] [CrossRef]
- Bisgaard, M.; Cour-Harbo, A.L.; Bendtsen, J.D. Swing Damping for Helicopter Slung Load Systems using Delayed Feedback. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Chicago, IL, USA, 10–13 August 2009. [Google Scholar]
- Bisgaard, M.; Cour-Harbo, A.L.; Johnson, E.N.; Bendtsen, J.D. Vision Aided State Estimator for Helicopter Slung Load System. In Proceedings of the 17th IFAC Symposium On Automatic Control In Aerospace, Toulouse, France, 25–29 June 2007; pp. 425–430. [Google Scholar]
- Shi, D.; Wu, Z.; Chou, W. Harmonic Extended State Observer Based Anti-Swing Attitude Control for Quadrotor with Slung Load. Electronics 2018, 7, 83. [Google Scholar] [CrossRef]
- Abbeel, P.; Coates, A.; Ng, A.Y. Autonomous Helicopter Aerobatics Through Apprenticeship Learning. Int. J. Rob. Res. 2010, 29, 1608–1639. [Google Scholar] [CrossRef]
- Zhang, D.; Zhao, X.; Han, J. Active Model-Based Control for Pneumatic Artificial Muscle. IEEE Trans. Ind. Electron. 2017, 64, 1686–1695. [Google Scholar] [CrossRef]
- Dai, B.; He, Y.; Gu, F.; Yang, L.; Han, J.; Xu, W. A Vision-Based Autonomous Aerial Spray System for Precision Agriculture. In Proceedings of the IEEE International Conference on Robotics and Biomimetics, Macau, China, 5–8 December 2017; pp. 507–513. [Google Scholar]
- Mellinger, D.; Kumar, V. Minimum Snap Trajectory Generation and Control for Quadrotors. In Proceedings of the IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 2520–2525. [Google Scholar]
- Qualisys Motion Capture System. Available online: https://www.qualisys.com/ (accessed on 12 August 2018).
- Reséndiz, V.M.A.; Rivas-Araiza, E.A. System Identification of a Quadrotor in X Configuration from Experimental Data. Res. Comput. Sci. 2016, 118, 77–86. [Google Scholar]
- Liu, J.; Shen, X.; Zhao, L. System Identification Theory and MATLAB Simulation; Publishing House of Electronics Industry: Beijing, China, 2013. [Google Scholar]
- Sheng, Z.; Xie, S.; Pan, C. Probability and Mathematical Statistics, 4th ed.; Higher Education Press: Beijing, China, 2008. [Google Scholar]

| State | of Nominal Model | of Nominal Model + Active Estimation | Improvement |
|---|---|---|---|
| x | m | m | 81.07% |
| y | m | m | 81.39% |
| z | m | m | 91.07% |
| rad | rad | 73.33% | |
| rad | rad | 58.28% | |
| rad | rad | 75.7% |
| State | of Nominal Control | of Nominal Control + Compensation Control | Improvement |
|---|---|---|---|
| x | m | m | 48.76% |
| y | m | m | 43.6% |
| z | m | m | 81.54% |
| rad | rad | 34% | |
| rad | rad | 27% | |
| rad | rad | 58.9% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yi, K.; Liang, X.; He, Y.; Yang, L.; Han, J. Active-Model-Based Control for the Quadrotor Carrying a Changed Slung Load. Electronics 2019, 8, 461. https://doi.org/10.3390/electronics8040461
Yi K, Liang X, He Y, Yang L, Han J. Active-Model-Based Control for the Quadrotor Carrying a Changed Slung Load. Electronics. 2019; 8(4):461. https://doi.org/10.3390/electronics8040461
Chicago/Turabian StyleYi, Kui, Xiao Liang, Yuqing He, Liying Yang, and Jianda Han. 2019. "Active-Model-Based Control for the Quadrotor Carrying a Changed Slung Load" Electronics 8, no. 4: 461. https://doi.org/10.3390/electronics8040461
APA StyleYi, K., Liang, X., He, Y., Yang, L., & Han, J. (2019). Active-Model-Based Control for the Quadrotor Carrying a Changed Slung Load. Electronics, 8(4), 461. https://doi.org/10.3390/electronics8040461





