Electronic Circuit with Controllable Negative Differential Resistance and its Applications
Abstract
:1. Introduction
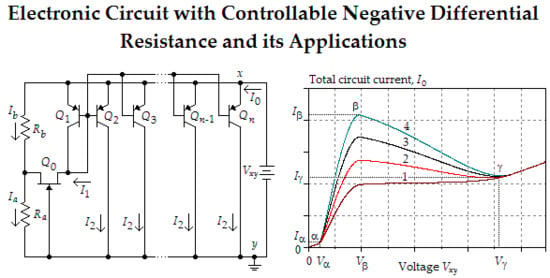
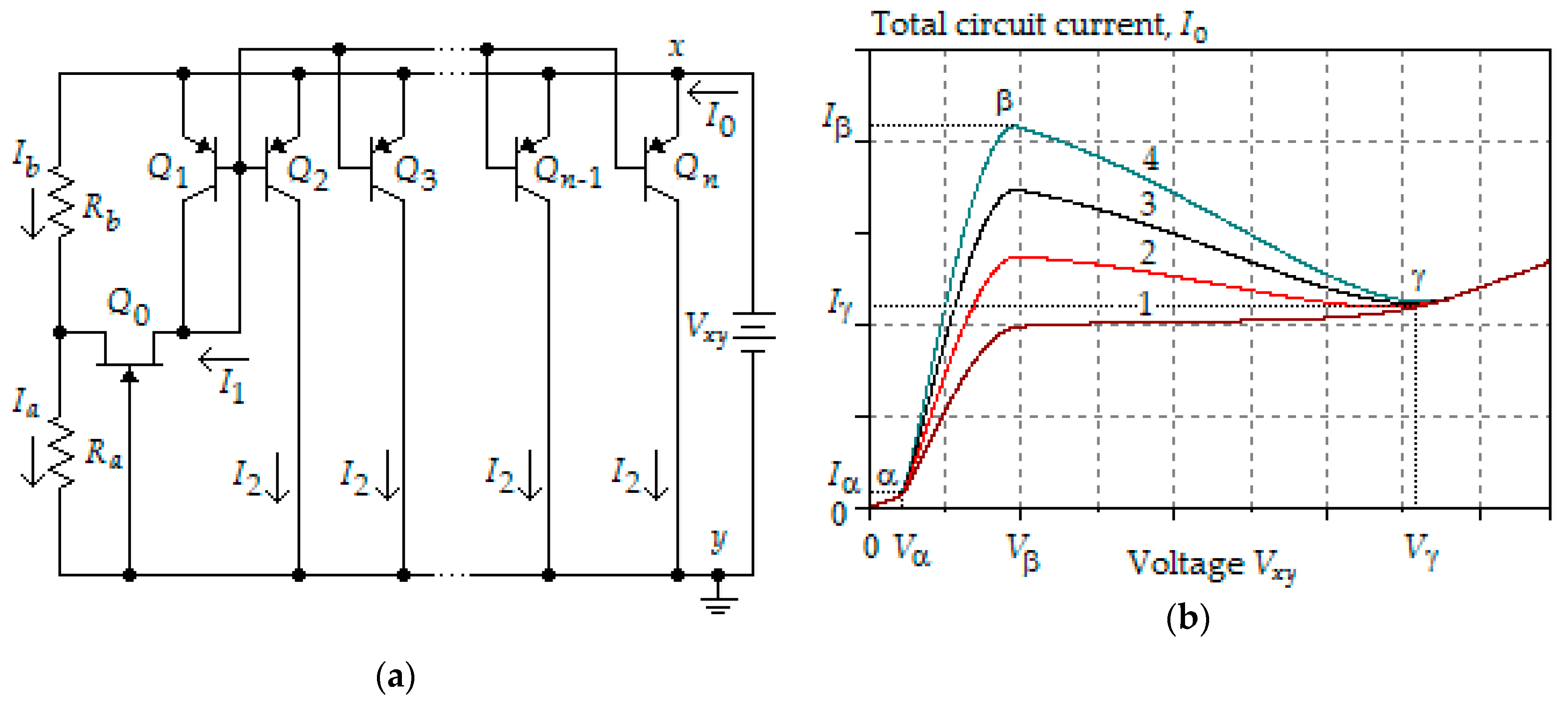
2. Circuit Operation
3. Circuit Applications
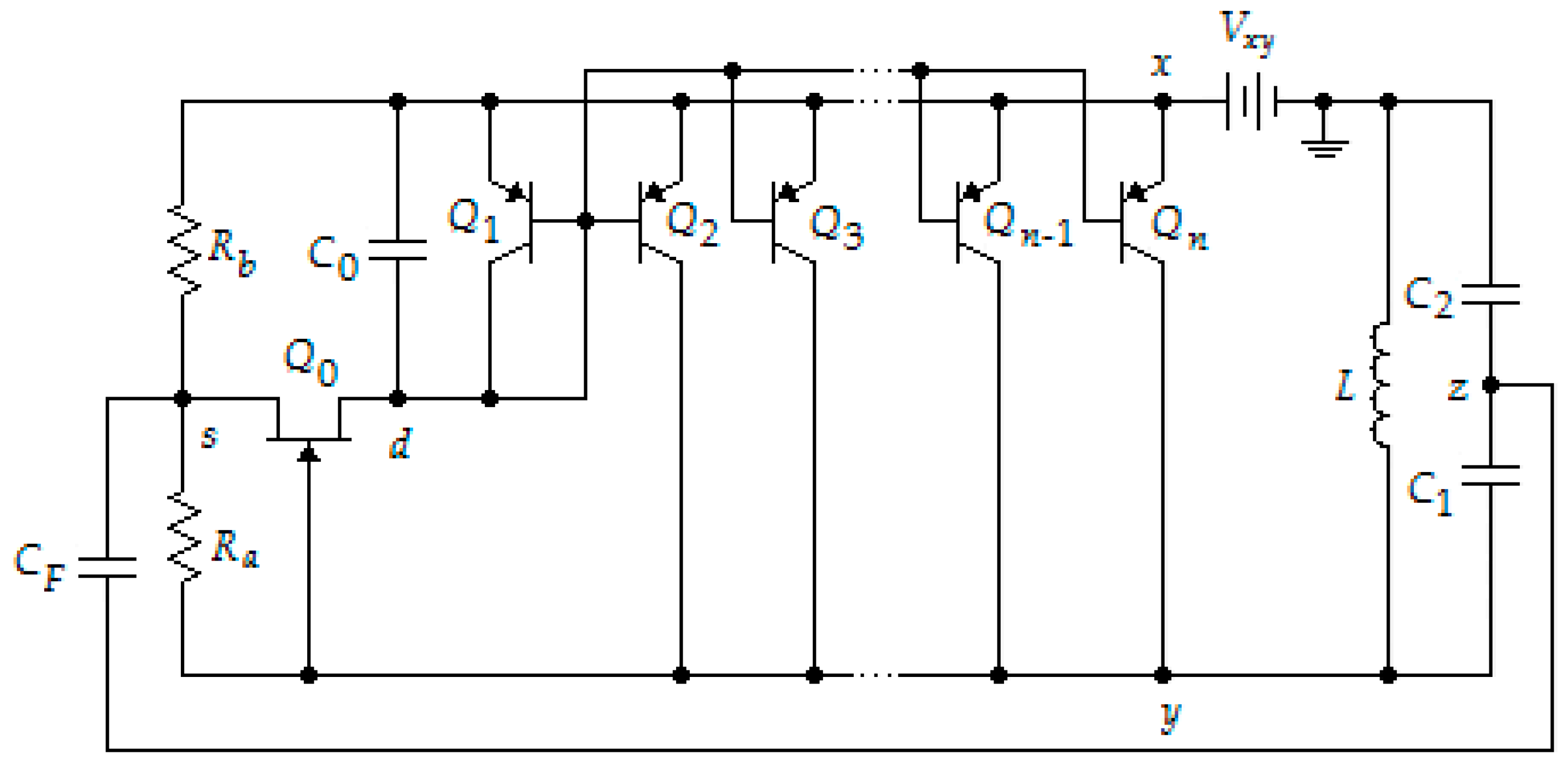
3.1. LC Oscillator
3.1.1. Simulation Results
3.1.2. Oscillator Prototype Implementation
3.2. LC Voltage Controlled Oscillator
LC Voltage-Controlled Oscillator Performance
4. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| BJT | Bipolar junction transistor |
| CM | Current mirror |
| CMOS | Complementary metal-oxide-semiconductor |
| FET | Field-effect transistor |
| FOM | Figure of merit |
| HBT | Heterojunction bipolar transistor |
| HEMT | High-electron-mobility transistor |
| JFET | Junction gate field-effect transistor |
| KCL | Kirchhoff’s current law |
| KVL | Kirchhoff’s voltage law |
| MESFET | Metal-semiconductor field-effect transistor |
| MOS | Metal-oxide-semiconductor |
| MOSFET | Metal-oxide-semiconductor field-effect transistor |
| NDR | Negative differential resistance |
| NENS | N-channel enhancement mode with load operated at saturation |
| PCB | Printed circuit board |
| PHEMT | Pseudomorphic high-electron-mobility transistor |
| PNP | Positive-negative-positive |
| RF | Radio frequency |
| SPICE | Simulation program with integrated circuit emphasis |
| THD | Total harmonic distortion |
| VCO | Voltage controlled oscillator |
References
- Tseng, P.; Chen, C.H.; Hsu, S.A.; Hsueh, W.J. Large negative differential resistance in graphene nanoribbon superlattices. Phys. Lett. A 2018, 382, 1427–1431. [Google Scholar] [CrossRef]
- Hwu, R.J.; Djuandi, A.; Lee, S.C. Negative differential resistance (NDR) frequency conversion with gain. IEEE Trans. Microw. Theory Tech. 1993, 41, 890–893. [Google Scholar] [CrossRef] [Green Version]
- Liang, D.S.; Gan, K.J. New D-Type Flip-Flop Design using negative differential resistance circuits. In Proceedings of the 4th IEEE International Symposium on Electronic Design, Test and Applications, Hong Kong, China, 23–25 January 2008; pp. 1–8. [Google Scholar]
- Chen, S.L.; Griffin, P.B.; Plummer, J.D. Negative differential resistance circuit design and memory applications. IEEE Trans. Electron Devices 2009, 56, 634–640. [Google Scholar] [CrossRef]
- Wang, S.; Pan, A.; Grezes, C.; Amiri, P.K.; Wang, K.L.; Chui, C.O.; Gupta, P. Leveraging nMOS negative differential resistance for low power, high-reliability magnetic memory. IEEE Trans. Electron Devices 2017, 64, 4084–4090. [Google Scholar] [CrossRef]
- Wu, Y.; Farmer, D.B.; Zhu, W.; Han, S.J.; Dimitrakopoulos, C.D.; Bol, A.A. Three-terminal graphene negative differential resistance devices. ACS Nano 2012, 6, 2610–2616. [Google Scholar] [CrossRef]
- Gan, K.J.; Hsiao, C.C.; Tsai, C.S.; Chen, Y.H.; Wane, S.Y.; Kuo, S.H. A novel voltage-controlled oscillator design by MOS-NDR devices and circuits. In Proceedings of the Fifth International Workshop on System-on-Chip for Real-Time Applications, Banff, AB, Canada, 20–24 July 2005; pp. 372–375. [Google Scholar]
- Tsai, C.S.; Hsiao, C.C.; Gan, K.J.; Wu, J.M.; Hsieh, M.Y.; Liao, C.C. An Oscillator Design Based on MOS-NDR Inverter. In Proceedings of the International Conference on Systems and Signals, Kaohsiung, Taiwan, 28–29 April 2005; pp. 1–5. [Google Scholar]
- Semenov, A. Mathematical model of the microelectronic oscillator based on the BJT-MOSFET structure with negative differential resistance. In Proceedings of the 2017 IEEE 37th International Conference on Electronics and Nanotechnology (ELNANO), Kiev, Ukraine, 18–20 April 2017; pp. 146–151. [Google Scholar]
- Gan, K.J.; Chun, K.Y.; Yeh, W.K.; Chen, Y.H.; Wang, W.S. Design of dynamic frequency divider using negative differential resistance circuit. Int. J. Recent Innov. Trends Comput. Commun. 2015, 3, 5224–5228. [Google Scholar]
- Stanley, I.W.; Ager, D.J. Two-terminal negative dynamic resistance. Electronic Lett. 1970, 6, 1–2. [Google Scholar] [CrossRef]
- Ulansky, V.V.; Ben Suleiman, S.F. Negative differential resistance based voltage-controlled oscillator for VHF band. In Proceedings of the 2013 IEEE International Scientific Conference on Electronics and Nanotechnology, Kiev, Ukraine, 16–19 April 2013; pp. 80–84. [Google Scholar]
- Kumar, U. Simulation of a novel bipolar-FET type-S negative resistance circuit. Act. Passiv. Electron. Compon. 2003, 26, 129–132. [Google Scholar] [CrossRef]
- Chua, L.O.; Yu, J.; Yu, Y. Bipolar-JFET-MOSFET negative resistance devices. IEEE Trans. Circuits Syst. 1985, 32, 46–61. [Google Scholar] [CrossRef]
- Ulansky, V.V.; Ben Suleiman, S.F.; Elsherif, H.M.; Abusaid, M.F. Optimization of NDR VCOs for microwave applications. In Proceedings of the 2016 IEEE 36th International Conference on Electronics and Nanotechnology (ELNANO), Kyiv, Ukraine, 19–21 April 2016; pp. 353–357. [Google Scholar]
- Akarvardar, K.; Chen, S.; Vandersand, J.; Blalock, B.; Schrimpf, R.; Prothro, B. Four-gate transistor voltage-controlled negative differential resistance device and related circuit applications. In Proceedings of the 2006 IEEE International SOI Conference, Niagara Falls, NY, USA, 2–5 October 2006; pp. 1–6. [Google Scholar]
- Shin, S.; Kim, K.R. Multiple negative differential resistance devices with ultra-high peak-to-valley current ratio for practical multi-valued logic and memory applications. Jpn. J. Appl. Phys. 2015, 54, 1–7. [Google Scholar] [CrossRef]
- Shin, S.; Kim, K.R. Novel five-state latch using double-peak negative differential resistance and standard ternary inverter. Jpn. J. Appl. Phys. 2016, 55, 1–6. [Google Scholar] [CrossRef]
- Gan, K.J.; Tsai, C.S.; Liang, D.S. Design and characterization of the negative differential resistance circuits using the CMOS and BiCMOS process. Analog Integr. Circuits Signal Process. 2010, 62, 63–68. [Google Scholar] [CrossRef]
- Gan, K.J.; Tsai, C.S.; Liang, D.S.; Wen, C.M.; Chen, Y.H. Tri-valued memory circuit using MOS-BJT-NDR circuits fabricated by standard SiGe process. Jpn. J. Appl. Phys. 2006, 45, 1–4. [Google Scholar] [CrossRef]
- Wu, C.Y.; Lai, K.N. Integrated Λ-type differential negative resistance MOSFET device. IEEE J. Solid-State Circuits 1979, 14, 1094–1101. [Google Scholar]
- Ulansky, V. Low phase-noise HEMT microwave voltage-controlled oscillator. In Proceedings of the IEEE Microwaves, Radar and Remote Sensing Symposium (MRRS), Kiev, Ukraine, 25–27 August 2011; pp. 55–58. [Google Scholar]
- Jagger, R.C.; Blalock, T.N. Microelectronic Circuit Design, 2nd ed.; McGraw-Hill: New York, NY, USA, 2004; pp. 251–254. [Google Scholar]
- Statz, H.; Newman, P.; Smith, W.; Pucel, R.A.; Haus, H.A. GaAs FET device and circuit simulation in Spice. IEEE Trans. Electron Devices 1987, 34, 160–169. [Google Scholar] [CrossRef]
- Converting GaAs FET Models for Different Nonlinear Simulators. Available online: https://docplayer.net/21705870-California-eastern-laboratories-an1023-converting-gaas-fet-models-for-different-nonlinear-simulators.html (accessed on 2 April 2003).
- ATF-33143. Low Noise Pseudomorphic HEMT in a Surface Mount Plastic Package. Data Sheet. Available online: https://cdn.datasheetspdf.com/pdf-down/A/T/F/ATF-33143-AVAGO.pdf (accessed on 6 January 2006).
- Conan Zhan, J.H.; Maurice, K.; Duster, J.; Kornegay, K.V. Analysis and design of negative impedance LC oscillators using bipolar transistors. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2003, 50, 1461–1464. [Google Scholar] [CrossRef]
- Ulansky, V.V.; Fituri, M.S.; Machalin, I.A. Mathematical modeling of voltage-controlled oscillators with the Colpitts and Clapp topology. Electron. Control Syst. 2009, 19, 82–90. [Google Scholar]
- Chung, C.; Chao, S. Robust Colpitts and Hartley oscillator design. In Proceedings of the 2014 IEEE International Frequency Control Symposium (FCS), Taipei, Taiwan, 19–24 May 2014; pp. 1–5. [Google Scholar]
- Ulansky, V.V.; Elsherif, H.M. A new method of designing UHF FET Colpitts oscillator. In Proceedings of the 2014 IEEE 34th International Scientific Conference on Electronics and Nanotechnology (ELNANO), Kyiv, Ukraine, 15–18 April 2014; pp. 388–392. [Google Scholar]
- Daliri, M.; Maymandi-Nejad, M. Analytical model for CMOS cross-coupled LC-tank oscillator. IET Circuits Devices Syst. 2014, 8, 1–5. [Google Scholar] [CrossRef]
- Hajimiri, A.; Lee, T.H. Design issues in CMOS differential LC oscillators. IEEE J. Solid-State Circuits 1999, 34, 717–724. [Google Scholar] [CrossRef] [Green Version]
- Hou, J.A.; Wang, Y.H. A 5 GHz differential Colpitts CMOS VCO using the bottom PMOS cross-coupled current source. IEEE Microw. Wirel. Compon. Lett. 2009, 19, 401–403. [Google Scholar]
- Grebennikov, A. RF and Microwave Transistor Oscillator Design; John Wiley & Sons Ltd.: Chichester, UK, 2007; 458p. [Google Scholar]
- Poole, C.; Darwazeh, I. Microwave Active Circuit Analysis and Design; Elsevier: Amsterdam, The Netherlands, 2016; 664p. [Google Scholar]
- Sze, S.M. Active Microwave Diodes in Modern Semiconductor Device Physics; Wiley: New York, NY, USA, 1997; pp. 343–407. [Google Scholar]
- Hegazi, E.; Sjoland, H.; Abidi, A.A. A filtering technique to lower LC oscillator phase noise. IEEE J. Solid-State Circuits 2001, 36, 1921–1930. [Google Scholar] [CrossRef] [Green Version]
- Bianchi, G. Phase-Locked Loop Synthesizer Simulation; McGraw-Hill: New York, NY, USA, 2005; pp. 64–78. [Google Scholar]
- Luong, H.C.; Leung, G.C.T. Low-Voltage CMOS RF Frequency Synthesizers; Cambridge University Press: Cambridge, UK, 2004; pp. 28–44. [Google Scholar]
- Leenaerts, D.; van der Tang, J. Circuit Design for RF Transceivers; Springer: Berlin, Germany, 2001; 323p. [Google Scholar]
- Kinget, P. Integrated GHz voltage-controlled oscillators. In Analog Circuit Design; Sansen, W., Huijsing, J., van de Plassche, R., Eds.; Springer: Berlin, Germany, 1999; pp. 353–381. [Google Scholar]
- Tiebout, M. Low Power VCO Design in CMOS; Springer: Berlin, Germany, 2006; 128p. [Google Scholar]
- Coilcraft. RF Inductor Comparison Tool. Q vs Frequency. Available online: https://www.coilcraft.com/apps/compare/compare_rf.cfm (accessed on 11 October 2018).
- Cai, H.L.; Yang, Y.; Qi, N. A 2.7-mW 1.36–1.86-GHz LC-VCO with a FOM of 202 dBc/Hz enabled by a 26%-size-reduced nano-particle-magnetic-enhanced inductor. IEEE Trans. Microw. Theory Tech. 2014, 62, 1221–1228. [Google Scholar] [CrossRef]
- Rout, P.K.; Nanda, U.K.; Acharya, D.P.; Panda, G. Design of LC VCO for optimal figure of merit performance using CMODE. In Proceedings of the 1st International Conference on Recent Advances in Information Technology (RAIT), Dhanbad, India, 15–17 March 2012; pp. 1–6. [Google Scholar]
- Kim, S.J.; Seo, D.I.; Kim, J.S. Compact CMOS LiT VCO achieving 198.6 dBc/Hz FoM. Electron. Lett. 2018, 54, 175–177. [Google Scholar] [CrossRef]
- Zailer, E.; Belostotski, L.; Plume, R. 8-GHz, 6.6-mW LC-VCO with small die area and FOM of 204 dBc/Hz at 1-MHz offset. IEEE Microw. Wirel. Compon. Lett. 2016, 26, 936–938. [Google Scholar] [CrossRef]
- Chung, T.W.; Huang, T.C.; Chung, S. A 2.7GHz 3.9mW mesh-BJT LC-VCO with −204dBc/Hz FOM in 65nm CMOS. In Proceedings of the IEEE Custom Integrated Circuits Conference, San Jose, CA, USA, 9–12 September 2012; pp. 1–6. [Google Scholar]
- Narayanan, A.T.; Kimura, K.; Deng, W. A pulse-driven LC-VCO with a figure-of-merit of −192dBc/Hz. In Proceedings of the 40th European Solid-State Circuits Conference (ESSCIRC), Venice Lido, Italy, 22–26 September 2014; pp. 1–5. [Google Scholar]
- Lin, Y.C.; Yeh, M.L.; Chang, C.C. A high figure-of-merit low phase noise 15-GHz CMOS VCO. J. Mar. Sci. Technol. 2013, 21, 82–86. [Google Scholar]
- Ghorbel, I.; Haddad, F.; Rahajandraibe, W. Optimization of voltage-controlled oscillator VCO using current-reuse technique. In Proceedings of the 26th International Conference on Microelectronics (ICM), Doha, Qatar, 14–17 December 2014; pp. 1–5. [Google Scholar]
- Bhat, M.V.; Jain, S.; Srivatsa, M.P. Design of low phase noise voltage-controlled oscillator for phase locked loop. In Proceedings of the International Conference on Microelectronic Devices, Circuits and Systems (ICMDCS), Vellore, India, 10–12 August 2017; pp. 1–5. [Google Scholar]
- Mirajkar, P.; Chand, J.; Aniruddhan, S.; Theertham, S. Low phase noise Ku-band VCO with optimal switched-capacitor bank design. IEEE Trans. Very Larg. Scale Integr. (VLSI) Syst. 2018, 26, 589–593. [Google Scholar] [CrossRef]
- Zuo, C.; der Spiegel, J.V.; Piazza, G. Dual-mode resonator and switchless reconfigurable oscillator based on piezoelectric AlN MEMS technology. IEEE Trans. Electron Devices 2011, 58, 3599–3603. [Google Scholar] [CrossRef]
- Rottava, R.E.; Camara Santes Junior, C.; Rangel de Sousa, F.; Nunes de Lima, R. Ultra-low-power 2.4 GHz Colpitts oscillator based on double feedback technique. In Proceedings of the IEEE International Symposium on Circuits and Systems, Beijing, China, 19–23 May 2013; pp. 1785–1788. [Google Scholar]
- Sachan, D.; Kumar, H.; Goswami, M.; Misra, P.K. A 2.4 GHz low power low phase-noise enhanced FOM VCO for RF applications using 180 nm CMOS technology. Wirel. Pers. Commun. 2018, 101, 391–403. [Google Scholar] [CrossRef]
- Thi Do, T.N.; Szhau Lai, S.; Horberg, M. A MMIC GaN HEMT voltage-controlled-oscillator with high tuning linearity and low phase noise. In Proceedings of the IEEE Compound Semiconductor Integrated Circuit Symposium (CSICS), New Orleans, LA, USA, 11–14 October 2015; pp. 1–4. [Google Scholar]
- Liu, H.; Zhu, X.; Boon, C.C. Design of ultra-low phase noise and high power integrated oscillator in 0.25µm GaN-on-SiC HEMT technology. IEEE Microw. Wirel. Compon. Lett. 2014, 24, 120–122. [Google Scholar] [CrossRef]
- Gray, P.R.; Hurst, P.J.; Lewis, S.H.; Meyer, R.G. Analysis and Design of Analog Integrated Circuits; John Wiley & Sons, Inc.: New York, NY, USA, 2001; 875p. [Google Scholar]
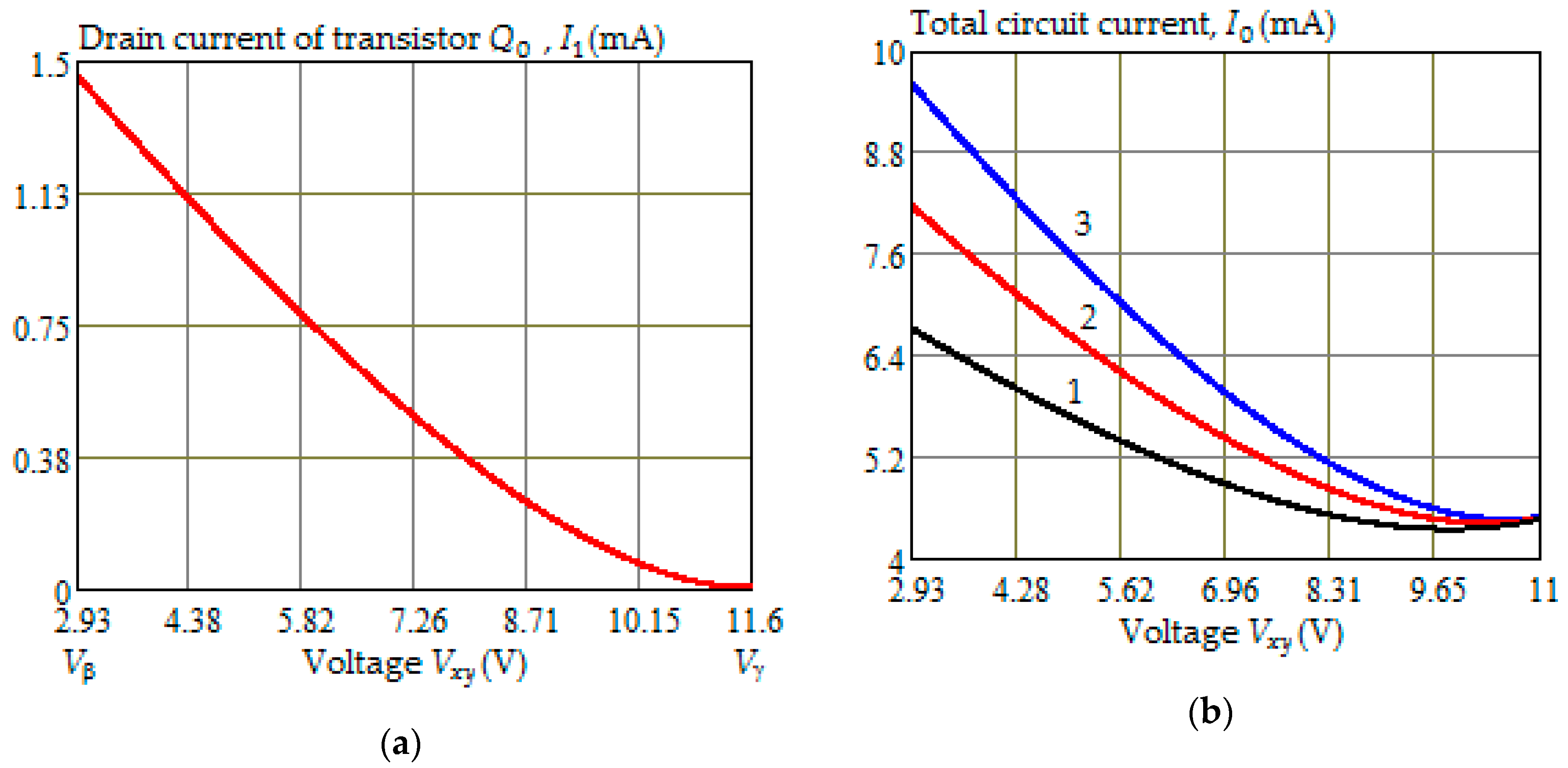
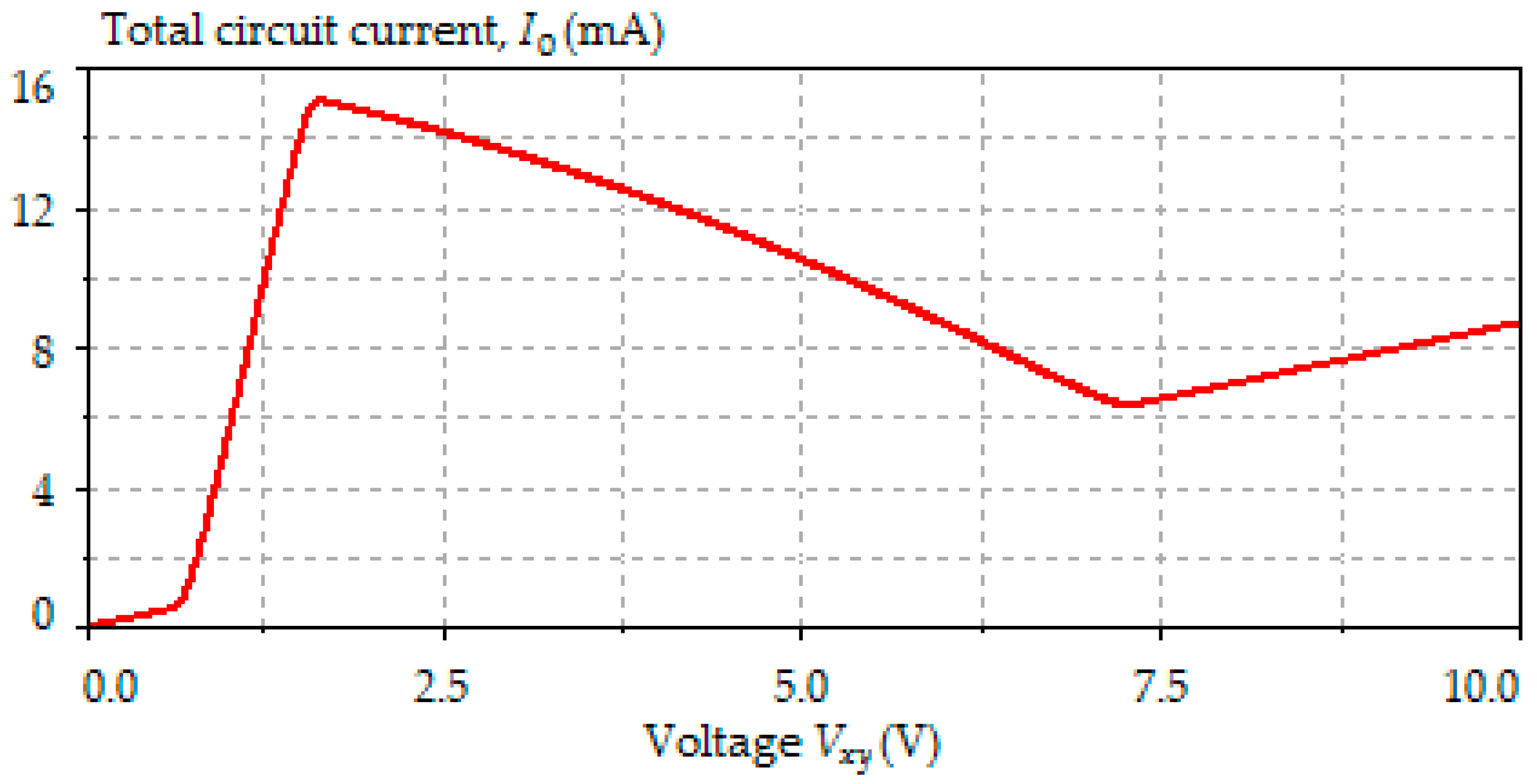
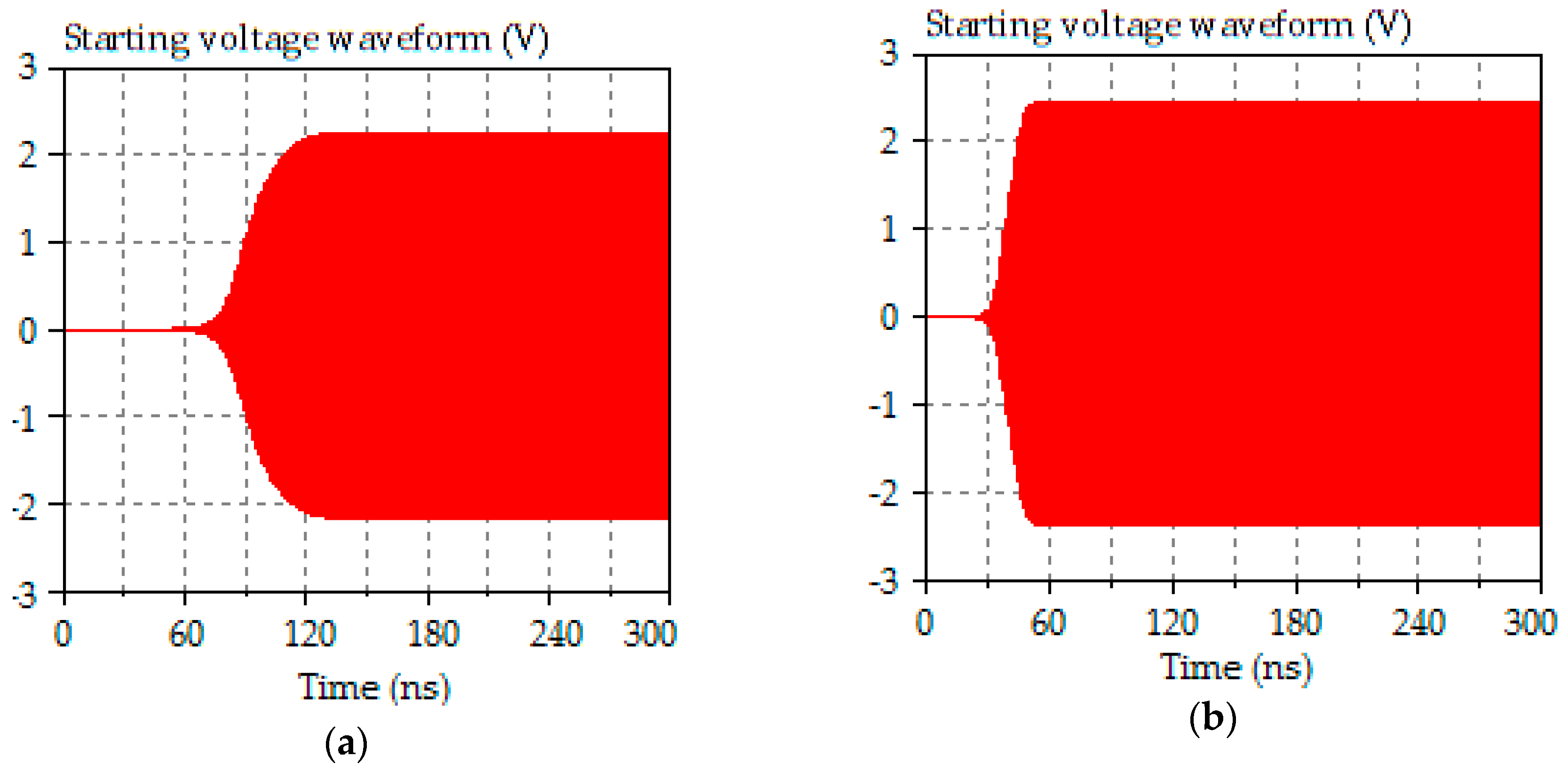
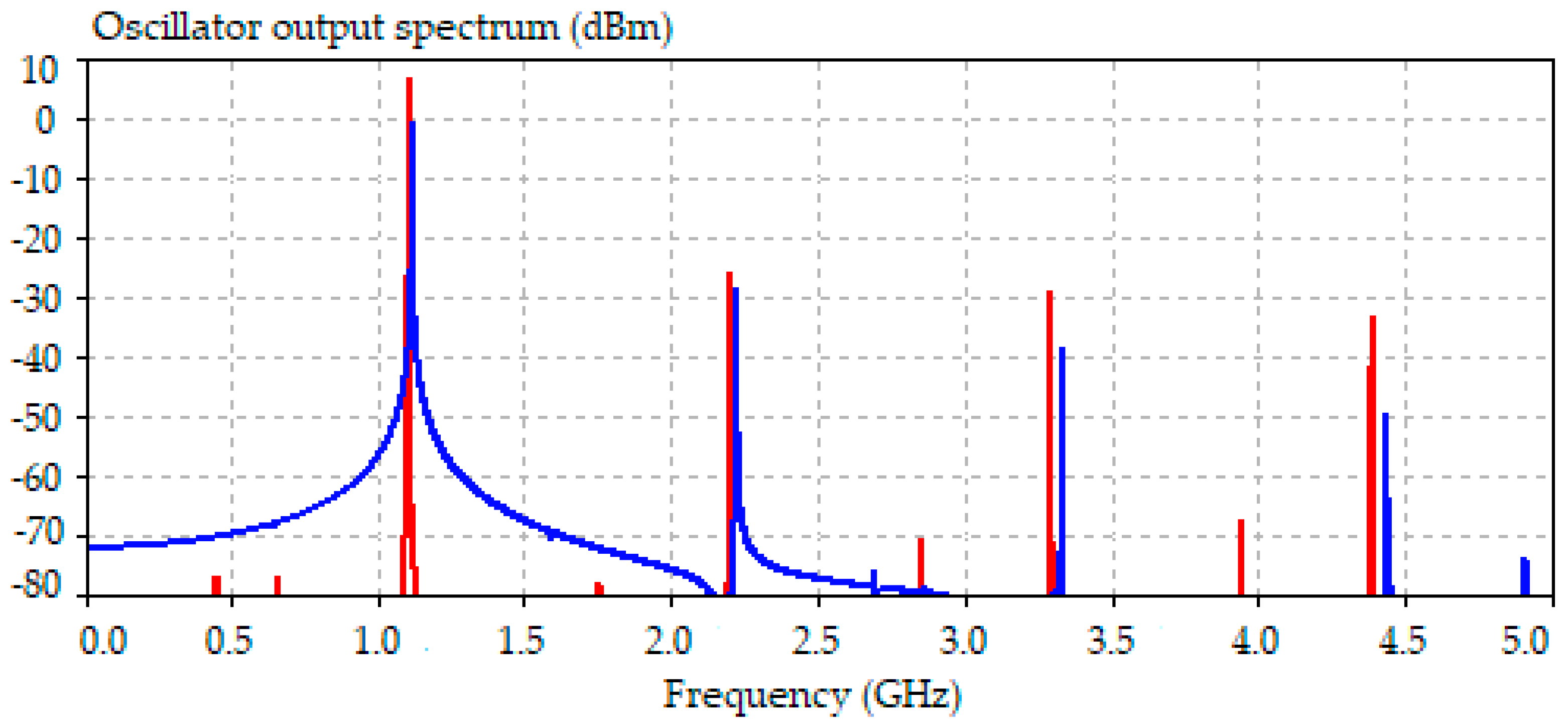
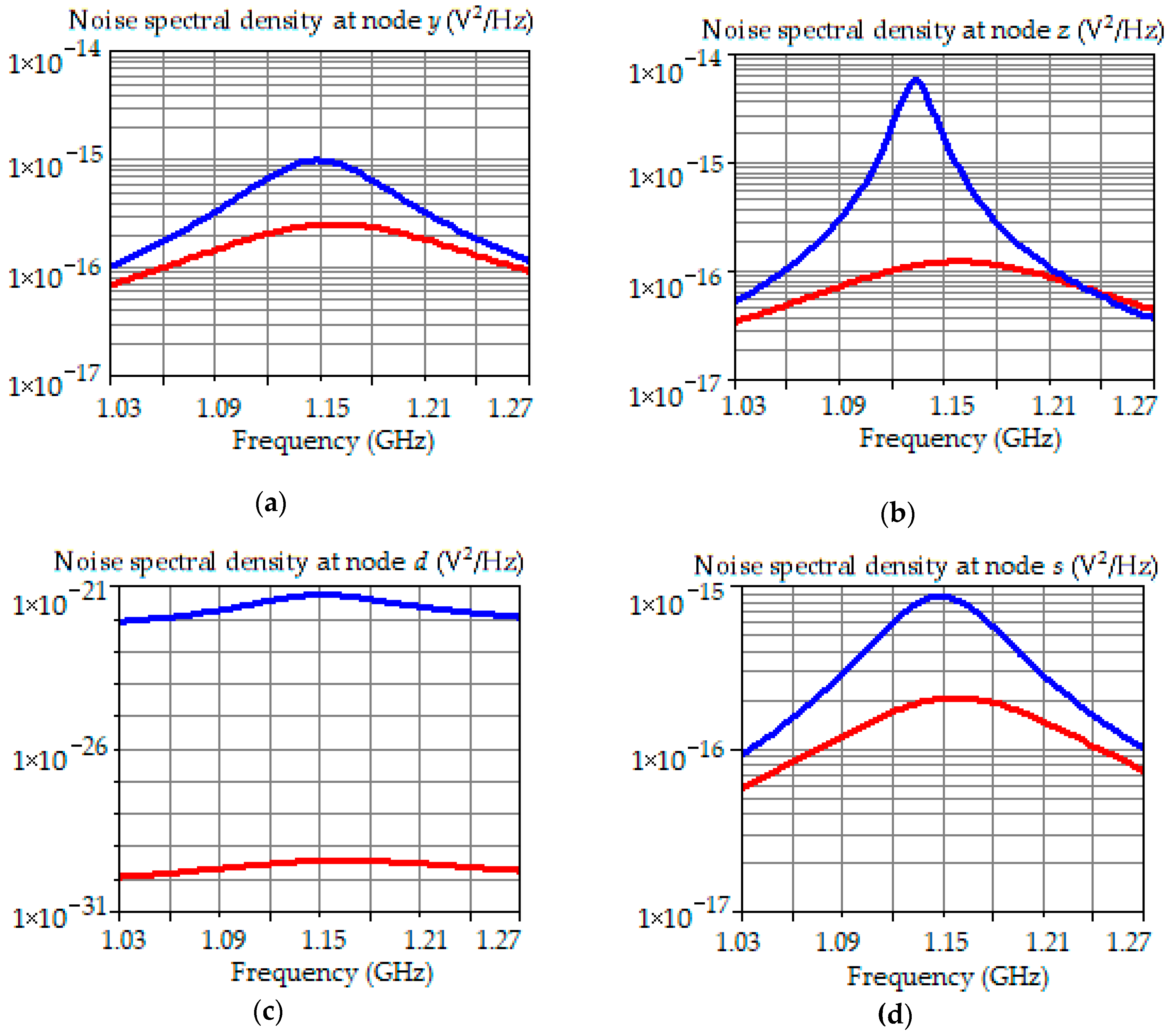

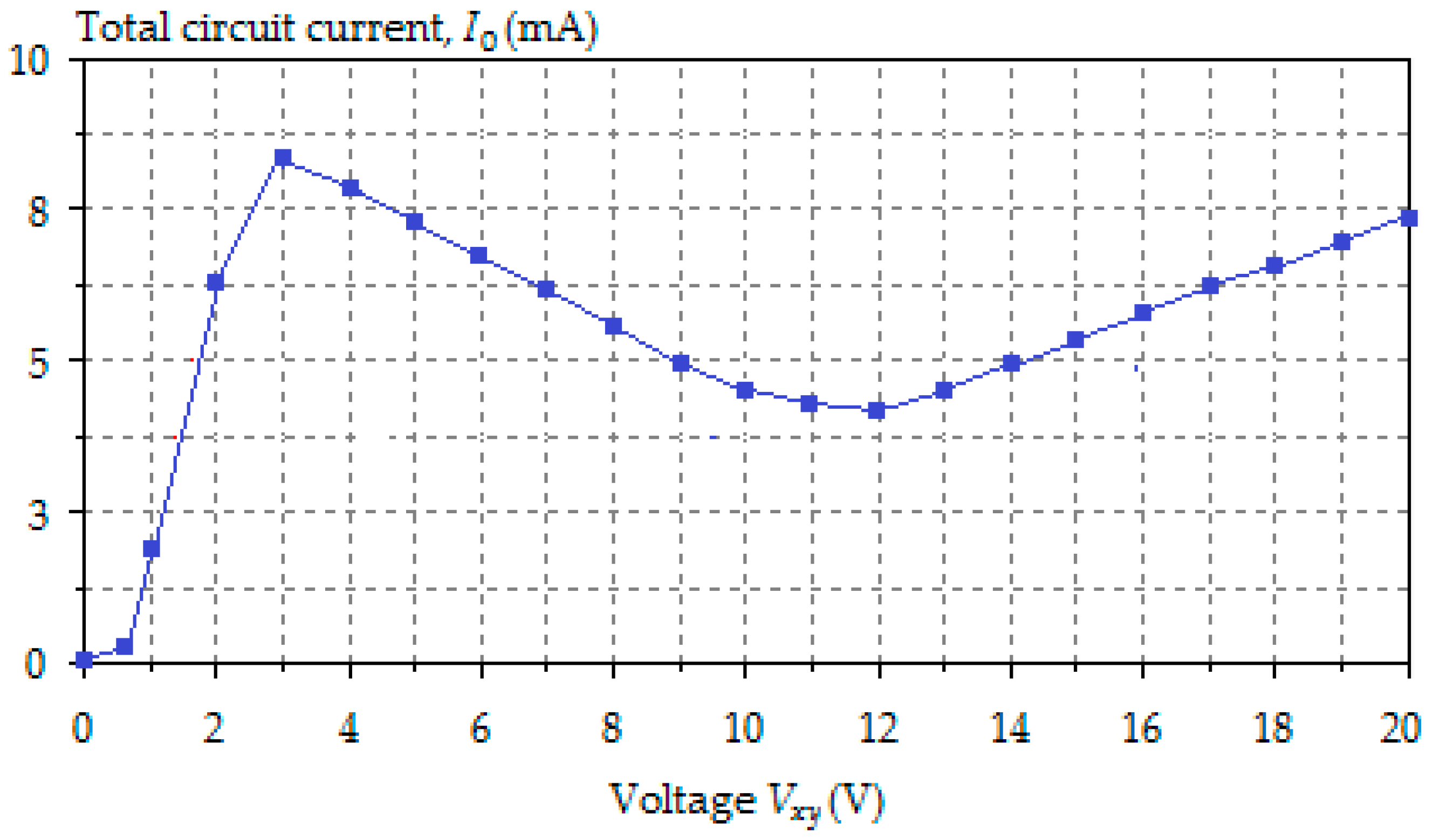
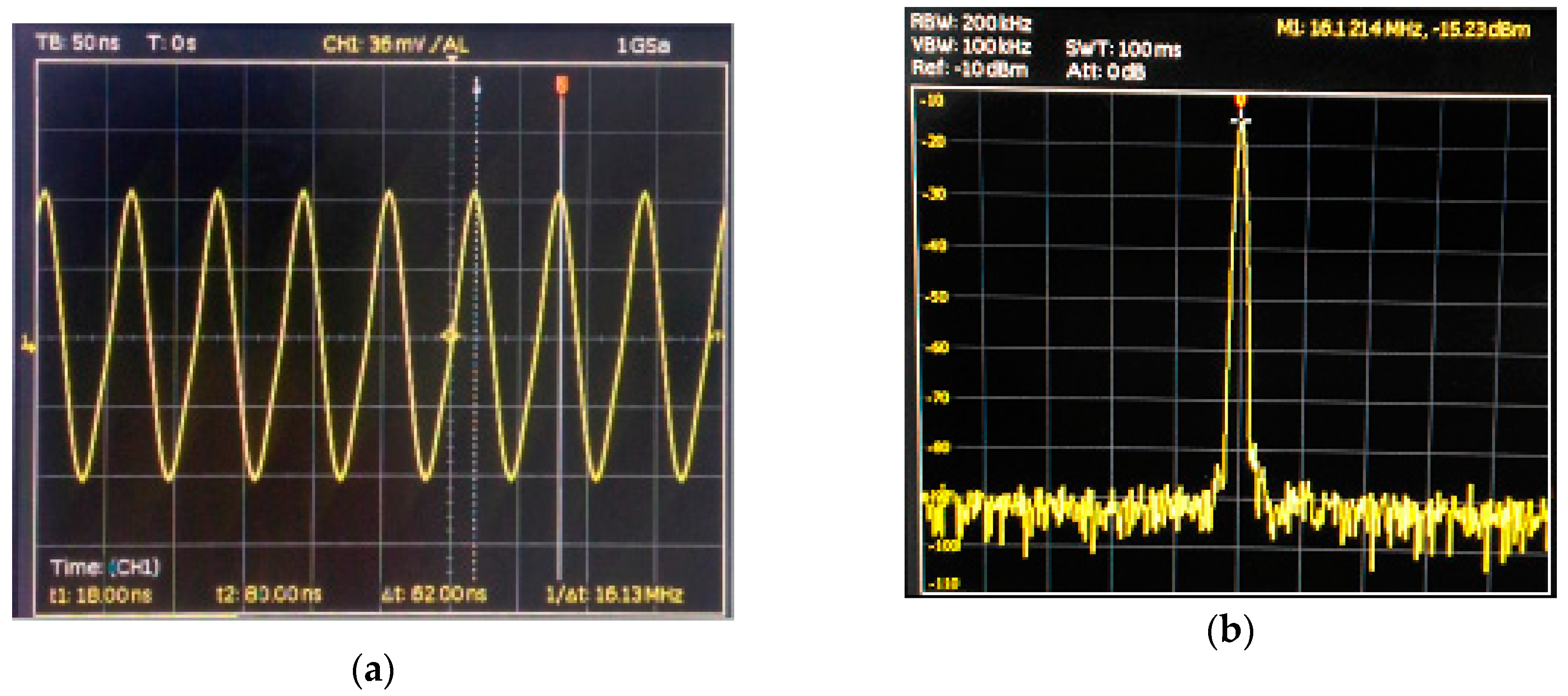
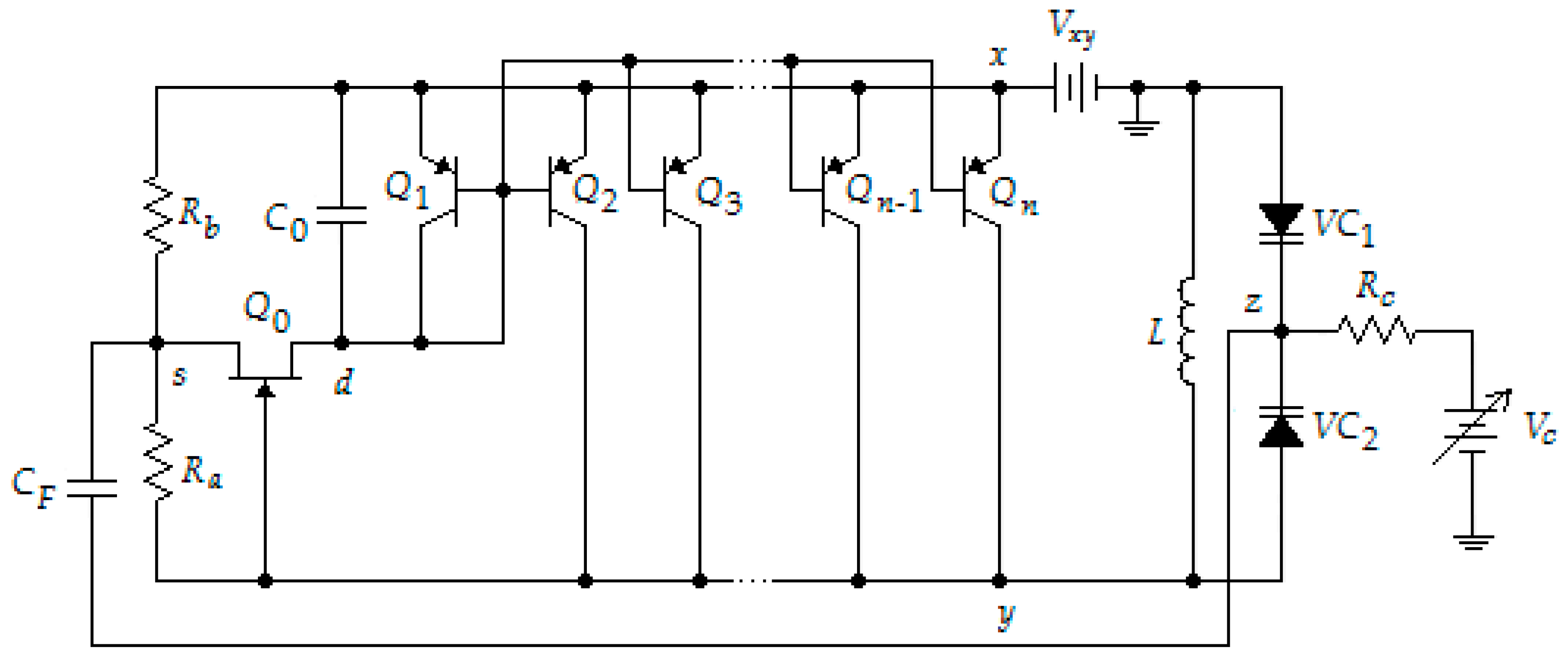
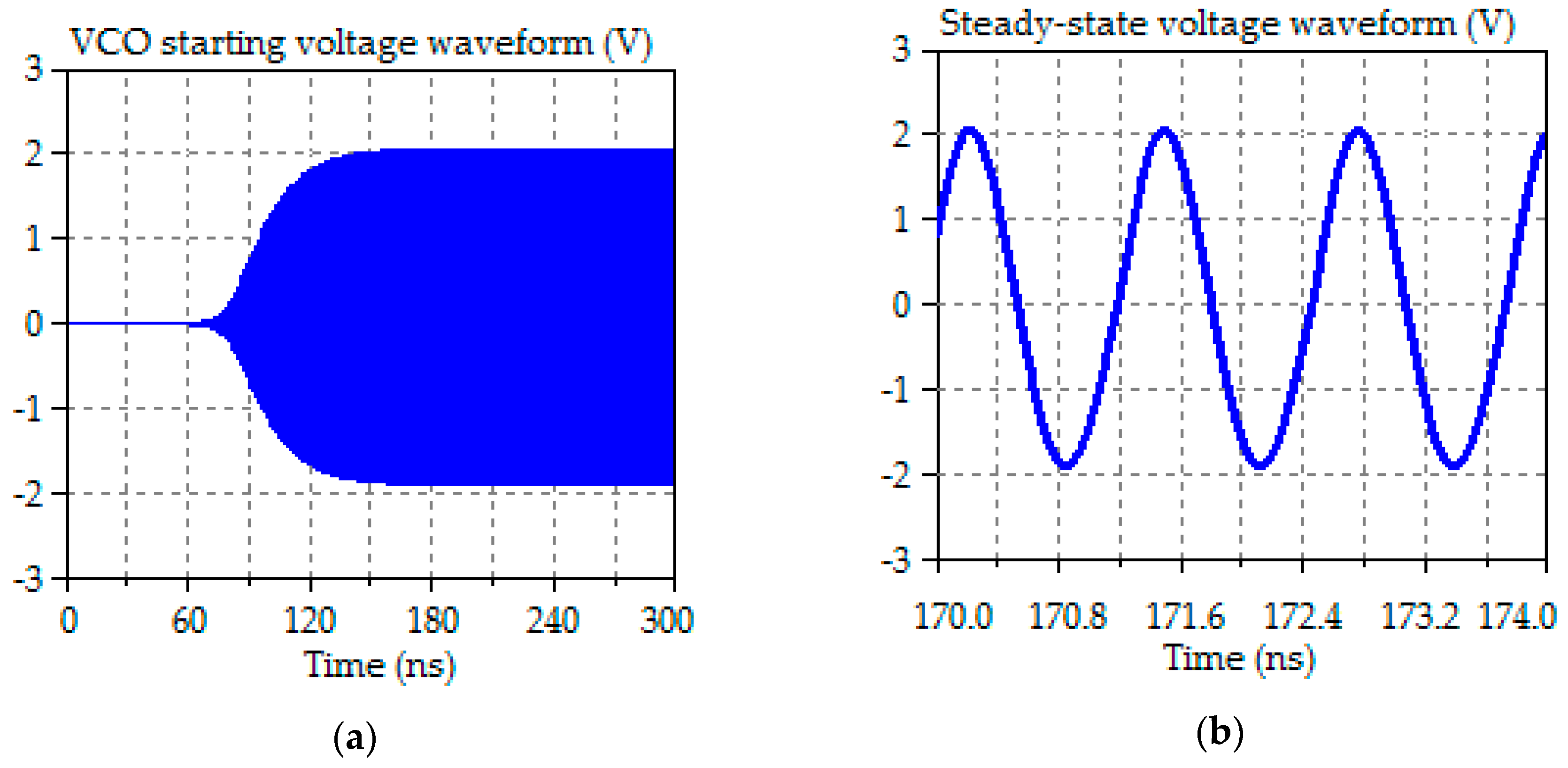
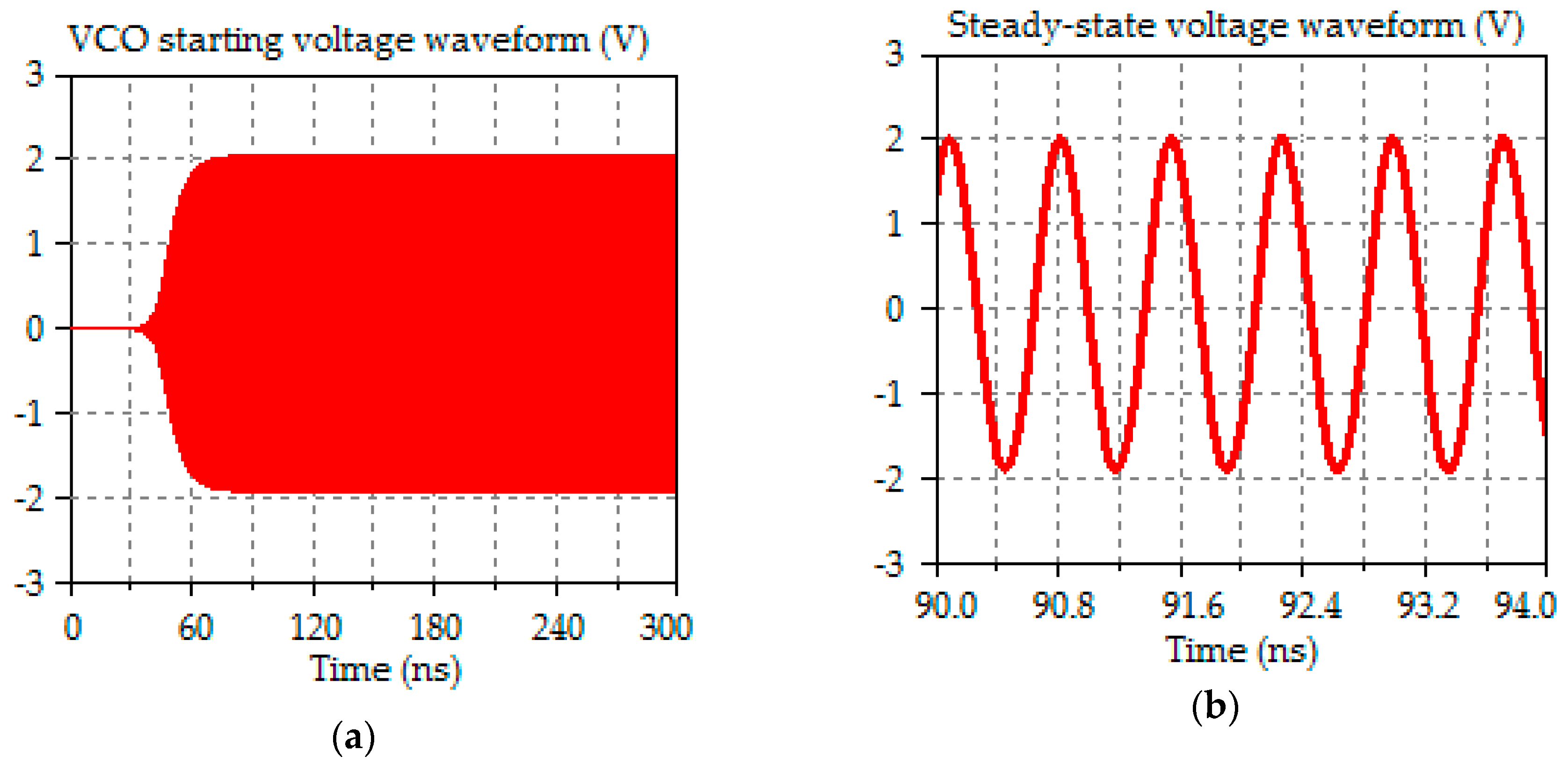
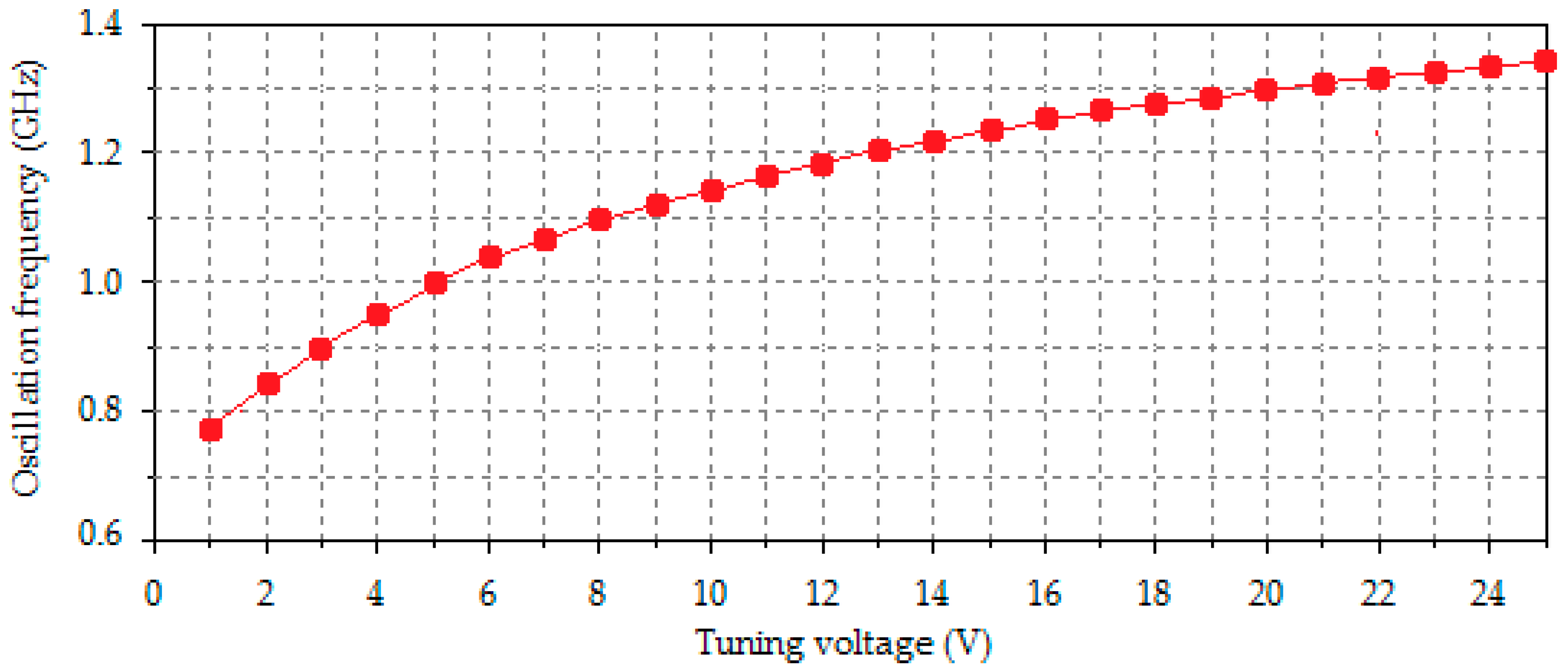
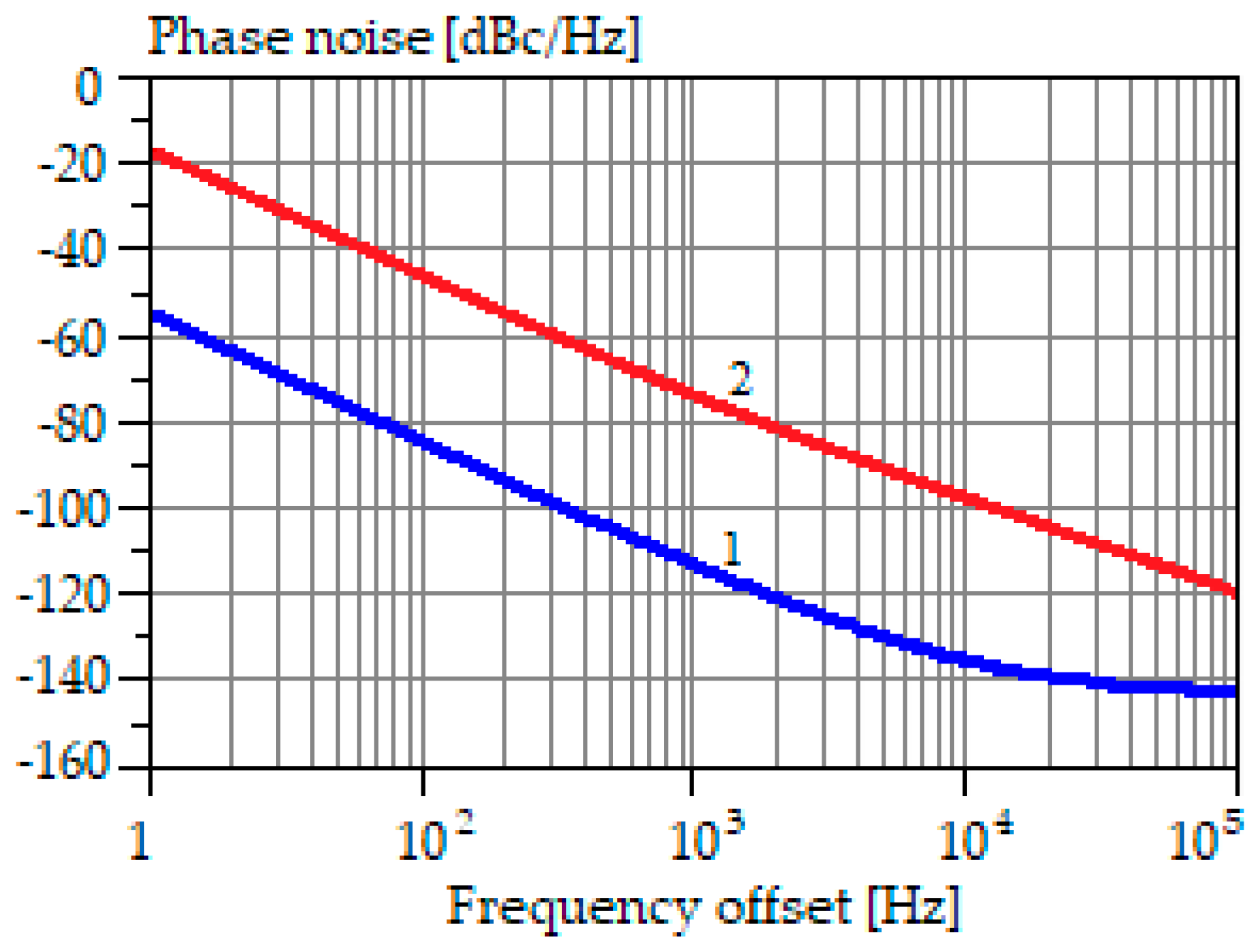
| Threshold | Calculated Value | Simulated Value | Error % |
|---|---|---|---|
| Vα (V) | 0.65 | 0.62 | −4.8% |
| Iα (mA) | 0.26 | 0.28 | 7.1% |
| Vβ (V) | 2.93 | 2.89 | −1.4% |
| Iβ (mA) | 8.22 | 8.30 | 1% |
| Vγ (V) | 11.60 | 11.05 | −5.0% |
| Iγ (mA) | 4.62 | 4.50 | −2.7% |
| Threshold | Calculated Value | Simulated Value | Error % |
|---|---|---|---|
| Vα (V) | 0.65 | 0.62 | −4.8% |
| Iα (mA) | 0.26 | 0.28 | 7.1% |
| Vβ (V) | 1.57 | 1.71 | 8.2% |
| Iβ (mA) | 7.18 | 6.92 | −3.8% |
| Vγ (V) | 4.75 | 4.73 | −0.4% |
| Iγ (mA) | 1.9 | 1.91 | 0.5% |
| Circuit Elements | Part Numbers |
|---|---|
| Transistor | NE722S01 |
| Transistors | MRF5211LT1 |
| Inductor L | 0201DS-3N3XJEU |
| Capacitor | C1608X5R1E105K |
| Capacitor | C0603C0G1E030C |
| Varactors | SMV1104-34 |
| Resistor | ERJ1GEJ471 |
| Resistor | ERJ2GEJ392 |
| VCO | Frequency GHz | Frequency Offset MHz | Phase Noise dBc/Hz | Power Dissipation mW | FOM dBc/Hz |
|---|---|---|---|---|---|
| [44] | 1.61 | 0.1 | −121 | 2.7 | −202 |
| [45] | 2.5 | 1 | −119.7 | 0.515 | −190.3 |
| [46] | 11.58 | 1 | −112.62 | 6 | −198.6 |
| [47] | 8 | 1 | −134.3 | 6.6 | −204 |
| [48] | 2.7 | 0.1 | −121.3 | 3.9 | −204 |
| [49] | 3.6 | 1 | −124 | 2.05 | −192 |
| [50] | 15.57 | 1 | −116.6 | 6 | −192.7 |
| [51] | 2.4 | 1 | −120 | 0.267 | −193.3 |
| [52] | 2.4 | 1 | −135.6 | 6.17 | −195.3 |
| [53] | 12.67 | 1 | −120.6 | 17.7 | −190 |
| [54] | 1.94 | 1 | −153 | 20 | −205.7 |
| [55] | 2.38 | 3 | −132.7 | 1 | −190.7 |
| [56] | 2.4 | 1 | −124 | 2.86 | −187.25 |
| [57] | 7 | 1 | −132 | 198 | −185.9 |
| [58] | 7.9 | 1 | −135 | 1456 | −181.3 |
| This work | 1.225 | 0.1 | −141.1 | 55.25 | −205.4 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ulansky, V.; Raza, A.; Oun, H. Electronic Circuit with Controllable Negative Differential Resistance and its Applications. Electronics 2019, 8, 409. https://doi.org/10.3390/electronics8040409
Ulansky V, Raza A, Oun H. Electronic Circuit with Controllable Negative Differential Resistance and its Applications. Electronics. 2019; 8(4):409. https://doi.org/10.3390/electronics8040409
Chicago/Turabian StyleUlansky, Vladimir, Ahmed Raza, and Hamza Oun. 2019. "Electronic Circuit with Controllable Negative Differential Resistance and its Applications" Electronics 8, no. 4: 409. https://doi.org/10.3390/electronics8040409
APA StyleUlansky, V., Raza, A., & Oun, H. (2019). Electronic Circuit with Controllable Negative Differential Resistance and its Applications. Electronics, 8(4), 409. https://doi.org/10.3390/electronics8040409