Green Computing in Sensors-Enabled Internet of Things: Neuro Fuzzy Logic-Based Load Balancing
Abstract
:1. Introduction
- Firstly, in the system model, a first-order energy radio model was used to examine the energy consumption throughout the network.
- Secondly, we designed an adaptive fuzzy logic inference system (AFLIS) with the help of fuzzy rules, sets, and membership functions that were updated (rules of AFLIS were updated) using input–output mapping of the hybrid systems. The output of the AFLIS was used as input for the neural network.
- Thirdly, in ANFCA, the metrics were input into the fuzzy logic inference system and output was produced, which provided the information about the sensor nodes, whether it was capable or not of playing the role of cluster head. The output of the fuzzy logic inference system was handed to the neuro fuzzy logic inference system to elect the cluster head for the next round. The ANFCA used a supervised learning strategy to adjust the weight of the membership function of the AFLIS.
- Fourthly, we present an approach to form clusters in which cluster heads aggregate data and send that data to the base station.
- Finally, the proposed algorithm was simulated and the results were compared with LEACH, CHEF, and LEACH-ERE algorithms to shows the effectiveness of the ANFCA.
2. Related Works
2.1. Green Computing without Heuristics
2.2. Green Computing Using Fuzzy-Centric Heuristics
3. Adaptive Neuro-Fuzzy for Green Computing in IoT
3.1. System Model
3.2. Adaptive Neuro-Fuzzy Clustering Algorithm
3.2.1. Adaptive Fuzzy Logic Inference System
- Fuzzification or Input Crisp Value: In this step, we input the three metrics: residual energy, node density, and distance to base station as crisp values in the fuzzy inference system. In this step, the inference system creates membership functions for each metric that is the intersection points.
- Knowledge Base or If–Then Rules: The knowledge base consists of all 27 rules, which runs concurrently on inputs and generates output as chance values. There are multiple inputs (three membership values), but selection is done among the minimum membership values which use fuzzy AND operator.
- Aggregation: There are 27 rules in the fuzzy inference system, which give multiple outputs. In this step, we aggregate all the output to generate a single fuzzy output set using union fuzzy OR operator which choose maximum of rule evaluation.
- Defuzzification: In this step, whether a sensor node can act as a cluster head or not is computed. For this purpose, we use a centroid method in the defuzzification step under the fuzzy set to get from aggregation, which is given by Equation (3).
3.2.2. Adaptive Neuro-Fuzzy Inference System
| Rule 1 = If RE is below, NDBS is adjacent and ND is deficient | Then = S1m + T1n + U1o + P1 |
| Rule 2 = If RE is below, NDBS is adjacent and ND is medium | Then = S2m + T2n + U2o + P2 |
| Rule 3 = If RE is below, NDBS is adjacent and ND is compact | Then = S3m + T3n + U3o + P3 |
| … | |
| Rule 25 = If RE is top, NDBS is distant and ND is deficient | Then = S25m + T25n + U25o + P25 |
| Rule 26 = If RE is top, NDBS is distant and ND is medium | Then = S26m + T26n + U26o + P26 |
| Rule 27 = If RE is top, NDBS is distant and ND is compact | Then = S27m + T27n + U27o + P27 |
- 1.
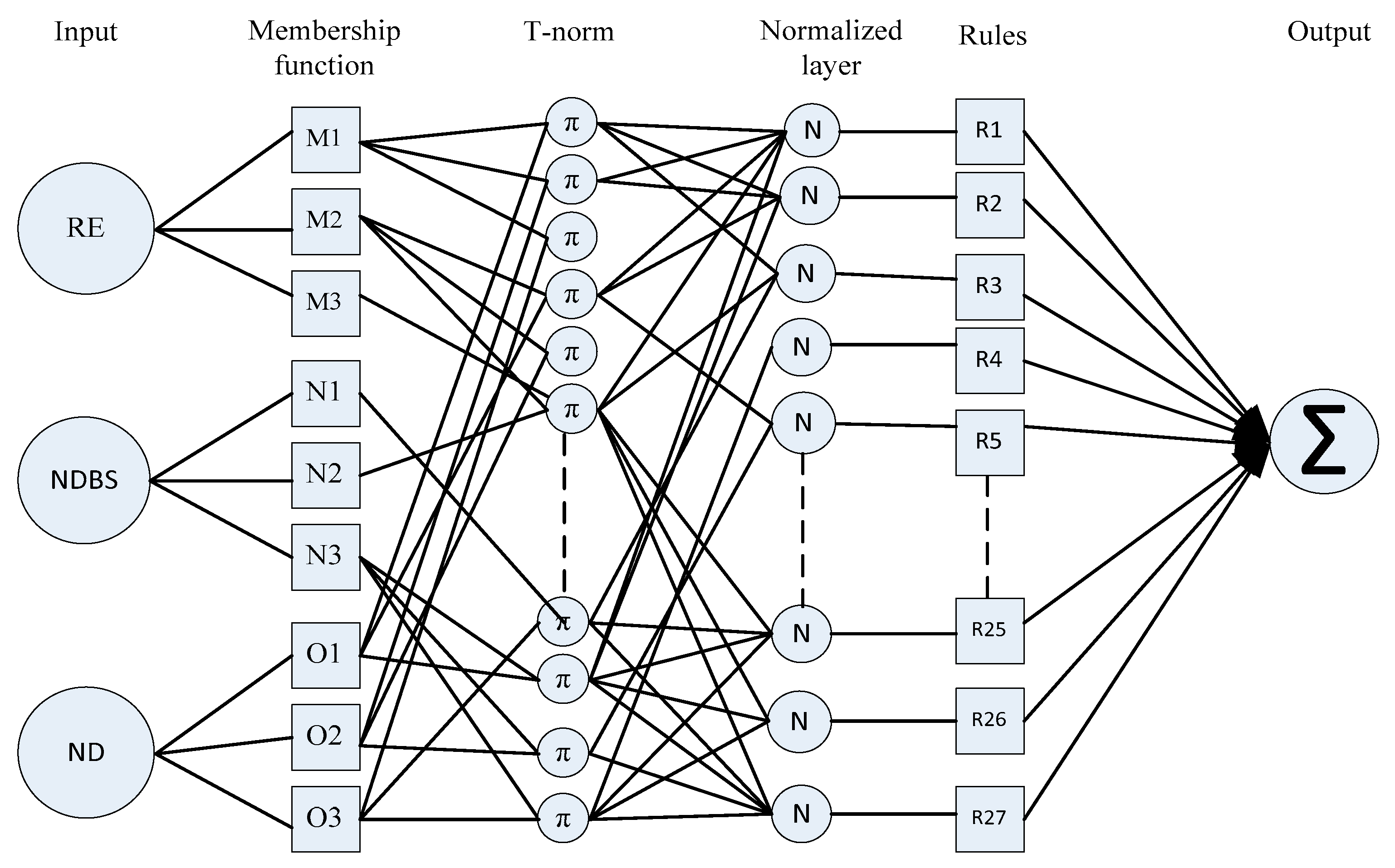
- Fuzzy Layer: This section describes the nature of the node which is actually flexible according to backward pass (denoted by square adaptable node) that resembles each input variable relative to membership function. The membership function graph is plotted against each adaptable node to describe their output. Membership function follows Gaussian distribution as shown in Equation (4) or generalized bell-shaped membership function (see Equation (5)) which gives a value in the range of 0 and 1.The output of the first layer is given bywhere is the input node to α and are the degree of membership function cross-ponding to linguistic variables , , and and {} are referred to as a parameter set of the membership function or premise parameter. The bell-shaped membership function varies along with the values of the premise parameter set. In this layer, we can also use the triangular and trapezoidal membership function for the input node; they are also valid quantifiers for this node.
- 2.
- T-Norm Layer: In this layer, each node is non-adaptive in nature, and called as rule nodes which are depicted by the circle labeled with (see Figure 5). These nodes represent the firing strength of each rule connected to it. To determine the results of each node, multiply all the signals (membership function) coming to the node. The T-norm operator uses generalized AND to calculate the antecedents/outputs at second layer of the rule.where is the output of each node which stands for each rule’s firing strength.
- 3.
- Normalized Layer: Non-adaptive in nature nodes found in the normalized layer, which is known as normalized mode, are depicted by circles labeled as N (see Figure 5). The output of every node is an estimation of the proportion between the th rule’s firing strength to the summation of firing strength of all rules. The result at the third layer or normalized output can be expressed as
- 4.
- Defuzzy Layer: This layer consists of those nodes which have adaptive essence depicted by a square (see Figure 5). The output of the node is the product of normalized firing strength and individual rule. The output at the fourth layer can be given bywhere is the normalized firing strength from the normalized layer and is a parameter in the node. Defuzzy layer parameters are also known as a consequent parameter.
- 5.
- Aggregated Output Layer: This layer consists of a single consolidated node as an output which is specified as non-adaptive in nature. This non-adaptive node gives information about the complete system performance evaluated by adding up all the approaching signals arriving at this layer from the previous node. Summation sign is used inside a circle to represent this aggregated output node. The output of the fifth layer is computed as
| Algorithm 1- Adaptive Neuro Fuzzy Clustering Algorithm (ANFCA) | |
| 1. | Begin |
| 2. | Input: Given input training pattern, {RE, NDBS, ND} and maximum number of Epoch to Emax. // obtained from first modeling mamdani type fuzzy inference system. |
| 3. | Output {CH} |
| 4. | Process |
| 5. | for E=1 to Emax. |
| 6. | Input the training data into first layer of Takagi-sugeno inference engine. |
| 7. | Membership function tuned using Equations (4) and (5). |
| 8. | Adjust the firing strength of each node (), using Equation (6) in non-adaptive T-norm layer. |
| 9. | Normalize the firing strength of each node () using Equation (7) in normalized layer. |
| 10. | Defuzzification of each node using Equation (8). |
| 11. | Aggregated output is produced for each node using Equation (9) in fifth layer. |
| 12. | END |
3.2.3. Phases of the Algorithm
Selection Phase
Cluster Formation Phase
Transfer Phase
4. Simulation
4.1. Simulation Environment
Evaluation Metrics
- ▪
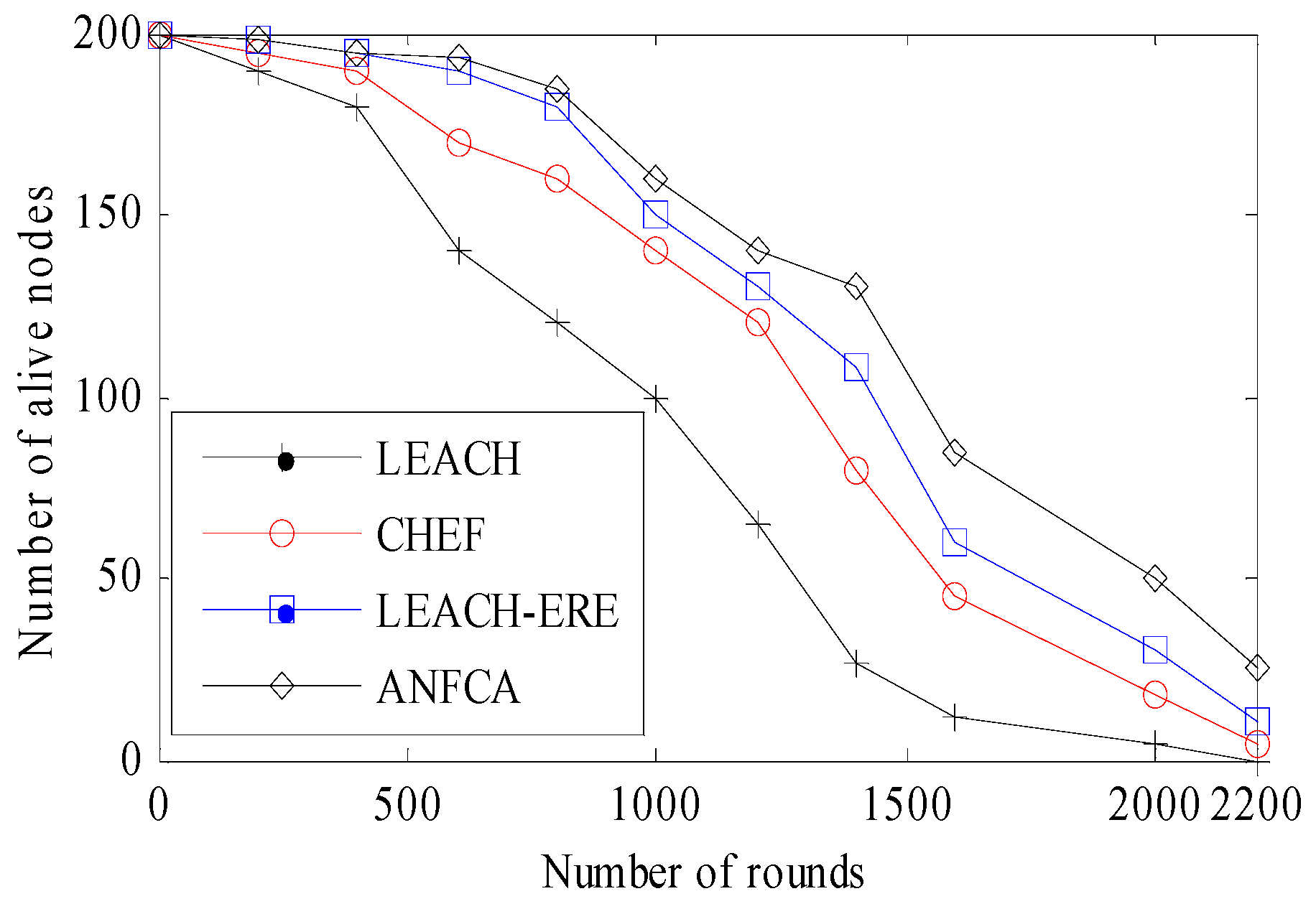
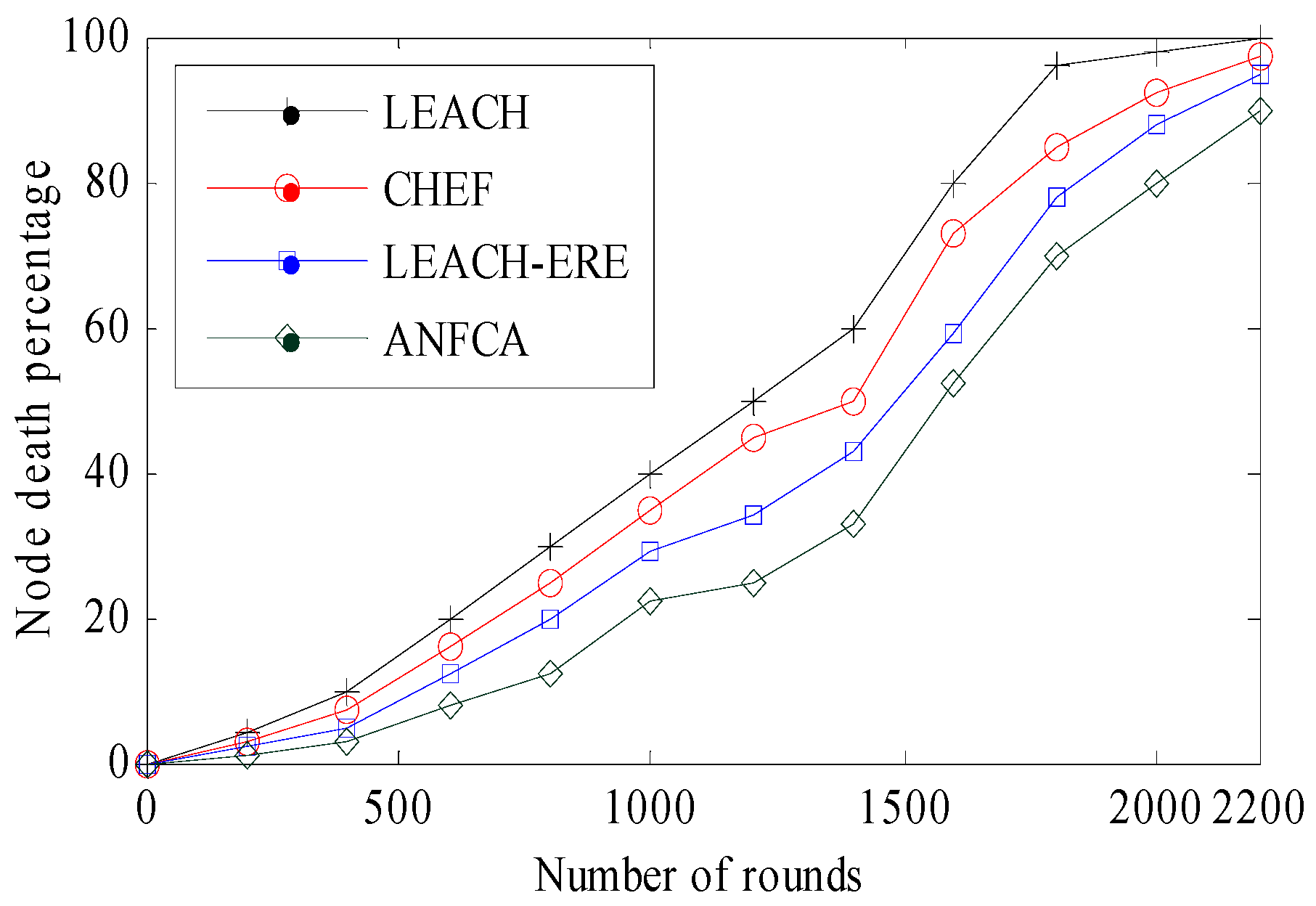
- Network Lifetime: Lifetime definition of the network is application dependent, and it may be stated that as the tenure spans from the start, it is the functioning of the network to a moment when a certain percentage of the nodes have died or the network will be disconnected. In this paper, we considered the simulation time until 90% of the nodes were dead.
- ▪
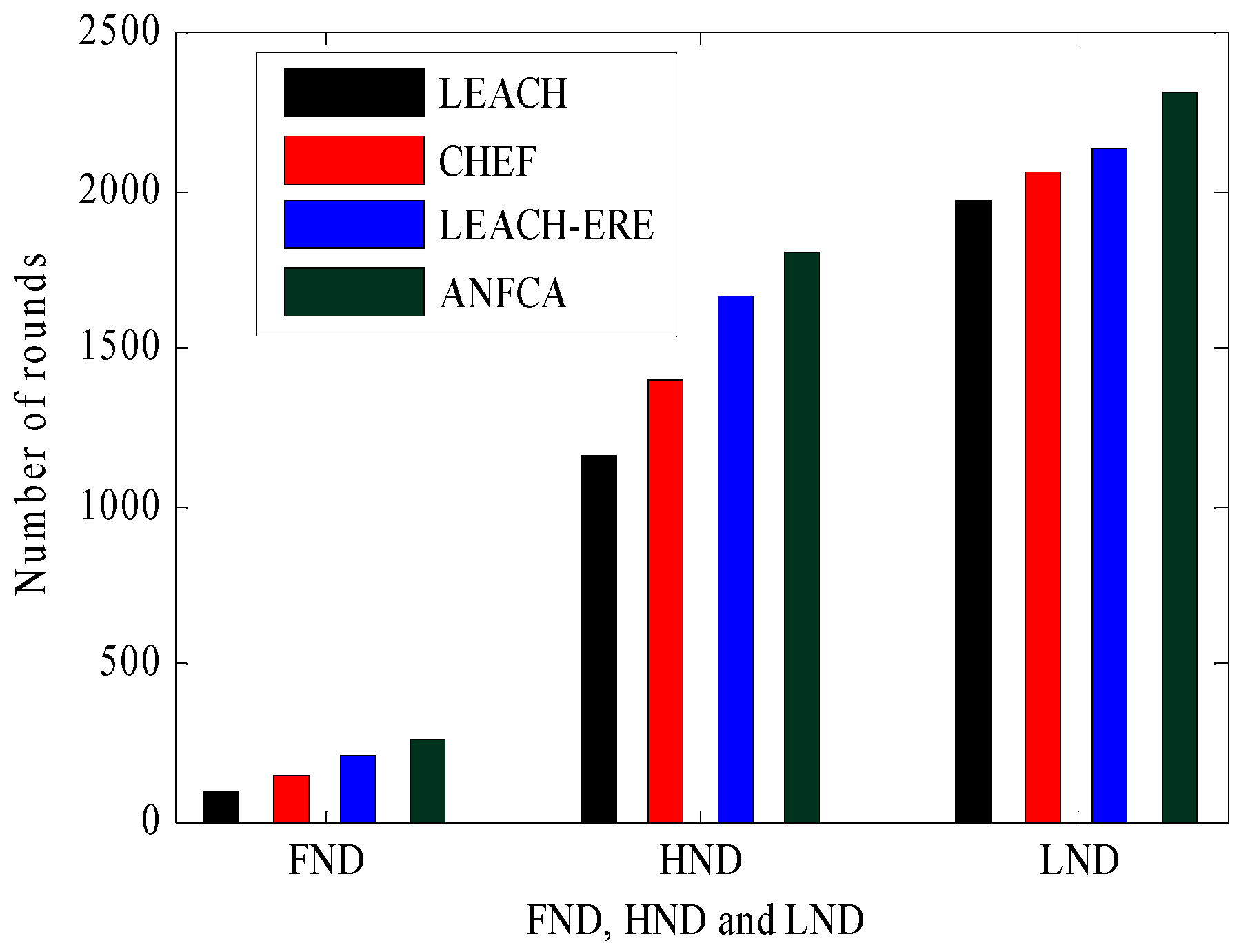
- (First node death) FND, (Half node death) HND and (Last node death) LND: The round at which the death of the first node occurred was defined as FND. Similarly, the round at which half of the nodes had died was defined as HND. The round at which the last node death has occurred was taken as LND.
- ▪
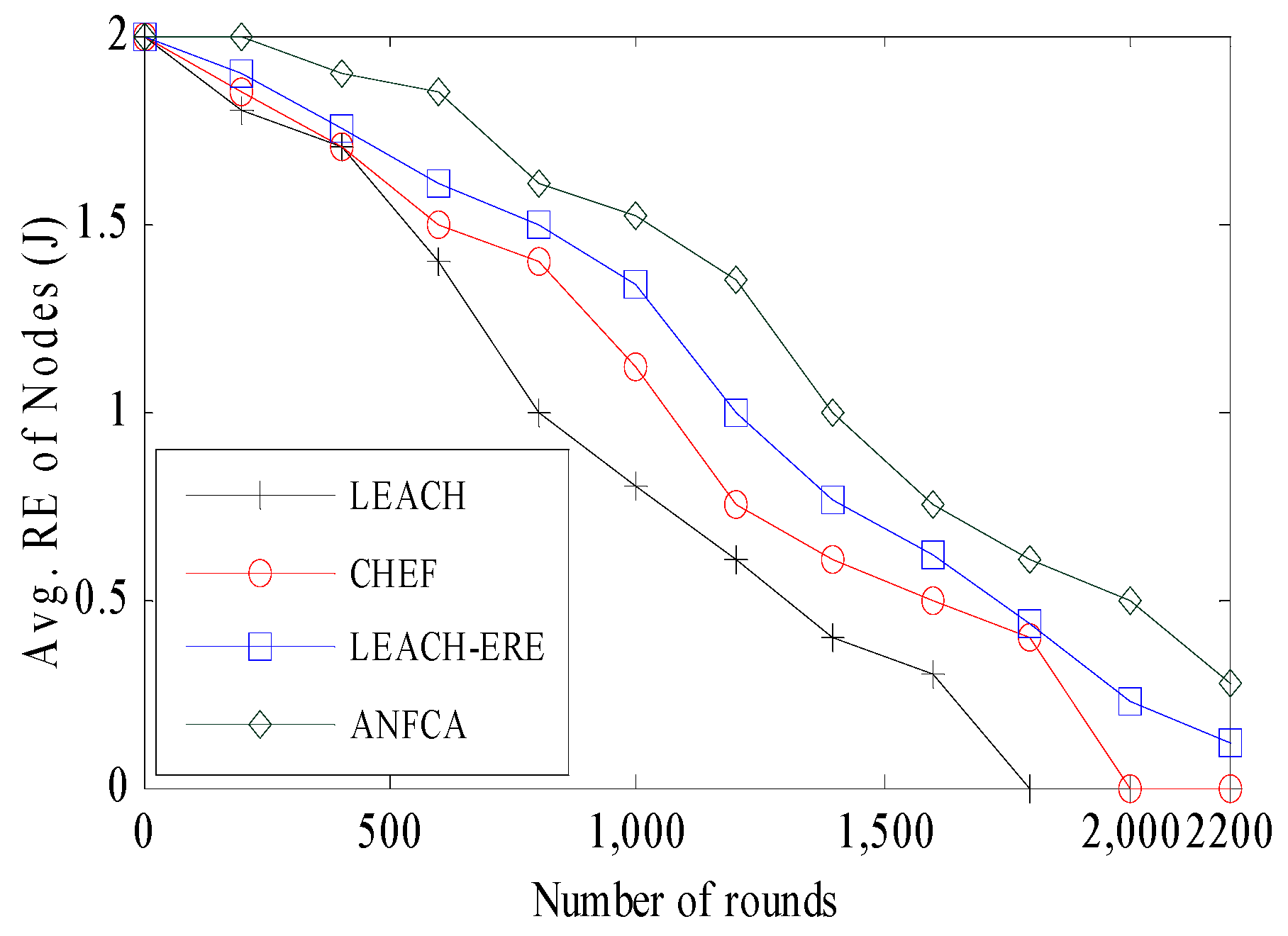
- Average Residual Energy: Defined as the mean of residual energy of alive nodes in the network with respect to rounds.
- ▪
- Average Energy Consumption: Defined as the summation of overall energy consumption taken place during the sensing and transmission by each sensor node to the number of sensor nodes with respect to rounds.
- ▪
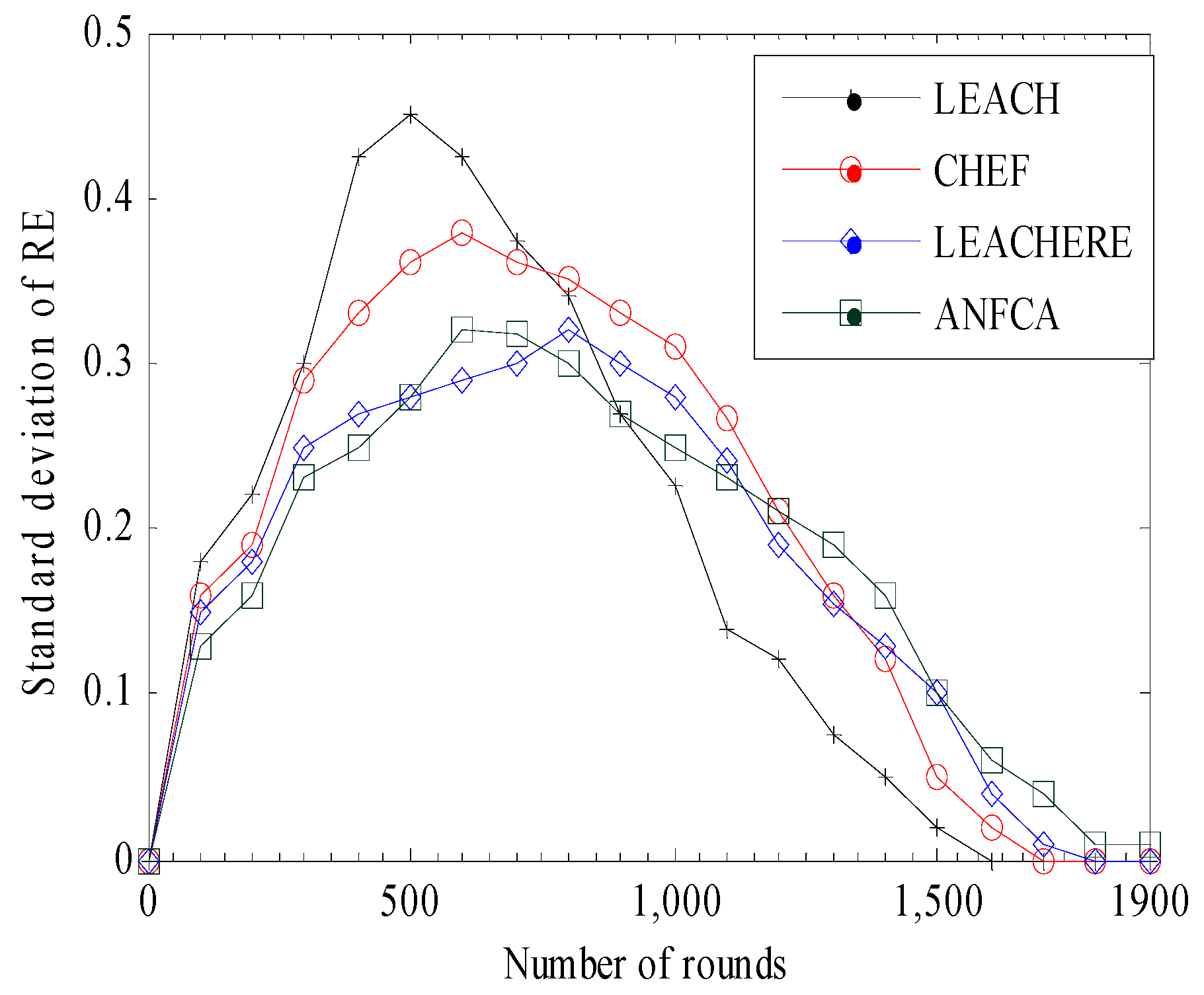
- Standard Deviation of Residual Energy: The standard deviation of residual energy is the square root of variance of residual energy of all the sensor nodes. It shows the variation of residual energy around the mean.
4.2. Simulation Results
4.2.1. Network Lifetime Over Rounds
4.2.2. Energy Expenditure over Rounds
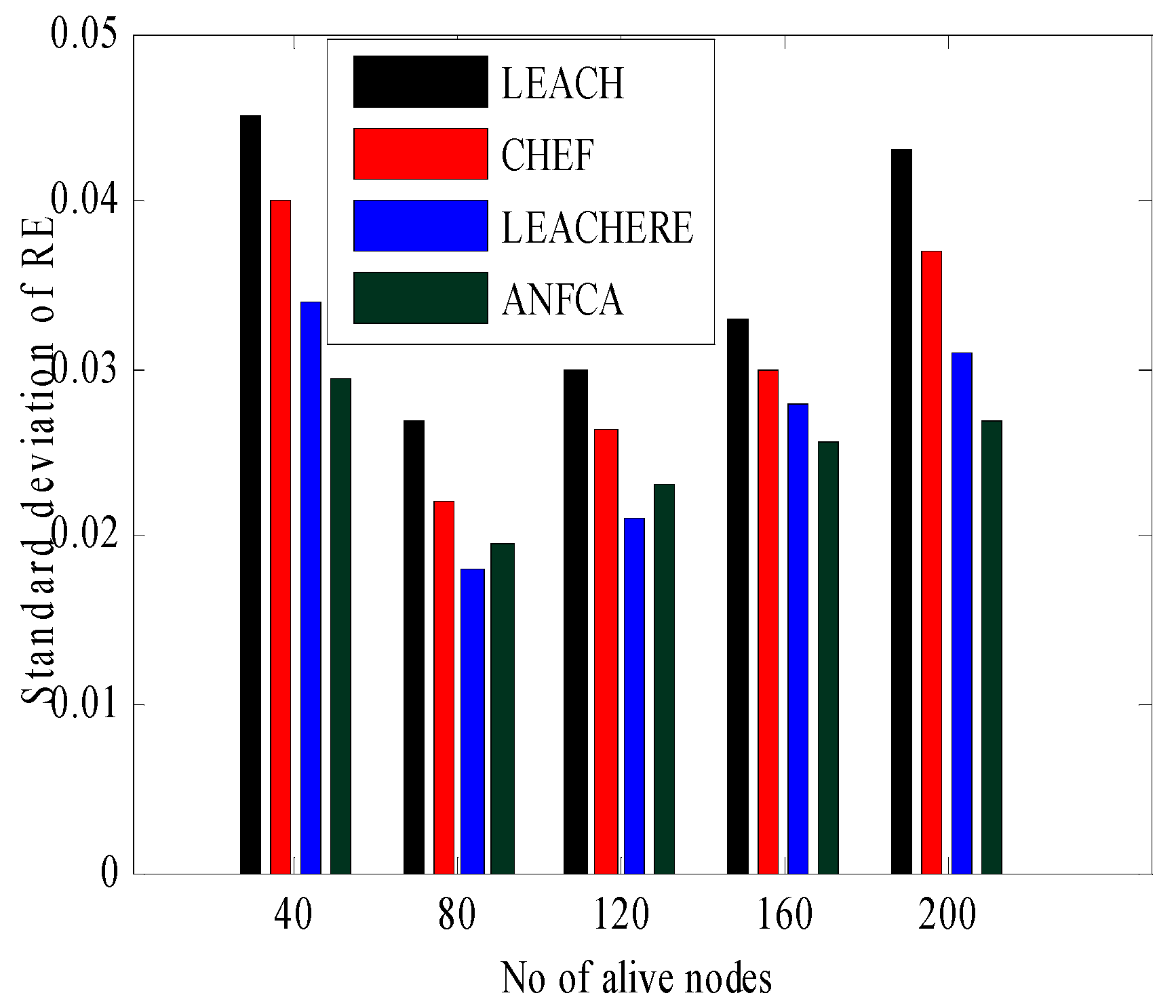
4.2.3. Standard Deviation of Residual Energy
5. Conclusions and Future Perspectives
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Farhan, L.; Kharel, R.; Kaiwartya, O.; Hammoudeh, M.; Adebisi, B. Towards green computing for Internet of things: Energy oriented path and message scheduling approach. Sustain. Cities Soc. 2018, 38, 195–204. [Google Scholar] [CrossRef]
- Aliyu, A.; Abdullah, A.H.; Kaiwartya, O.; Cao, Y.; Lloret, J.; Aslam, N.; Joda, U.M. Towards video streaming in IoT Environments: Vehicular communication perspective. Comput. Commun. 2018, 118, 93–119. [Google Scholar] [CrossRef]
- Kaiwartya, O.; Abdullah, A.H.; Cao, Y.; Altameem, A.; Prasad, M.; Lin, C.T.; Liu, X. Internet of Vehicles: Motivation, Layered Architecture, Network Model, Challenges, and Future Aspects. IEEE Access 2016, 4, 5356–5373. [Google Scholar] [CrossRef]
- Kumar, K.; Kumar, S.; Kaiwartya, O.; Cao, Y.; Lloret, J.; Aslam, N. Cross-Layer Energy Optimization for IoT Environments: Technical Advances and Opportunities. Energies 2017, 10, 2073. [Google Scholar] [CrossRef]
- Verma, J.K.; Kumar, S.; Kaiwartya, O.; Cao, Y.; Lloret, J.; Katti, C.P.; Kharel, R. Enabling green computing in cloud environments: Network virtualization approach toward 5G support. Trans. Emerg. Telecommun. Technol. 2014, 25, 81–93. [Google Scholar] [CrossRef]
- Kaiwartya, O.; Kumar, S.; Lobiyal, D.; Abdullah, A.; Hassan, A. Performance improvement in geographic routing for vehicular Ad Hoc networks. Sensors 2014, 14, 22342–22371. [Google Scholar] [CrossRef] [PubMed]
- Ullah, F.; Abdullah, A.; Kaiwartya, O.; Arshad, M. Traffic priority-aware adaptive slot allocation for medium access control protocol in wireless body area network. Computers 2017, 6, 9. [Google Scholar] [CrossRef]
- Cao, Y.; Yang, S.; Min, G.; Zhang, X.; Song, H.; Kaiwartya, O.; Aslam, N. A Cost-Efficient Communication Framework for Battery-Switch-Based Electric Vehicle Charging. IEEE Commun. Mag. 2017, 55, 162–169. [Google Scholar] [CrossRef]
- Kaiwartya, O.; Kumar, S.; Abdullah, H.A. Analytical model of Deployment Methods for Application of Sensors in non-Hostile Environment. Wireless Pers. Commun. 2017, 97, 1517–1536. [Google Scholar] [CrossRef]
- Kaiwartya, O.; Abdullah, A.H.; Cao, Y.; Raw, R.S.; Kumar, S.; Lobiyal, D.K.; Isnin, I.F.; Liu, X.; Shah, R.R. T-MQM: Testbed-Based Multi-Metric Quality Measurement of Sensor Deployment for Precision Agriculture—A Case Study. IEEE Sens. J. 2016, 16, 8649–8664. [Google Scholar] [CrossRef]
- Dohare, U.; Lobiyal, D.K.; Kumar, S. Energy balanced model for lifetime maximization in randomly distributed wireless sensor networks. Wireless Pers. Commun. 2014, 78, 407–428. [Google Scholar] [CrossRef]
- Aanchal, Kumar, S.; Kaiwartya, O.; Abdullah, A.H. Green computing for wireless sensor networks: Optimization and Huffman coding approach. Peer-to-Peer Netw. Appl. 2017, 10, 592–609. [Google Scholar] [CrossRef]
- Liu, A.-F.; Zhang, P.-H.; Chen, Z.-G. Theoretical analysis of the lifetime and energy hole in cluster based wireless sensor networks. Journal of parallel and distributed computing. J. Parallel Distrib. Comput. 2011, 71, 1327–1355. [Google Scholar] [CrossRef]
- Khasawneh, A.; Latiff, M.; Kaiwartya, O.; Chizari, H. Next forwarding node selection in underwater wireless sensor networks (UWSNs): Techniques and challenges. Information 2016, 8, 3. [Google Scholar] [CrossRef]
- Khatri, A.; Kumar, S.; Kaiwartya, O.; Aslam, N.; Meena, N.; Abdullah, A.H. Towards green computing in wireless sensor networks: Controlled mobility–aided balanced tree approach. Int. J. Commun. Syst. 2017, 31, e3463. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Takagi, T.; Sugeno, M. Fuzzy identification of systems and its applications to’ modeling and control. IEEE Trans. Syst. Man Cybern. 1985, 15, 116–132. [Google Scholar] [CrossRef]
- McCulloch, W.S.; Pitts, W.H. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Rosenblatt, F. The Perceptron: A Probabilistic Model for Information Storage and Organization in the Brain. Psychol. Rev. 1958, 65, 386–408. [Google Scholar] [CrossRef]
- Rosenblatt, F. Principles of Neurodynamics; Perceptrons and the Theory of Brain Mechanisms; Spartan Books: Washington, DC, USA, 1962; Available online: https://catalog.hathitrust.org/Record/000203591 (accessed on 21 February 2019).
- Rosenblatt, F. On the Convergence of Reinforcement Procedures in Simple Perceptron; Cornell Aeronautical Laboratory: Buffalo, NY, USA, 1960. [Google Scholar]
- Widrow, B.; Lehr, M.A. 30 years of adaptive neural networks: perceptron, Madaline, and back propagation. Proc. IEEE 1990, 78, 1415–1442. [Google Scholar] [CrossRef]
- Widrow, B.; Winter, R.G.; Baxter, R.A. Layered neural nets for pattern recognition. IEEE Trans. Acoust. Speech Signal Process. 1988, 36, 1109–1118. [Google Scholar] [CrossRef]
- Winter, R.; Widrow, B. MADALINE RULE II: A training algorithm for neural networks. In Proceedings of the IEEE 1988 International Conference on Neural Networks, San Diego, CA, USA, 24–27 July 1988; pp. 401–408. [Google Scholar]
- Lin, C.-T.; Lee, C.S.G. Neural-network-based fuzzy logic control and decision system. IEEE Trans. Comput. 1991, 40, 1320–1336. [Google Scholar] [CrossRef]
- Berenji, H.R.; Khedkar, P. Learning and tuning fuzzy logic controllers through reinforcements. IEEE Trans. Neural Netw. 1992, 3, 724–740. [Google Scholar] [CrossRef]
- Nauck, D.; Kruse, R. Neuro-Fuzzy Systems for Function Approximation. Fuzzy Sets Syst. 1999, 101, 261–271. [Google Scholar] [CrossRef]
- Lin, C.-T. FALCON: A fuzzy adaptive learning control network. In NAFIPS/IFIS/NASA ′94, Proceedings of the First International Joint Conference of The North American Fuzzy Information Processing Society Biannual Conference. The Industrial Fuzzy Control and Intellige, San Antonio, TX, USA, 18–21 December 1994; IEEE: Piscataway, NJ, USA; pp. 228–232.
- Tano, S.; Oyama, T.; Arnold, T. Deep Combination of Fuzzy Inference. Fuzzy Sets Syst. 1996, 8, 338–353. [Google Scholar]
- Juang, C.F.; Lin, C.-T. An online self-constructing neural fuzzy inference network and its applications. IEEE Trans. Fuzzy Syst. 1998, 6, 12–32. [Google Scholar] [CrossRef]
- Figueiredo, M.; Gomide, F. Design of fuzzy systems using neuro fuzzy networks. IEEE Trans. Neural Netw. 1999, 10, 815–827. [Google Scholar] [CrossRef]
- Nauck, D.; Kalwon, F.; Kruse, R. Foundation of Neuro-Fuzzy Systems; John Wiley & Sons, Inc.: New York, NY, USA, 1997. [Google Scholar]
- Jang, R. Neuro-Fuzzy Modeling: Architectures, Analysis and Application. Ph.D. Thesis, University of California, Berkley, CA, USA, July 1992. [Google Scholar]
- Heinzelman, W.R.; Chandrakasan, A.; Balakrishnan, H. Energy efficient communication protocol for wireless micro sensor networks. In Proceedings of the 33rd Annual Hawaii International Conference on System Sciences, Maui, HI, USA, 7 January 2000; pp. 3005–3014. [Google Scholar]
- Heinzelman, W.B.; Chandrakasan, A.P.; Balakrishnan, H. An application-specific protocol architecture for wireless micro sensor networks. IEEE Trans. Wirel. Commun. 2002, 1, 660–670. [Google Scholar] [CrossRef]
- Younis, O.; Fahmy, S. HEED: A Hybrid, Energy Efficient, Distributed clustering approach for Ad Hoc sensor networks. IEEE Trans. Mobile Comput. 2004, 3, 366–379. [Google Scholar] [CrossRef]
- Lindsey, S.; Raghavendra, C.S. PEGASIS: Power efficient gathering in sensor information systems. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 9–16 March 2002; pp. 1125–1130. [Google Scholar]
- Sampalli, S.; Riordan, D.; Gupta, I. Cluster-head election using fuzzy logic for wireless sensor networks. In Proceedings of the 3rd Annual Communication Networks and Services Research Conference, Halifax, NS, Canada, May 2005. [Google Scholar]
- Kim, J.; Park, S.; Han, Y.; Chung, T. CHEF: Cluster head election mechanism using fuzzy logic in wireless sensor networks. In Proceedings of the 2008 10th International Conference on Advanced Communication Technology, Gangwon-Do, Korea, 17–20 February 2008; pp. 654–659. [Google Scholar]
- Ran, G.; Zhang, H.; Gong, S. Improving on LEACH protocol of wireless sensor networks using fuzzy logic. J. Inf. Comput. Sci. 2010, 7, 767–775. [Google Scholar]
- Lee, J.S.; Cheng, W.L. Fuzzy-Logic-Based Clustering Approach for Wireless Sensor Networks Using Energy Predication. IEEE Sens. J. 2012, 12, 2891–2897. [Google Scholar] [CrossRef]
- Nayak, P.; Devulapalli, A. A Fuzzy Logic-Based Clustering Algorithm for WSN to Extend the Network Lifetime. IEEE Sens. J. 2016, 16, 137–144. [Google Scholar] [CrossRef]
- Nayak, P.; Anurag, D.; Bhargavi, V.V.N.A. Fuzzy based method super cluster head election for wireless sensor network with mobile base station (FM-SCHM). In Proceedings of the 2nd International Conference Advance Computational Methodology; 2013; pp. 422–427. [Google Scholar]
- Abidoye, A.P.; Obagbuwa, I.C. Models for integrating wireless sensor networks into the Internet of Things. IET Wirel. Sens. Syst. 2017, 7, 65–72. [Google Scholar] [CrossRef]
- Li, Y.; Sun, Z.; Han, L.; Mei, N. Fuzzy Comprehensive Evaluation Method for Energy Management Systems Based on an Internet of Things. IEEE Access 2017, 5, 21312–21322. [Google Scholar] [CrossRef]
- Kasana, R.; Kumar, S.; Kaiwartya, O.; Kharel, R.; Lloret, J.; Aslam, N.; Wang, T. Fuzzy-Based Channel Selection for Location Oriented Services in Multichannel VCPS Environments. IEEE Internet Things J. 2018, 5, 4642–4651. [Google Scholar] [CrossRef]
- Hu, Q.; Wu, C.; Zhao, X.; Chen, X.; Ji, Y.; Yoshinaga, T. Vehicular Multi-Access Edge Computing With Licensed Sub-6 GHz, IEEE 802.11p and mmWave. IEEE Access 2018, 6, 1995–2004. [Google Scholar] [CrossRef]
- Kaiwartya, O.; Abdullah, A.H.; Cao, Y.; Lloret, J.; Kumar, S.; Shah, R.R.; Prasad, M.; Prakash, S. Virtualization in wireless sensor networks: Fault tolerant embedding for internet of things. IEEE Internet Things J. 2018, 5, 571–580. [Google Scholar] [CrossRef]
- Jang, J.S.R. ANFIS: adaptive-network-based fuzzy inference system. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
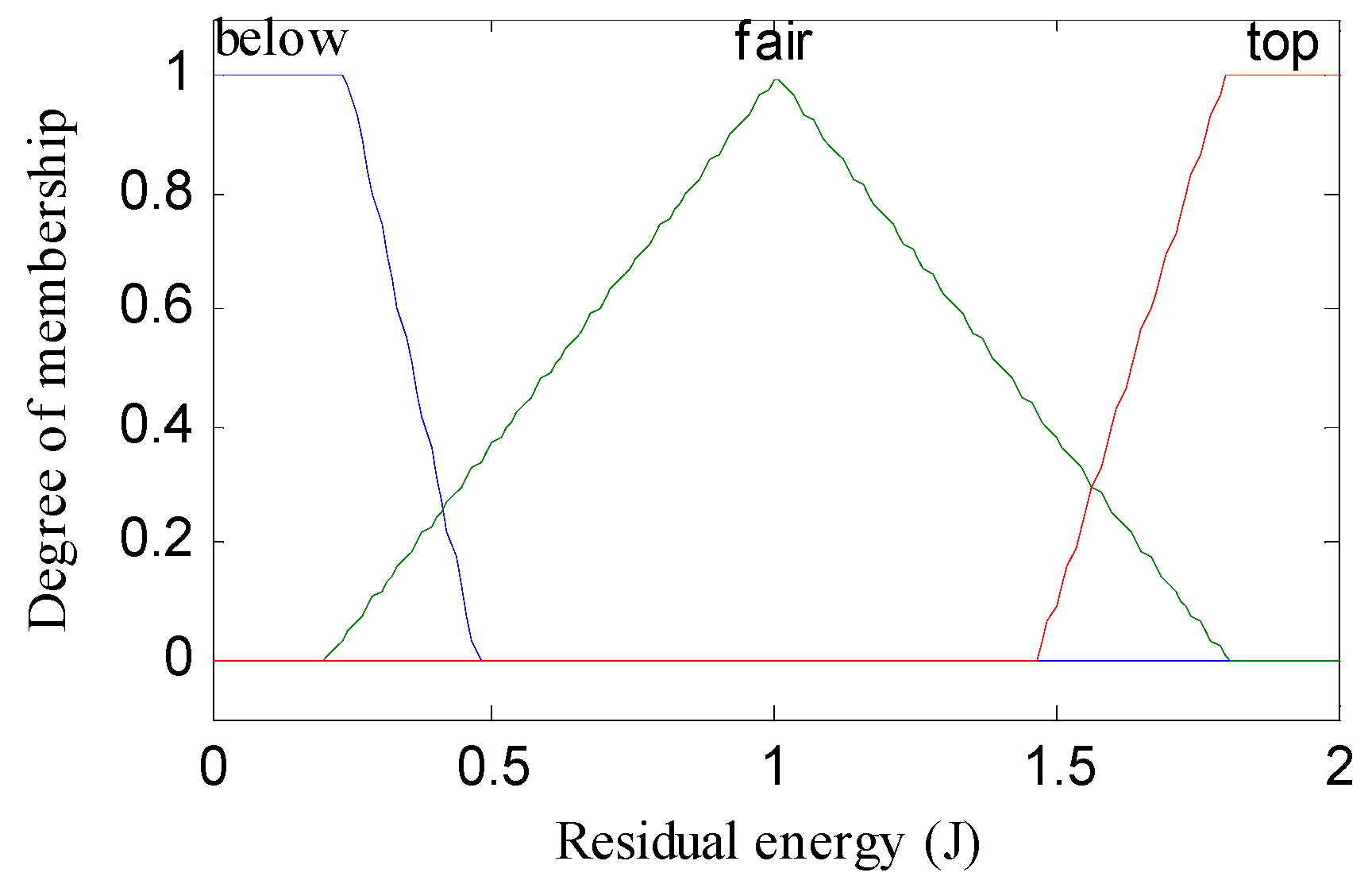


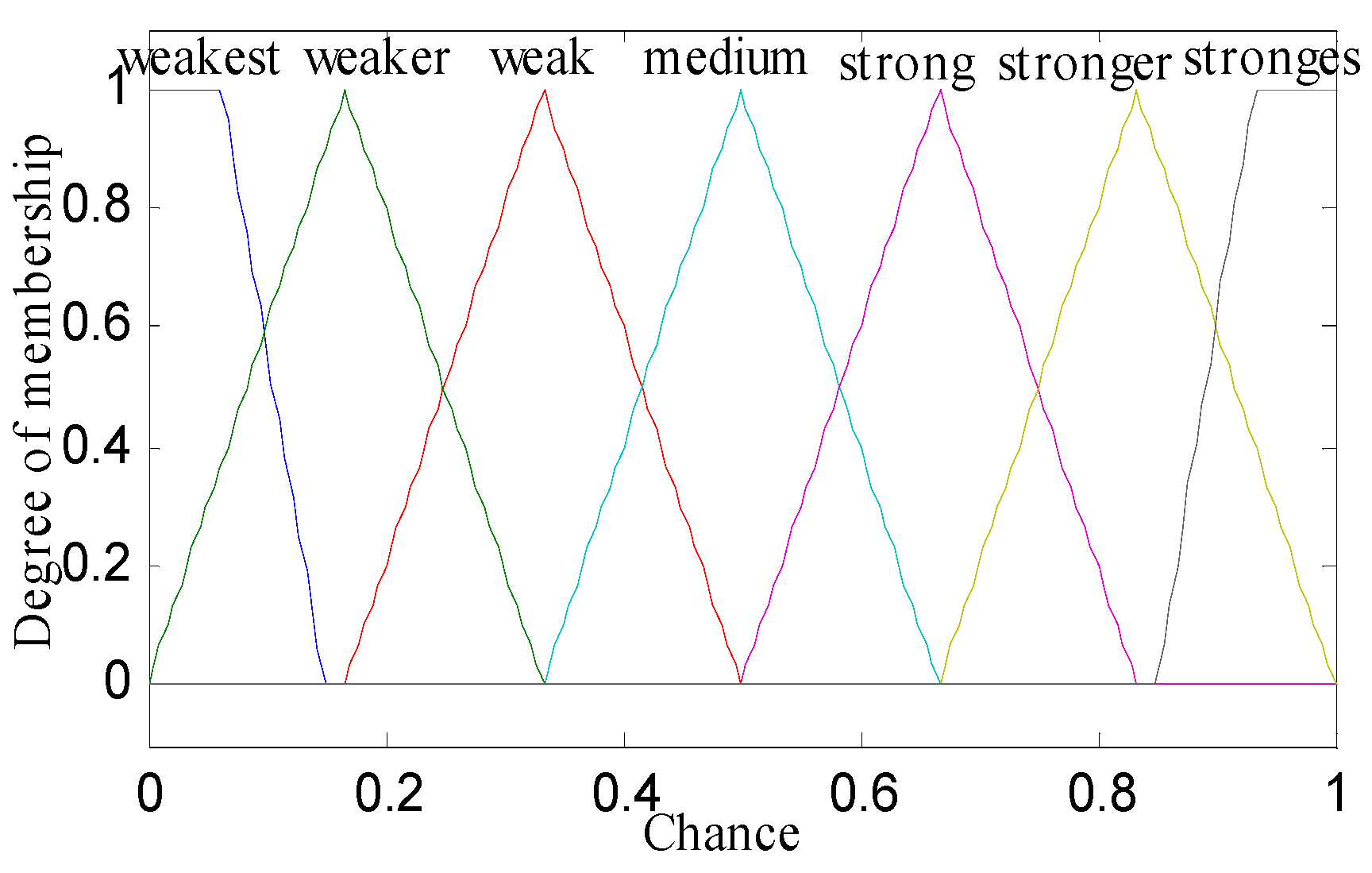

| Rule | IF THEN | Rule | IF THEN | ||||||
|---|---|---|---|---|---|---|---|---|---|
| RE | NDBS | ND | CH | RE | NDBS | ND | CH | ||
| 1. | below | adjacent | deficient | weakest | 15. | fair | midway | compact | medium |
| 2. | below | adjacent | medium | weaker | 16. | fair | distant | deficient | weakest |
| 3. | below | adjacent | compact | weak | 17. | fair | distant | medium | weaker |
| 4. | below | midway | deficient | weakest | 18. | fair | distant | compact | weaker |
| 5. | below | midway | medium | weakest | 19. | top | adjacent | deficient | strong |
| 6. | below | midway | compact | weaker | 20. | top | adjacent | Medium | stronger |
| 7. | below | distant | deficient | weaker | 21. | top | adjacent | compact | strongest |
| 8. | below | distant | medium | weakest | 22. | top | midway | deficient | medium |
| 9. | below | distant | compact | weakest | 23. | top | midway | medium | strong |
| 10. | fair | adjacent | deficient | weak | 24. | top | midway | compact | stronger |
| 11. | fair | adjacent | medium | medium | 25. | top | distant | deficient | strong |
| 12. | fair | adjacent | compact | strong | 26. | top | distant | medium | stronger |
| 13. | fair | midway | deficient | weak | 27. | top | distant | compact | stronger |
| 14. | fair | midway | medium | weak | - | - | - | - | - |
| Metrics | Specification |
|---|---|
| Number of nodes | 200 |
| Rectangular area | 200 × 200 m2 |
| Node sensing range | 5 m |
| Node transmission range | 25 m |
| Base station location | (200,170) |
| Packet size m | 512 bits |
| Initial Energy | 2 J |
| 5 nJ/bit/message | |
| 50 nJ/bit | |
| 10 pJ/bit/m2 | |
| 0.0013 pJ/bit/m4 | |
| Cycle time | 60 µs |
| Death Percentage (%) | LEACH | CHEF | LEACH-ERE | ANFCA |
|---|---|---|---|---|
| FND | 96 | 150 | 205 | 260 |
| 20 | 600 | 827 | 1107 | 1224 |
| 40 | 934 | 1223 | 1536 | 1707 |
| HND | 1167 | 1400 | 1665 | 1810 |
| 60 | 1386 | 1631 | 1885 | 1972 |
| 80 | 1600 | 1795 | 1994 | 2206 |
| LND | 1970 | 2056 | 2140 | 2310 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumar Kashyap, P.; Kumar, S.; Dohare, U.; Kumar, V.; Kharel, R. Green Computing in Sensors-Enabled Internet of Things: Neuro Fuzzy Logic-Based Load Balancing. Electronics 2019, 8, 384. https://doi.org/10.3390/electronics8040384
Kumar Kashyap P, Kumar S, Dohare U, Kumar V, Kharel R. Green Computing in Sensors-Enabled Internet of Things: Neuro Fuzzy Logic-Based Load Balancing. Electronics. 2019; 8(4):384. https://doi.org/10.3390/electronics8040384
Chicago/Turabian StyleKumar Kashyap, Pankaj, Sushil Kumar, Upasana Dohare, Vinod Kumar, and Rupak Kharel. 2019. "Green Computing in Sensors-Enabled Internet of Things: Neuro Fuzzy Logic-Based Load Balancing" Electronics 8, no. 4: 384. https://doi.org/10.3390/electronics8040384
APA StyleKumar Kashyap, P., Kumar, S., Dohare, U., Kumar, V., & Kharel, R. (2019). Green Computing in Sensors-Enabled Internet of Things: Neuro Fuzzy Logic-Based Load Balancing. Electronics, 8(4), 384. https://doi.org/10.3390/electronics8040384






