Wireless-Powered Cooperative MIMO NOMA Networks: Design and Performance Improvement for Cell-Edge Users

Abstract

In this paper, we study two transmission scenarios for the base station (BS) in cellular networks to serve the far user, who is located at the cell-edge area in such a network. In particular, we show that wireless-powered non-orthogonal multiple access (NOMA) and the cell-center user in such a model can harvest energy from the BS. To overcome disadvantages of the cell-edge user due to its weak received signal, we fabricate a far NOMA user with multiple antennas to achieve performance improvement. In addition, the first scenario only considers a relay link deployed to forward signals to a far NOMA user, while both direct links and relay links are generally enabled to serve a far user in the second scenario. These situations, together with their outage performance, are analyzed and compared to provide insights in the design of a real-multiple-antenna NOMA network, in which the BS is also required to equip multiple antennas for robust quality of transmission. Higher complexity in computations is already known in consideration of outage metrics with respect to performance analysis, since the system model employs multiple antennas. To this end, we employ a transmit antenna selection (TAS) policy to formulate closed-form expressions of outage probability that satisfies the quality-of-service (QoS) requirements in the NOMA network. Our simulation results reveal that the performance of the considered system will be improved in cases of higher quantity of transmit antennas in dedicated devices. Finally, the proposed design in such a NOMA system cannot only ensure a downlink with higher quality to serve a far NOMA user, but also provide significant system performance improvement compared to a traditional NOMA networks using a single antenna.

1. Introduction

Recently, to deploy the next generation of wireless networks, one of the potential technologies referred to as a promising application in 5G is Non-Orthogonal Multiple Access (NOMA) [1,2,3]. With more advantages compared to Orthogonal Multiple-Access (OMA) schemes, NOMA allows a superior number of users to be connected to a wireless network concurrently [4]. Furthermore, cooperative NOMA is considered to be extended work, and it can be developed from traditional relaying networks [5,6,7,8] with a NOMA scheme. More specifically, outage performance is examined since the conditions of extended coverage and energy harvesting are guaranteed [6,7]. To investigate the further challenges in cooperative NOMA, a full-duplex (FD), together with device-to-device, is proposed for a cooperative NOMA scheme, as studied in [9], in which the outage performance can be enhanced with respect to satisfying the quality requirements of NOMA users. A decoding and forward relaying scheme was proposed, and two metrics, including the outage probabilities and average throughput of the paired users, are derived in closed-form [10]. To achieve wireless-powered NOMA, the degraded performance of NOMA as a result of the of inter-cell interference can be examined [11]. In particular, the authors in [12] showed the impacts of relay selection schemes in the analysis of physical-layer security for such a NOMA. In other system models, the concept of both downlink and uplink NOMA (termed as DU-CNOMA) is proposed, which considered system performance [13]. In [13], the authors investigated ergodic sum capacity, outage probability, and outage sum capacity. In [14], an optimum joint user and relay selection procedure was suggested to employ dual-hop transmission in cooperative NOMA networks, in which multiple Amplify-and-Forward (AF) relays forward signals from multiple users to two terminals. Other emerging trends need to be considered, i.e., the authors in [15] considered a two-tier heterogeneous network (HetNet) with non-uniform small cell deployment for cooperative NOMA to establish a NOMA-based HetNet model. In particular, critical performance metrics are analyzed, such as coverage probability and achievable rate.

More recently, when considering the random location of relay in NOMA systems, some stochastic geometry models can be applied for performance evaluation. For instance, in [16], to improve the security of a random network, large-scale NOMA systems were examined in terms of physical-layer security. In addition, the authors in [16] proposed a secured zone containing the source node. More specifically, the emerging techniques, including NOMA and energy harvesting, have been implemented for next generation wireless networks [17]. By allowing energy harvesting, the system maintains distinct power levels when the users commence NOMA transmissions [18]. It is worth noting that harvested energy is re-used for signal processing in a 3-phase scheme of energy-harvesting NOMA [19]. In particular, the authors in [19] presented the case in which the NOMA user harvests energy from the received downlink signals to further the process on the uplink, which leads to improving the average ergodic rate of the system. In recent work, a low-complexity iterative algorithm has been proposed to maximize the energy efficiency of the D2D pair in an energy harvesting-enabled device-to-device (D2D) NOMA [20]. The main result is that such a system is discovered in the case of the existence of D2D communications underlaying a NOMA-based cellular network while guaranteeing the quality of service of cellular users [20]. In other metrics of multi-objective resource optimization problems, simultaneous wireless information and power transfer, together with a NOMA cognitive radio (CR-NOMA) network, is investigated under a practical non-linear energy-harvesting model [21]. Furthermore, there is an information–energy trade-off in CR-NOMA, and the analytical results confirmed that CR-NOMA can outperform OMA if the channel power gains of users are sufficiently different [22].

In other trends of research on NOMA, multiple-input multiple-output (MIMO) is incorporated with NOMA to introduce a new scheme with favorable results [23,24,25,26]. In particular, a user-pairing algorithm classifying users into clusters is proposed. For instance, Ding et al. [23] and Al-Abbasi et al. [24] considered a multi-user MIMO downlink channel. The authors used a beamforming technique to avoid inter-cluster interference, whereas NOMA is used to manage intra-cluster interference. In [25], the authors developed a novel transceiver for the MIMO NOMA system and showed its efficiency in terms of power consumption. More general frameworks in NOMA technique using Successive Interference Cancellation (SIC) for MIMO systems are provided in [26]. It was assumed that the instantaneous channel state information (CSI) is available at the base station ($BS$). They also assumed that each user is equipped with several antennas equal to or higher than the number of antennas at the base station (BS) so that users can eliminate inter-cluster interference and manage intra-cluster interference using SIC. It was shown that NOMA enhances the performance of MIMO systems in terms of the spectrum efficiency and user fairness.

Regarding multiple-input single-output (MISO) NOMA systems, the authors in [27] recommended a sub-optimal precoding design for minimization of the transmit power. Regarding transmit antenna selection, the performance of MISO NOMA systems was presented in [28]. In [29], MIMO using a single carrier (SC) applied in NOMA systems is proposed to achieve a substantially higher spectral efficiency compared to the traditional MIMO SC-OMA systems, by exploiting the degrees of freedom (DoF) offered in both the spatial domain and the power domain. On the other hand, the application of NOMA to improve the fairness and spectrum use in multi-carrier (MC) systems was studied in [30,31,32]. In [30], to consider the weighted system throughput in single-antenna MC-NOMA systems, the authors developed a sub-optimal sub-carrier and power allocation algorithm. Optimal sub-carrier and power allocation algorithms for minimization of the total transmitted power and maximization of the weighted system throughput in MC-NOMA systems were proposed in [31,32], respectively. Most of the above works on NOMA systems have considered a single-antenna NOMA user. However, recent studies have shown that outage performance can be improved effectively in the spatial domain, if multiple antennas are used [33]. These recent analyses motivate us to consider situations where multiple antennas are deployed at the BS and destination. In particular, it is important to study outage performance regarding the multi-antenna NOMA user in cooperative NOMA networks.

Our main contributions are summarized as follows:

• Extending our previous work in terms of single-input single-output (SISO) NOMA strategy [17], we introduce a realistic scenario with multiple antennas which is equipped at the far NOMA user in the considered NOMA. This model also employs multiple-antenna BS. To provide the capability for energy harvesting, the near NOMA user can re-use the harvested power to serve the far NOMA user, who has a weaker channel condition. Two schemes are investigated with or without the existence of a direct link between the BS, and hence performance of far NOMA user is determined.
• We first examine outage performance at the near user, who has a single antenna. Then, we derive outage probability expressions for the near NOMA user and the outage comparison is exhibited with the far NOMA user. The number of deployed antennas or location arrangement of the BS, relay, and destination node are examined as crucial impacts on the considered outage performance.
• In addition, to extract further metrics and highlight the system behavior, throughput performance of these users is presented. Targeting the threshold signal-to-noise ratio (SNR), optimal throughput can be achieved via a numerical method. Such an evaluation is presented in the numerical results section.
• Our findings reveal that a higher number of transmit antennas at the BS provides a superior outage probability for both the near and far users compared to the traditional model. In addition, outage performance of the far NOMA user will be improved when increasing the number of its received antennas. Moreover, comparing the proposed multiple-antenna NOMA system with different locations of the user and energy-harvesting time, we provide detailed guidelines for the design of real cooperative NOMA, achieving better outage performance.

The rest of the paper is structured as follows. Section 2 describes the system model and antenna selection policy. Section 3 studies the outage performance and the throughput performance of NOMA with two proposed schemes, while Section 4 investigates the numerical results of the NOMA system. In particular, the numerical results are presented and Monte Carlo simulations are applied to verify the accuracy of the proposed analysis. Finally, Section 5 concludes the paper

Notation: This paper needs some main notations to easy considerations on following analysis: the Euclidean norm of the vector is $∥.∥$, $E\left\{.\right\}$ shows expectation computation; $f_X\left(.\right),F_X\left(.\right)$ denote the probability density function (PDF) and cumulative distribution function (CDF) of a random variable (RV) X, respectively. $P\left(.\right)$ is represented as probability operation. $E_n\left(.\right)$ stands for the exponential integrals function, $\Gamma \left(.\right)$ is the gamma function.

2. System Model

In this study, a cooperative cellular scenario deploying NOMA is considered with respect to performance evaluation for downlink as in Figure 1. Two transmission modes are introduced—direct and relay mode. In particular, the system model includes one base station ($BS$), which intends to transmit information to two NOMA mobile users with the help of a DF relay $D_1$ in relay mode to distant node $D_2$, but in direct mode $D_2$ can also receive the signal directly from the BS without assistance of relay. For robust and effective transmission, both source $BS$ and mobile user $D_2$ are equipped with many antennas. However, in this case only a single antenna is equipped for the relay node $D_1$ due to some disadvantages, such as small size and limited power. Relay is only provided by wireless power transfer scheme from the $BS$. In practice, relay is often installed at intermediate positions (outdoor). As a result, the construction of a power grid is hard, and hence wireless-powered relay needs to be designed. In particular, relay can perform signal processing and harvest energy, and such an energy signal can be extracted from the same received signal. In the context of energy harvesting, such a signal is transferred from the $BS$ via an RF signal transmission environment. It is noted that all the nodes operate in a half-duplex mode due to simple deployment. All the wireless links are assumed to exhibit frequency non-selective Rayleigh block fading, and additive white Gaussian noise (AWGN). For mathematical tractability, we restrict our attention primarily to transmit antenna selection (TAS) topology, in which such antenna selection criteria are required to enhance system performance with low cost of computations.

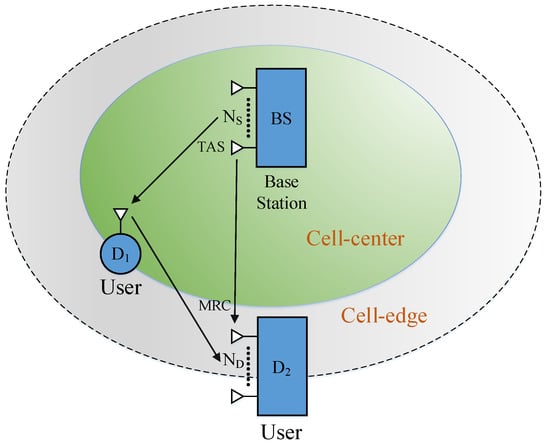
Figure 1. The proposed system model of NOMA facilitating multiple antennas at the $BS$ and cell-edge user.

In the concerned system, two scenarios are examined in this paper:

• Scheme I: The $BS$ intends to communicate with the far user $D_2$ under the assistance of the near user $D_1$. In this situation, $D_1$ is regarded as the relaying user and the DF protocol is employed to decode and forward information to $D_2$. A direct link does not exist between $BS$ and $D_2$.
• Scheme II: Under the existence of a direct link between $BS$ and $D_2$, a relay link is still employed to support $D_2$. As a result, a more complex process can be seen at the far NOMA user, as two signal streams are received. The question is of which scheme is suitable for application in such a NOMA network.

In this situation as Figure 1, $BS$ is equipped with $N_S$ transmit antennas while $D_2$ has $N_D$ received antennas. In the first phase, $BS$ transmits mixed-signal $x_S$ to $D_1$ and $BS$ employs a single antenna selected from given $N_S$ antennas. At $BS$, the transmit antenna, maximizing the instantaneous SNR at $D_1$, is selected for such transmission. Here, mixed-signal $x_S=\sqrt{a_1{P}_S}{x}_1+\sqrt{a_2{P}_S}{x}_2$ is a summation of the coded modulation symbol of the two NOMA users, where $a_i$, $i\in \left\{1,2\right\}$ are the power allocation coefficients to satisfy $a_1+a_2=1$, $P_S,P_R$ are transmit power at the $BS,D_1$, respectively. Without loss of generality, it is assumed that the effective channel gains are ordered to support the signal decoding operation of each NOMA user, and we assume that $a_2>a_1$. It can be assumed that the $N_S\times 1$ channel vector between $BS$ and $D_1$ is known as ${\mathbf{h}}_{S{D}_1}=\left[h_{1,1},\dots ,h_{1,i},\dots h_{1,N_S}\right]$ while link $BS$ and $D_2$ is modeled ${\mathbf{h}}_{S{D}_2}=\left[h_{0,1},\dots ,h_{0,j},\dots ,h_{0,N_D}\right]$, $i\in \left[1,N_S\right],j\in \left[1,N_D\right]$. In this case, we assume that Rayleigh fading channels are deployed in such a model, i.e., $h_{1,i}$, $h_{0,i}$ are selected to perform signal transmission from the $BS$ to $D_1$ in Scheme I and link $BS-D_2$, respectively; ${\mathbf{h}}_{D_2}$ characterizes for link from $D_1$ to $D_2$. We continue to denote the average channel power gains in links $BS-D_1,D_1-D_2,BS-D_2$ are modeled as ${\Omega }_1,{\Omega }_2,{\Omega }_0$. Interestingly, only $D_1$ can furnish the capability of wireless energy transfer [5,6], due to the lower load of signal processing required here. The main reason for this is that we intend to design a single antenna at relay $D_1$ to reduce the complex computation at the intermediate device.

Following from the principle of wireless power transfer to relay node $D_1$ in such NOMA, the relay can harvest the amount of energy from the multiple-antenna $BS$ and then the received power at the $D_1$ is given by [5,6]

$$P_R=\alpha \eta P_S{\left|h_{1,i}\right|}^2,$$

(1)

where $\alpha ,\eta$ are the percentage of time for energy harvesting in the whole time of frame processing and energy efficiency factor (depending on how effective the circuit can operate), respectively.

The received signal can be given at $D_1$ as

$$y_{D_1}=\sqrt{(1-\alpha )P_S}{h}_{1,i}\left(\sqrt{a_1{P}_S}{x}_1+\sqrt{a_2{P}_S}{x}_2\right)+n_{D_1},$$

(2)

where $n_{D_1}$ is denoted as AWGN noise with variance of ${\sigma }^2$ at node $D_1$. In the first computation, the received signal-to-interference-and-noise ratio (SINR) at $D_1$ to detect the $D_2$’s message $x_2$ is given by

$${\gamma }_{1i,D_1{x}_2}=\frac{(1-\alpha )P_S{\left|h_{1,i}\right|}^2{a}_2}{(1-\alpha )P_S{\left|h_{1,i}\right|}^2{a}_1+{\sigma }^2}.$$

(3)

In such NOMA, SIC will be carried out at the users. Therefore, the instantaneous SNR between the i-th antenna at $BS$ and $D_1$ can be derived to evaluate outage performance. Applying the principle of NOMA for Scheme I, SIC is employed at $D_1$. After SIC, the received SNR at $D_1$ to detect its own message $x_1$ is given by

$${\gamma }_{1i,D_1{x}_1}=\frac{(1-\alpha )P_S{\left|h_{1,i}\right|}^2{a}_1}{{\sigma }^2}.$$

(4)

Regarding the TAS scheme, we deploy an interesting policy of maximal SNR to improve system performance. In particular, the optimal transmit antenna selection is employed at relay link as below, and the index of the antenna is selected with respect to $x_2,x_1$ respectively as

$$i^{*}=arg\underset{1\le i\le N_S}{max}\left({\gamma }_{1i,D_1{x}_2}\right).$$

(5)

and

$$i^{*}=arg\underset{1\le i\le N_S}{max}\left({\gamma }_{1i,D_1{x}_1}\right).$$

(6)

3. Exact Outage and Throughput in Delay-Limited Mode of Two Proposed Schemes

3.1. Scheme I: NOMA Network without Direct Link between $BS$ and Far User $D_2$

The coexistence of near/far users and multiple/single antennas in NOMA systems is the main factor that results in varying performance for these users. For example, the performance of far users with poor channel conditions will be changed, and hence we improve the outage probability of them. It is worth noting that this multiple-antenna architecture at both the $BS$ and $D_2$ is suitable for practical situations, wherein the far users are much farther away from the BS in comparison with near users and thus the poor channel conditions need to be considered. We then examine outage probability of $D_1,D_2$ as below.

According to the NOMA protocol, the complementary events of outage at $D_1$ can be explained as: $D_1$ can detect $x_2$ as well as its own message $x_1$. From the above description, the outage probability of $D_1$ with respect to threshold SNRs for NOMA user $D_1,D_2$ (denoting ${\gamma }_{th1}$, ${\gamma }_{th2}$, respectively) and such outage probability can be expressed as below

$$\mathcal{O}{\mathcal{P}}_{1,x_1}=1-Pr\left({\gamma }_{1i,D_1{x}_2}>{\gamma }_{th2},{\gamma }_{1i,D_1{x}_1}>{\gamma }_{th1}\right),$$

(7)

where ${\gamma }_{th1}=2^{2R_1}-1$ with $R_1$ being the target rate at $D_1$ to detect $x_1$ and ${\gamma }_{th2}=2^{2R_2}-1$ with $R_2$ being the target rate at $D_2$ to detect $x_2$. It is rewritten in following formula

$$\begin{array}{cc}\hfill \mathcal{O}{\mathcal{P}}_{1,x_1}& =1-Pr\left(\underset{1\le i\le N_S}{\underbrace{max}}\left\{{\left|h_{1,i}\right|}^2\right\}>\xi \right)\hfill \\ & =\sum _{n=0}^{N_S}\left(\begin{array}{c}{N}_S\\ n\end{array}\right){\left(-1\right)}^{n}exp\left(-n\xi \right),\hfill \end{array}$$

(8)

where $\xi =max\left(\frac{{\gamma }_{th2}}{(1-\alpha ){\overline{\gamma }}_1\left(a_2-{\gamma }_{th2}{a}_1\right)},\frac{{\gamma }_{th1}}{(1-\alpha ){\overline{\gamma }}_1{a}_1}\right)$, ${\overline{\gamma }}_1=\frac{P_S{\Omega }_1}{{\sigma }^2}$. It is noted that (8) is derived on the condition of $a_2>a_1{\gamma }_{th2}$. In the second phase, $D_1$ first decodes the received source signal, and then forwards the detected symbol by using the harvested energy. We then compute SNR for second-hop $D_1-D_2$ transmission during the second phase and it is given by

$${\gamma }_{2i}=\frac{P_R{\left|\left|{\mathbf{h}}_{D_2}\right|\right|}_F^2}{{\sigma }^2}=\alpha \eta \frac{P_S}{{\sigma }^2}{\left|h_{1,i}\right|}^2{\left|\left|{\mathbf{h}}_{D_2}\right|\right|}_F^2.$$

(9)

In this case, the DF protocol is deployed at user $D_1$. Thus, when the i-th antenna at $BS$ is selected, the instantaneous SNR of end-to-end $BS-D_1-D_2$ link can be expressed as

$${\gamma }_{S{D}_1{D}_2}=min\left({\gamma }_{1i,D_1{x}_2},{\gamma }_{2i}\right).$$

(10)

Using several expressions of SNR as previous calculations, i.e., ${\gamma }_{1i,D_1{x}_2}=\frac{(1-\alpha )P_S{\left|h_{1,i}\right|}^2{a}_2}{(1-\alpha )P_S{\left|h_{1,i}\right|}^2{a}_1+{\sigma }^2}$, ${\gamma }_{2i}=\alpha \eta \frac{P_s}{{\sigma }^2}{\left|h_{1,i}\right|}^2{\left|\left|{\mathbf{h}}_{D_2}\right|\right|}_F^2$ we further compute an outage event related to $D_2$ to provide system performance analysis.

More specifically, the outage event of $D_2$ can be explained for two reasons. The first is that $D_1$ cannot detect $x_2$ . The second is that $D_2$ cannot detect its own message $x_2$ on the condition that $D_1$ can detect $x_2$ successfully. Based on this, the outage probability of $D_2$ can be expressed as below. In particular, the outage probability at the far user $D_2$ is given by

$$\begin{array}{cc}\hfill \mathcal{O}{\mathcal{P}}_{2,x_2}=& Pr\left({\gamma }_{1i,D_1{x}_2}<{\gamma }_{th2}\right)\hfill \\ & +Pr\left(min\left\{{\gamma }_{1i,D_1{x}_1},{\gamma }_{2i}\right\}<{\gamma }_{th2},{\gamma }_{1i,D_1{x}_2}>{\gamma }_{th2}\right).\hfill \end{array}$$

(11)

Next, it can be re-expressed by

$$\begin{array}{c}O{P}_{2,x_2}=Pr\left(\underset{1\le i\le N_S}{max}\left(\frac{(1-\alpha )P_S{\left|h_{1,i}\right|}^2{a}_2}{(1-\alpha )P_S{\left|h_{1,i}\right|}^2{a}_1+{\sigma }^2}\right)<{\gamma }_{th2}\right)\hfill \\ +Pr\left(\begin{array}{c}\underset{1\le i\le N_S}{max}min\left\{{\gamma }_{1i,D_1{x}_1},{\gamma }_{2i}\right\}<{\gamma }_{th2},\underset{1\le i\le N_S}{max}\left(\frac{(1-\alpha )P_s{\left|h_{1,i}\right|}^2{a}_2}{(1-\alpha )P_s{\left|h_{1,i}\right|}^2{a}_1+{\sigma }^2}\right)>{\gamma }_{th2}\hfill \end{array}\right)\hfill \end{array}.$$

(12)

To ease understanding, we divide the two components to compute independently as below $J_1,J_2$. It is worth noting that new denotation $J_1$ is given by

$$\begin{array}{cc}\hfill J_1& =Pr\left(\frac{(1-\alpha )P_S{\left|h_{1,i}\right|}^2{a}_2}{(1-\alpha )P_S{\left|h_{1,i}\right|}^2{a}_1+{\sigma }^2}<{\gamma }_{th2}\right)\hfill \\ & =\sum _{n=0}^{N_S}\left(\begin{array}{c}{N}_S\\ n\end{array}\right){\left(-1\right)}^{n}exp\left(-\frac{n{\gamma }_{th2}}{\left(a_2-a_1{\gamma }_{th2}\right){\overline{\gamma }}_1(1-\alpha )}\right)\hfill \end{array}.$$

(13)

Lemma 1.

It can be expressed the following outage event as

$$J_2=Pr\left\{\underset{1\le i\le N_S}{max}min\left\{{\gamma }_{1i,D_1{x}_1},{\gamma }_{2i}\right\}<{\gamma }_{th2}\right\}.$$

(14)

And it is shown in the closed-form expression as

$$\begin{array}{cc}\hfill J_2& =1-\frac{N_S{\gamma }_{th}}{{\overline{\gamma }}_1\left(1-\alpha \right)}\sum _{n=0}^{N_S-1}\left(\begin{array}{c}{N}_S-1\\ n\end{array}\right)\sum _{m=0}^{N_D-1}\sum _k^{\infty }\frac{{(-1)}^{k+n}}{m!k!}\hfill \\ & \times {\left(\frac{1-\alpha }{\alpha \mu {\Omega }_2}\right)}^{m+k}{\mathrm{E}}_{m+k}\left(\frac{{\gamma }_{th}\left(n+1\right)}{(1-\alpha ){\overline{\gamma }}_1}\right).\hfill \end{array}$$

(15)

Proof. 

See in Appendix A. □

Finally, by applying Lemma 1, we obtain the outage probability for signal $x_2$ at $D_2$ as

$$\mathcal{O}{\mathcal{P}}_{2,x_2}=J_1+J_2\left(1-J_1\right),$$

(16)

where $J_1$, $J_2$ are calculated as previous steps.

3.2. Scheme II: NOMA with Presence of Direct Link between $BS$ and Far User $D_2$

In this scenario, extending signal gained at relaying link, the $BS$ intends to serve directly $D_2$ based on selected antenna at index j, $h_{0,j}$. In particular, the observation on the received signal at $D_2$ for the direct link can be written as

$${\mathbf{y}}_{D_2}={\mathbf{h}}_{0,j}\left(\sqrt{a_1{P}_S}{x}_1+\sqrt{a_2{P}_S}{x}_2\right)+{\mathbf{n}}_{D_2}.$$

(17)

where ${\mathit{n}}_{D_2}$ is noise matrix at $D_2$ following AWGN .

Similarly, the instantaneous SINR between transmitter on the j-th antenna at $BS$ and $D_2$ during the first phase can be expressed as below. The received SINR at $D_2$ to detect $x_2$ is given by

$${\gamma }_{0j,D_2{x}_2}=\frac{P_S{\left|\left|{\mathbf{h}}_{0,j}\right|\right|}_F^2{a}_2}{P_S{\left|\left|{\mathbf{h}}_{0,j}\right|\right|}_F^2{a}_1+{\sigma }^2}.$$

(18)

Due to existence of the relaying link, $D_2$ has two links to achieve a composed signal. More importantly, to reduce the implementation cost of the system, we adopt the TAS policy at $BS$ and the selection-combining technique at $D_2$ to combine the direct signal and the relaying signal. Thus, the instantaneous end-to-end SNR of the system with the j-th antenna selected at $BS$ is derived as

$${\gamma }_{e,j^{*}}=max({\gamma }_{0j,D_2{x}_2},{\gamma }_{S{D}_1{D}_2}).$$

(19)

Then, the general expression to examine outage performance at $D_2$ is given by

$$\mathcal{O}{\mathcal{P}}_{2,x_2}=Pr({\gamma }_{e,j^{*}}<{\gamma }_{th2}).$$

(20)

Based on obtained expressions of SNR, it can be achieved that

$$\mathcal{O}{\mathcal{P}}_{2,x_2}=\mathrm{Pr}\left(\underset{1\le i\le N_S}{\underbrace{max}}max\left\{{\gamma }_{0i,D_2{x}_2},min\left\{{\gamma }_{1i,D_1{x}_1},{\gamma }_{2i}\right\}\right\}<{\gamma }_{th2}\right).$$

(21)

Proposition 1.

The outage probability for $D_2$ in Scheme II can be expressed by

$$\begin{array}{cc}\hfill \mathcal{O}{\mathcal{P}}_{2,x_2}& ={\left[1-\frac{1}{\Gamma \left(N_D\right)}\Gamma \left(N_D,\frac{\frac{{\gamma }_{th2}}{a_2-a_1{\gamma }_{th2}}}{{\overline{\gamma }}_0}\right)\right]}^{N_S}\hfill \\ & \times \left[1-\frac{N_S{\gamma }_{th2}}{\left(1-\alpha \right)a_1{\overline{\gamma }}_1}\sum _{n=0}^{N_S-1}\left(\begin{array}{c}{N}_S-1\\ n\end{array}\right)\sum _{m=0}^{N_D-1}\sum _k^{\infty }\frac{{(-1)}^{k+n}}{m!k!}\right.\hfill \\ & \left.\times {\left(\frac{\left(1-\alpha \right)a_1}{\alpha \mu {\Omega }_2}\right)}^{m+k}{\mathrm{E}}_{m+k}\left(\frac{{\gamma }_{th2}\left(n+1\right)}{(1-\alpha )a_1{\overline{\gamma }}_1}\right)\right].\hfill \end{array}$$

(22)

where ${\overline{\gamma }}_0=\frac{P_S{\Omega }_0}{{\sigma }^2}$

Proof. 

See in Appendix B. □

Remark 1.

Such outage performance exhibits optimal value for consideration on varying time-splitting allocation for the function of energy harvesting. However, due to the complexity in the derived expressions of these outage probabilities, exact expressions of such optimal time to achieve lowest outage performance cannot be found. Fortunately, we can show the optimal time-splitting coefficient by exploiting numerical methodology. In addition, from such a derived formula, it is worth noting that the transmit SNR at the BS and the target rates are the main factors affecting outage performance. This can be verified in numerical results section.

To further the comparison, we consider a special case where such a network only contains a direct link. It is based on obtained SNR ${\gamma }_{0j,D_2{x}_2}=\frac{P_S{\left|\left|{\mathbf{h}}_{\mathbf{0},\mathit{j}}\right|\right|}_F^2{a}_2}{P_S{\left|\left|{\mathbf{h}}_{\mathbf{0},\mathit{j}}\right|\right|}_F^2{a}_1+{\sigma }^2}$, and by performing SIC at destination $D_2$, we have SNR to detect $x_1$.

$${\gamma }_{0j,D_2{x}_1}=\frac{P_S{\left|\left|{\mathbf{h}}_{0,j}\right|\right|}_F^2{a}_1}{{\sigma }^2}.$$

(23)

However, we only examine the outage probability for $D_2$ as detecting signal $x_1$

$$\begin{array}{cc}\hfill \mathcal{O}{\mathcal{P}}_{3,x_1}& =Pr\left({\gamma }_{0j,D_2{x}_1}<{\gamma }_{th2}\right)\hfill \\ & ={\left[1-\frac{1}{\Gamma \left(N_D\right)}\Gamma \left(N_D,\frac{{\gamma }_{th2}}{a_1{\overline{\gamma }}_0}\right)\right]}^{N_S}.\hfill \end{array}$$

(24)

3.3. Throughput Performance

For the delay-limited transmission mode, the source $BS$ transmits at a constant rate $R_1=\frac{1}{2}log\left(1+{\gamma }_{th1}\right)$ and $R_2=\frac{1}{2}log\left(1+{\gamma }_{th2}\right)$ corresponding requirement of each signal $x_1,x_2$, which may be subjected to outage due to fading. Hence the average throughput can be expressed as

$${\tau }_{k,x_l}=\left(1-\mathcal{O}{\mathcal{P}}_{n,x_l}\right)R_l,$$

(25)

where $n=\left\{1,2,3\right\}$ and $l=\left\{1,2\right\}$

Remark 2.

We firstly recall among many promising strategies to exploit multiple antennas in NOMA, TAS has widely been used in the traditional (MIMO) NOMA systems. In such a TAS scheme, there is excellent performance with full diversity, and it is simple to implement. Secondly, from the derived expressions here, the number of transmit and receive antennas contributes to a smaller outage value and exhibits outage performance with expected improvement. Furthermore, an extra advantage of TAS is that it requires only very low feedback signaling overhead.

4. Numerical Results

In this section, it is assumed that the BS, the near NOMA user (relay), and the far NOMA user are located in approximate a straight line. We denote $d_0$ as the distance between $BS$ and $D_2$, $d_1$ as the distance between $BS$ and $D_1$, and $d_2$ as the distance between $D_1$ and the $D_2$. To ease computation, the distance between $BS$ and the NOMA users is normalized with a factor m as $d_1+d_2=5\mathrm{m}$. Furthermore, we can obtain ${\Omega }_0={\left(1+d_0^z\right)}^{-1}$, ${\Omega }_1={\left(1+d_1^z\right)}^{-1}$ and ${\Omega }_2={\left(1+d_2^z\right)}^{-1}$, where z is denoted as the path-loss exponent. Here, $z=2$. The time-switching factor for the energy-harvesting phase is $\alpha =0.5$ and energy conversion efficiency $\eta =1$. To satisfy requirements of QoS for each NOMA user, we set $R_1=R_2$ = 0.5 bps/Hz.

In Figure 2, we illustrate the outage performance versus transmit SNR at the $BS$. There is an excellent agreement between the exact analytical results and the simulations observed, and the performance gap of two users $D_1,D_2$ can be raised significantly across the whole range of SNR. Most important is that the system outage performance can be improved significantly by increasing the number of antennas at the BS while the relay node has a single antenna. Moreover, it reveals that the outage performance of user $D_2$ is worse than that of $D_1$. The main reason for this is that a lower amount of transmit power at the relay for signal processing second-hop $D_1-D_2$ results in deceasing the outage performance of the second hop, and the total outage performance of two-hop transmission link falls as well. To show the impact of the number of received antennas at the far NOMA user, we perform a similar simulation to Figure 3. In this case, we keep the number of transmit antennas at the $BS$ as $N_S=2$, then the outage performance will be enhanced with an increasing number of received antennas at $D_2$. It is shown that $N_S=2,N_D=3$ exhibits the best performance of $D_2$ among three illustrated cases. Please note that two NOMA users have different power allocation factors. Since NOMA allocates different power allocation factors for two NOMA users, then it is the existence of performance gap between the two NOMA users.

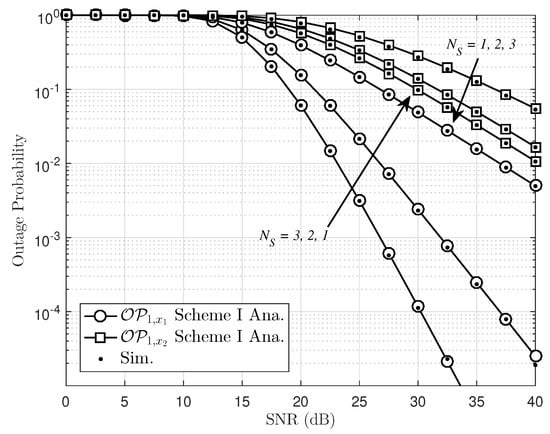
Figure 2. Outage probability of Scheme I with different numbers of transmit antennas at the $BS$, $N_D=1$, $d_1=2\mathrm{m}$, $d_2=3\mathrm{m}$, $a_1=0.2$ and $a_2=0.8$.

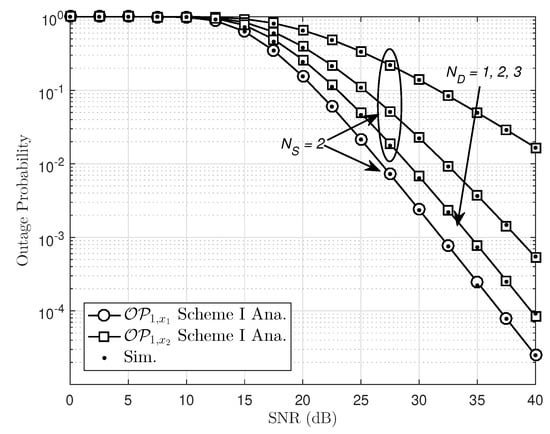
Figure 3. Outage probability of Scheme I with different $N_D$, $N_S=2$, $d_1=2\mathrm{m}$, $d_2=3\mathrm{m}$, $a_1=0.2$ and $a_2=0.8$.

In Figure 4, we present the outage performance by varying the number of transmit antennas at $BS$. We compare three cases of Scheme II as fixed single antenna at $D_2$, i.e., $N_D=1$. It can be observed that with more transmit antennas at the $BS$, the outage performance will be improved. It confirms that the direct link in Scheme II has outage performance worse than the combined scheme, in which relay and direct link join to serve the far NOMA user. Furthermore, we compare these cases of such proposed NOMA relaying networks, and the worst performance can be seen with a conventional single-antenna NOMA, i.e., $N_S=N_D=1$.

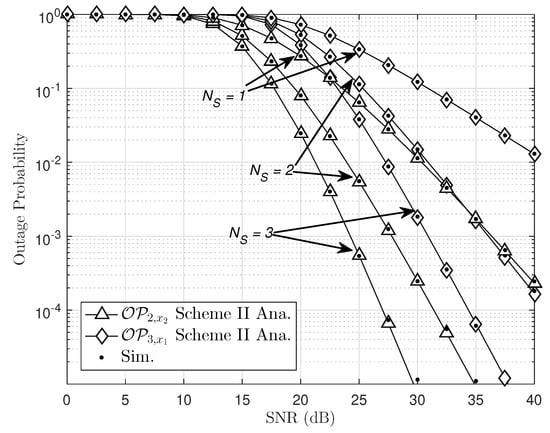
Figure 4. Outage probability of schemes II with different number of antennas $N_S$, $N_D=1$, $d_1=2\mathrm{m}$, $d_2=3\mathrm{m}$, $a_1=0.2$ and $a_2=0.8$.

In Figure 5, the impact number of received antennas at $D_2$ on outage performance can be illustrated by keeping a fixed number of transmit antennas at the $BS$, i.e., $N_S=2$. It can be confirmed that the highest number of transmit/receive antennas at the $BS,D_2$ provide the best outage performance. As a result, it shows the advantage of multiple antennas assigned to proper users. Besides, energy harvesting is reasonable when facing the energy shortage situation at $D_1$. By employing the time-switching factor $\alpha =0.5$ in the energy-harvesting approach, outage performance will be satisfied as multiple antennas are provided.

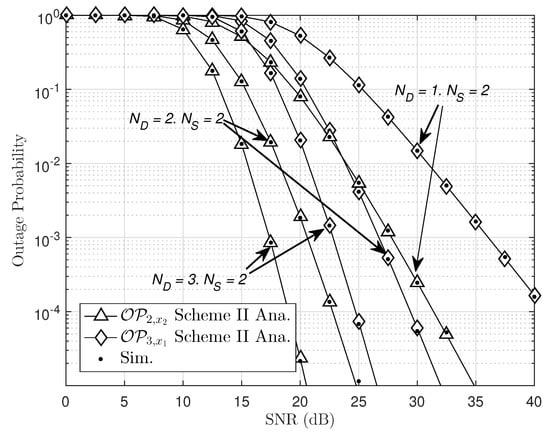
Figure 5. Outage probability of Scheme II with different $N_D$, $N_S=2$, $d_1=2\mathrm{m}$, $d_2=3\mathrm{m}$, $a_1=0.2$ and $a_2=0.8$.

In Figure 6, we compare two schemes in terms of outage performance. The first observation is that the best outage performance at $D_1$ in single-antenna NOMA. The worst performance can be raised at $D_2$ in Scheme I as only the relay link is implemented. It can be seen clearly that outage performance at $D_2$ in Scheme II is better than that in Scheme I. In the case of multiple antennas assigned at the $BS,D_2$, performance of $D_2$ can be improved significantly. In particular, outage probability at $D_2$ when $N_S=N_D=4$ is the best case among the four simulated curves. It reveals that multiple antennas at the far NOMA user contribute to outage improvement.

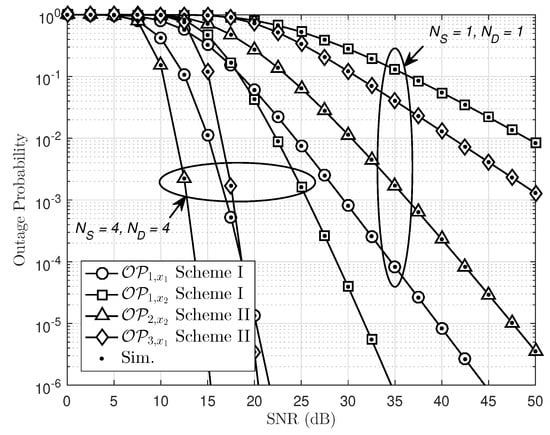
Figure 6. Comparison study on outage probability between Scheme I and Scheme II with $d_1=2\mathrm{m}$, $d_2=3\mathrm{m}$, $a_1=0.2$ and $a_2=0.8$.

In Figure 7, we present the outage performance by varying the location of the relay $D_1$. It is noted that the curve showing outage performance of only the direct link in Scheme II is not affected by varying such distance $d_1$. Three users have different optimal relay locations, while outage performance of $D_2$ is slightly changed in the considered range of distance $d_1$. The most important observation is that the outage performance of $D_1$ falls significantly at locating $D_1$ far from the $BS$. Since NOMA allocates less transmit power to the users with better channel conditions, the optimal relay location for the user with better channel conditions should be nearer to $BS$ to achieve its high SNR. It confirms that optimal location arrangement plays an important role in the remaining outage performance at an acceptable level.

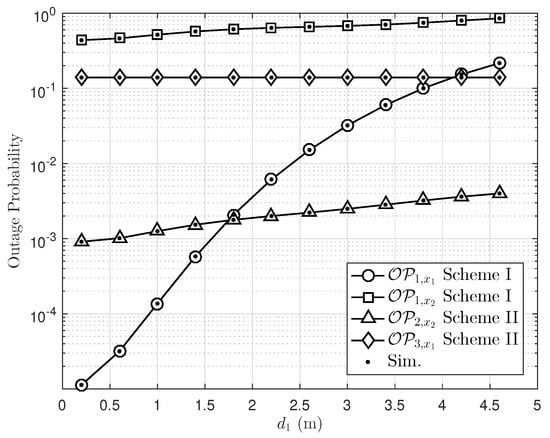
Figure 7. The impact of relay location on outage probability with $N_S=2$, $N_D=2$, $P_S=20$ dB, $a_1=0.2$ and $a_2=0.8$.

Next, we further examine how the time-switching factor of energy-harvesting policy affects outage performance, as in Figure 8. In this case, the special case of Scheme II, the direct link between the $BS$ and $D_2$ is not supported by wireless power charge, and hence outage performance here is constant. Interestingly, optimal outage performance of $D_2$ can be seen at approximately $\alpha =0.65$ for both schemes, while when changing time-switching factor in energy harvesting $\alpha =0.1$ to $\alpha =0.9$ we obtain higher power at $D_1$, which can harvest wireless energy. However, the remaining time for signal processing is inversely proportion to the time allocated for energy harvesting. The main reason is that a small amount of time for energy harvesting corresponding to a larger amount of time for signal processing at the first hop $BS-D_1$ causes better outage performance of $D_1$, and the best case occurs at around $\alpha =0.1$.

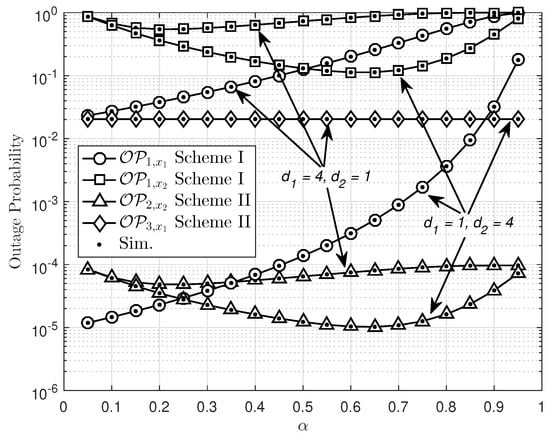
Figure 8. Outage probability versus the power-splitting ratio $\alpha$ with $N_S=2$, $N_{\mathrm{D}}=3$, $P_S=20$ dB, $a_1=0.2$ and $a_2=0.8$.

In Figure 9, we present the throughput performance by varying the threshold rate ${\gamma }_{th1}={\gamma }_{th2}={\gamma }_{th}$. It is noted that the highest curve showing throughput performance of $D_2$ is in Scheme II at set values $N_S=N_D=4$. However, throughput will be decreased at a high threshold rate. A higher number of transmit antennas at the $BS$ and receive antennas at $D_2$ leads to improved throughput performance, and they can be affordable with higher threshold data rates. Once again, we proved that multiple antennas design leads to system performance improvement.

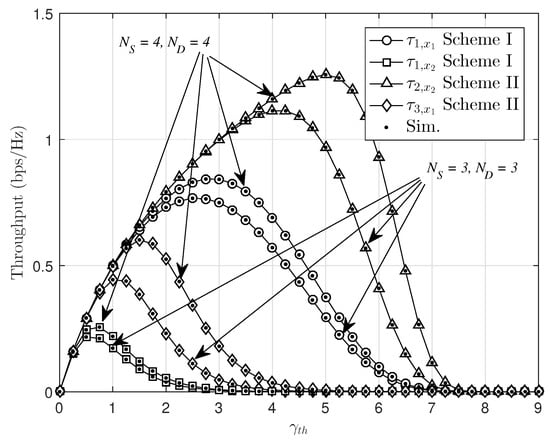
Figure 9. Impact of outage threshold on the throughput with transmit SNR at source $SNR=20dB$, $d_0=5$ m, $d_1=3\mathrm{m}$, $d_2=2\mathrm{m}$, $a_1=0.1$ and $a_2=0.9$.

5. Conclusions

In this paper, we studied the impact of the number of transmit antennas at $BS$ on outage performance in a multiple-antenna NOMA. In this paper, we compare two schemes related to the existence or non-existence of direct link between the $BS$ and the far NOMA user. It is confirmed that optimal TAS policy deployed in this paper helps to improve performance in such a NOMA since multiple antennas lead to higher diversity order compared to single-antenna NOMA system. Simulation results revealed that the considered multiple-antenna NOMA system employing energy harvesting and a TAS scheme can achieve significantly higher performance than many situations of such systems. Furthermore, our results confirmed the robustness of the proposed scheme can be seen with respect to varying distance of these nodes, time-switching factors for energy harvesting, number of antennas at both the $BS$, and the far NOMA user. There are, intuitively, results can improve the performance of the far NOMA user, when considering and selecting various appropriate system parameters to achieve performance improvement.