GPU Acceleration and Game Engines for Wireless Channel Estimation in Millimeter Waves
Abstract
:1. Introduction
2. Materials and Methods
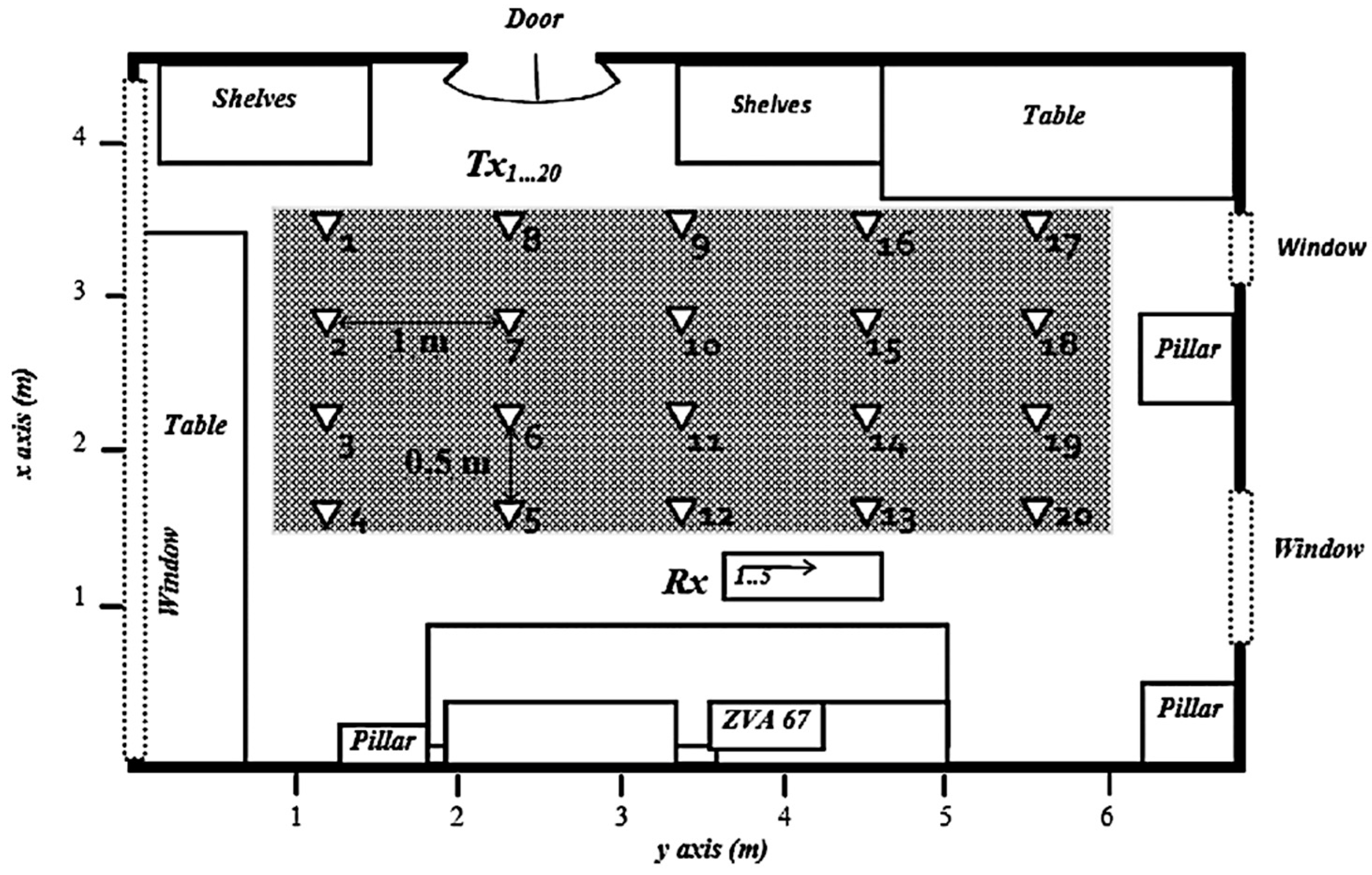
2.1. Description of the Test Scenario
2.2. Channel Modeling
2.3. Ray Propagation
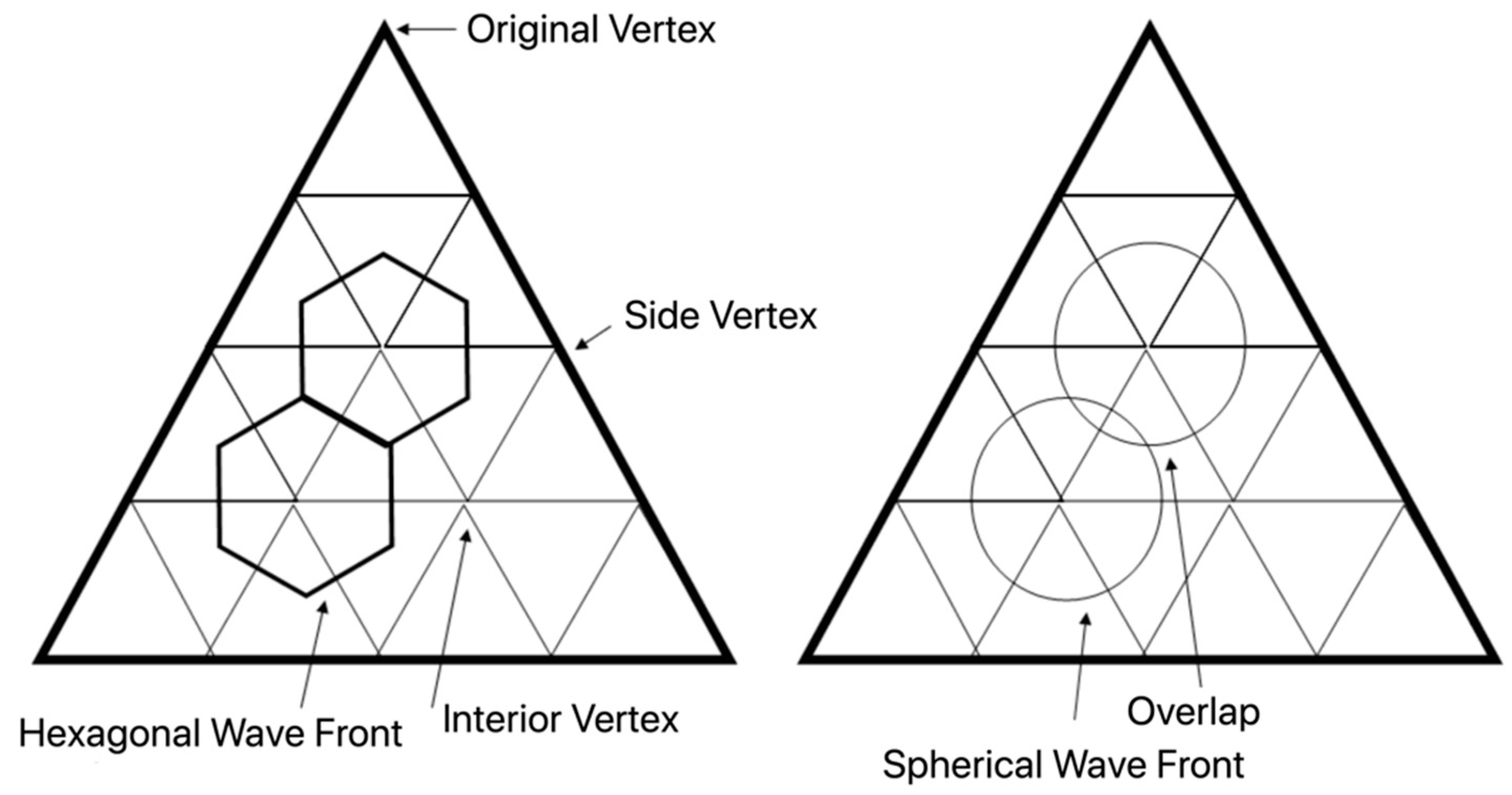
2.4. Launch Algorithm
2.5. Reception Algorithm
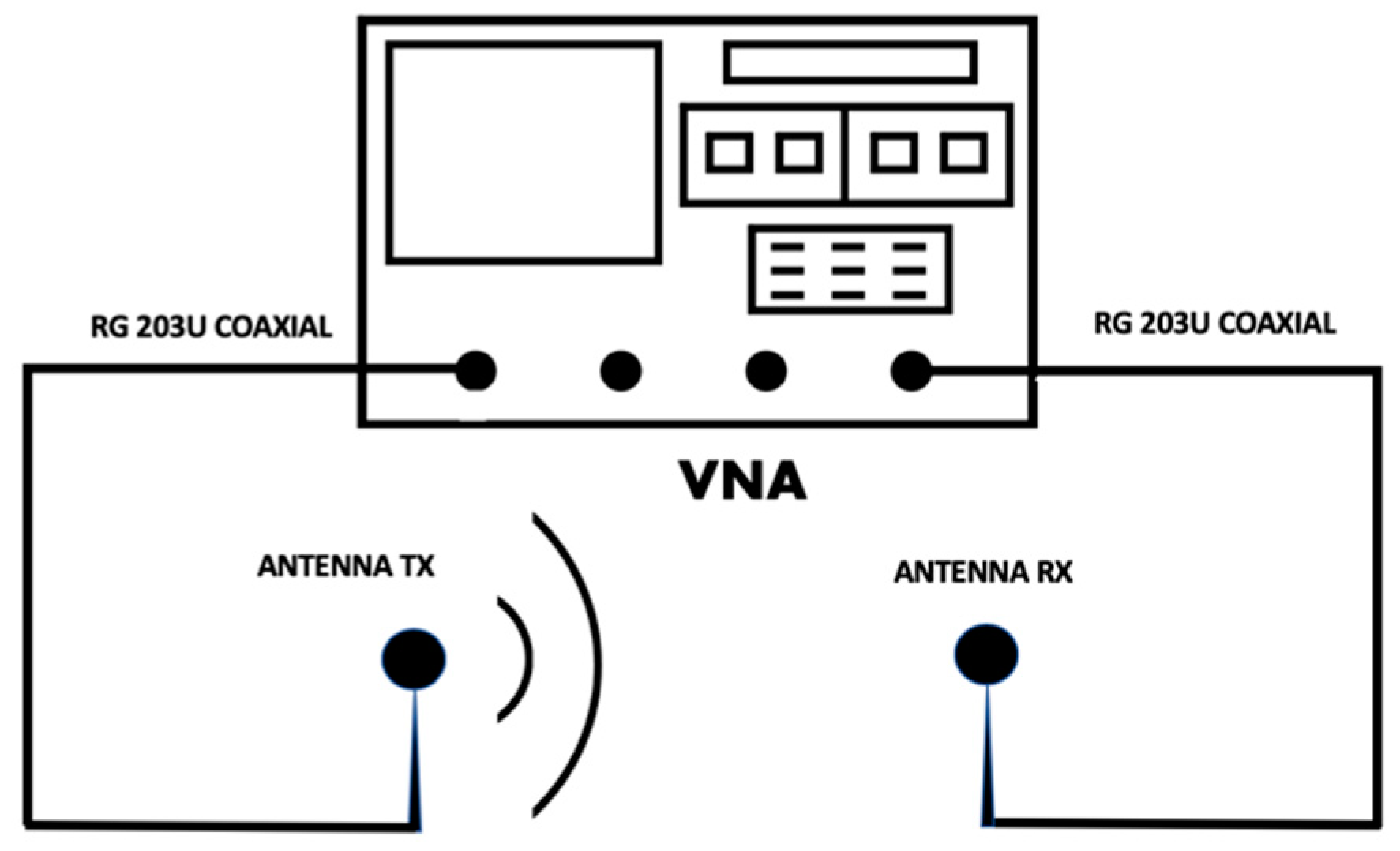
2.6. Hardware Acceleration
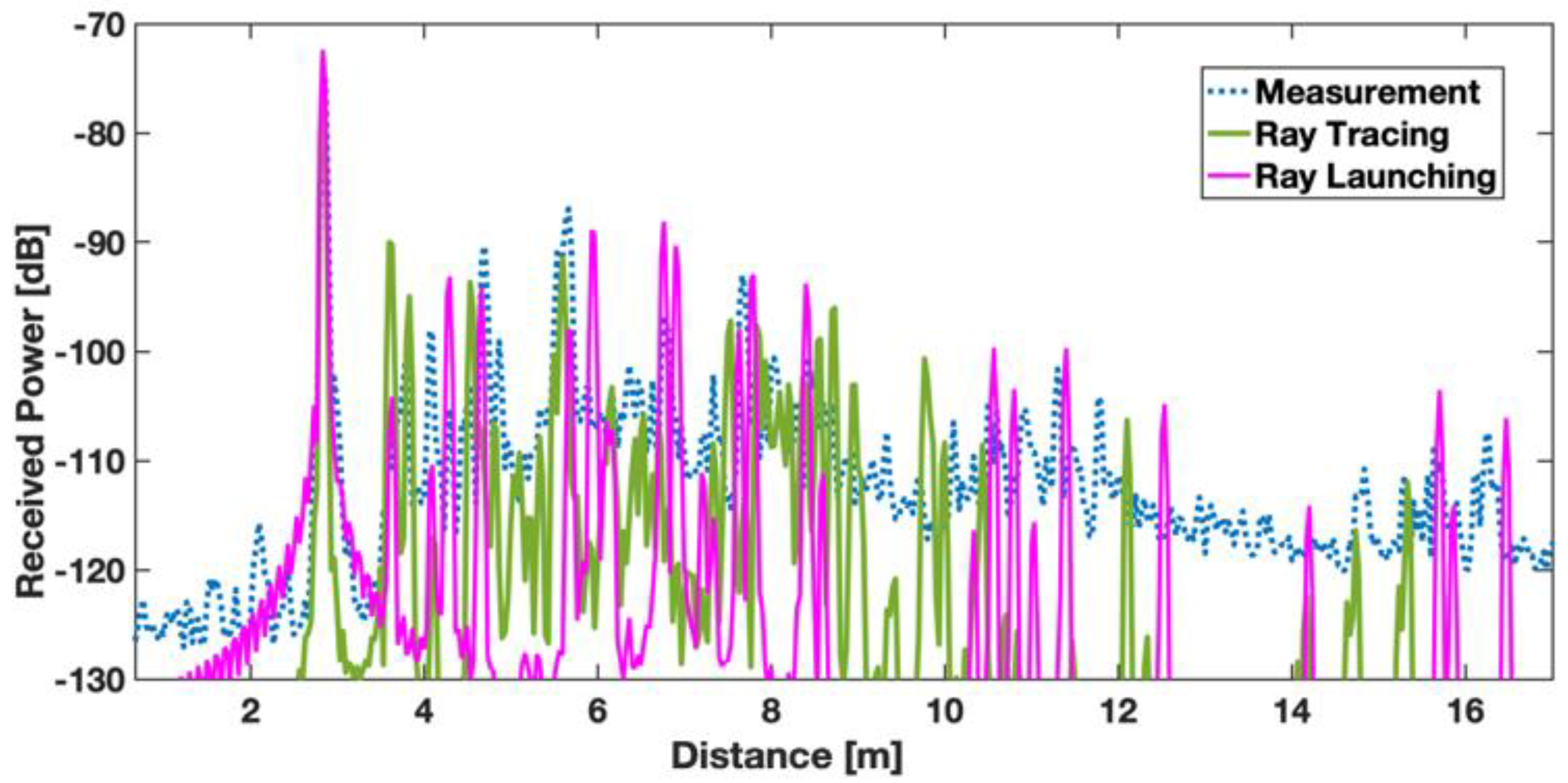
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Calabuig, J.; Monserrat, J.F.; Gomez-Barquero, D. 5th Generation Mobile Networks: A New Opportunity for the Convergence of Mobile Broadband and Broadcast Services. IEEE Commun. Mag. 2015, 53, 198–205. [Google Scholar] [CrossRef]
- Fettweis, G.; Alamouti, S. 5G: Personal mobile internet beyond what cellular did to telephony. IEEE Commun. Mag. 2014, 52, 140–145. [Google Scholar] [CrossRef]
- International Wireless Industry Consortium (IWPC), Evolutionary & Disruptive Visions Towards Ultra High Capacity Networks. Available online:https://www.iwpc.org (accessed on 1 July 2019).
- Gupta, A.; Jha, R.K. A Survey of 5G Network: Architecture and Emerging Technologies. IEEE Access 2015, 3, 1206–1232. [Google Scholar] [CrossRef]
- Chandrasekhar, V.; Andrews, J.G.; Gatherer, A. Femtocell Networks: A Survey. IEEE Commun. Mag. 2008, 46, 59–67. [Google Scholar] [CrossRef]
- Thompson, J.; Ge, X.; Wu, H.-C.; Irmer, R.; Jiang, H.; Fettweis, G.; Alamouti, S. 5G Wireless Communication Systems: Prospects and Challenges. IEEE Commun. Mag. 2014, 52, 62–64. [Google Scholar] [CrossRef]
- Busari, S.A.; Mumtaz, S.; Al-Rubaye, S.; Rodríguez, J. 5G Millimeter-Wave Mobile Broadband: Performance and Challenges. IEEE Commun. Mag. 2018, 56, 137–143. [Google Scholar] [CrossRef]
- Ni, Y.; Liang, J.; Shi, X.; Ban, D. Research on key technology in 5G mobile communication network. In Proceedings of the 2019 International Conference on Intelligent Transportation, Big Data & Smart City (ICITBS), Changsha, China, 12–13 January 2019. [Google Scholar]
- Degli-Esposti, V. Ray Tracing propagation modelling: Future prospects. In Proceedings of the 8th European Conference on Antennas and Propagation (EuCAP 2014), The Hague, The Netherlands, 6–11 April 2014. [Google Scholar]
- Rao, C.V.K.P. Signal modeling with stochastic and deterministic data: A lossless inverse scattering approach. In Proceedings of the ICASSP-88., International Conference on Acoustics, Speech, and Signal Processing, New York, NY, USA, 11–14 April 1988. [Google Scholar]
- Key, C.; Troksa, B.; Kunkel, F.; Savic, S.V.; Ilic, M.M.; Notaros, B.M. Comparison of three sampling methods for shooting-bouncing ray tracing ssing a simple waveguide model. In Proceedings of the 2018 IEEE International Symposium on Antennas and Propagation & USNC/URSI National Radio Science Meeting, Boston, MA, USA, 8–13 July 2018. [Google Scholar]
- Martinez-Ingle, M.-T.; Pascual-García, J.; Rodríguez, J.-V.; Molina-Garcia-Pardo, J.-M.; Juan-Llácer, L.; Gaillot, D.P.; Liénard, M.; Degauque, P. Indoor radio channel characterization at 60 GHz. In Proceedings of the 2013 7th European Conference on Antennas and Propagation (EuCAP), Gothenburg, Sweden, 8–12 April 2013. [Google Scholar]
- Martinez-Ingles, M.-T.; Gaillot, D.P.; Pascual-Garcia, J.; Molina-Garcia-Pardo, J.-M.; Lienard, M.; Rodriguez, J.-V. Deterministic and Experimental Indoor mmW Channel Modeling. IEEE Antennas Wirel. Propag. Lett. 2014, 13, 1047–1050. [Google Scholar] [CrossRef]
- Zhu, M.; Singh, A.; Tufvesson, F. Measurement based ray launching for analysis of outdoor propagation. In Proceedings of the 2012 6th European Conference on Antennas and Propagation (EUCAP), Prague, Czech Republic, 26–30 March 2012. [Google Scholar]
- Lai, Z.; Bessis, N.; de LaRoche, G.; Song, H.; Zhang, J.; Clapworthy, G. An intelligent ray launching for urban prediction. In Proceedings of the 2009 3rd European Conference on Antennas and Propagation, Berlin, Germany, 23–27 March 2009. [Google Scholar]
- Weng, J.; Tu, X.; Lai, Z.; Salous, S.; Zhang, J. Modelling the mmWave channel based on intelligent ray launching model. In Proceedings of the 2015 9th European Conference on Antennas and Propagation (EuCAP), Lisbon, Portugal, 13–17 April 2015. [Google Scholar]
- Durgin, G.; Patwari, N.; Rappaport, T.S. An advanced 3D ray launching method for wireless propagation prediction. In Proceedings of the 1997 IEEE 47th Vehicular Technology Conference, Phoenix, AZ, USA, 4–7 May 1997. [Google Scholar]
- Lu, W.; Chan, K. Advanced 3D Ray Tracing Method for Indoor Propagation Prediction. Electron. Lett. 1998, 34, 1259–1260. [Google Scholar] [CrossRef]
- Navarro, A.; Guevara, D.; Gomez, J. A Proposal to Improve Ray Launching Techniques. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 143–146. [Google Scholar] [CrossRef]
- Liang, G.; Bertoni, H. A New Approach to 3-D Ray Tracing for Propagation Prediction in Cities. IEEE Trans. Antennas Propag. 1998, 46, 853–863. [Google Scholar] [CrossRef]
- Navarro, A.; Guevara, D.; Cardona, N.; Gomez, J. Heuristic UTD Coefficients for Delay Spread Prediction in an Indoor Scenario. In Proceedings of the 11th European Conference on Antennas and Propagation (EUCAP), Paris, France, 19–24 March 2017. [Google Scholar]
- Chen, S.-H.; Jeng, S.-K. An SBR/Image Approach for Radio Wave Propagation in Indoor Environments with Metallic Furniture. IEEE Trans. Antennas Propag. 1997, 45, 98–106. [Google Scholar] [CrossRef]
- Yun, Z.; Iskander, M.F. Ray Tracing for Radio Propagation Modeling: Principles and Applications. IEEE Access 2015, 3, 1089–1100. [Google Scholar] [CrossRef]
- Schneider, C.; Sommerkorn, G.; Narandzic, M.; Kaske, M.; Hong, A.; Algeier, V.; Kotterman, W.A.T.; Thoma, R.S.; Jandura, C. Multi-user MIMO channel reference data for channel modelling and system evaluation from measurements. In Proceedings of the 2009 International ITG Workshop on Smart Antennas, Berlin, Germany, 16–18 February 2009. [Google Scholar]
- Rautiainen, T.; Wolfle, G.; Hoppe, R. Verifying path loss and delay spread predictions of a 3D ray tracing propagation model in urban environment. In Proceedings of the IEEE 56th Vehicular Technology Conference, Vancouver, BC, Canada, 24–28 September 2002. [Google Scholar]
- Navarro, A.; Guevara, D.; Gomez, J. Prediction of delay spread using ray tracing and game engine based on measurement. In Proceedings of the 2015 IEEE 81st Vehicular Technology Conference (VTC Spring), Glasgow, UK, 11–14 May 2015. [Google Scholar]

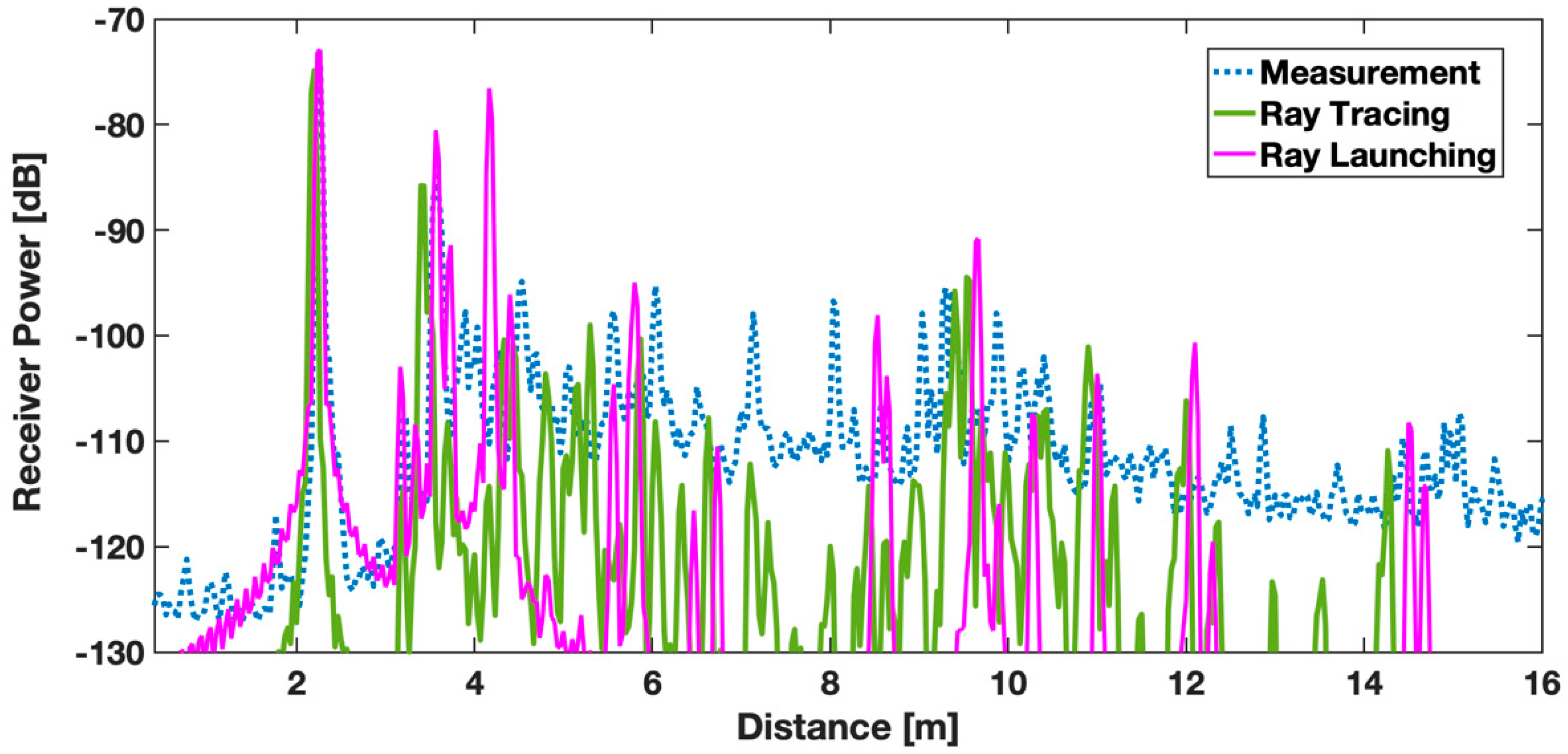
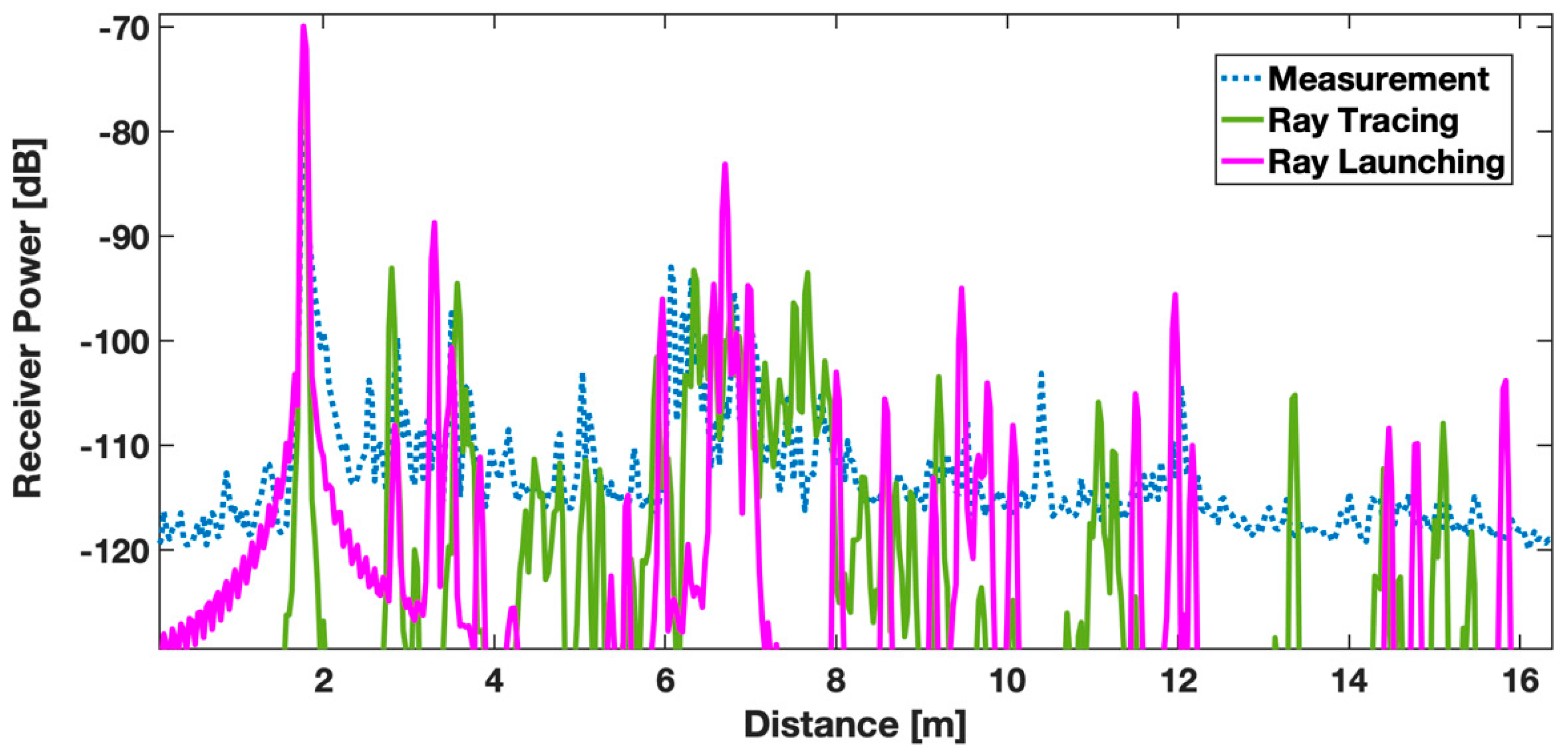
| Element | Relative Permittivity | Conductivity (S/m) |
|---|---|---|
| Floor and Columns | 6.5–0.43i | 1.43 |
| Walls and Drop-Down Ceiling | 2.81–0.046i | 0.15 |
| Furniture | 1.54–0.095i | 0.32 |
| Metal | 1 | 1 |
| Glass | 6.94–0.176i | 0.59 |
| RMS [ns] | |||||
| Position | Measure | Tracer | % | Launcher | % |
| 3 | 4.22 | 4.41 | 95.5 | 3.92 | 92.9 |
| 7 | 3.77 | 3.52 | 93.4 | 4.05 | 92.57 |
| 18 | 4.32 | 3.70 | 83.2 | 3.81 | 88.2 |
| Medium Delay [ns] | |||||
| Position | Measure | Tracer | % | Launcher | % |
| 3 | 11.22 | 11.01 | 98.1 | 10.7 | 89 |
| 7 | 6.90 | 6.70 | 97.0 | 6.92 | 99.7 |
| 18 | 8.98 | 8.26 | 91.3 | 9.76 | 91.3 |
| PL [dB] | |||||
| Position | Measure | Tracer | Dif. | Launcher | Dif. |
| 3 | 71 | 74 | 3 | 69.7 | 1.3 |
| 7 | 72 | 70 | 2 | 67.2 | 4.8 |
| 18 | 71 | 72 | 1 | 67.88 | 2.12 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gomez-Rojas, J.; Guevara, D.; Navarro, A.; Pascual-Garcia, J. GPU Acceleration and Game Engines for Wireless Channel Estimation in Millimeter Waves. Electronics 2019, 8, 1121. https://doi.org/10.3390/electronics8101121
Gomez-Rojas J, Guevara D, Navarro A, Pascual-Garcia J. GPU Acceleration and Game Engines for Wireless Channel Estimation in Millimeter Waves. Electronics. 2019; 8(10):1121. https://doi.org/10.3390/electronics8101121
Chicago/Turabian StyleGomez-Rojas, Jorge, Dinael Guevara, Andres Navarro, and Juan Pascual-Garcia. 2019. "GPU Acceleration and Game Engines for Wireless Channel Estimation in Millimeter Waves" Electronics 8, no. 10: 1121. https://doi.org/10.3390/electronics8101121
APA StyleGomez-Rojas, J., Guevara, D., Navarro, A., & Pascual-Garcia, J. (2019). GPU Acceleration and Game Engines for Wireless Channel Estimation in Millimeter Waves. Electronics, 8(10), 1121. https://doi.org/10.3390/electronics8101121






