Research on Adaptive Reaction Null Space Planning and Control Strategy Based on VFF–RLS and SSADE–ELM Algorithm for Free-Floating Space Robot
Abstract
1. Introduction
2. Dynamic Model of the Space Robot
3. Adaptive Reaction Null Space (ARNS) Planning Strategy and Adaptive Robust Control Algorithm
3.1. Adaptive Reaction Null Space (ARNS) Planning Strategy Based on Variable Forgetting Factor Recursive Least Squares (VFF–RLS)
3.2. Adaptive Control Algorithm Based on Strategy Self-Adaptation Differential Evolution–Extreme Learning Machine (SSADE–ELM)
3.3. Robust Control Algorithm
3.4. Stability Analysis
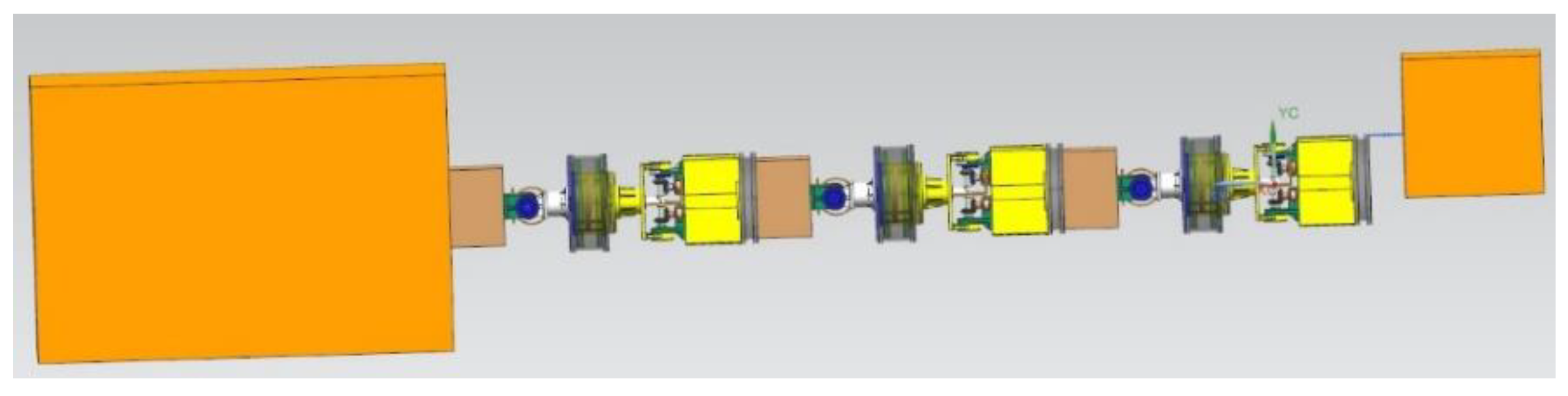
4. Simulation
4.1. Parameter Settings
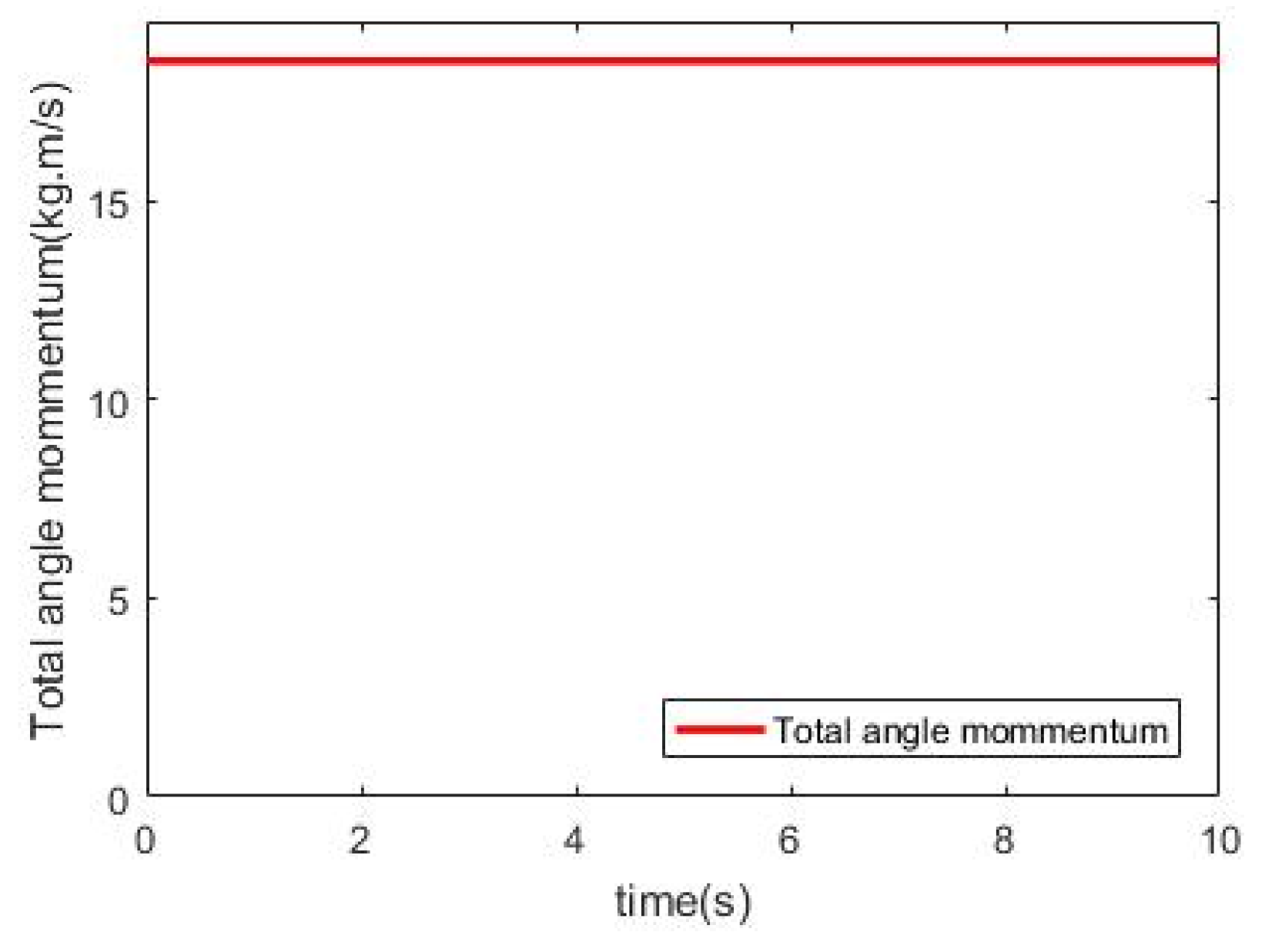
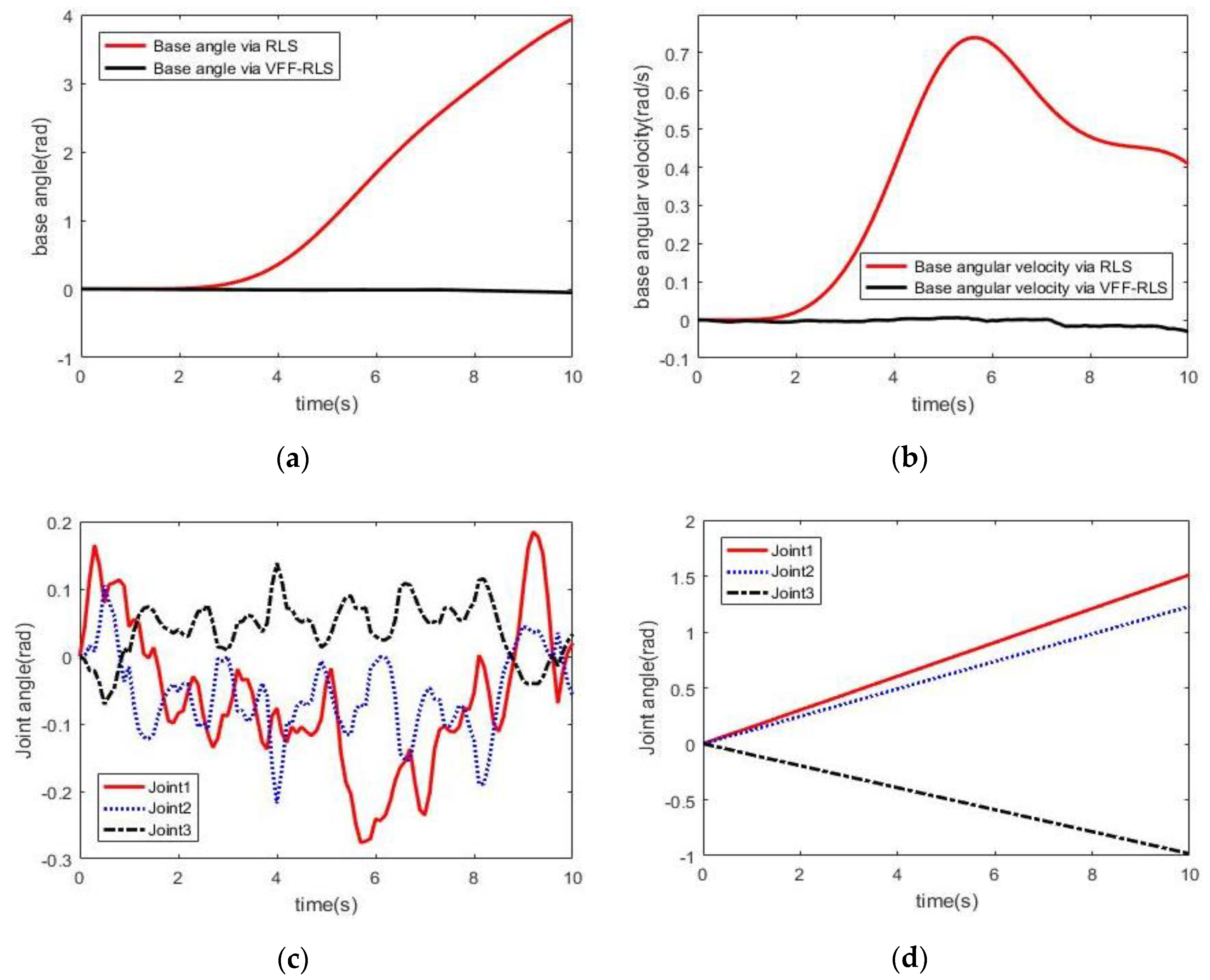
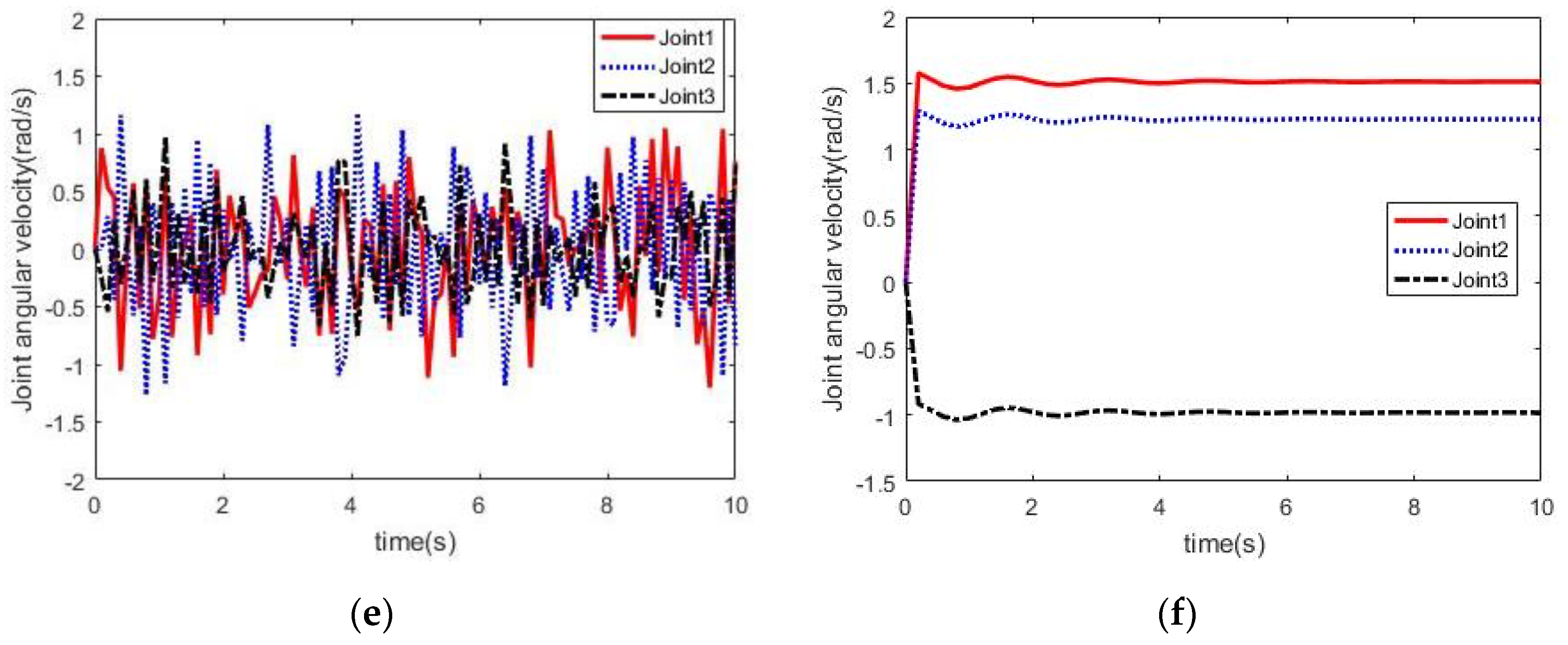
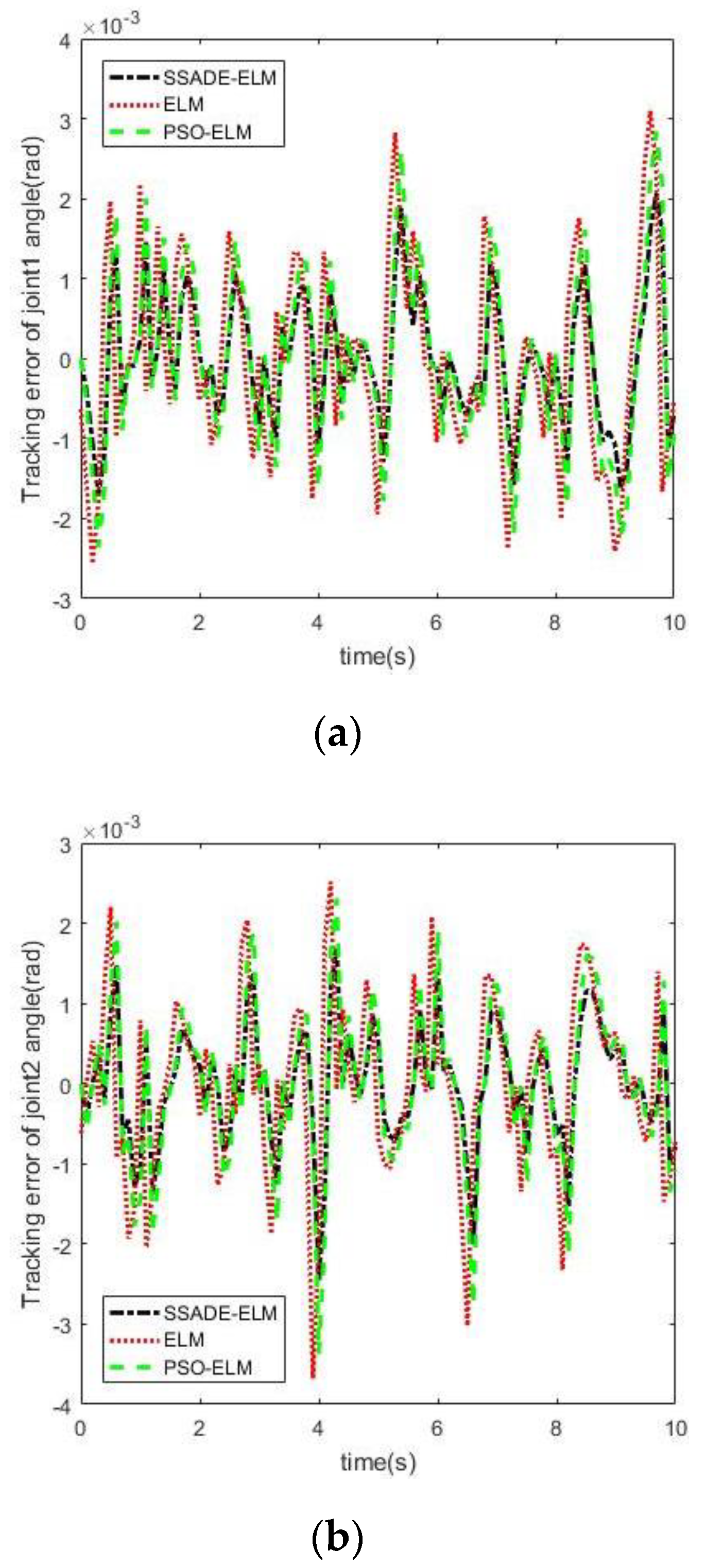
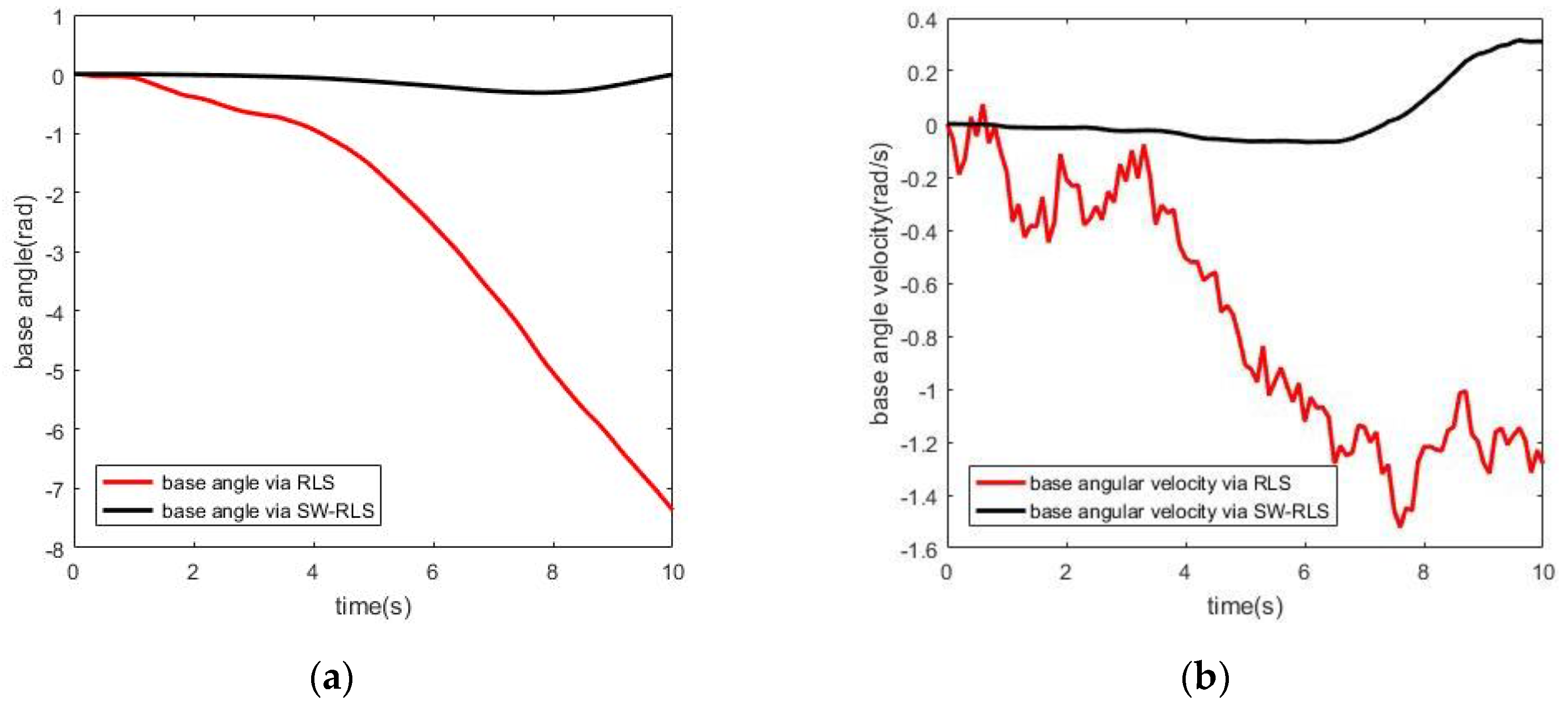
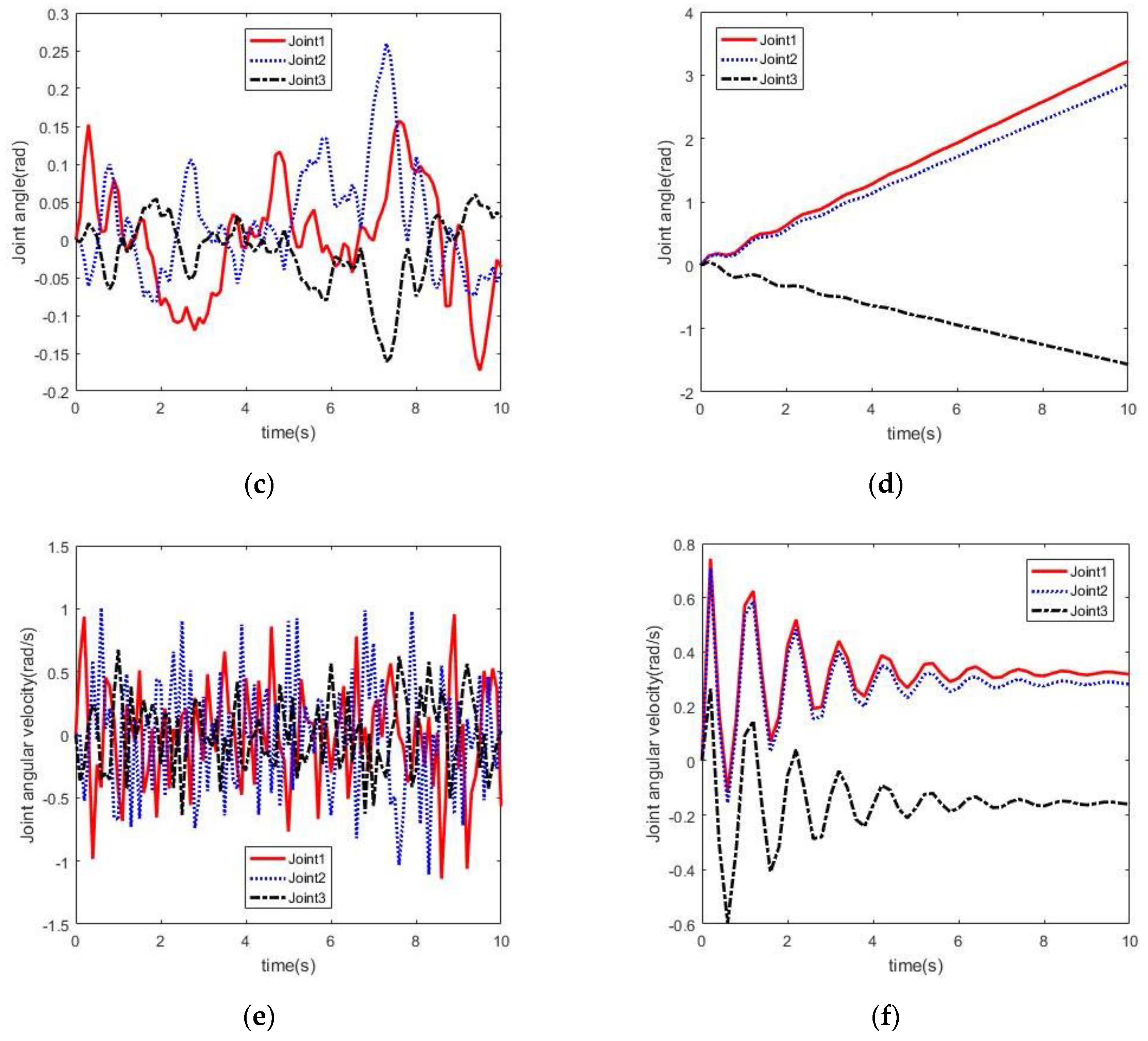
4.2. Simulation Results
5. Experiment
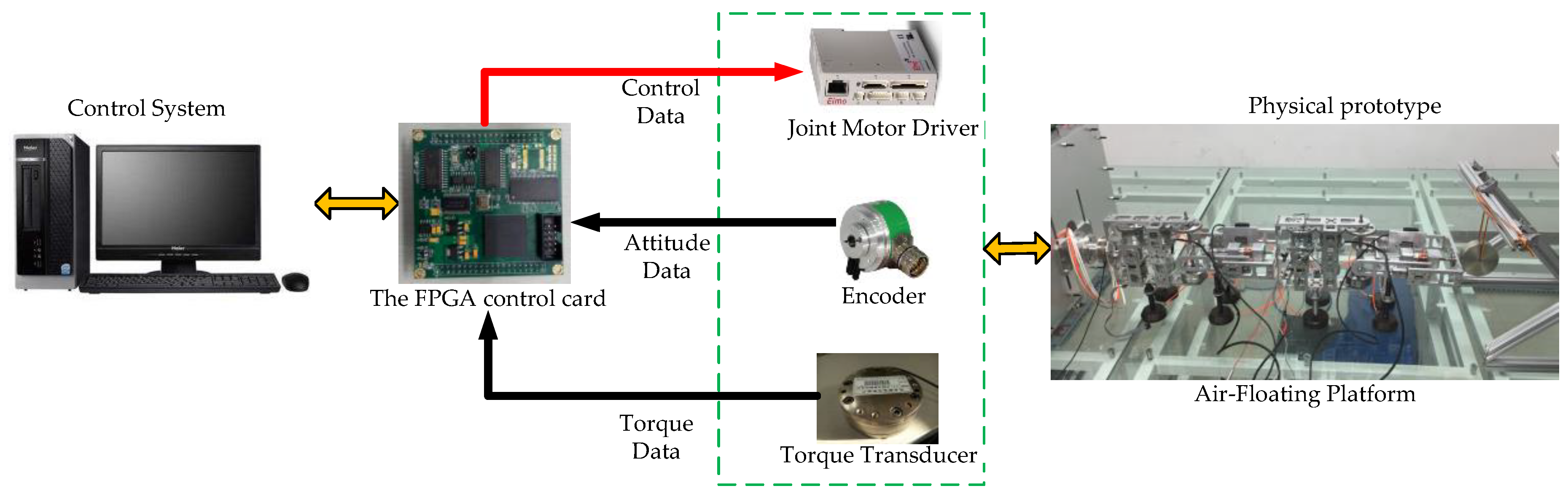
5.1. Experimental Setting
5.2. Experimental Results
6. Discussion
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ellery, A. Tutorial Review on Space Manipulators for Space Debris Mitigation. Robotics 2019, 8, 34. [Google Scholar] [CrossRef]
- Li, W.-J.; Cheng, D.-Y.; Liu, X.-G.; Wang, Y.-B.; Shi, W.-H.; Tang, Z.-X.; Gao, F.; Zeng, F.-M.; Chai, H.-Y.; Luo, W.-B.; et al. On-orbit service (OOS) of spacecraft: A review of engineering developments. Prog. Aerosp. Sci. 2019, 108, 32–120. [Google Scholar] [CrossRef]
- Liang, B.; Xu, W.F. Space Robot: Modeling, Planning, and Control, 1st ed.; Tsinghua University Press: Beijing, China, 2017; pp. 26–27. [Google Scholar]
- Flores-Abad, A.; Crain, A.; Nandayapa, M.; Garcia-Teran, M.A.; Ulrich, S. Disturbance Observer-Based Impedance Control for a Compliance Capture of an Object in Space. In Proceedings of the 2018 AIAA Guidance, Navigation, and Control Conference, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar] [CrossRef]
- Yoon, H.; Chung, S.; Kang, H.; Hwang, M. Trapezoidal Motion Profile to Suppress Residual Vibration of Flexible Object Moved by Robot. Electronics 2019, 8, 30. [Google Scholar] [CrossRef]
- Wang, Y.; Liang, X.; Gong, K.; Liao, Y. Kinematical Research of Free-Floating Space-Robot System at Position Level Based on Screw Theory. Int. J. Aerosp. Eng. 2019, 2019, 1–13. [Google Scholar] [CrossRef]
- Crain, A.D. Optimal Trajectory Planning and Compliant Spacecraft Capture Using a Space Robot. Ph.D. Thesis, Carleton University, Ottawa, ON, Canada, 2018. [Google Scholar]
- Gasbarri, P.; Pisculli, A. Dynamic/control interactions between flexible orbiting space-robot during grasping, docking and post-docking manoeuvres. Acta Astronaut. 2015, 110, 225–238. [Google Scholar] [CrossRef]
- Yu, X.-Y.; Chen, L. Modeling and observer-based augmented adaptive control of flexible-joint free-floating space manipulators. Acta Astronaut. 2015, 108, 146–155. [Google Scholar] [CrossRef]
- Nenchev, D.N. Reaction null space of a multibody system with applications in robotics. Mech. Sci. 2013, 4, 97–112. [Google Scholar] [CrossRef]
- Xie, R.; Shi, P.; Zhao, Y. Zero Reaction Coordinated Motion Planning for Free-Floating Space Manipulators. In Proceedings of the 34th Chinese Control Conference (CCC), Hangzhou, China, 28–30 July 2015; pp. 5830–5834. [Google Scholar]
- Wei, C.; Gu, H.; Liu, Y.; Zhao, Y. Attitude reactionless and vibration control in space flexible robot grasping operation. Int. J. Adv. Robot. Syst. 2018, 15. [Google Scholar] [CrossRef]
- Nguyen-Huynh, T.C.; Sharf, I. Adaptive reactionless motion and parameter identification in postcapture of space debris. J. Guid. Control Dyn. 2013, 36, 404–414. [Google Scholar] [CrossRef]
- Yang, C.; Wu, H.; Li, Z.; He, W.; Wang, N.; Su, C.-Y. Mind control of a robotic arm with visual fusion technology. IEEE Trans. Ind. Inform. 2018, 14, 3822–3830. [Google Scholar] [CrossRef]
- Xu, S.; Wang, H.; Zhang, D.; Yang, B. Adaptive zero reaction motion control for free-floating space manipulators. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 1067–1076. [Google Scholar] [CrossRef]
- Lu, X.; Jia, Y. Adaptive coordinated control of uncertain free-floating space manipulators with prescribed control performance. Nonlinear Dyn. 2019, 97, 1541–1566. [Google Scholar] [CrossRef]
- Zhang, B. Research on Trajectory Planning and Control of Space Robot After Autonomously Taking Over a Noncooperative Target. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, 2017. [Google Scholar]
- Jiao, C.; Liang, B.; Wang, X. Adaptive Reaction Null-Space Control of Dual-Arm Space Robot for Post-Capture of Non-Cooperative Target. In Proceedings of the 2017 29th Chinese Control and Decision Conference (CCDC), Chongqing, China, 28–30 May 2017; pp. 531–537. [Google Scholar]
- Nguyen Huynh, T.C. Adaptive Reactionless Control of a Space Manipulator for Post-Capture of an Uncooperative Tumbling Target. Ph.D. Thesis, McGill University, Montreal, QC, Canada, 2013. [Google Scholar]
- Chu, Z.; Ma, Y.; Cui, J. Adaptive reactionless control strategy via the PSO-ELM algorithm for free-floating space robots during manipulation of unknown objects. Nonlinear Dyn. 2018, 91, 1321–1335. [Google Scholar] [CrossRef]
- Yang, C.; Jiang, Y.; He, W.; Na, J.; Li, Z.; Xu, B. Adaptive parameter estimation and control design for robot manipulators with finite-time convergence. IEEE Trans. Ind. Electron. 2018, 65, 8112–8123. [Google Scholar] [CrossRef]
- Wang, L.; Zeng, Y.; Chen, T. Back propagation neural network with adaptive differential evolution algorithm for time series forecasting. Expert Syst. Appl. 2015, 42, 855–863. [Google Scholar] [CrossRef]
- Daachi, M.E.; Madani, T.; Daachi, B.; Djouani, K. A radial basis function neural network adaptive controller to drive a powered lower limb knee joint orthosis. Appl. Soft Comput. 2015, 34, 324–336. [Google Scholar] [CrossRef]
- Smith, A.M.C.; Yang, C.; Ma, H.; Culverhouse, P.; Cangelosi, A.; Burdet, E. Novel hybrid adaptive controller for manipulation in complex perturbation environments. PLoS ONE 2015, 10, e0129281. [Google Scholar] [CrossRef]
- Chu, Z.; Cui, J.; Sun, F. Fuzzy adaptive disturbance-observer-based robust tracking control of electrically driven free-floating space manipulator. IEEE Syst. J. 2014, 8, 343–352. [Google Scholar] [CrossRef]
- Huang, G.-B.; Zhu, Q.-Y.; Siew, C.-K. Extreme learning machine: A new learning scheme of feedforward neural networks. Neural Netw. 2004, 2, 985–990. [Google Scholar]
- Zhao, J.T. Extreme learning machine control algorithm for control saturated systems. Sci. Technol. Eng. 2019, 19, 173–177. [Google Scholar]
- Rong, H.-J.; Wei, J.-T.; Bai, J.-M.; Zhao, G.-S.; Liang, Y.-Q. Adaptive neural control for a class of MIMO nonlinear systems with extreme learning machine. Neurocomputing 2015, 149, 405–414. [Google Scholar] [CrossRef]
- Petković, D.; Danesh, A.S.; Dadkhah, M.; Misaghian, N.; Shamshirband, S.; Zalnezhad, E.; Pavlović, N.D. Adaptive control algorithm of flexible robotic gripper by extreme learning machine. Robot. Comput. Integr. Manuf. 2016, 37, 170–178. [Google Scholar] [CrossRef]
- Yang, C.; Huang, K.; Cheng, H.; Li, Y.; Su, C.-Y. Haptic identification by ELM-controlled uncertain manipulator. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 2398–2409. [Google Scholar] [CrossRef]
- Figueiredo, E.M.N.; Ludermir, T.B. Investigating the use of alternative topologies on performance of the PSO-ELM. Neurocomputing 2014, 127, 4–12. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, J.; Cai, Z.; Zhang, P.; Chen, L. Memetic extreme learning machine. Pattern Recognit. 2016, 58, 135–148. [Google Scholar] [CrossRef]
- Cao, J.; Lin, Z.; Huang, G.-B. Self-adaptive evolutionary extreme learning machine. Neural Process. Lett. 2012, 36, 285–305. [Google Scholar] [CrossRef]
- Tang, X.; Chen, L. A self-adaptive evolutionary weighted extreme learning machine for binary imbalance learning. Prog. Artif. Intell. 2018, 7, 95–118. [Google Scholar] [CrossRef]
- Das, S.; Mullick, S.S.; Suganthan, P.N. Recent advances in differential evolution—An updated survey. Swarm Evol. Comput. 2016, 27, 1–30. [Google Scholar] [CrossRef]







| Description | Symbol | Value | Unit |
|---|---|---|---|
| Base mass | 100 | kg | |
| Joints mass | , , | 5 | kg |
| Base inertia | 6.67 | kg·m2 | |
| Joints inertia | , , | 0.2 | kg·m2 |
| Target mass | 5 | kg | |
| Target inertia | 2.5 | kg·m2 | |
| Vector from center of the base to the centroid of the first joint | 0.5 | m | |
| Vectors from center of the ith joint to the centroid of the ith body | , , | 0.5 | m |
| Vectors from the centroid of the ith body to the center of the (i + 1)th joint | , , | 0.5 | m |
| Vectors from center of the Target to the centroid of the end | 0.1 | m | |
| Initial base angle | 0 | rad | |
| Initial base angular velocity | 0 | rad/s | |
| Initial base linear velocity | 0 | m/s | |
| Initial joint angle | [0, 0, 0] | rad | |
| Initial joint angular velocity | [0, 0, 0] | rad/s |
| Algorithm | Description | Symbol | Value |
|---|---|---|---|
| Strategy Self-Adaptation Differential Evolution–Extreme Learning Machine (SSADE–ELM) | Amount of hidden layer nodes of ELM network | 60 | |
| Max iteration | 1000 | ||
| Population size | NP | 30 | |
| Stage control factor | c | 0.85 | |
| Arbitrary non-zero vector | [1, 1, 1] | ||
| Upper bound of error | 1 | ||
| The gain of the PD control algorithm | K | Diag (100, 50) | |
| Positive diagonal coefficient matrix | Diag (2, 1) | ||
| Extreme Learning Machine (ELM) | Amount of hidden layer nodes of ELM network | 60 | |
| Max iteration | 1000 | ||
| Population size | NP | 30 | |
| Input weight | rand (0, 1) | ||
| Hidden layer bias | rand (0, 1) | ||
| Arbitrary non-zero vector | [1, 1, 1] | ||
| Upper bound of error | 1 | ||
| The gain of the PD control algorithm | K | Diag (100, 50) | |
| Positive diagonal coefficient matrix | Diag (2, 1) | ||
| Particle Swarm Optimization–ELM (PSO–ELM) | Amount of hidden layer nodes of ELM network | 60 | |
| Max iteration | 1000 | ||
| Population size | NP | 30 | |
| The weights of the stochastic acceleration terms | 0.2 | ||
| The inertial weight serving as a tradeoff between the global and local exploration capabilities of the swarm | 2 | ||
| Arbitrary non-zero vector | [1, 1, 1] | ||
| Upper bound of error | 1 | ||
| The gain of the PD control algorithm | K | Diag (100, 50) | |
| Positive diagonal coefficient matrix | Diag (2, 1) |
| Algorithm | SSADE–ELM | ELM | PSO–ELM |
|---|---|---|---|
| Average error | −3.0 × 10−7 | −4.5 × 10−7 | −4.2 × 10−7 |
| Algorithm | SSADE–ELM | ELM | PSO–ELM |
|---|---|---|---|
| Average error | −5.3 × 10−6 | −7.6 × 10−6 | −6.9 × 10−6 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, X.; Dong, Z.-H.; Hong, J.-C. Research on Adaptive Reaction Null Space Planning and Control Strategy Based on VFF–RLS and SSADE–ELM Algorithm for Free-Floating Space Robot. Electronics 2019, 8, 1111. https://doi.org/10.3390/electronics8101111
Ye X, Dong Z-H, Hong J-C. Research on Adaptive Reaction Null Space Planning and Control Strategy Based on VFF–RLS and SSADE–ELM Algorithm for Free-Floating Space Robot. Electronics. 2019; 8(10):1111. https://doi.org/10.3390/electronics8101111
Chicago/Turabian StyleYe, Xin, Zheng-Hong Dong, and Jia-Cai Hong. 2019. "Research on Adaptive Reaction Null Space Planning and Control Strategy Based on VFF–RLS and SSADE–ELM Algorithm for Free-Floating Space Robot" Electronics 8, no. 10: 1111. https://doi.org/10.3390/electronics8101111
APA StyleYe, X., Dong, Z.-H., & Hong, J.-C. (2019). Research on Adaptive Reaction Null Space Planning and Control Strategy Based on VFF–RLS and SSADE–ELM Algorithm for Free-Floating Space Robot. Electronics, 8(10), 1111. https://doi.org/10.3390/electronics8101111





