1. Introduction
The need for higher data rates at the user end is the major motivation for new multiple-input multiple output (MIMO) schemes in modern communication systems. These modern techniques dispensing with the large number of antennas also enable spectral efficiency and increased transmit-energy efficiency, although all antennas do not contribute equally [
1,
2,
3,
4]. This is laudable in the study of massive MIMO (mMIMO) systems that are being pursued by researchers and industrialists alike for coping with the growing demand for higher data rates in modern telecommunication services. In the 5G standard, for example, the mmWavebands have been selected due to the abundance of unused spectrum resources [
5]. However, while the high data rate problem can be overcome easily by deploying large bandwidths, the scarcity of the electromagnetic spectrum subtends some efficiency limitations in using large bandwidths to satisfy the high data rate demand. One of the ways of realizing such data rates (on which the mMIMO can rely), for example in wireless communication systems, is by enabling higher antenna configurations or by optimizing the available/known configuration techniques. In this study, we explore the methods of both optimizing the present MIMO design methods and exploring higher order antenna configurations with potentials for mMIMO.
Space-time block coding (STBC) [
6,
7], for example, is a MIMO technique that exploits time and antenna dimensions to achieve high data rates with minimum error probability. In [
8], it was shown that under similar spectral efficiencies, STBCs outperform spatial modulation in terms of bit error ratio (BER) metrics. STBCs can be combined with beamforming to minimize the error probability of MIMO systems [
9,
10,
11] and presently studied for systems supporting mMIMO schemes [
3]. Other methods include the use of large antennas at the transmitting base stations [
3].
Although STBCs combined with beamforming are good hybrids when minimum BER is desired, the conventional orthogonal STBC (STBC) [
6] is limited to only two transmit antennas (
= 2) as higher order antenna configurations do not achieve orthogonality [
12]. These limitations are overcome by specially combining the O-STBCs to increase the spatial diversity capability of the scheme [
13]. Such codes are referred to as QO-STBCs [
11,
14]. The standard QO-STBC scheme provides
over similar spectral conditions as the O-STBC with better performance and also dispenses with the full spatial rate, but not full diversity. Unfortunately, also, QO-STBC complicates the receiver design due to the lack of orthogonality among the codes. Such a limitation also leads to ISI in the decoding matrix of the QO-STBC receiver and diminishes the BER performance.
In terms of the detection matrix, these off-diagonal (ISI) terms are described also as self-interference terms [
15]. Usually, it is difficult to decouple transmitted symbols using linear processing at the receiver of a standard QO-STBC system. Consequently, several solutions have been offered by researchers to eliminate the ISI, namely using Givens-rotation [
16], eigenvalue decomposition (EVD) [
17,
18] and Hadamard matrices [
1,
17]. Although both the Givens-rotation technique and the EVDs approach yielded similar results [
19], the EVD method is less complex to implement. The Hadamard matrices are equivalent modal matrices of the EVD with non-zero entries to enhance full-diversity realization of the ISI-free QO-STBCs. In [
17], the authors proposed a QO-STBC code structure of with no off-diagonal terms in its detection matrix. Unfortunately, however, the output ISI-free matrix is complex, and it will be demonstrated later in this study to have a poor BER performance (compared to the Givens-rotations and EVD methods). This is due to the degradation of the true gain by the power of the ISI terms (removed from the rest off-diagonal points), which are greater than the ISIs of the Givens-rotation and EVD methods.
Initially, this present work was first introduced in [
1] for multiple input single output (MISO) systems; we extend our results to include large-antenna (
), MIMO, receivers up to
receiving antennas and spectrally-efficient modulation schemes (e.g., 16 quadrature amplitude modulation (QAM) and 128 QAM). Large antenna systems provide three advantages, namely: the effect of small-scale fading is averaged out; the random channel between
and
become pairwise orthogonal as the elements grow; and lastly, it allows for transmit power efficiency in massive MIMO [
20]. We apply modal matrices from the eigenvalues of the QO-STBCs provided by the Hadamard matrices to orthogonalize the detection matrix and enable linear processing. This is achieved by deriving an equivalent virtual channel matrix (EVCM) first, which can be used to reduce the complexity of decoupling the space-time transmitted messages at the receiver. With the EVCM approach, the design and study of QO-STBC become attractive since there exist only the estimates of the originally
-transmitted messages received at the receiver. Using the EVCM approach also, the receiver complexity is thus transferred to the transmitters such as the base stations, which have the flexibility of supporting very-large/mMIMO antennas (as in [
21]) and also complex algorithms better than the receivers [
14], such as mobile phones. This is attractive for massive MIMO as linear processing does not require the complex detection process required as well in dirty paper coding [
22]. In mMIMO, the capacities when
can be verified using a left-truncated Gaussian distribution [
23]. Furthermore, given that the conventional STBC has found applications in multi-directional MIMO designs [
9], the proposed QO-STBC can also impact mMIMO multi-directional QO-STBCs being explored in [
24,
25]. Our results, in future studies, can enhance the performance of large antenna wireless sensor networks (WSNs) design [
20] in mMIMO systems since the total power consumption decays by
as
becomes very large [
26], satisfying the power efficiency criteria of large antennas [
20]. In addition, the linear process of our proposed technique will be useful for low-complexity implementations at the decision fusion centres (DFCs) over inhomogeneous large-scale fading between the sensors and the DFC as in [
27], although, massive MIMO trade antennas at the FDCs for energy efficiency at the sensors of WSNs [
28].
QO-STBCs with non-sparse matrices enable a well-performing peak-to-average power ratio (PAPR) [
29,
30]. Thus, since the modal matrices of our system do not have zero entries, then we present among other properties a QO-STBC design scheme with well-performing PAPR. In addition, our system exhibits full diversity, increased SNR performance that minimizes the BER and supports linear decoding. The standard QO-STBC is combined with the modal matrices of the Hadamard matrices motivated by EVD to construct new QO-STBC with no ISI and achieves full diversity. Furthermore, we have also shown in the literature that the true gain is significantly reduced by the eliminated ISI terms for
receiving antennas in [
8] and also that realistic receivers may not support more than
without severe mutual coupling degradation.
In
Section 2, the system model is described for specific QO-STBC characteristics. An introduction to full-diversity QO-STBC including the proposed full-diversity QO-STBC is presented in
Section 3. We presented the pairwise error probability in
Section 4 and our simulation results in
Section 5 with the conclusions following in
Section 6.
2. System Model
Given a standard STBC code with a full rate (
) (e.g., [
6]), the ratio of the space (number of antennas) and time (number of timeslots) can be expressed as
. Then, for an orthogonal-STBC (O-STBC) system (e.g., [
6]) with two transmit antennas (
) and one receiver (
), the received signal at the receiver can be represented as:
where
,
,
is a multipath Rayleigh fading channel with
,
and
represent the additive white Gaussian noise (AWGN) and
and
represent the channel coefficients from Rayleigh fading and
in the above example. Note that
represents the transpose of
, and
represents the complex conjugate.
Although the STBC code described in [
6] achieves full rate criteria and full diversity, its major disadvantage is that the design does not support
. This problem can be solved by deploying QO-STBC, which can be formed from the STBCs. The QO-STBC can dispense with
and complex entries. It achieves full spatial rate [
12,
13,
31], but it does not attain full diversity; QO-STBCs exhibit full spatial rate (
) when, for example
. Meanwhile, consider a QO-STBC code with
as follows [
18,
31]:
where
and
follow the standard Alamouti STBC of [
6]. Unfortunately, (
2) does not satisfy the
condition
. This property has also motivated the proposal for the QO-STBC design discussed in [
32].
The QO-STBC signal,
, can be a phase-shift keying (PSK) or quadrature amplitude modulation (QAM) modulated signal,
, of length
N. Unlike the case of
where there are
, the QO-STBC (e.g., (
2)) involves
antenna spaces. Assuming that there are
antenna spaces over which the QO-STBC symbols of (
2) can be transmitted at different timeslots with one receiver (
), then combining the QO-STBC of (
2) with the channel
, the receiver obtains:
The result in (
3) follows from combining (
2) and the channel vector
so that the received symbols can be expressed as:
where
. The design in (
3) complicates the receiver since the received signals cannot be linearly processed without difficulty. For instance, it is difficult to decouple the transmitted messages at the receiver using linear processing. Thus, an EVCM is derived to enable the linear processing, simplifying the decoding of only
and also the decoupling of received symbols into the estimates of
(namely
). As an example, computing the conjugates of the second and fourth rows of (
3) and rearranging the results,
A major advantage of the (
5) architecture is that if
but
and
, then it is therefore impossible for an eavesdropper to compromise
over a time varying condition, hence making the scheme secure. The result realized in (
5) enables that the channel
given in (
1) can be expressed as:
where (
6) represents the EVCM,
. In the literature, an EVCM can be described as a matrix with ones on its leading diagonal and at least
zeros at its off-diagonal positions and its remaining (self-interference) entries being bounded in magnitude by 1 [
33]. Representatively,
where
is a sparse matrix. To reduce the system complexity, we apply the EVCM, which simplifies decoding at the receiver. If there exists an optimum detector of a maximal ratio combining (MRC) output, namely using zero-forcing (ZF),
, such that
, then
. For instance, let the received signal estimate be:
where
is the conjugate transpose of
. It can be verified that
is the detection matrix that implements a QO-STBC systems with
and
. In relation to (
7), we define:
where
and
. The mutual interference terms outside the leading diagonal can be expressed as
and
. Of course, the interference term diminishes the performance of this style of QO-STBC, for example the signal-to-noise ratio (SNR) and consequently the BER. Our interest is to minimize the impact of
so that the SNR can be maximized and then the BER minimized. An example is in constructing a suitable channel matrix whose decoding matrix is devoid of the ISI of (
9).
3. Full-Diversity QO-STBC Using EVD and the Proposed
In [
34], a zero-forcing detection was discussed for the QO-STBC design; this is similar to the eigenvalue method proposed in [
18]. Since the matrices that orthogonalize the detection of symbols are non-singular, the received noise estimate is non-Gaussian. Similarly, also, the pre-whitening process of the noise further amplifies the noise, so that the BER statistics are impacted to reduction. In [
32], the author explored the method of the analytical derivation of the closed-form expression of the pairwise error probability (PEP). The models described in [
32,
34] sacrifice the data rates and would require switching off the first two antennas or the last two antennas at the RF-chain during each timeslot; this can be expensive.
Meanwhile, QO-STBCs that exhibit no-ISI in the detection matrices are said to achieve full diversity. For example, the ISI-free QO-STBC is achieved through the rotation of one-half of the symbol constellation set [
35,
36,
37], multidimensional rotation [
38,
39,
40], Givens-rotations [
16], EVD [
17,
18] and Hadamard matrices [
1,
17]. Although the EVD approach is less complex and will be followed, the results can be enhanced if an equivalent modal matrix can be derived without zeros terms.
Definition 1. [1]: If is a square matrix and is a column matrix (), let , where v is a scalar, then is an eigenvalue and an eigenvector. The vector can be formed into a square matrix , usually called a modal matrix. If the eigenvalue of is the leading diagonal of a matrix , then ; both and share the same eigenvalues; is an identity matrix. It follows that . Here, we use Definition 1 to demonstrate our proposal using a handy
and show also that this can easily be extended to other higher antenna configurations, namely
. Substituting for
using
in Definition 1, it can be observed that:
We formulate the modal matrices depending on the number of transmitting antennas to eliminate the interfering terms in the detection matrix; this results in different modal matrix sizes. By applying (
10), namely
to (
9), the QO-STBC scheme can attain full diversity; this is the principle of diagonalizing a matrix [
41]. The matrix
therefore achieves the required interference-free detection. By (
9), the resulting modal matrix of the QO-STBC system under study with
and
T = 4 can be expressed as:
A new EVCM can be formed by post-multiplying
by
, such as:
Note that if the channel is defined as (
12), the linear model will be expressed as (
1). On the other hand, if the system has channel coefficients given by
, then the system can be described (in linear form) as (
4).
Definition 2. (see Theorem 5.5.1 of [12]): A complex generalized linear processing orthogonal design in variables 0, , , exists if and only if there exists a complex generalized linear processing orthogonal design in the same variables and of the same size, such that . Notably, only the Alamouti STBC achieves this condition without other post- (or pre-) processing. Now, rewrite (
4) in the following form,
then the receiver receives:
From (
13), the encoding matrix
of (
2) simplifies to
only. On the other hand, the term
in (
13) also permits linear decoding and eliminates the off-diagonal
interfering terms, such as:
Observe that
provides:
as the new detection matrix with no ISI. Furthermore, observe that the eliminated ISI impacts the true power gain. For a large number of antenna configurations, some antenna branches contribute more than others [
2]. In (
14) for example, the energy of the last two antenna branches are reduced by the eliminated off-diagonal ISI terms so that the resulting gains are more on the first two antenna branches. This can be useful with RF-chain switching and also when using directional communications to concentrate power including the antenna selection technique.
For the 4 × 1 configuration,
, while for the 3 × 1 configuration
but within the QO-STBC design. The
configuration is achieved by setting
; for example, using the method of (
12), it is possible to construct an EVCM suitable for
with
such as:
On the other hand, formulating the equivalent symbol matrix involves eliminating the fourth column of the matrix [
16] since only three antenna spaces are required, for example:
With a receiver dispensing with a maximum likelihood (ML) detection, the receiver finds signals that have the closest Euclidean distance nearest to the original transmitted QO-STBC signals as follows . In this case, the error matrix can be expressed as . We assume that the channel is quasi-static for consecutive timeslots.
3.1. Combined Standard QO-STBC and Hadamard Matrices for QO-STBC Design
Although one can easily verify that
, the limitations of (
11) include poor PAPR performance due to the sparsity of the EVD modal matrix [
30] and poor BER resulting from the zero terms [
8]. Since QO-STBC matrices can be diagonalized using modal matrices (
), then Hadamard matrices can also be used to diagonalize QO-STBC systems. For an
matrix, Hadamard matrices have
entries with the columns (and rows) being pairwise orthogonal [
42,
43], for example:
where
is an identity matrix. Considering the system example under study, the Hadamard matrix of
order can be expressed as:
where:
It can be observed in (
17) that there exist no zero (0) entries as there are in (
11). These zero entries limit the BER performance as they null-out the channel gains. From (
16), it can be observed that use of the Hadamard matrix as the modal matrix gives the advantage of the
multiple of the diagonalized matrix.
In
Section 3, we discussed that modal matrices are applied to QO-STBC systems in order to eliminate the off-diagonal (ISI) terms. This phenomenon also led to the proposal of applying Hadamard matrices to ensure that QO-STBC systems attain full diversity by eliminating the off-diagonal terms. Since the 0’s null-out the channel gains, the modal matrix in (
11) diminishes the SNR and consequently worsens the BER performance of the QO-STBC systems. For instance, the channel gains are eliminated when combined with a zero. Second, the presence of these zeros leads to poorer PAPR performance (see [
29,
30] and the references therein). The modal matrices subtended by the Hadamard matrices do not have these limitations, consequently QO-STBC codes constructed from it would exhibit better BER and better PAPR advantages. Meanwhile, our interest in this study is in minimizing the error probability (BER). Thus, we combine (
6) and (
17) so that the channel matrix can be expressed as:
At the receiver, linear processing can be applied as follows:
where:
The result in (
18) can be discussed in terms of the advantages it provides. As an example, it eliminates the nonlinear decoding that existed in standard QO-STBC. Additionally, comparing (
19) with (
14), using the proposed modal matrix technique improves the gain by
-times the power gain. Consequently, the received SNR is thus improved by
-times. With
, the channel term namely
is set to zero (0) [
16,
17]. As an example, we express:
If
, where
were sent in (
18), then
where
are required in the case of
. Thus, the fourth column of (
20) is ignored so that the EVCM for
becomes:
This phenomenon (as in (
21)) can be extended to designing QO-STBC systems with
= 5, 6, 7, 9, 10, 11, etc. for higher order antenna configurations.
In terms of complexity in comparison to the EVD method, the number of terms is exactly the same except that when the standard QO-STBC matrix terms are multiplied by the null terms from the sparse eigenvalues of the EVD matrix, it nulls-out the channel gains so that the resulting EVCM matrix is reduced in the number of terms; this is pronounced in the analysis results discussed in
Section 3 of this paper (see (
12)).
Theorem 1. The standard QO-STBCs can achieve full diversity if the detection matrix exhibits no off-diagonal terms and its modal matrix has non-zero entries.
In [
30], it was shown that full-diversity Toeplitz STBC codes exhibit well-reduced PAPR if the codes have non-zero entries. Meanwhile, the PAPR can be calculated as:
where
is the time domain orthogonal frequency division multiplexing (OFDM) symbol vector of
with length
K. Since the scheme involves multiple
transmit branches, the OFDM driver is performed along each of the transmit branches, and the PAPR is measured using the complementary cumulative distribution function (CCDF), namely
where
.
and
are the probability of
and the target symbol amplitude threshold, respectively. The indicative PAPR is therefore an average of the PAPRs over each transmitting branch.
Corollary 1. As a corollary of Theorem 1, it can be established that modal matrices with no zero entries yield better PAPR performing QO-STBCs.
Similar to the foregoing discussion, when the antenna configuration is increased to
, the method of realizing (
6) can be used. However, the process can be simplified by formulating two EVCMs from
as follows; define the EVCM for antenna Indices 5 to 8 as:
Then, combining (
23) and (
6) in the regime of (
2) and then multiplying by the necessary modal matrix,
Using the method that subtends (
24), other higher antenna configurations (namely,
) can be explored. For other base stations equipped with
, the process that subtended (
21) can be used.
3.2. Diagonalized Hadamard STBC
Other methods of constructing new codes from the standard QO-STBC have been reported [
17,
30]. The method described in [
30] does not adopt the use of the Hadamard matrix and does not achieve the full rate. However, [
17] combined cyclic matrices with Hadamard matrices to form new codes. The cyclic matrix does not achieve orthogonality, hence its combination with the Hadamard matrix. In [
17], the authors introduced a new QO-STBC design from cyclic matrices called diagonalized Hadamard STBC (DHSTBC). For instance, the DHSTBC can be expressed as [
17]:
Given the knowledge of modal matrices proposed in this study, the equivalent symbol matrix is discussed. As the modal matrix of
from
was used to form an EVCM in (
12), similarly from
, the equivalent symbol matrix can be discussed knowing that
is the modal matrix of
. Considering (
25), the equivalent symbol matrix can be derived as
; this is realized by combining a cyclic matrix of (
25) and a Hadamard matrix to obtain the DHSTBC code, which was defined as [
17]:
Recall a system model of (
4). Similar to the (
4) model, if the symbols matrix is defined from the cyclic matrix of (
25), then the channel matrix can also be expressed as:
Then, constructing an EVCM for linear decoding involves combining the EVCM and the Hadamard-based modal matrix (
17), as:
Similar to (
18), the receiver receives:
where
. The detection matrix is fat in terms of elements, for example:
where:
where
. Furthermore, if
is formed as
instead of
, then
(where
) as the sequel to the Hadamard criteria. The resulting matrix is huge and complex; these have their respective implications that will be enumerated shortly. For instance, since there are additional interfering terms in (
27) after expanding
, then, when compared to the results of the ISI-free QO-STBC in (
37), the terms
further diminish the BER performance, so that the DHSTBC scheme performs poorly.
Comparing the proposed QO-STBC result (
18) with the earlier Hadamard algorithm of DHSTBC in (
27), the proposed QO-STBC has well-reduced computational complexity. For instance, expanding
, it can be observed that there are 16 terms involved in the earlier DHSTBC, while there are only eight terms involved in the proposed one; there exist
ISI terms. In terms of performance, the earlier Hadamard QO-STBC (DHSTBC) involves eight additional interfering terms (apart from
) that would degrade its BER performance.
3.3. MIMO QO-STBC
In the earlier discussions, we have supposed that there are
receiver antennas; here, we consider the case of
. Thus, each of the channel terms from the
can be treated respectively as a vector of the form:
where:
If the equivalent channel can be derived, then the MRC when there are
maximum receiving elements can be described. Assuming perfect channel state information (CSI) (i.e., the channel coefficients are perfectly available at the receiver), the detector attains the optimal maximum likelihood (ML) rule as [
44]:
where
. The term
is the Euclidean distance metric for an ML decoding. If an equivalent channel is known (e.g., the EVCM), the maximal ratio combining (MRC) rule from [
33,
44] provides that:
where
,
and
for each receiver antenna branch. In the case of [
1], we only studied the QO-STBC scheme for a multiple-input and single-output (MISO) system; thus,
, but in this version, we have extended the study to include
.
Considering the MIMO scheme in (
29), both
and the gain
influence the amplitude of the received signal. Then, the noise part is amplified by the
. This is because the EVCM is unitary (see (
37)), except that they are scaled by the gains. Notice that
,
represents an identity matrix impacted (as in the case
) by the channel gains, such as
. The noise term is rather amplified by
,
. The degree of impact of
on the noise term impacts the Euclidean distance metric at the receiver; this depends on the fading of the channel. The complexity in the decoupling of the transmitted message in the receiver reduces to finding only
for all of the receiving branches. STBCs that support linear transceiver systems incur a loss in capacity over channels with multiple receive antennas [
45]. This is even more noticeable in the case of conventional QO-STBCs due to ISI and worst when DHSTBC is used to enable transmitter diversity because the ISI terms (
) will grow as the
increases, in fact up to the point of no more diversity gain.
4. Pairwise Error Probability of the QO-STBCs
Usually, the channel is considered quasi-static throughout each symbol block so that the Chernoff bound is averaged over a Rayleigh fading channel as [
9]:
where
is the pairwise error probability (PEP), which responds to the received SNR and
is the expectation value over each symbol block. The conditional PEP, for a given channel say
, is described using the well-discussed Chernoff bound of the form:
where
is from the circularly-symmetric additive white Gaussian noise with zero mean and variance
; this is the case when
. Indeed, the Gaussian
Q-function is the complementary error function expressed as:
In terms of (
32), the conditional PEP is summarized as:
where
is the SNR at the maximal ratio combining (MRC) receiver output. The performance bound then follows as [
9]:
where
and
is from the detection matrix. Meanwhile, from the Cauchy–Schwartz inequality,
Furthermore, define
as an
matrix, then its Frobenius norm
then
. Rewrite
as
, such that:
where
[
46]. If
estimates the error detection metrics, then
. Furthermore,
. The likelihood of erroneously decoding the transmitted signals can be used to discuss the diversity product of the scheme [
47]. However, for any ISI-free QO-STBC,
where
and
is the gain power.
4.1. The SNR Performance of EVD and DHSTBC
The conventional O-STBC achieves full diversity, and there exists only
. For
, one can express the SNR at the receiver of the ISI-free QO-STBC (
14) from EVD as:
where
and
. For an ISI-free QO-STBC, although the results in (
35) and (
27) are similar, the impacts of the channel matrix are different. When the detection matrix is a diagonal matrix, for instance,
when
= 2, while
when
= 4, and so on, the Euclidean distance metrics are also different both for different QAM constellations and different
. Now, the probability that
was detected can be expressed as:
where
. In [
9],
for
. Then, for
,
and
. Notice that when
, then
, which can be described further in terms of
being the Euclidean distance metric at the receiver. Sometimes, the Chernoff bound of the Gaussian function can be used to approximate the
Q-function, such as in [
8]. The method of DHSTBC does not perform any better. For example, the ISI is greater in the DHSTBC (see (
27)) than using either the EVD (
14) or the proposed technique (
19). The effects of the ISI on diminishing the true-power gain of the DHSTBC will be reduced as evidently shown in the BER results discussed in
Section 5.
4.2. The SNR Performance of Proposed Full-Diversity QO-STBC
Although one can easily verify that
, the limitations of (
11) include poor PAPR performance due to the sparsity of the modal matrix [
30] and poor BER resulting from the zero terms of
[
1] because the SNR and the BER performance depend on the power gain contributed by
. The proposed modal matrix is
and the proposed channel matrix is
. Thus, the SNR at the receiver can be described as:
One can also verify that:
Equation (
37) provides the SNR statistics at the MRC output of the receiver and provides information of the BER performance of the EVD ISI-free QO-STBC from the Hadamard modal matrix. Notice that
provides
with an extra factor,
impacting the power gain, which will further minimize the BER statistics; similarly,
. Consequently, the SNR can be well described as:
Since
provides:
then (
38) can be rewritten as:
where
is a
Hadamard matrix when
. Comparing (
38) and (
37), it is clear that the power gain in using
is
-times greater than using
. The use of
thus affects the slope of the BER so that the full-diversity method of the proposed QO-STBC becomes better. In general, the method of constructing
antenna configurations described in
Section 3.1 can be extended to any higher order design, namely
, 16, 32, etc.
Remark 1. We refer the reader to our earlier discussion in [1,48] for other designs that do not enable the full rate, but maintain full diversity. 5. Simulation Results and Discussion
In [
1], we have studied only the cases of MISO using QPSK and
, and here (in this study), we extend the MISO configuration to include
. For fair comparisons, the simulation environments are similar except for the use of suitable EVCM configurations for different numbers of antenna configurations and code design styles. The symbols we have used are not coded; in other words, no forward error correction is applied. At the receiver, the optimum detector is assumed so that an MRC combining method is adopted. We do not present the simulation results for
and
in this work, as these have been addressed in [
1]. Meanwhile, the Rayleigh fading channel model is used, which is considered to be quasi-static over each symbol block. The model has zero mean with unit variance.
5.1. MISO and MIMO QO-STBC Design Using Eight Transmit Antennas
This study implements the standard QO-STBC code system described in
Section 2 in the transmitter and an ML detection dispensing with MRC in the receiver to construct a
,
and
MIMO system using 16 and 128 QAM;
and these are simulated over the MATLAB environment. In the process, random symbols are generated; this involves
symbols averaged over each channel block. These are mapped using the aforementioned mapping schemes, demultiplexed and processed over the EVCM channels that enabled
when
and
transmit antennas are used, respectively.
Using EVCM simplifies detection to linear processing so that the estimates of the transmitted symbols,
, are easily decoupled. Since there are
transmitting branches, then each branch receives
messages up to a total of
(where
for MISO design) receptions. The receiver finds estimates
whose Euclidean distance,
, is closest to the transmitted messages; then, afterwards, M-QAM signal demodulation is performed. The transmitted message (
) and the received message (
) are then compared for the error value as
; the BER is computed, and the results are shown in the following
Figure 1,
Figure 2,
Figure 3,
Figure 4,
Figure 5 and
Figure 6.
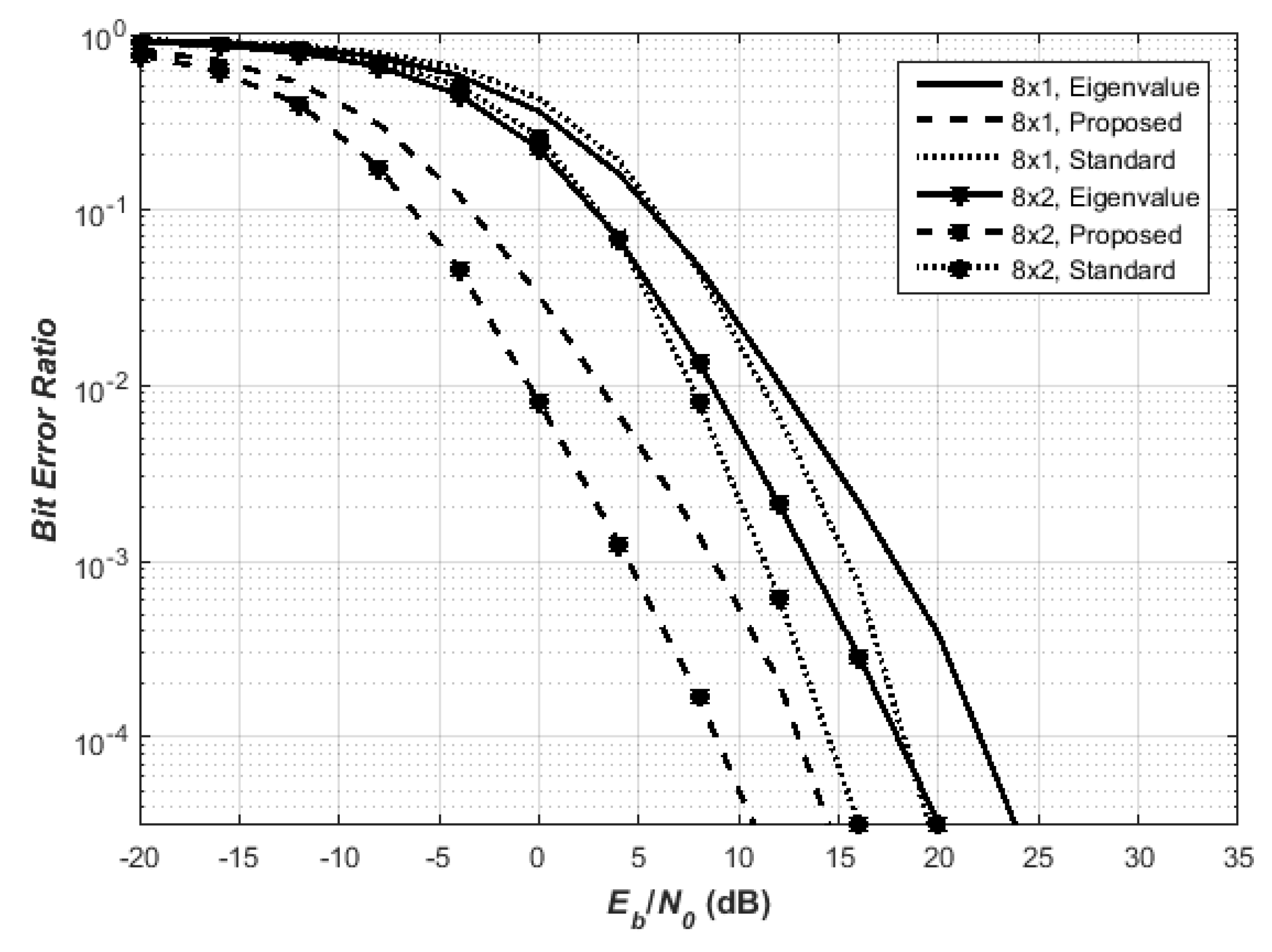
In
Figure 1, the proposed QO-STBC outperforms the standard and eigenvalue QO-STBC styles. Specifically, at
BER, the proposed outperforms eigenvalue QO-STBC by 10 dB and better than the standard QO-STBC by 5 dB. For the MIMO design, namely
, the proposed technique outperforms the standard QO-STBC by 6 dB and better than the eigenvalue QO-STBC technique by 9 dB. The degradation is from the eliminated off-diagonal terms that diminishes the true power of the received signal.
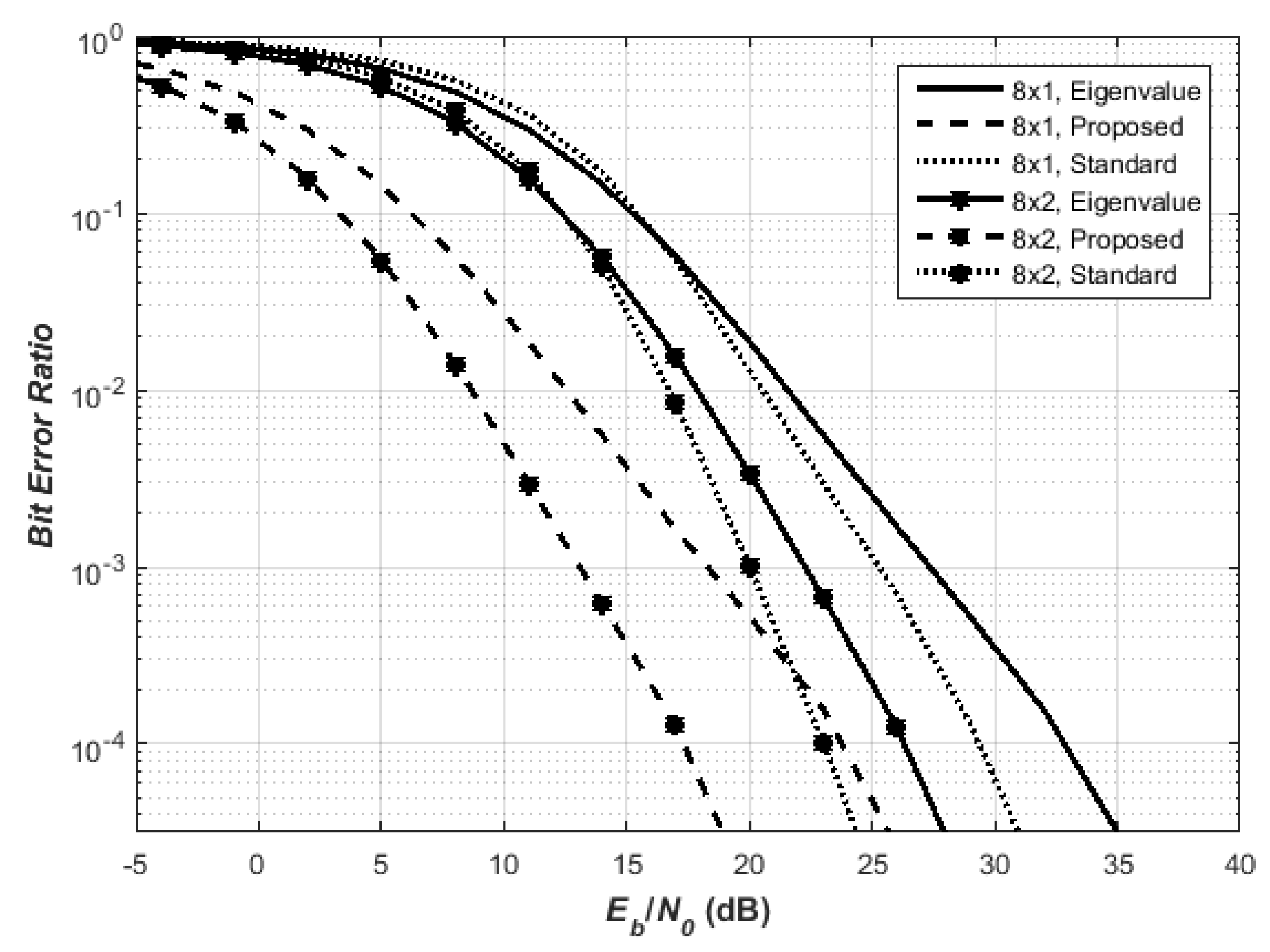
We extend our investigation to 128 QAM as shown in
Figure 2; it is found that the proposed also outperforms both the eigenvalue technique and the standard QO-STBC.
From (
18), the gain
and
impact the amplitude of the received signal while only
impacts the noise. The
amplifies the amplitude of the received signal such that the power gain is improved (see (
18)) compared to the eigenvalue interference-free QO-STBC in
Figure 2. Furthermore, in
Figure 2, this proposed QO-STBC technique translates to a 6-dB gain in comparison to the earlier eigenvalue-based QO-STBC scheme. Significantly, two parts are involved (
and
);
is an interference term that degrades the
gain
. Any method that can eliminate
would further improve the BER performance.
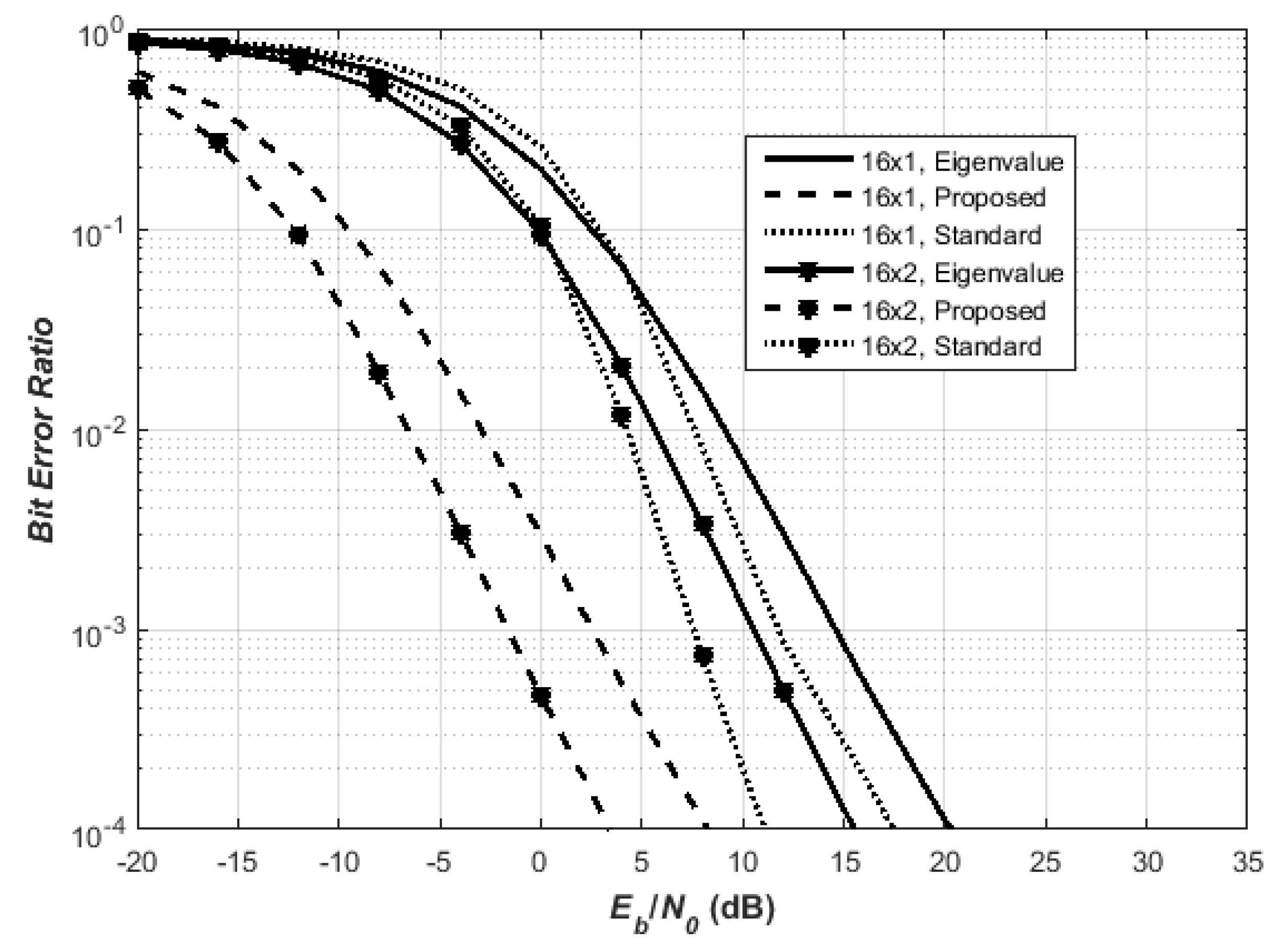
5.2. MISO and MIMO QO-STBC Design Using 16 Transmit Antennas
In (
18), it is found that the result of the proposed QO-STBC (in
Figure 3) satisfied the Hadamard criteria in (
18). For
with the
QO-STBC scheme, the proposed outperformed the eigenvalue QO-STBC. Clearly, the
-times amplitude gain of the Hadamard criteria in (
18) is reflected also in
Figure 3, as the proposed QO-STBC consistently outperformed both the standard and eigenvalue-based QO-STBCs by about 10 dB and 13 dB, respectively, at
BER. In all cases, the proposed method outperformed all other QO-STBCs.
Although the symbols transmitted over antenna spaces are typically unique, however, the EVCM are constructed with respect to
Section 2 of this study. In the receiver, AWGN terms,
, are constructed and added to each receiver antenna branch. Since there are
transmitting branches, then each branch receives
messages up to a total of
(where
for MIMO design) receptions. Again, using the EVCM simplifies the detection of the transmitted symbol for a linear processing so that the estimates of the transmitted symbols,
, are easily decoupled. The receiver finds estimates of
whose Euclidean distance,
, is closest to the transmitted messages; then, 128 QAM signal demodulation is performed in
Figure 4. The proposed method clearly outperformed both the standard and eigenvalue approaches. Both techniques show falling BER measures due to some irreducible errors from the “untrue-gain” and the noise-power enhancement.
In (
27), linear detection was performed; for the QO-STBC discussed in [
17], it was shown that the detection matrix (
27) is huge, complex and contains further degrading elements that limit the improvement from the true gain (
); on the other hand, the QO-STBC method of [
48] provided a matrix that precludes these limitations.
The investigation is further extended to a higher modulation scheme, such as 16 QAM; the results are shown in
Figure 5.
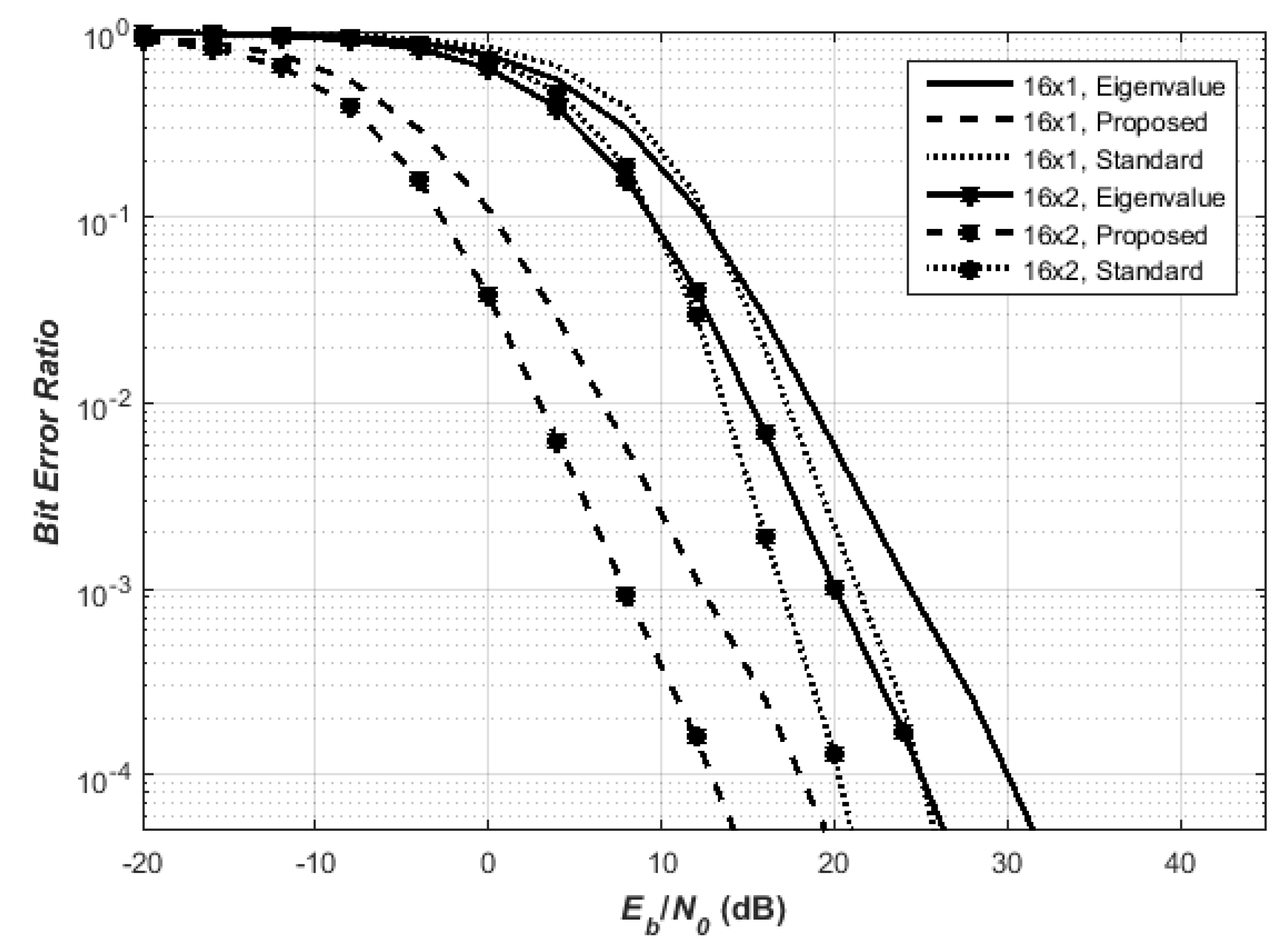
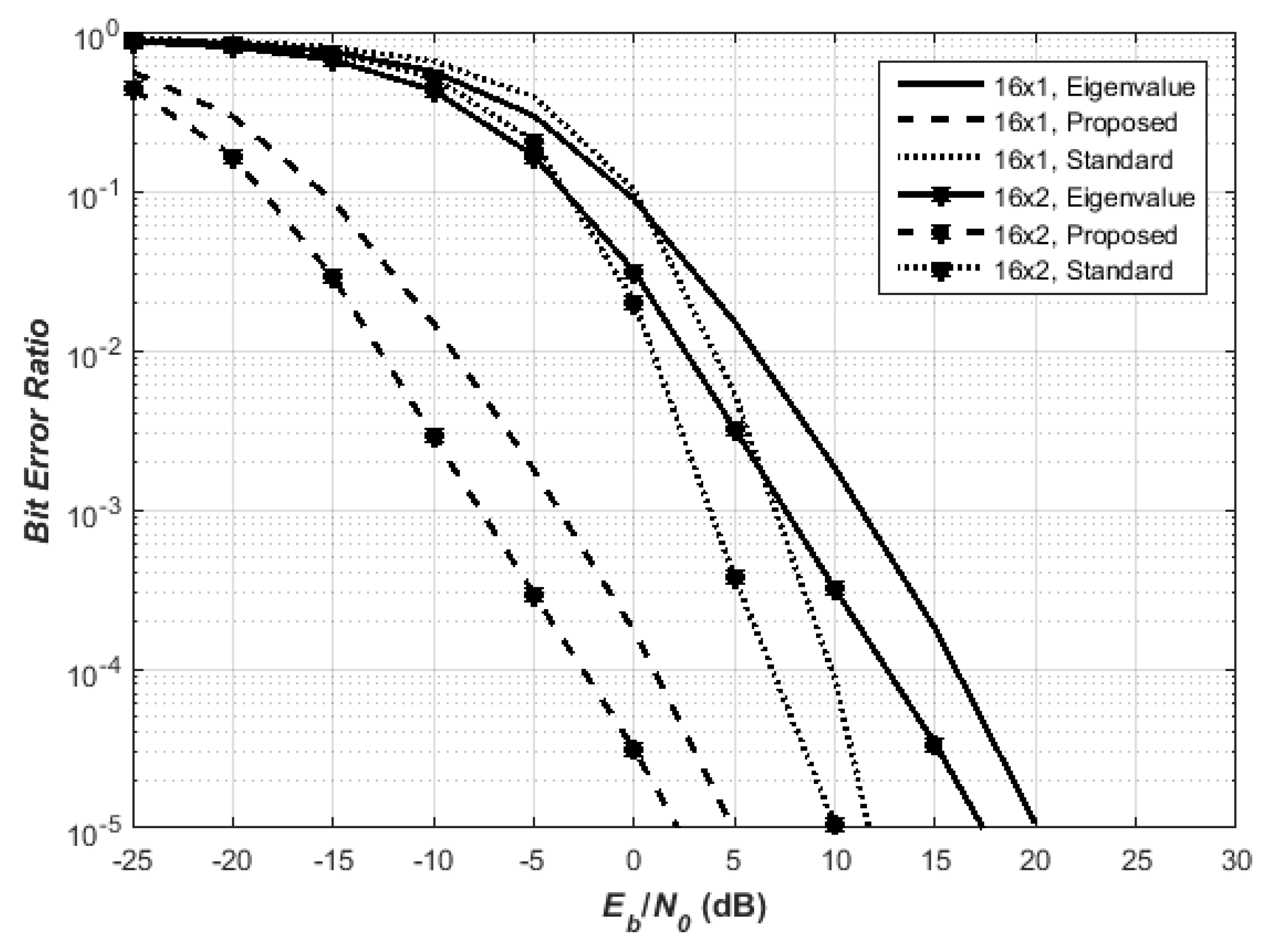
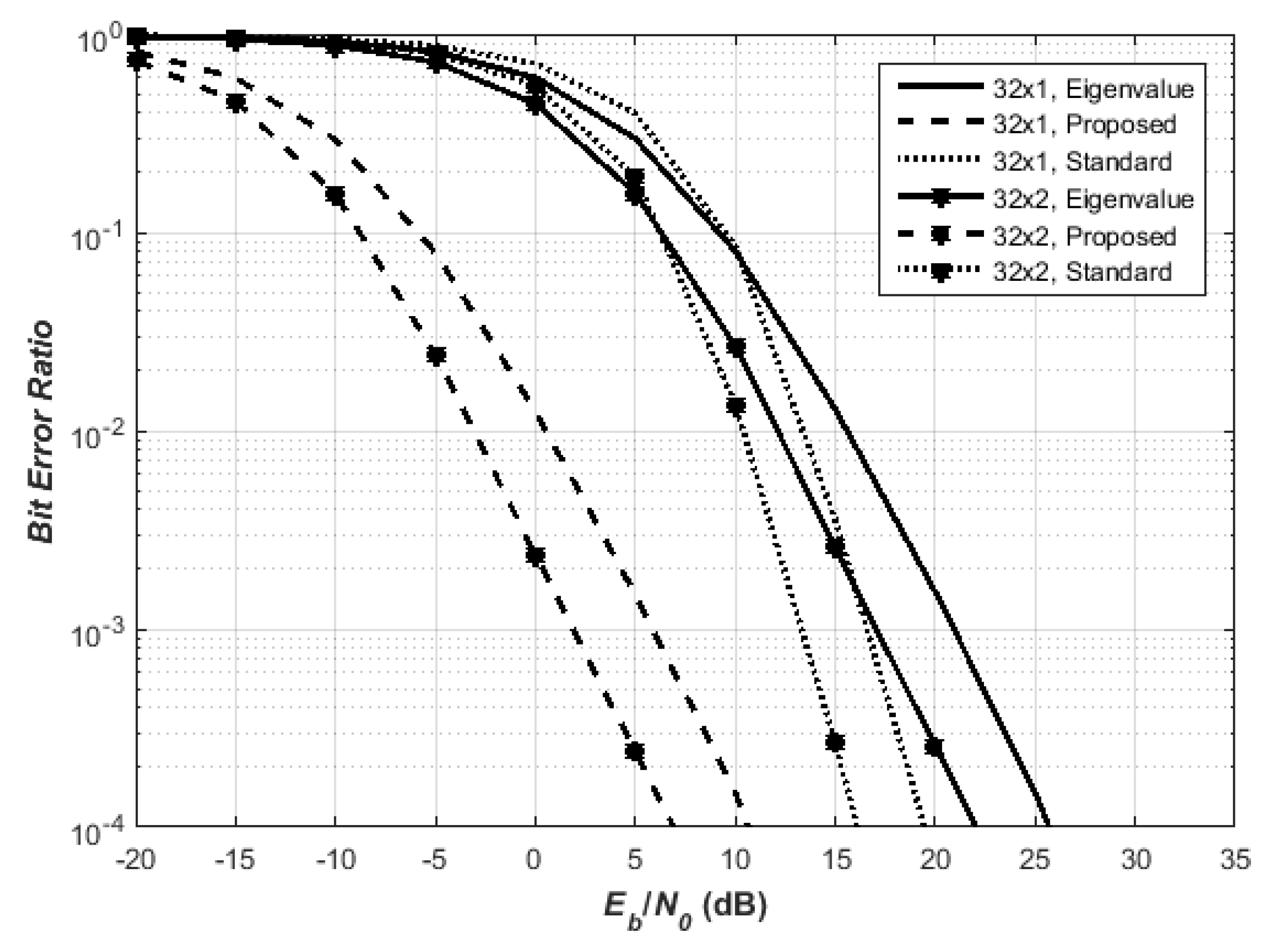
5.3. MISO and MIMO QO-STBC Design Using 32 Transmit Antennas
Finally, we report in
Figure 5 and
Figure 6 the results for
with
using 16 and 128 QAM, respectively. In
Figure 5, the proposed QO-STBC for the 16 × 1 antenna design at
BER outperformed eigenvalue QO-STBC by 15 dB and better than the standard QO-STBC by 8 dB. Consider the design also for the 16 × 2 antenna configurations at
BER, the proposed QO-STBC outperformed eigenvalue-based QOSTBC by 15 dB.
Similarly, the proposed Hadamard-based QO-STBC performs better than the standard QOSTBC technique by 10 dB. From the proposed QO-STBC design coupled with the MRC rule in the receiver, it follows that the performance of the MIMO design method using MRC provides improvement to the QO-STBC system design for independently fading channels, thus showing increasing power gain with increasing receivers. By increasing the transmitter diversity and using a higher order and spectrally-efficient modulation scheme as in
Figure 6, the results for 128-QAM also corroborate the foregoing performance gains achieved by the proposed QO-STBC over other similarly-configured QO-STBC techniques. For example, at
BER for
with
, the proposed QO-STBC design achieves 15 dB better than eigenvalue-based QO-STBC. Similarly, when the receiver diversity is increased from
to
, it can be seen that the proposed scheme achieves 15 dB better than the eigenvalue-based QO-STBC and 12 dB better than the standard QO-STBC.
In general, the off-diagonal interfering terms further reduce the performance of the QO-STBC scheme of the eigenvalue-based QO-STBC design.
Note that due to amplitude modulation in QAM modulators, a normalization of the received symbol amplitudes must be observed before demodulation to realize these results. For PSK symbols, there are no bias-energy terms, and thus, it can be more tolerant than the QAM modulators.
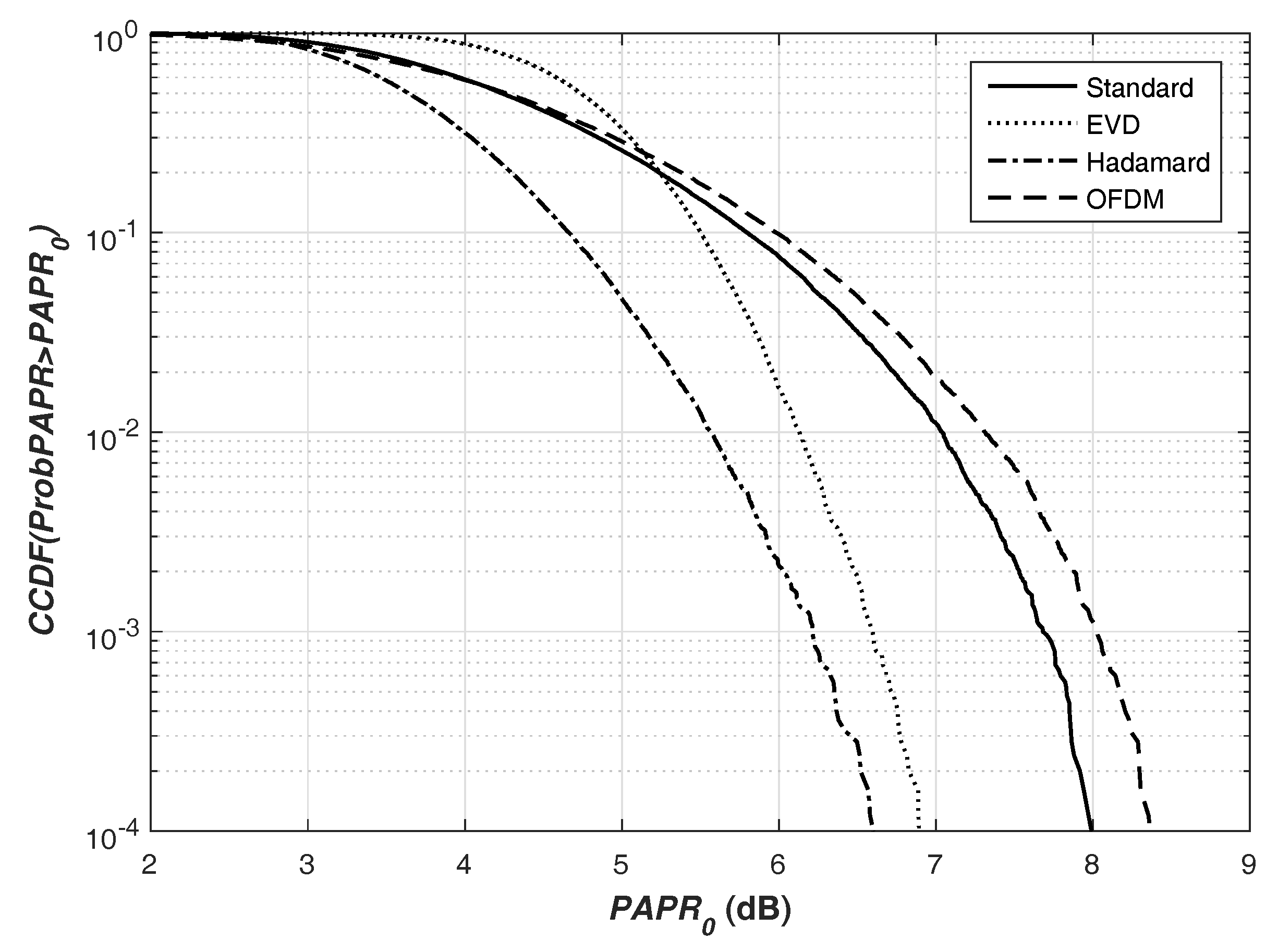
5.4. PAPR Evaluation of Different QO-STBC Schemes
In this section, we evaluate the performances of these different QO-STBC schemes in our foregoing discussion. We show in
Figure 7 the performances of the PAPR metrics of the three QO-STBCs under study using
and 128 QAM modulation.
From the results, the Hadamard technique proffers better PAPR than the rest EVD and standard techniques in all cases. On the other hand, while the Hadamard technique volunteers a better PAPR than the EVD technique, the EVD QO-STBC is also 1 dB better than the standard QO-STBC scheme, which is slightly better than the conventional OFDM system. Meanwhile, the performance of the Hadamard-based (and similarly, the EVD) QO-STBC system can be improved by adopting any of the well-known PAPR reduction techniques. Such techniques must also appeal to the aim of this work, which is geared towards reducing the complexity of the receiver, as the receiver modules are general small in nature, and this will eliminate the unnecessary depletion of the limited-battery power of such devices. Examples of such light-weight PAPR reduction techniques include companding and iterative clipping and filtering.