Abstract
Chromosomes are essential carriers of human genetic material, and karyotype diagnosis plays a crucial role in prenatal diagnostics, genetic disease identification, and medical research. Physicians rely heavily on karyotype images to diagnose potential abnormalities in chromosome numbers and structure. However, the process is tedious and challenging. To improve diagnostic efficiency and accuracy, artificial intelligence (AI) researchers have developed convolutional neural networks (CNNs) for chromosome image classification. Despite this progress, the gap between cytogeneticists and AI experts results in a time-consuming workflow. In this study, we propose a framework based on improved Differentiable Architecture Search (DARTS) to automatically design convolutional architectures for the classification task. The improvement strategies based on DARTS are implemented in two stages. First, a procedural approach was designed to comprehensively analyze the evolution of architectural parameters. Based on this analysis, the search space of the DARTS algorithm was refined, resulting in an optimized search space. Next, an entropy-based regularization term was incorporated into the supernetwork’s objective function to guide the algorithm in searching for a more effective architecture. Then, extensive experiments were conducted on CIFAR-10, ImageNet, and the Copenhagen datasets to evaluate the performance of the searched architecture in comparison with related works. The network composed of the searched architecture achieved accuracies of 97.27 0.05%, 75.40%, and 98.64% on the three datasets, respectively. These results demonstrate that the architecture is high-performing and the proposed framework for designing networks for chromosome classification is effective.
1. Introduction
Chromosomes are the specific form in which DNA exists during mitosis or meiosis, and they are easily stained by basic dyes. They serve as the primary carriers of the genetic material of humans. Under normal conditions, the somatic cells of humans contain 23 pairs (46 chromatids) without structural changes [1]. Diseases caused by abnormalities in chromosome structure or number during cell division are referred to as chromosomal disorders. Chromosomal structural abnormalities include cases such as deletions, duplications, translocations, and inversions of segments. If such abnormalities occur during embryonic development, severe cases can result in halted development and miscarriage. Moreover, a few survivors may exhibit deformities, intellectual disabilities, or developmental delays.
Chromosome karyotype analysis is a commonly used clinical method for diagnosing chromosomal abnormalities [2]. This technique involves studying chromosomes during the metaphase stage of cell division and employing banding techniques for the digital imaging of chromosomes. After imaging, professional geneticists manually segment chromosomes from the image, separating them from other impurities. The chromosomes are then semi-automatically classified and paired based on their characteristics in the image, such as length, banding pattern, centromere position, the presence or absence of satellite bodies, and the ratio of the short and long arms. The task of classifying segmented chromosome images into 1 of 24 categories (chromosomes 0–22 and the X/Y sex chromosomes) is known as chromosome image classification (hereinafter referred to as chromosome classification). Once the chromosomes are paired, they are arranged according to the International Standard for Human Cytogenetic Nomenclature (ISCN) and analyzed to determine whether numerical or structural abnormalities are present [3].
Traditional karyotype analysis mainly relies on cytogenetics experts or doctors to preprocess the collected chromosome images, segment and classify chromosomes, pair them, and analyze abnormalities. Among the tasks of segmentation, classification, and counting, chromosome classification and pairing are the most time-consuming steps in clinical practice. This process is influenced by various factors, including the quality of chromosome images, the technical expertise of the physician, and their level of concentration during the operation, making it a low-efficiency and error-prone part of karyotype analysis. Therefore, accurate and efficient chromosome identification is of great importance for automated karyotype analysis.
With the development of computer vision technology, automated chromosome karyotype analysis has gained significant attention from researchers [1,2,4]. Initially, researchers focused on the morphological characteristics of chromosomes, such as the chromosome length, centromere position, and band patterns, using manually designed features or shallow artificial neural networks to extract features for classification [1]. However, constrained by the representational capabilities of manual features, these methods fail to meet the requirements for automated karyotype analysis. In 2012, AlexNet, a deep CNN, achieved remarkable performance on natural image datasets. Researchers discovered that the feature representation capabilities of deep CNNs far surpassed those of manually designed features [5]. Consequently, some researchers began using CNNs to perform tasks in chromosome karyotype analysis, such as classification and segmentation, achieving significant results and advancing the automation of karyotype analysis [6,7,8,9,10,11]. Therefore, the progress of research in automating karyotype analysis heavily relies on the development of CNNs.
In various computer vision tasks, researchers have consistently viewed the architecture as a crucial factor influencing the performance of CNNs and have continuously designed numerous advanced architectures [5,12,13,14]. However, manually designing an architecture for a task, even by experienced experts, is time-consuming and requires extensive trial-and-error experimentation [15]. To improve the efficiency of architecture design, researchers have proposed algorithms to automatically design CNN architectures under constrained conditions. This technology is known as neural architecture search (NAS) [16]. NAS mainly consists of three approaches: reinforcement learning (RL) [16], evolutionary algorithms (EAs) [17], and DARTS [18]. Researchers have proposed numerous improvements based on these methods and have applied NAS to various vision tasks [19], such as human sperm image assessment [20], hyperspectral image classification [21], and multi-modal classification [22], to automatically design suitable CNN architectures for these tasks.
To the best of our knowledge, there are few researchers who have utilized the technology to design a CNN architecture for chromosome image classification. On the other hand, due to the unique feature of dark and light bands in chromosomes, it is difficult for computer vision researchers without a background in genetics to manually design an architecture using prior knowledge. To overcome the extensive demand for additional knowledge and the inefficiency of manual design, this study proposes a framework based on an improved DARTS algorithm, named E-DARTS, to automatically and efficiently design CNN architectures for chromosome recognition tasks. We conducted extensive experiments on Copenhagen, CIFAR-10 [23], and ImageNet [24], achieving accuracies of 98.64%, 97.27 0.05%, and 75.40%, respectively. The results demonstrate that using the algorithm to design architectures for chromosome classification tasks is efficient and feasible.
2. Materials and Methods
2.1. The Dataset
This study involves three publicly available datasets: CIFAR-10, ImageNet, and Copenhagen. Following DARTS and related works, the architecture search phase uses the CIFAR-10 as a proxy dataset to prevent memory overflow when directly using the target dataset. The evaluation network is constructed using the searched cell, and its performance is first tested on two standard datasets, CIFAR-10 and ImageNet. Subsequently, the network is transferred to the Copenhagen Chromosome Dataset for further experimentation.
2.1.1. CIFAR-10
CIFAR-10 is a natural image dataset with 10 classes, including airplane, automobile, bird, cat, deer, dog, frog, horse, ship, and truck. It consists of 50,000 training images and 10,000 testing images, both with a resolution of 32 × 32 pixels. During the architecture search phase, the training set is split into two halves: one half is used to train the convolutional kernel parameters of the candidate operations, while the other half is used to train the architecture parameters. After deriving the cells from the search phase to construct the evaluation network, the network is trained on the full training set, and its performance is assessed based on the accuracy achieved on the test set.
2.1.2. ImageNet
ImageNet is one of the most widely recognized datasets for image classification research. It contains approximately 1,280,000 images in the training set and 50,000 images in the validation set, spanning 1000 categories. This dataset was led by Feifei Li to address the issues of overfitting and generalization in machine learning, and its test results serve as the gold standard for evaluating network architecture performance. Therefore, we also evaluated the performance of the evaluation network on this dataset.
2.1.3. Copenhagen
Copenhagen, created by Lundsteen et al. [25], is one of the most widely used datasets for chromosome classification, along with Edinburgh and Philadelphia [2]. There are 180, 125, and 130 cells in these datasets, respectively. A total of 8106 chromatid images were derived from these Copenhagen cells. Since the image quality of Copenhagen is better than that of the others, it was selected for the chromosome classification experiments. Due to the varying resolutions of the samples, we applied a preprocessing step to standardize them for input into the CNN. Specifically, we placed all samples on a 200 × 200 black background to ensure a consistent resolution across the dataset.
2.2. Methods
In this study, we propose a framework based on improved DARTS for chromosome classification, as illustrated in Figure 1. Based on the observed similarity between the visualized convolutional kernels of AlexNet [5] and the banding patterns of chromosomes, we assume that an architecture capable of extracting features layer by layer from natural image datasets can also be used for chromosome classification tasks. Based on this assumption, we developed an improved network architecture search algorithm from both the search space and search algorithm perspectives. Finally, the network constructed from the cell searched by the algorithm was used for chromosome classification.
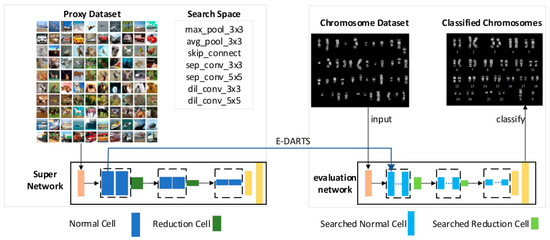
Figure 1.
The proposed NAS framework for chromosome classification.
2.2.1. Overall Framework
In this study, we present an algorithmic framework to design CNN for chromosome classification, which is primarily divided into two phases: the search phase within a constrained search space (as illustrated on the left side of Figure 1) and the phase in which a classification network is constructed via cells searched using the algorithm (as shown on the right side of Figure 1).
The search phase involves three key components: selecting a proxy dataset, designing the search space, and constructing a supernetwork. First, to maintain similar GPU memory requirements as DARTS, we used CIFAR-10 with a lower resolution for the search phase rather than a chromosome dataset. As illustrated in Figure 1, our supernetwork adopts the same configuration as DARTS—it is composed of d cells, where the d/3rd and the 2d/3rd cells are reduction cells, while all the remaining cells are normal cells. In a normal cell, each convolutional layer maintains the spatial resolution through padding, whereas a reduction cell reduces the spatial resolution of the feature maps by applying a stride of 2 at its input layer. We further refine the DARTS search space by reducing the number of candidate operations. At the end of the search phase, our algorithm outputs a normal cell and a reduction cell, both of which are then used to build the classification network.
In the classification network construction phase, there are two key components: evaluating the performance of the classification network and using it for chromosome classification. Network architecture search algorithms typically build a deeper CNN based on the discovered cells and assess its performance on CIFAR-10 and ImageNet. To facilitate comparison with related algorithms, we conducted performance evaluation experiments, the details of which are provided in Section 3. Additionally, to validate our earlier hypothesis, we applied the same classification network to a chromosome dataset to perform the chromosome image classification task.
2.2.2. Principle of DARTS
DARTS uses cells as the basic units for architecture search, represented by directed acyclic graphs. This graph consists of several ordered nodes and directed edges connecting the nodes, where the nodes represent feature maps of the network and the directed edges represent transformation operations between nodes. A cell defined by DARTS consists of 7 ordered nodes, including 2 input nodes, 4 intermediate nodes, and 1 output node. Each intermediate node is connected to the input nodes and its preceding intermediate nodes through directed edges, as defined in Equation (1).
Here, represents an intermediate node in the cell, represent a preceding node of , denotes the transformation operation connecting and , and and represent the node indices.
The transformation operations represented by the edges in a cell are mixed operations—weighted sums of candidate operations and architecture parameters. Each architecture parameter serves as the weight for its corresponding candidate operation. To ensure that all architecture parameters share a uniform value range, the algorithm applies the softmax function to relax these parameters, normalizing their values within the (0, 1) interval. After applying softmax, the transformation operation in Equation (1) is rewritten as follows:
In Equation (2), represents a candidate operation, and denotes the relaxed transformation operation. and represent the architecture parameters corresponding to candidate operations or on the directed edge . The indices and indicate node numbers. represents the set of candidate operations, which includes a total of 8 operations: 3 × 3/5 × 5 separable convolution (sep_conv), 3 × 3/5 × 5 dilated separable convolution (dil_conv), 3 × 3 average/max pooling (avg/max_pool), skip connection (skip_connect), and no connection (none).
DARTS incorporates architecture parameters into the cells and constructs a supernetwork by stacking these cells for end-to-end training, transforming the discrete architecture search problem into a parameter optimization problem within a continuous space. As the supernetwork is trained, the architecture parameters in the transformation operation gradually converge.
Based on these converged architecture parameters, the importance of candidate operations in the transformation operation can be assessed, leading to the derivation of a simplified cell. This derivation process involves two steps. The first step is candidate operation simplification: among the 8 candidate operations on a directed edge, only the operation with the highest weight (excluding ‘none’) is retained; the second step is directed edge simplification: after candidate operation simplification, only the two edges with the top 2 weights are kept among those connecting each intermediate node to all preceding nodes.
2.2.3. Search Space of E-DARTS
According to the DARTS algorithm strategy, Equation (2) defines the architecture parameters from two perspectives:
- Architecture parameters indicate the importance of candidate operators in transformation operations.
- The architecture parameters are relaxed to normalize them within the (0, 1) interval, with the sum of the parameters for all candidate operations on a directed edge constrained to equal 1.
With this constraint, the algorithm aims to use the architecture parameters as quantitative indicators to compare the importance of candidate operations once the supernetwork has been optimized, retaining the candidate operation with the highest parameter value as the optimal one. However, excluding the ‘none’ operation during derivation may introduce potential issues. To evaluate whether the above strategy achieves its intended goal, we plot the curves of all architecture parameters over the course of supernetwork optimization iterations, as shown in Figure 2.
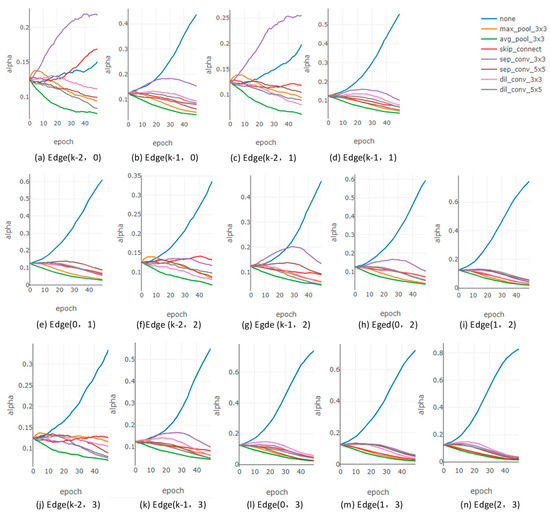
Figure 2.
The curves of all architecture parameters of normal cells during search in DARTS. (a,b) illustrate the architecture parameters corresponding to all candidate operations connecting node 0 and its predecessor nodes. (c–e) illustrate the architecture parameters corresponding to all candidate operations connecting node 1 and its predecessor nodes. (f–i) illustrate the architecture parameters corresponding to all candidate operations connecting node 2 and its predecessor nodes. (j–n) illustrate the architecture parameters corresponding to all candidate operations connecting node 3 and its predecessor nodes.
Using a procedural analysis approach, we found that the architecture parameters of all directed edges exhibit two main trends. The trend shown in Figure 2a,c appears on the shallowest connecting edges of the intermediate nodes (i.e., edges connecting intermediate nodes to input nodes). In contrast, the trend shown in Figure 2e,i,n is observed on all other deeper edges (i.e., edges where the predecessor node of the current node is another intermediate node rather than an input node).
In Figure 2a,c, the values of the architecture parameters are relatively dispersed, and the candidate operations selected according to the first step of the derivation strategy generally align with DARTS’s design principle of selecting the optimal operation based on architecture parameters. For other directed edges, the architecture parameter corresponding to the ‘none’ operation is the largest and holds an overwhelming advantage. Additionally, since the sum of all architecture parameters equals 1, the parameters corresponding to other candidate operations are constrained to a very small range and show minimal distinction in their values. Further analysis reveals that the ‘none’ operation’s architecture parameter exhibits an increasingly dominant advantage on deeper directed edges (for example, as shown in Figure 2i,n).
According to the first step of the DARTS derivation strategy, the ‘none’ operation is excluded from the maximum weight evaluation. This strategy results in the ‘none’ operation suppressing other effective candidate operations in deeper edges when using architecture parameters as a quantitative metric to determine the optimal candidate, leading to very low architecture parameter values for effective operations. This compromises the algorithm’s intended goal of selecting the optimal candidate operation based on architecture parameters. The issue caused by the first step of the derivation strategy further impacts step two. During directed edge simplification, the effective candidate operations retained in deeper edges have smaller parameter values, making it difficult for them to compete equally with those retained in shallower edges. Consequently, the algorithm ultimately favors cell architectures with shallow connections. Shu et al. also identified this issue and noted that such cells have poor generalization [26].
We argue that the root cause of the aforementioned issue is the inclusion of the ‘none’ operation, which is ineffective for derivation, in the set of candidate operations. As the supernetwork is trained, the ‘none’ operation increasingly dominates over other operations, which we interpret as a form of overfitting in the supernetwork. From the perspective of the DARTS derivation strategy, this leads to the inclusion of ‘none’ operations in the cells defined during the search phase, ultimately resulting in ‘none’ operations dominating the architecture parameters in the derivation phase.
Building on the procedural analysis above and the derivation strategy of the DARTS algorithm, we identified the root cause of how the ‘none’ operation affects the optimization of architecture parameters. Based on these insights, we propose an optimized search space in which the candidate operation set excludes the ‘none’ operation and consists of only seven effective operations: 3 × 3/5 × 5 sep_conv, 3 × 3/5 × 5 dil_conv, 3 × 3 avg_pool, 3 × 3 max_pool, and skip_connect.
After optimizing the search space, we also employed a procedural analysis approach, as shown in Figure 3. The evolution trends of the architecture parameters after the search space optimization are shown in Figure 3a,c for shallower edges, which exhibit minimal differences compared to those before optimization. For deeper edges, the evolution of architecture parameters after the search space optimization is illustrated in Figure 3e,i,n. Before the search space optimization, the ‘none’ operation in Figure 2e had an overwhelming advantage in this deep edge, severely affecting other effective candidate operations. After the search space optimization, the values of the architecture parameters for candidate operations in Figure 3e are more dispersed compared to Figure 2e.
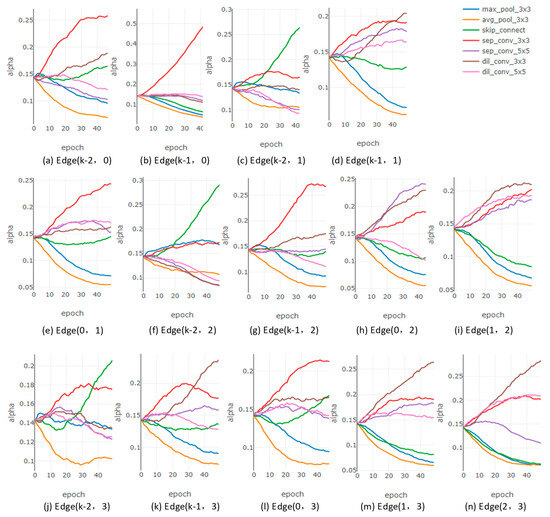
Figure 3.
The curves of all architecture parameters of normal cells after search space optimization. (a,b) illustrate the architecture parameters corresponding to all candidate operations connecting node 0 and its predecessor nodes. (c–e) illustrate the architecture parameters corresponding to all candidate operations connecting node 1 and its predecessor nodes. (f–i) illustrate the architecture parameters corresponding to all candidate operations connecting node 2 and its predecessor nodes. (j–n) illustrate the architecture parameters corresponding to all candidate operations connecting node 3 and its predecessor nodes.
Comparing Figure 2 and Figure 3 reveals that when selecting the optimal candidate operation based on architecture parameters as a quantitative indicator, the optimized search space enables effective candidate operations to prevail during the derivation phase. Furthermore, during directed edge simplification, the winning candidate operations in deeper edges can be fairly compared with those from shallower edges, aligning better with the expectations of the search algorithm and derivation strategy.
Figure 3 also reveals that, as the supernetwork is trained, the architecture parameters corresponding to parameterless candidate operations (pool and skip) and those of parameterized candidate operations (sep_conv and dil_conv) gradually differentiate. In most directed edges, the architecture parameters for parameterized candidate operations are greater than those for parameterless ones. This trend favors the parameterized candidate operations in competition, reducing the potential number of skips in the derived cell to some extent and mitigating the risk of performance degradation caused by excessive skip connections in the derived cell [27].
2.2.4. Search Algorithm of E-DARTS
The DARTS algorithm creatively integrates architecture parameters into the definition of the search cell. During the architecture search phase, this strategy transforms the discrete architecture search problem into a continuous parameter optimization problem. In the architecture evaluation phase, these optimized architecture parameters need to be converted from their continuous representation to a discrete one-hot encoded representation. To achieve this, DARTS introduces a corresponding derivation strategy. While this strategy enables the discretization of architecture parameters and the derivation of a cell, the discrepancy between the two representations of architecture parameters is not adequately addressed.
To quantify this discrepancy, Xie et al. linked architecture parameters to entropy at the level of directed edges, defining ‘certainty’ as a measure to quantify the likelihood that the derived architecture is the optimal architecture in the parameter space [28]. They observed that after the supernetwork completes its training, the architecture parameter distributions for each edge retain relatively high entropy. High entropy indicates low certainty in the supernetwork regarding the selected architecture, implying a reduced likelihood that the derived architecture represents the optimal one. This low certainty results in a ‘gap’ between the performance of the cell based on transformation operation in the supernetwork and the derived architecture on the validation set.
We consider that if the search algorithm could guide architecture parameters toward the final discrete one-hot representation, encouraging their convergence into one-hot vectors, it would reduce the entropy of the architecture during the optimization of the supernetwork. This would increase the certainty of the supernetwork regarding the search results, narrow the discrepancy between the continuous and discrete representations of the architecture parameters, and mitigate the performance gap.
Inspired by the work of Xie et al., this study interprets the architecture parameters—normalized to the (0, 1) interval according to the DARTS definition of a cell—as the probabilities of their corresponding candidate operations being selected as the optimal ones by the supernetwork. Building on this perspective and leveraging the concept of entropy, we define architecture entropy based on the vector of all normalized architecture parameters, as shown in Equation (3). This metric quantifies the certainty of the supernetwork in its search results, with a reduction in architecture entropy indicating an increase in the supernetwork’s certainty.
In Equation (3), represents the architecture entropy, and and denote the normalized architecture parameter of a normal cell and reduced cell, respectively. refers to the directed edge between node and node .
In this study, is introduced as a regularization term in the objective function of the DARTS algorithm during the architecture search phase. The goal is to reduce discrepancies between cells at different stages and enhance the supernetwork’s confidence in the discovered architecture. The objective function of the supernetwork is defined as shown in Equation (4).
In Equation (4), represents the validation loss, denotes the convolutional kernel parameters within the candidate operations, and is the coefficient used to balance and .
3. Experiments
Following the experimental setup of DARTS and related works, the architecture search phase utilizes the CIFAR-10 dataset as a proxy to prevent memory overflow when directly using the target dataset. The evaluation network is constructed using the searched cell, and its performance is first assessed on two standard datasets, CIFAR-10 and ImageNet. Subsequently, it is employed as a classification network for further experimentation on the Copenhagen Chromosome Dataset.
The experimental setup for the search phase was conducted on a single Nvidia GeForce GTX 1080Ti GPU (It was manufactured by MSI and sourced from Guangzhou, China). For evaluation on the Copenhagen dataset, both training and testing were performed using a single Nvidia GeForce GTX 1080Ti. On the CIFAR-10 dataset, training and testing utilized two Nvidia GeForce GTX 1080Ti GPUs, while on the ImageNet dataset, four Nvidia Titan RTX GPUs (They were manufactured by Nvidia and sourced from Guangzhou, China) were used for training and testing. All experiments were implemented using PyTorch 1.2.
3.1. Results on CIFAR-10
Besides differences in the search space and optimization objective function, the construction of the supernetwork during the search phase remains consistent with DARTS. The supernetwork consists of eight cells, where the third and sixth cells are reduction cells, and the remaining are normal cells. The supernetwork is trained for 50 epochs with a batch size of 64, employing a first-order approximation optimization strategy [18]. The regularization coefficient is set to 0.05, selected from the set (0, 0.01, 0.05, 0.1, 1) based on four experimental runs for each value. To optimize the convolutional kernel parameters of the candidate operations, stochastic gradient descent (SGD) is used with an initial learning rate of 0.025, a momentum of 0.9, and a weight decay coefficient of 3 × 10−4. To optimize the architectural parameters, the adaptive moment estimation (Adam) algorithm is applied with an initial learning rate of 3 × 10−4 and a weight decay coefficient of 10−4.
Based on the previously described setup, the cells searched using the algorithm are illustrated in Figure 4. Compared to the cells obtained by the DARTS algorithm, the cells derived in this study have more layers and exhibit a deeper structure. The results validate our earlier hypothesis that optimizing the search space by excluding the ‘none’ operation effectively prevents the dominance of optimal operations in shallow edges, which would otherwise lead to an overall shallow cell structure.
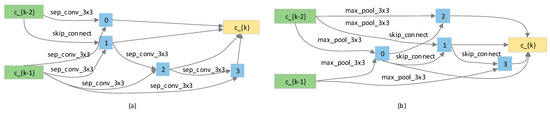
Figure 4.
The searched cells of E-DARTS. (a) The normal cell searched using the algorithm; (b) the reduction cell searched using the algorithm.
This study follows the same experimental setup as DARTS and constructs an evaluation network with a depth parameter d = 20. In this network, the cells at d/3 and 2d/3 are reduction cells, while all others are normal cells. Table 1 presents the results on the CIFAR-10 dataset, along with a comparison of classification accuracy against architectures derived from related methods on the same dataset. Following the setup of DARTS, we also report the mean and standard deviation of 10 independent runs in Table 1.

Table 1.
A comparison of accuracy with related work on CIFAR-10.
As presented in Table 1, the evaluation network constructed in this study achieved a test accuracy of 97.21 0.17% on CIFAR-10 when utilizing only the optimized search space (denoted as E-DARTS_S). When the regularization term was further introduced into the objective function based on the optimized search space, the test accuracy of the evaluation network increased to 97.27 % (denoted as E-DARTS). Using the same first-order approximation optimization strategy as DARTS, this approach improved accuracy by 0.27 % over DARTS. Additionally, the test accuracy surpassed that of ENAS [29] and SNAS [28]. In terms of search time, the architecture search time in this study was comparable to that of P-DARTS [27] and β-DARTS [30], demonstrating high search efficiency. Considering both accuracy and search time, the proposed method demonstrates competitive performance compared to state-of-the-art (SOTA) approaches. The results demonstrate the effectiveness of the proposed method.
3.2. Results on ImageNet
CIFAR-10 is a relatively small-scale image classification dataset. On this dataset, many network architectures designed by different algorithms achieve comparable performance. Consequently, most architectures are further evaluated on ImageNet to test their performance on a large-scale dataset. In this study, we adopted the evaluation methodology used by DARTS and its related algorithms. Specifically, the cell obtained from the search phase was used to construct a complete network, which was then trained and evaluated on ImageNet. The evaluation network has a depth of d = 14 and an initial channel number of C0 = 48. The training strategy for the evaluation network follows that of P-DARTS. A comparison of the performance of the proposed architecture and that obtained using related methods on ImageNet is presented in Table 2. In the table, the symbol ‘~’ denotes approximate values.

Table 2.
A performance comparison with related work on ImageNet.
The network built using the cell derived from our algorithm achieved a classification accuracy of 75.4% on ImageNet. Compared to manually designed architectures, this accuracy surpasses Inception-v1 by 5.6%, MobileNets by 4.8%, and ShuffleNet by 1.7%. These results demonstrate that the architecture discovered by our algorithm outperforms several classic human-designed networks.
Compared to other NAS methods, the architecture derived from our algorithm outperforms those searched by DARTS [18], SNAS [28], CARS [31], and PC-DARTS [32] while achieving performance comparable to architectures searched by P-DARTS [27] and DaNAS [33]. From a computational cost perspective, our architecture achieves higher classification accuracy than architectures like CARS-I [31] and PNAS [34], which have similar computational requirements. Moreover, the proposed algorithm completed the architecture search in just 0.3 days, achieving a 0.1-day improvement in efficiency over DARTS and matching the speed of P-DARTS [27], DaNAS [33], and β-DARTS [30], second only to PC-DARTS [32].
Since ImageNet is the most authoritative dataset for image classification, the experimental results on this dataset provide strong evidence of the transferability of the cells discovered by the proposed algorithm. Considering three key factors—classification accuracy, search time, and computational cost—the results demonstrate that the network composed of the searched cells achieves a high level of performance compared to related studies.
3.3. Results on Copenhagen
The experiments on ImageNet and CIFAR-10 demonstrate that the architecture derived in this study exhibits strong feature extraction capabilities and achieves competitive performance compared to related works. We hypothesize that this capability is also well suited for chromosome image classification. To further investigate the transferability of the searched architecture, we conducted experiments on the chromosome dataset and compared its performance with other networks and related works on the same dataset [5,6,12,13,14,35,36].
Given that the resolution of chromosome samples (200 × 200) is similar to that of ImageNet samples (224 × 224), the evaluation network was constructed following the configuration used on the ImageNet dataset, comprising a total of 14 cells. To evaluate the performance of the classification network stacked by the searched cells on Copenhagen, we compared it against several architectures designed by experts manually, including the classic networks AlexNet, VGG16, ResNet18, and DenseNet, as well as two chromosome-classification-specific networks, Sharma and Verifocal-Net. These networks were also manually designed by experts and have demonstrated strong performance. Notably, Verifocal-Net is a two-stage model. For a fair comparison, we only considered its G-Net component.
During training, the models were initialized from scratch with learning rates of 0.1, 0.01, 0.001, and 0.0001. The learning rate was reduced by a factor of 10 every 25 epochs, for a total of 100 epochs. After training, the best-performing result was recorded as shown in Table 3.

Table 3.
A performance comparison of classical architectures on Copenhagen.
As shown in Table 3, the classification network constructed using the cells searched by our algorithm achieved an accuracy of 98.64% on the Copenhagen chromosome dataset. Compared to manually designed classic networks, its classification accuracy is approximately 2 percentage points higher than AlexNet [5], 1 percentage point higher than VGG16 [12], and 0.6 percentage points higher than ResNet [13] and DenseNet [14]. When compared to networks designed explicitly for chromosome classification, it outperforms the network proposed by Sharma et al. [6] by about 1 percentage point and achieves the same accuracy as G-Net [36]. It is worth noting that while G-Net uses standard convolutions, our method employs lightweight depthwise separable convolutions. Compared to standard convolutions, depthwise separable convolutions require significantly fewer parameters, resulting in a more compact network at the same depth. As a result, our deeper classification network achieves accuracy comparable to that of G-Net.
These results indicate that the architecture discovered by our algorithm using CIFAR-10 as a proxy dataset performs competitively on the chromosome dataset. This highlights the effectiveness of our approach in transferring from natural image classification tasks to the classification of specialized chromosome image data.
3.4. Ablation Experiments
Building upon the DARTS algorithm, this study optimizes the design of the search space and introduces architecture entropy as a regularization term in the supernetwork’s objective function. To assess the impact of these two strategies, ablation experiments were conducted on CIFAR-10 and ImageNet. Each algorithm was run four times on CIFAR-10, with both the average and the best performance recorded. The architectures corresponding to the best results were selected as the final output of the algorithm and were further evaluated on ImageNet to evaluate their performance. The results are shown in Table 4.

Table 4.
The ablation experiment results of the improved strategy.
The experimental results indicate that only applying the search space optimization strategy leads to a moderate improvement over the original DARTS. This suggests that refining the search space effectively eliminates the interference of the ‘none’ operation with other valid candidate operations, thereby enabling the algorithm to search higher-performing architectures.
However, when solely introducing the architectural entropy constraint to DARTS (denoted as E-DARTS-R), the performance of the network drops significantly. This decline occurs because DARTS inherently suffers from the suppression of valid candidate operations due to the ‘none’ operation. The evolution of the architecture parameters is shown in Figure 5. Without first addressing this issue, introducing an additional constraint further exacerbates the dominance of the ‘none’ operation, leading to degraded performance.
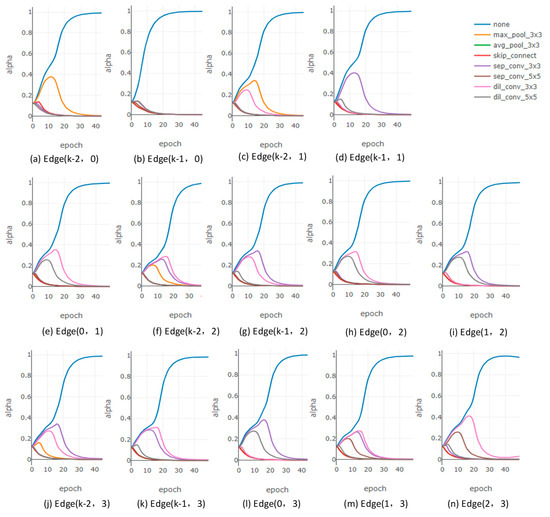
Figure 5.
The curves of all architecture parameters of normal cells when solely introducing the architectural entropy constraint. (a,b) illustrate the architecture parameters corresponding to all candidate operations connecting node 0 and its predecessor nodes. (c–e) illustrate the architecture parameters corresponding to all candidate operations connecting node 1 and its predecessor nodes. (f–i) illustrate the architecture parameters corresponding to all candidate operations connecting node 2 and its predecessor nodes. (j–n) illustrate the architecture parameters corresponding to all candidate operations connecting node 3 and its predecessor nodes.
Conversely, when both strategies are applied—first optimizing the search space and then incorporating the architectural entropy constraint—the algorithm is able to search superior architectures. This is because the optimized search space removes the suppression effect of the ‘none’ operation on valid candidates, while the entropy constraint further reduces the gap between the supernetwork and the derived architectures, ultimately yielding better results.
4. Discussion
Intuitively, the Copenhagen chromosome dataset differs significantly from the natural image dataset CIFAR-10, making it seem unlikely that they could share the same network architecture. This raises concerns that performing neural architecture search using CIFAR-10 as a proxy dataset might not yield satisfactory classification performance on the final target dataset. However, the experimental results presented in this study suggest that such concerns are unnecessary.
We believe that there are generally two approaches to designing a convolutional neural network (CNN) for an image classification task. The first approach involves using a general dataset (such as CIFAR-10 or ImageNet) as input and then designing the CNN architecture—either manually or automatically—by determining key elements such as the network depth, kernel size, and types of convolutional operations. Once an architecture demonstrates strong performance on the general dataset, it can be transferred to other, task-specific datasets. In fact, this approach is also commonly seen in object detection, where well-established image classification models are often adopted as backbone networks. The second approach is to directly use the target dataset for network design. This typically requires a deeper understanding of the dataset itself in order to properly set hyperparameters and architectural choices. We argue that, regardless of whether the dataset is Copenhagen or CIFAR-10, CNNs are inherently capable of extracting hierarchical features, from low-level local features to high-level semantic representations. Consequently, a CNN architecture that effectively extracts features from natural images should, in principle, also be capable of progressively extracting features from chromosome images. The framework proposed in this study, which utilizes CIFAR-10 as a proxy dataset and subsequently transfers the searched architecture to the chromosome classification task, benefits from the inherent transferability of CNN architectures.
We believe that directly using the chromosome dataset as the target dataset for the architecture search might yield even better results. However, to maintain consistency with related works in experimental settings and due to GPU memory limitations, we did not conduct such experiments in this study. Nevertheless, we consider this an interesting direction for future exploration.
The approach of downsampling the chromosome image dataset to match the resolution of CIFAR-10 and using it as a proxy dataset presents two major issues: First, chromosomes typically contain more than ten, sometimes over twenty, distinct bands. When the image resolution is too low, each band would be represented by only one or two pixels along the vertical axis, significantly reducing the amount of texture information available in each sample. On the other hand, using higher-resolution images leads to substantial GPU memory consumption. Second, the chromosome dataset is much smaller in scale compared to CIFAR-10, which could negatively impact the performance of the search algorithm.
In the results in Table 3, we observe a general trend where classification performance on the Copenhagen dataset tends to correlate positively with network depth. However, despite having the greatest depth, DenseNet does not achieve the best performance. We speculate that this may be due to a mismatch between the network architecture and the dataset size, preventing the model from fully realizing its potential. We also observe that although the network derived from E-DARTS is deeper, it only achieves the same classification accuracy as G-Net. According to the corresponding literature, G-Net employs standard convolutions. In contrast, the search space used in DARTS-related studies mainly consists of lightweight separable convolutions, which have fewer parameters and weaker representational capacity compared to standard convolutions. As a result, E-DARTS needs a deeper architecture to match the classification performance of G-Net.
As research progresses, network architectures are becoming increasingly powerful, suggesting that datasets for chromosome classification, such as Copenhagen, may also need to scale accordingly. We believe that the release of larger, publicly accessible chromosome datasets would significantly accelerate research on the automation of karyotyping analysis or medical image classification [37].
5. Conclusions
The algorithm framework proposed in this study, which incorporates an improved DARTS algorithm and uses CIFAR-10 as a proxy dataset, successfully searches for high-performance cells with a computational cost of just 0.3 GPU·days. From the perspective of design efficiency, this approach is highly efficient. Based on the derived cell, a complete neural network was constructed and tested on two natural image datasets. The experimental results demonstrate the effectiveness of the proposed approach. Further experiments on a chromosome image dataset reveal that the discovered cell excels at extracting chromosome features and achieves excellent classification performance. These findings indicate that the strategy of searching for network architectures on natural image datasets and transferring them to chromosome image classification tasks is feasible.
Author Contributions
Methodology, J.L., C.Z. and J.Z.; software, M.Z.; validation, J.L. and M.Z.; formal analysis, Z.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was sponsored by Fundamental Research Funds for the Central Universities J2022-046, 24CAFUC04015; Independent Research Project of the Key Laboratory of Civil Aviation Flight Technology and Flight Safety, FZ2022ZZ01; Funds for Civil Aviation Safety Capacity Building, ASSA2024/30.
Data Availability Statement
The CIFAR-10 dataset is publicly available at https://www.cs.toronto.edu/~kriz/cifar.html (accessed on 20 March 2025). The ImageNet dataset is publicly available at https://image-net.org (accessed on 20 March 2025).
Acknowledgments
All authors sincerely appreciate Piper for their enthusiastic assistance and detailed explanations in obtaining the Copenhagen dataset for this study.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Meenakshisundaram, N.; Ramkumar, G. A combined deep CNN-LSTM network for chromosome classification for metaphase selection. In Proceedings of the 2022 International Conference on Inventive Computation Technologies (ICICT), Lalitpur, Nepal, 20–22 July 2022; pp. 1005–1010. [Google Scholar]
- Somasundaram, D.; Madian, N.; Goh, K.M.; Suresh, S. Chromosome segmentation and classification: An updated review. Knowl. Inf. Syst. 2025, 67, 977–1011. [Google Scholar] [CrossRef]
- Menaka, D.; Vaidyanathan, S.G. Chromenet: A CNN architecture with comparison of optimizers for classification of human chromosome images. Multidimens. Syst. Signal Process. 2022, 33, 747–768. [Google Scholar] [CrossRef]
- Piper, J.; Granum, E. On fully automatic feature measurement for banded chromosome classification. Cytom. J. Int. Soc. Anal. Cytol. 1989, 10, 242–255. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012, 25, 1097–1105. [Google Scholar] [CrossRef]
- Sharma, M.; Saha, O.; Sriraman, A.; Hebbalaguppe, R.; Vig, L.; Karande, S. Crowdsourcing for chromosome segmentation and deep classification. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, HI, USA, 21–26 July 2017; pp. 34–41. [Google Scholar]
- Jindal, S.; Gupta, G.; Yadav, M.; Sharma, M.; Vig, L. Siamese networks for chromosome classification. In Proceedings of the IEEE International Conference on Computer Vision Workshops, Venice, Italy, 22–29 October 2017; pp. 72–81. [Google Scholar]
- Lin, C.; Zhao, G.; Yang, Z.; Yin, A.; Wang, X.; Guo, L.; Chen, H.; Ma, Z.; Zhao, L.; Luo, H. Cir-net: Automatic classification of human chromosome based on inception-resnet architecture. IEEE/ACM Trans. Comput. Biol. Bioinform. 2020, 19, 1285–1293. [Google Scholar] [CrossRef]
- Liu, X.; Fu, L.; Chun-Wei Lin, J.; Liu, S. SRAS-net: Low-resolution chromosome image classification based on deep learning. IET Syst. Biol. 2022, 16, 85–97. [Google Scholar] [CrossRef]
- Xiao, L.; Luo, C. DEEPACC: Automate chromosome classification based on metaphase images using deep learning framework fused with priori knowledge. In Proceedings of the 2021 IEEE 18th International Symposium on Biomedical Imaging (ISBI), Nice, France, 13–16 April 2021; pp. 607–610. [Google Scholar]
- Sun, X.; Li, J.; Ma, J.; Xu, H.; Chen, B.; Zhang, Y.; Feng, T. Segmentation of overlapping chromosome images using U-Net with improved dilated convolutions. J. Intell. Fuzzy Syst. 2021, 40, 5653–5668. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. In Proceedings of the 3rd International Conference on Learning Representations (ICLR 2015), San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4700–4708. [Google Scholar]
- Ang, K.M.; Lim, W.H.; Tiang, S.S.; Sharma, A.; Towfek, S.; Abdelhamid, A.A.; Alharbi, A.H.; Khafaga, D.S. MTLBORKS-CNN: An innovative Approach for automated convolutional neural Network design for image classification. Mathematics 2023, 11, 4115. [Google Scholar] [CrossRef]
- Zoph, B.; Le, Q.V. Neural architecture search with reinforcement learning. arXiv 2016, arXiv:1611.01578. [Google Scholar]
- Real, E.; Aggarwal, A.; Huang, Y.; Le, Q.V. Regularized evolution for image classifier architecture search. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; pp. 4780–4789. [Google Scholar]
- Liu, H.; Simonyan, K.; Yang, Y. DARTS: Differentiable architecture search. arXiv 2018, arXiv:1806.09055. [Google Scholar]
- Chitty-Venkata, K.T.; Emani, M.; Vishwanath, V.; Somani, A.K. Neural architecture search benchmarks: Insights and survey. IEEE Access 2023, 11, 25217–25236. [Google Scholar] [CrossRef]
- Miahi, E.; Mirroshandel, S.A.; Nasr, A. Genetic Neural Architecture Search for automatic assessment of human sperm images. Expert Syst. Appl. 2022, 188, 115937. [Google Scholar] [CrossRef]
- Lu, Z.; Liang, S.; Yang, Q.; Du, B. Evolving block-based convolutional neural network for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–21. [Google Scholar] [CrossRef]
- Fu, P.; Liang, X.; Qian, Y.; Guo, Q.; Zhang, Y.; Huang, Q.; Tang, K. Multi-Scale Features Are Effective for Multi-Modal Classification: An Architecture Search Viewpoint. IEEE Trans. Circuits Syst. Video Technol. 2024, 35, 1070–1083. [Google Scholar] [CrossRef]
- Krizhevsky, A. Learning Multiple Layers of Features from Tiny Images. 2009. Available online: https://www.cs.toronto.edu/~kriz/learning-features-2009-TR.pdf (accessed on 20 March 2025).
- Deng, J.; Dong, W.; Socher, R.; Li, L.-J.; Li, K.; Li, F.-F. Imagenet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- Lundsteen, C.; Lind, A.M.; Granum, E. Visual classification of banded human chromosomes. I. Karyotyping compared with classification of isolated chromosomes. Ann. Hum. Genet. 1976, 40, 87–97. [Google Scholar] [CrossRef]
- Shu, Y.; Wang, W.; Cai, S. Understanding architectures learnt by cell-based neural architecture search. arXiv 2019, arXiv:1909.09569. [Google Scholar]
- Chen, X.; Xie, L.; Wu, J.; Tian, Q. Progressive differentiable architecture search: Bridging the depth gap between search and evaluation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 1294–1303. [Google Scholar]
- Xie, S.; Zheng, H.; Liu, C.; Lin, L. SNAS: Stochastic neural architecture search. arXiv 2018, arXiv:1812.09926. [Google Scholar]
- Pham, H.; Guan, M.; Zoph, B.; Le, Q.; Dean, J. Efficient neural architecture search via parameters sharing. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 4095–4104. [Google Scholar]
- Ye, P.; Li, B.; Li, Y.; Chen, T.; Fan, J.; Ouyang, W. b-DARTS: Beta-decay regularization for differentiable architecture search. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 10874–10883. [Google Scholar]
- Yang, Z.; Wang, Y.; Chen, X.; Shi, B.; Xu, C.; Xu, C.; Tian, Q.; Xu, C. Cars: Continuous evolution for efficient neural architecture search. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 1829–1838. [Google Scholar]
- Xu, Y.; Xie, L.; Zhang, X.; Chen, X.; Qi, G.-J.; Tian, Q.; Xiong, H. PC-DARTS: Partial channel connections for memory-efficient architecture search. arXiv 2019, arXiv:1907.05737. [Google Scholar]
- Zhang, B.; Wu, X.; Miao, H.; Guo, C.; Yang, B. Dependency-Aware Differentiable Neural Architecture Search. In Proceedings of the European Conference on Computer Vision, Milan, Italy, 29 September–4 October 2024; pp. 219–236. [Google Scholar]
- Liu, C.; Zoph, B.; Neumann, M.; Shlens, J.; Hua, W.; Li, L.-J.; Li, F.-F.; Yuille, A.; Huang, J.; Murphy, K. Progressive neural architecture search. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 19–34. [Google Scholar]
- Li, J.; Chen, B.; Sun, X.; Feng, T.; Zhang, Y. Banded chromosome images recognition based on dense convolutional network with segmental recalibration. J. Biomed. Eng. 2021, 38, 122–130. [Google Scholar]
- Qin, Y.; Wen, J.; Zheng, H.; Huang, X.; Yang, J.; Song, N.; Zhu, Y.-M.; Wu, L.; Yang, G.-Z. Varifocal-net: A chromosome classification approach using deep convolutional networks. IEEE Trans. Med. Imaging 2019, 38, 2569–2581. [Google Scholar] [CrossRef]
- Hussain, T.; Shouno, H.; Hussain, A.; Hussain, D.; Ismail, M.; Mir, T.H.; Hsu, F.R.; Alam, T.; Akhy, S.A. EFFResNet-ViT: A Fusion-based Convolutional and Vision Transformer Model for Explainable Medical Image Classification. IEEE Access 2025, 13, 54040–54068. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).