A Graphene Nanoribbon Electrode-Based Porphyrin Molecular Device for DNA Sequencing
Abstract
1. Introduction
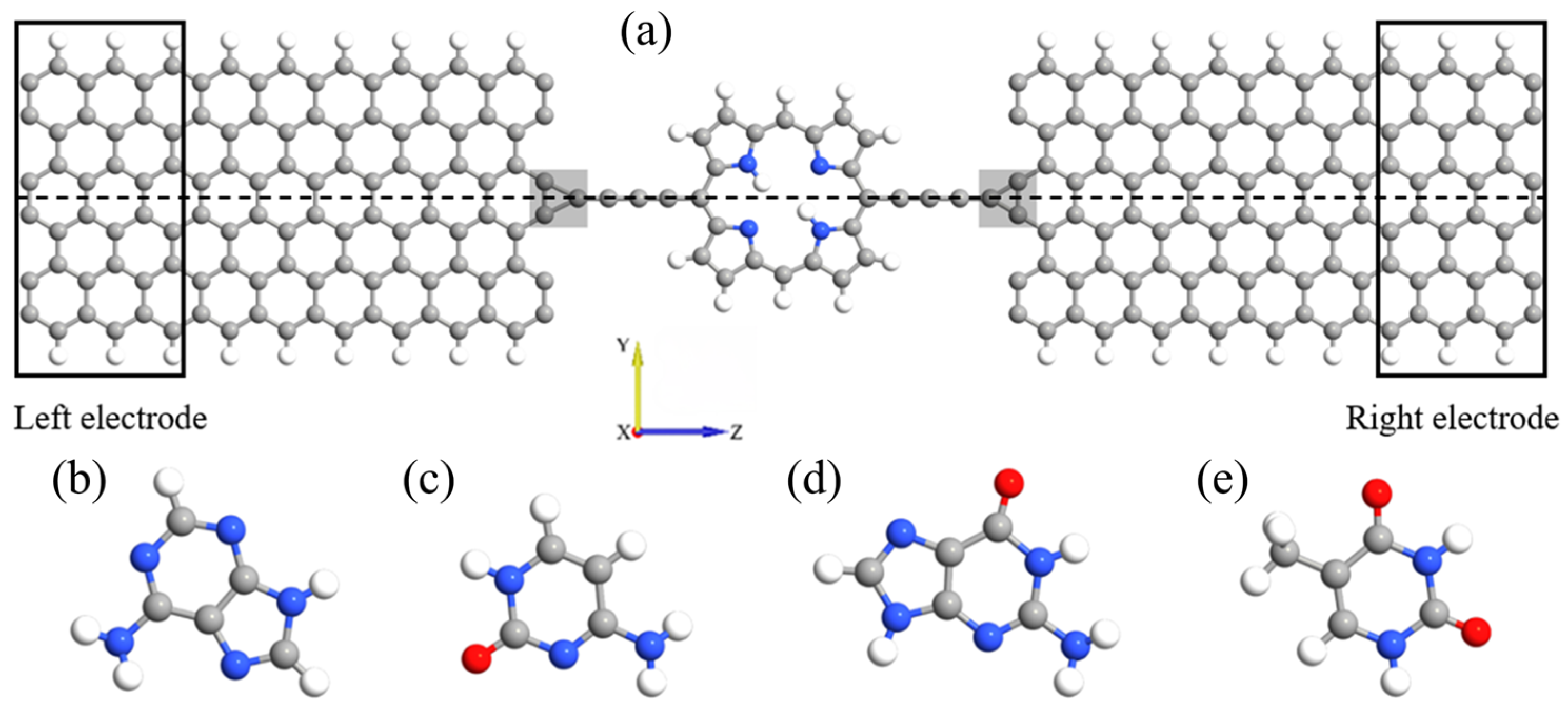
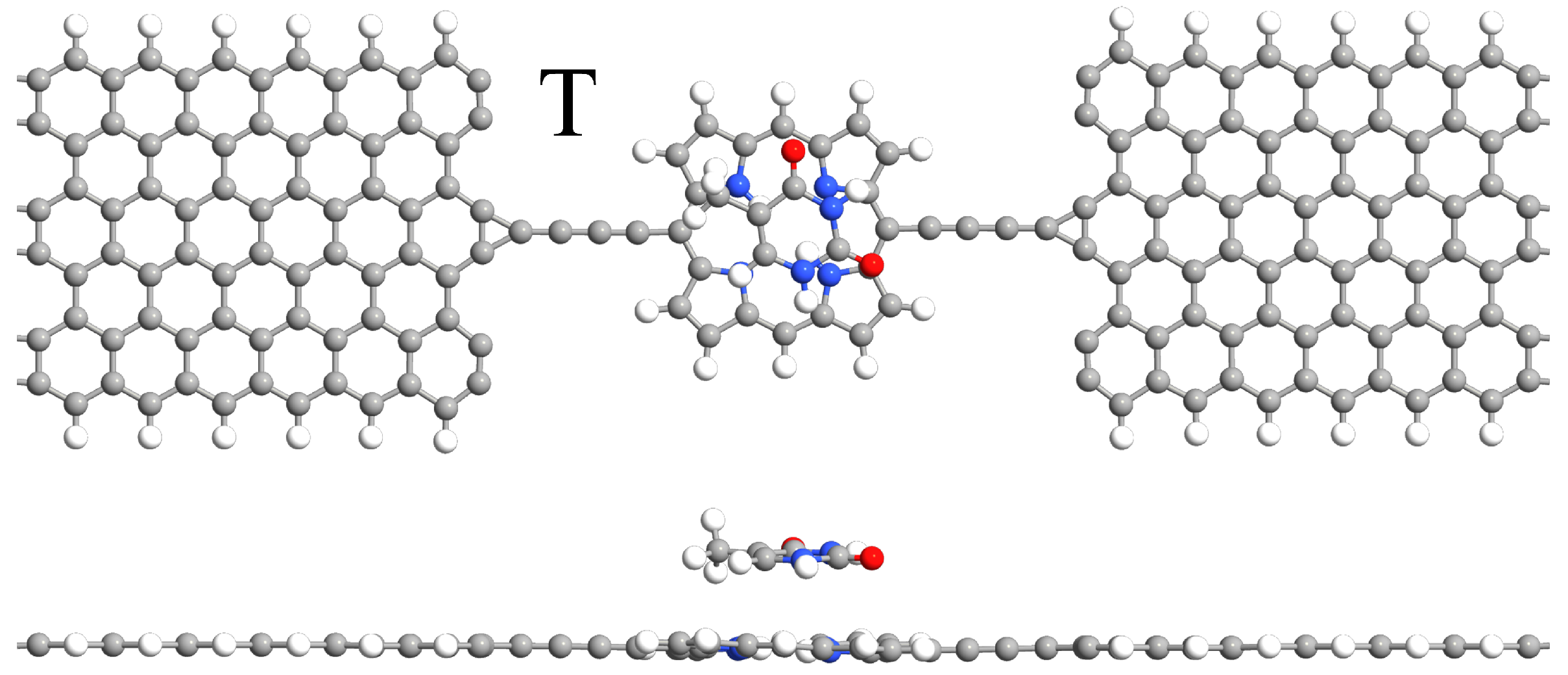
2. Model and Computational Details
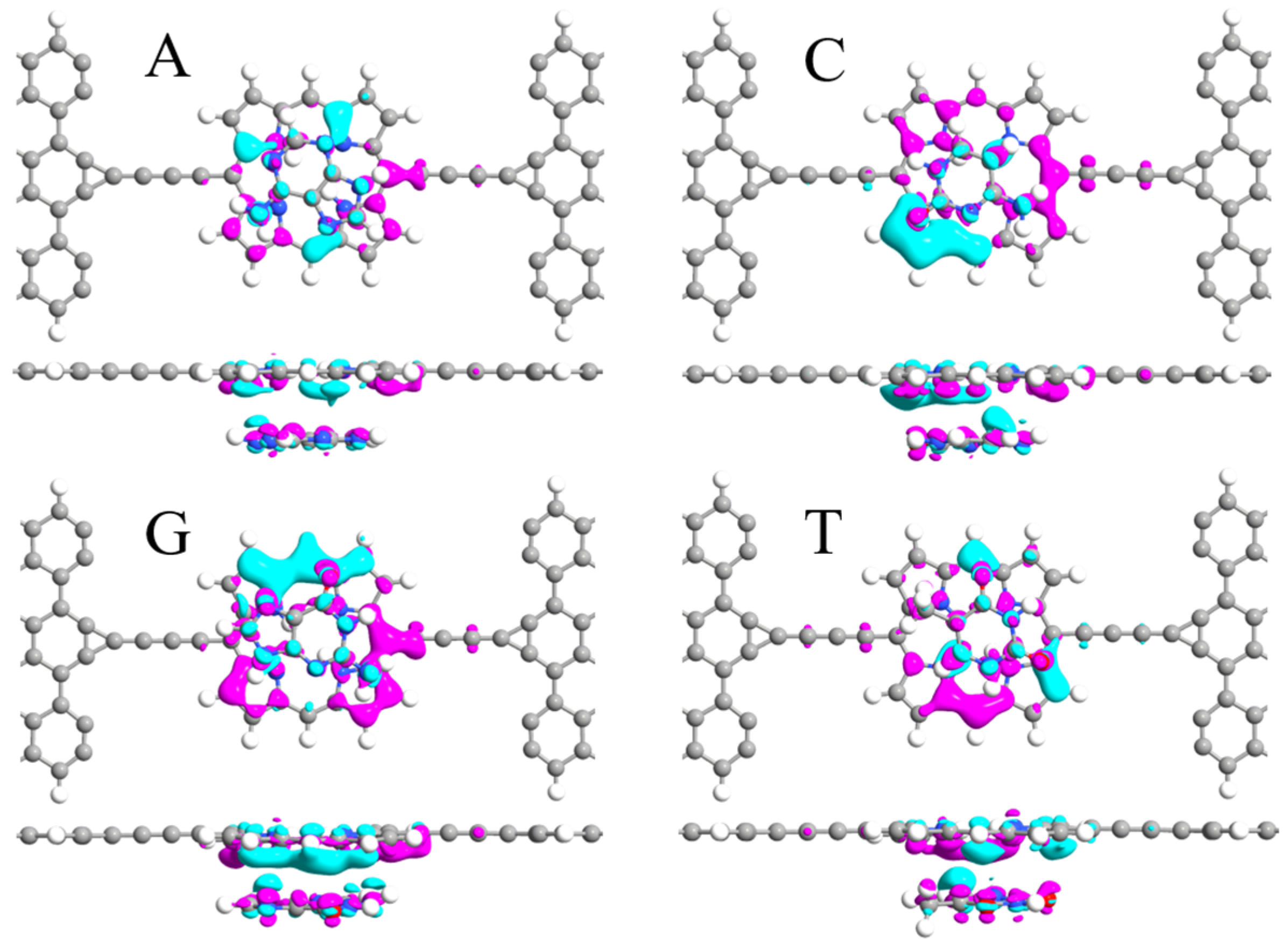
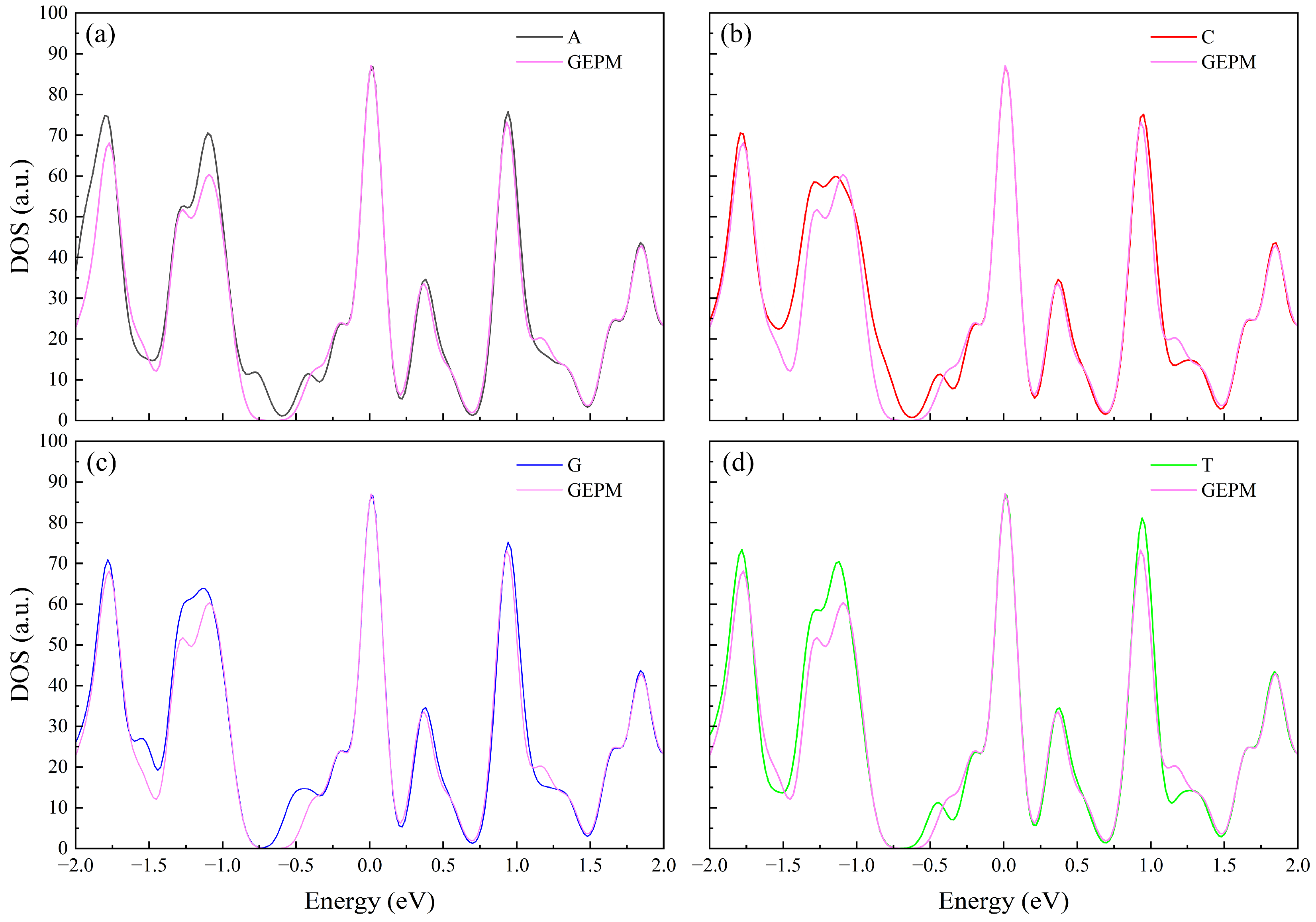
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shendure, J.; Ji, H. Next-Generation DNA Sequencing. Nat. Biotechnol. 2008, 26, 1135–1145. [Google Scholar] [CrossRef]
- Steinbock, L.J.; Radenovic, A. The Emergence of Nanopores in Next-Generation Sequencing. Nanotechnology 2015, 26, 074003. [Google Scholar] [CrossRef] [PubMed]
- Rabbani, B.; Mahdieh, N.; Hosomichi, K.; Nakaoka, H.; Inoue, I. Next Generation Sequencing: Implications in Personalized Medicine and Pharmacogenomics. Mol. BioSyst. 2016, 12, 1818–1830. [Google Scholar] [CrossRef] [PubMed]
- Zhong, Y.; Xu, F.; Wu, J.; Schubert, J.; Li, M.M. Application of Next Generation Sequencing in Laboratory Medicine. Ann. Lab. Med. 2021, 41, 25–43. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Kang, Y.; Luo, J.; Pang, K.; Xu, X.; Wu, J.; Li, X.; Jin, S. Next-Generation Sequencing Reveals the Progression of COVID-19. Front. Cell. Infect. Microbiol. 2021, 11, 632490. [Google Scholar] [CrossRef]
- Seo, G.; Lee, G.; Kim, M.J.; Baek, S.H.; Choi, M.; Ku, K.B.; Lee, C.S.; Jun, S.; Park, D.; Kim, H.G.; et al. Rapid Detection of COVID-19 Causative Virus (SARS-CoV-2) in Human Nasopharyngeal Swab Specimens Using Field-Effect Transistor-Based Biosensor. ACS Nano 2020, 14, 5135–5142. [Google Scholar] [CrossRef]
- Ciotti, M.; Angeletti, S.; Minieri, M.; Giovannetti, M.; Benvenuto, D.; Pascarella, S.; Sagnelli, C.; Bianchi, M.; Ciccozzi, M.; Bernardini, S. The COVID-19 Pandemic. Crit. Rev. Clin. Lab. Sci. 2020, 57, 365–388. [Google Scholar] [CrossRef]
- Lee, J.-H.; Choi, Y.-K.; Kim, H.-J.; Scheicher, R.H.; Cho, J.-H. Physisorption of DNA Nucleobases on h-BN and Graphene: vdW-Corrected DFT Calculations. J. Phys. Chem. C 2013, 117, 24242–24249. [Google Scholar] [CrossRef]
- Prasongkit, J.; Grigoriev, A.; Pathak, B.; Ahuja, R.; Scheicher, R.H. Theoretical Study of Electronic Transport through DNA Nucleotides in a Double-Functionalized Graphene Nanogap. J. Phys. Chem. C 2013, 117, 15421–15428. [Google Scholar] [CrossRef]
- Kumawat, R.L.; Garg, P.; Bhattacharyya, G.; Pathak, B. Electronic Transport through DNA Nucleotides in BC3 Nanogap for Rapid DNA Sequencing. ACS Appl. Electron. Mater. 2020, 2, 1218–1225. [Google Scholar] [CrossRef]
- Kumawat, R.L.; Pathak, B. Functionalized Carbon Nanotube Electrodes for Controlled DNA Sequencing. Nanoscale Adv. 2020, 2, 4041–4050. [Google Scholar] [CrossRef] [PubMed]
- Shukla, V.; Jena, N.K.; Grigoriev, A.; Ahuja, R. Prospects of Graphene-hBN Heterostructure Nanogap for DNA Sequencing. ACS Appl. Mater. Interfaces 2017, 9, 39945–39952. [Google Scholar] [CrossRef] [PubMed]
- Kumawat, R.L.; Pathak, B. Extended Topological Line Defects in Graphene for Individual Identification of DNA Nucleobases. Mater. Adv. 2020, 1, 2908–2916. [Google Scholar] [CrossRef]
- Kumawat, R.L.; Jena, M.K.; Pathak, B. Individual Identification of Amino Acids on an Atomically Thin Hydrogen Boride System Using Electronic Transport Calculations. J. Phys. Chem. C 2020, 124, 27194–27202. [Google Scholar] [CrossRef]
- Hayden, E.C. Technology: The $1000 Genome. Nature 2014, 507, 294–295. [Google Scholar] [CrossRef]
- Pathak, B.; Löfås, H.; Prasongkit, J.; Grigoriev, A.; Ahuja, R.; Scheicher, R.H. Double-Functionalized Nanopore-Embedded Gold Electrodes for Rapid DNA Sequencing. Appl. Phys. Lett. 2012, 100, 023701. [Google Scholar] [CrossRef]
- Mardis, E.R. A Decade’s Perspective on DNA Sequencing Technology. Nature 2011, 470, 198–203. [Google Scholar] [CrossRef]
- Siwy, Z.S.; Davenport, M. Graphene Opens up to DNA. Nat. Nanotechnol. 2010, 5, 697–698. [Google Scholar] [CrossRef]
- Arjmandi-Tash, H.; Belyaeva, L.A.; Schneider, G.F. Single Molecule Detection with Graphene and other Two-Dimensional Materials: Nanopores and Beyond. Chem. Soc. Rev. 2016, 45, 476–493. [Google Scholar] [CrossRef]
- Liu, H.; He, J.; Tang, J.; Liu, H.; Pang, P.; Cao, D.; Krstic, P.; Joseph, S.; Lindsay, S.; Nuckolls, C. Translocation of Single-Stranded DNA Through Single-Walled Carbon Nanotubes. Science 2010, 327, 64–67. [Google Scholar] [CrossRef]
- Branton, D.; Deamer, D.W.; Marziali, A.; Bayley, H.; Benner, S.A.; Butler, T.; Ventra, M.D.; Garaj, S.; Hibbs, A.; Huang, X.; et al. The Potential and Challenges of Nanopore Sequencing. Nat. Biotechnol. 2008, 26, 1146–1153. [Google Scholar] [CrossRef] [PubMed]
- Nelson, T.; Zhang, B.; Prezhdo, O.V. Detection of Nucleic Acids with Graphene Nanopores: Ab Initio Characterization of a Novel Sequencing Device. Nano Lett. 2010, 10, 3237–3242. [Google Scholar] [CrossRef] [PubMed]
- Traversi, F.; Raillon, C.; Benameur, S.M.; Liu, K.; Khlybov, S.; Tosun, M.; Krasnozhon, D.; Kis, A.; Radenovic, A. Detecting the Translocation of DNA through a Nanopore Using Graphene Nanoribbons. Nat. Nanotechnol. 2013, 8, 939–945. [Google Scholar] [CrossRef] [PubMed]
- Garaj, S.; Hubbard, W.; Reina, A.; Kong, J.; Branton, D.; Golovchenko, J.A. Graphene as a Subnanometre Trans-Electrode Membrane. Nature 2010, 467, 190–193. [Google Scholar] [CrossRef]
- Liu, K.; Feng, J.; Kis, A.; Radenovic, A. Atomically Thin Molybdenum Disulfide Nanopores with High Sensitivity for DNA Translocation. ACS Nano 2014, 8, 2504–2511. [Google Scholar] [CrossRef]
- Saha, K.K.; Drndić, M.; Nikolić, B.K. DNA Base-Specific Modulation of Microampere Transverse Edge Currents through a Metallic Graphene Nanoribbon with a Nanopore. Nano Lett. 2012, 12, 50–55. [Google Scholar] [CrossRef]
- Prasongkit, J.; Grigoriev, A.; Pathak, B.; Ahuja, R.; Scheicher, R.H. Transverse Conductance of DNA Nucleotides in a Graphene Nanogap from First Principles. Nano Lett. 2011, 11, 1941–1945. [Google Scholar] [CrossRef]
- Kumawat, R.L.; Garg, P.; Kumar, S.; Pathak, B. Electronic Transport through DNA Nucleotides in Atomically Thin Phosphorene Electrodes for Rapid DNA Sequencing. ACS Appl. Mater. Interfaces 2018, 11, 219–225. [Google Scholar] [CrossRef]
- Prasongkit, J.; Martins, E.F.; Souza, F.A.L.; Scopel, W.L.; Amorim, R.G.; Amornkitbamrung, V.; Rocha, A.R.; Scheicher, R.H. Topological Line Defects Around Graphene Nanopores for DNA Sequencing. J. Phys. Chem. C 2018, 122, 7094–7099. [Google Scholar] [CrossRef]
- Chang, S.; Huang, S.; He, J.; Liang, F.; Zhang, P.; Li, S.; Chen, X.; Sankey, O.; Lindsay, S. Electronic Signatures of all Four DNA Nucleosides in a Tunneling Gap. Nano Lett. 2010, 10, 1070–1075. [Google Scholar] [CrossRef]
- Postma, H.W.C. Rapid Sequencing of Individual DNA Molecules in Graphene Nanogaps. Nano Lett. 2010, 10, 420–425. [Google Scholar] [CrossRef] [PubMed]
- He, H.; Scheicher, R.H.; Pandey, R.; Rocha, A.R.; Sanvito, S.; Grigoriev, A.; Ahuja, R.; Karna, S.P. Functionalized Nanopore-Embedded Electrodes for Rapid DNA Sequencing. J. Phys. Chem. C 2008, 112, 3456–3459. [Google Scholar] [CrossRef]
- Min, S.K.; Kim, W.Y.; Cho, Y.; Kim, K.S. Fast DNA Sequencing with a Graphene-Based Nanochannel Device. Nat. Nanotechnol. 2011, 6, 162–165. [Google Scholar] [CrossRef]
- Rajan, A.C.; Rezapour, M.R.; Yun, J.; Cho, Y.; Cho, W.J.; Min, S.K.; Lee, G.; Kim, K.S. Two Dimensional Molecular Electronics Spectroscopy for Molecular Fingerprinting, DNA Sequencing, and Cancerous DNA Recognition. ACS Nano 2014, 8, 1827–1833. [Google Scholar] [CrossRef]
- Cho, Y.; Min, S.K.; Kim, W.Y.; Kin, K.S. The Origin of Dips for the Graphene-Based DNA Sequencing Device. Phys. Chem. Chem. Phys. 2011, 13, 14293–14296. [Google Scholar] [CrossRef]
- Mittal, S.; Pathak, B. A Step toward Amino Acid-Labeled DNA Sequencing: Boosting Transmission Sensitivity of Graphene Nanogap. ACS Appl. Bio Mater. 2023, 6, 218–227. [Google Scholar] [CrossRef]
- Dong, Y.-J.; Wang, X.-F.; Zhai, M.-X.; Wu, J.-C.; Zhou, L.; Han, Q.; Wu, X.-M. Effects of Geometry and Symmetry on Electron Transport through Graphene-Carbon-Chain Junctions. J. Phys. Chem. C 2013, 117, 18845–18850. [Google Scholar] [CrossRef][Green Version]
- Ke, S.H.; Yang, W.; Baranger, H.U. Quantum-Interference-Controlled Molecular Electronics. Nano Lett. 2008, 8, 3257–3261. [Google Scholar] [CrossRef]
- Kim, W.Y.; Choi, Y.C.; Min, S.K.; Cho, Y.; Kim, K.S. Application of Quantum Chemistry to Nanotechnology: Electron and Spin Transport in Molecular Devices. Chem. Soc. Rev. 2009, 38, 2319–2333. [Google Scholar] [CrossRef]
- Bolotin, K.I.; Sikes, K.I.; Jiang, Z.; Klima, M.; Fudenberg, G.; Hone, J.; Kim, P.; Stormer, H.L. Ultrahigh electron mobility in suspended graphene. Solid State Commun. 2008, 146, 351–355. [Google Scholar] [CrossRef]
- Balandin, A.A.; Ghosh, S.; Bao, W.; Calizo, I.; Teweldebrhan, D.; Miao, F.; Lau, C.N. Superior Thermal Conductivity of Single-Layer Graphene. Nano Lett. 2008, 8, 902–907. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.; Wei, X.; Kysar, J.W.; Hone, J. Measurement of the Elastic Properties and Intrinsic Strength of Monolayer Graphene. Science 2008, 321, 385–388. [Google Scholar] [CrossRef] [PubMed]
- Cao, C.; Chen, L.; Huang, W.; Xu, H. Electronic Transport of Zigzag Graphene Nanoribbons with Edge Hydrogenation and Oxidation. Open Chem. Phys. J. 2012, 4, 1–7. [Google Scholar] [CrossRef][Green Version]
- Hou, Z.; Yee, M. Electronic and Transport Properties of Graphene Nanoribbons. In Proceedings of the 2007 7th IEEE Conference on Nanotechnology (IEEE NANO) 2007, Hong Kong, China, 2–5 August 2007; pp. 554–557. [Google Scholar]
- Treske, U.; Ortmann, F.; Oetzel, B.; Hannewald, K.; Bechstedt, F. Electronic and Transport Properties of Graphene Nanoribbons. Phys. Status Solidi (a) 2010, 207, 304–308. [Google Scholar] [CrossRef]
- Xiao, H.P.; Yu, Z.; Peng, X.Y.; Sun, L.Z.; Zhong, J. Zigzag Graphene Nanoribbons: Flexible and Robust Transparent Conductors. Solid State Sci. 2012, 14, 711–714. [Google Scholar] [CrossRef]
- Mittal, S.; Jena, M.K.; Pathak, B. Amplifying Quantum Tunneling Current Sensitivity through Labeling Nucleotides Using Graphene Nanogap Electrodes. ACS Appl. Nano Mater. 2022, 5, 9356–9366. [Google Scholar] [CrossRef]
- Qiu, H.; Zhou, W.; Guo, W. Nanopores in Graphene and Other 2D Materials: A Decade’s Journey toward Sequencing. ACS Nano 2021, 15, 18848–18864. [Google Scholar] [CrossRef]
- Cao, Z.; Yadav, P.; Farimani, A.B. Which 2D Material is Better for DNA Detection: Graphene, MoS2, or MXene? Nano Lett. 2022, 22, 7874–7881. [Google Scholar] [CrossRef]
- Jena, M.K.; Pathak, B. Development of an Artificially Intelligent Nanopore for High-Throughput DNA Sequencing with a Machine-Learning-Aided Quantum-Tunneling Approach. Nano Lett. 2023, 23, 2511–2521. [Google Scholar] [CrossRef]
- Xue, X.; Lindstrom, A.; Li, Y. Porphyrin-Based Nanomedicines for Cancer Treatment. Bioconjug. Chem. 2019, 30, 1585–1603. [Google Scholar] [CrossRef]
- Asselin, P.; Harvey, P.D. Visible-Light-Driven Production of Solar Fuels Catalyzed by Nanosized Porphyrin-Based Metal-Organic Frameworks and Covalent-Organic Frameworks: A Review. ACS Appl. Nano Mater. 2022, 5, 6055–6082. [Google Scholar] [CrossRef]
- Mathew, D.; Sujatha, S. Interactions of Porphyrins with DNA: A Review Focusing Recent Advances in Chemical Modifications on Porphyrins as Artificial Nucleases. J. Inorg. Biochem. 2021, 219, 111434. [Google Scholar] [CrossRef] [PubMed]
- Kumawat, R.L.; Pathak, B. Electronic Conductance and Current Modulation through Graphdiyne Nanopores for DNA Sequencing. ACS Appl. Electron. Mater. 2021, 3, 3835–3845. [Google Scholar] [CrossRef]
- Majumder, C.; Mahadevan, P.; Mizuseki, H.; Kawazoe, Y. Binding of DNA Nucleobases and Nucleosides with Graphene. J. Phys. Chem. C 2009, 113, 15182–15188. [Google Scholar]
- Taylor, J.; Guo, H.; Wang, J. Ab Initio Modeling of Quantum Transport Properties of Molecular Electronic Devices. Phys. Rev. B 2001, 63, 245407. [Google Scholar] [CrossRef]
- Brandbyge, M.; Mozos, J.L.; Ordejón, P.; Taylor, J.; Stokbro, K. Density-Functional Method for Nonequilibrium Electron Transport. Phys. Rev. B 2002, 65, 165401. [Google Scholar] [CrossRef]
- Ordejón, P.; Artacho, E.; Soler, J.M. Self-Consistent Order-N Density-Functional Calculations for Very Large Systems. Phys. Rev. B 1996, 53, R10441–R10444. [Google Scholar] [CrossRef]
- Sánchez-Portal, D.; Ordejón, P.; Artacho, E.; Soler, J.M. Density-Functional Method for Very Large Systems with LCAO Basis Sets. Int. J. Quantum Chem. 1997, 65, 453–461. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Setten, M.J.; Giantomassi, M.; Bousquet, E.; Verstraete, M.J.; Hamann, D.R.; Gonze, X.; Rignanese, G.M. The PseudoDojo: Training and Grading a 85 Element Optimized Norm-Conserving Pseudopotential Table. Comput. Phys. Commun. 2018, 226, 39–54. [Google Scholar] [CrossRef]
- Borlido, P.; Doumont, J.; Tran, F.; Marques, M.A.L.; Botti, S. Validation of Pseudopotential Calculations for the Electronic Band Gap of Solids. J. Chem. Theory Comput. 2020, 16, 3620–3627. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar]
- Chadi, D.J.; Cohen, M.L. Special Points for Brillouin-Zone Integrations. Phys. Rev. B 1977, 16, 1746–1747. [Google Scholar] [CrossRef]
- Chen, D.; Zhang, X.; Tang, J.; Cui, Z.; Cui, H. Pristine and Cu Decorated Hexagonal InN Monolayer, a Promising Candidate to Detect and Scavenge SF₆ Decompositions Based on First-Principle Study. J. Hazard. Mater. 2019, 363, 346–357. [Google Scholar] [CrossRef]
- Das Sarma, S.; Adam, S.; Hwang, E.H.; Rossi, E. Electronic Transport in Two-Dimensional Graphene. Rev. Mod. Phys. 2011, 83, 407–470. [Google Scholar] [CrossRef]
- Büttiker, M.; Imry, Y.; Landauer, R.; Pinhas, S. Generalized Many-Channel Conductance Formula with Application to Small Rings. Phys. Rev. B 1985, 31, 6207–6215. [Google Scholar] [CrossRef]
- Babar, V.; Sharma, S.; Shaikh, A.R.; Oliva, R.; Chawla, M.; Cavallo, L. Sensing Hachimoji DNA Bases with Janus MoSH Monolayer Nanodevice: Insights from Density Functional Theory (DFT) and Non-Equilibrium Green’s Function Analysis. ACS Omega 2024, 9, 48173–48184. [Google Scholar] [CrossRef]
- Gao, F.; Zhang, Y.; He, L.; Gao, S.; Brandbyge, M. Control of the Local Magnetic States in Graphene with Voltage and Gating. Phys. Rev. B 2021, 103, L241402. [Google Scholar] [CrossRef]
- Li, Z.; Li, S.; Xu, Y.; Tang, N. Recent Advances in Magnetism of Graphene from 0D to 2D. Chem. Commun. 2023, 59, 6286–6300. [Google Scholar] [CrossRef]

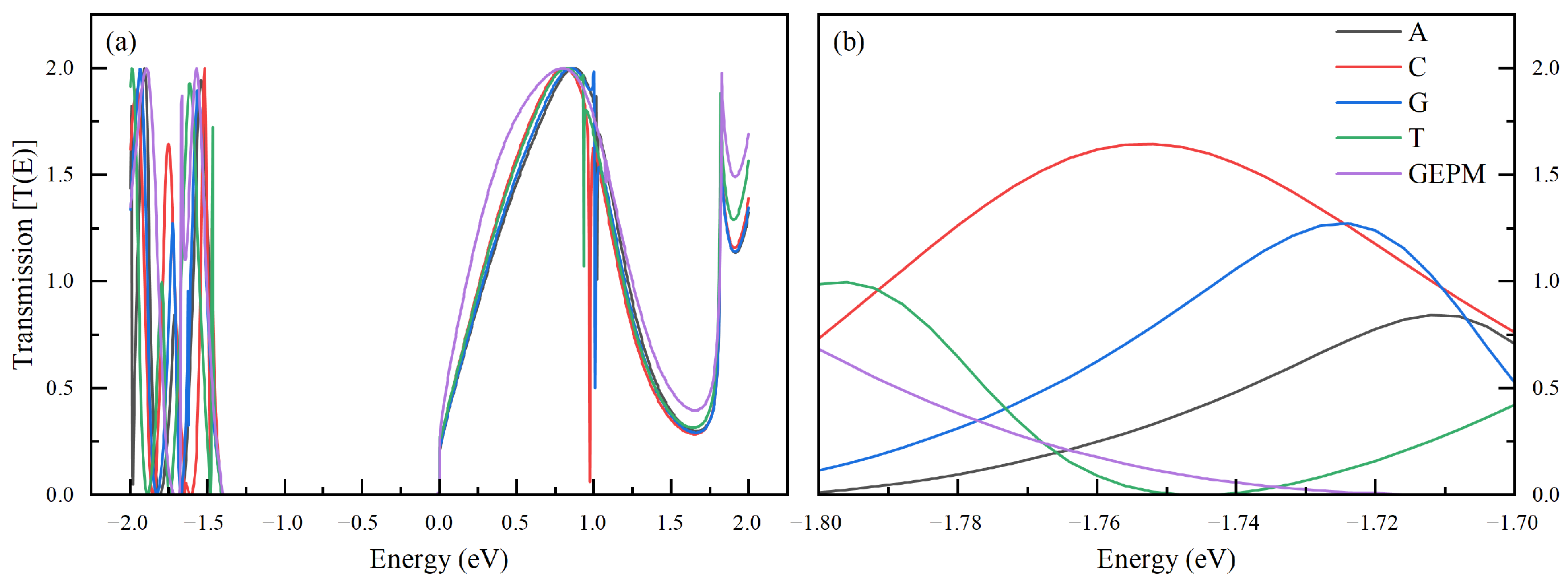
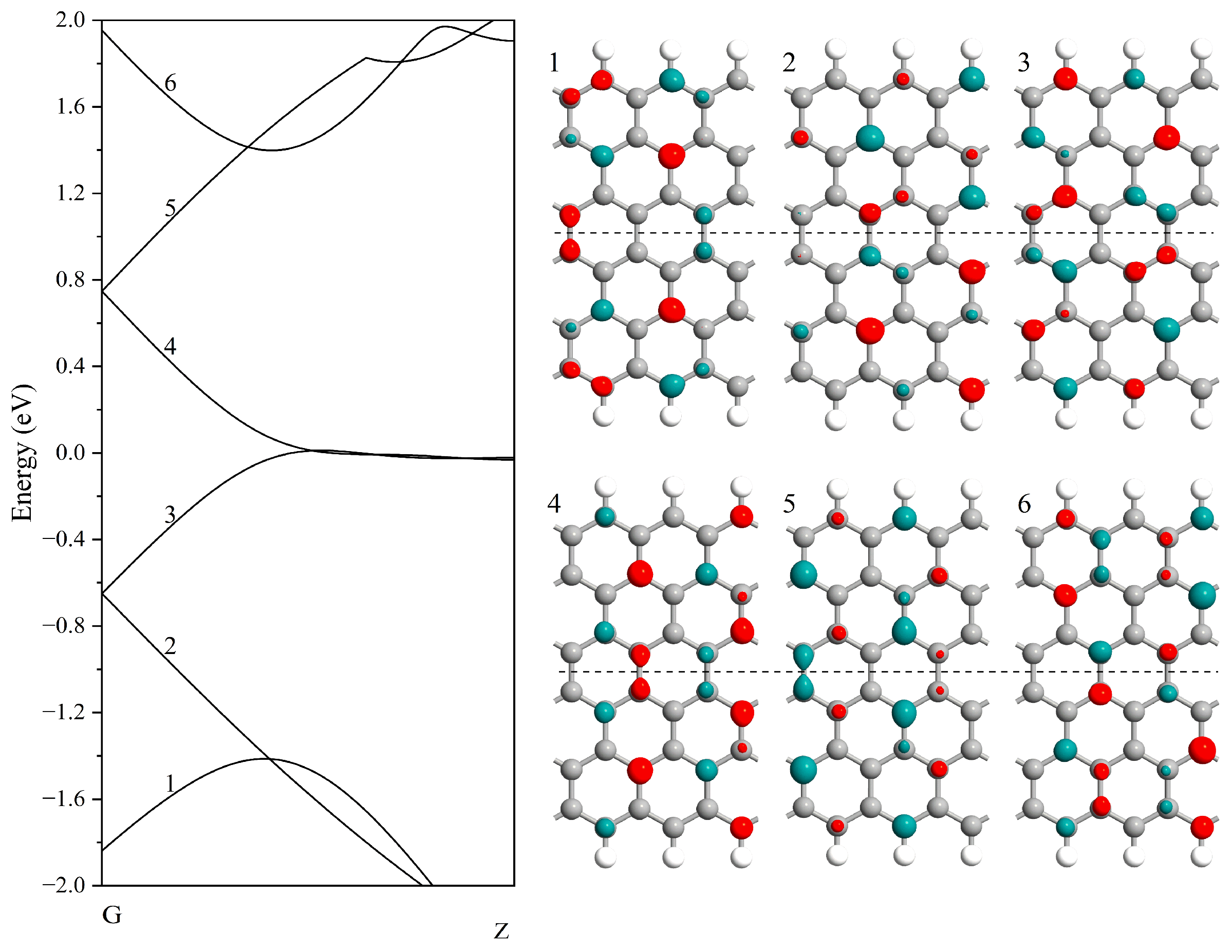
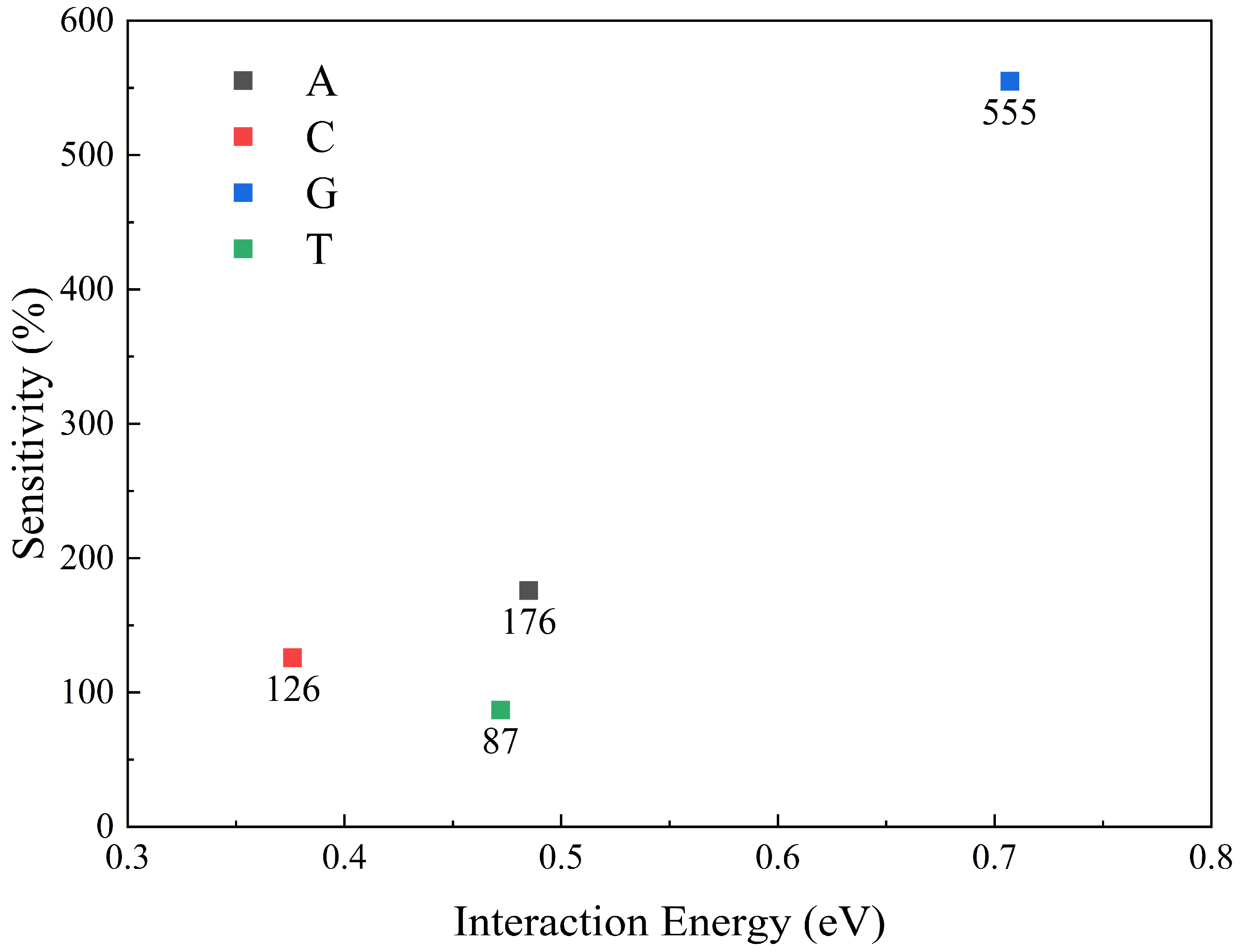
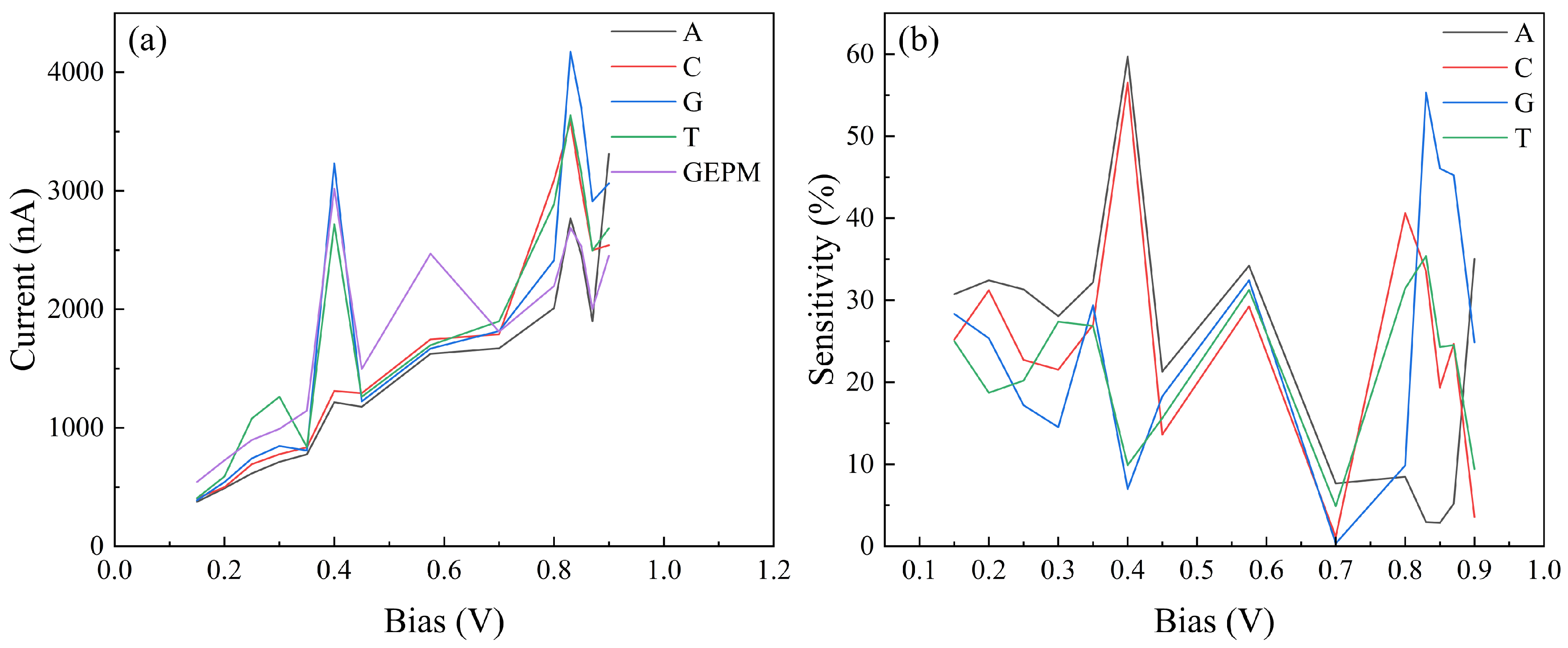

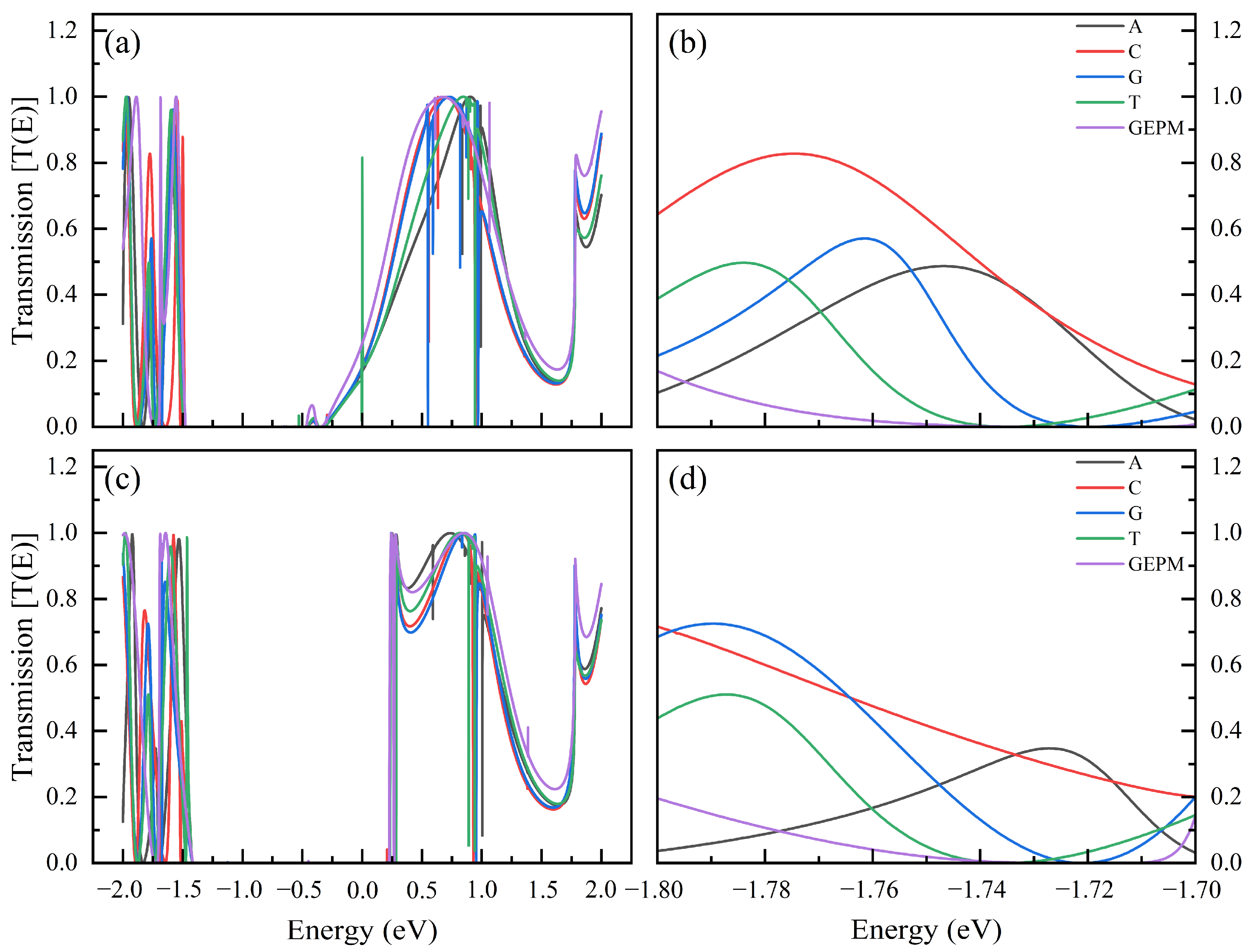
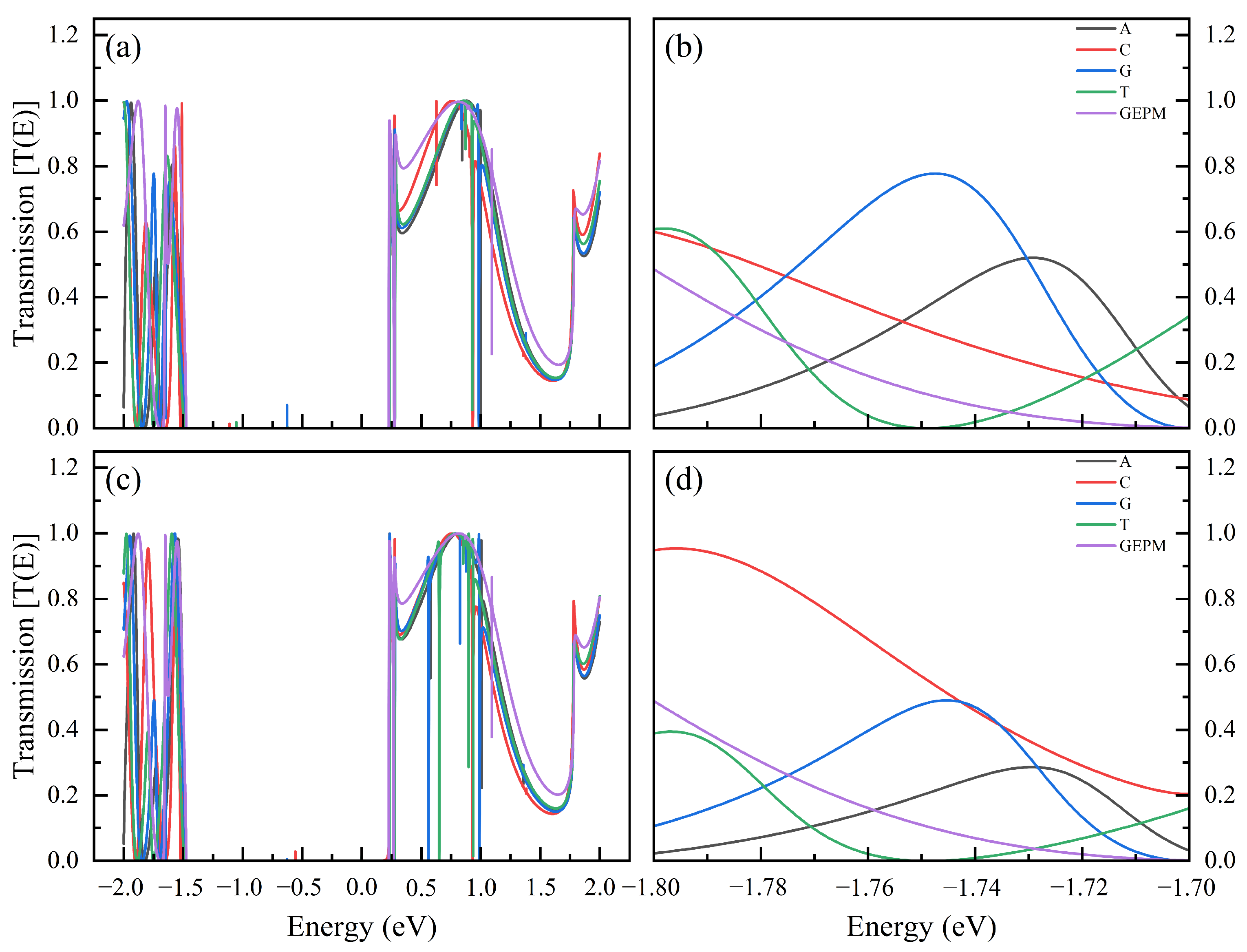
| Nucleobase | Distance (Å) | SG (%) | SI (%) | Ei GEPM (eV) | Ei Theo (eV) | Ei Ref [8] (eV) |
|---|---|---|---|---|---|---|
| A | 3.06 | 176.2 | 2.9 | 0.485 | 1.10 | 1.00 |
| C | 2.92 | 126.6 | 19.4 | 0.376 | 0.97 | 0.93 |
| G | 2.97 | 555.7 | 46.1 | 0.707 | 1.30 | 1.18 |
| T | 3.07 | 87.97 | 24.3 | 0.472 | 1.01 | 0.95 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.-K.; Zhou, L.-P.; Wang, X.-F.; Vasilopoulos, P.; You, W.-L.; Liu, Y.-S. A Graphene Nanoribbon Electrode-Based Porphyrin Molecular Device for DNA Sequencing. Electronics 2025, 14, 1814. https://doi.org/10.3390/electronics14091814
Li Y-K, Zhou L-P, Wang X-F, Vasilopoulos P, You W-L, Liu Y-S. A Graphene Nanoribbon Electrode-Based Porphyrin Molecular Device for DNA Sequencing. Electronics. 2025; 14(9):1814. https://doi.org/10.3390/electronics14091814
Chicago/Turabian StyleLi, Yong-Kang, Li-Ping Zhou, Xue-Feng Wang, Panagiotis Vasilopoulos, Wen-Long You, and Yu-Shen Liu. 2025. "A Graphene Nanoribbon Electrode-Based Porphyrin Molecular Device for DNA Sequencing" Electronics 14, no. 9: 1814. https://doi.org/10.3390/electronics14091814
APA StyleLi, Y.-K., Zhou, L.-P., Wang, X.-F., Vasilopoulos, P., You, W.-L., & Liu, Y.-S. (2025). A Graphene Nanoribbon Electrode-Based Porphyrin Molecular Device for DNA Sequencing. Electronics, 14(9), 1814. https://doi.org/10.3390/electronics14091814






