High-Resolution Building Indicator Mapping Using Airborne LiDAR Data
Abstract
1. Introduction
1.1. Cadastral Data in Spatial Planning
1.2. Three-Dimensional (3D) Data in Spatial Planning
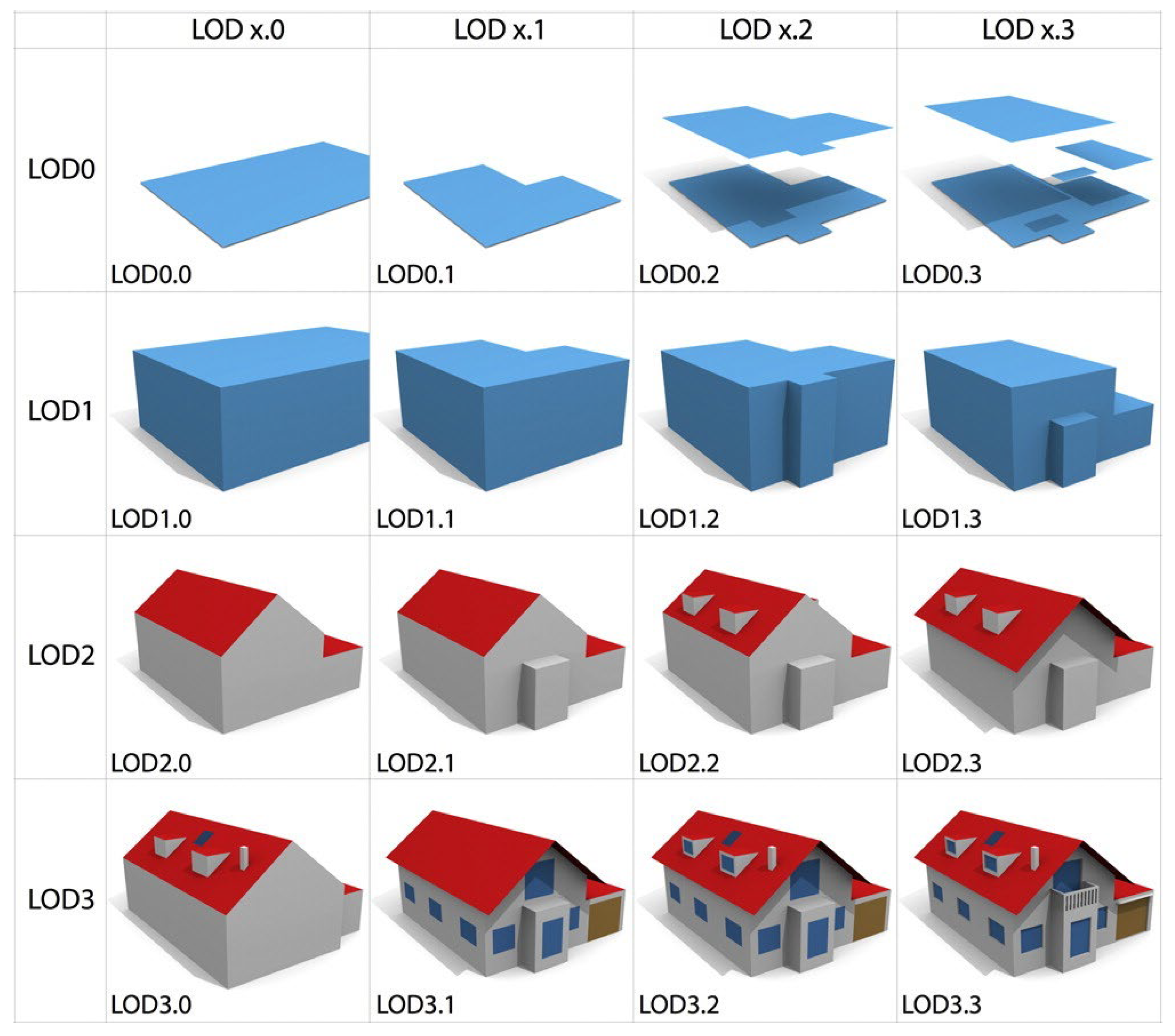
1.3. Quality of 3D Models
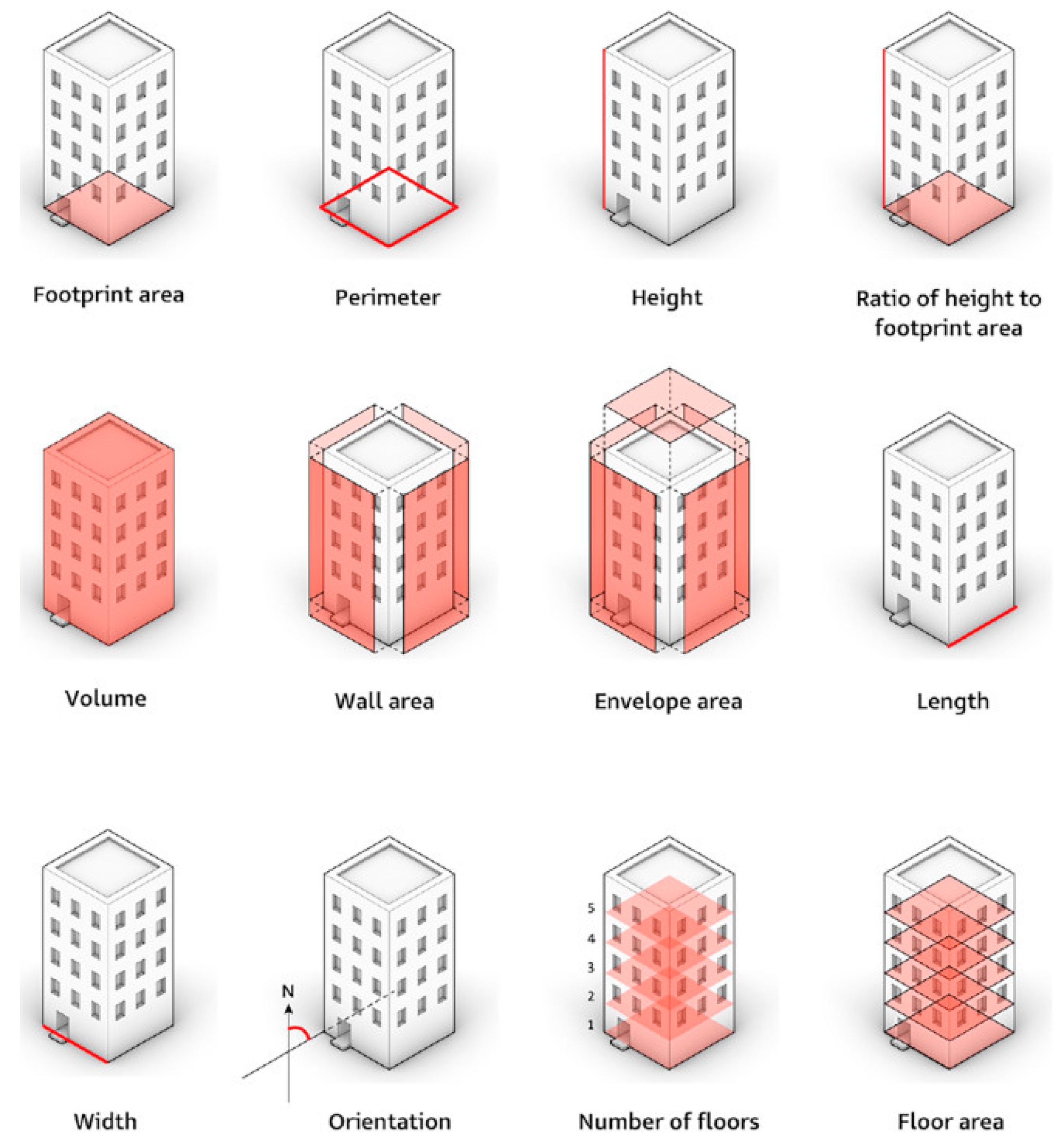
1.4. Three-Dimensional (3D) Urban Space Indicators
1.5. Aim of the Research
- The automatic creation of 2D and 3D building indicators from the LiDAR point cloud.
- Timesaving in smart city management and monitoring.
- Evaluation of the building area and volume calculated using LiDAR data.
- Opening the door to calculating most of a building’s 2D and 3D indicators automatically from LiDAR data.
- Accuracy assessment and formulation of target indicators.
- Advancements in 3D urban indicator calculations using LiDAR data.
2. Datasets
3. Suggested Approach
3.1. DSM Resolution Calculation
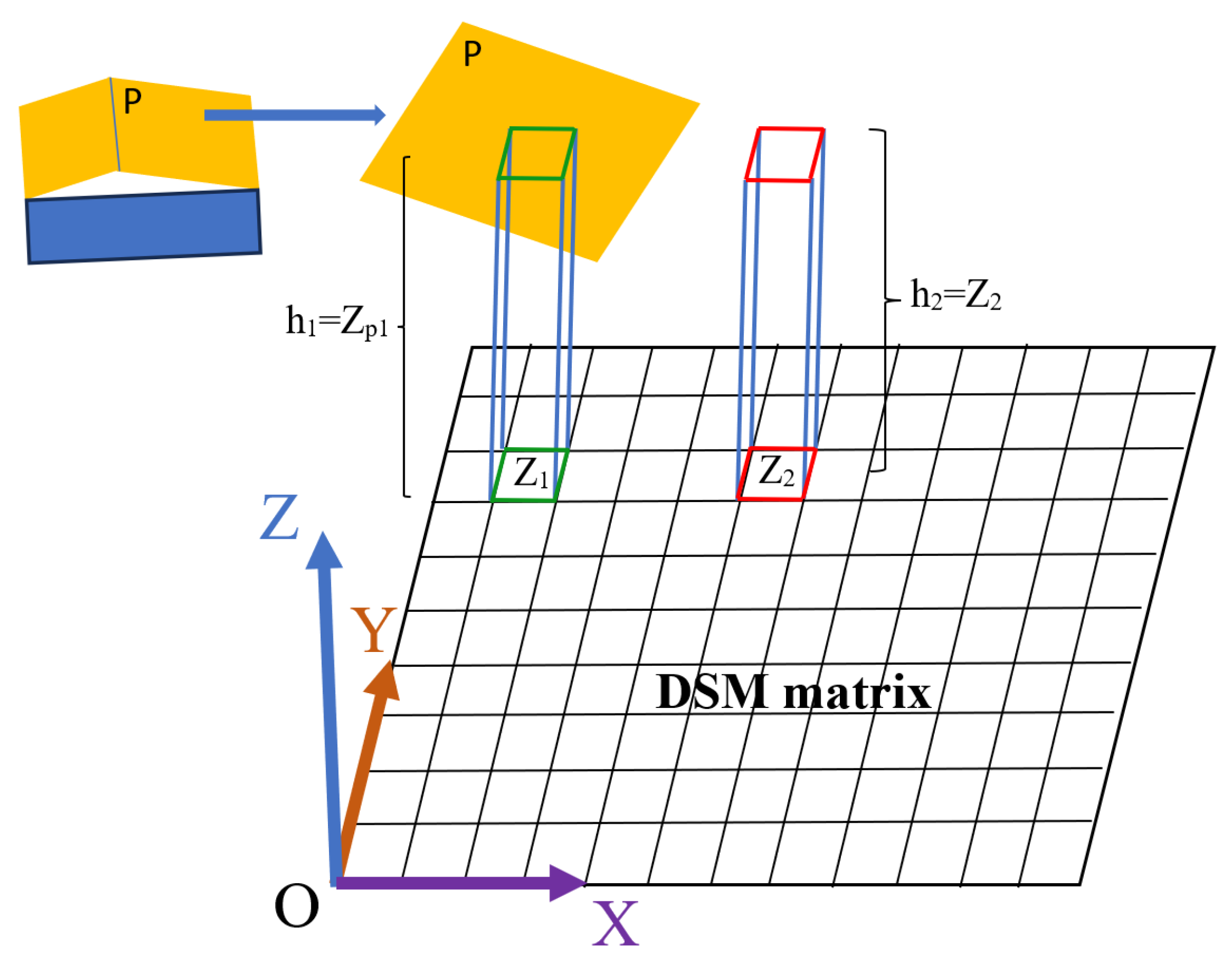
3.2. Calculation of the Building DSM
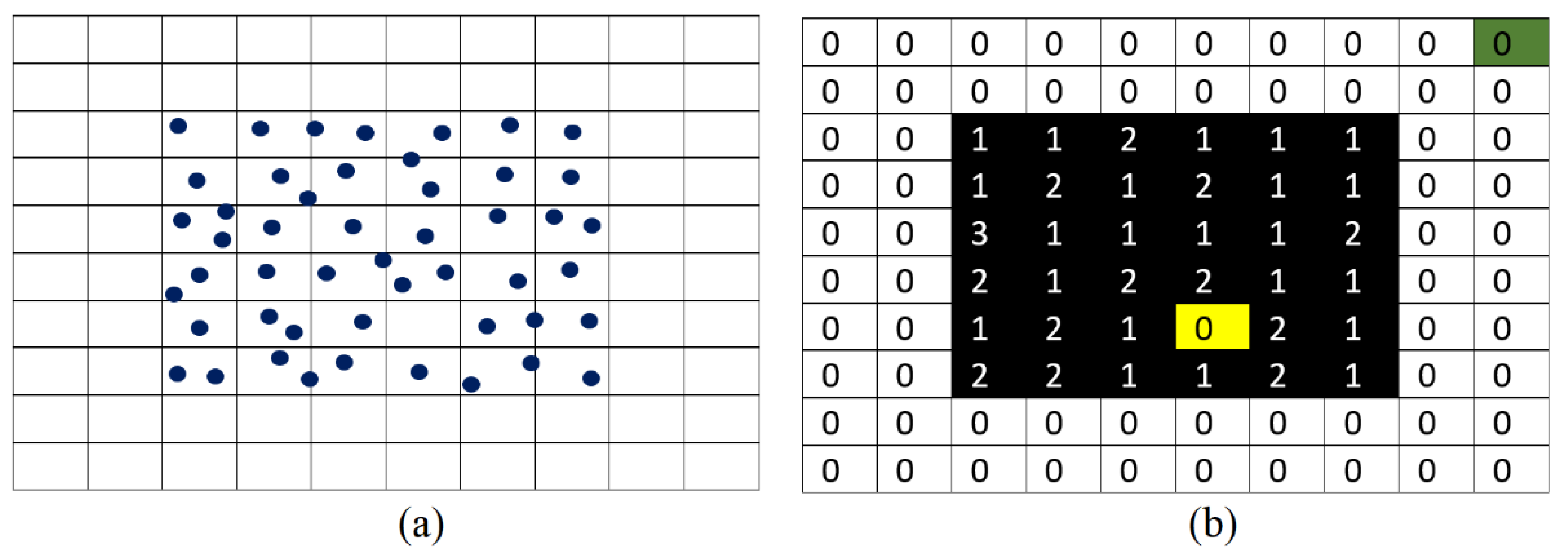
3.3. Building Area Calculation and Accuracy Estimation
3.4. Multi-Story Building Area and Building Intensity Index
3.5. Building Volume Calculation and 3D Building Intensity Index
- All building DSM pixels located outside the building boundary polygon, which was calculated in Section 3.3, will be eliminated.
- For building boundary pixels located on the boundary polygon, only the parts situated inside that polygon will be considered.
- Pixels belonging to the building body and having values smaller than a given threshold will be neglected. This threshold is related to the level height, i.e., the threshold will equal the ground level . Indeed, these kinds of pixels can be in connection with the building boundary, and they may represent a confusing noise. That is why they are kept at the classification stage.
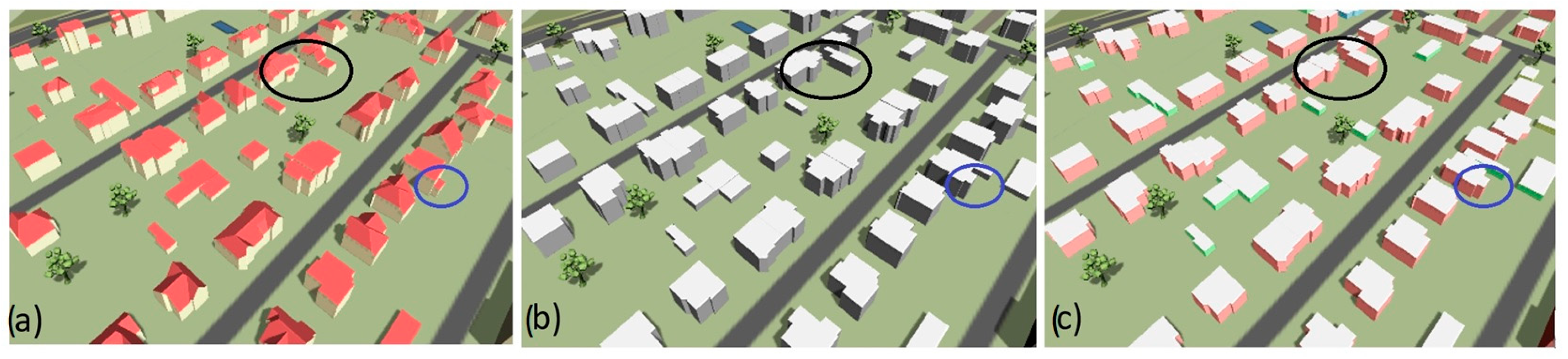
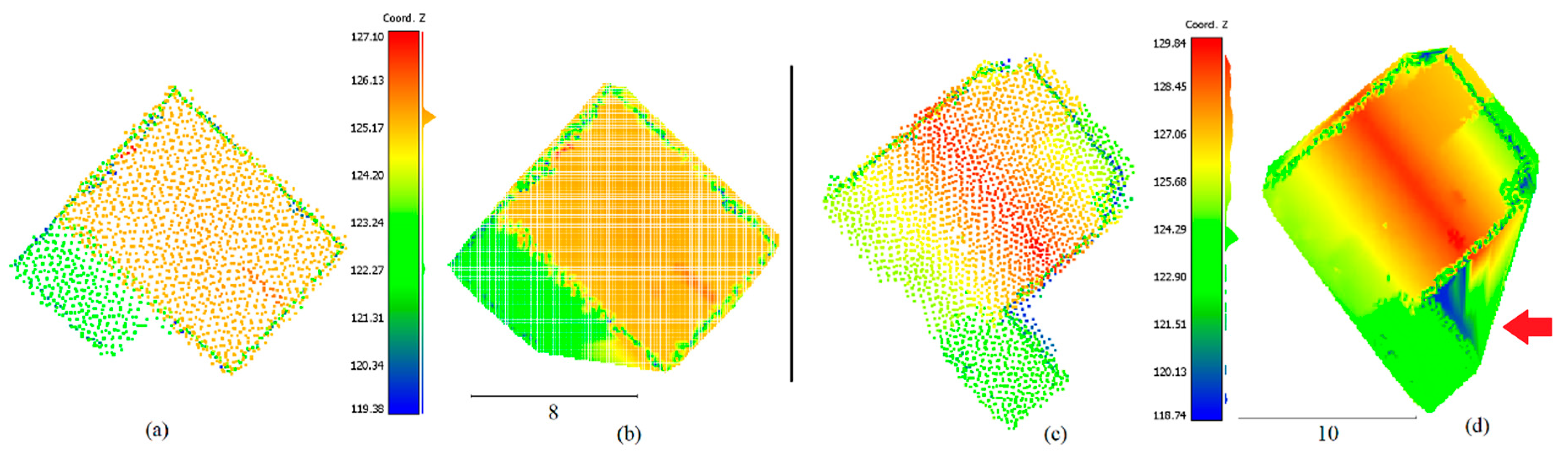
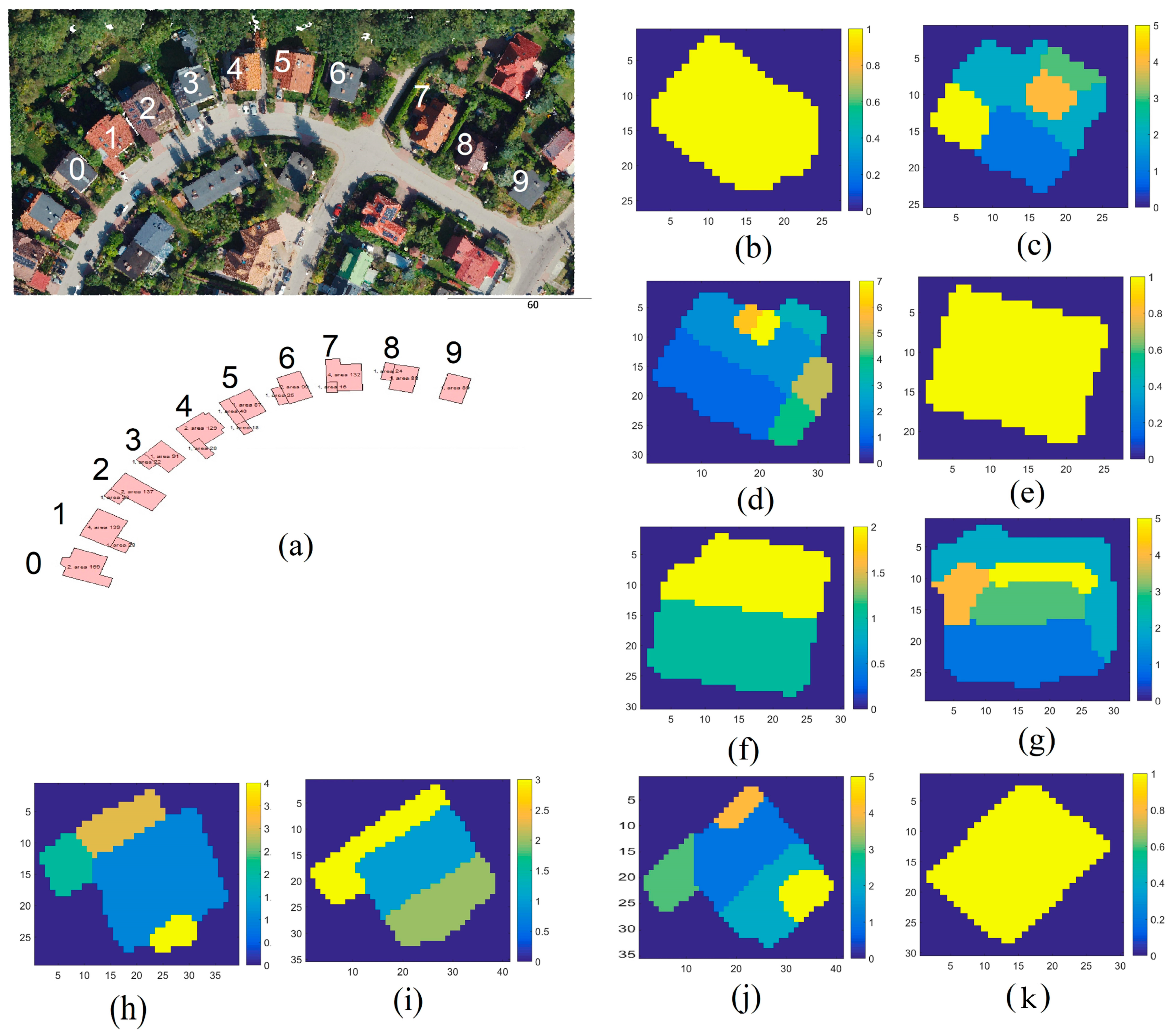
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Huang, L.; Wu, J.; Yan, L. Defining and Measuring Urban Sustainability: A Review of Indicators. Landscape Ecol. 2015, 30, 1175–1193. [Google Scholar] [CrossRef]
- Pira, M. A Novel Taxonomy of Smart Sustainable City Indicators. Humanit. Soc. Sci. Commun. 2021, 8, 197. [Google Scholar] [CrossRef]
- Angelakoglou, K.; Nikolopoulos, N.; Giourka, P.; Svensson, I.-L.; Tsarchopoulos, P.; Tryferidis, A.; Tzovaras, D. A Methodological Framework for the Selection of Key Performance Indicators to Assess Smart City Solutions. Smart Cities 2019, 2, 269–306. [Google Scholar] [CrossRef]
- Olewiler, N. Environmental Sustainability for Urban Areas: The Role of Natural Capital Indicators. Cities 2006, 23, 184–195. [Google Scholar] [CrossRef]
- Nassauer, J.I.; Wu, J.G.; Xiang, W.-N. Actionable Urban Ecology in China and the World: Integrating Ecology and Planning for Sustainable Cities. Landsc. Urban Plan. 2014, 125, 207–208. [Google Scholar] [CrossRef]
- Jorge-Ortiz, A.; Braulio-Gonzalo, M.; Bovea, M.D. Assessing Urban Sustainability: A Proposal for Indicators, Metrics and Scoring—A Case Study in Colombia. Environ. Dev. Sustain. 2023, 25, 11789–11822. [Google Scholar] [CrossRef]
- Garcia, C.; López-Jiménez, P.A.; Sánchez-Romero, F.-J.; Pérez-Sánchez, M. Assessing Water Urban Systems to the Compliance of SDGs through Sustainability Indicators. Implementation in the Valencian Community. Sustain. Cities Soc. 2023, 96, 104704. [Google Scholar] [CrossRef]
- Gavaldà, O.; Gibbs, C.; Eicker, U. A Review of Current Evaluation Urban Sustainability Indicator Frameworks and a Proposal for Improvement. Sustainability 2023, 15, 15425. [Google Scholar] [CrossRef]
- Boeing, G.; Higgs, C.; Liu, S.; Giles-Corti, B.; Sallis, J.F.; Cerin, E.; Lowe, M.; Adlakha, D.; Hinckson, E.; Moudon, A.V.; et al. Using open data and open-source software to develop spatial indicators of urban design and transport features for achieving healthy and sustainable cities. Lancet Glob. Health 2022, 10, E907–E918. [Google Scholar] [CrossRef]
- Tan, S.; Hu, B.; Kuang, B.; Zhou, M. Regional differences and dynamic evolution of urban land green use efficiency within the Yangtze River Delta, China. Land Use Policy 2021, 106, 105449. [Google Scholar] [CrossRef]
- Pozoukidou, G.; Angelidou, M. Urban Planning in the 15-Minute City: Revisited under Sustainable and Smart City Developments until 2030. Smart Cities 2022, 5, 1356–1375. [Google Scholar] [CrossRef]
- Krüger, A.; Kolbe, T.H. Building Analysis for Urban Energy Planning Using Key Indicators on Virtual 3D City Models—The Energy Atlas Of Berlin. Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 2012, XXXIX-B2, 145–150. [Google Scholar] [CrossRef]
- Liu, B.; Guo, X.; Jiang, J. How Urban Morphology Relates to the Urban Heat Island Effect: A Multi-Indicator Study. Sustainability 2023, 15, 10787. [Google Scholar] [CrossRef]
- Hu, Y.; Dai, Z.; Guldmann, J.-M. Modeling the Impact of 2D/3D Urban Indicators on the Urban Heat Island over Different Seasons: A Boosted Regression Tree Approach. J. Environ. Manag. 2020, 266, 110424. [Google Scholar] [CrossRef]
- Biljecki, F.; Stoter, J.; Ledoux, H.; Zlatanova, S.; Çöltekin, A. Applications of 3D City Models: State of the Art Review. ISPRS Int. J. Geo-Inf. 2015, 4, 2842–2889. [Google Scholar] [CrossRef]
- Willenborg, B.; Sindram, M.; H. Kolbe, T. Applications of 3D City Models for a Better Understanding of the Built Environment. In Understanding of the Built Environment; Behnisch, M., Meinel, G., Eds.; Trends in Spatial Analysis and Modelling; Geotechnologies and the Environment; Springer: Cham, Switzerland, 2017; Volume 19. [Google Scholar] [CrossRef]
- Kang, Y. Visualization analysis of urban planning assistant decision network 3D system based on intelligent computing. Heliyon 2024, 10, e31321. [Google Scholar] [CrossRef]
- Brasebin, M.; Perret, J.; Mustière, S.; Weber, C. Measuring the impact of 3D data geometric modeling on spatial analysis: Illustration with Skyview factor. Usage Usability Util. 3D City Models 2012, 02001. [Google Scholar] [CrossRef]
- Liang, X.; Chang, J.H.; Gao, S.; Zhao, T.; Biljecki, F. Evaluating human perception of building exteriors using street view imagery. Build. Environ. 2024, 263, 111875. [Google Scholar] [CrossRef]
- Biljecki, F.; Lim, J.; Crawford, J.; Moraru, D.; Tauscher, H.; Konde, A.; Adouane, K.; Lawrence, S.; Janssen, P.; Stouffs, R. Extending CityGML for IFC-sourced 3D city models. Autom. Constr. 2021, 121, 103440. [Google Scholar] [CrossRef]
- Kutzner, T.; Chaturvedi, K.; Kolbe, T.H. CityGML 3.0: New functions open up new applications. PFG J. Photogramm. Remote Sens. Geoinf. Sci. 2020, 88, 43–61. [Google Scholar] [CrossRef]
- Kolbe, T.H.; Kutzner, T.; Smyth, C.S.; Nagel, C.; Roensdorf, C.; Heazel, C. OGC City Geography Markup Language (CityGML) Part 1: Conceptual Model Standard, 2021. Available online: https://www.opengis.net/doc/IS/CityGML-1/3.0 (accessed on 26 April 2025).
- Kutzner, T.; Smyth, C.S.; Nagel, C.; Coors, V.; Vinasco-Alvarez, D.; Ishi, N. OGC City Geography Markup Language (CityGML) Part 2: GML Encoding Standard, 2023. Available online: http://www.opengis.net/doc/IS/CityGML-2/3.0 (accessed on 26 April 2025).
- Biljecki, F.; Ledoux, H.; Stoter, J. An improved LOD specification for 3D building models. Computers. Environ. Urban Syst. 2016, 59, 25–37. [Google Scholar] [CrossRef]
- Domińczak, M. Metodyka regulacji intensywności zabudowy w ujęciu historycznym–zarys problematyki. Methodology of building density regulation—Historical aspects. Builder 2021, 294, 12–15. [Google Scholar] [CrossRef]
- Bansal, V.K. Use of geographic information systems in spatial planning: A case study of an institute campus. J. Comput. Civ. Eng. 2014, 28, 05014002. [Google Scholar] [CrossRef]
- Michalik, A.; Załuski, D.; Zwirowicz-Rutkowska, A. Rozważania nad intensywnością zabudowy w kontekście praktyki urbanistycznej oraz potencjału technologii GIS (Considerations on the intensity of development in the context of urban practice and the potential of GIS technology). Rocz. Geomatyki 2015, 13, 133–145. [Google Scholar]
- Michalik, A.; Zwirowicz-Rutkowska, A. Geoportal Supporting Spatial Planning in Poland: Concept and Pilot Version. Geomat. Environ. Eng. 2023, 17, 2. [Google Scholar] [CrossRef]
- Guler, D. Implementation of 3D spatial planning through the integration of the standards. Trans. GIS 2023, 27, 2252–2277. [Google Scholar] [CrossRef]
- Gui, S.; Qin, R. Automated LoD-2 model reconstruction from very-high-resolution satellite-derived digital surface model and orthophoto. ISPRS J. Photogramm. Remote Sens. 2021, 181, 1–19. [Google Scholar] [CrossRef]
- Lewandowicz, E.; Tarsha Kurdi, F.; Gharineiat, Z. 3D LoD2 and LoD3 Modeling of Buildings with Ornamental Towers and Turrets Based on LiDAR Data. Remote Sens. 2022, 14, 4687. [Google Scholar] [CrossRef]
- Tarsha Kurdi, F.; Lewandowicz, E.; Gharineiat, Z.; Shan, J. Modeling Multi-Rotunda Buildings at LoD3 Level from LiDAR Data. Remote Sens. 2023, 15, 3324. [Google Scholar] [CrossRef]
- Tarsha Kurdi, F.; Gharineiat, Z.; Campbell, G.; Dey, E.K.; Awrangjeb, M. Full Series Algorithm of Automatic Building Extraction and Modelling from LiDAR Data. In Proceedings of the 2021 Digital Image Computing: Techniques and Applications (DICTA), Gold Coast, Australia, 29 November–1 December 2021; pp. 1–8. [Google Scholar]
- Peters, R.; Dukai, B.; Vitalis, S.; Van Liempt, J.; Stoter, J. Automated 3D Reconstruction of LoD2 and LoD1 Models for All 10 Million Buildings of the Netherlands. Photogramm. Eng. Remote Sens. 2022, 88, 165–170. [Google Scholar] [CrossRef]
- Bizjak, M.; Žalik, B.; Štumberger, G.; Lukač, N. Large-scale estimation of buildings’ thermal load using LiDAR data. Energy Build. 2021, 231, 110626. [Google Scholar] [CrossRef]
- Zhang, Z.; Qian, Z.; Zhong, T.; Chen, M.; Zhang, K.; Yang, Y.; Zhu, R.; Zhang, F.; Zhang, H.; Zhou, F.; et al. Vectorized rooftop area data for 90 cities in China. Sci. Data 2022, 9, 66. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Luo, Y.P.; Jiang, T.; Gong, H.; Luo, S.; Zhang, X.W. A new classification method for LIDAR data based on unbalanced support vector machine. In Proceedings of the 2011 International Symposium on Image and Data Fusion, Tengchong, China, 9–11 August 2011; pp. 1–4. [Google Scholar] [CrossRef]
- Wen, C.; Yang, L.; Li, X.; Peng, L.; Chi, T. Directionally constrained fully convolutional neural network for airborne LiDAR point cloud classification. ISPRS J. Photogramm. Remote Sens. 2020, 162, 50–62. [Google Scholar] [CrossRef]
- Maltezos, E.; Doulamis, A.; Doulamis, N.; Ioannidis, C. Building extraction from LiDAR data applying deep convolutional neural networks. IEEE Geosci. Remote Sens. Lett. 2018, 16, 155–159. [Google Scholar] [CrossRef]
- Yuan, J. Learning building extraction in aerial scenes with convolutional networks. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 2793–2798. [Google Scholar] [CrossRef]
- Kuras, A.; Brell, M.; Rizzi, J.; Burud, I. Hyperspectral and Lidar Data Applied to the Urban Land Cover Machine Learning and Neural-Network-Based Classification: A Review. Remote Sens. 2021, 13, 3393. [Google Scholar] [CrossRef]
- Zhou, L.; Geng, J.; Jiang, W. Joint Classification of Hyperspectral and LiDAR Data Based on Position-Channel Cooperative Attention Network. Remote Sens. 2022, 14, 3247. [Google Scholar] [CrossRef]
- Pang, H.E.; Biljecki, F. 3D building reconstruction from single street view images using deep learning. Int. J. Appl. Earth Obs. Geoinf. 2022, 112, 102859. [Google Scholar] [CrossRef]
- Xu, Y.; Stilla, U. Towards Building and Civil Infrastructure Reconstruction from Point Clouds: A Review on Data and KeyTechniques. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 2857–2885. [Google Scholar] [CrossRef]
- Zhuang, J.; Li, G.; Xu, H.; Xu, J.; Tian, R. TEXT-TO-CITY Controllable 3D Urban Block Generation with Latent Diffusion Model. In Proceedings of the 29th International Conference of the Association for Computer-Aided Architectural Design Research in Asia (CAADRIA), Singapore, 20–26 April 2024; Volume 2, pp. 169–178. Available online: https://www.researchgate.net/publication/380124047_TEXT-TO-ITYControlla-ble_3D_Urban_Block_Generation_with_Latent_Diffusion_Model (accessed on 14 August 2024).
- Li, J.; Yang, B.; Chen, C.; Habib, A. NRLI-UAV: Non-rigid registration of sequential raw laser scans and images for low-cost UAV LiDAR point cloud quality improvement. ISPRS J. Photogramm. Remote Sens. 2019, 158, 123–145. [Google Scholar] [CrossRef]
- Mongus, D.; Lukač, N.; Žalik, B. Ground and building extraction from LiDAR data based on differential mor-phological profiles and locally fitted surfaces. ISPRS J. Photogramm. Remote Sens. 2014, 93, 145–156. [Google Scholar] [CrossRef]
- Yang, B.; Li, J. A hierarchical approach for refining point cloud quality of a low cost UAV LiDAR system in the urban environment. ISPRS J. Photogramm. Remote Sens. 2022, 183, 403–421. [Google Scholar] [CrossRef]
- Gilani, S.A.N.; Awrangjeb, M.; Lu, G. An Automatic Building Extraction and Regularisation Technique Using LiDAR Point Cloud Data and Orthoimage. Remote Sens. 2016, 8, 258. [Google Scholar] [CrossRef]
- Lukač, N.; Mongus, D.; Žalik, B.; Štumberger, G.; Bizjak, M. Novel GPU-accelerated high-resolution solar potential estimation in urban areas by using a modified diffuse irradiance model. Appl. Energy 2024, 353 Pt A, 122129. [Google Scholar] [CrossRef]
- Orthuber, E.; Avbelj, J. 3D Building Reconstruction from Lidar Point Clouds by Adaptive Dual Contouring. ISPRS Ann. Photogramm. Remote Sens. Spatial Inf. Sci. 2015, II-3/W4, 157–164. [Google Scholar] [CrossRef]
- Bizjak, M.; Mongus, D.; Žalik, B.; Lukač, N. Novel Half-Spaces Based 3D Building Reconstruction Using Airborne LiDAR Data. Remote Sens. 2023, 15, 1269. [Google Scholar] [CrossRef]
- Tarsha Kurdi, F.; Lewandowicz, E.; Shan, J.; Gharineiat, Z. 3D modeling and visualization of single tree Lidar point cloud using matrixial form. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 2024. [Google Scholar] [CrossRef]
- Tarsha Kurdi, F.; Amakhchan, W.; Gharineiat, Z. Random Forest machine learning technique for automatic vegetation detection and modeling in LiDAR data. Int. J. Environ. Sci. Nat. Resour. 2021, 28, 556234. [Google Scholar]
- Tarsha Kurdi, F.; Lewandowicz, E.; Gharineiat, Z.; Shan, J. Accurate Calculation of Upper Biomass Volume of Single Trees Using Matrixial Representation of LiDAR Data. Remote Sens. 2024, 16, 2220. [Google Scholar] [CrossRef]
- Dong, L.; Du, H.; Han, N.; Li, X.; Zhu, D.; Mao, F.; Zhang, M.; Zheng, J.; Liu, H.; Huang, Z.; et al. Application of Convolutional Neural Network on Lei Bamboo Above-Ground-Biomass (AGB) Estimation Using Worldview-2. Remote Sens. 2020, 12, 958. [Google Scholar] [CrossRef]
- Zhou, L.; Xuejian, L.; Bo, Z.; Jie, X.; Yulin, G.; Cheng, T.; Huaguo, H.; Huaqiang, D. Estimating 3D Green Volume and Aboveground Biomass of Urban Forest Trees by UAV-Lidar. Remote Sens. 2022, 14, 5211. [Google Scholar] [CrossRef]
- Lucchi, E.; Buda, A. Urban green rating systems: Insights for balancing sustainable principles and heritage conservation for neighbourhood and cities renovation planning. Renew. Sustain. Energy Rev. 2022, 161, 112324. [Google Scholar] [CrossRef]
- Richa, J.P.; Deschaud, J.-E.; Goulette, F.; Dalmasso, N. AdaSplats: Adaptive Splatting of Point Clouds for Accurate 3D Modeling and Real-Time High-Fidelity LiDAR Simulation. Remote Sens. 2022, 14, 6262. [Google Scholar] [CrossRef]
- Biljecki, F.; Shin Chow, Y. Global Building Morphology Indicators. Comput. Environ. Urban Syst. 2022, 95, 101809. [Google Scholar] [CrossRef]
- Bibri, S.E. A novel model for data-driven smart sustainable cities of the future: The institutional transformations required for balancing and advancing the three goals of sustainability. Energy Inform. 2021, 4, 1. [Google Scholar] [CrossRef]
- USTAWA z dnia 27 marca 2003 r. o Planowaniu i Zagospodarowaniu Przestrzennym. Tekst jednolity z 2023 r. t.j. Dz. U. z 2023 Nr. 80 poz. 717, s. 20-21. (ACT of 27 March 2003 on Spatial Planning and Development. Consolidated Text of 2023, i.e., Journal of Laws of 2023, No. 80 Items 717, s 20-21). Available online: https://isap.sejm.gov.pl/isap.nsf/download.xsp/WDU20030800717/U/D20030717Lj.pdf (accessed on 26 April 2025).
- Rozporządzenie Ministra Rozwoju I Technologii z dnia 15 lipca 2024 r. w Sprawie Sposobu Ustalania Wymagań Dotyczących Nowej Zabudowy i Zagospodarowania Terenu w Przypadku Braku Miejscowego Planu Zagospodarowania Przestrzennego. Dziennik Ustaw 2024 poz. 1116, s. 1-2. (Regulation of the Minister of Development and Technology of 15 July 2024 on the Method of Determining the Requirements for New Development and Land Development in the Absence of a Local Spatial Development Plan). Journal of Laws of 2024, Items 1116, s. 1-2. Available online: https://isap.sejm.gov.pl/isap.nsf/download.xsp/WDU20240001116/O/D20241116.pdf (accessed on 26 April 2025).
- Chen, J.; Chuanbin, Z.; Feng, L. Quantifying the green view indicator for assessing urban greening quality: An analysis based on Internet-crawling street view data. Ecol. Indic. 2020, 113, 106192. [Google Scholar] [CrossRef]
- Sargent, I.; Holland, D.; Harding, J. The Building Blocks of User-Focused 3D City Models. ISPRS Int. J. Geo-Inf. 2015, 4, 2890–2904. [Google Scholar] [CrossRef]
- Jjumba, A.; Dragićević, S. Sppatial indices for measuring three-dimensional patterns in a voxel-based space. J. Geogr. Syst. 2016, 18, 183–204. [Google Scholar] [CrossRef]
- McTegg, S.J.; Tarsha Kurdi, F.; Simmons, S.; Gharineiat, Z. Comparative approach of unmanned aerial vehicle restrictions in controlled airspaces. Remote Sens. 2022, 14, 822. [Google Scholar] [CrossRef]
- Bydłosz, J.; Bieda, A.; Parzych, P. The Implementation of Spatial Planning Objects in a 3D Cadastral Model. ISPRS Int. J. Geo-Inf. 2018, 7, 153. [Google Scholar] [CrossRef]
- Indrajit, A.; van Loenen, B.; Ploeger, H.; van Oosterom, P. Developing a spatial planning information package in ISO 19152 land administration domain model. Land Use Policy 2020, 98, 104111. [Google Scholar] [CrossRef]
- Wolak, P. Topographic Data as a Basis for 3D Visualization Using Object Models Available in the GIS Program and Other Libraries. Engineering Diploma Thesis, University of Warmia and Mazury in Olsztyn, Olsztyn, Poland, 2025. [Google Scholar]
- Schutz, M.; Porte, L. FreeBSD (2-Clause BSD). Available online: https://github.com/potree/potree (accessed on 26 April 2025).
- Tarsha Kurdi, F.; Awrangjeb, M.; Munir, N. Automatic filtering and 2D modelling of LiDAR building point cloud. Trans. GIS J. 2021, 25, 164–188. [Google Scholar] [CrossRef]
- Tarsha Kurdi, F.; Landes, T.; Grussenmeyer, P.; Smigiel, E. New approach for automatic detection of buildings in airborne laser scanner data using first echo only. In Proceedings of the ISPRS Commission III Symposium, Photogrammetric Computer Vision, Bonn, Germany, 20–22 September 2006; International Archives of Photogrammetry and Remote Sensing and Spatial Information Sciences; International Society of Photogrammetry and Remote Sensing (ISPRS): Hannover, Germany, 2006; Volume XXXVI, Part 3, pp. 25–30. [Google Scholar]

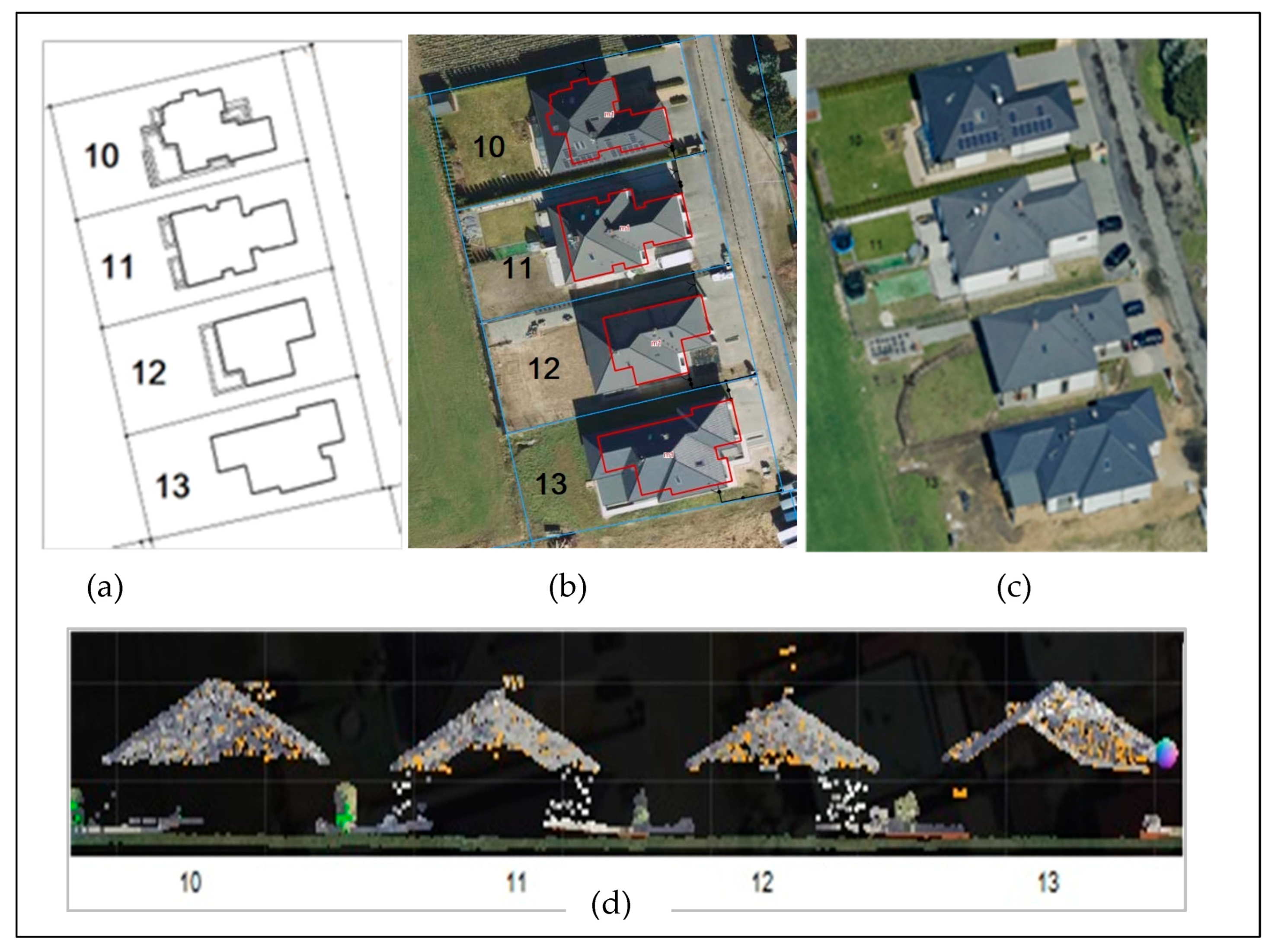
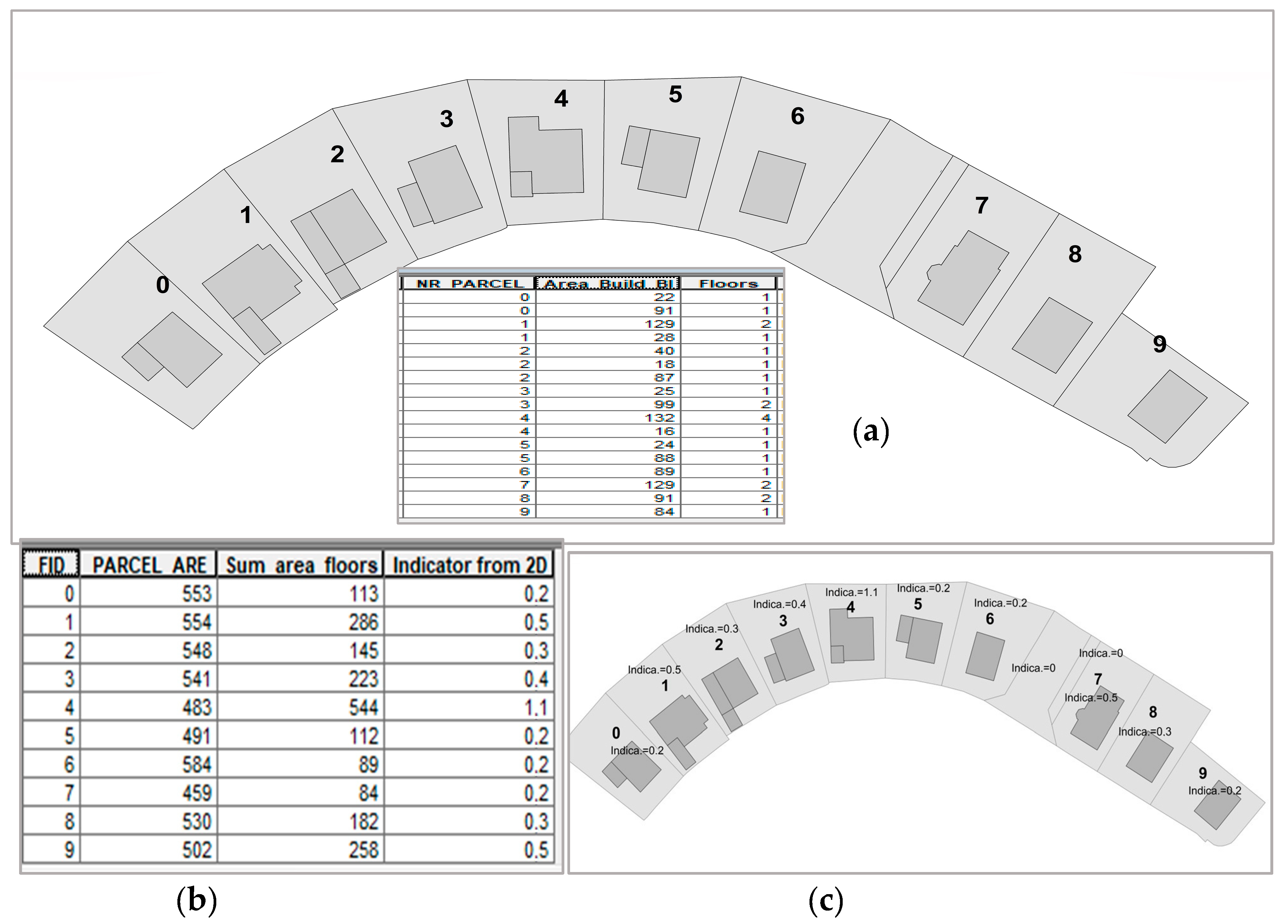



| Parcel Area m2 | Building Area m2 | Floor | Indicator | |
|---|---|---|---|---|
| 10 | 836 | 175 | 1 | 0.2 |
| 11 | 817 | 215 | 1 | 0.3 |
| 12 | 816 | 168 | 1 | 0.2 |
| 13 | 818 | 232 | 1 | 0.3 |
| Building ID | Number of Points | DSM Pixel Size (m) | Number of Building Pixels Containing LiDAR Points | Number of Empty Building Pixels | Area Without Filling Empty Pixels (m2) | Area with Filling Empty Pixels (m2) | Reference Area (Ground Truth) (m2) |
|---|---|---|---|---|---|---|---|
| 0 | 2094 | 0.10 | 1977 | 12102 | 19.77 | 140.79 | 113 |
| 0.25 | 1470 | 815 | 91.88 | 142.81 | |||
| 0.40 | 861 | 49 | 137.76 | 145.6 | |||
| 0.60 | 400 | 15 | 144 | 149.4 | |||
| 1 | 3272 | 0.10 | 3055 | 20,252 | 30.55 | 233.07 | 157 |
| 0.25 | 2320 | 1431 | 145 | 234.44 | |||
| 0.40 | 1334 | 150 | 213.38 | 237.44 | |||
| 0.60 | 620 | 57 | 223.2 | 243.72 | |||
| 5 | 2674 | 0.10 | 2573 | 16171 | 25.73 | 187.44 | 112 |
| 0.25 | 2035 | 1014 | 127.19 | 190.56 | |||
| 0.40 | 1167 | 36 | 186.72 | 192.48 | |||
| 0.60 | 543 | 7.44 | 195.48 | 198.00 | |||
| 6 | 1664 | 0.10 | 1600 | 10,846 | 16.00 | 124.46 | 89 |
| 0.25 | 1257 | 756 | 78.56 | 125.81 | |||
| 0.40 | 738 | 58 | 118.08 | 127.36 | |||
| 0.60 | 350 | 15 | 126.00 | 131.40 |
| Building ID | Footprint Area (m2) | Footprint Ref Area (Ground Truth) (m2) | Underhung Ref Area (Ground Truth) (m2) | Footprint MLA (m2) | Underhung MLA Ref (Ground Truth) (m2) | Area Error (m2) | Parcel Area (Ground Truth) (m2) | II % | II Ref (Ground Truth) % |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 131.35 | 129.99 | 113 | 131.35 | 113 | 14.28 | 553 | 0.2 | 0.2 |
| 1 | 205.26 | 200.53 | 157 | 339.52 | 286 | 20.31 | 554 | 0.6 | 0.5 |
| 2 | 218.71 | 221.97 | 145 | 218.71 | 145 | 20.52 | 548 | 0.4 | 0.3 |
| 3 | 163.08 | 162.62 | 124 | 263.09 | 223 | 12.86 | 541 | 0.5 | 0.4 |
| 4 | 196.78 | 193.67 | 148 | 602.31 | 544 | 23.32 | 483 | 1.2 | 1.1 |
| 5 | 175.1 | 171.51 | 112 | 175.1 | 112 | 19.91 | 491 | 0.4 | 0.2 |
| 6 | 112.6 | 108.52 | 89 | 112.60 | 89 | 8.61 | 584 | 0.2 | 0.2 |
| Building ID | Vol 1 (m3) | Vol 2 (m3) | Vol Ref (m3) (Ground Truth) | ∆Vol 2 | Vol Error (m3) | VRA (%) | 3D II 1 | 3D II 2 |
|---|---|---|---|---|---|---|---|---|
| 0 | 860.56 | 860.32 | 818.29 | 42.03 | 58.95 | 6.9 | 0.3 | 0.3 |
| 1 | 1454.25 | 1454.35 | 1378.37 | 75.98 | 86.93 | 6.0 | 0.5 | 0.5 |
| 2 | 1371.75 | 1371.25 | 1283.67 | 87.58 | 83.21 | 6.1 | 0.5 | 0.5 |
| 3 | 914.82 | 914.67 | 1015.79 | −101.12 | 61.65 | 6.7 | 0.3 | 0.3 |
| 4 | 1621.71 | 1623.82 | 1522.85 | 100.97 | 94.36 | 5.8 | 0.7 | 0.7 |
| 5 | 1423.81 | 1429.36 | 1316.87 | 112.49 | 85.56 | 6.0 | 0.6 | 0.6 |
| 6 | 619.46 | 618.01 | 618.29 | −0.28 | 46.45 | 7.5 | 0.2 | 0.2 |
| Building ID | Vol 1 (m3) | Vol 2 (m3) | Vol Error (m3) | VRA (%) | 3D II 1 | 3D II 2 |
|---|---|---|---|---|---|---|
| 10 | 1332.18 | 1312.63 | 86.42 | 6.5 | 0.3 | 0.3 |
| 11 | 862.55 | 869.44 | 67.35 | 7.8 | 0.2 | 0.2 |
| 12 | 905.57 | 896.24 | 70.42 | 7.8 | 0.2 | 0.2 |
| 13 | 1450.34 | 1441.80 | 92.52 | 6.4 | 0.4 | 0.4 |
| Building ID | Footprint Area (m2) | Footprint Ref Area (Ground Truth) (m2) | Underhung Ref Area (Ground Truth) (m2) | Footprint MLA (m2) | Underhung MLA Ref (Ground Truth) (m2) | Area Error (m2) | Parcel Area (Ground Truth) (m2) | II % | II Ref (Ground Truth) % |
|---|---|---|---|---|---|---|---|---|---|
| 10 | 250.65 | 248.34 | 175.00 | 250.65 | 175.00 | 30.26 | 836 | 0.3 | 0.2 |
| 11 | 244.42 | 245.86 | 215.00 | 244.42 | 215.00 | 22.83 | 817 | 0.3 | 0.3 |
| 12 | 229.56 | 230.05 | 168.50 | 229.56 | 168.50 | 23.65 | 816 | 0.3 | 0.2 |
| 13 | 306.19 | 305.47 | 233.5 | 306.19 | 233.5 | 32.63 | 818 | 0.4 | 0.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tarsha Kurdi, F.; Lewandowicz, E.; Gharineiat, Z.; Shan, J. High-Resolution Building Indicator Mapping Using Airborne LiDAR Data. Electronics 2025, 14, 1821. https://doi.org/10.3390/electronics14091821
Tarsha Kurdi F, Lewandowicz E, Gharineiat Z, Shan J. High-Resolution Building Indicator Mapping Using Airborne LiDAR Data. Electronics. 2025; 14(9):1821. https://doi.org/10.3390/electronics14091821
Chicago/Turabian StyleTarsha Kurdi, Fayez, Elżbieta Lewandowicz, Zahra Gharineiat, and Jie Shan. 2025. "High-Resolution Building Indicator Mapping Using Airborne LiDAR Data" Electronics 14, no. 9: 1821. https://doi.org/10.3390/electronics14091821
APA StyleTarsha Kurdi, F., Lewandowicz, E., Gharineiat, Z., & Shan, J. (2025). High-Resolution Building Indicator Mapping Using Airborne LiDAR Data. Electronics, 14(9), 1821. https://doi.org/10.3390/electronics14091821









