How to Use Redundancy for Memory Reliability: Replace or Code?

Abstract

Modern digital systems rely on DRAM as main memory and flash-based SSDs for storage, forming the backbone of today’s computing infrastructure. As demands for faster processing and larger data services increase, the memory subsystems have become denser, pushing technologies to their physical limits and increasing susceptibility to faults. To ensure data integrity, two complementary approaches are employed: replacement-based techniques, which map defective cells to redundant areas, and error-correcting code (ECC) methods, which dynamically detect and correct errors. This paper theoretically investigates the most efficient use of redundancy for DRAM reliability by categorizing detects into hard faults and soft errors. Each scenario is evaluated in terms of required redundancy and residual error rate, using finite-length channel coding capacity. We compare the ECC schemes with BCH codes, which are widely favored in on-die ECC applications due to their low latency and decoding complexity.

1. Introduction

In modern digital systems, DRAM is commonly employed as the main memory, while flash-based SSDs serve as the primary storage solution [1,2,3]. Both DRAM and flash memory technologies have achieved significant success, becoming key pillars of today’s computing infrastructure. As demands for faster processing and large-scale data services continue to escalate, the industry has prioritized creating larger, faster, and more energy-efficient memory subsystems. Consequently, the densification of memory cells in silicon dies has accelerated to unprecedented levels, pushing the technology toward its fundamental physical limits [2,4]. However, this extreme density renders modern memory devices more susceptible to various faults and errors [5,6]. To address these vulnerabilities, advanced error protection schemes are increasingly imperative for ensuring data integrity and reliability in cutting-edge computing environments.

As DRAM technology continues to scale, ensuring reliability has become a critical challenge due to process variations, retention failures, and inherent defects. Enhancements in DRAM reliability are achieved through two key approaches: replacement-based techniques and error-correcting code (ECC)-based techniques. Replacement-based methods mitigate faults by mapping defective memory cells to redundant, functional regions, while ECC-based methods detect and correct errors dynamically to maintain data integrity. These approaches complement each other, with replacement techniques addressing permanent faults and ECC handling transient and soft errors.

First, replacement-based techniques generally map faulty memory cells to redundant, functional regions. Redundant row/column sparing dynamically replaces defective rows or columns with pre-allocated spares, minimizing defects with minimal overhead [7]. Laser fusing permanently disables faulty cells during fabrication and redirects access to spare units, improving yield [8]. Post-packaging repair (PPR) enables EEPROM-based remapping, allowing in-field correction of memory faults, thereby extending DRAM lifespan [9]. These replacement-based strategies collectively enhance DRAM reliability across manufacturing and operational phases.

On the other hand, ECC technologies have become increasingly important for DRAM [10,11]. ECC techniques are applied in various ways to enhance reliability and data integrity. Rank-level ECC provides robust error protection by applying ECC at the DRAM rank level, ensuring resilience against multi-bit errors [12]. In-DRAM ECC detects and corrects errors within the DRAM chip itself, reducing the dependency on external memory controllers and improving efficiency [13]. Multi-tier ECC optimizes performance by separating error detection (ED) and error correction (EC), allowing for more flexible and efficient error handling.

These diverse ECC strategies collectively strengthen DRAM reliability across different failure scenarios. In spite of these various DRAM reliability solutions, there is no theoretical study on the joint optimization of the two approaches. In this paper, from a theoretical standpoint, we investigate how to use redundancy most efficiently for DRAM reliability. In order to know the theoretical limitation, we put some practical considerations (implementation friendliness, etc.) aside.

More specifically, we classify the defects in cells as hard faults and soft errors and categorize the scenarios. For each scenario, error protection methods are evaluated in terms of required redundancy or remaining error rate. For evaluation of the capacity of ECC schemes, finite-length capacity of channel coding [14] is used and compared with BCH codes [15] as they and their variations are most preferred in on-die ECC applications due to their low decoding complexity and short decoding latency.

In Section 2, the system model and notations are introduced. In Section 3, replacement and ECC techniques are separately evaluated in terms of error-free rate. In Section 4, we study the ECC performance behavior for soft errors and a unified approach for the two schemes where both hard faults and soft errors are existing. Conclusions are given in Section 5.

2. System Model

In order to develop a simplified model, we approximate the DRAM redundancy techniques as a resource allocation problem. First, we consider only two classes of errors: one class is ‘hard fault’ and the other class is ‘soft error’, although DRAM errors occur in various patterns due to different causes. Here, hard faults are permanent errors, normally originating from fabrication or manufacturing processes. The soft errors are the non-permanent errors, which occur occasionally. For basic analysis, we assume soft errors arise independently.

We assume the number of available cells is N among the cells, D cells are used for data, and R cells are allocated for redundancy for the DRAM reliability mechanism. Resultantly,

$$N=D+R.$$

Let $\rho =R/D$ be called the redundancy rate. As every cell cannot be handled separately, we consider block-wise operation. Let $k_B$ be the block size, which is a system parameter; then, the number of cell blocks in the system is $N_B=\lfloor N/k_B\rfloor$. Then, we can count the data and redundancy size in terms of the number of blocks: $N_D=\lfloor D/k_B\rfloor$ is the number of data blocks and $N_R=\lfloor R/k_B\rfloor$ the number of redundant blocks.

Because the goal of this study is to provide a comprehensive guide for efficient use of redundancy or overhead in memory systems, we assume that coding parameters can be freely determined. This is indeed an infeasible assumption. However, in this paper, we focus on the theoretical limit of coding. More practical considerations can be used after the theoretical bound is established, or practical solutions can be evaluated by how far it is from the limit.

As mentioned, there are two types of errors that one addresses: hard faults and soft errors. First of all, it has been considered that hard faults can be coped with through the test and replacement method. If a cell is detected as a fault or a bad cell, then the bad cell’s data block (say, a faulty block) can be replaced with one from the spare cells. However, soft errors cannot be prevented by replacement. Since soft errors occur in a random fashion, a proper error protection technique should be applied. The ECC method can handle this problem.

Replacement can be achieved by allocating a new data block from spare cells to the memory address of a faulty block. In Figure 1, the replacement task is demonstrated. The device or controller should memorize the list of newly allocated addresses. For soft errors, ECC techniques should be applied to protect the data blocks from randomly occurring errors. The error protection capability varies regarding the coding parameters, such as block length and overhead (or coding rate). Here, we will consider two types of coding performances: the theoretical finite-length capacity [14] and one with practical binary block codes preferred in memory applications. The ECC method is also visualized in Figure 1b.

3. Error Protection from Hard Faults

In this section, we investigate how to deal with hard faults in memory systems. Hard faults can be tackled by two types of error protection mechanisms: replacement and error correction coding. We investigate behavior when the two methods are exclusively applied.

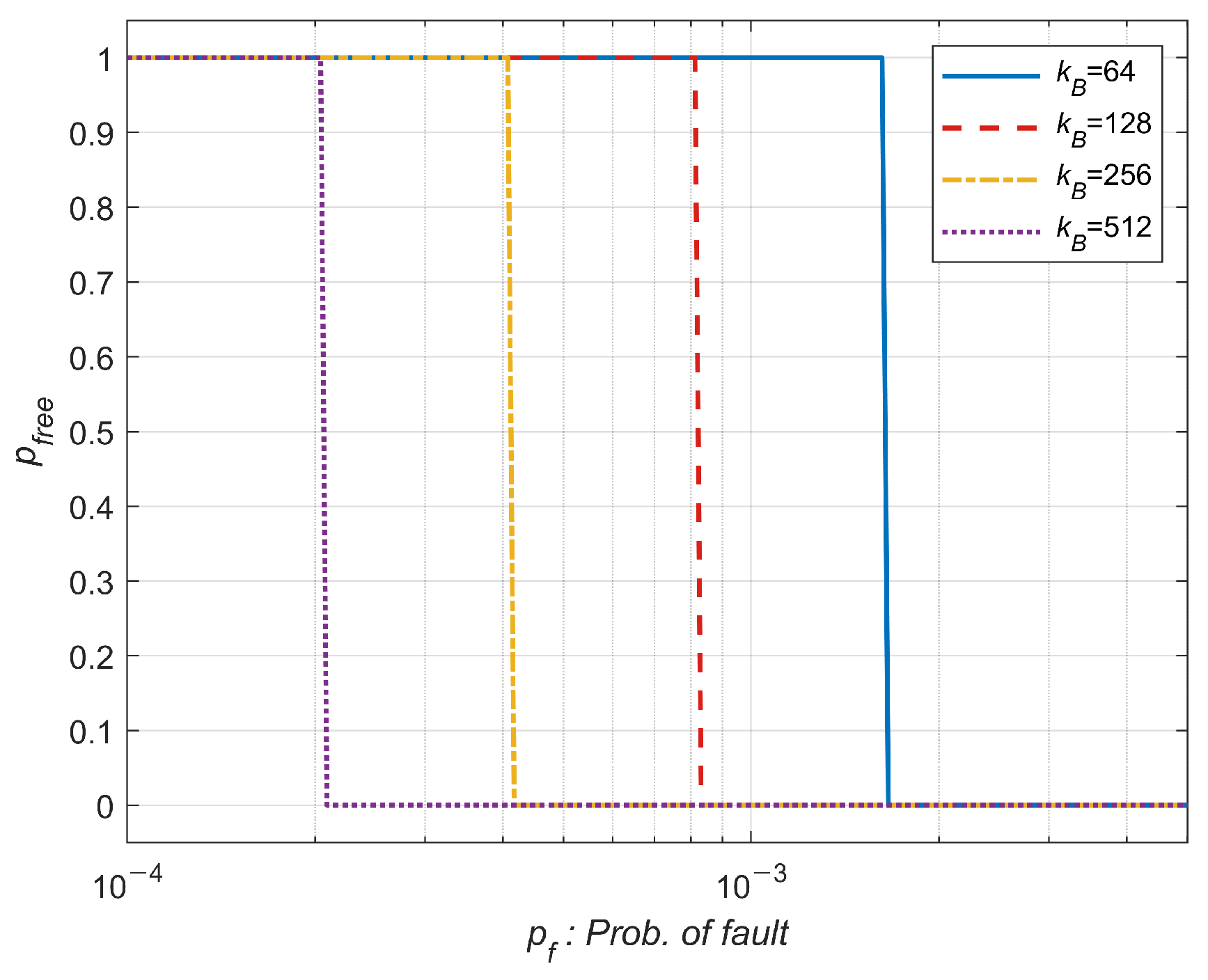
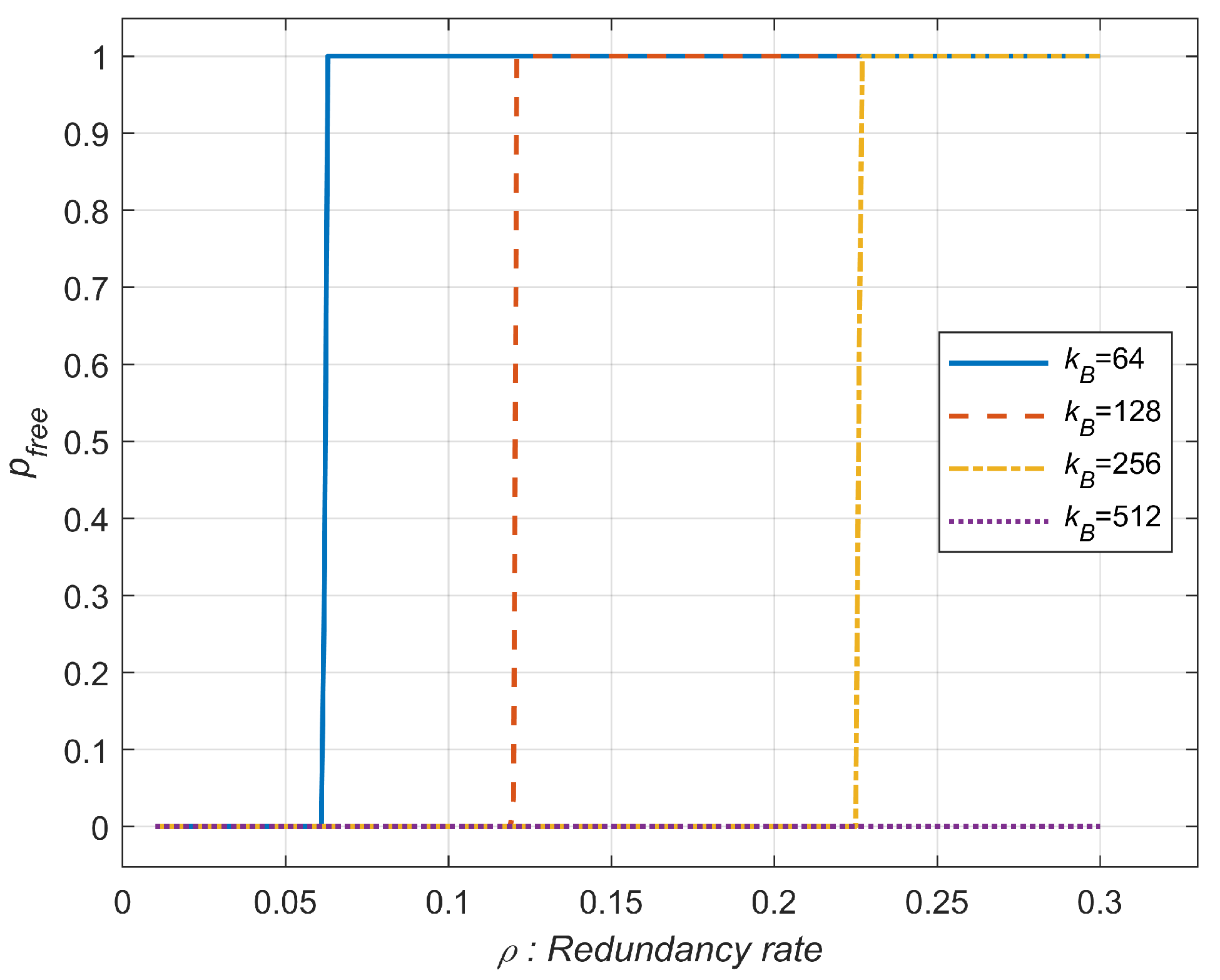
3.1. Replacement Approach

In the manufacturing and fabrication process, defects such as faults may occur, which should be avoided and fixed to protect the integrity of the memory system [16]. Under the assumption that we can test a memory block to know if there is a fault, the logical replacement of the memory block would be the best way to enhance the yield rate. The replacement can also be called ‘repair’.

Redundant cells should be augmented in the memory chip for the replacement process. The proper allocation of the redundant cells in a chip is crucial in the economics of memory production. Having the faults replaced, both the yield rate and the lifetime of the memory chip can be enhanced. Here, we investigate the yield rate (virtual) behavior according to a target fault rate, which can be measured in the real world.

We investigate this problem based on the assumption of uniformly random occurrence of hard faults, which may not precisely analyze the practice. However, at least the study results provide a lower (or upper limit) of practical metrics. In addition, analysis can be improved by more accurate or practical channel modeling. For mathematical modeling, some should be defined.

Let $p_f$ be the probability of a fault occurring in an individual cell; faults are assumed to be distributed randomly and independently. Let $p_{\mathrm{FB}}$ denote the probability of a faulty block, which is a function of $p_f$ and the size of the block $k_B$. The probability that the entire system (or a chip) is fault-free is denoted by $p_{\mathrm{free}}$. We have $p_{free}=1-p_{fail}$, where $p_{\mathrm{fail}}$ is the probability of system failure.

The replacement method is very simple. We ignore a faulty cell block by redirecting the address of the block to a redundant cell block. We consider the chip is alive if all faulty blocks are replaced by sound redundancy blocks. The probability of a faulty block is

$$p_{FB}=1-{(1-p_f)}^{k_B},$$

(1)

where $p_f$ is the probability of a faulty cell. This simple formula in (1) will be used to analyze the $p_{free}$ of the replacement scheme.

For reference, if there is no redundancy part and replacement cannot apply, then the system survives only when all data blocks are good, or equivalently, all cells are good. Thus,

$$p_{free}={(1-p_f)}^N={(1-p_f)}^{N_D{k}_B},$$

(2)

where $N_D$ is the number of blocks. In this case, $p_{free}$ quickly decreases as $N_D$ becomes larger. Figure 2 exhibits $p_{\mathrm{free}}$ versus $p_f$. The yield rate quickly diminishes where $p_f$ is still very low. There is no notable change depending on the block size $k_B$. Let us see what changes if we apply the replacement (or repair) technique.

Now, let us incorporate the replacement scheme by allocating a redundancy portion. We consider a typical value of the redundancy rate, $\rho =R/D=0.1$, corresponding to a 10% overhead. Let $N_f$ be the number of faulty blocks in the system, where $N_{f,D}$ and $N_{f,R}$ are the numbers of faulty blocks in data and redundancy parts, respectively. Based on the replacement policy, the failure of chip integrity occurs if

$$N_{f,D}>N_R-N_{f,R},$$

the event that the number of faulty data blocks exceeds the number of healthy remaining redundant blocks. This condition is equivalent to

$$N_f>N_R,$$

which we call an ‘outage’ event.

The metric $N_f$ is binomial-distributed and is approximated by a Gaussian random variable with mean $\mu =N_B{p}_{\mathrm{FB}}$ and variance ${\sigma }^2=N_B{p}_{\mathrm{FB}}(1-p_{\mathrm{FB}})$ due to the central limit theorem. The distribution is given as

$$f_{N_f}\left(x\right)={\displaystyle \frac{1}{\sqrt{2\pi {\sigma }^2}}}exp\left({\displaystyle \frac{-{(x-\mu )}^2}{2{\sigma }^2}}\right).$$

The outage probability $p_{\mathrm{free}}$ can be simply evaluated by the Q function as

$$p_{fail}=\mathrm{Pr}[N_f>N_R]={\int }_{N_R}^{\infty }{f}_{N_f}\left(x\right)dx=Q\left({\displaystyle \frac{N_f-\mu }{\sigma }}\right).$$

Figure 3 shows $p_{free}=1-p_{fail}$ versus $p_f$ under the basic setting. A threshold behavior is observed: $p_{free}$ surges from zero to probability 1 at a critical threshold as $p_f$ decreases. This phenomenon results from the law of large numbers associated with the large $N_B$. It is observed that as the block length $k_B$ increases, the threshold for $p_f$ decreases. The same mathematical result is drawn in terms of the redundancy rate $\rho$ in Figure 4. A similar threshold behavior is again observed. As the available repair resources increase, $p_{free}$ surges at a threshold. When the block size is larger, more redundancy is required to achieve $p_{free}\approx 1$.

By applying replacement, it is shown that $p_{free}\approx 1$ is achieved at a much higher raw fault rate $p_f$. For a fixed $p_f$, $p_{free}$ jumps as the block length becomes smaller. For a fixed redundancy rate, $p_{free}$ also has a sharp transition from zero to one as the block length decreases. In simple terms, a smaller block length is more advantageous for the replacement scheme if we disregard the control overhead. It is worth noting that the block length plays a crucial role in the performance of replacement schemes, whereas it does not affect the probability of a fault-free system when no protection is applied.

3.2. Error Correction Coding Approach

Here, we consider using ECC schemes for handling hard faults. For now, soft errors are not taken into account. Although ECCs are good for random errors, they can still be effective in improving the probability of a fault-free system $p_{free}$. Here, we assume that ECC is applied as a blind fault protection mechanism against hard faults. Thus, the detection of the faulty block is not required.

The performance of ECCs depends on the block length [14,17]. The finite-length capacity of ECCs has been analyzed by a theoretical study over various channels [14]. We consider the capacity of achieving finite-length codes, which is much superior to existing memory codes such as the single error correction codes [18,19] or BCH codes [15], to reveal the theoretical limit of this approach.

In the evaluation of the ECC approach, the $p_{free}$ is the performance metric. Because the ECC can correct a number of hard faults in a block, the faulty block with a smaller number of errors than the error correction capability can be considered error-free. Therefore, the probability of a fault-free system, $p_{free}$, can be evaluated regarding the error correction capability.

Let us first discuss the setting. We assume the entire redundancy part is used for ECC parity. Overall, D data cells are encoded with R redundant cells, resulting in a code rate of $r=D/(D+R)$, where D and R are the numbers of data and redundant cells, respectively. Since data are handled in $k_B$-bit blocks, the redundancy part should also be partitioned into $k_P(\doteq k_{B}R/D)$-bit blocks. A data block of $k_B$ bits and a parity block of $k_P$ bits form a codeword. The block error rate (BLER) of BCH codes (after decoding) is directly related to their error-correcting capability. Let $p_{B,BCH}$ denote the BLER of BCH codes, which is given as

$$p_{B,BCH}=\mathrm{P}(\mathrm{number}\mathrm{of}\mathrm{errors}>t).$$

This can be formulated using the binomial probability distribution derived from the bit error probability or the probability of fault $p_f$:

$$p_{B,BCH}=\sum _{i=t+1}^n\left({\displaystyle \genfrac{}{}{0pt}{}{n}{i}}\right){\left(p_f\right)}^i·{(1-p_f)}^{n-i}.$$

This formula represents the probability that more than t errors occur in a block of length n. Hence, the corresponding fault-free probability is given by

$$p_{free,BCH}={(1-p_{B,BCH})}^{N_D},$$

(3)

according to Equations (1) and (2).

As the block length is determined, the BLER can be also evaluated by the finite-length analysis. Let $l_B$ be the length of a codeword, which is $k_{B}N/D$. Then, the BLER is given by the following formula:

$$p_{B,NA}=Q\left(\left(1-h\left(p_f\right)-r+{\displaystyle \frac{{\log }_2\left(l_B\right)}{2l_B}}\right)/\left(\sqrt{{\displaystyle \frac{p_f(1-p_f)}{l_B}}}{\log }_2\left({\displaystyle \frac{1-p_f}{p_f}}\right)\right)\right),$$

(4)

where

$$h\left(x\right)=-(1-x){\log }_2(1-x)-x{\log }_2\left(x\right).$$

Because there are $N_D$ codewords,

$$p_{free,NA}={(1-p_{B,NA})}^{N_D}.$$

(5)

In Figure 5, the $p_{free}$ (from Equations (2), (3) and (5)) is plotted versus $p_f$ for various error protection configurations, when the faults are recovered by ECC in a blind manner. For the ‘Repair$(n,k_B)$’ curves, $(n,k_B)$ indicates a block of $k_B$ data cells is encoded and $(n-k_B)$ parity bits are generated. For the BCH curves, the parameters indicate $(n,k_B,t)$ of BCH codes. For finite-length codes’ normal approximation, the parameter indicates $k_B$.

The BCH results demonstrate that increasing the block length improves the error correction performance, gradually approaching the theoretical finite-length limit predicted by the normal approximation. This aligns with the expected behavior of ECCs, where longer codes yield higher decoding reliability. In contrast, the repair approach exhibits better $p_{free}$ performance with shorter block lengths, as smaller blocks reduce the likelihood of multiple faults occurring within a single block. As the block length increases, the benefit of simple replacement diminishes. These results highlight the distinct tradeoffs between hard fault repair and soft error correction.

As $p_f$ increases, $p_{free}$ drops gradually from one to zero. The slope of the drop is modest in this case. Compared with the replacement method, the BCH codes perform poorly for small to moderate block lengths. (That is because the ECC method is a blind protection.) As the block length increases, the gap between the BCH coding and replacement methods narrows since the performance of BCH codes improves with the block length increase and the number of blocks decreases. But for optimal finite-length codes, this tendency is shown at smaller block lengths. In our tested block lengths, the replacement method is better than the optimal coding only at the smallest length $k_B=128$.

Note that we evaluate the error protection performance against randomly deployed hard faults in the manufacturing process of a chip. Although ignored in this work, the local coherence in cell quality over a chip may be relevant. More precise models should be developed for better analysis. However, the overall trends may not change much.

The $p_{free}$ improves as the block length increases because long codes have a better capacity in general and the number of blocks in a chip decreases. No threshold behavior occurs; instead, gradual enhancement is shown. It is interesting to see that for large block lengths, the ECC approach can be better than the replacement approach.

Note that although an ECC method can overcome hard faults to some extent, the error tolerance of ECC schemes is not as good as the replacement method in general. The blocks with hard faults are more prone to soft errors than other blocks as well.

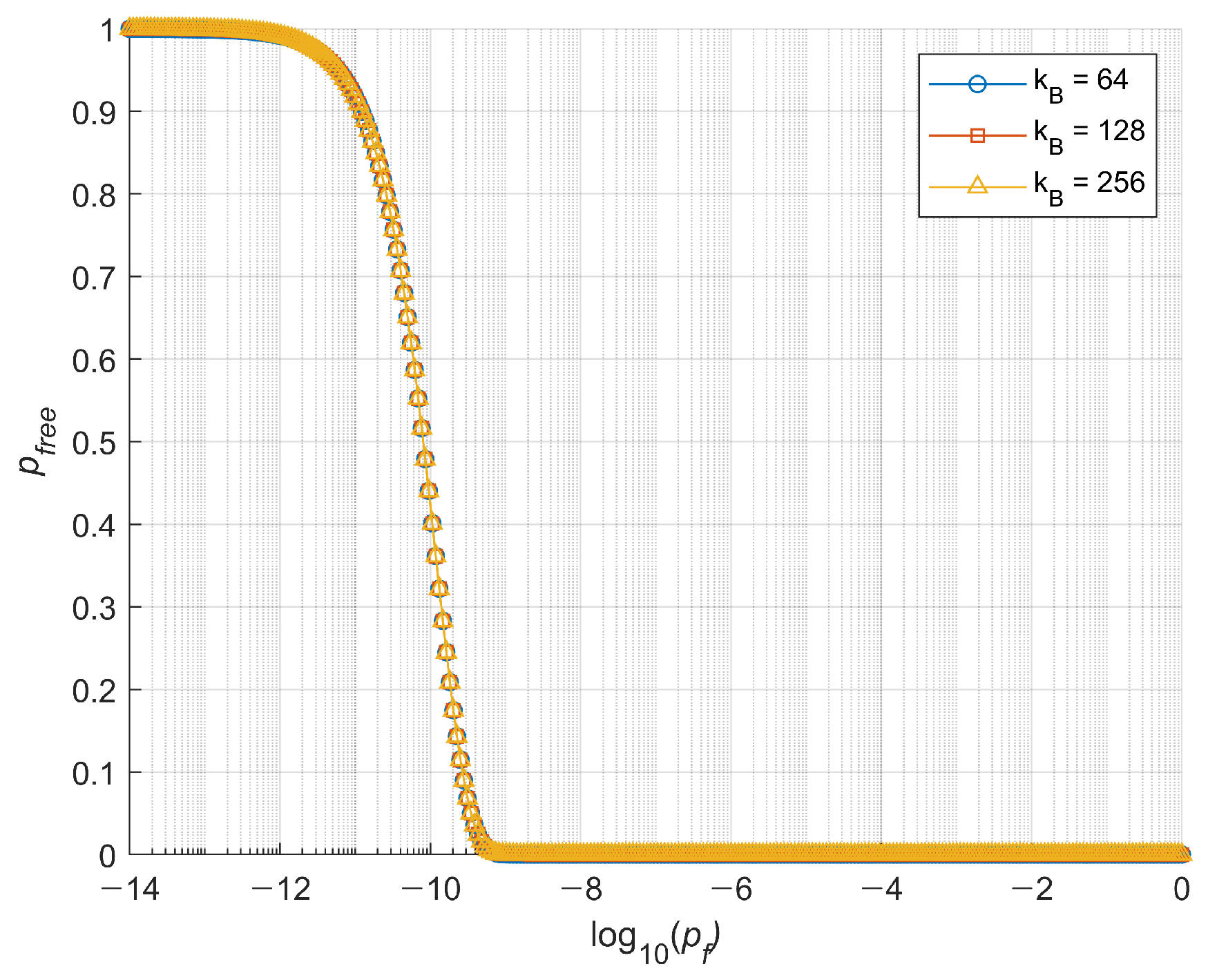
4. Error Protection from Soft Errors

In this section, we incorporate soft errors in our problem. First, the soft error only scenario is considered, and then a mixed case is addressed. We assume soft errors occur randomly and independently of the location. Therefore, every cell suffers from the same soft error probability. It is worth noting that in reality, some cells degrade earlier than others, and they thus make more errors. Soft errors cannot be removed by a replacement method because testing cannot locate the source of soft errors. It is assumed that there is no remaining hard fault because they are removed by the repair process in the production. Soft errors can then be corrected by normal ECC methods.

4.1. Soft Error Only Scenario

In this section, we consider a soft error scenario. We discuss how to handle soft errors where there is no hard fault. All redundancy bits are used for ECC parity. Let $R^{\prime }$ be the number of remaining redundant cells. If we ignore pre-processing, we can consider $R^{\prime }=R$ for this problem only. Hard faults are now assumed to be nonexistent or all repaired in the pre-processing step. The code rate r is

$$r=N/(N+R^{\prime }).$$

This scenario is evaluated by $P_B$, the BLER. In this paper, as a practical coding scheme for DRAM or main memory, the BCH codes are considered. Even though several codes, such as Hsiao codes [19], Dutta codes, and Petro codes, have been developed, they are basically variants of the single error correction code and they are more focused on improving implementation aspects of the code. Since we only consider the error correction performance in this paper, employing multiple error-correcting binary BCH code families is sufficient for providing practical reference performance.

Let $p_e$ be the probability of soft errors, which occur independently and uniform-randomly. The BLER of practical t error-correcting codes is computed as

$$p_B=1-\sum _{i=1}^t\left({\displaystyle \genfrac{}{}{0pt}{}{l_B}{i}}\right){p_e}^i{(1-p_e)}^{l_B-i}.$$

On the other hand, for ideal finite-length codes, the BLER is computed by (4). Let us compare the BLER performances of the two schemes. Figure 6 exhibits the BLER performances of the two code families. The parameters of BCH codes are chosen closest to those of basic $k_B$ and $l_B$ settings. Note that the BLER is for a single individual block. As can be expected, the performance improves as the block length increases. The BCH codes are severely outperformed by the optimal codes. Also, the performance improvement of the BCH codes due to block length increase is marginal compared with the optimal coding performance.

It is observed that the optimal finite-length performance is much better than that of BCH codes. As the block length increases, $p_B$ decreases in general (for both codes). An increase in block length is desired as long as the circumstances such as complexity or latency allow. The performance of BCH codes and its long code improvement is limited compared with the optimal codes. There is a big gap between the existing solutions (individual BCH coding) and theoretical limits (the performance of optimal finite-length coding).

4.2. How to Handle the Mixture of Hard Faults and Soft Errors

We now consider a case where both hard faults and soft errors occur. The amount of redundancy cells is first given. An optimization problem is formed. First, it is clear that hard faults are better replaced. Therefore, a two-step approach—replace faults first and correct soft errors—is very reasonable based on the wisdom we obtained from the former chapters. Although the redundancy part for replacement is solely determined, the block length should be determined. The block length affects both the replacement and error correction efficiencies. The block length optimization problem is addressed in this section under a fixed redundancy amount constraint.

Here, the problem is organized:

• Assign replacement cells fitted to the target $p_f$. (We assume aging can increase $p_f$, and the repair process can be conducted after production.)
• The block length can be optimized in terms of the final BLER.

If we operate the scheme, all data blocks with hard faults are replaced first, or for future usage at the target hard fault rate, the redundant space for replacement is reserved. Thus, ECC runs without a hard fault and only has to deal with soft errors. The block length controls the replacement efficacy and the ECC’s protection performance. It is worth finding the optimal block length. One might claim that block length for replacement and coding can be different. However, we assume they are the same because it can cause a large overhead when they are different.

In Figure 7a, the BLER is shown versus the processing block length $k_B$ when $N=2^{33}$, with $\rho \in \{0.1,0.143\}$ and $p_f={10}^{-5}$. Both the practical BCH codes and ideal finite-length codes are considered. Because of the tradeoff between replacement efficiency and the soft error correction efficiency, we observe a clean convex curve for the optimal codes. The BLER is minimized at a block length of 3600 for optimal codes at $p_f={10}^{-5}$. A similar behavior is shown for BCH codes. Note that for shortened BCH codes, the error correction capability does not improve gradually with the block length. This is because the error correction capability t can be the same even if $k_B$ increases. (If $k_B$ continues to increase, t increases stepwise.) For parameter setting, given $k_B$ and the code rate, we searched for all possible shortened BCH code candidates and selected the one whose t is the largest, and then the rate is closest to the target. However, the curve still shows a convex shape from which a minimum can be found.

The BLER is minimized at a block length of 3683 for optimal codes where $\rho =0.1$ and $p_f={10}^{-5}$. The tradeoff curve and the optimal value $k_B$ may vary according to the redundancy rate $\rho$. The results in Figure 7 confirm that the optimal $k_B$ increases as $\rho$ increases, but the optimal $k_B$ consistently lies in the range of several thousands for proper $\rho$ values. The reason that the optimal length becomes larger for higher $\rho$ is that more redundancy leads to a large repair margin and low ECC BLER, due to remaining redundancy.

For the redundancy rate $\rho$ corresponding to the code rate considered in a typical DRAM system, the optimal $k_B$ is on the order of several thousand bits, as shown in Figure 7. However, it is infeasible to use such a long $k_B$ due to hardware constraints such as target decoding latency and power/thermal budget. Today’s technology thus uses a small $k_B$. Therefore, as the analysis curve suggests, it is better to increase the block length if possible.

Figure 8 exhibits the case where the information block size is an integer multiple of the replacement block length (say, $k_R$). For a given asymmetry, still we obtain an optimal block length to achieve the lowest BLER. As asymmetry increases, the optimal BLER performance improves.

5. Conclusions

In this paper, we investigated the efficient use of redundancy for memory reliability. We examined two error protection methods: replacement and ECC. Then, we analyzed the performances of the two methods to address hard faults and soft errors and their mixed cases. In particular, we considered practical codes such as BCH codes and ideal finite-length codes to know the gap between the theoretical limits and practice. Based on our analysis, it is better to address hard faults with the replacement method. Then, soft errors are preferred to be protected by ECC schemes. There is a tradeoff between hard fault repair and soft error protection in terms of processing block length. Specifically, the fundamental tradeoff lies between the inefficiency of replacement and the improved error correction capability of ECC due to a larger block length. The optimal processing block length can be found from the relation. Practical coding schemes operate with a block length far from the theoretically optimal value, which justifies the application of multi-level coding, which can encode much larger data blocks with low processing complexity with short component codes. However, such multi-level coding schemes should be designed carefully to avoid the coherence of the structural error patterns and the weaknesses of the multi-level scheme.

For future works, more rigorous optimization can be studied for mixed cases. For instance, not all hard faults are repaired, and ECC deals with both hard faults and soft errors. A non-uniform fault or error probability scenario can be investigated. Also, correlated and structured faults or soft errors and their countermeasures, such as multi-level coding, may be studied.