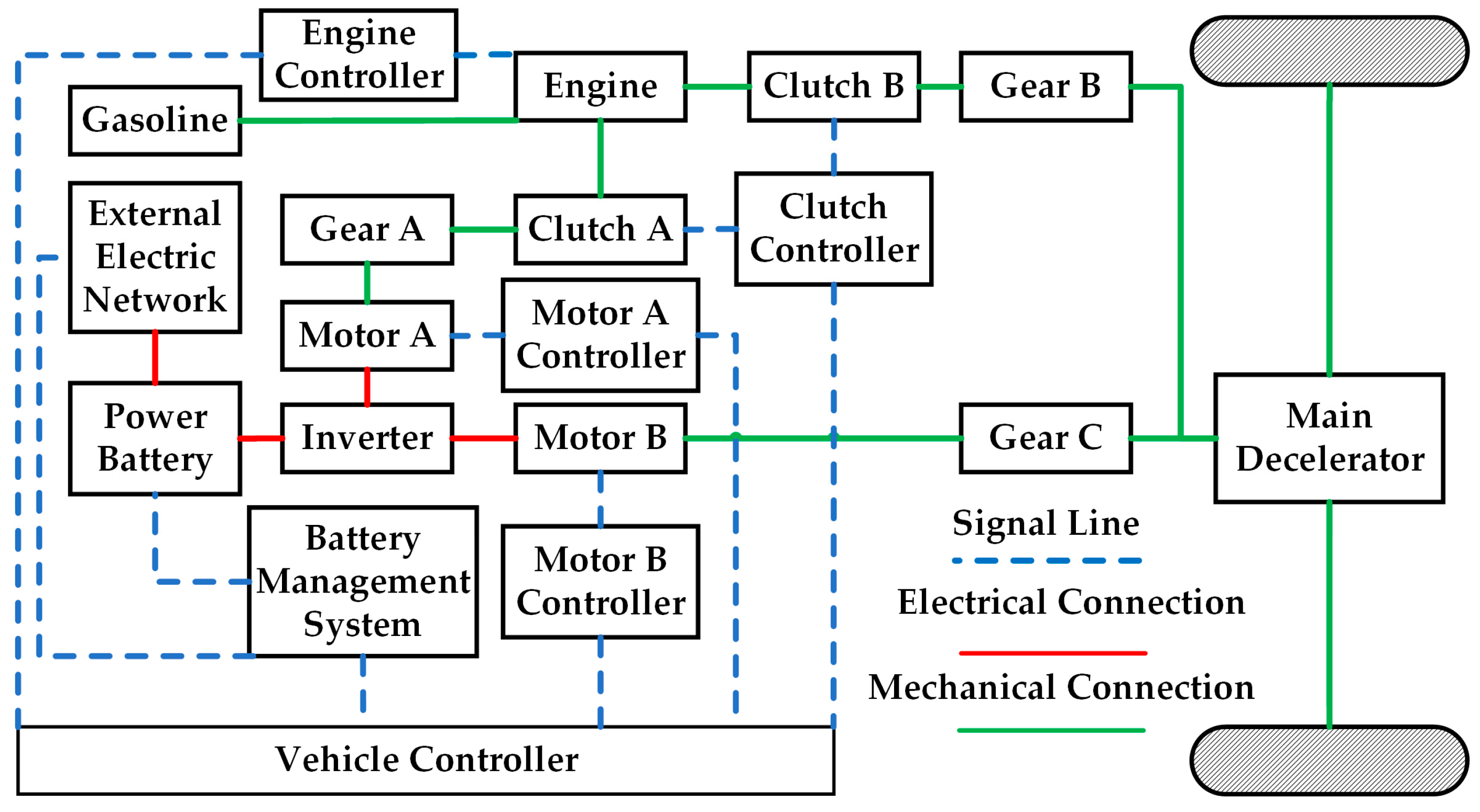
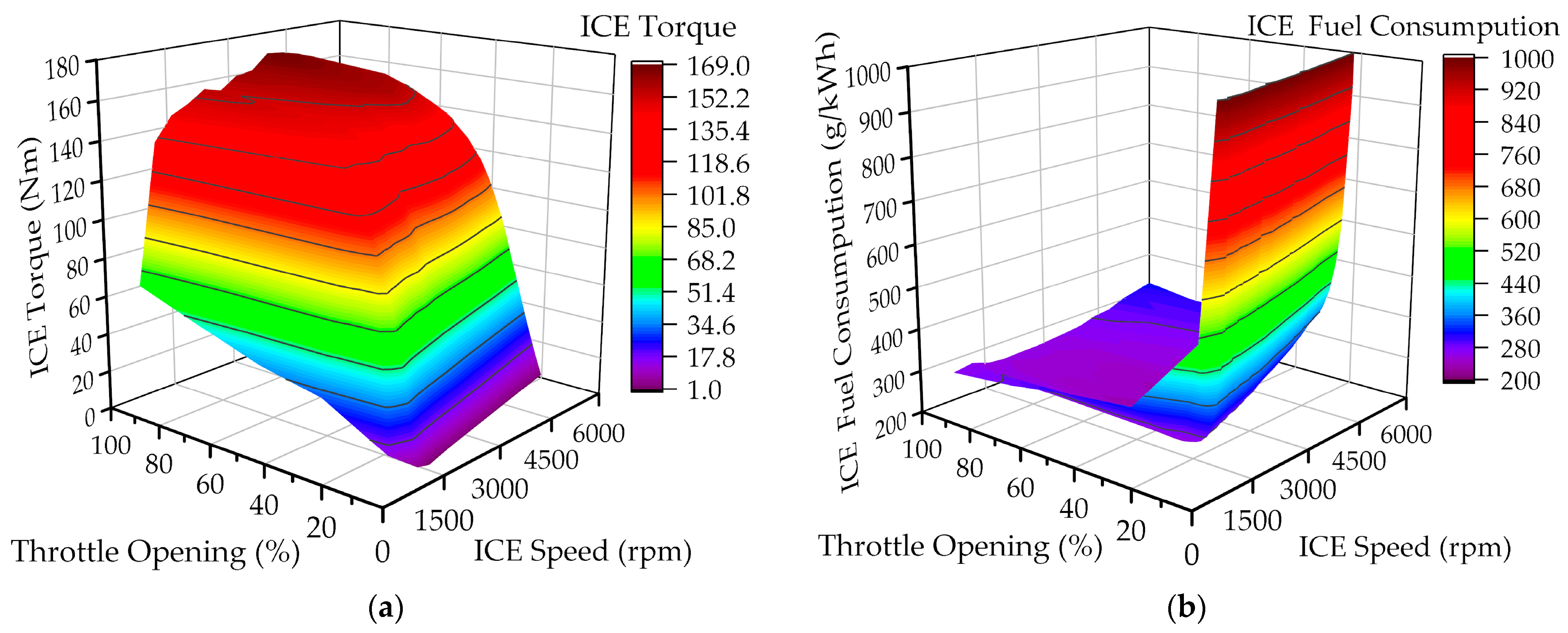
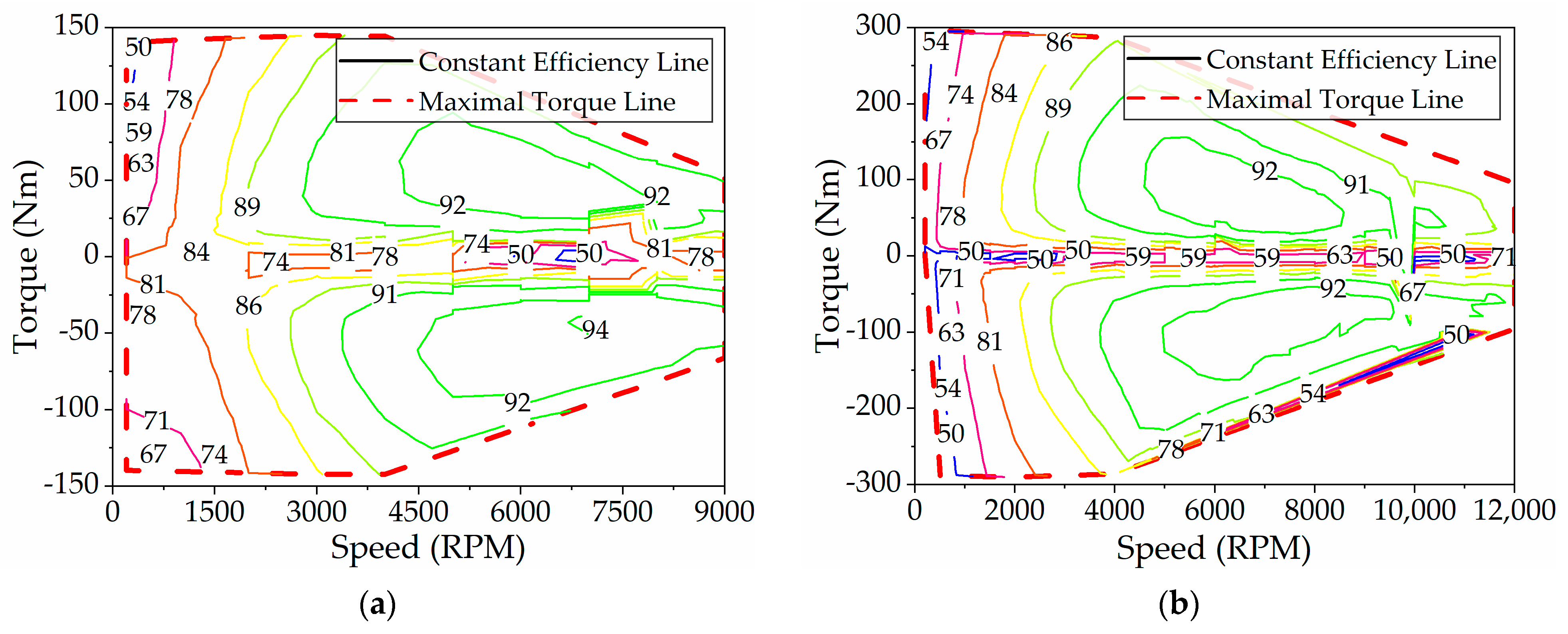
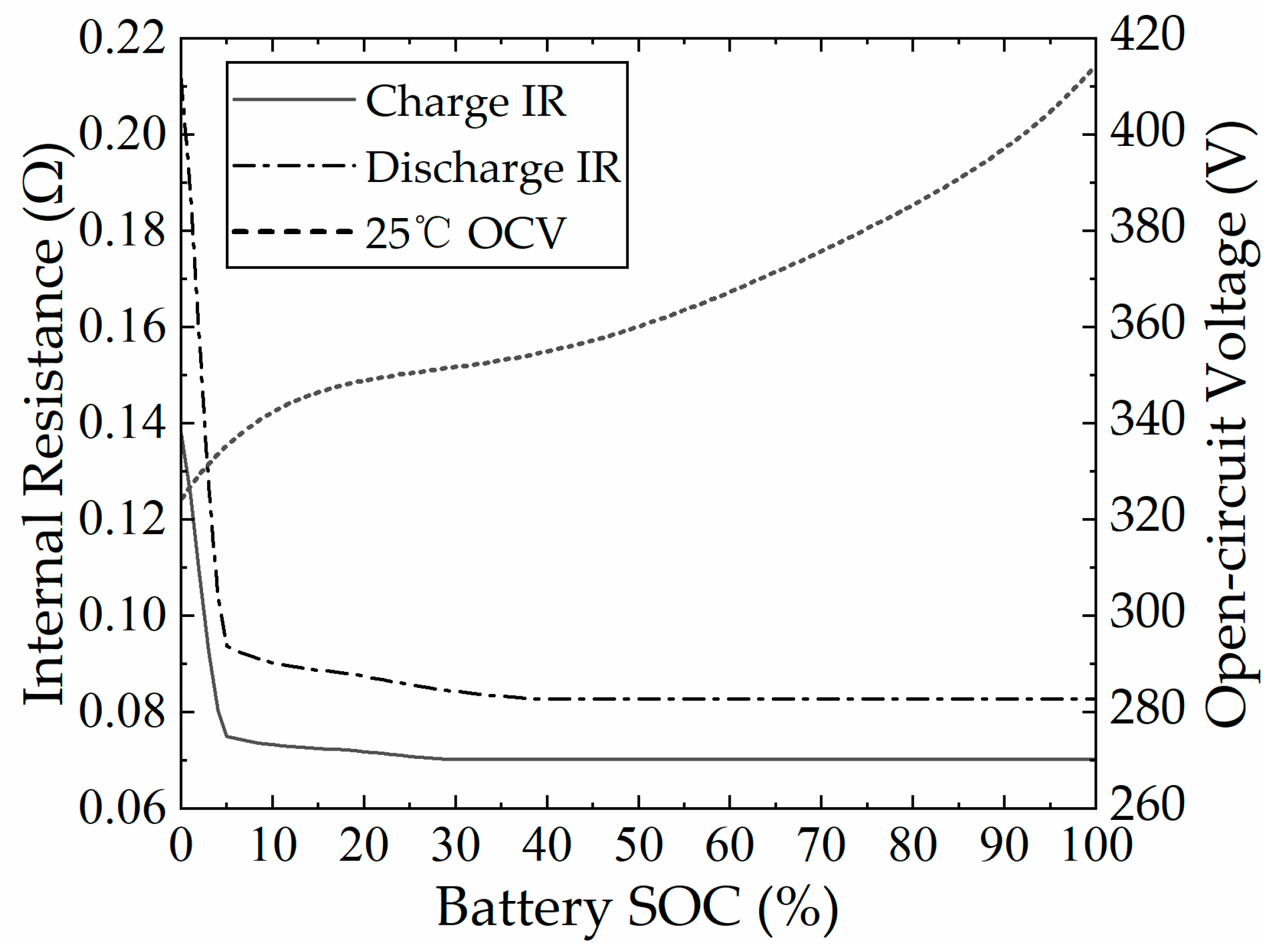
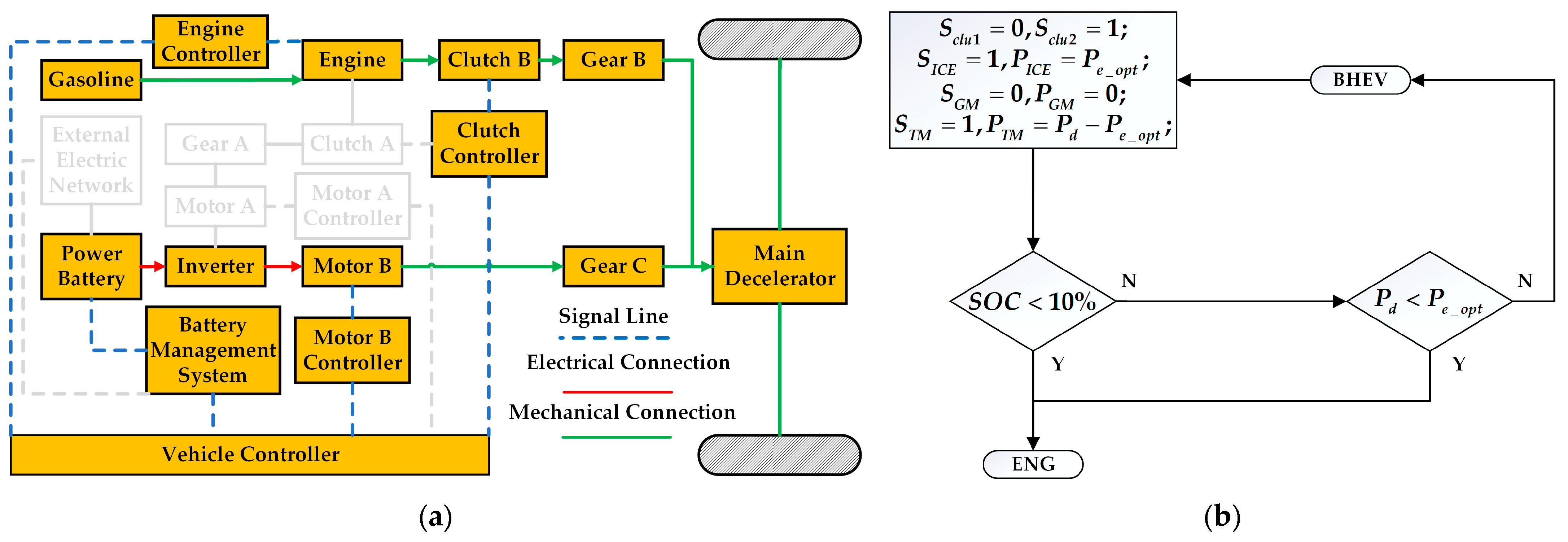
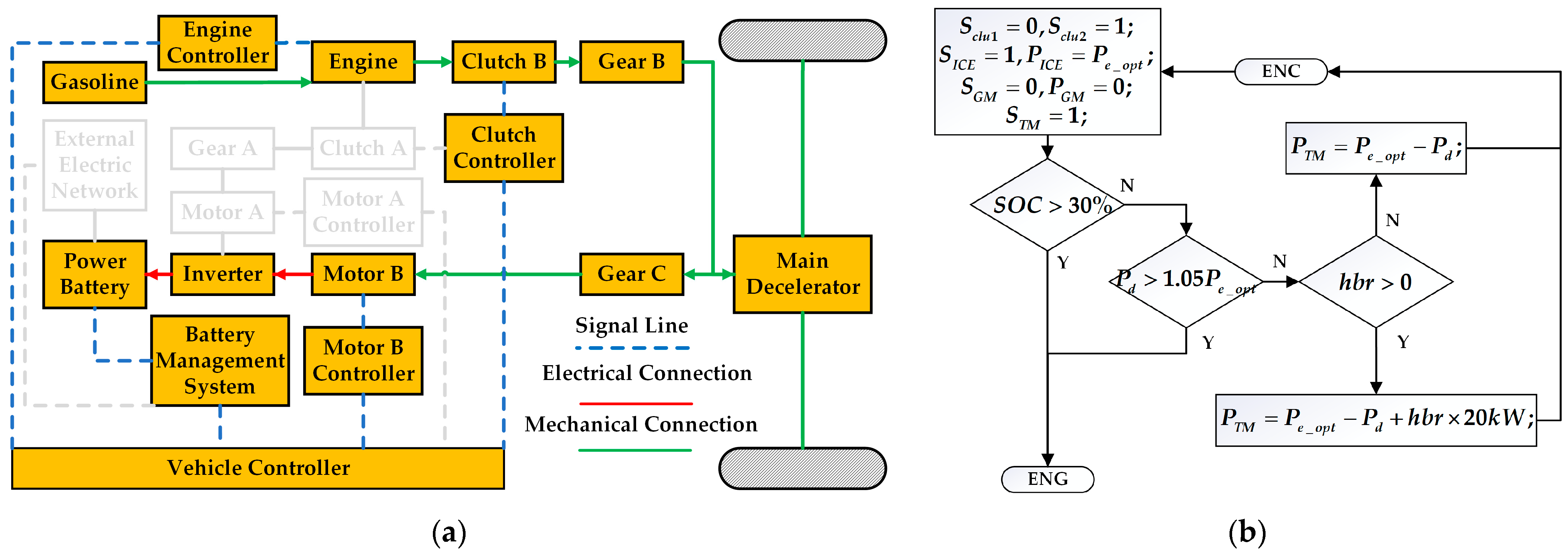
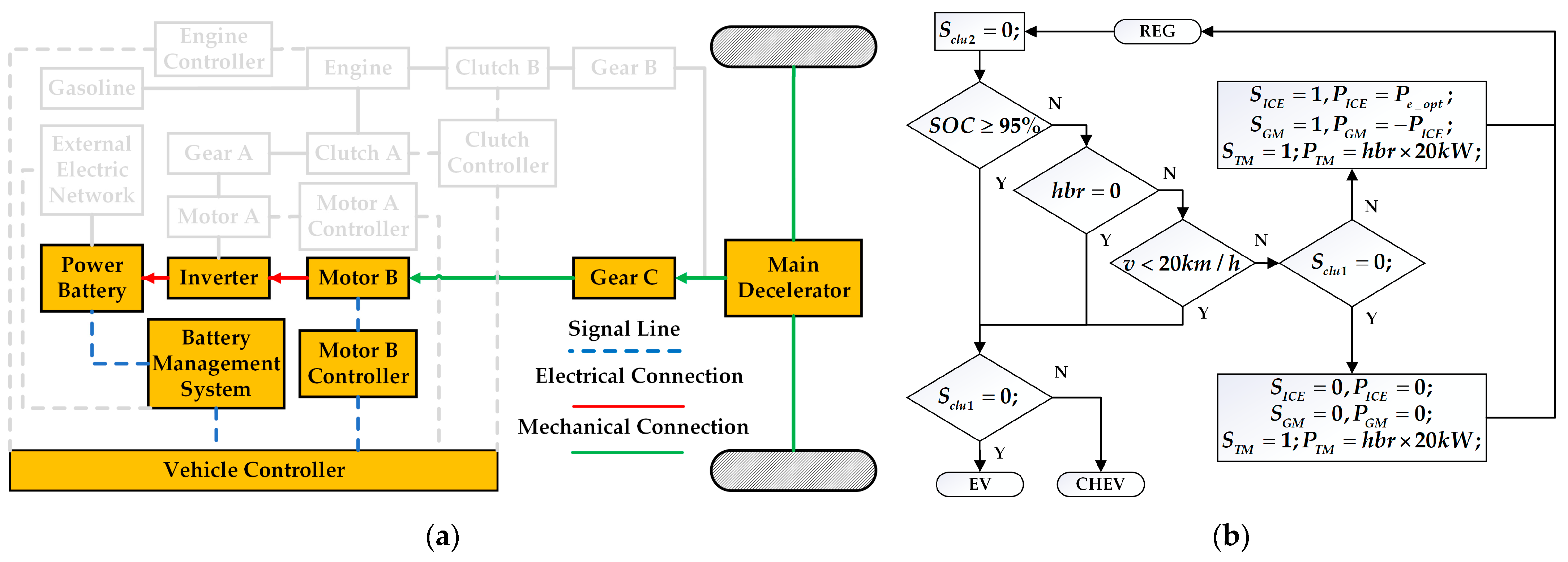
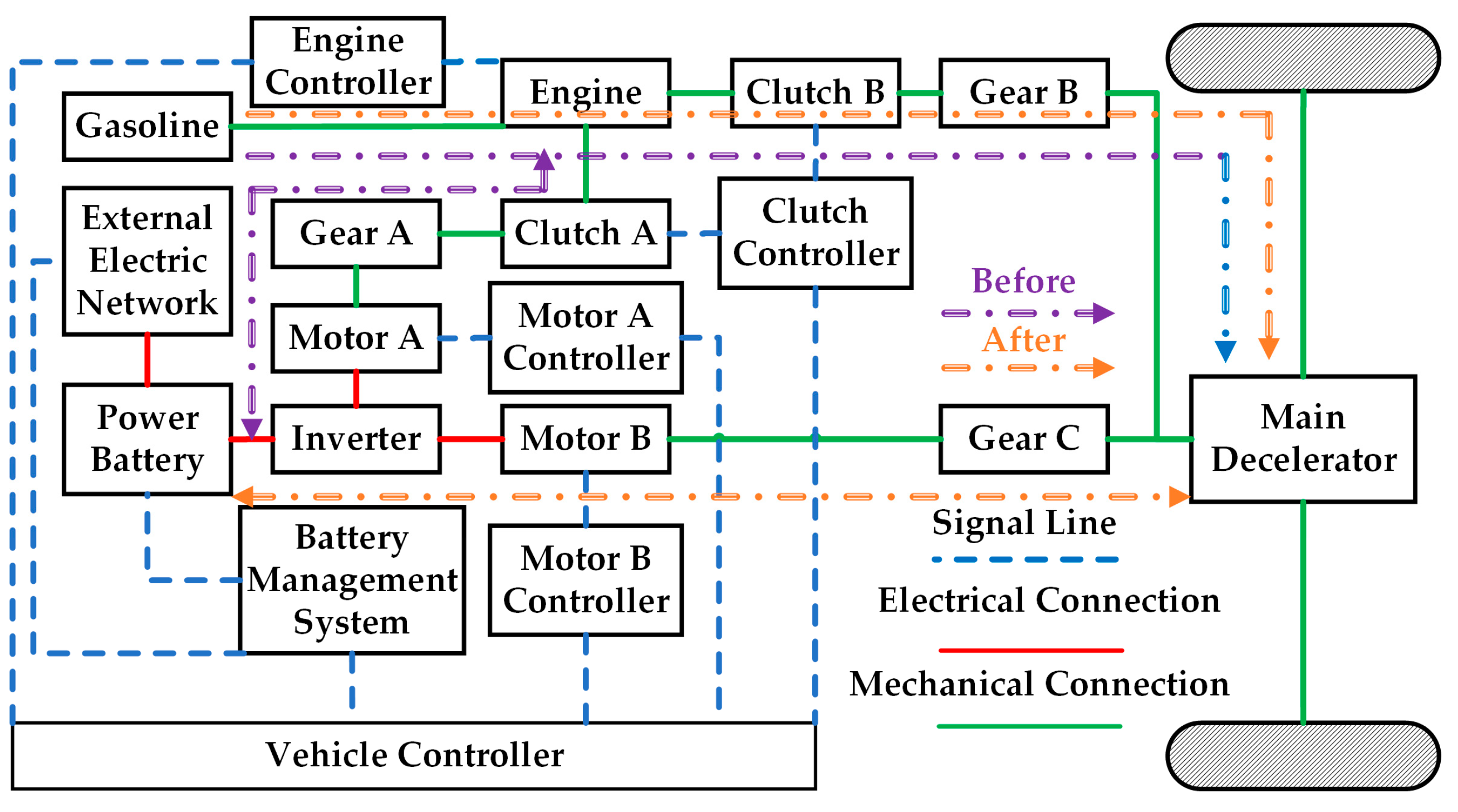
1. Introduction
To address growing concerns over energy scarcity and environmental degradation, new energy vehicles—including electric vehicles, hybrid electric vehicles, and fuel cell vehicles—have undergone widespread development due to their economic viability and reduced emissions [
1]. As a form of new energy vehicle, plug-in hybrid electric vehicles (PHEVs) can be powered by charging from an external grid. They not only have the low-cost advantages of all-electric vehicles, but they also have the advantages of traditional fuel vehicles, as they do not cause cruising range anxiety. Therefore, PHEV technology plays an important role in the development of new energy vehicles [
2].
The hybrid electric vehicle (HEV) utilizes a multi-source powertrain system. A control strategy ensures efficient power distribution and coordinated control among components, improving overall vehicle performance [
3]. Control algorithms have seen continuous optimization in recent years, with many novel algorithms being introduced. Research institutions and automotive manufacturers have developed HEV control algorithms that are typically classified into three main categories: rule-based methods, optimization-based techniques, and intelligent control approaches. Optimization-based algorithms are further categorized into real-time and global optimization strategies [
4].
Algorithm engineers designed the rule-based control strategy using test data and insights gained from engineering iterations. This method requires less controller computing resources and is easy to implement, so it is the most commonly used control strategy in actual vehicles [
5]. Hajer et al. [
6] developed a fuzzy logic-based control strategy for hybrid power systems, while Wang et al. [
7] introduced a logic threshold control approach incorporating battery state-of-charge and power capability estimation to enhance battery longevity. After implementation, it remains static and cannot handle parameter changes due to the wear and tear of vehicle components. Simultaneously, the system’s need for real-time operation and stability limits its ability to achieve better fuel efficiency and emission optimization [
8].
In global optimization control strategies, the problem is first discretized, and then optimization methods are applied to achieve optimal energy distribution for a fixed driving cycle. Representative optimization techniques in this domain encompass dynamic programming (DP) [
9], Pontryagin’s minimum principle (PMP) [
10], as well as metaheuristic approaches including particle swarm optimization (PSO) [
11] and simulated annealing (SA) [
12]. Hu et al. [
13] integrated a mapping-based approach with DP to optimize engine-battery power allocation, resulting in minimized fuel consumption. The rapid dynamic programming (Rapid-DP) method, introduced by Yang et al. [
14], is an approximation of the DP approach designed to shorten decision-making time. Experimental results showed that combining PSO with the multi-mode configuration achieved maximum fuel efficiency when component parameters were optimally tuned. Although globally optimized energy management strategies enhance fuel efficiency, they necessitate prior driving condition information and experience a sharp increase in computational complexity and time as mileage grows. The limited processing power of modern automotive controllers prevents their real-time deployment.
Real-time optimization control strategies focus on reducing fuel consumption in the present or near future. Leading methodologies in this domain comprise model predictive control (MPC) [
15] and equivalent consumption minimization strategy (ECMS) [
16]. Optimization of control parameters (mode-switching thresholds and ECMS coefficients) by Li et al. [
17] substantially improved commuter HEV performance. Nevertheless, the ECMS approach exhibits significant dependence on precise system modeling and parameter calibration, especially regarding initial state-of-charge (SOC) estimation, while its inherent limitation in long-term global optimization capacity substantially increases implementation complexity. The novel approach by Guo et al. [
18] employed deep learning techniques to forecast driving patterns and dynamically optimize SOC trajectories, successfully balancing fuel efficiency and battery degradation in plug-in hybrids. However, the practical application of MPC is constrained by its computationally intensive nature and strong dependence on high-fidelity system models, resulting in substantial implementation challenges and elevated operational costs. The real-time optimization control algorithm, which does not consider driving conditions or mileage, performs less effectively than the global optimization algorithm. Current research predominantly focuses on conventional HEVs, where the operational state of the hybrid powertrain significantly impacts the vehicle’s overall energy consumption characteristics. Since both driving state determination and obstacle avoidance maneuvers rely exclusively on human driver cognition and control inputs, conventional energy management systems prioritize fuel consumption optimization over computational speed [
19].
The integration of machine learning with connected intelligent networks has established a new research direction for intelligent control algorithms, enabling data-driven optimization and self-adaptive system behaviors. Through interactive learning between intelligent agents and the environment, the strategy is continuously updated, enabling strong learning and adaptability to complex and changing working conditions [
20]. Utilizing transfer learning, Lian et al. [
21] introduced a method to share knowledge across energy management strategies using deep reinforcement learning, improving the efficiency of developing strategies for hybrid electric vehicles. A rolling time domain control strategy considering real-time traffic information prediction was proposed by Xu et al. [
22]. The results show that timely information updates contribute to the improved economy of the control strategy. Intelligent control algorithms hold potential for hybrid power system energy management, but their application in vehicle energy management remains underdeveloped and requires further study.
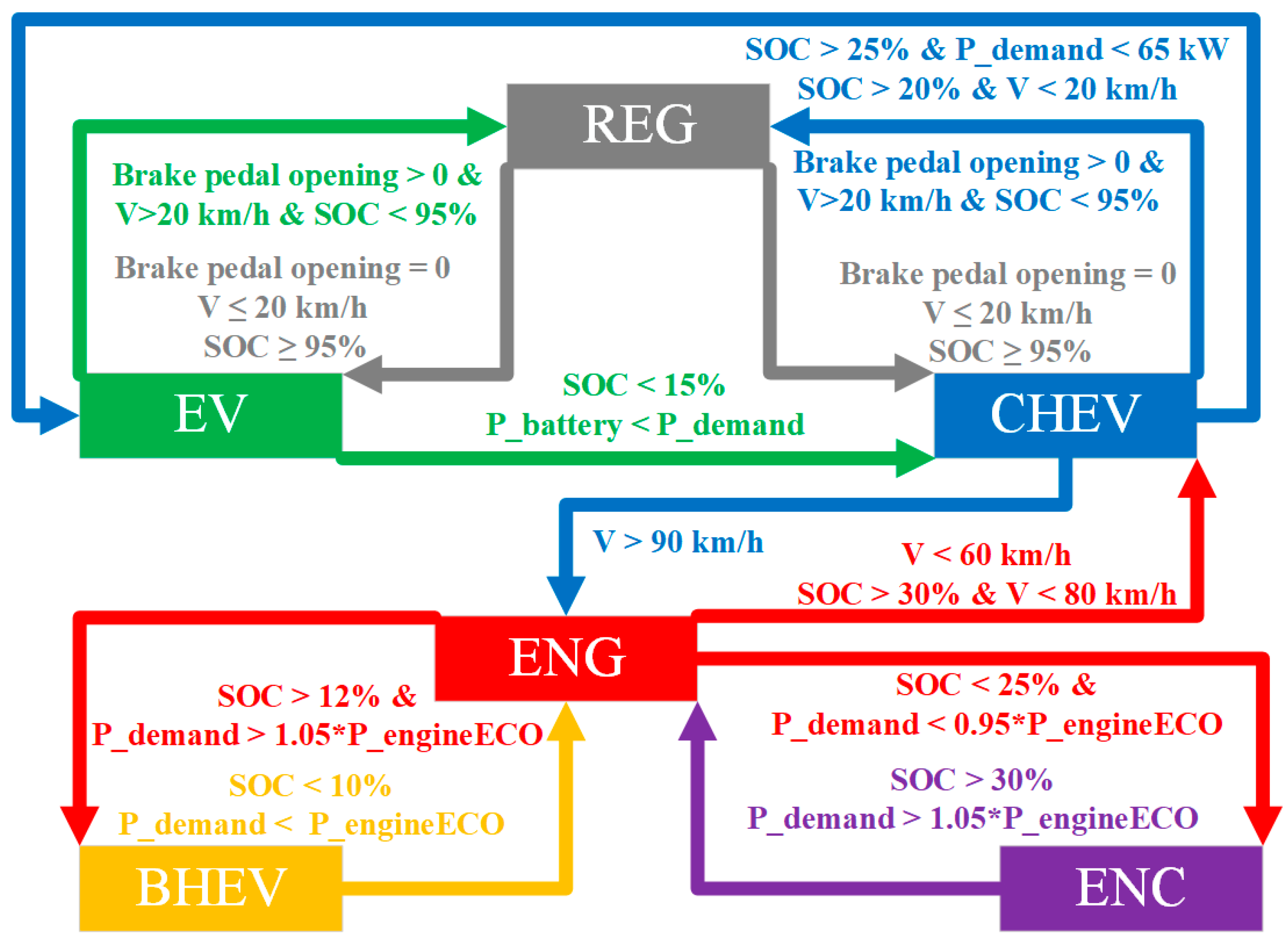
The novel dual-motor plug-in hybrid electric vehicle in this paper combines the features and benefits of pure electric, series, and parallel configurations, increasing the complexity of mode selection and energy distribution among power sources. The inherent complexity of modern hybrid systems precludes the reliable establishment of mode-switching thresholds through empirical engineering judgment alone. For instance, in pure electric mode, energy distribution between motor braking and hydraulic braking can be adjusted. In series hybrid configuration, optimal power allocation between the engine-generator unit and battery pack can be achieved through energy management. Conversely, parallel hybrid operation enables dynamic torque distribution between the internal combustion engine and dual electric traction motors. Since pure electric, series, and parallel modes can generally meet driver demands, determining the optimal operational mode and corresponding energy allocation strategy to maximize overall system performance remains a critical research challenge in hybrid vehicle control.
Although the method based on optimization has excellent fuel economy, the complex operation of the coupled power system of hybrid electric vehicle poses an obstacle to the online application of control strategy. In view of this, some researchers introduce the optimal information in the optimal control into the rule-based strategy, forming a rule extraction method. The control scheme in this area involves multiple logic or mapping rules, which include fuel-saving operations based on global or suboptimal data sets. This approach reduces computational complexity while maintaining energy efficiency. Wang et al. [
23] developed a rule extraction method for series-parallel AMT hybrid vehicles, using dynamic positioning optimization to determine the driving mode and shift line. Parallel to this work, Yu et al. [
24] established a rule-based control architecture specifically tailored for dual-motor EV powertrains.
The dynamic programming approach exhibits remarkable adaptability, imposing minimal restrictions on both system state equations and performance index formulations, thereby accommodating data-driven system modeling paradigms [
25]. Moreover, the fuel consumption optimization problem for hybrid electric vehicles on a given path fits the dynamic programming framework, as it lacks aftereffects or overlapping sub-problems. This makes dynamic programming an ideal approach for solving optimal control problems in hybrid electric vehicles [
4]. Primarily, the DP algorithm guarantees global optimality for hybrid electric vehicle energy management along predefined driving cycles, thereby establishing benchmark solutions for heuristic control strategy development. Then, key control parameters can be derived from dynamic optimization results to improve and adjust the control strategy of hybrid electric vehicles [
26]. Therefore, this paper adopts the rule-based control strategy to develop the controller of the dual-motor plug-in hybrid electric vehicle, and at the same time optimizes the rule control logic by using the global optimal strategy based on the DP algorithm, thus realizing the adjustment and improvement of the energy management strategy of the dual-motor plug-in hybrid electric vehicle.
The rest of this article is as follows:
Section 2 describes the modeling of the power system and rule-based control strategies.
Section 3 introduces the control strategy based on DP algorithm, obtains its simulation results, and improves the rule control strategy. The discussion and analysis of the results before and after rule control optimization are described in
Section 4.
Section 5 summarizes the main conclusions.
3. Control Strategy Based on DP Algorithm
3.1. DP Theory
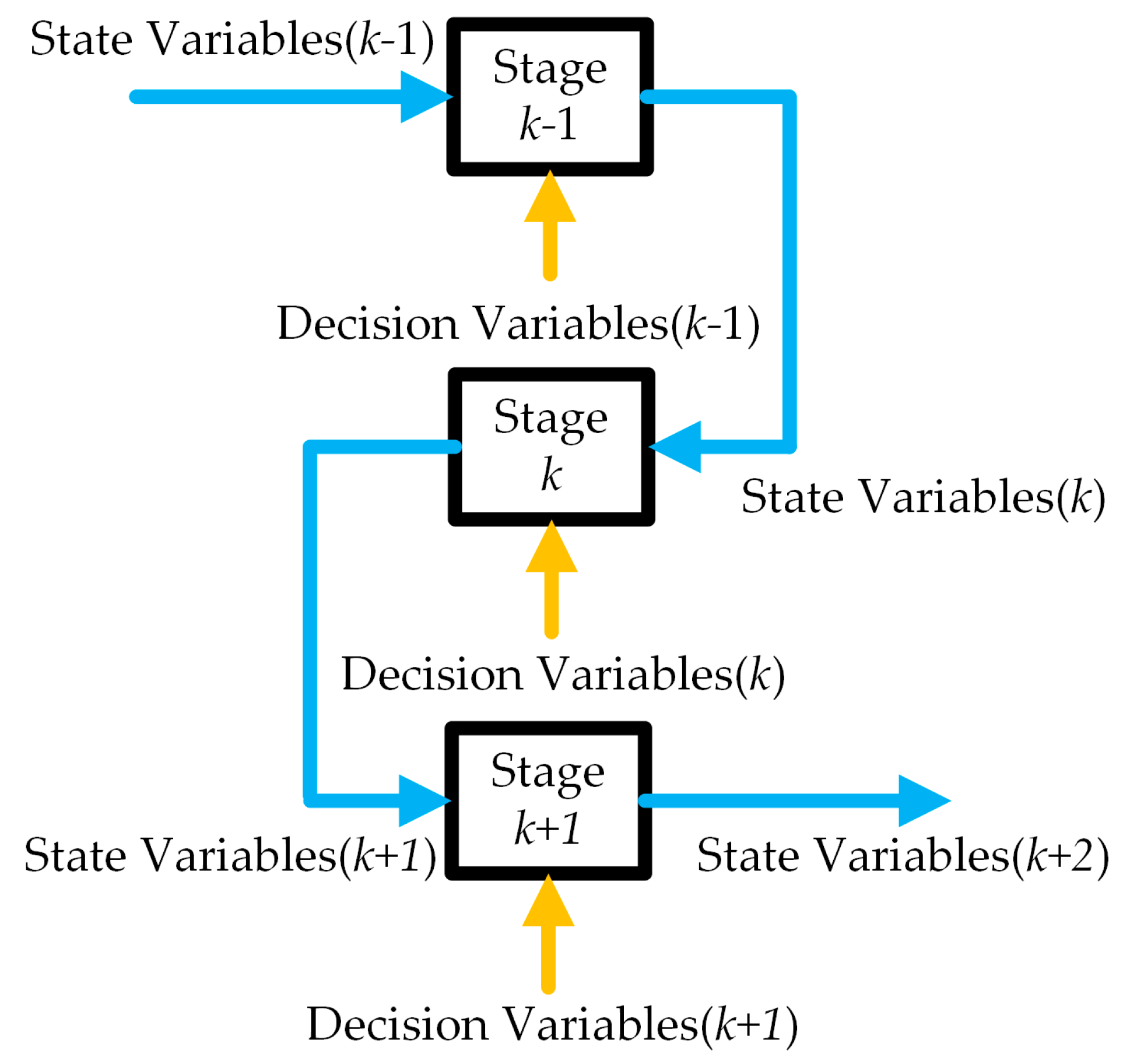
By partitioning the optimization problem into multiple interconnected stages, the DP algorithm employs carefully chosen state variables, control variables, and cost functions to decompose the original problem into a sequence of similar subproblems. Each subproblem’s solution builds on the results of the previous one, and the optimal solution for the final subproblem serves as the global optimum.
Figure 12 provides a block diagram of the dynamic programming algorithm’s process [
28]. When optimizing the entire process, the initial state is known, so each stage’s decision depends solely on its current state. This allows the optimal strategy and state at each stage to be adjusted to determine the best route. Rule-based control strategies, which often rely on empirical and constrained parameter settings, cannot fully exploit the benefits of PHEVs. In contrast, DP effectively handles constraints and nonlinearities, finding the global optimal solution. The minimum fuel solution for a given driving cycle is obtained by DP through cost function optimization at each operational stage.
3.2. Problem Formulation
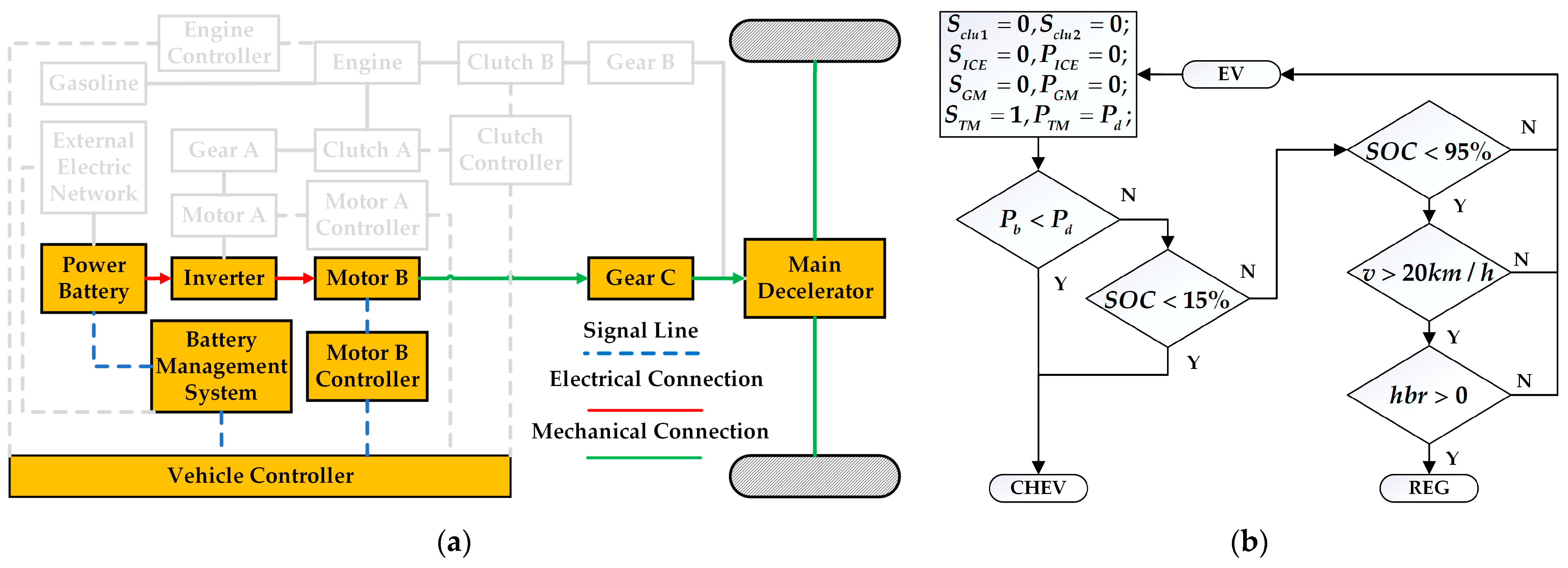
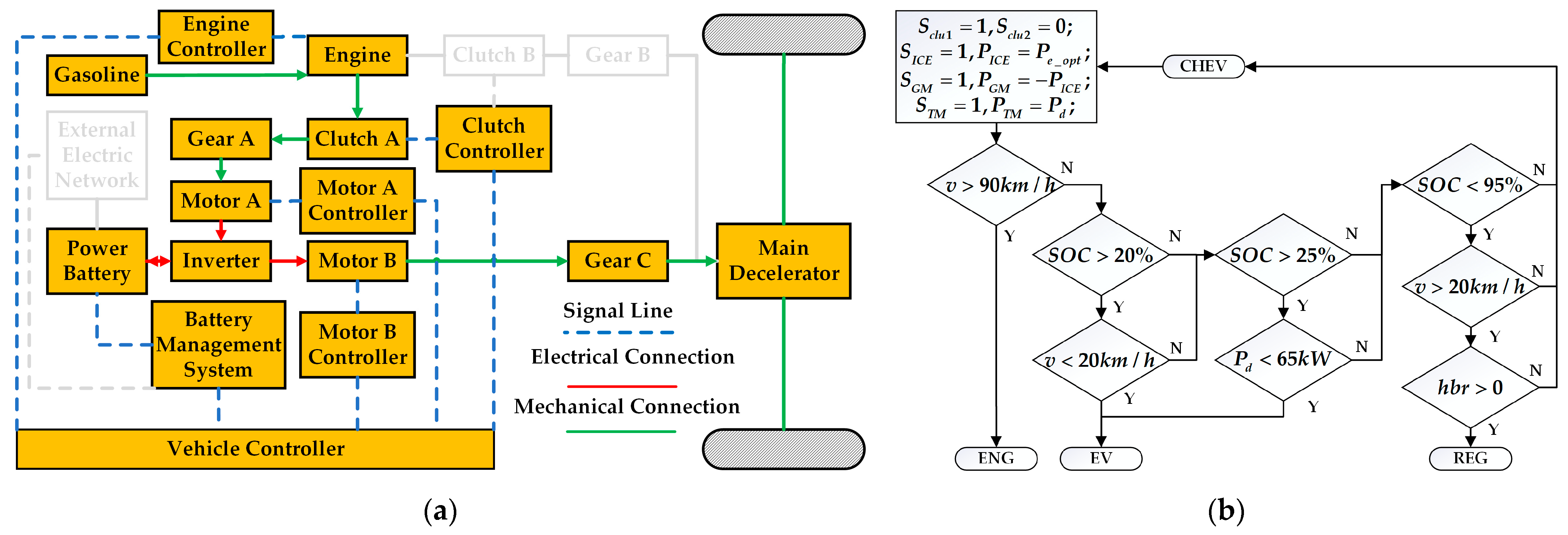
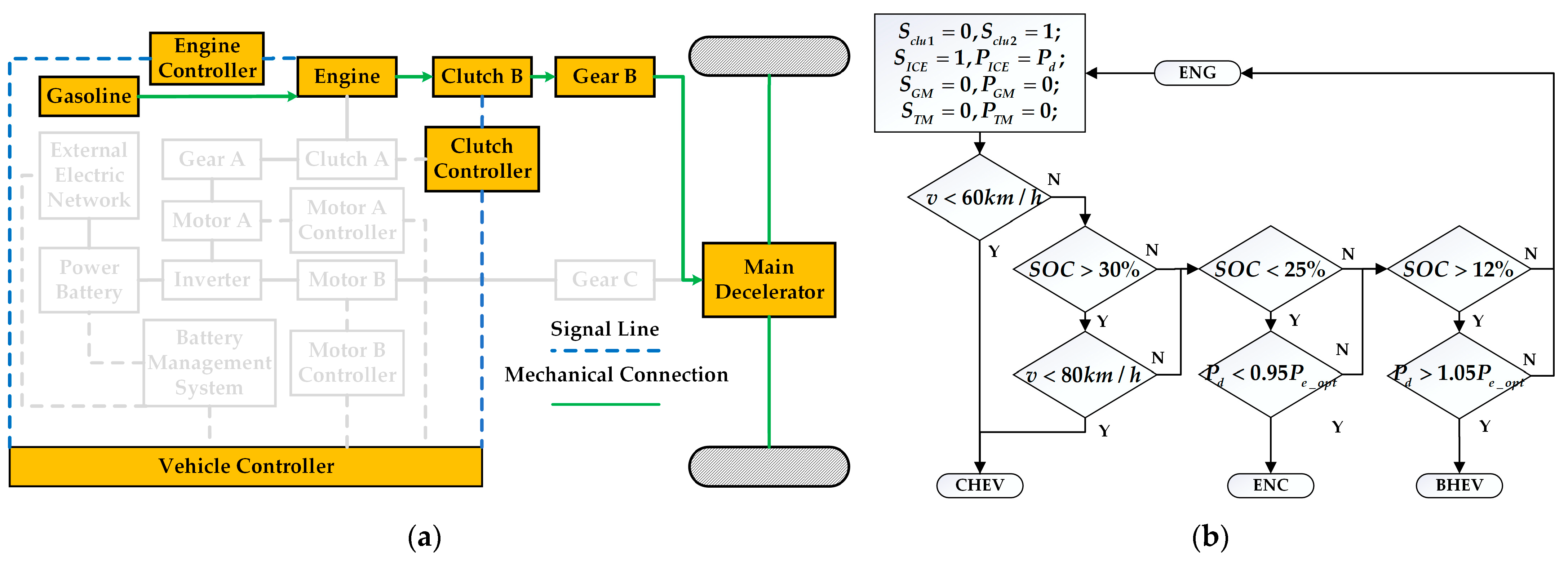
The trip is segmented into several interconnected stages based on known future road conditions, with driving information (e.g., speed, acceleration, and battery SOC) known at the start of each stage. Other conditions are treated as state and phase variables. The energy management optimization problem for hybrid vehicles generally aims to minimize comprehensive fuel consumption. As speed demands change over time, different state variables emerge, and their variations significantly affect fuel consumption. Therefore, the battery SOC is designated as the state variable, while the ICE’s torque and speed, along with the driving motor’s torque, are established as the three decision variables in the DP formulation.
Consequently, the state variable
at stage
k is mathematically defined as the battery state of charge:
The control variable
at the
k-th stage is defined by the ICE torque
, ICE speed
and TM torque
as follows:
Plug-in hybrid electric vehicles typically feature higher-capacity batteries, allowing them to curtail fossil fuel consumption by drawing power from the grid. This paper focuses on optimizing the vehicle’s fuel consumption, taking into account the driving cost associated with electric energy consumption. Therefore, the energy management strategy optimization objective minimizes the HEV’s comprehensive vehicle cost. The system’s cumulative cost function
represents the summation of stage-wise cost objectives throughout the optimization horizon. The instantaneous cost function
combines both fuel and electrical energy expenditures at each stage:
In this equation, is the fuel consumption of the ICE output torque at the k-th moment (L), is the gasoline price (CNY/L), is the electricity price (CNY/kWh), and is the battery’s discharge/charge energy (kWh).
The key power components of the hybrid vehicle must adhere to the following inequality constraints. Prior to torque/power distribution computations, all component physical constraints must be enforced to meet vehicular speed and torque demands, thus guaranteeing driving safety and operational stability.
where the subscripts “
min” and “
max” signify the smallest and largest values of the associated variables, respectively.
3.3. Implementing DP
The driving cycle is segmented into
N stages using time steps, and the state transition equations are defined in discrete state space based on the driving cycle’s time sequence.
Equation (18) is recursively applied to evaluate the stage cost function for subsequent states. Under cyclic boundary conditions, the control variable determines the state transition from stage k to k + 1, where denotes the admissible control set. At each stage, the optimal path for transitioning state variables to the next stage is chosen by assessing the control variables. Thus, the selected optimal path minimizes the system’s total cost objective over the complete operating cycle.
This minimum-cost trajectory is completely specified by the optimal control policy:
The DP problem is solved backward to minimize the cost function, with the recursive Equations (22) and (23) describing the sub-problems. For the (
)-th step:
For the
-th step (
):
In this context, denotes the optimal value function representing the minimum cumulative cost from state at stage k to the terminal condition. The state transition follows as specified in Equation (23), where is the applied control input.
3.4. Simulation Results of DP-Based Control Strategy
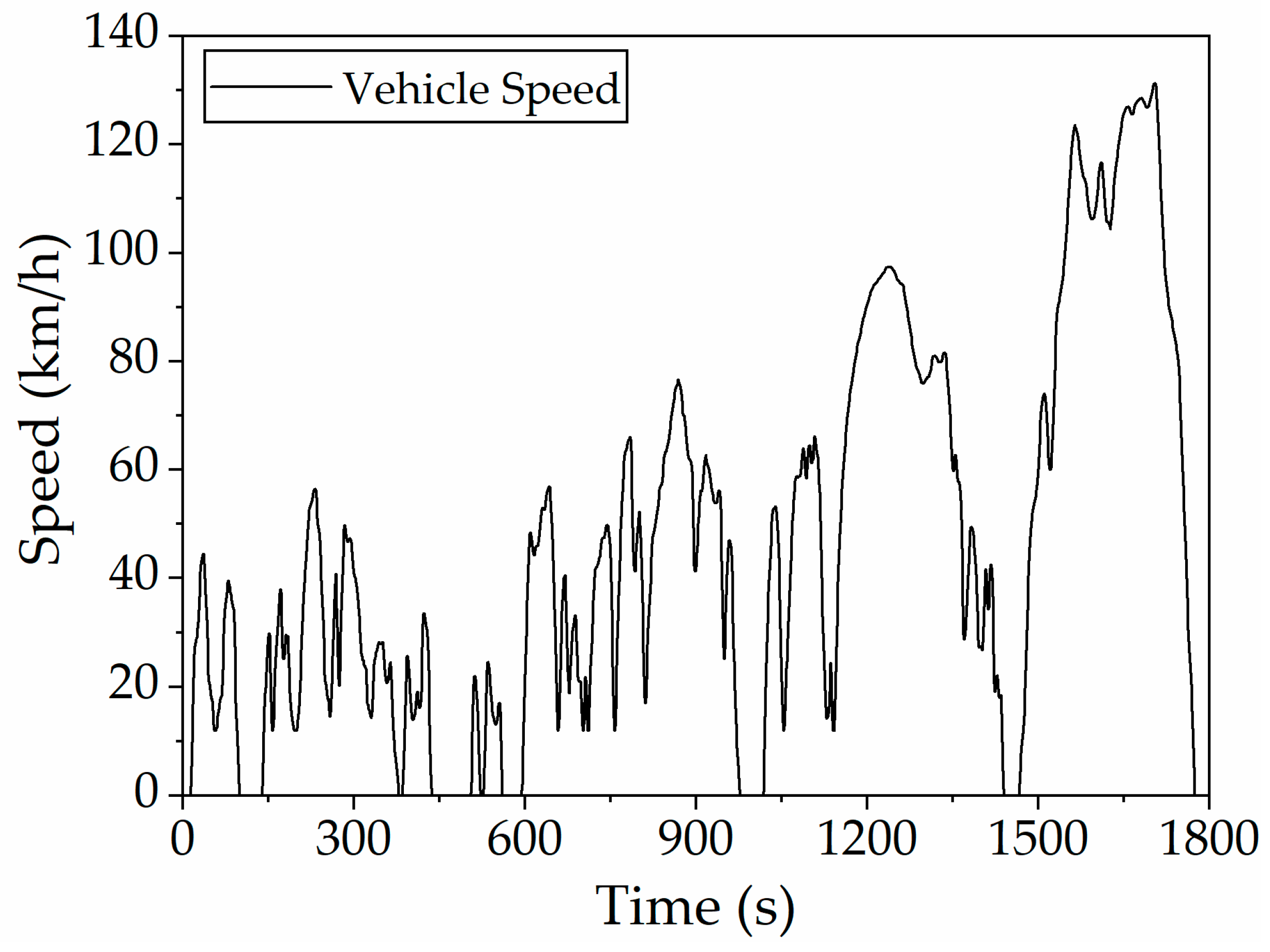
In previous chapters, the state variables, control variables, and cost objective functions for the hybrid vehicle energy management dynamic programming problem have been established. The control strategy based on dynamic programming algorithm is developed on MATLAB (R2022b) software platform. The simulation employs the World Light Vehicle Test Cycle (WLTC), illustrated in
Figure 13, spanning 22.73 km over a duration of 1800 s.
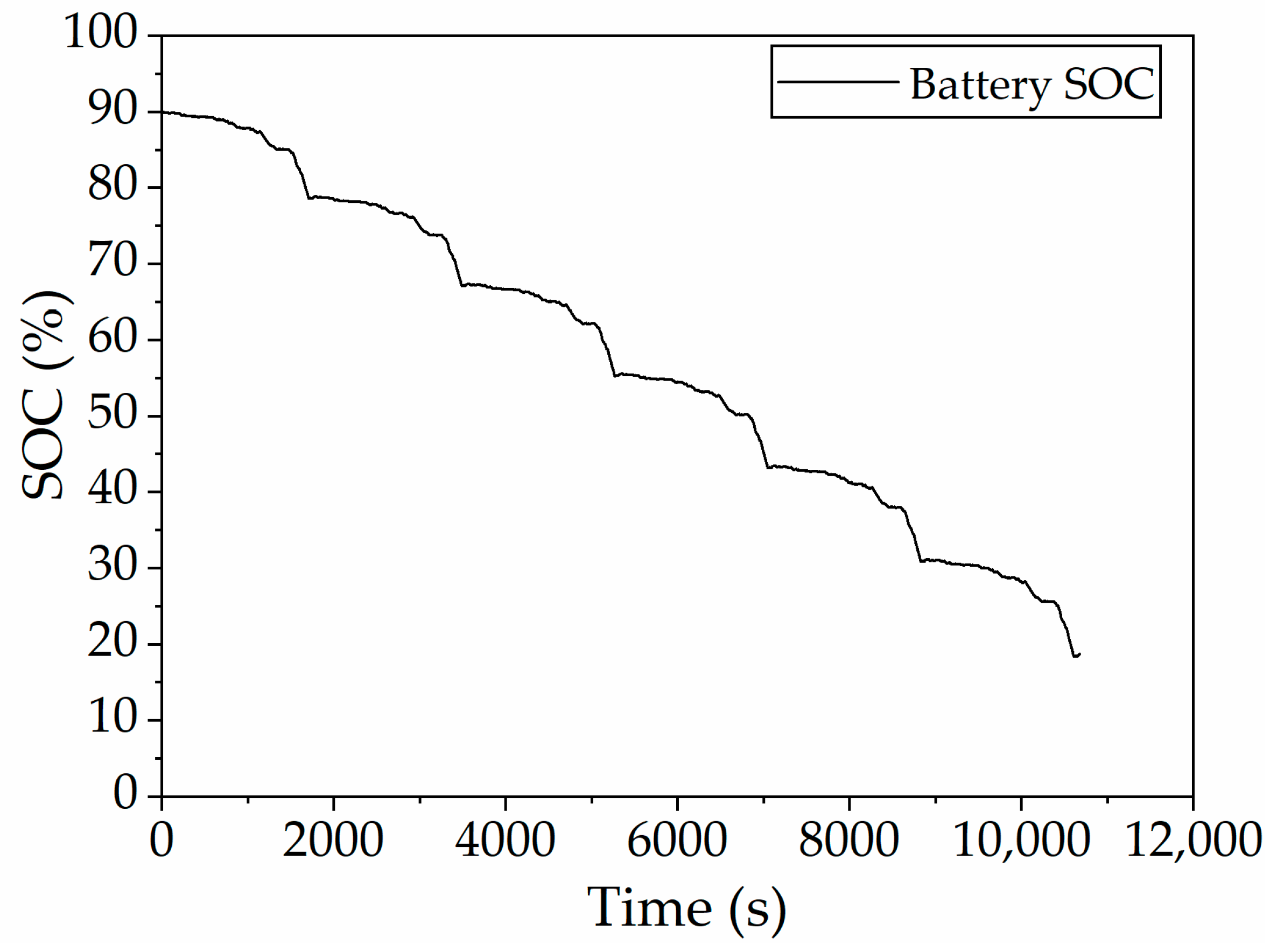
The initial SOC is set to 0.9, and the SOC threshold considering the battery SOC balance based on rule control is 0.15. Six consecutive WLTC driving cycles are simulated. As shown in
Figure 14, the SOC drops in a nearly linear manner under DP control, and the energy consumption results are provided in
Table 2. In order to simplify the complexity of calculation, a more efficient range of the ICE at 3200 speed is selected for output power generation, and it is obtained that each liter of gasoline can generate 3.0095 kWh of power. According to the mechanical and electrical efficiency loss of generator GM and battery charging, the fuel consumption required for vehicle electricity consumption in this simulation time can be converted to 4.373 L/100 km. The dual-motor plug-in hybrid electric vehicle, optimized with the dynamic programming algorithm, demonstrates a comprehensive energy consumption of 6.423 L/100 km under WLTC conditions.
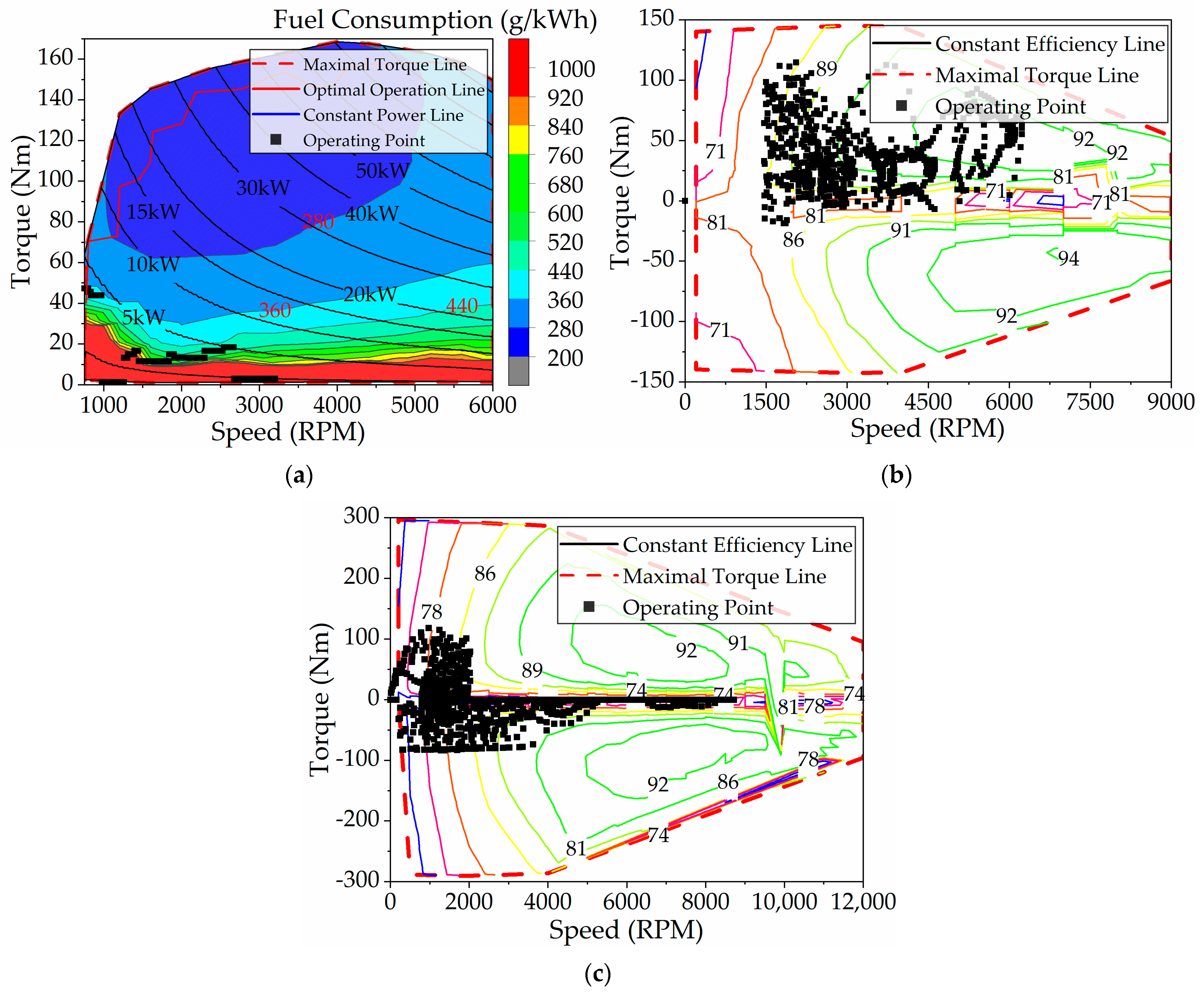
Figure 15 shows the operating points of the ICE, TM, and GM. Notably, the ICE does not operate along the optimal efficiency curve, and its torque output is comparatively modest. The output torque is about 45 N·m at low speed (below 1000 rpm) and about 18 N·m at high speed (above 1000 rpm). In the whole driving cycle, the required torque is mainly provided by the motor, while the ICE accounts for a relatively small proportion. GM works in high efficiency range, and the distribution range of working points is wider than TM. In addition, in the whole working condition, most GMs are in the driving state, and the power generation state is less. The overall efficiency of TM is lower than that of GM, and its working point is mainly within 2000 rpm. Under DP control, when the TM speed exceeds 2000 rpm, the TM hardly outputs the drive torque, only the brake torque. DP control optimizes fuel consumption but necessitates advance knowledge of the driving cycle and substantial computational resources. Therefore, extracting key parameters from DP outcomes can improve rule-based energy management approaches.
3.5. Improved Rule-Based Control Strategy
The DP adopted in this paper is an offline optimization method that pursues global optimization and does not fall under real-time optimization algorithms. The unsuitability of DP for real-time optimization stems from three primary limitations: First, high computational complexity—the state space grows exponentially with the problem scale, making it difficult to complete calculations within a constrained timeframe. Second, heavy reliance on pre-computation—requiring the prior construction of a complete state table, which lacks dynamic adaptability to real-time inputs. Third, the pursuit of global optimization—exhaustive traversal of all possible states’ conflicts with the “rapid response” imperative inherent to real-time optimization.
Within the DP framework, only the optimal output states of vehicle powertrain components and their corresponding operating modes are considered, with no inclusion of mode-switching processes. Consequently, strategy execution incurs no delay. Precisely for this reason, DP yields globally optimal solutions but cannot be directly implemented in vehicle controllers.
In the rule-based control strategy, transitions between vehicle operating modes involve clutch actions encompassing three states: engagement, synchronization, and disengagement. To accurately model this behavior, corresponding clutch and controller models were developed in the simulation environment, with strategy execution delays incorporated. However, due to the brevity of clutch actuation durations, the six operating modes corresponding to the dual clutches in the model are categorized as transient states and thus not exhaustively elaborated in the main text. It is emphasized that the rule-based control strategy retains identical transient operating modes before and after optimization.
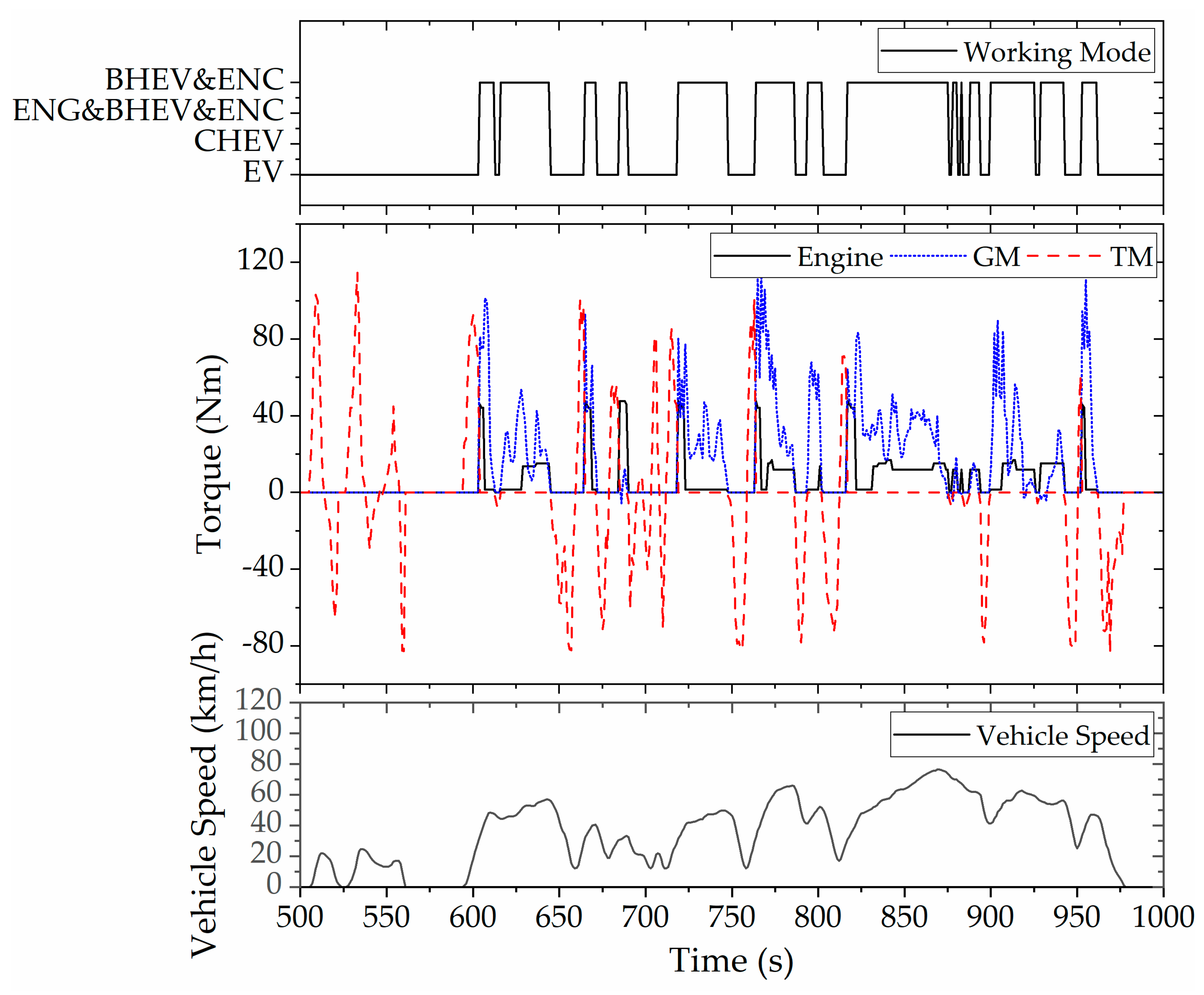
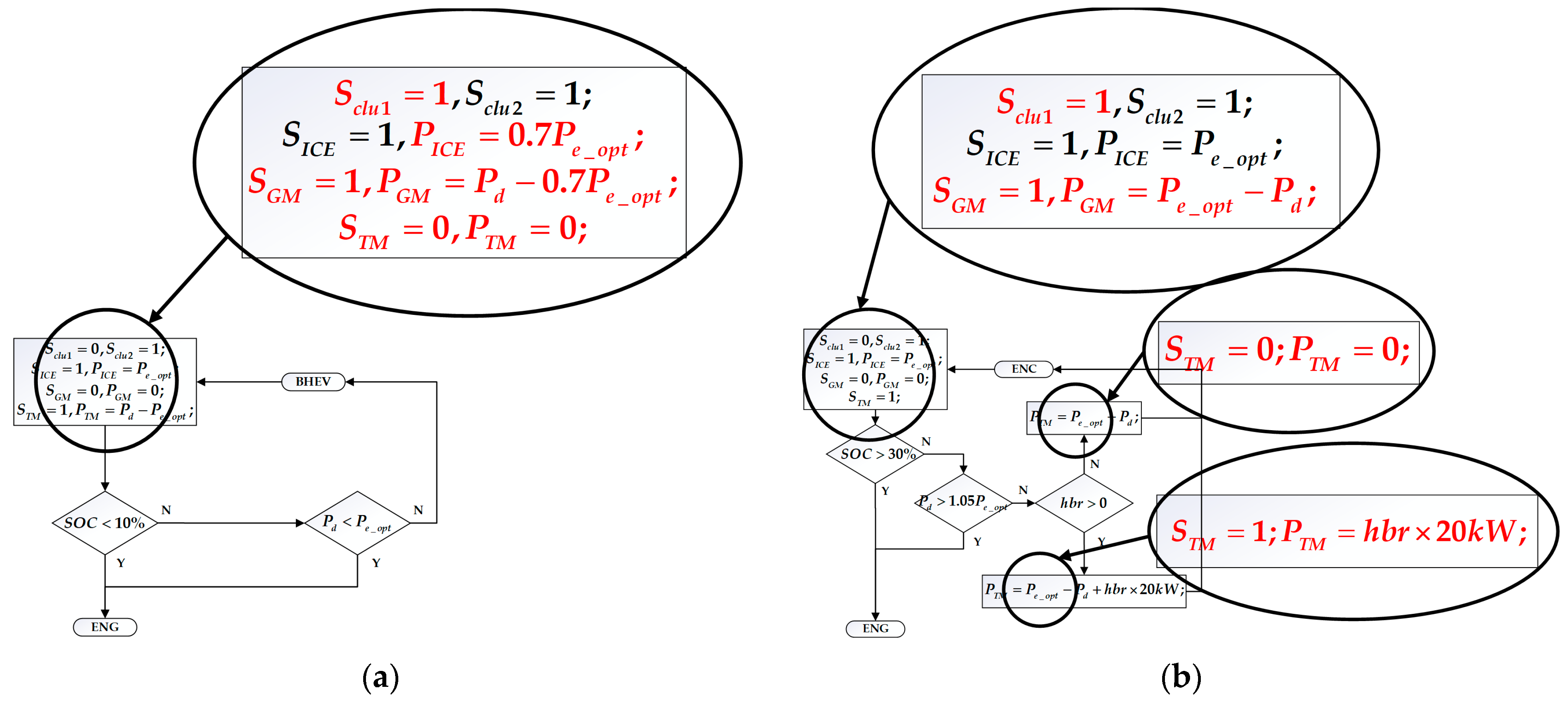
The original rule-based energy control strategy is adjusted by using the results of DP optimization, and the optimized rule-based control strategy is obtained, which is mainly reflected in three aspects, as shown in
Figure 16.
Firstly, it can be seen from the working mode switching curve of the vehicle that the vehicle is hardly driven in series mode but is switched between pure electric mode and parallel mode (ENG, BHEV, and ENC). In addition, when the vehicle is in parallel mode (BHEV and ENC), both the ICE and the GM output power, and the TM does not output torque at this time. It is different from the parallel mode (BHEV and ENC), which is composed of ICE and TM in the previous rule control, and the power source combination of the improved rule control is shown in
Figure 17.
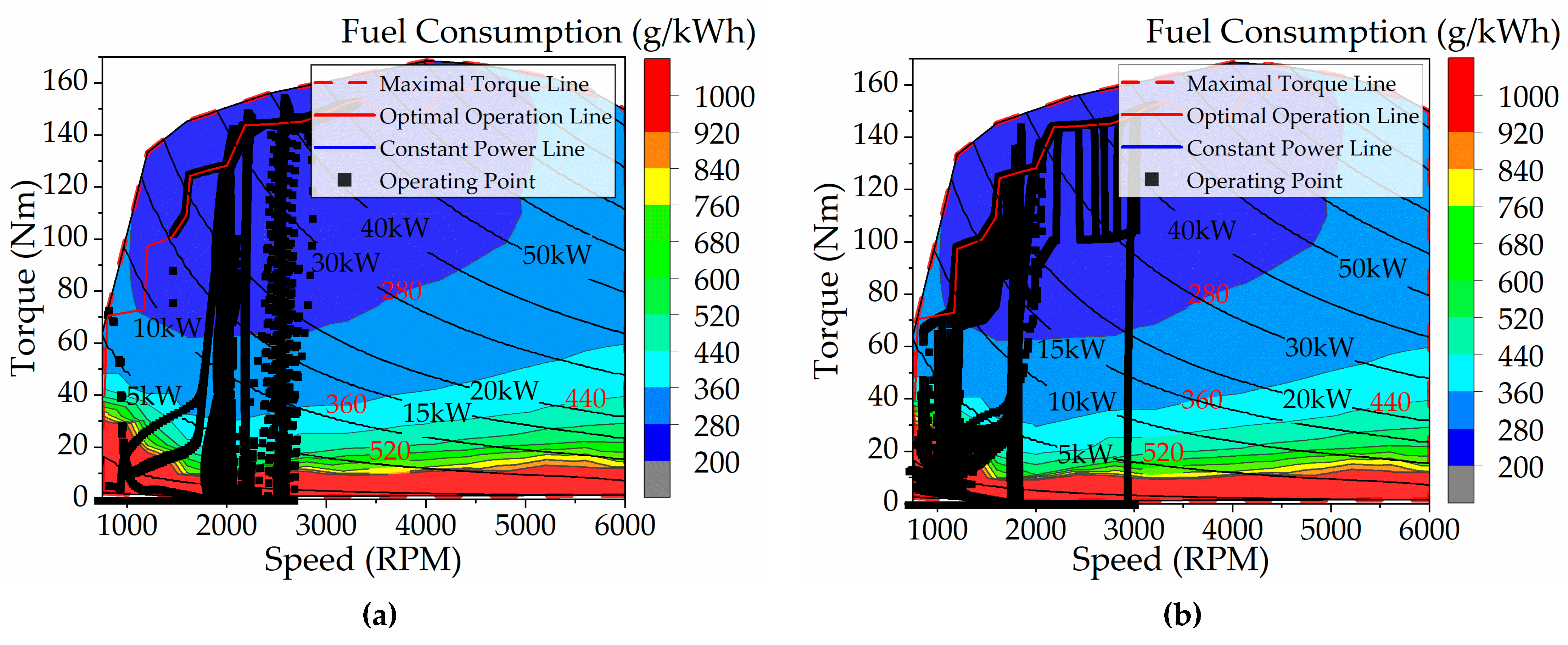
Secondly, from the output torque curve of each power element, it can be seen that when driving in parallel, the output torque of the ICE is not high, instead of working on the optimal economic curve, GM provides more torque. Therefore, when the vehicle is driven in parallel, the proportion of the ICE can be appropriately reduced in the distribution of the driver’s required torque. As shown in
Figure 18, under the improved rule strategy, in BHEV mode, the output power of ICE still follows the trend of the optimal economic curve, but its power is reduced to 70%. In ENC mode, because the battery needs to be charged at this time, the output power of ICE is not adjusted, but the TM is changed to GM, as described in
Figure 17.
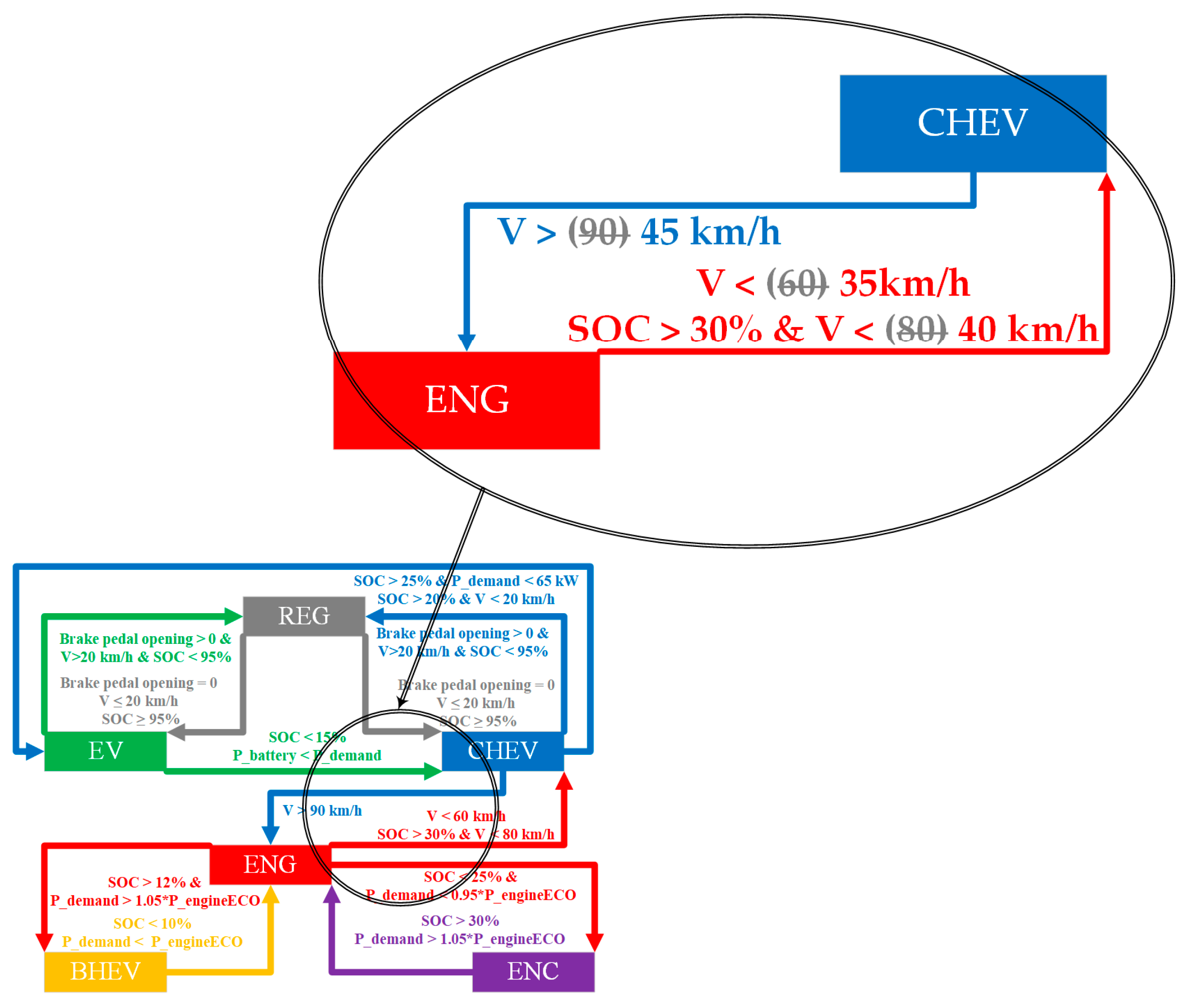
Thirdly, according to the corresponding relationship between vehicle speed and mode switching, under DP control, when the vehicle speed exceeds 40 km/h, the ICE will start to enter the parallel mode. Therefore, compared with the speed threshold of 90 km/h mentioned above, it will be more beneficial to reduce the comprehensive fuel consumption if the ICE is involved in vehicle driving in advance. As shown in
Figure 19, the improved rule strategy switches to ENG mode when the vehicle speed threshold is reduced to 45 km/h, and at the same time, the vehicle speed threshold for exiting ENG mode is correspondingly reduced to 35 km/h or 40 km/h.
4. Optimization Results and Discussion
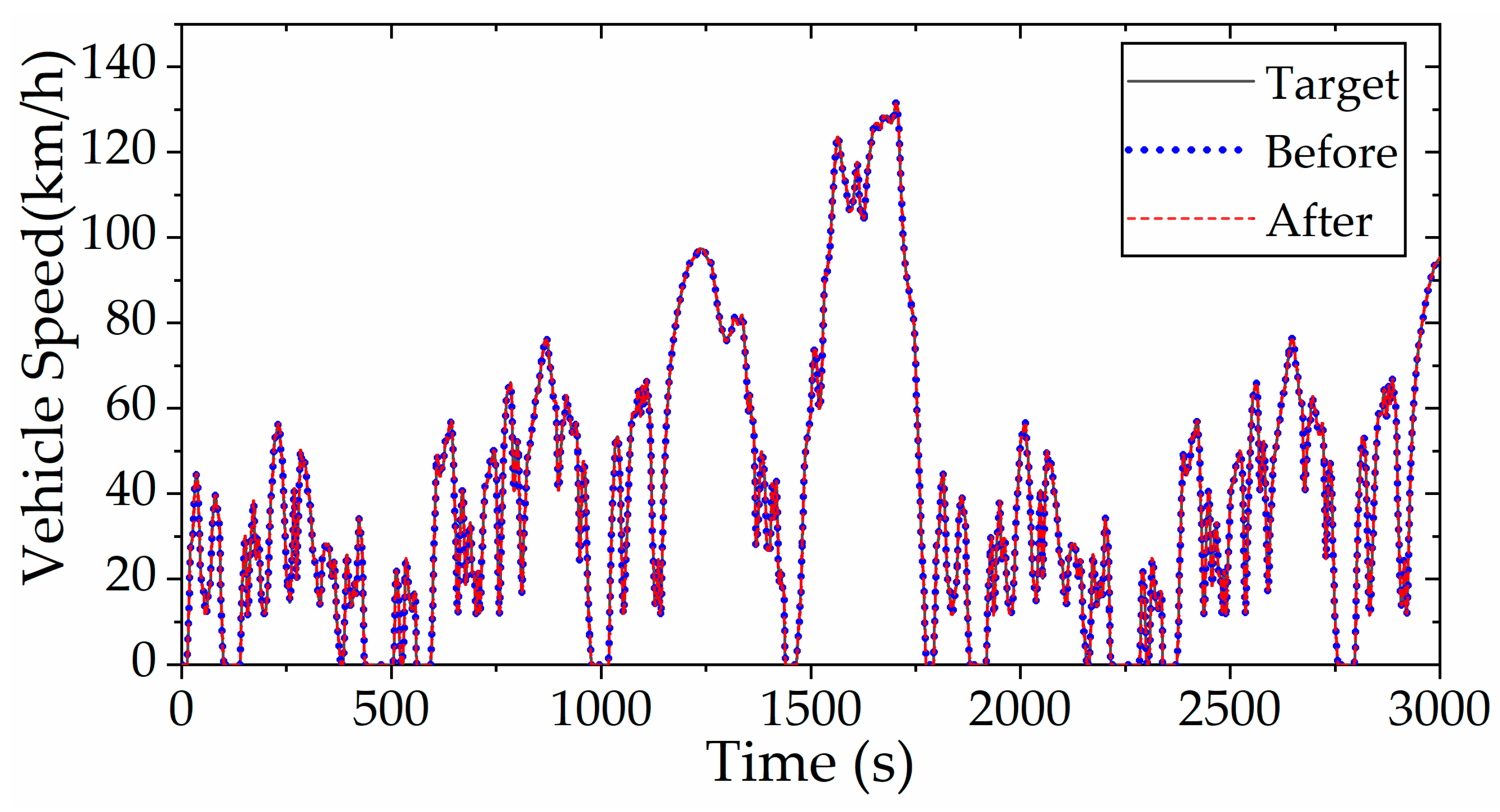
Figure 20 presents a comparative analysis between the simulated PHEV speed profiles (with and without enhanced rule-based control strategy) and the reference WLTC target speed. The results confirm that both control implementations successfully track the prescribed velocity trajectory while satisfying all power demands, demonstrating the robustness of the developed control framework.
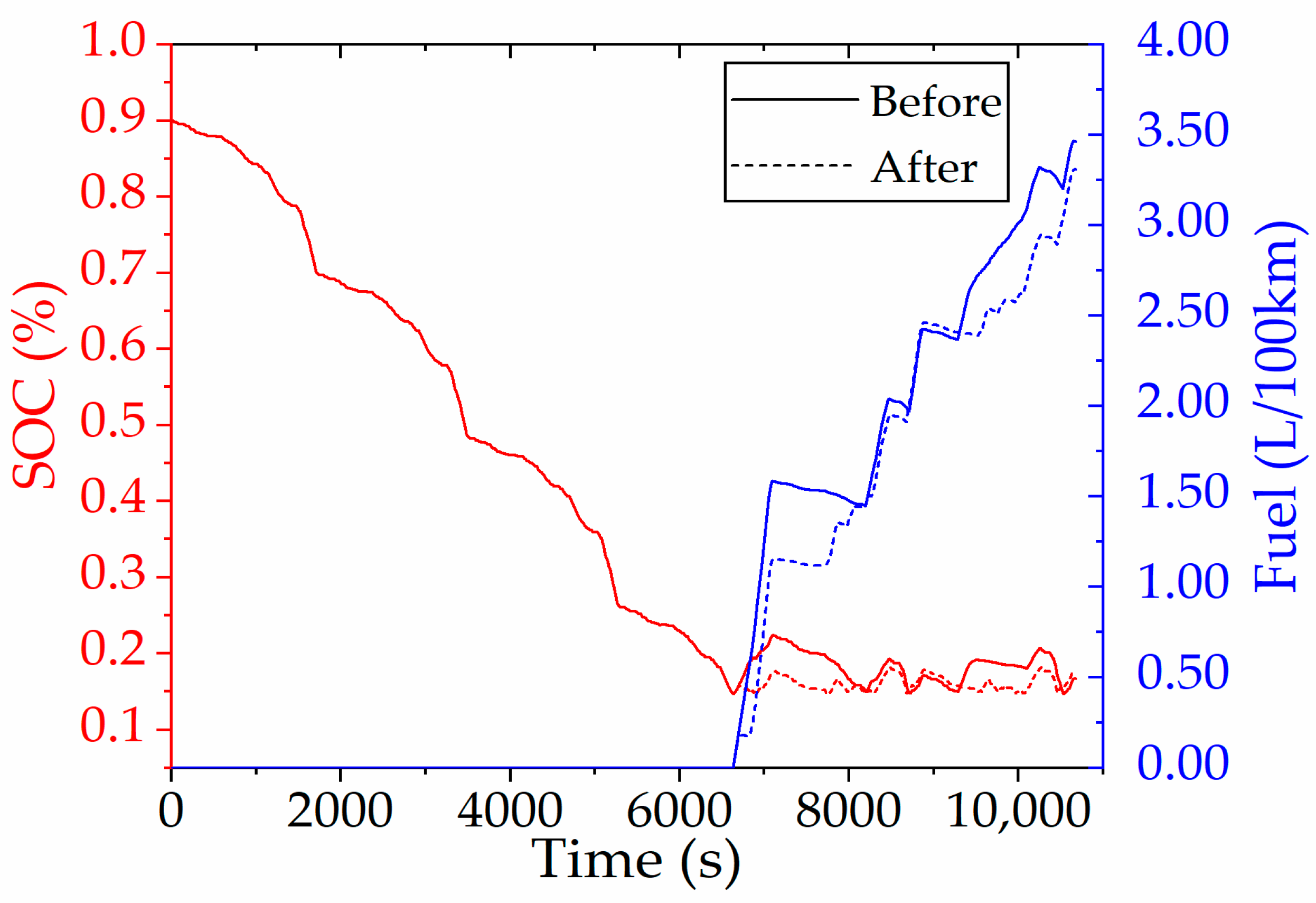
With the initial SOC set to 0.9 before improving the rule-based control strategy,
Figure 21 presents the fuel consumption and SOC fluctuations during six continuous driving cycles. The driving distance is 136.379 km and the fuel consumption is 3.463 L/100 km. In rule-based control, the vehicle’s operating state is usually divided into two stages: the charge depleting stage (CD) and the charge sustaining stage (CS), based on the operating state of the battery SOC. Around 6600 s, the PHEV shifted from the CD stage to the CS stage, ending the trip with an SOC of 16.71%. The fuel consumption per 100 km rose by 23.88% compared to DP control, highlighting substantial room for improving the rule-based strategy to achieve better fuel economy.
After the rule-based control strategy is improved, the same driving cycle is carried out and the initial state of charge is also set to 0.9. From the comparison of
Figure 21, it can be seen that since PHEV runs in EV mode during the CD stage, the changes in SOC and fuel consumption are consistent with the changes in the control strategy before the improvement. After entering the CS stage, SOC and fuel consumption change more gently, and the final SOC and fuel consumption are 17.87% and 3.307 L/100 km, respectively.
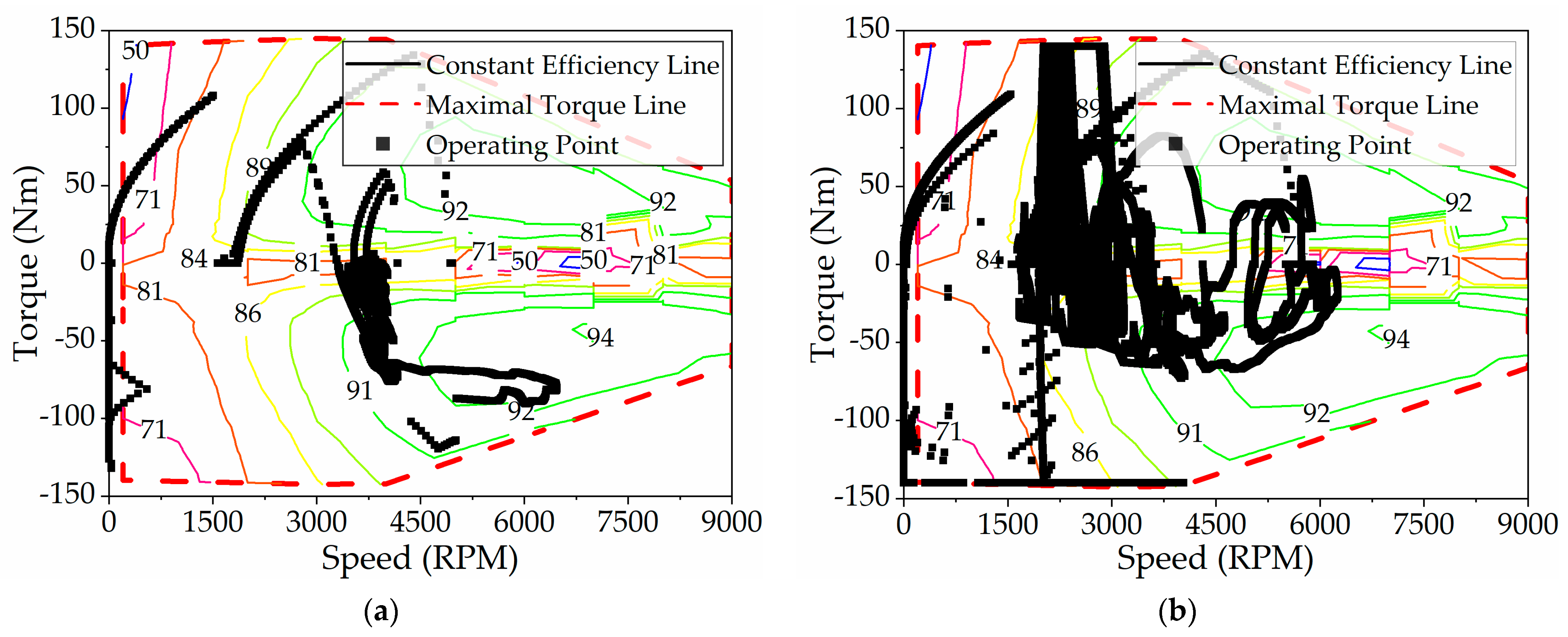
The distribution of TM working points before and after the improvement of rule-based energy strategy is shown in
Figure 22. As can be seen from the figure, the operation of TM decreases at high speed, and the TM in particular is hardly in the power generation state. This is because the combination of ICE and GM is used in parallel mode instead of the combination of ICE and TM, while TM is only used in a small amount of braking energy recovery mode.
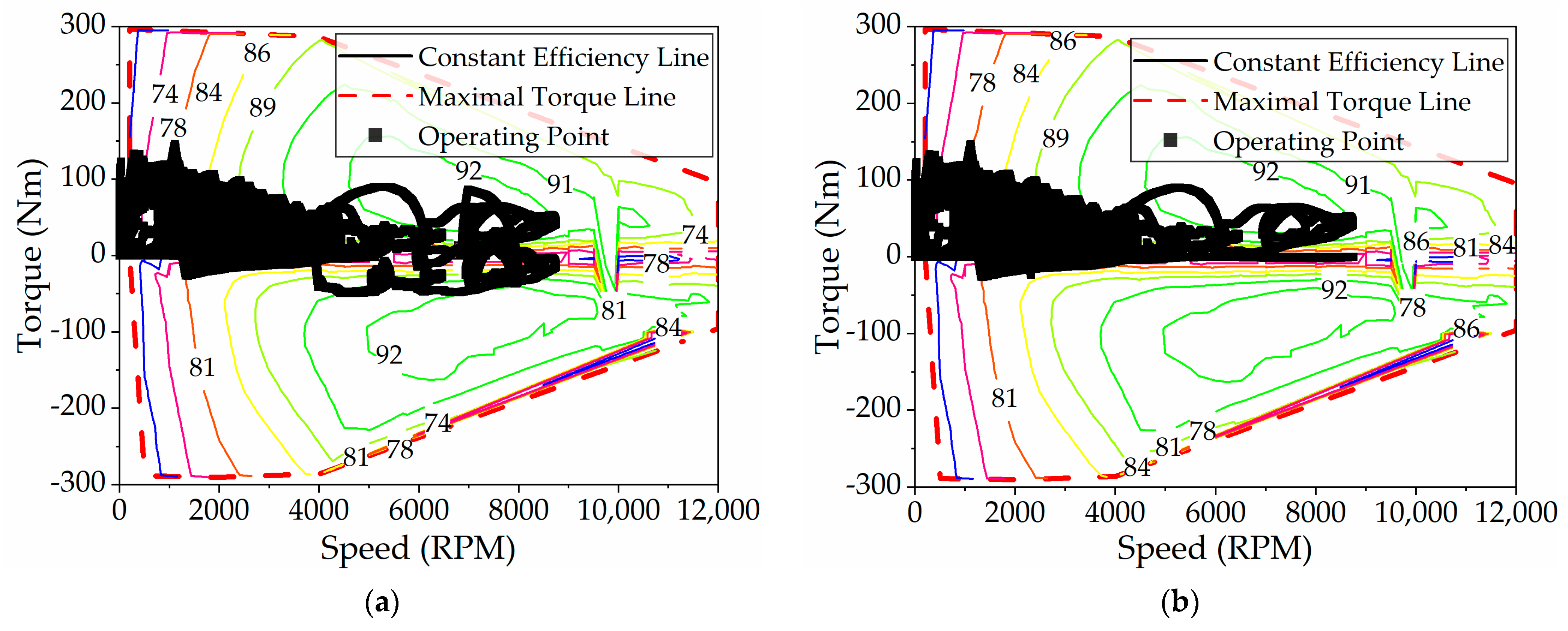
Figure 23 displays the working point distribution of the GM before and after improvement. It is evident that the GM participates more extensively in driving and power generation, operating primarily within the high-efficiency zone. In addition, the overall efficiency of its working point is higher than that of TM. This is because the rated power of GM is smaller than that of TM, its redundant power is lower, and the parallel mode combined with ICE has more energy-saving advantages, which is consistent with the results of DP control.
Figure 24 shows the ICE’s operating points. Prior to the rule improvements, the ICE’s operating speeds were mostly between 1800 rpm and 2700 rpm, suggesting that, compared to the DP-based energy management strategy, the ICE ran at higher speeds and needed its output power to be provided later. In addition, the torque at its working point is mainly concentrated on the optimal economic curve, which forces the ICE to output more power. After the improvement of the rules, the working area of the ICE is larger than that before the improvement, and it is in the range of 750 rpm to 3000 rpm, which indicates that the ICE participates in driving the vehicle earlier. The ICE’s working points lie both on the optimal economic curve and slightly below it, demonstrating that the ICE’s output power is efficiently reduced while ensuring improved fuel efficiency.
Figure 25 shows the switching of vehicle working modes. It can be seen from the figure that after the improvement of the rules, the CHEV mode is reduced, the BHEV mode and ENC mode are increased, and the running time of the ICE is increased. Using the inspiration of DP optimal control strategy, the vehicle can enter parallel mode driving at medium speed. In addition, the difference between ENG, BHEV, and ENC is that the output torque of GM is positive, negative, and zero, which does not involve complicated switching process. Therefore, the improved rule control strategy does not increase the control difficulty that cannot be achieved, nor does it bring frequent mode switching.
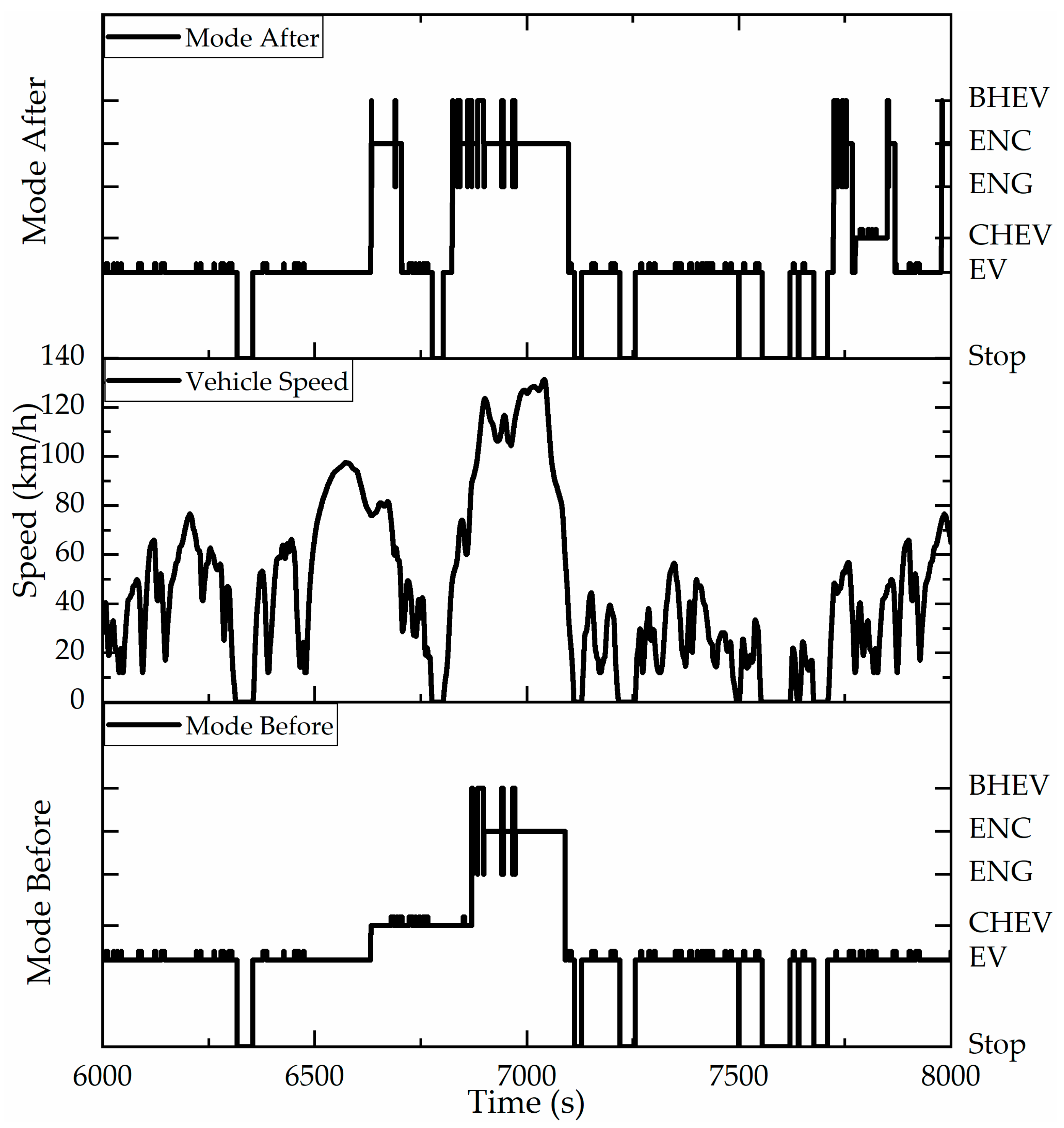
The simulation encompasses six consecutive WLTCs. Given the insufficient temporal resolution in
Figure 25, the dynamic transitions between vehicle working mode during the simulation cannot be fully resolved. Therefore,
Figure 26 provides a systematic visualization of the spatiotemporal distribution patterns characterizing these working modes. As shown in
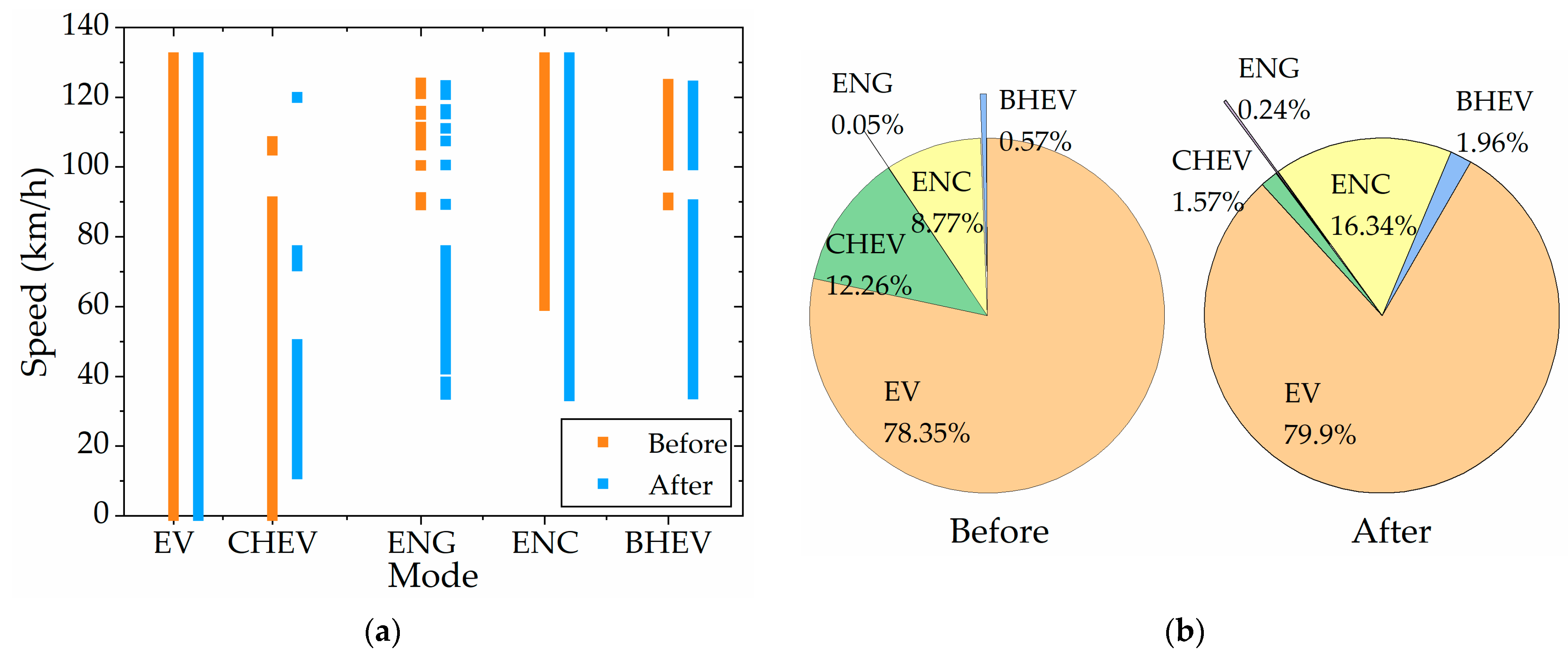
Figure 26a, the EV mode covers the whole vehicle speed range, so the rule control before and after improvement is the same. The improved rule-based control strategy compresses the distribution of vehicle speed in the CHEV mode, not only when the vehicle speed is lower than 10 km/h but also when the vehicle speed is higher than 50 km/h, so that it will actively enter other modes. The improved rule-based control strategy, whether ENG mode (single power source) or ENC and BHEV mode (multi-power source), has a wider range of engine power output to the wheels, except for at low speeds. As can be seen from
Figure 26b, since the improved rule-based control strategy still adopts the same power control method of CD-CS as that of the original rule-based control strategy, the time proportion of EV mode is almost the same. The proportion of CHEV mode changed greatly, from 12.26% before improvement to 1.57% after improvement, while the time proportion of ENC mode increased the most, from 8.77% to 16.34%. However, the time proportion of the ENG mode and BHEV mode increased from 0.05% and 0.57% to 0.24% and 1.96%, respectively. That is, the time when CHEV mode was originally adopted was replaced by ENC, ENG, and BHEV mode.
Table 3 compares the performance of different control strategies. After improving the rule-based strategy, the fuel consumption for six consecutive driving cycles is 4.423 L/100 km, with a final SOC of 17.87%. Fuel consumption per 100 km decreased by 4.504%, and electricity consumption decreased by 1.580%, leading to a 2.853% reduction in comprehensive energy consumption per 100 km. Nevertheless, fuel consumption per 100 km is still 38.010% higher than DP control, and electricity consumption is 1.130% higher.
5. Conclusions
In this paper, the dual-motor PHEV is examined, and the control strategy for the hybrid electric system is developed and explored using a model-based development methodology.
Within the MATLAB/Simulink framework, the key components and controller of the hybrid electric vehicle are modeled. The control strategy is designed based on the vehicle’s operational modes. The DP-based energy management strategy is explored, and an optimal control strategy is developed using MATLAB (R2022b). The vehicle’s working modes and torque distribution are analyzed, and the control strategy is extracted and refined using the optimal control strategy.
- (1)
The optimized internal combustion engine (ICE) operating point is not only near the fuel economy curve but it also reduces the output power of the internal combustion engine (ICE).
- (2)
After optimization, the working point efficiency of the dual-motor is improved and the cooperation with the internal combustion engine (ICE) is better.
- (3)
The optimized working mode switch is more active, making full use of the advantages of various working modes and improving the economy of the system.
The findings show that the DP-based energy management strategy improves the allocation and torque distribution of power components in various operating modes, optimizes the timing of mode switching, and significantly enhances the fuel economy of PHEVs. Fuel consumption per 100 km decreased by 4.504%, and electricity consumption per 100 km decreased by 1.580%, leading to a 2.853% reduction in comprehensive energy consumption per 100 km.
The proposed application framework of the DP algorithm-enhanced rule-based strategy can be extended to other passenger or commercial vehicle models, demonstrating strong commercialization potential. Furthermore, this methodology provides a template for developing energy management systems in emerging hybrid architectures, including hydrogen-fueled hybrids. Although the DP algorithm, as an offline global optimization method, cannot be directly deployed in vehicle controllers, it can still identify local–global optima within constrained temporal and spatial domains, enabling real-time optimization processes—a key direction for our future research. Meanwhile, leveraging the global optimal benchmark derived from DP allows the formulation of diverse rule-based control strategies. By generating training datasets under various rule-based strategies, reinforcement learning can extend multi-objective optimization capabilities across diverse driving styles, fuel consumption, and electricity usage, thereby automating calibration engineering tasks. This will constitute a primary focus of our subsequent work.