An Evolutionary Game-Theoretic Approach to Triple-Strategy Coordination in RRT*-Based Path Planning

Abstract

To address the limitations of the RRT-series algorithm and its variants, which have demonstrated a lack of dynamic adaptability in various environments, poor path quality, slow convergence rates, and a tendency to become trapped in local optima, this paper aims to propose a dynamic multi-strategy path-planning algorithm based on EG-DRRT* (Evolutionary Game-Theoretic Dynamic RRT*). The integration of evolutionary game theory allows the algorithm to use the concept of dynamically updating replicators to develop the payoff function for a fusion of multi-strategies. This enables a dynamic adjustment of the usage ratios of RRT*, Dijkstra, and Goal Bias algorithms. This approach directs the search process toward converging on the goal point, ultimately achieving an ESS (Evolutionarily Stable Strategy) equilibrium. The experimental results reveal that EG-DRRT* successfully establishes a dynamic balance between global exploration and local optimization across various environments, demonstrating remarkable adaptability and robustness. Additionally, EG-DRRT* shows substantial advantages compared to existing algorithms.

1. Introduction

The increasing use of UAVs and autonomous driving technology is driving significant advancements in path-planning technology. As a fundamental aspect of autonomous navigation in unmanned systems, effective path planning directly impacts the success rate of missions and overall operational efficiency [1,2]. Modern path planning aims to overcome the limitations of traditional algorithms. It not only addresses the fundamental challenges of graph search and obstacle avoidance but also considers the adaptability to dynamic environments. Furthermore, it takes into account the dynamics and kinematics constraints, as well as various optimization requirements [3,4]. The RRT family of algorithms, which rely on probabilistic sampling methods, plays a significant role in exploring high-dimensional spaces today. Additionally, graph-search-planning algorithms, such as A* and Dijkstra, are becoming increasingly important in structured environments [5,6,7]. Path-planning technology is making significant advancements, enabling robots to not only perform their primary task of autonomous navigation but also improve their ability to adapt to different environments. This progress is crucial for the future development of an intelligent society and will play a vital role in facilitating collaborative operations among various intelligent systems [8,9,10].

Kuffner and LaValle first proposed the RRT algorithm [11]. The algorithm rapidly explores the high-dimensional search space by random sampling and incrementally constructing trees. It has the advantages of simple implementation and adaptability and is widely used in robot path planning. However, the RRT algorithm was originally designed to find a feasible path quickly, does not guarantee the optimality of the path, and exhibits the disadvantage of low expansion efficiency in narrow-channel environments. Karaman and Frazzoli proposed the RRT* algorithm [12]. It is an improved version of the traditional RRT algorithm. RRT* achieves asymptotic convergence performance to the globally optimal solution and theoretically overcomes the path suboptimality problem of RRT by continuously optimizing the path cost during the expansion process. However, the cost of RRT* is that it significantly increases the computation time and complexity of the algorithm, especially in high-dimensional spaces or complex environments, where its performance is limited by the number of nodes and computational resources, and its real-time performance is difficult to meet the demand of dynamic planning. The RRT-Connect algorithm, proposed by Kuffner and LaValle [13], enhances path-planning efficiency through bi-directional search. However, the paths it generates often lack smoothness, leading to a decline in path quality. Seeking to improve upon this aspect, Marcucci T et al. introduced a path-planning algorithm based on an improved PRM [14], which enhances path smoothness through a post-optimization step. However, this optimization process adds extra computational overhead. The reinforcement learning approach combined with path planning, as proposed by Wang et al. [15], has demonstrated significant adaptability in complex environments. However, the training process for this method relies heavily on a substantial amount of labeled data, making it challenging to generalize to unfamiliar environments. A common issue faced by existing algorithms is generating high-quality paths in complicated settings while maintaining computational efficiency. The Adapt-RRT algorithm, introduced by Choudhury et al. [16], seeks to improve adaptation to complex environments by optimizing the sampling region. Nevertheless, its performance remains suboptimal in areas with dense obstacles. In contrast, Dang et al. developed a path-planning framework known as SIL-RRT* [17], which integrates deep learning with path optimization. This approach has made notable advancements in navigating complex dynamic environments, yet its practical application is hindered by the lengthy training time required for the model. Recently, Y and HE proposed a two-layer optimized A* algorithm that utilizes a dynamic window approach for UAV path planning in complex environments [18], incorporating specific rules for clipping neighboring nodes. While this method shows effectiveness in such intricate settings, further investigation is needed to determine its adaptability across diverse environments. As a result, enhancing the adaptability of path-planning algorithms in complex environments remains a vital area for future research.

An analysis of the aforementioned classical algorithms reveals that, despite significant progress in path planning, they exhibit several key limitations: the absence of strict guarantees for path optimality, inadequate adaptability in complex environments, and substantial computational demands. These issues highlight a clear direction for improvement in the EG-DRRT* algorithm proposed in this paper. Specifically, the aim is to enhance the efficiency and adaptability of path planning by integrating the global optimality of Dijkstra’s algorithm with the asymptotic optimality of the RRT* algorithm, alongside the dynamic adjustment of the policy.

The rest of this paper is organized as follows: Section 2 presents an overview of the RRT algorithm and Dijkstra’s algorithm, along with a description of the problem being addressed. Section 3 offers a detailed explanation of the EG-DRRT* algorithm. In Section 4, we compare our algorithm with other existing algorithms and present the results of our simulation experiments. Finally, Section 5 summarizes the advantages of the EG-DRRT* algorithm and proposes directions for future research.

2. Related Research Background

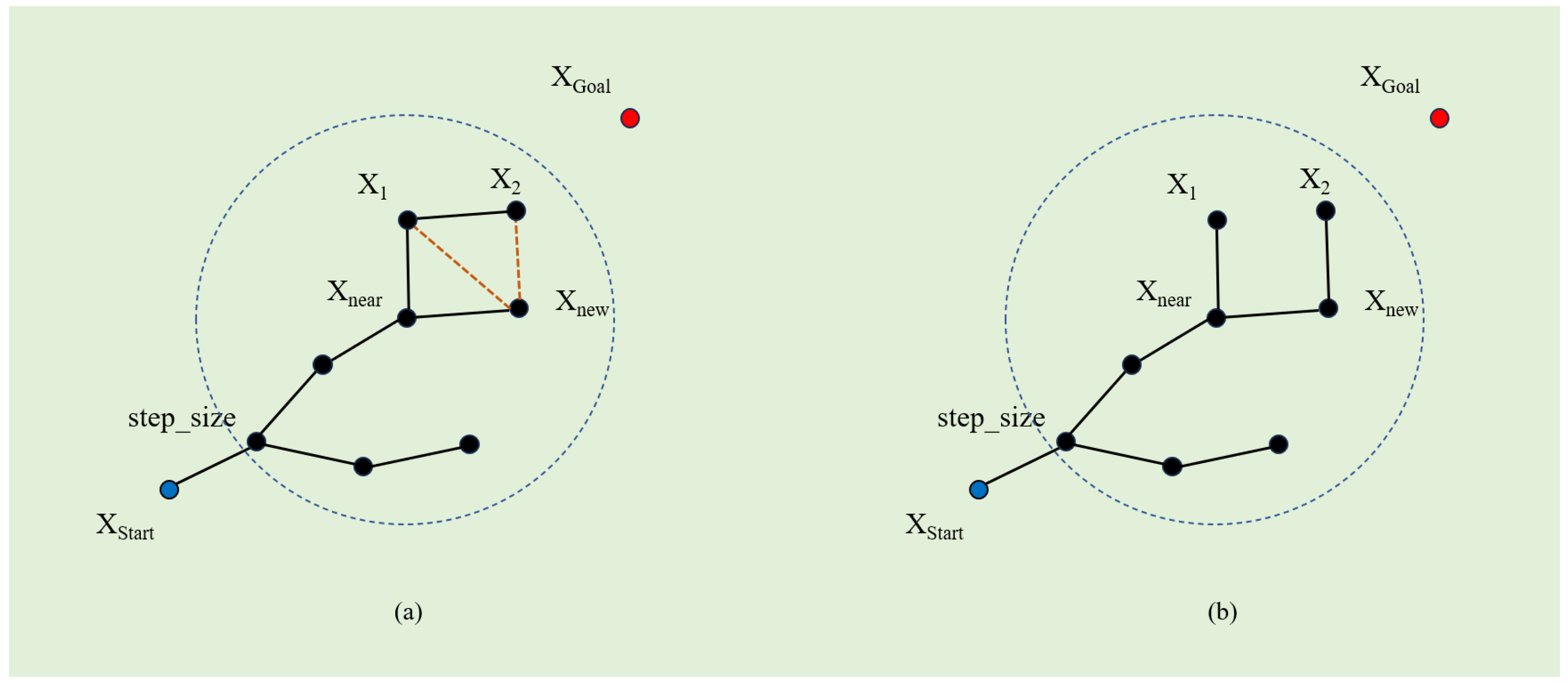
2.1. Analysis of Classical RRT* Algorithm

The main steps in the path expansion process of the RRT* algorithm include:

Firstly, as in Figure 1a, the existing path is extended to the current node $x_{near}$ from the start node $x_{Start}$. Based on this, a search radius $step\_size$ is defined around $x_{near}$ to generate a new path node $x_{new}$, and all nodes within this radius are considered candidate parent nodes. From the candidate parent nodes, the one with the shortest distance from $x_{Start}$ and the lowest cost is selected as the new parent. The new node $x_{new}$ is connected to the chosen parent node at this stage, creating a new path. During the expansion process, the algorithm optimizes the overall structure of the path by selecting an appropriate parent node connected to $x_{new}$. Specifically, $x_1$ expands further in the search space by connecting to $x_{new}$ as a temporary node. Based on this, the expansion continues, and $x_2$ is added to the path and reconnected with $x_{new}$. Path optimization is further implemented in step (2). The node $x_2$ becomes part of the new path, updating the connections to minimize total cost by re-evaluating all parent nodes, as detailed in Algorithm 1.

Algorithm 1 RRT*

Input: Start node $x_{start}$, goal node $x_{goal}$, maximum iterations max_iter; Output: Optimal path; 1: Initialize an empty tree T with root at $x_{start}$; 2: for $i=1$ to max_iter do 3:       $x_{rand}\leftarrow \mathrm{Randomly}\mathrm{sample}\mathrm{a}\mathrm{point}$; 4:       $x_{near}\leftarrow \mathrm{Randomly}\mathrm{sample}\mathrm{a}\mathrm{point}\mathrm{in}$ T; 5:       $x_{new}\leftarrow$ Move towards $x_{rand}$ from $x_{near}$; 6:       if $x_{new}$ is collision-free then 7:             Add $x_{new}$ to T; 8:             Optimize parent of $x_{new}$ within its neighbors; 9:             Rewire neighbors of $x_{new}$ to move the path; 10:       end if 11: end for 12: return the best path from $x_{start}$ to $x_{goal}$;

The RRT* algorithm utilizes random sampling for planning, but this approach may result in many invalid nodes and increase computational costs [19].

2.2. Analysis of Classical Dijkstra’s Algorithm

Dijkstra’s algorithm is a classical method for finding the shortest path from a single source node in a graph. It progressively explores neighboring nodes based on a greedy approach. This algorithm is widely used in various path-planning problems due to its effectiveness in searching for the shortest paths [20,21,22]. Dijkstra’s algorithm considers the edge weights of the graph as the costs of the paths, typically defining these weights as the Euclidean distance between two nodes. For two points $x=(x_1,x_2,\cdots ,x_n)$ and $y=(y_1,y_2,\cdots ,y_n)$ in n-dimensional space, the Euclidean distance can be expressed as follows:

$$d(x,y)=\sqrt{\sum _{i=1}^n{\left(x_i-y_i\right)}^2}$$

(1)

Dijkstra’s algorithm maintains a predecessor node for each node in the graph. It records the shortest distance to be added to the priority queue. As nodes are processed, Dijkstra compares the distances of each node with its neighboring nodes. If a shorter path to a neighboring node is found, the predecessor node is updated, and the new distance is reinserted into the priority queue. This process continues until all nodes have been completed, as detailed in Algorithm 2. Dijkstra’s algorithm consistently seeks the shortest path using a fixed greedy approach. However, it lacks the flexibility to incorporate other search strategies. In high-dimensional spaces or large-scale graphs, this global search characteristic results in high computational complexity, leading to limited adaptability in complex environments.

Algorithm 2 Dijkstra

Input: Graph G, start node $x_{start}$; Output: Shortest path distances from $x_{start}$; 1: Initialize distances: $\mathrm{dist}\left[x_{start}\right]=0$, others = $+\infty$; 2: Add $x_{start}$ to priority queue Q; 3: while Q is not empty do 4:      u ← Extract node with the smallest distance from Q; 5:      for each neighbor v of u do 6:             if $\mathrm{dist}\left[u\right]+\cos \mathrm{t}(u,v)<\mathrm{dist}\left[v\right]$: then 7:                   Update $\mathrm{dist}\left[v\right]\leftarrow \mathrm{dist}\left[u\right]+\cos \mathrm{t}(u,v)$; 8:                   Update priority of v to u; 9:                   Add v to Q 10:            end if 11:       end for 12: end while 13: return distances;

3. The Proposed Algorithm

As environmental complexity and the diversity of task requirements increase, traditional path-planning algorithms often struggle to handle various environmental features effectively. To better adapt to these diverse scenarios, we propose a dynamic multi-strategy path-planning algorithm called EG-DRRT*. This algorithm leverages the complementary strengths of RRT*, Dijkstra, and Goal Bias by dynamically adjusting the proportion of each strategy used during the search process. In this chapter, we provide a detailed description of the core design of the EG-DRRT* algorithm. First, Section 3.1 will analyze the design principles and implementation details of the strategy evolution mechanism. Following that, Section 3.2 will elaborate on the specific implementation of integrating strategy evolution with path planning.

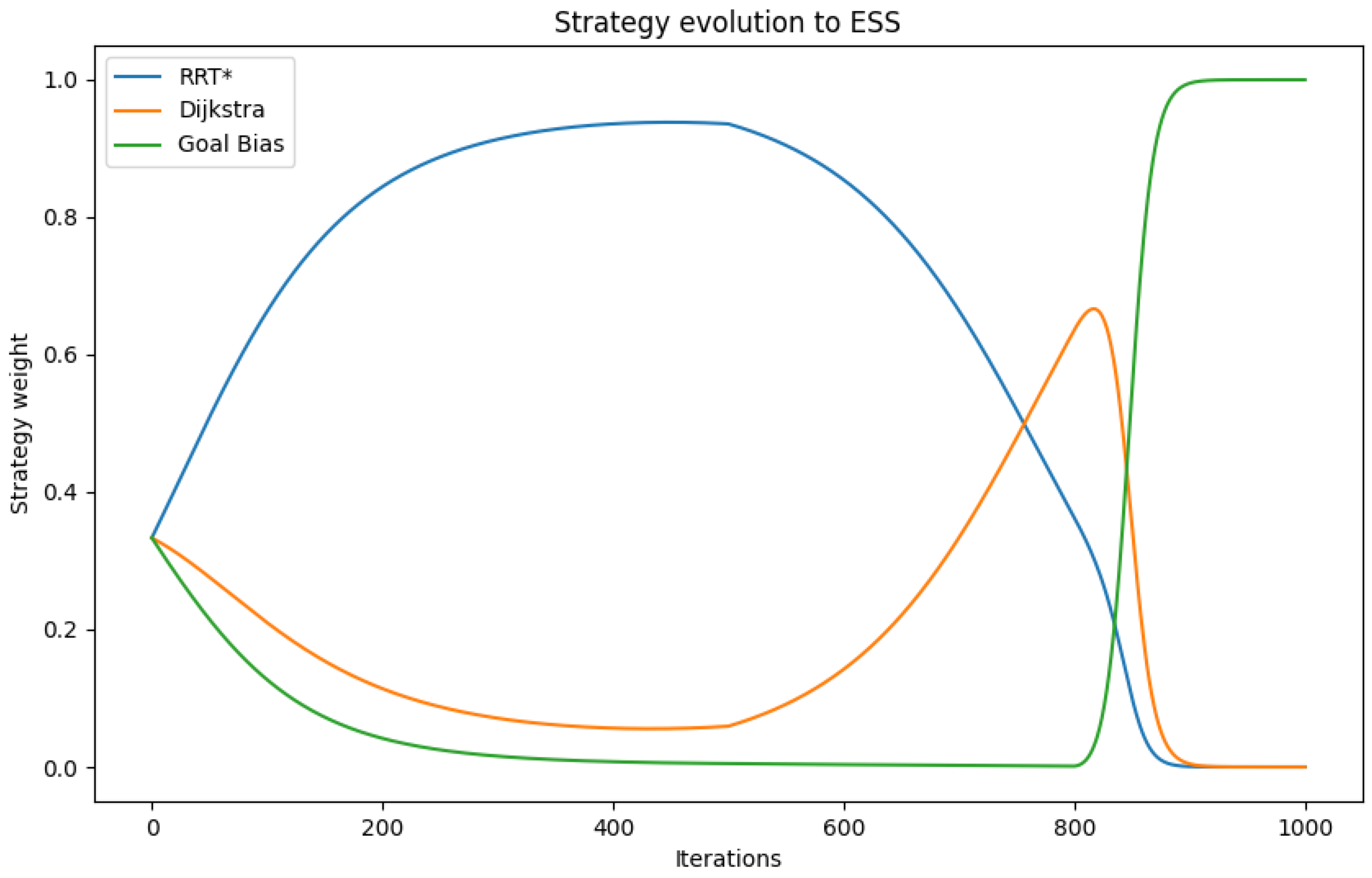
3.1. Mechanisms for Evolving Strategies

Evolutionary game theory originated in biology and was initially applied in economic theory to analyze the dynamic evolutionary processes of various strategies in competitive and cooperative environments. The goal is to optimize system performance by adjusting strategy distribution based on the payoff function [23]. Evolutionary game theory offers a flexible and effective approach to solving path-planning problems through dynamic adjustments, adaptive optimization, and management of group strategy distribution [24]. Its unique features not only address the limitations of traditional game methods but also provide a theoretical foundation for tackling complex optimization challenges that involve multi-strategy collaboration. Evolutionary game theory manages the adjustment of strategy weights by utilizing dynamic equations, allowing for continuous optimization of strategy proportions. In contrast, traditional adaptive weight adjustment relies on historical performance to modify weights, which can lead to a bias towards a single strategy and may result in local optimization issues. Overall, evolutionary game theory offers superior adaptability and stability compared to traditional methods. In this algorithm, the three strategies—RRT*, Dijkstra, and Goal Bias—each have their advantages and disadvantages. By incorporating evolutionary game theory, we calculate the priority of each strategy at different stages based on a payoff function. This allows us to adjust the proportion of each strategy adaptively during the algorithm’s iterative process, achieving a dynamic balance of strategies as the search progresses. Each strategy (RRT*, Dijkstra, and Goal Bias) is considered an independent player in the game model, and its payoff is determined by performance in the current search phase. To assess the performance of the current search phase, set the environment attribute vector as follows:

$$S\left(t\right)=[s_1\left(t\right),s_2\left(t\right),s_3\left(t\right)]$$

(2)

In this context, $s_1\left(t\right)$ represents the density of obstacles, which is positively correlated to its value. $s_2\left(t\right)$ refers to the known degree of the map; the higher the value, the more comprehensively the map is understood. $s_3\left(t\right)$ indicates the proximity to the target, meaning that a larger value signifies that the search is closer to the target point. The dynamic gain function is formulated based on the environmental attribute vector.

$$\begin{array}{cc}\hfill R_1\left(t\right)& =(1-{\displaystyle \frac{t}{T}})·{\displaystyle \frac{1}{1+s_1\left(t\right)}}+{\lambda }_1·s_3\left(t\right)\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill R_2\left(t\right)& ={\displaystyle \frac{t}{T}}·s_2\left(t\right)+{\lambda }_2(1-s_1\left(t\right))\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill R_3\left(t\right)& ={\displaystyle \frac{1}{1+e^{-\gamma (\frac{t}{T}-\theta )}}}·(1-s_3\left(t\right))+\mu \left(t\right)Q_i\hfill \end{array}$$

(5)

In this context, $T=max\_iter$ represents the maximum number of iterations, while $R_1\left(t\right)$, $R_2\left(t\right)$, and $R_3\left(t\right)$ indicate the gains achieved by the three strategies: RRT*, Dijkstra, and Goal Bias, as the number of iterations varies. The parameters ${\lambda }_1,{\lambda }_2>0$ are tuning parameters that reflect the impact of proximity to the goal and the density of obstacles on the gains, respectively. A larger value of ${\lambda }_1$ will significantly increase the gain of the RRT* algorithm when the goal is closer. Similarly, increasing ${\lambda }_2$ will lead to a greater gain for Dijkstra’s algorithm. To balance these two gains, both ${\lambda }_1$ and ${\lambda }_2$ are set to 1 in this experiment.

To quickly adapt to the optimal strategy for achieving the goal, mutation gains are introduced in this evolutionary game concept, along with the mutation probability.

$$\mu \left(t\right)=min\{1,\alpha (\mathsf{\Delta }d-d\left(t\right)\left)\right\}$$

(6)

The parameter $\alpha >0$ regulates the sensitivity of mutation. A higher value of $\alpha$ increases the probability of mutation, which accelerates convergence. Conversely, a smaller $\alpha$ slows down the mutation process. To balance these two effects, $\alpha$ is set to 0.05 in the experiment. $d\left(t\right)$ denotes the current distance to the target point. $\mathsf{\Delta }d$ is the predetermined step size. When $\mathsf{\Delta }d$ exceeds $d\left(t\right)$, a mutation occurs to quickly reach the target point, thereby conserving time and resources. The distribution of the target strategy after this mutation is as follows:

$$Q_i=\left\{\begin{array}{cc}1,\hfill & i=3\hfill \\ 0,\hfill & i=1,2\hfill \end{array}\right.$$

(7)

The overall complexity of the weight update formula is $O\left(N\right)$, with N representing the number of strategies involved in the game. This indicates that the impact of strategy updates on overall computational efficiency is linear. Consequently, the overall computational complexity of the algorithm is primarily determined by the path-planning algorithm. This algorithm employs three independent strategies: RRT*, Dijkstra, and Goal Bias. Previous studies have shown that these strategies demonstrate good scalability in three-dimensional space. Additionally, the computational complexity of updating weights is minimal compared to the overall algorithm, allowing it to run efficiently even in scenarios with high real-time requirements. To maximize the effectiveness of the strategies at any given moment, this algorithm also introduces a competitive penalty factor, denoted as $\beta$. It modifies the extent of the return adjustments based on t. Higher values increase competition among strategies, while lower values weaken their impact on strategy selection. This factor enables the concept of negative feedback in the weight-updating process, penalizing the underperforming current strategy by reducing its weight. This approach encourages the system to transition toward a plan that demonstrates better performance. Let $\beta \left(t\right)$ represent the competitive penalty factor at the current moment; its dynamic adjustment is as follows:

$$\beta \left(t\right)={\beta }_{min}+({\beta }_{max}-{\beta }_{min})·{\displaystyle \frac{t}{T}}$$

(8)

The maximum competitive penalty factor, ${\beta }_{max}=0.5$, is pre-set, while the minimum value is ${\beta }_{min}=0.1$. Initially, the competition penalty factor is low, which allows for the retention of a greater number of strategies and enhances exploitability. As the process advances, the competition penalty factor is gradually increased to encourage a focus on better-performing strategies. Towards the end of the process, the competitive penalty factor approaches its maximum value, indicating that the offsetting strategy is no longer a factor in the decision making. As the number of iterations, denoted as t, increases, the competitive penalty factor gradually rises from its minimum value ${\beta }_{min}$ to its maximum value ${\beta }_{max}$. This trend applies to the overall phase adjustment of the algorithm and aligns with the evolutionary mechanism of the strategy.

Using the concept of dynamic updating of replicators, the returns for each strategy are adjusted based on their respective weights. The formula for the dynamic adjustment update in the evolutionary game is as follows:

$${\tilde{\omega }}_i(t+1)={\omega }_i\left(t\right)[1+\beta \left(t\right)·(R_i\left(t\right)-\overline{R}\left(t\right)]]$$

(9)

where ${\omega }_i\left(t\right)$ represents the current strategy weight of RRT*, Dijkstra, and Goal Bias at time t, and $\overline{R}\left(t\right)$ denotes the average of the strategy returns.

$$\overline{R}\left(t\right)=\sum _{j=1}^3{\omega }_j\left(t\right)R_j\left(t\right)$$

(10)

3.2. Strategy Implementation and Route Planning

The weights for each of the strategies calculated earlier are normalized and updated.

$${\omega }_i(t+1)=(1-\mu \left(t\right))·{\displaystyle \frac{{\tilde{\omega }}_i(t+1)}{{\sum }_{j=1}^3{\omega }_i(j+1)}}$$

(11)

The normalized weights serve as the probability for selecting the final path in the planning process.

$$P_i(t+1)={\omega }_i(t+1)$$

(12)

The adjustment of strategy weights is determined by the dynamic equation for replication:

$${\displaystyle \frac{d{P}_i\left(t\right)}{dt}}=P_i\left(t\right)\left(R_i\left(t\right)-\overline{R}\left(t\right)\right),i\in \{1,2,3\}$$

(13)

The rate of weight change is shown to be proportional to the deviation of strategy returns. Based on the probabilistic model described above, a current execution strategy is chosen during each path search by generating a random number $r\in [0,1]$. The rules for strategy selection are as follows:

$$Strategy(t+1)=\left\{\begin{array}{cc}\mathrm{RRT}*,\hfill & \mathrm{if}r<P_1(t+1)\hfill \\ \mathrm{Dijkstra},\hfill & \mathrm{if}{P}_1(t+1)\le r<P_1(t+1)+P_2(t+1)\hfill \\ \mathrm{Goal}\mathrm{Bias},\hfill & \mathrm{if}r\ge P_1(t+1)+P_2(t+1)\hfill \end{array}\right.$$

(14)

The sampling point $x_{rand}$ is generated based on the following probability distribution:

$$P\left(x_{rand}\right)=\left\{\begin{array}{cc}{P}_{goal},\hfill & \mathrm{if}{x}_{rand}=x_{goal}\hfill \\ 1-P_{goal},\hfill & otherwise\hfill \end{array}\right.$$

(15)

When $P_{goal}$ represents the predefined target-point bias probability, employing the target bias strategy can efficiently and quickly correspond to the target point, as illustrated in Figure 2.

The tuning strategy for the evolutionary game is outlined as follows: At the beginning of the exploration phase, the RRT* strategy takes precedence, facilitating rapid global expansion to explore the unknown environment and ensure comprehensive path coverage. During this phase, the weights assigned to Dijkstra and Goal Bias are kept low. As the search process progresses, the influence of Dijkstra’s algorithm gradually increases to improve the quality of the path. This enhancement is achieved by optimizing the connections between critical points on the path, utilizing the algorithm’s precise capability to find the shortest route. Toward the end of the exploration, the weight assigned to the Goal Bias strategy is significantly increased, which helps the search process converge rapidly toward the target point. This method not only shortens the path length but also reduces the computational time. The system can gradually converge to a final adaptive steady state, where the strategy combinations become balanced and an efficient path is established. From the perspective of system theory, the iteration of this algorithm treats the behavior of group strategies as a dynamic system. During this process, each strategy’s behavior and its relationship with the group are depicted by the principle of time irreversibility. This approach leads to the establishment of a final strategy that achieves the target goal without interference from other strategies. Compared to the Nash equilibrium, this method demonstrates absolute robustness and aligns with the ESS equilibrium, as illustrated in the accompanying Figure 3.

4. Experimental Results and Discussion

To evaluate the performance of the EG-DRRT* algorithm, we compared it with the RRT, RRT*, and RRT-Connect algorithms in various environments, including simple, complex, and 3D settings. To adhere to the principle of controlling variables, we maintained consistent parameter settings across all comparison experiments. During the pre-experimental phase, we tested various parameter combinations and found that their effects on the optimization results were minimal, with all configurations converging to the ESS equilibrium. As a result, we selected a set of parameters that effectively balanced computational efficiency and algorithm performance. Due to the randomness inherent in RRT-series algorithms, we averaged the experimental data over 1000 iterations. The experiments were conducted using Python 3.12 on a Windows 11 operating system, with hardware specifications of a 2.60 GHz Intel (R) Core (TM) i5-13600KF CPU (Intel Corporation, Santa Clara, CA, USA) and 32 GB of RAM.

Figure 4 compares the success rates of four algorithms in simple, complex, and 3D environments. EG-DRRT* achieves high success rates across these different environments, particularly in simple and 3D scenarios. In contrast, the traditional RRT, RRT*, and RRT-Connect algorithms significantly decrease success rates in high-complexity situations, indicating that they are less robust when dealing with complex environments. Meanwhile, EG-DRRT* demonstrates a stronger ability to adapt.

4.1. Simple Environment

In a simple 100 × 100 environment, the starting point is at (5, 95) and the goal point is at (95, 5). While the RRT family of algorithms typically requires many iterations to find a clear path and is effective for path planning in complex, unstructured environments, it can generate a significant number of unnecessary and redundant branches in simpler paths. This issue can lead to increased time and resource consumption.

In the simple environment presented in

Table 1. The experimental data on four algorithms tested in a simple environment.

Algorithm Category	Time/s	Length/m	Iterations
EG-DRRT*	0.12	155.81	745.3
RRT	0.29	172.76	1212.0
RRT*	1.53	150.83	1369.5
RRT-Connect	0.63	166.53	1246.7

and Figure 5, EG-DRRT* demonstrates a significant advantage in computation time compared to RRT, RRT*, and RRT-Connect, indicating that it can provide quick responses. Additionally, the path length is reduced by 9.8% compared to RRT and by 8.4% compared to RRT-Connect. EG-DRRT* also has the lowest number of iterations among all the algorithms. Although the path generated by RRT* is 3.2% shorter than that of EG-DRRT*, the time cost for RRT* is considerably higher. Overall, EG-DRRT* achieves a better balance between efficiency and path length.

4.2. Complex Environment

In the 100 × 100 complex environment, the starting point is located at (5, 95), while the goal point is at (95, 5). This environment presents more obstacles, fewer feasible paths, and a denser layout compared to the simpler environment. Our algorithm demonstrates a level of randomness comparable to the other three algorithms in the initial stages. However, it reaches the goal point more quickly in the later stages, especially when the complexity of obstacles is lower. This efficiency reduces both the time needed and computational redundancy, as illustrated in Figure 6.

As shown in

Table 2. The experimental data on four algorithms tested in a complex environment.

Algorithm Category	Time/s	Length/m	Iterations
EG-DRRT*	19.38	596.13	17,764.8
RRT	19.86	611.09	17,742.7
RRT*	74.82	598.59	18,450.3
RRT-Connect	35.79	603.33	18,896.2

, the computation time of EG-DRRT* is reduced by 74.1% compared to RRT*. Additionally, the path length is shortened by 2.45% compared to RRT, 0.41% compared to RRT*, and 1.19% compared to RRT-Connect. Even when employing heuristic search and bi-directional expansion, EG-DRRT* remains superior. The number of iterations is reduced by 3.72% compared to RRT* and by 5.99% compared to RRT-Connect, although this reduction is slightly greater than that of RRT. Overall, the time efficiency and quality of paths produced by EG-DRRT* demonstrate its superiority in complex environments.

4.3. Three-Dimensional Environment

In a 100 × 100 × 20 3D environment, the starting point is at (10, 10, 0), and the target point is at (90, 90, 5). There are column obstacles with heights of 3, 4, and 5 positioned at (50, 50), (30, 40), and (70, 70), respectively. Figure 7 illustrates the path-planning results of the EG-DRRT* algorithm in this 3D environment. The path successfully navigates through the irregularly distributed obstacle regions and reaches the target point, demonstrating the effectiveness of the algorithm in a 3D setting.

The random tree generated by EG-DRRT* is sparser, as shown in Figure 8. This sparsity leads to a reduction in redundant nodes, lowers search complexity, and enhances the efficiency of the expansion strategy. According to

Table 3. The experimental data on four algorithms tested in a 3D environment.

Algorithm Category	Time/s	Length/m	Iterations
EG-DRRT*	6.42	157.78	4217.6
RRT	8.35	169.52	3727.7
RRT*	15.63	163.06	5317.8
RRT-Connect	9.33	160.25	5236.8

, the time taken by EG-DRRT* is reduced by 23.1% compared to RRT, 58.9% compared to RRT*, and 31.2% compared to RRT-Connect. Additionally, the path length is shortened by 6.9%, 3.2%, and 1.5%, respectively. This indicates that EG-DRRT* maintains the fastest search speed and the shortest path length in 3D path planning. While the number of iterations is slightly higher than that of RRT, it is still lower by 20.7% and 19.5% when compared to RRT* and RRT-Connect, respectively. This demonstrates EG-DRRT*’s effectiveness in controlling the number of node extensions in a 3D environment.

5. Conclusions

Our proposed EG-DRRT* algorithm performs simulation experiments in three different environments by integrating evolutionary game theory, which emphasizes dynamically changing adaptations and strategies. The algorithm shows significant improvements in search time for simple environments, achieving an average path-length reduction of 5.0%. In complex environments, it reports an impressive average search-time reduction of 39.9% and a path-length reduction of 1.35%. For 3D environments, the search time is reduced by an average of 37.7%, while the average path length decreases by 3.9%. Overall, the expected results in terms of path dimension, complexity, time, and path length have been successfully met, effectively enhancing traditional RRT-series algorithms that typically exhibit poor dynamic adaptability and insufficient robustness in various environments.

While the algorithm has made notable strides in improving path-planning efficiency and quality, the fetch-random-point-type algorithm remains influenced by its initial parameter settings. Future studies will include experimental validation on the PX4 open-source UAV platform, along with the ROS operating system, building on the current research conducted within a simulation environment. Future theoretical research will concentrate on further optimizing the evolutionary game theory model, developing a more refined strategy for calculating payoff functions, and exploring the creation of path-replanning mechanisms in dynamic obstacle environments. These efforts aim to augment the versatility and practical application of the EG-DRRT* algorithm for unmanned systems.