A Machine Learning Evaluation of the Impact of Bit-Depth for the Detection and Classification of Wireless Interferences in Global Navigation Satellite Systems
Abstract
1. Introduction
2. Related Work
2.1. Related Work on Machine Learning
2.2. Related Work on Neural Networks and Deep Learning
- With a good degree of novelty, the CNN is applied to the digital artifacts created by the GNSS receiver instead of the spectral domain representation of the signal in space. Even if the application of the CNN to the observables may be more challenging because the original Radio Frequency (RF) signal is pre-processed and some information could be lost, the approach is more practical and realistic because it relies only on the output of the GNSS receiver and no additional components (e.g., spectrum analyzer) are needed.
- For the first time in the literature, the impact of the bit-depth storage and reproduction of the original GNSS signal is evaluated in combination with CNN and the artifacts for the problem of detection and classification of interferences in GNSSs.
- A CNN with a multi-head attention layer is used for classification, which is more sophisticated than the CNN architectures used in the literature so far.
- The authors have produced a novel (because it is based on data) and comprehensive data set with different types of interference, levels of attenuation, and bit-depths, which was not made available before to the research community. This data set will be available after the publication of the manuscript.
3. Methodology
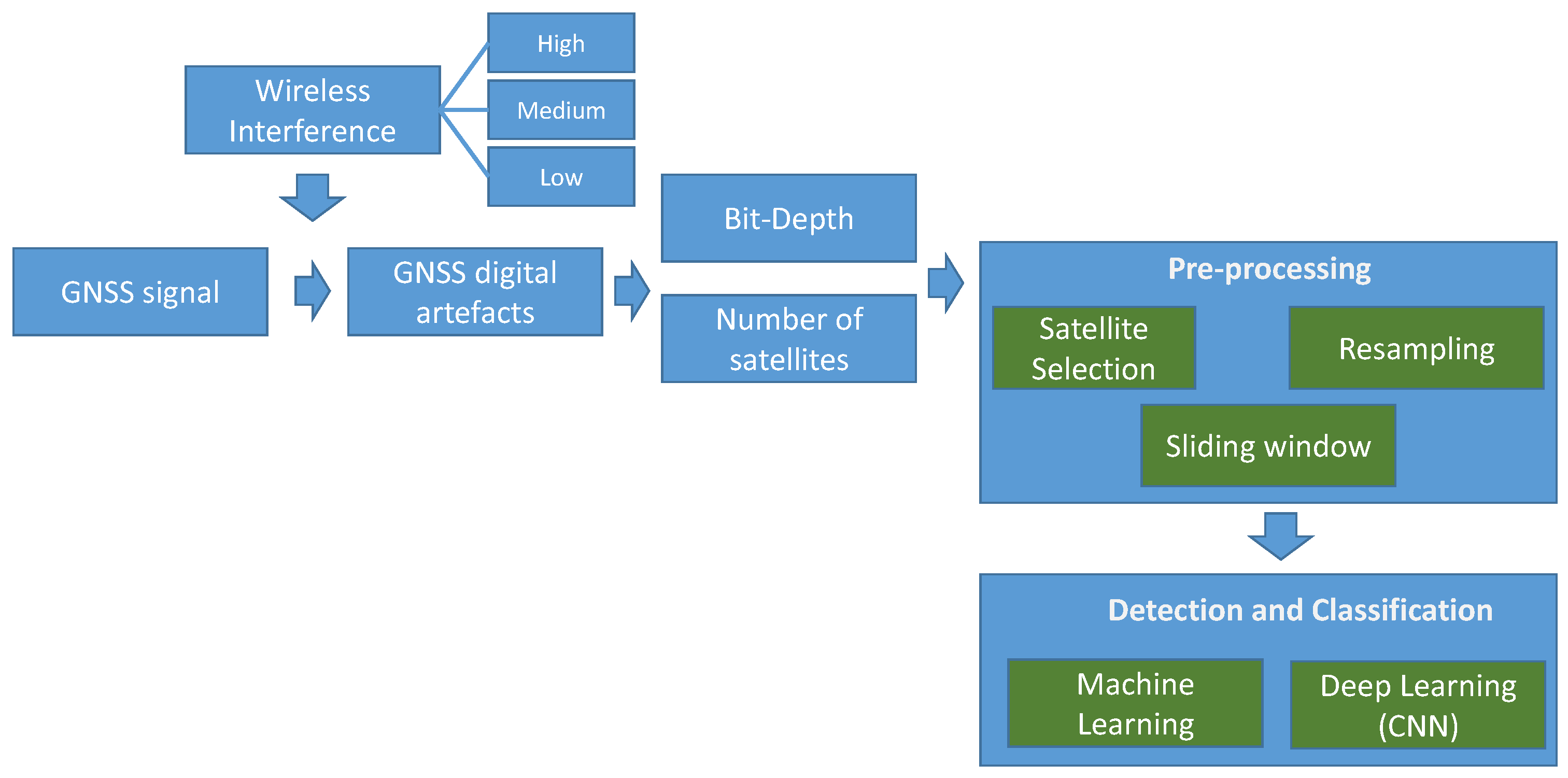
3.1. Main Flow and Procedures of the Proposed Approach
3.2. Feature-Based Approach with Machine Learning Algorithms
3.3. CNN Architecture and Hyper-Parameters
3.4. Metrics of Evaluation
3.5. Computing Platform
4. Data Set Generation and Processing
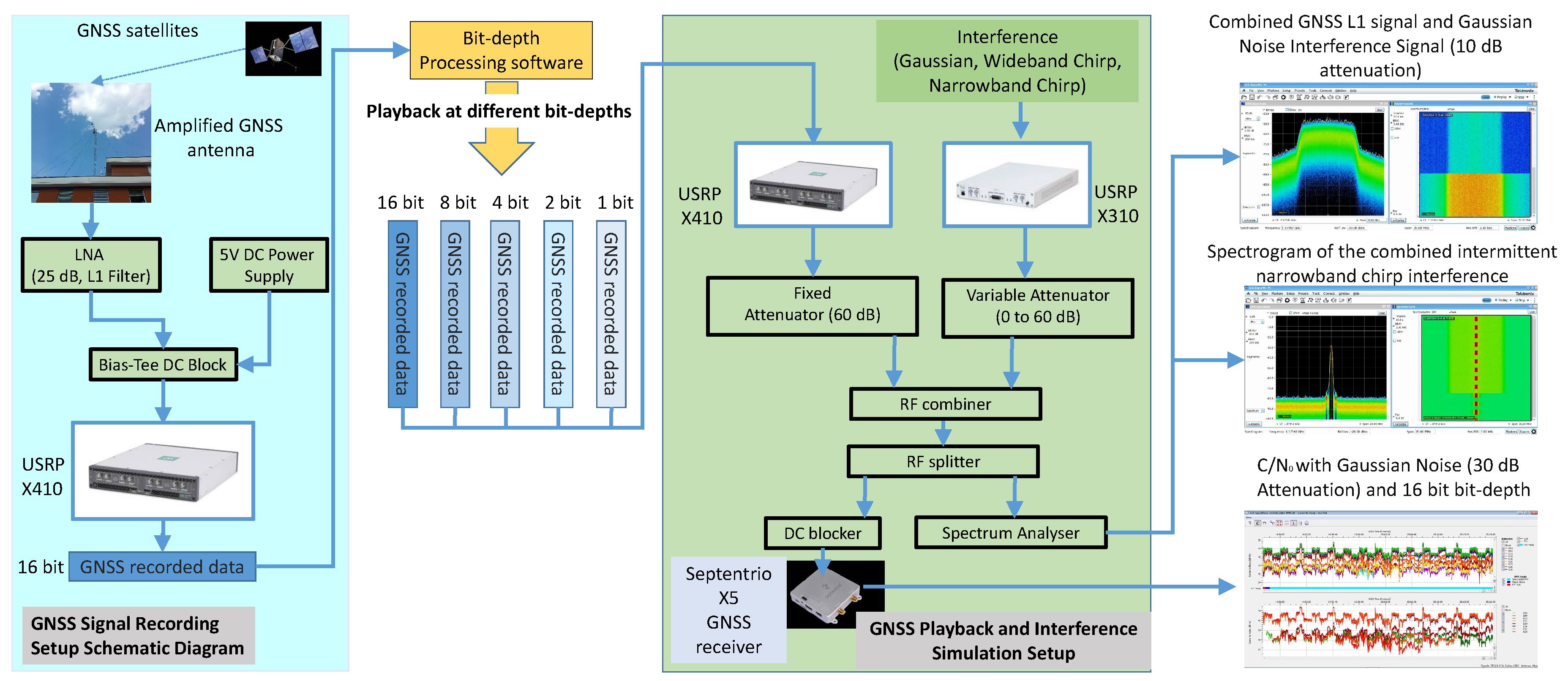
4.1. Test Bed Setup
- Hardware component USRP X410, which is the primary GNSS recording and playback system, configured with a custom LabVIEW-based application. Labview is a graphical system design and development platform produced and distributed by National Instruments. National Instruments is based in Austin, TX, USA.
- Hardware component X310 (interferent signal generation) is utilized with GNU’s Not Unix (GNU) Radio on Ubuntu to generate diverse interferent signals, including Gaussian noise, narrowband chirp, and wideband chirp.
- Variable attenuator precisely controls the power level of the interferer.
- Software component Windows Platform LabVIEW-based application with standard LabVIEW driver based on USRP Hardware Driver (UHD) was chosen for its compatibility with the X410 Universal Software Radio Peripheral (USRP) and for the implementation of bit-depth reduction.
- Software component Ubuntu Environment GNU Radio is used for generating the interference signals.
4.2. GNSS Signal Model and Types of Interference
4.3. GNSS Signal and Playback with Specific Bit-Depth
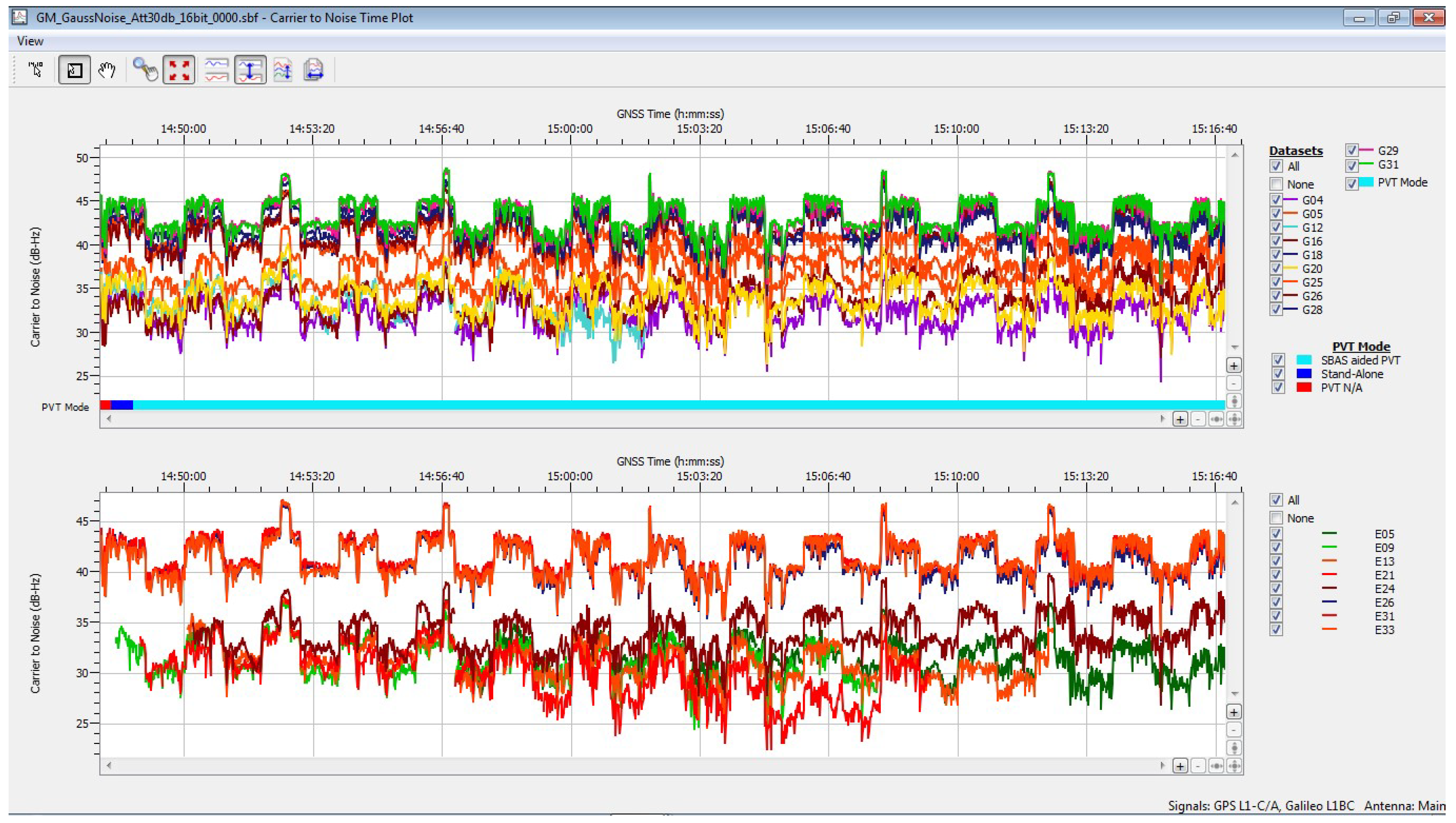
4.4. GNSS Receiver Configuration and Generated Digital Artifacts
4.5. Data Set Structure and Format
5. Results and Discussion
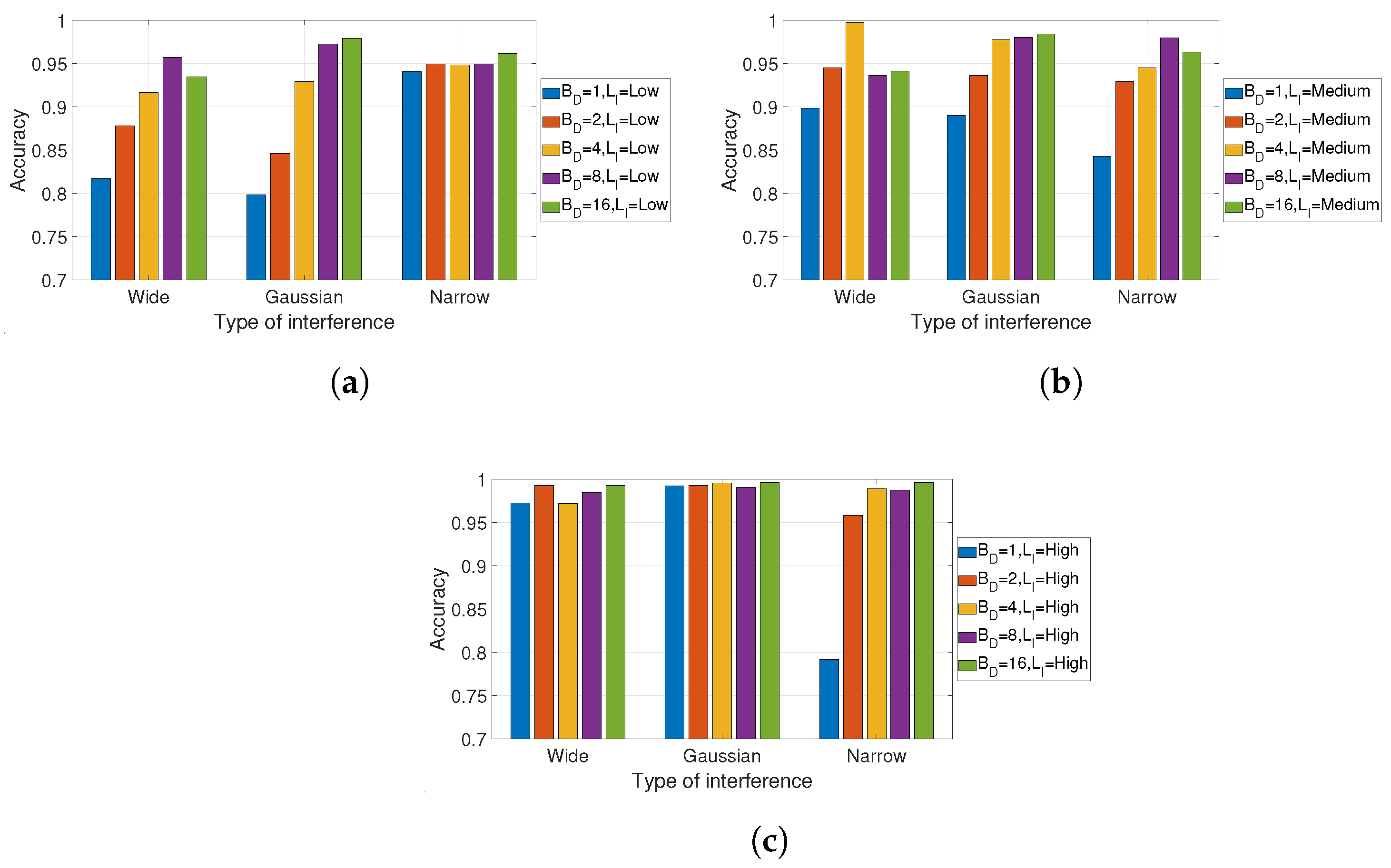
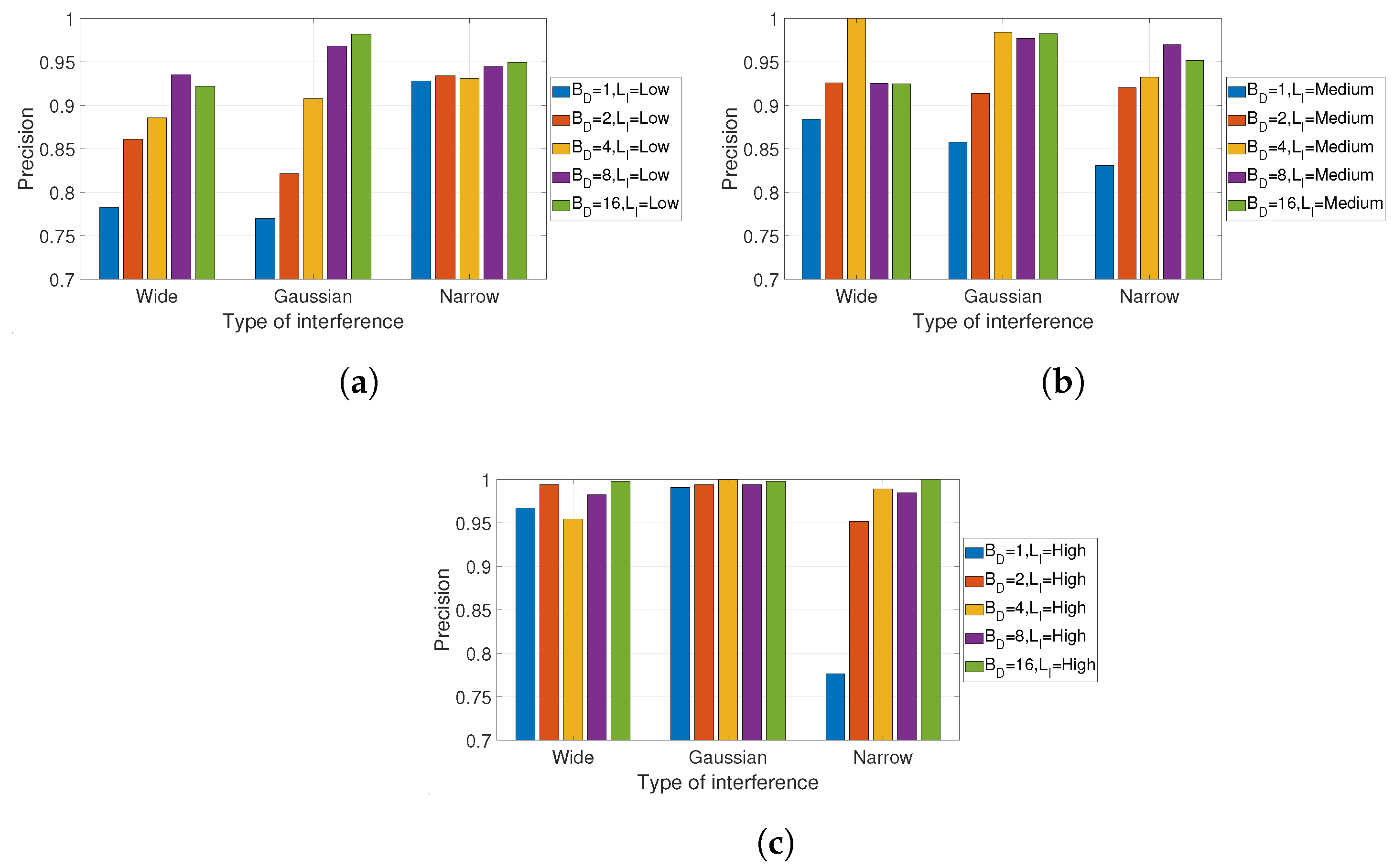
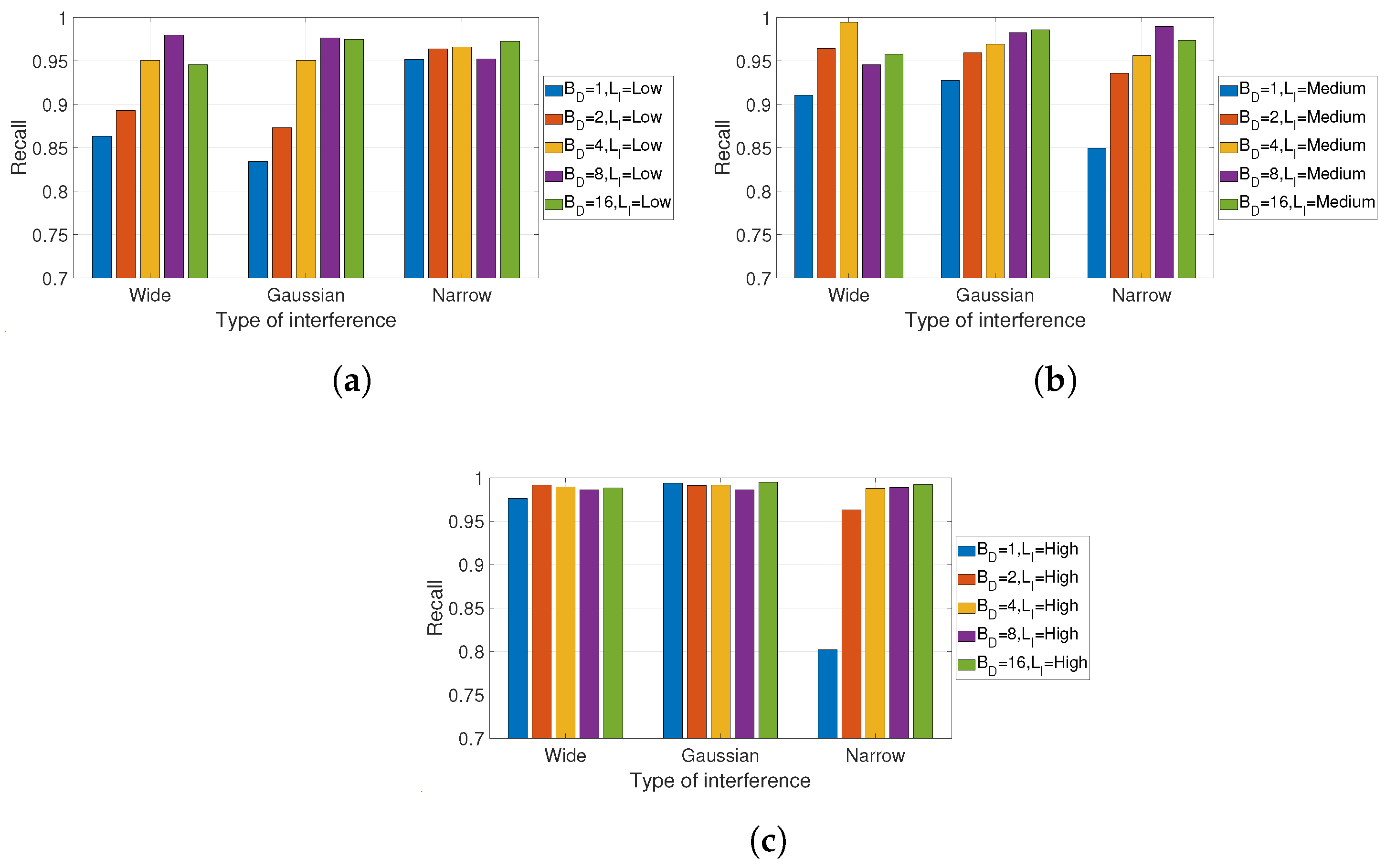
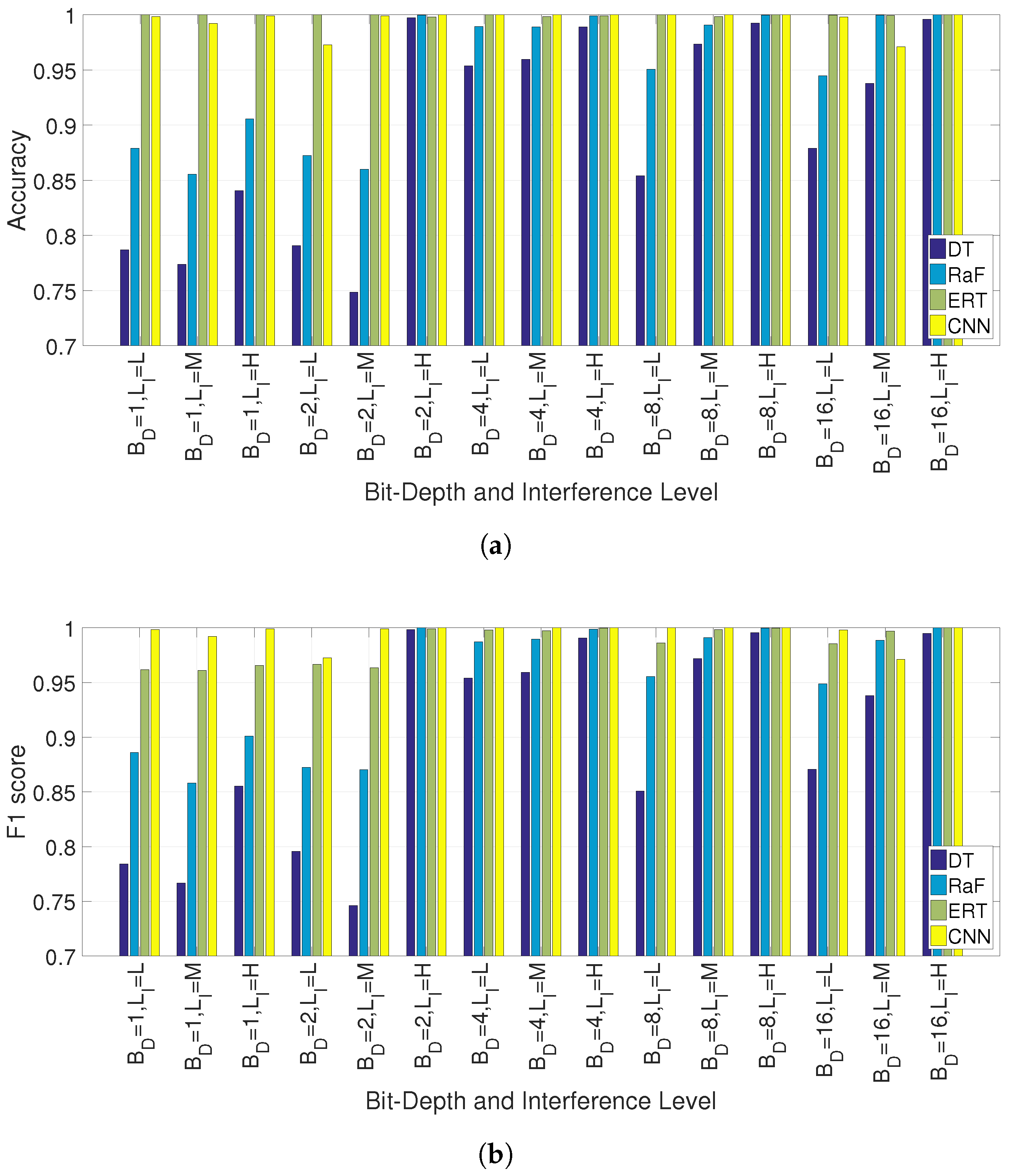
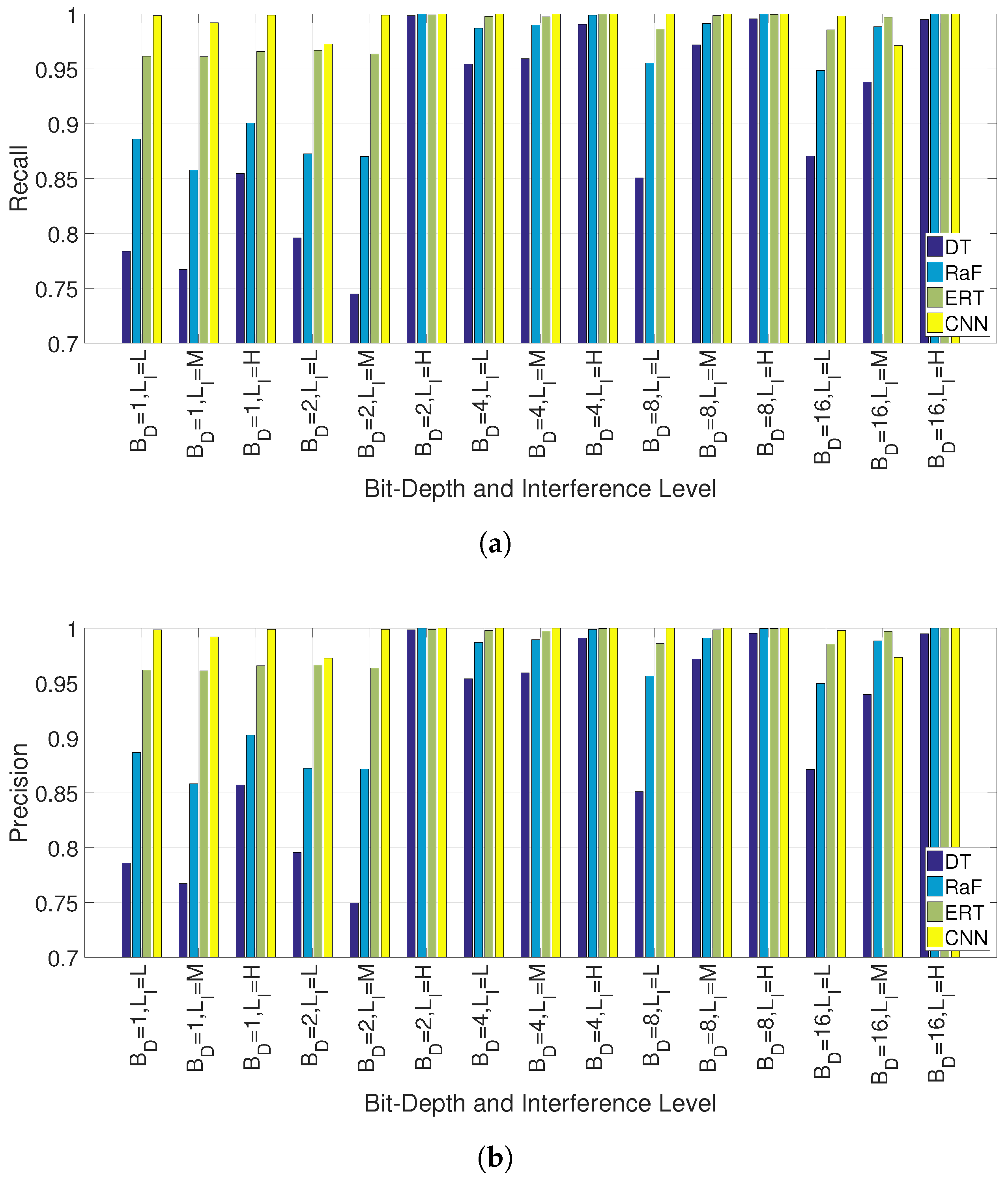
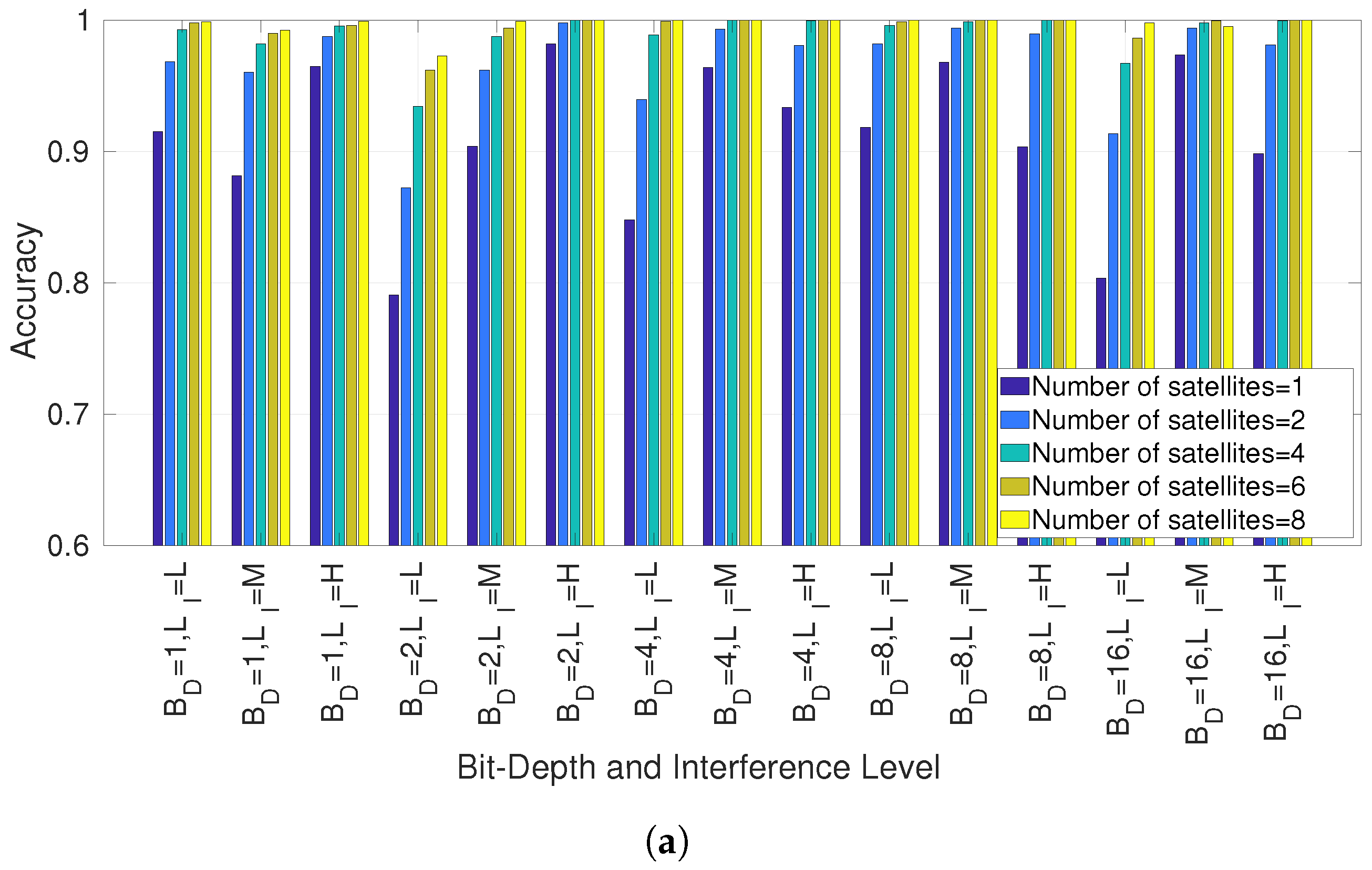
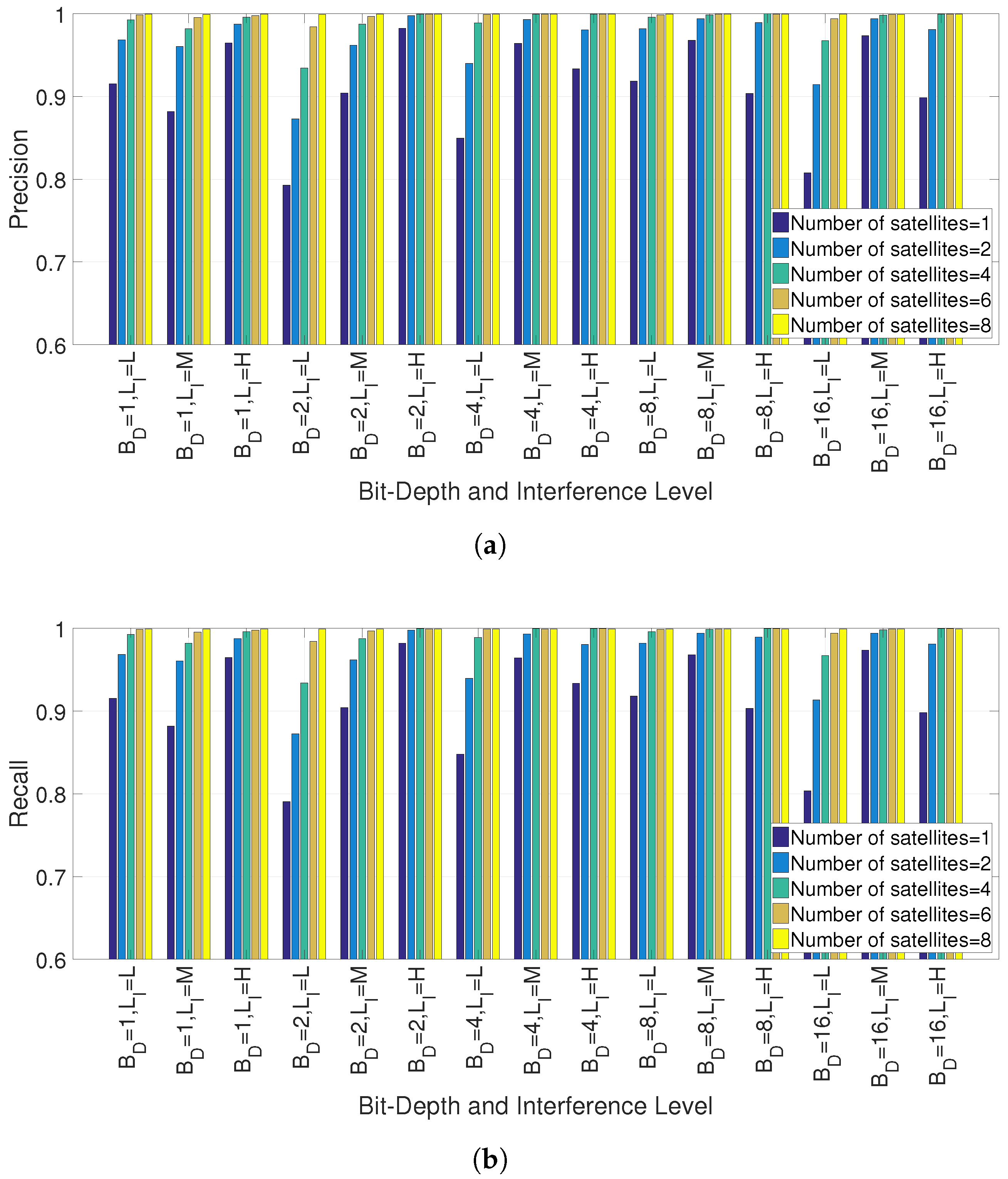
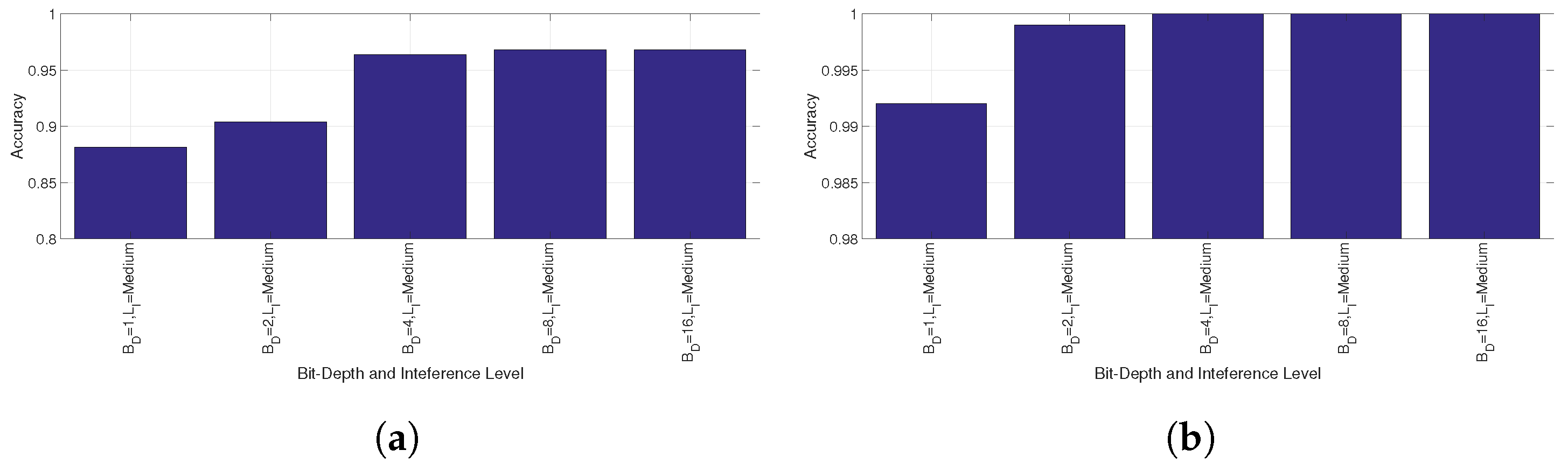
5.1. Detection of Interference
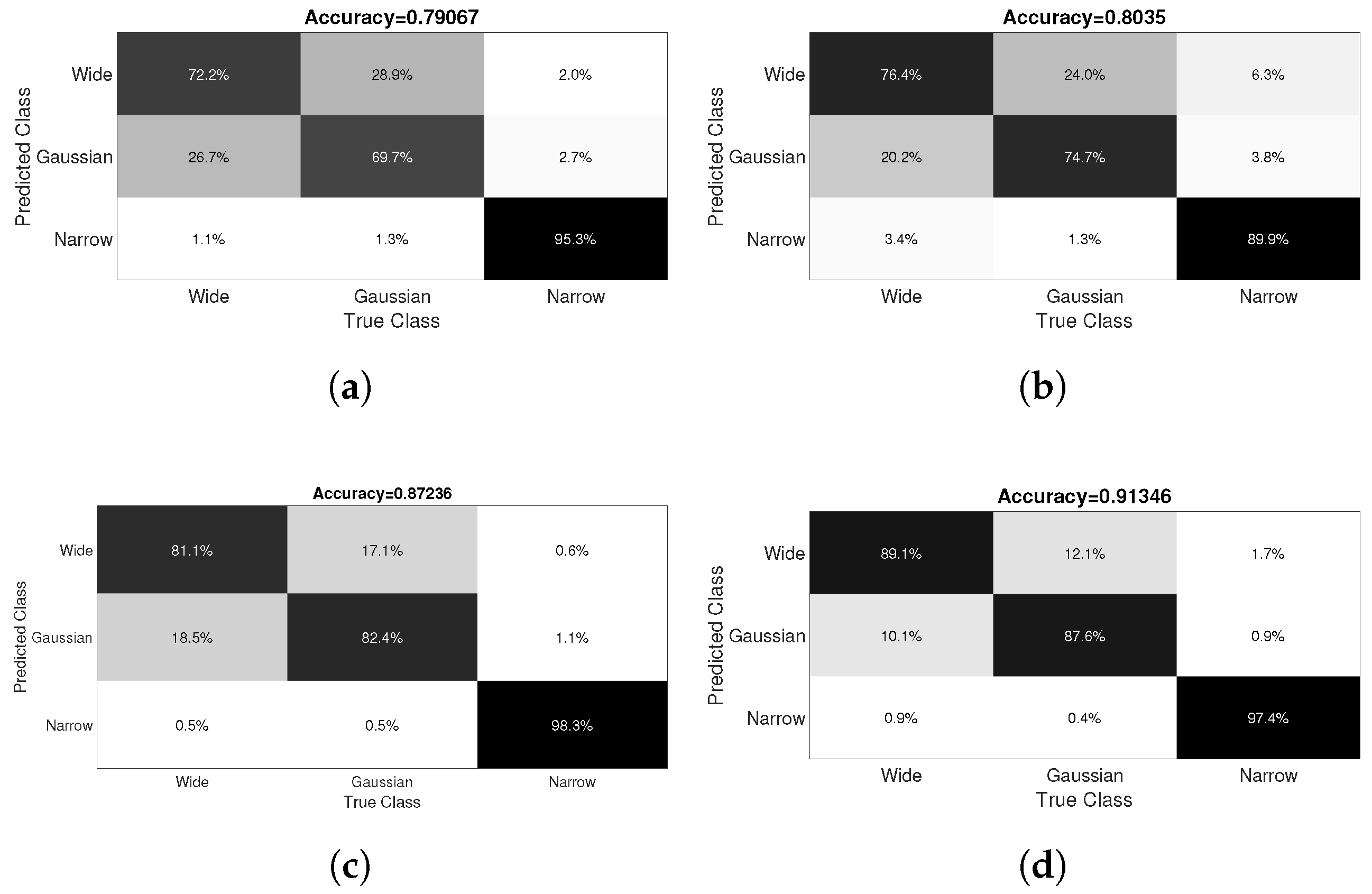
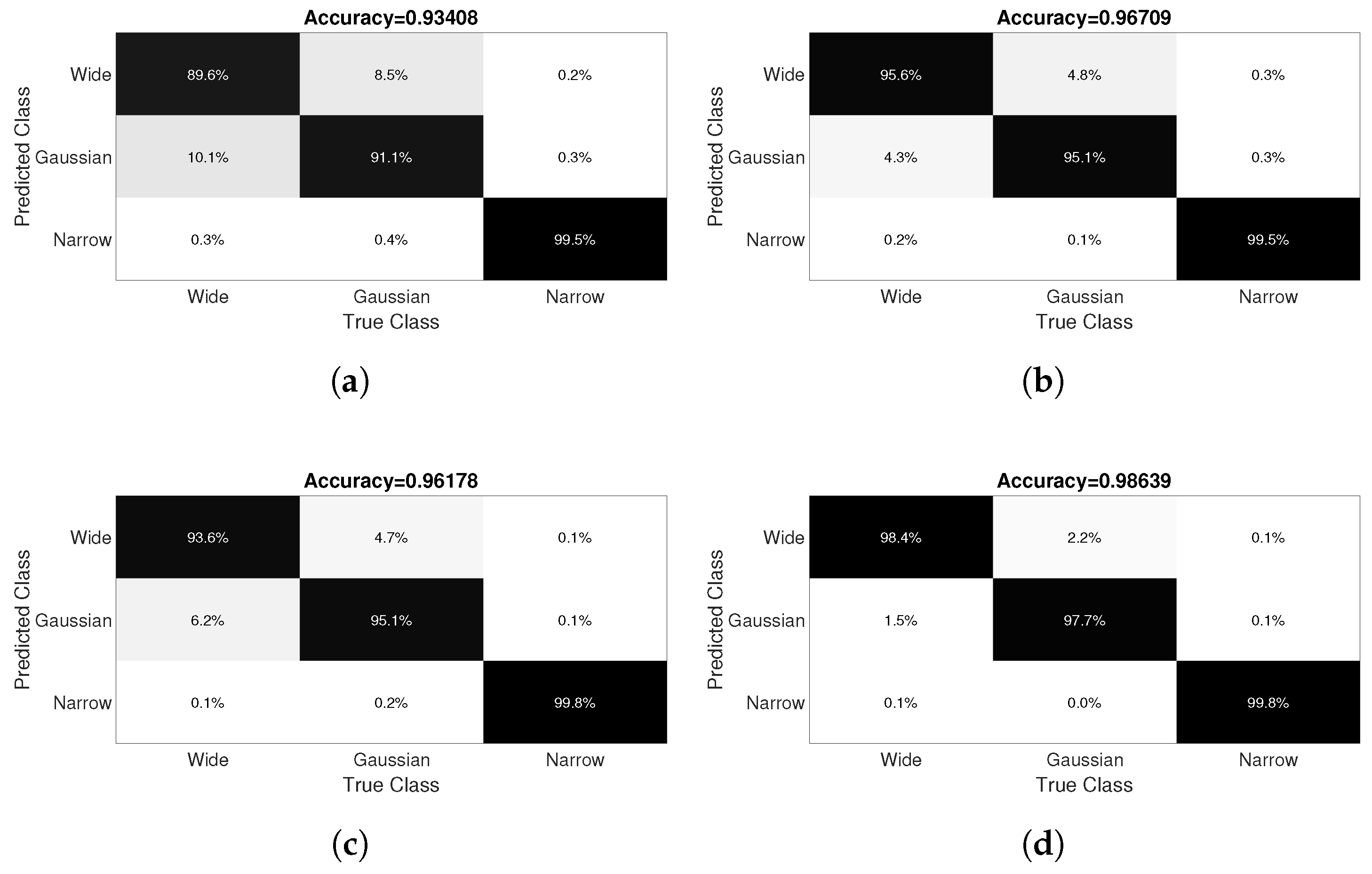
5.2. Classification of Interference
5.3. Discussion on the Limitations of the Proposed Approach
6. Conclusions and Future Developments
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Adam | Adaptive moment estimation |
| AGC | Automatic Gain Control |
| AWGN | Additive White Gaussian Noise |
| CNN | Convolutional Neural Network |
| CNR | Carrier-to-Noise Ratio |
| DC | Direct Current |
| DL | Deep Learning |
| ERT | Extremely Randomized Tree |
| FPGA | Field-Programmable Gate Array |
| GPS | Global Positioning System |
| GNSS | Global Navigation Satellite System |
| HDOP | Horizontal Dilution Of Precision |
| IF | Intermediate Frequency |
| IQ | in-phase (I) and quadrature (Q) |
| JRC | Joint Research Centre |
| LNA | Low Noise Amplifier |
| ML | Machine Learning |
| RFI | Radio Frequency Interference |
| SVM | Support Vector Machine |
| TF | Time Frequency |
| UHD | USRP Hardware Driver |
| USRP | Universal Software Radio Peripheral |
| VCO | Voltage-Controlled Oscillator |
| VDOP | Vertical Dilution Of Precision |
References
- Siemuri, A.; Selvan, K.; Kuusniemi, H.; Valisuo, P.; Elmusrati, M.S. A systematic review of machine learning techniques for GNSS use cases. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 5043–5077. [Google Scholar] [CrossRef]
- Dimc, F.; Bažec, M.; Borio, D.; Gioia, C.; Baldini, G.; Basso, M. An Experimental Evaluation of Low-Cost GNSS Jamming Sensors. Navig. J. Inst. Navig. 2017, 64, 93–109. [Google Scholar] [CrossRef]
- Zhong, W.; Xiong, H.; Hua, Y.; Shah, D.H.; Liao, Z.; Xu, Y. TSFANet: Temporal-Spatial Feature Aggregation Network for GNSS Jamming Recognition. IEEE Trans. Instrum. Meas. 2024, 73, 3375975. [Google Scholar] [CrossRef]
- Baldini, G.; Bonavitacola, F.; Chareau, J.M. Wireless Interference Identification with Convolutional Neural Networks based on the FPGA implementation of the LTE Cell Specific Reference Signal (CRS). IEEE Trans. Cogn. Commun. Netw. 2023, 10, 48–63. [Google Scholar] [CrossRef]
- Ma, J.; Zhang, J.; Xiao, L.; Chen, K.; Wu, J. Classification of power quality disturbances via deep learning. IETE Tech. Rev. 2017, 34, 408–415. [Google Scholar] [CrossRef]
- Li, W.; Huang, Z.; Lang, R.; Qin, H.; Zhou, K.; Cao, Y. A real-time interference monitoring technique for GNSS based on a twin support vector machine method. Sensors 2016, 16, 329. [Google Scholar] [CrossRef] [PubMed]
- Semanjski, S.; Muls, A.; Semanjski, I.; De Wilde, W. Use and validation of supervised machine learning approach for detection of GNSS signal spoofing. In Proceedings of the 2019 IEEE International Conference on Localization and GNSS (ICL-GNSS), Nuremberg, Germany, 4–6 June 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Wu, Z.; Zhao, Y.; Yin, Z.; Luo, H. Jamming signals classification using convolutional neural network. In Proceedings of the 2017 IEEE International Symposium on Signal Processing and Information Technology (ISSPIT), Bilbao, Spain, 18–20 December 2017; pp. 62–67. [Google Scholar] [CrossRef]
- Morales Ferre, R.; de la Fuente, A.; Lohan, E.S. Jammer classification in GNSS bands via machine learning algorithms. Sensors 2019, 19, 4841. [Google Scholar] [CrossRef]
- Pérez, A.; Querol, J.; Park, H.; Camps, A. Radio-frequency interference location, detection and classification using deep neural networks. In Proceedings of the IGARSS 2020—2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 6977–6980. [Google Scholar] [CrossRef]
- Brieger, T.; Raichur, N.L.; Jdidi, D.; Ott, F.; Feigl, T.; van der Merwe, J.R.; Rügamer, A.; Felber, W. Multimodal learning for reliable interference classification in GNSS signals. In Proceedings of the International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2022), Denver, CO, USA, 19–23 September 2022; pp. 19–23. [Google Scholar] [CrossRef]
- Guo, C.; Tu, W. GNSS interference signal recognition based on deep learning and fusion time-frequency features. In Proceedings of the 34th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2021), St. Louis, MI, USA, 20–24 September 2021; pp. 855–863. [Google Scholar] [CrossRef]
- Mehr, I.E.; Dovis, F. Detection and classification of GNSS jammers using convolutional neural networks. In Proceedings of the 2022 IEEE International Conference on Localization and GNSS (ICL-GNSS), Tampere, Finland, 7–9 June 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Ding, M.; Chen, W.; Ding, W. Performance analysis of a normal GNSS receiver model under different types of jamming signals. Measurement 2023, 214, 112786. [Google Scholar] [CrossRef]
- Taylor, L.; Nitschke, G. Improving deep learning with generic data augmentation. In Proceedings of the 2018 IEEE Symposium Series on Computational Intelligence (SSCI), Bangalore, India, 18–21 November 2018; pp. 1542–1547. [Google Scholar] [CrossRef]
- Hernández-García, A.; König, P. Further advantages of data augmentation on convolutional neural networks. In Proceedings of the Artificial Neural Networks and Machine Learning–ICANN 2018: 27th International Conference on Artificial Neural Networks, Rhodes, Greece, 4–7 October 2018; Proceedings, Part I 27. Springer: Berlin/Heidelberg, Germany, 2018; pp. 95–103. [Google Scholar] [CrossRef]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely randomized trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef]
- Spirent. Testing Infinity: Bringing Realism into Your GNSS Testing with RF Record and Playback. 2022. Available online: https://www.spirent.com/ (accessed on 12 February 2025).
- Cucchi, L.; Fortuny, J.; Baldini, G.; Fernandez-Hernandez, I.; Martinez, B.; Vecchione, G. A GNSS Jamming/Spoofing Test Suite for Smart Tachograph Applications. In Proceedings of the 33rd International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2020), Virtual, 22–25 September 2020; pp. 1490–1514. [Google Scholar] [CrossRef]
- Kubo, N.; Kobayashi, K.; Furukawa, R. GNSS multipath detection using continuous time-series C/N0. Sensors 2020, 20, 4059. [Google Scholar] [CrossRef] [PubMed]
- Yozevitch, R.; Moshe, B.B.; Weissman, A. A robust GNSS los/nlos signal classifier. Navig. J. Inst. Navig. 2016, 63, 429–442. [Google Scholar] [CrossRef]
- Xu, H.; Angrisano, A.; Gaglione, S.; Hsu, L.T. Machine learning based LOS/NLOS classifier and robust estimator for GNSS shadow matching. Satell. Navig. 2020, 1, 15. [Google Scholar] [CrossRef]
- Chen, J.; Wang, J.; Zheng, S.; Liu, Y.; Li, Z.; Xie, S.; Wang, Q. Improving NLOS/LOS Classification Accuracy in Urban Canyon Based on Channel-Independent Patch Transformer with Temporal Information. In Proceedings of the 2024 International Technical Meeting of the Institute of Navigation, Long Beach, CA, USA, 23–25 January 2024; pp. 869–882. [Google Scholar]





| CNN Parameter | Value |
|---|---|
| Width, filter size, and number of filters of the 1st convolutional layer | 16, 16, 32 |
| Width, filter size, and number of filters of the 2nd convolutional layer | 8, 8, 16 |
| 1st pooling layer | Max pooling (4,4) with Stride (2,2) |
| 2nd pooling layer | Max pooling (2,2) with Stride (2,2) |
| Activation functions | REctified Linear Unit (RELU) |
| Number of heads in the attention layer | 8 |
| Number of channels for keys and queries in the attention layer | 64 |
| Maximum number of epochs | 30 |
| Interference Type | = H (High) Attenuation Value | = M (Medium) Attenuation Value | = L (Low) Attenuation Value |
|---|---|---|---|
| Gaussian Noise | 10 dB | 20 dB | 30 dB |
| Wideband Chirp | 10 dB | 20 dB | 30 dB |
| Narrowband Chirp | 0 dB | 5 dB | 10 dB |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baldini, G.; Bonavitacola, F. A Machine Learning Evaluation of the Impact of Bit-Depth for the Detection and Classification of Wireless Interferences in Global Navigation Satellite Systems. Electronics 2025, 14, 1147. https://doi.org/10.3390/electronics14061147
Baldini G, Bonavitacola F. A Machine Learning Evaluation of the Impact of Bit-Depth for the Detection and Classification of Wireless Interferences in Global Navigation Satellite Systems. Electronics. 2025; 14(6):1147. https://doi.org/10.3390/electronics14061147
Chicago/Turabian StyleBaldini, Gianmarco, and Fausto Bonavitacola. 2025. "A Machine Learning Evaluation of the Impact of Bit-Depth for the Detection and Classification of Wireless Interferences in Global Navigation Satellite Systems" Electronics 14, no. 6: 1147. https://doi.org/10.3390/electronics14061147
APA StyleBaldini, G., & Bonavitacola, F. (2025). A Machine Learning Evaluation of the Impact of Bit-Depth for the Detection and Classification of Wireless Interferences in Global Navigation Satellite Systems. Electronics, 14(6), 1147. https://doi.org/10.3390/electronics14061147







