Abstract
In view of the future of the Internet of Things (IoT), the number of edge devices and the amount of sensing data and communication data are expected to increase exponentially. With the emergence of new computing-intensive tasks and delay-sensitive application scenarios, terminal devices need to offload new business computing tasks to the cloud for processing. This paper proposes a joint transmission and offloading task scheduling strategy for the edge computing-enabled low Earth orbit satellite networks, aiming to minimize system costs. The proposed system model incorporates both data service transmission and computational task scheduling, which is framed as a long-term cost function minimization problem with constraints. The simulation results demonstrate that the proposed strategy can significantly reduce the average system cost, queue length, energy consumption, and task completion rate, compared to baseline strategies, thus highlighting the strategy’s effectiveness and efficiency.
1. Introduction
Traditional terrestrial networks, like 5G, rely on base stations as their fundamental units of operation. These stations enable the delivery of real-time and rapid services [1]. Nonetheless, terrestrial network deployment faces certain challenges. Primarily, the reach of terrestrial base stations is limited, making it difficult to establish them in regions such as deserts, forests, or mountains. Additionally, terrestrial base stations are susceptible to natural disasters. When events like typhoons, tsunamis, and earthquakes damage these stations, communication systems can fail, and restoring them swiftly is challenging, which leads to severe societal and economic disruptions due to interrupted communications. Consequently, satellite communication systems, especially the low Earth orbit (LEO) satellite networks, offer a flexible deployment option with global coverage, effectively complementing terrestrial networks [2,3]. In densely populated regions, satellite communication networks can provide substantial support, utilizing their resources for communication, computing, and storage to ease the burden on terrestrial systems. In locales where terrestrial networks are unable to reach, satellite networks can assume the role of transmitting information, thus complementing the terrestrial networks [4].
In the forthcoming era of the Internet of Things (IoT), achieving global connectivity and intelligence will lead to an exponential increase in the number of edge devices and the volume of sensing and communication data. Traditional centralized cloud networks will no longer be able to efficiently process the massive amounts of data generated by the IoT [5,6]. The advent of augmented reality, enhanced reality, high-definition live streaming, and other novel application scenarios further accentuates this challenge. Limitations in terminal computing power and navigation capabilities may result in suboptimal user experiences, such as the inability to interact in real time. Mobile Edge Computing (MEC), a pivotal technology in fifth-generation mobile communications, addresses these issues by decentralizing resources from central devices to network edge devices. This enables edge devices to possess certain computing capabilities for processing user requests locally, providing users with low-latency, high-bandwidth data processing services. Consequently, MEC alleviates the pressure on core network resources and effectively resolves problems such as data traffic bottlenecks in the core network [7,8,9].
In traditional satellite communication systems, satellites usually act as relays for transferring data from user devices. With the emergence of new computing-intensive tasks and delay-sensitive application scenarios, terminal devices need to offload new business computing tasks to the cloud for processing. However, the traditional mode of uploading data to the cloud for processing cannot meet the current computing-intensive business needs in terms of low latency and high bandwidth transmission. Therefore, the integration of satellite communication and edge computing is the development trend of future satellite networks. Moreover, LEO satellite communication systems inherently offer low-latency communication due to their proximity to the Earth’s surface and typically orbit at altitudes between 500 and 2000 km [10]. This close proximity significantly reduces the signal propagation delay compared to Geostationary Earth Orbit (GEO) satellites, which orbit at approximately 35,786 km. As a result, LEO satellites can achieve round-trip signal latencies as low as 20–30 ms, making them suitable for real-time and delay-sensitive applications [10,11]. The deployment of LEO satellite constellations enhances communication reliability through redundant coverage and seamless handover capabilities.
These low-latency and high-reliability characteristics of satellite communication systems, combined with edge computing and storage resources deployed on satellites, can provide users with strong computing and storage resource support [12,13,14]. This can significantly reduce data transmission between the edge and the central cloud, reduce delay, and lower energy consumption. In addition, with the increasing demand for computing and storage resources in new application scenarios, satellite edge computing can provide strong computing and storage resource support for new applications.
By integrating MEC technology with LEO satellite communication networks, satellites not only can receive and forward tasks to ground stations but also deploy MEC servers onboard, enabling LEO satellites to possess computing and storage resources. This is crucial for expanding service capabilities. Considering the characteristics of the LEO satellite communication networks and MEC technology, their integration can fully utilize the flexible satellite chain routes of LEO communication networks for efficient transmission [14]. Additionally, by deploying satellite servers, we can meet the needs of end users for faster, better, and safer applications. Therefore, building a LEO satellite edge computing network is an inevitable trend in the development of communication networks [15]. In our initial result [16], integrating edge computing technology with LEO networks can significantly reduce the service response time of LEO satellites, enhance the autonomous task processing capabilities of satellites, and improve network performance. Moreover, dynamic task offloading and transmission scheduling are critical for optimizing performance in satellite networks as they must adapt to various dynamic factors such as fluctuating user demand, the movement of satellites, changes in network topology, and environmental conditions. This adaptability ensures that tasks are efficiently offloaded to the most suitable resources in real time, thereby enhancing overall system performance and responsiveness.
The existing challenges of latency issues and bandwidth allocation must be addressed to improve system optimization. Although satellite networks are known for their low latency advantages, certain applications may still experience latency issues, especially when bandwidth is constrained during peak usage periods. Effective bandwidth allocation is crucial as it directly influences task processing speed and response times. Furthermore, optimizing bandwidth is essential in enhancing resource utilization efficiency, which ultimately contributes to better overall system performance. The LEO satellite systems integrated with edge computing need to communicate through satellites and ground stations, and there is a certain signal transmission delay between satellites and ground stations. This delay may adversely affect real-time applications and tasks that require rapid data processing; the bandwidth of satellite communications is relatively limited and insufficient for supporting large-scale data transmission and processing needs. This means that bottlenecks may be encountered when processing large-scale data sets and performing complex computing tasks; the LEO satellite systems integrated with edge computing require a large amount of energy supply to support their computing and communication needs. However, current solar battery technology and battery capacity limitations restrict the energy supply capacity of satellite systems. This may lead to the system being unable to meet the needs of high-intensity computing tasks. Additionally, satellite systems still face difficulties in maintenance and updates, as well as high costs.
The major contributions of this paper are as follows:
- This paper proposes a novel integration of Mobile Edge Computing (MEC) technology with LEO satellite communication networks while comprehensively considering constraints such as onboard computing and transmission, satellite–ground and inter-satellite links, and traffic conservation.
- This paper formulates the problem of efficient task offloading in the integrated LEO satellite edge computing network. It defines a cost function based on caching and energy consumption and models the dynamic task offloading and transmission scheduling problem as a constrained long-term cost function minimization problem.
- The original optimization problem is divided into two key components: data task transmission scheduling and computation task offloading. The data task transmission scheduling problem focuses on determining the most efficient routes for data transmission from observation satellites to ground stations, utilizing Dijkstra’s algorithm to identify the shortest paths while accounting for energy consumption. In contrast, the computation task offloading and computation scheduling problem is modeled as a Markov Decision Process (MDP), where dynamic factors such as the arrival of IoT device tasks and the status of relay satellite buffers are considered. This approach enables the application of reinforcement learning techniques, specifically the Deep Q-Network (DQN) algorithm, to develop optimal strategies for task offloading and computation scheduling, which minimize long-term system costs under varying conditions.
- Extensive simulations are performed to evaluate the proposed scheme compared with the existing peers.
The rest of the paper is organized as follows. Section 2 presents an overview of related work. Section 3 describes the system model, and Section 4 formulates the joint transmission, task offloading, and computation scheduling problem. The proposed schemes are introduced in Section 5. Simulation results are presented in Section 6. Finally, we conclude this paper in Section 7.
2. Related Works
This section outlines the current research related to task offloading and resource scheduling in LEO satellite networks.
2.1. Task Offloading in LEO Satellite Networks
In scenarios involving task offloading in LEO satellite networks, references [17,18] suggest energy-efficient algorithms for task offloading. The work in [17] examines a ground network supported by LEO satellites and offers a cloud–edge collaborative offloading strategy that accounts for service quality constraints, facilitating efficient energy offloading within a satellite network. It provides separate solutions utilizing deep reinforcement learning and game theory. Meanwhile, Ref. [18] explores a hybrid cloud–edge LEO satellite computing network with a three-layer structure, focusing on reducing total energy consumption for ground users. This research applies game theory to devise task offloading strategies for each ground user.
Studies [19,20,21] introduce algorithms that optimize delay in task offloading. Ref. [19] presents a network architecture integrating space and ground components to deliver edge computing services to LEO satellites and UAVs, focusing on reducing task execution delays through deep reinforcement learning for offloading decisions. Ref. [20] examines task offloading challenges within modern small satellite systems, proposing a strategy that optimizes delay while offloading and dismantling tasks. For satellite relay computing, Ref. [21] suggests a collaborative computing approach between satellite and ground to specifically reduce task response delays.
Other works [22,23,24,25] focus on creating energy-efficient and delay-optimized strategies for task offloading. Ref. [22] analyzes the time delays inherent in satellite–ground communications within relay computing scenarios, proposing a heuristic search algorithm to balance the computational load and reduce system energy consumption and task execution delay. Ref. [23] introduces a task offloading method employing a heuristic search algorithm specifically to lower both energy consumption and task execution delay for ground users. Ref. [24] also focuses on modern small satellite systems, suggesting a delay-optimized strategy for both offloading and dismantling tasks. Ref. [25] proposes a local search matching algorithm to determine the optimal task offloading strategy, targeting a reduction in energy usage and delay for ground users.
2.2. Resource Scheduling Algorithms for LEO Satellite Networks
The works of [26,27,28] examine the challenge of satellite transmission delays. Specifically, Ref. [26] explores the use of ground stations, high-altitude platforms, and LEO satellites to offer data offloading services to ground users. Meanwhile, Ref. [27] investigates using satellite chains for data offloading to ground stations, suggesting optimization algorithms to enhance the download throughput of data at these stations and for data transfer among cooperative satellites and from satellites to ground stations. Ref. [28] develops a transmission scheduling algorithm to maximize bandwidth usage in satellite constellations by enhancing inter-satellite link capacity. Furthermore, Ref. [29] examines the integration of LEO satellite networks with terrestrial networks, proposing a matching algorithm aimed at maximizing data transmission rates and user access, factoring in various capacity constraints.
Additionally, Refs. [30,31,32,33] delve into the scheduling of computing and storage resources in LEO satellite networks. For instance, Ref. [30] introduces a hybrid satellite–ground network utilizing software-defined networking, focusing on optimizing the long-term usage efficiency of communication, storage, and computing resources despite variable network, storage, and computing states, employing deep Q-learning algorithms for joint resource allocation optimization. Ref. [31] considers LEO satellites equipped with MEC platform computing and storage resources, proposing a service request scheduling approach to optimize resource use and service quality while reducing system costs. Ref. [32] suggests a strategy for satellite network storage resource scheduling to maintain user experience quality, and Ref. [33] explores the joint optimization of wireless resource allocation and task offloading in satellite networks to leverage the computing power of edge nodes effectively.
2.3. Task Offloading and Resource Scheduling Algorithms for LEO Networks
In addressing the challenges of task offloading and resource scheduling within LEO network environments, Ref. [34] examines the varying aspects of task segmentation and the energy priorities of edge devices. The study introduces an energy-efficient task offloading and resource scheduling algorithm to minimize both overall delay and energy usage.
Studies [35,36] put forward joint task offloading and resource scheduling algorithms leveraging deep reinforcement learning. Specifically, Ref. [35] employs a distributed algorithm grounded in convex optimization to tackle the task offloading and resource scheduling issue, recasting it as a direct optimization problem of computing resource scheduling for LEO satellites and simulating the system to maintain high energy efficiency. Meanwhile, Ref. [36] utilizes a deep reinforcement learning approach for resource allocation, addressing task offloading to the edge device and task segmentation issues, and applies a deep reinforcement learning strategy to identify the optimal offloading approach to minimize delay and energy consumption at the edge device.
Moreover, Refs. [37,38] suggest joint task offloading and resource scheduling frameworks using deep reinforcement learning. For instance, Ref. [37] proposes an integrated strategy for computing resource allocation and task offloading that adapts to dynamic changes in the network environment to enhance energy efficiency long-term, employing deep reinforcement learning to modulate the offloading strategy dynamically. Meanwhile, Ref. [38] evaluates LEO network architecture with edge computing, focusing on minimizing user task processing delay and energy use at the edge node, and proposes a comprehensive strategy for task offloading and computing resource scheduling to achieve long-term reductions in delay and energy consumption. Furthermore, Ref. [39] considers dynamic shifts in the locations of edge devices, satellites, and the network setting, using a deep reinforcement learning algorithm to optimize user association, offloading, computing, and communication resource allocation strategy for minimal long-term delay and energy use. Additionally, Ref. [40] presents a joint task offloading and resource scheduling strategy tailored for LEO edge computing aimed at minimizing system costs, with simulation outcomes indicating that the proposed strategy can notably decrease the average system cost.
Despite significant advancements in LEO satellite task offloading research, there remains a substantial gap in fully leveraging satellite collaboration for efficient resource utilization. Existing studies, summarized in the Table 1, primarily focus on optimizing task execution delay and energy efficiency without accounting for the dynamic nature of LEO networks and the potential of satellite cooperation. To address these gaps, our research makes the following unique contributions. We propose a groundbreaking integration of Mobile Edge Computing (MEC) technology with LEO satellite communication networks. This integration considers unique constraints such as onboard computing capabilities, satellite–ground and inter-satellite link capacities, and traffic conservation laws, which have not been collectively addressed in prior works.

Table 1.
Comparison of related works on task offloading in LEO satellite networks.
3. System Model
This section considers the system model comprising the network model, task and computation model, transmission service model, and link transmission rate model.
3.1. Network Model
The proposed LEO satellite network includes N observation satellites, K relay satellites, M IoT devices, and a ground station. Observation satellites equipped with sensors and instruments to collect data from the Earth’s surface, such as imagery or environmental measurements, focus on data acquisition and initial data processing [41,42]. Relay satellites are defined as satellites that facilitate communication by receiving data from observation satellites or IoT devices [43,44] and forwarding it to other satellites, ground stations, or processing nodes. They possess greater computational and communication capabilities to handle data relay and task offloading.
In this paper, we distinguish between two types of information handled by satellites: data and tasks. Data refer to raw information transmitted or forwarded without additional processing, such as images relayed from an observation satellite to a ground station. Tasks, on the other hand, involve computational workloads where data need to be processed to extract useful insights. For example, an IoT sensor may collect temperature readings, which require analysis to detect anomalies. In our model, if data only require transmission, we classify it as ‘data’; if computation is required, we classify it as a ‘task’.
When direct communication between an observation satellite and the ground station is not possible due to their relative positions, observation satellites gather data from the Earth’s surface and transmit it to relay satellites, which then relay the data to the ground station cache. For example, the data can be raw or processed information, such as images, sensor readings, and measurements that need to be transmitted to ground stations. Computational tasks may originate from IoT devices and require offloading to relay satellites for processing due to limited device capabilities. IoT devices create computational tasks and transmit them either to relay satellites or directly to the ground station for processing. Computational tasks encompass processing activities generated by IoT devices or satellites, requiring computational resources to execute functions like data analysis, image processing, and complex calculations. Accordingly, IoT devices establish connections with relay satellites through an association process, where each device selects an appropriate relay satellite for communication and task offloading based on factors such as signal quality, available resources, and connectivity status.
Let denote the n-th observation satellite, denote the k-th relay satellite with a computational capacity of , and denote the m-th IoT device. Each relay satellite’s sub-channel offers a bandwidth of B, allowing multiple IoT devices to connect with relay satellites via Orthogonal Frequency Division Multiple Access (OFDMA) technology. The specific system layout is depicted in Figure 1.
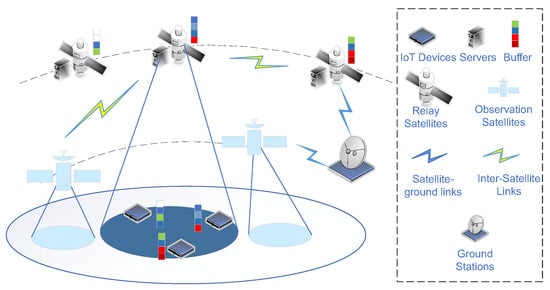
Figure 1.
System model.
In the dynamic LEO satellite scenario explored in this paper, to more clearly illustrate the system’s link dynamics, we consider that the system time T is divided into continuous intervals of duration . Given the nature of inter-satellite links in the LEO network, each LEO satellite is equipped with four interconnections with other satellites. The links between satellites within the same orbit are comparatively stable, while those between satellites in adjacent orbits achieve relative stability through steerable beam technology. Therefore, the inter-satellite network topology is assumed to remain stable. To describe the connection status of the inter-satellite communication links, we define as the physical link indicator between the observation satellite and the relay satellite . If , a physical link exists between and ; otherwise, . Similarly, represents the link indicator between relay satellites and , where indicates that a link exists, and indicates no link. The satellite-to-ground network topology is assumed to change with each time slot, yet it remains constant within a single time slot. To describe the satellite-to-ground link status, is used to indicate the existence of a physical link between the IoT device and the relay satellite at time slot t. Here, indicates a link exists, otherwise . Likewise, serves as the indicator for a link between the relay satellite and the ground station at time t, where symbolizes an existing link, and symbolizes its absence.
3.2. Task and Computation Model
Consider that the computational tasks for IoT devices arrive unpredictably during each time slot and conform to a Poisson distribution. Let signify the computational task that arrives at IoT device during time slot t. This task is characterized as , where denotes the size of the task , and indicates the CPU cycle count necessary to process each bit of data in the task , where signifies the typical task arrival rate for device .
Considering that IoT devices often have limited computational capabilities and constrained energy resources due to their compact size and design, they are not suited for processing computationally intensive tasks locally. Performing such tasks would result in significant delays and quickly deplete the device’s battery life. Therefore, rather than executing computational tasks themselves, IoT devices offload these tasks to relay satellites. Relay satellites possess enhanced processing power and energy availability, enabling them to handle tasks efficiently either through onboard computation or by forwarding tasks to ground stations for processing. This offloading strategy not only conserves the limited resources of IoT devices but also improves overall system performance by leveraging the capabilities of more powerful network nodes. Define as the variable indicating the transmission of task . A value of means that the task is sent to the relay satellite during time slot , while means it is not. Furthermore, let denote the decision variable for selecting the ground station offloading mode for task . If , it signifies that the relay satellite chooses the ground station mode for task during time slot , whereas indicates otherwise.
3.3. Transmission Service Model and Transmission Model
In the scenario outlined in this paper, observation satellites are tasked with continuously monitoring the ground and collecting data transmission services at the outset of system operations. Denote by the data collected by the observation satellite . Assume that, following data collection, an observation satellite is required to relay the data to the ground station through relay satellites in the following time slots. Define as the selection variable for satellite transmission relays concerning observation satellites. A value of indicates that the observation satellite sends data to relay satellite in time slot t, whereas indicates no transmission. Let represent the transmission selection variable between relay satellites. If , relay satellite forwards data to relay satellite in time slot t; otherwise, . Additionally, let be the variable for selecting the ground station transmission from relay satellites. If , the relay satellite transmits data to the ground station in the time slot t; if not, then .
3.4. Link Transmission Model
Define as the data rate between the IoT device and the satellite at time t:
Here, is the transmission power, and are antenna gains, is path loss, is rain attenuation, and is noise power. The antenna gains and free space path loss are critical components in the link budget analysis. They determine the signal-to-noise ratio (SNR) at the receiver, which in turn affects the achievable data rate as per Shannon’s capacity formula. Higher antenna gains improve the SNR, while larger path losses deteriorate it. According to Equation in [45], where c is the speed of light, is the distance, and f is the frequency.
Let represent the link rate between the relay satellite and the ground station in time slot t. It is given by the following:
where is the relay satellite’s transmission power to the ground station, is the transmission antenna gain, is the receiving antenna’s gain, denotes the rain attenuation, and indicates the free space loss, which is defined as follows: where is the distance between and the ground station during time slot t.
Let represent the link rate between the observation satellite and the relay satellite , which is given by Equation in [46]:
where is the observation satellite’s transmission gain, is the relay satellite’s receiving gain, is the power of , is the free space loss between and , is the Boltzmann constant, is the system noise temperature, is the energy per bit, and is the noise power spectral density. is the distance between and .
specifies the rate between the relay satellites and , which is given by the following:
where and are the relay satellite k’s transmission gain and ’s receiving gain, is the power for inter-satellite transmission, is the free space loss between and . is the distance between and .
4. Optimization Problem Modeling
This section first models the system’s cache queue and energy consumption then defines the system cost function based on the cache queue and energy consumption. Next, it considers constraints such as association and computation limitations to model the joint task offloading and resource scheduling problem as a long-term cost function minimization problem under these constraints.
The dynamic nature of LEO networks requires a flexible approach to resource scheduling. As the number of IoT devices and their corresponding tasks vary, our system dynamically schedules the transmission and computation resources to ensure efficient processing and transmission. Continuous assessment of the operational status of satellites and ground stations allows our framework to respond promptly to changes in network conditions. The quality of communication channels is monitored to optimize data transmission paths, ensuring reliable connectivity. The relationships between satellites are considered, allowing for adaptive scheduling based on the current inter-satellite network topology.
To effectively manage these dynamic factors, our resource scheduling strategy is designed to adapt in real time. By modeling the task offloading and computation scheduling processes as a Markov Decision Process (MDP), we enable our system to make informed decisions based on the current state of the network. This approach ensures that both the data transmission and computational tasks are scheduled efficiently, minimizing latency and maximizing throughput.
4.1. System Cache Queue Modeling
As the computational tasks for IoT devices appear unpredictably and are sent to relay satellites in successive time slots, it is necessary to model the computation task cache queue at the devices. Given that relay satellites might handle data transmission services, accept and transfer computational tasks, and perform onboard tasks in each time slot, it is important to model a queue at the relay satellites to illustrate the caching scenario. Inspired by the analysis and modeling in [47,48,49], we model the queueing as follows.
4.1.1. IoT Device Queues
Let represent the length of the task queue for computations at the IoT device during time slot t. The formula for updating the queue is given by the following:
where denotes the maximum allowable length of the cache queue for the IoT device and denotes the incoming data.
4.1.2. Relay Satellite Queues
Define as the queue size for the relay satellite at time t. The update equation for the queue at the satellite is given by the following:
Here, denotes the upper limit of the queue for ; is a binary task indicator for the satellite’s task execution. A value of 1 signals that processes the task at time t. The symbol stands for the computational capacity of , and indicates the workload associated with task for at t. The workload update is defined as follows:
Initially, for satellite is determined by the following:
Equation (8) implies that the task is considered empty when there are no incoming data from the IoT devices, and it reflects the total task size once task execution begins.
4.2. System Energy Consumption Model
Let denote the energy consumption for executing tasks at time t, comprising energy spent transmitting tasks from IoT devices to relay satellites, relay satellites computing tasks, and transmitting tasks to ground stations. The energy consumed by ground stations is neglected due to their ample power. is given by the following:
In Equation (9),
- is the energy to transmit a task from IoT device to relay at t;
- is the energy for to compute at t where is the energy coefficient for ;
- is the energy to send from to ground stations at t.
Define as the energy needed for data transmission at time t, incorporating data transfer from observation satellites to relay satellites, among relay satellites, and from relay satellites to ground stations. The formula for is
where the following holds:
- denotes the energy for observation satellite to send the data to the relay satellite at t;
- quantifies the energy for relay satellite to transmit the data to another relay satellite at t;
- defines the energy for to transmit the data to ground stations at t.
4.3. System Cost Model
The system cost function, denoted by U, takes into account both the task queue length and energy usage and is represented as follows:
Here, indicates the cost at each time t. The energy consumed, , includes computation and data transmission at time t, while reflects the system’s queue length at the same time. The parameters and prioritize energy and queue length, respectively.
4.4. Optimization Constraints
Considering transmission links, link availability, flow conservation, and other constraints, the optimization problem needs to satisfy the following constraints.
4.4.1. Transmission Link Constraints
This study assumes that, for any time t, each IoT device can link to only one relay satellite, which is expressed as follows:
Similarly, at any given t, each observation satellite is restricted to a connection with a single relay satellite, which is expressed as follows:
For the relay satellites, at any moment t, data transfer is limited to transmitting from one observation satellite. This is denoted by the following:
Further, at any point in time t, each relay satellite can only facilitate the transmission of data from one observation satellite within a single relay transfer:
Finally, each relay satellite is also constrained to transmitting data from a single observation satellite to the ground station. This is defined by the following:
4.4.2. Link Availability
IoT devices can transmit computational tasks to relay satellites only when connectivity is established, which is defined by
where is an indicator function that returns 1 if x is true and 0 otherwise. Similarly, relay satellites can relay data to ground stations only with an active link:
For data transfer from observation satellites to relay satellites, a valid connection is necessary:
Finally, data can only be exchanged between relay satellites if they are interconnected:
The term ‘x’ serves as an indicator of link availability between IoT devices and satellites. When , it signifies that the link is not available; thus, the transmission variables must be set to zero, reflecting the inability to transmit data. This is supported by the indicator function, which will yield a value of 1 under these circumstances. Conversely, if , which indicates an available link, the transmission variables can assume non-zero values, allowing for data communication. This logical structure ensures that our model accurately represents the conditions of link availability within the network.
4.4.3. Task Computation
Given that the relay satellite initiates computing tasks only when all tasks have been transmitted and that they process just one task in each time slot, we have
4.4.4. Flow Conservation
In the transmission of user data via inter-satellite and satellite-to-ground communications, it is essential to adhere to flow conservation laws for both observation and relay satellites. The flow conservation constraint for an observation satellite is defined by the following:
Equation (24) ensures that each observation satellite (where n is the index of the satellite) must transmit its data to exactly one relay satellite within the time frame . The summation over k (relay satellites) and t (time slots) ensures that the total number of transmissions initiated by each observation satellite equals 1. This reflects the principle that each observation satellite must transmit its data to exactly one relay satellite during the defined time horizon, maintaining data flow from observation satellites to relay satellites.
For a relay satellite handling the data , the constraint is formulated as follows:
Equation (25) enforces the principle of flow conservation at each relay satellite for data originating from a given observation satellite . It ensures that the total incoming data flow into the relay satellite equals the total outgoing data flow from , preserving the continuity of the data flow within the network. The left-hand side represents the total incoming flow into the relay satellite , which includes data directly transmitted from the observation satellite and relayed from other relay satellites. The right-hand side represents the total outgoing flow from the relay satellite , which includes data relayed to the other relay satellite and transmitted to the ground station.
Equations (24) and (25) embody the principle of flow conservation, stating that for any given node in the network, the total data inflow must equal the total data outflow. This principle is vital for maintaining the integrity and efficiency of data transmission within the satellite network. By applying this conservation principle, we ensure that our model accurately tracks data movement and resource utilization across the network, thereby facilitating optimal routing and task offloading strategies.
4.5. Optimization Model
Considering constraints such as link availability and computation limitations, the optimization model for the joint dynamic task offloading and transmission scheduling problem based on the long-term cost function minimization under the constraints is the following:
where is the set of all variables.
5. Proposed Schemes for Joint Task Offloading and Transmission Scheduling
Solving the long-term cost minimization problem modeled in (26) involves dynamic task offloading and computation scheduling strategies for observation satellite data tasks, IoT device computation tasks, and inter-satellite network topology stability. The original optimization problem is divided into data task transmission scheduling and computation task offloading and scheduling problems. For the data task transmission scheduling problem, a transmission scheduling strategy based on Dijkstra’s algorithm [50] is proposed. For the dynamic task offloading and scheduling problem, considering the Markov decision process, a deep learning method is adopted to propose a dynamic task offloading and scheduling strategy based on DQN.
5.1. Data Task Transmission Scheduling
This section models and addresses the data task transmission scheduling issue, aiming to devise a transmission strategy. Assuming a static inter-satellite network topology, the problem is simplified to a directed shortest path with weighted edges. Dijkstra’s algorithm is utilized to find the shortest routes from observation satellites to the ground station. To solve the capacity limitations of relay satellites, an enhanced scheduling strategy is introduced. Excluding conflicts among relay satellites, a scheduling strategy for observation satellites maps the data transmission route to ground stations. The link weights, determined by energy consumption, help model this as a directed shortest path problem. Let be the cumulative energy expenditure from to the ground station, which is represented by the following:
Here, denotes the link weight between the observation satellite and relay satellite , the link weight for the data between the relay satellites and , and the link weight for the data from the relay satellite to the ground station at time t. These weights are computed as follows.
From (28), it is observed that greater transmission energy reduces link weight. The shortest path problem between the observation satellite and the ground station is modeled as follows:
The inter-satellite link’s state over time is modeled by representing the ground station as T nodes, , with . At each time t, link weights to relay satellites depend on link conditions. Using Dijkstra’s algorithm [50] for shortest path calculations, super nodes are employed, and virtual ground station nodes have link weights set to zero. Specifically, to model the time-varying nature of the satellite–ground links, we represent the ground station as a set of virtual nodes for each time slot t. Each virtual ground station node corresponds to the ground station at time t, capturing the link availability and conditions at that specific time. To facilitate the application of Dijkstra’s algorithm, we introduce a ‘super node’. The super node serves as a single common destination node and is connected to all virtual ground station nodes with edges of zero weight. This construction ensures that the shortest path algorithm can effectively consider all possible paths reaching the ground station over different time slots.
The graph is constructed, where V includes observation satellites , relay satellites, and virtual ground station nodes; E consists of satellite–ground station links, and contains link weights. All link weights from ground stations to super nodes are zero. By constructing the time-expanded graph , we capture the dynamic topology of the inter-satellite network over time. The vertices V include the observation satellite , relay satellites at different time slots, virtual ground station nodes representing the ground station at time t, and the super node serving as the common destination. Edges E represent possible transmissions between nodes at consecutive time slots, with weights Wn indicating the transmission costs. We apply Dijkstra’s algorithm to this graph to find the shortest path from to the super node. This path denotes the optimal sequence of transmissions through relay satellites and time slots, minimizing the overall transmission cost to the ground station.
Figure 2 illustrates a schematic of the link formed by one observation satellite and six relay satellites. Applying Dijkstra’s algorithm to the augmented graph identifies the shortest path between and the virtual ground station nodes. Let represent the data set from to . Due to multiple hops and the dynamic nature of the inter-satellite link, the original transmission strategy may become infeasible, requiring adjustments. The strategy set is checked for conflicts. If the maximum conflict time of the relay satellite transmission strategy exceeds t, the strategy is invalidated; if , the strategy set is retained. The strategy with the minimum weight is selected as the local transmission scheduling strategy set for .
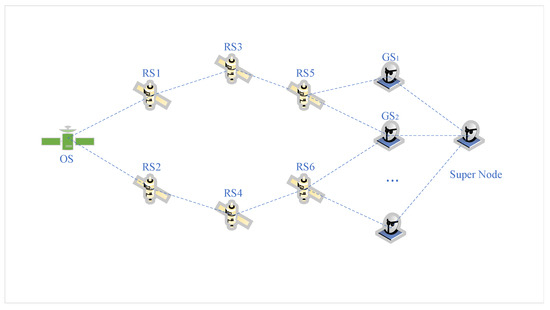
Figure 2.
Diagram of link state.
In the context of independently designing transmission scheduling strategies for observation satellites, instances may arise where two distinct data tasks commence transmission from a similar origin and are destined for the same endpoint concurrently. Such scenarios precipitate a transmission scheduling conflict. To address this issue, the following section introduces an algorithm capable of adjusting transmission strategies through prioritization. For illustrative purposes, consider the transmission strategies and associated with the conflicting data and , respectively. The algorithm’s fundamental concept is developed as follows:
- Assess the Priority of Present Data Tasks:At the current time, evaluate the transmission energy expended by both conflicting data tasks, assuming that the task with greater accumulated transmission energy is accorded higher priority. Define as the total transmission energy accumulated by the data task preceding time . The expression for is given by the following:The accumulated energy in Equation (30) quantifies the total energy expended for transmitting data task up to time , considering both observation-to-relay and relay-to-relay transmissions. Specifically, for conflicting data tasks and , if , the data task is granted higher priority (i.e., the one that has already consumed more energy up to time ). This metric is crucial for prioritizing tasks during scheduling conflicts as tasks with higher accumulated energy are considered to have greater investment and are, therefore, prioritized to minimize system cost and resource waste.
- Modify Transmission Strategy in Accordance with Priority:The aforementioned data task , enjoying higher precedence, will implement the strategy encapsulated in . Here, denotes the designated set of strategies for transmitting the data task . Consequently, the optimal scheduling strategy set is . For the data task possessing a subordinate priority, it is imperative to revert to the observation satellite and reformulate the transmission scheduling strategy, as detailed in the Dijkstra-based algorithm developed above. To circumvent subsequent conflicts, careful consideration must be given to arranging the set containing strategy , ultimately achieving the refined strategy set .
5.2. Dynamic Task Offloading and Computation Scheduling Problem Modeling and Solving
With the transmission scheduling strategy for data tasks established, the relay satellite’s buffer queue status is known for each time slot. Due to the relay satellite’s limited buffer capacity, dynamic satellite–ground links, and the random arrival of IoT device computation tasks, the task offloading and computation scheduling problem becomes highly complex and dynamic.
This complexity makes traditional optimization methods less effective, as they may not efficiently handle the high-dimensional and stochastic nature of the problem. Therefore, we model the problem as a Markov Decision Process (MDP). By formulating the problem as an MDP, we can employ reinforcement learning techniques to find optimal policies. Specifically, we utilize the Deep Q-Network (DQN) algorithm, which integrates deep learning with Q-learning. DQN is adept at estimating the state–action value function in high-dimensional spaces, making it suitable for our model. The algorithm leverages deep neural networks to approximate the optimal Q-values and incorporates experience replay and target networks to enhance learning stability and efficiency.
The application of DQN enables the agent (relay satellite) to learn optimal task offloading and computation scheduling strategies through interactions with the environment, ultimately minimizing the long-term system cost in the face of uncertainty and dynamic conditions.
Consider the function as indicative of the cost associated with the relay satellite’s activities in managing the offloading of tasks and scheduling of computational procedures at time instance t. The function is defined mathematically as follows:
The challenge surrounding the optimization model for dynamic task offloading and computation scheduling is formulated by the following:
Through solving the above-stated Equation (32), it becomes possible to determine the strategic approach for selecting computation modes by the relay satellite, denoted as . Additionally, this leads to the identification of strategies for offloading mode selection by the ground station, represented by , along with determining the computation scheduling strategy denoted by .
5.2.1. Markov Decision Process Modeling
When we closely examine Equation (32), it becomes apparent that we are dealing with a long-term optimization challenge that incorporates randomness through its variables. To effectively address this problem, it is structured as a Markov decision process, which is mathematically characterized by the tuple . Here, S signifies the array of system states, signifies the suite of potential actions, and stands for the immediate reward function associated with the process [51]. The constituents of the state space, action space, and reward function within this context are further detailed as follows. Let denote the array of system states at a given time t, with each state conceptualized as follows:
In this expression, captures the buffer queue conditions for each relay satellite at time t; reflects the buffer queue status for each IoT device during the same period; indicates the rain attenuation coefficient relevant to the communication link connecting each IoT device and each relay satellite at time t; and depicts the status of logical link existence between each IoT device and each relay satellite at this time instance. At time t, IoT devices have the capability to transfer computation tasks stored within their buffer queues to relay satellites. Accordingly, let denote the comprehensive set of actions available at time t, where each action encapsulates the strategies for selecting task offloading modes by IoT devices at that specific moment and can be expressed as follows:
Under the scenario wherein IoT devices occupy state and undertake action , the resulting immediate reward is meticulously designed as follows:
5.2.2. Determining Satellite Dynamic Link Strategy Based on DQN
Figure 3 illustrates the developed framework for task offloading and scheduling. The algorithm of DQN, introduced by the DeepMind group, is a reinforcement learning algorithm integrating deep learning principles widely used in current complex satellite networks design [19,30,52,53,54]. Unlike traditional Q-learning, DQN is adept at managing complex state spaces characterized by high dimensionality. In the realm of Q-learning, such state spaces often pose dimensionality challenges, impeding effective learning. DQN circumvents these limitations by employing deep neural networks as function approximators, which allows for the efficient handling of high-dimensional spaces by representing states as continuous variables, thus enhancing learning efficacy. Moreover, conventional Q-learning mandates a discrete action space, thereby restricting its utility in scenarios necessitating continuous action spaces. DQN addresses this limitation by leveraging deep neural networks to estimate the Q-values for each possible action, thus enabling the handling of continuous action spaces and the selection of the optimal action via optimization techniques [55]. The integration of an experience replay mechanism permits the storage of the agent’s experiences in a replay buffer, from which samples are randomly extracted for training. This approach alleviates the correlation between successive training data, thereby mitigating the sample correlation issue and bolstering training efficiency and stability. Consequently, the DQN method is proficient at maximizing interactions between intelligent agents and stochastic environments. The ‘Environment’ encapsulates the temporal dynamics that influence the state, allowing the model to maintain a distinction between the current conditions and the actions taken, until such action results in a transition to a ‘Next State’.
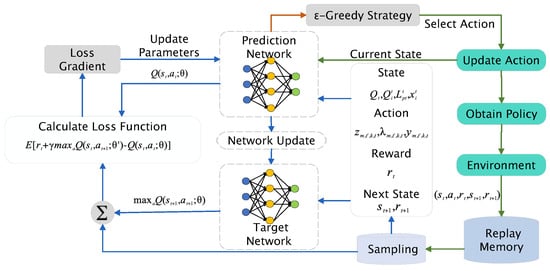
Figure 3.
Proposed DQN-based task offloading algorithm framework.
Figure 3 illustrates the iterative process of the Deep Q-Network (DQN) learning cycle. Although the figure does not explicitly show an entry point, the process naturally begins with the first observation of the environment, denoted as the initial state . This initial state is used to determine the first action , initiating the sequence of interactions between the agent and the environment. From this point forward, the system continuously updates states and actions based on learned policies. This design aligns with conventional DQN representations, where the emphasis is on the continuous reinforcement learning process rather than a discrete starting point.
During the training phase of the DQN (Deep Q-Network) algorithm, the strengths of both convolutional and recurrent neural networks are harnessed to proficiently estimate the state–action value function, known as the Q-function. The architecture of DQN comprises two distinct networks: the prediction network tasked with generating experience replay data, and the target network, which computes the state–action value, referred to as the Q-value. To expedite convergence, DQN employs an experience replay strategy, which involves the random sampling of accumulated data for training, alongside a smoothing technique for managing the data effectively. When IoT devices execute actions during the state , the associated action value function Q is updated as follows:
In Equation (36), denotes the learning rate, and represents the discount factor. To tackle the computational intricacies of Equation (36), and prevent divergence of Q-values, DQN introduces a prediction network and a target network , which are responsible for predicting and assessing the Q-values, respectively. Herein, and are the parameters of the prediction network and target network. The parameters are updated by reducing the loss function:
where signifies the step size, and denotes the Q-value loss function, which is expressed as follows:
In Equation (38), symbolizes samples randomly extracted from the experience replay buffer D, and is the output generated by the target network at time t, which is given by the following:
The detailed procedures for the computation task offloading and scheduling algorithm, rooted in the DQN learning algorithm for interactions between satellite and IoT devices, are outlined in Algorithm 1. Begin by initializing the prediction and target networks alongside the state, action, and parameters within the experience replay buffer. Within the state , implement the -greedy policy to identify the optimal action for the target network, facilitating the transition of the system state from to . Record the experience tuple in the experience replay buffer, whose maximum capacity is denoted as . Select a random batch of samples with size from this buffer and feed them into the prediction network to generate predicted Q-values. The target Q-values are computed in line with Equation (36). Then, determine the discrepancy between the predicted and target Q-values to update the parameters of the prediction network via Equation (37). The target network parameters are periodically revised utilizing the prediction network’s parameters. Iterate these steps until convergence is reached.
We define ‘resource scheduling’ in the context of our study as the strategic scheduling and management of computational and communication resources within the satellite network. This encompasses both data scheduling, which prioritizes data packet transmission, and task offloading, which involves distributing computational tasks among various network nodes. Although our primary focus is on optimizing data scheduling paths and task offloading strategies, these actions are intrinsically linked to efficient resource utilization, ensuring that the network operates optimally in conjunction with its available resources.
| Algorithm 1 DQN-Based Task Offloading and Scheduling |
|
6. Simulation Results and Analysis
This section uses the STK simulation software version 6.0 to build a system scenario in order to obtain real satellite and inter-satellite physical link information, apply Pytorch 2.2.2 and MATLAB 2024a to simulate the algorithms proposed in this paper and the algorithm in the literature [40], and analyze the performance differences between the two. This paper presents a novel cost model for an LEO satellite edge computing system, addressing the challenges of computation offloading. It introduces a joint computation offloading and resource allocation strategy, which decomposes the problem into two sub-problems: optimizing computation offloading using game theory and allocating communication resources via the Lagrange multiplier method. Ref. [40] is selected as a baseline due to its relevance to IoT applications and its use of energy consumption as a cost metric, which aligns with our study’s objectives. However, our approach differs significantly in methodology, as we employ a DQN-based optimization rather than the game-theoretic and Lagrange multiplier methods used in [40]. To enable a fair comparison, we replace our proposed DQN-based optimization algorithm with the JCORA method from [40] while keeping all other simulation parameters unchanged. This allows us to directly compare the performance impact of different optimization strategies under the same system conditions.
Simulation Scenario
In the simulation scenario of this paper, a LEO satellite network is built using the STK satellite tool (version 6.0), which includes 24 medium-orbit satellites distributed in three orbital planes with an altitude of 1000 km, 10 observation satellites, and one ground station. This section uses MATLAB (version 2024a) the Python programming language (version 3.8) and a Pytorch (version 2.1.2) simulation environment based on the Gym reinforcement learning environment to simulate the DQN network. During the simulation process, the number of training steps is set to 4000 steps, and the number of training episodes is set to 30 h. The parameters of the DQN network and other parameters are shown in Table 2. This section averages the simulation results of 600 independent experiments and compares the proposed algorithm with the algorithm in the literature.

Table 2.
Parameter settings for DQN network and simulation.
Figure 4 and Figure 5 show the impact of different learning rates and discount factors on long-term rewards. As shown in the figure, a learning rate of 0.1 is very clear that the DQN network does not converge and fluctuates significantly. This is because the learning rate is too large, and the network jumps directly to the local optimal value, resulting in suboptimal results. When the learning rate is 0.0001, the network converges slowly, and even after 400 training steps, there is still a large fluctuation. This is because, during the learning process, the network converges slowly and requires more training steps to reach the final reward. When the learning rate is 0.001, the network can reach the optimal reward after 1000 steps and maintain the reward through continuous training.
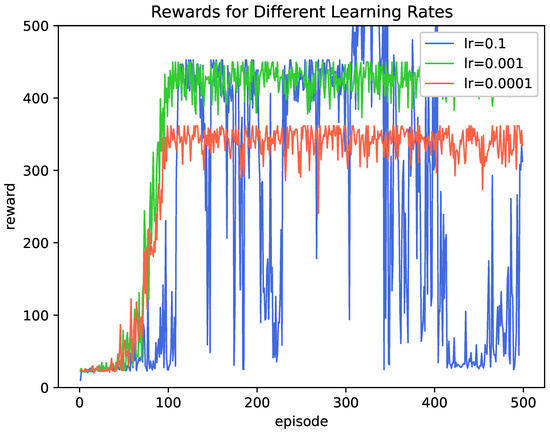
Figure 4.
Long-term reward versus number of training steps (with different learning rates).
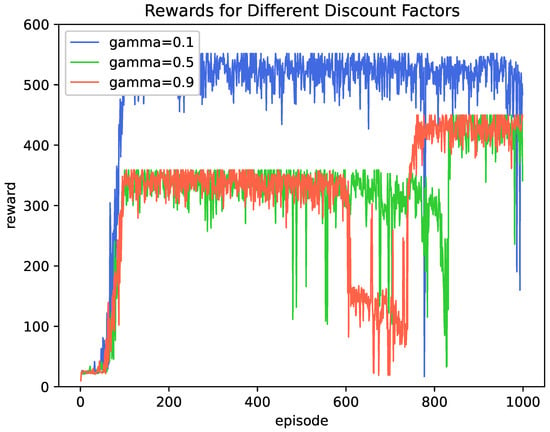
Figure 5.
Long-term reward versus number of training steps (with different discount factors).
Figure 5 illustrates the impact of different discount factors on the long-term rewards during the training of our DQN-based task offloading and computation scheduling algorithm. The discount factor is a critical parameter in reinforcement learning algorithms, determining how future rewards are valued relative to immediate rewards. When , the agent exhibits slow convergence with high fluctuations in rewards. This low discount factor implies that the agent undervalues future rewards, leading to shortsighted decisions that do not contribute to long-term system optimization. For , the agent shows improved convergence and reduced fluctuations. The balance between immediate and future rewards allows the agent to learn better policies but still falls short of optimal performance. With , the agent achieves rapid convergence and higher steady-state rewards. The high emphasis on future rewards enables the agent to learn strategies that significantly minimize the long-term system cost. This result indicates that a higher discount factor is beneficial in the context of our satellite edge computing network, where long-term planning is essential due to the dynamic and continuous nature of tasks and resources.
In Figure 6, we illustrate the connection between the relay satellite’s maximum queue length and the system cost, alongside analysis of varied scenarios concerning task computation difficulty. The figure reveals that as the relay satellite’s maximum queue length grows, the system cost declines. This occurs because a longer queue allows the satellite to manage more data transmission tasks and adjust computation task scheduling, enhancing the system’s capacity to prevent data loss and stabilize cost fluctuations. Notably, the system cost achieved by our proposed method in this study is lower than that reported in prior research, and with a task computation difficulty of 1000 cycles, the cost reduction using our approach is slower compared to the method from the literature [40].
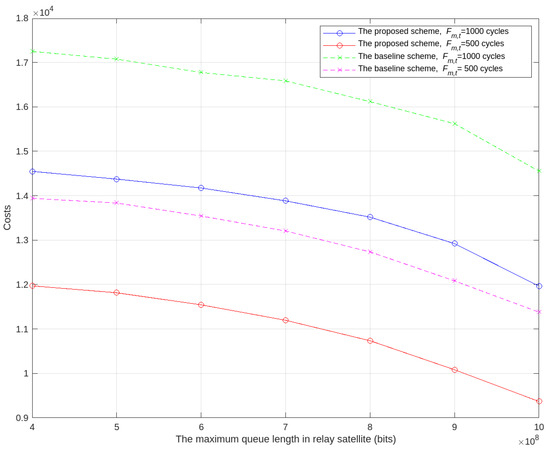
Figure 6.
System cost versus maximum queue length of relay satellites.
Figure 7 presents the correlation between the relay satellite’s computation capability and system cost. It demonstrates that as the satellite’s computation capability increases, the system cost decreases unevenly across various methods. Figure 7 demonstrates the relationship between the computational capability of relay satellites and the system cost in the proposed LEO satellite edge computing network. As the computational capability of relay satellites increases, the system cost decreases significantly due to improved task processing efficiency and reduced communication overhead. However, the curve exhibits a diminishing return effect, where further increases in computational capability yield only marginal reductions in system cost. This highlights the importance of balancing computational resources to achieve cost-effective performance. The figure underscores the efficiency of the proposed joint task offloading and resource scheduling strategy in optimizing system performance while minimizing costs.
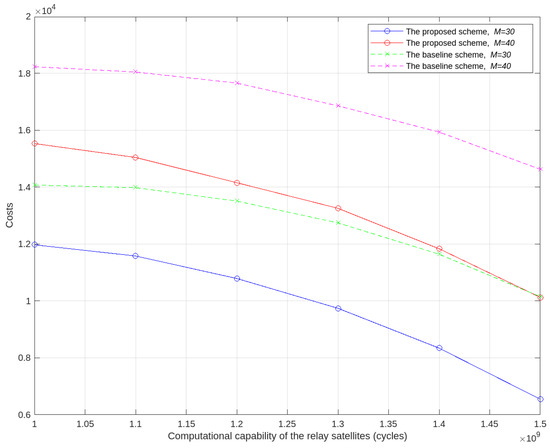
Figure 7.
System cost versus computing capability of relay satellites.
Furthermore, an increase in IoT device numbers also results in uneven decreases in system costs. This is due to the reduction in task computation time as satellite computation improves, allowing the task queue to remain stable within a reasonable timeframe, thus lowering costs. Moreover, a rise in device data quantity leads to more tasks for the system to process, adding to the costs. The cost via our proposed methodology notably surpasses that of previous approaches [40], and with enhanced satellite computation, our method’s cost increase is slower than that of existing methods, underscoring the benefits of our approach.
Figure 8 evaluates the relationship between the average task arrival rate and system cost under different numbers of IoT devices for the proposed algorithm in this chapter and the algorithm from [40]. As shown in the figure, as the task arrival rate increases, the system cost decreases. This is because a higher task arrival rate leads to greater utilization of the network’s computational, communication, and caching resources, resulting in increased system costs. Moreover, the system cost achieved by the proposed algorithm in this chapter is lower than that of the algorithm in [40]. Furthermore, as the task arrival rate increases, the cost under the proposed algorithm increases at a relatively slower rate.
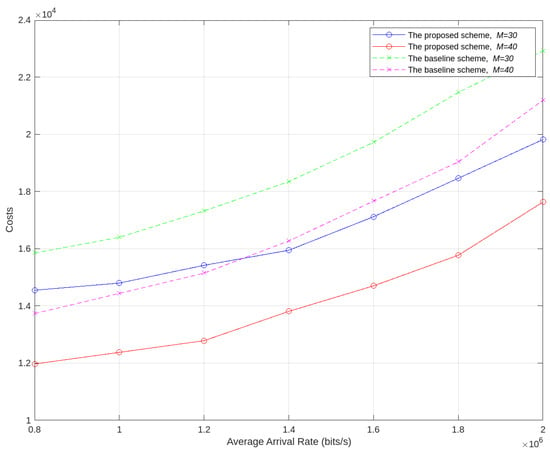
Figure 8.
System cost versus the average arrival rate of the tasks.
The system cost metric used in this study incorporates energy consumption, task processing delays, and other operational factors. By minimizing system costs, the proposed method achieves significant energy savings in addition to reducing delays and improving task completion rates. This holistic evaluation provides a comprehensive assessment of the system’s performance.
7. Conclusions
This paper has comprehensively addressed the joint dynamic task offloading and resource scheduling problem in LEO satellite edge computing networks. The proposed system model incorporates both data service transmission and computational task offloading and is framed as a long-term cost function minimization problem with constraints. Key contributions include the development of a priority-based policy adjustment algorithm for handling transmission scheduling conflicts and a DQN-based algorithm for dynamic task offloading and computation scheduling. These methods are integrated into a joint scheduling strategy that optimizes overall system performance. Simulation results demonstrate significant improvements in average system cost, queue length, energy consumption, and task completion rate, compared to baseline strategies, highlighting the strategy’s effectiveness and efficiency. Future work will extend the framework to more complex network scenarios and explore the integration of advanced machine learning techniques to further enhance security performance [56,57].
Author Contributions
Conceptualization, J.L. and R.C.; methodology, J.L. and K.G.; software, K.G. and R.C.; formal analysis, J.L.; writing—original draft preparation, J.L.; writing—review and editing, R.C. and C.L.; project administration, C.L.; funding acquisition, C.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Science and Technology Innovation Key R&D Program of Chongqing grant number: CSTB2023TIAD-STX0025.
Data Availability Statement
Access to the experimental data presented in this article can be obtained by contacting the corresponding authors.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Chen, M.; Li, J.; Chai, R. 5G Multi-Service-Oriented User Association and Routing Algorithm for Integrated Terrestrial-Satellite Networks. In Proceedings of the 13th International Conference on Wireless Communications and Signal Processing (WCSP), Changsha, China, 20–22 October 2021; pp. 1–5. [Google Scholar]
- De Gaudenzi, R.; Ottersten, B.; Perez-Neira, A.; Yanikomeroglu, H.; Heyn, T.; Lichten, S.M. Guest Editorial Space Communications New Frontiers: From Near Earth to Deep Space. IEEE J. Sel. Areas Commun. 2024, 42, 1023–1028. [Google Scholar] [CrossRef]
- Huang, Y.; Cui, H.; Hou, Y.; Hao, C.; Wang, W.; Zhu, Q.; Li, J.; Wu, Q.; Wang, J. Space-based electromagnetic spectrum sensing and situation awareness. Space Sci. Technol. 2024, 4, 0109. [Google Scholar] [CrossRef]
- Bai, L.; Zhu, L.; Zhang, X.; Zhang, W.; Yu, Q. Multi-satellite relay transmission in 5G: Concepts, techniques, and challenges. IEEE Netw. Mag. 2018, 32, 38–44. [Google Scholar] [CrossRef]
- De Cola, T.; Bisio, I. QoS Optimisation of eMBB Services in Converged 5G-Satellite Networks. IEEE Trans. Veh. Technol. 2020, 69, 12098–12110. [Google Scholar] [CrossRef]
- Li, B.; Fei, Z.; Zhou, C.; Zhang, Y. Physical-layer Security in Space Information Networks: A Survey. IEEE Internet Things J. 2019, 7, 33–52. [Google Scholar] [CrossRef]
- Ranaweera, P.; Jurcut, A.D.; Liyanage, M. Survey on Multi-Access Edge Computing Security and Privacy. IEEE Commun. Surv. Tutorials 2021, 23, 1078–1124. [Google Scholar] [CrossRef]
- Abbas, N.; Zhang, Y.; Taherkordi, A.; Skeie, T. Mobile Edge Computing: A Survey. IEEE Internet Things J. 2017, 5, 450–465. [Google Scholar] [CrossRef]
- Pan, J.; McElhannon, J. Future Edge Cloud and Edge Computing for Internet of Things Applications. IEEE Internet Things J. 2018, 5, 439–449. [Google Scholar] [CrossRef]
- Al-Hraishawi, H.; Chougrani, H.; Kisseleff, S.; Lagunas, E.; Chatzinotas, S. A survey on nongeostationary satellite systems: The communication perspective. IEEE Commun. Surv. Tutor. 2022, 25, 101–132. [Google Scholar] [CrossRef]
- Huang, Y.; Dong, M.; Mao, Y.; Liu, W.; Gao, Z. Distributed Multi-Objective Dynamic Offloading Scheduling for Air–Ground Cooperative MEC. IEEE Trans. Veh. Technol. 2024, 73, 12207–12212. [Google Scholar] [CrossRef]
- Liu, J.; Shi, Y.; Fadlullah, Z.M.; Kato, N. Space-Air-Ground Integrated Network: A Survey. IEEE Commun. Surv. Tutor. 2018, 20, 2714–2741. [Google Scholar] [CrossRef]
- Xie, R.; Tang, Q.; Wang, Q.; Liu, X.; Yu, F.R.; Huang, T. Satellite-Terrestrial Integrated Edge Computing Networks: Architecture, Challenges, and Open Issues. IEEE Netw. 2020, 34, 224–231. [Google Scholar] [CrossRef]
- Huang, C.; Chen, G.; Xiao, P.; Xiao, Y.; Han, Z.; Chambers, J.A. Joint offloading and resource allocation for hybrid cloud and edge computing in SAGINs: A decision assisted hybrid action space deep reinforcement learning approach. IEEE J. Sel. Areas Commun. 2024, 42, 1029–1043. [Google Scholar] [CrossRef]
- Tang, Q.; Xie, R.; Fang, Z.; Huang, T.; Chen, T.; Zhang, R.; Yu, F.R. Joint service deployment and task scheduling for satellite edge computing: A two-timescale hierarchical approach. IEEE J. Sel. Areas Commun. 2024, 42, 1063–1079. [Google Scholar] [CrossRef]
- Li, J.; Gui, A.; Rong, C.; Liang, C. Cost-Optimized Dynamic Offloading and Resource Scheduling Algorithm for Low Earth Orbit Satellite Networks. In Proceedings of the 19th EAI International Conference on Communications and Networking in China, Chongqing, China, 2–3 November 2024; p. 1. [Google Scholar]
- Tang, Z.; Zhou, H.; Ma, T.; Yu, K.; Shen, X.S. Leveraging LEO assisted cloud-edge collaboration for energy efficient computation offloading. In Proceedings of the 2021 IEEE Global Communications Conference (GLOBECOM), Madrid, Spain, 7–11 December 2021; pp. 1–6. [Google Scholar]
- Tang, Q.; Fei, Z.; Li, B.; Han, Z. Computation offloading in LEO satellite networks with hybrid cloud and edge computing. IEEE Internet Things J. 2021, 8, 9164–9176. [Google Scholar] [CrossRef]
- Xu, F.; Yang, F.; Zhao, C.; Wu, S. Deep reinforcement learning based joint edge resource management in maritime network. China Commun. 2020, 17, 211–222. [Google Scholar] [CrossRef]
- Chen, Y.; Ai, B.; Niu, Y.; Zhang, H.; Han, Z. Energy-constrained computation offloading in space-air-ground integrated networks using distributionally robust optimization. IEEE Trans. Veh. Technol. 2021, 70, 12113–12125. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, W.; Tseng, F.-H. Satellite mobile edge computing: Improving QoS of high-speed satellite-terrestrial networks using edge computing techniques. IEEE Netw. 2019, 33, 70–76. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, J.; Guo, X.; Qu, Z. A game-theoretic approach to computation offloading in satellite edge computing. IEEE Access 2019, 8, 12510–12520. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, J.; Zhang, X.; Wang, P.; Liu, L. A computation offloading strategy in satellite terrestrial networks with double edge computing. In Proceedings of the 2018 IEEE International Conference on Communication Systems (ICCS), Chengdu, China, 19–21 December 2018; pp. 450–455. [Google Scholar]
- Pang, B.; Gu, S.; Zhang, Q.; Zhang, N.; Xiang, W. CCOS: A coded computation offloading strategy for satellite-terrestrial integrated networks. In Proceedings of the 2021 International Wireless Communications and Mobile Computing (IWCMC), Harbin, China, 28 June–2 July 2021; pp. 242–247. [Google Scholar]
- Zhang, L.; Zhang, H.; Guo, C.; Xu, H.; Song, L.; Han, Z. Satellite-aerial integrated computing in disasters: User association and offloading decision. In Proceedings of the ICC 2020—2020 IEEE International Conference on Communications (ICC), Dublin, Ireland, 7–11 June 2020; pp. 554–559. [Google Scholar]
- Alsharoa, A.; Alouini, M.S. Improvement of the global connectivity using integrated satellite-airborne-terrestrial networks with resource optimization. IEEE Trans. Wirel. Commun. 2020, 19, 5088–5100. [Google Scholar] [CrossRef]
- Zhang, M.; Zhou, W. Energy-efficient collaborative data downloading by using inter-satellite offloading. In Proceedings of the 2019 IEEE Global Communications Conference (GLOBECOM), Waikoloa, HI, USA, 9–13 December 2019; pp. 1–6. [Google Scholar]
- Yarr, N.; Ceriotti, M. Optimization of intersatellite routing for real-time data download. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 2356–2369. [Google Scholar] [CrossRef]
- Di, B.; Zhang, H.; Song, L.; Li, Y.; Li, G.Y. Ultra-dense LEO: Integrating terrestrial-satellite networks into 5G and beyond for data offloading. IEEE Trans. Wirel. Commun. 2018, 18, 47–62. [Google Scholar] [CrossRef]
- Qiu, C.; Yao, H.; Yu, F.R.; Xu, F.; Zhao, C. Deep Q-learning aided networking, caching, and computing resources allocation in software-defined satellite-terrestrial networks. IEEE Trans. Veh. Technol. 2019, 68, 5871–5883. [Google Scholar] [CrossRef]
- Li, C.; Zhang, Y.; Hao, X.; Huang, T. Jointly optimized request dispatching and service placement for MEC in LEO network. China Commun. 2020, 17, 199–208. [Google Scholar] [CrossRef]
- Jiang, D.; Wang, F.; Lv, Z.; Mumtaz, S. QoE-aware efficient content distribution scheme for satellite-terrestrial networks. IEEE Trans. Mob. Comput. 2021, 22, 443–458. [Google Scholar] [CrossRef]
- Wang, G.; Zhou, S.; Niu, Z. Radio resource allocation for bidirectional offloading in space-air-ground integrated vehicular network. J. Commun. Inf. Netw. 2019, 4, 24–31. [Google Scholar] [CrossRef]
- Song, Z.; Hao, Y.; Liu, Y.; Sun, X. Energy-efficient multiaccess edge computing for terrestrial-satellite Internet of Things. IEEE Internet Things J. 2021, 8, 14202–14218. [Google Scholar] [CrossRef]
- Ding, C.; Wang, J.-B.; Zhang, H.; Lin, M.; Li, G.Y. Joint optimization of transmission and computation resources for satellite and high altitude platform assisted edge computing. IEEE Trans. Wirel. Commun. 2021, 21, 1362–1377. [Google Scholar] [CrossRef]
- Cui, G.; Long, Y.; Xu, L.; Wang, W. Joint offloading and resource allocation for satellite assisted vehicle-to-vehicle communication. IEEE Syst. J. 2020, 15, 3958–3969. [Google Scholar] [CrossRef]
- Cheng, N.; Lyu, F.; Quan, W.; Zhou, C.; He, H.; Shi, W.; Shen, X. Space/aerial-assisted computing offloading for IoT applications: A learning-based approach. IEEE J. Sel. Areas Commun. 2019, 37, 1117–1129. [Google Scholar] [CrossRef]
- Wei, K.; Tang, Q.; Guo, J.; Zeng, M.; Fei, Z.; Cui, Q. Resource scheduling and offloading strategy based on LEO satellite edge computing. In Proceedings of the 2021 IEEE 94th Vehicular Technology Conference (VTC2021-Fall), Norman, OK, USA, 27–30 September 2021; pp. 1–6. [Google Scholar]
- Cui, G.; Li, X.; Xu, L.; Wang, W. Latency and energy optimization for MEC enhanced SAT-IoT networks. IEEE Access 2020, 8, 55915–55926. [Google Scholar] [CrossRef]
- Wang, B.; Feng, T.; Huang, D. A joint computation offloading and resource allocation strategy for LEO satellite edge computing system. In Proceedings of the 2020 IEEE 20th International Conference on Communication Technology (ICCT), Nanning, China, 28–31 October 2020; pp. 649–655. [Google Scholar]
- Tani, S.; Hayama, M.; Nishiyama, H.; Kato, N.; Motoyoshi, K.; Okamura, A. Multi-carrier relaying for successive data transfer in earth observation satellite constellations. In Proceedings of the 2017 IEEE Global Communications Conference, Singapore, 4–8 December 2017; pp. 1–5. [Google Scholar]
- He, C.; Dong, Y. Multi-Satellite Observation-Relay Transmission-Downloading Coupling Scheduling Method. Remote. Sens. 2023, 15, 5639. [Google Scholar] [CrossRef]
- Qu, Z.; Zhang, G.; Cao, H.; Xie, J. LEO satellite constellation for Internet of Things. IEEE Access 2017, 5, 18391–18401. [Google Scholar] [CrossRef]
- Cui, G.; Duan, P.; Xu, L.; Wang, W. Latency optimization for hybrid GEO–LEO satellite-assisted IoT networks. IEEE Internet Things J. 2022, 10, 6286–6297. [Google Scholar] [CrossRef]
- Saeed, N.; Elzanaty, A.; Almorad, H.; Dahrouj, H.; Al-Naffouri, T.Y.; Alouini, M.-S. CubeSat communications: Recent advances and future challenges. IEEE Commun. Surv. Tutor. 2020, 22, 1839–1862. [Google Scholar] [CrossRef]
- Golkar, A.; i Cruz, I.L. The federated satellite systems paradigm: Concept and business case evaluation. Acta Astronaut. 2015, 111, 230–248. [Google Scholar] [CrossRef]
- Han, D.; Chen, W.; Fang, Y. Joint channel and queue aware scheduling for latency sensitive mobile edge computing with power constraints. IEEE Trans. Wirel. Commun. 2020, 19, 3938–3951. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, Q. Computation resource allocation for heterogeneous time-critical IoT services in MEC. In Proceedings of the 2020 IEEE Wireless Communications and Networking Conference (WCNC), Virtually, 25–28 May 2020; pp. 1–6. [Google Scholar]
- Hu, H.; Song, W.; Wang, Q.; Hu, R.Q.; Zhu, H. Energy efficiency and delay tradeoff in an MEC-enabled mobile IoT network. IEEE Internet Things J. 2022, 9, 15942–15956. [Google Scholar] [CrossRef]
- Zheng, F.; Wang, C.; Zhou, Z.; Pi, Z.; Huang, D. LEO laser microwave hybrid inter-satellite routing strategy based on modified Q-routing algorithm. Eurasip J. Wirel. Commun. Netw. 2022, 2022, 36. [Google Scholar] [CrossRef]
- Kallus, N.; Uehara, M. Double reinforcement learning for efficient off-policy evaluation in Markov decision processes. J. Mach. Learn. Res. 2020, 21, 6742–6804. [Google Scholar]
- Lyu, Y.; Liu, Z.; Fan, R.; Zhan, C.; Hu, H.; An, J. Optimal computation offloading in collaborative LEO-IoT enabled MEC: A multi-agent deep reinforcement learning approach. IEEE Trans. Green Commun. Netw. 2022, 7, 996–1011. [Google Scholar] [CrossRef]
- Wu, M.; Guo, K.; Li, X.; Lin, Z.; Wu, Y.; Tsiftsis, T.A.; Song, H. Deep reinforcement learning-based energy efficiency optimization for RIS-aided integrated satellite-aerial-terrestrial relay networks. IEEE Trans. Commun. 2024, 72, 4163–4178. [Google Scholar] [CrossRef]
- Zhang, H.; Zhao, H.; Liu, R.; Kaushik, A.; Gao, X.; Xu, S. Collaborative Task Offloading Optimization for Satellite Mobile Edge Computing Using Multi-Agent Deep Reinforcement Learning. IEEE Trans. Veh. Technol. 2024; 1–16, early access. [Google Scholar] [CrossRef]
- Chen, T.; Liu, J.; Tang, Q.; Huang, T.; Liu, Y. Deep reinforcement learning based data offloading in multi-layer Ka/Q band LEO satellite-terrestrial Networks. In Proceedings of the 2021 IEEE 21st International Conference on Communication Technology (ICCT), Tianjin, China, 13–16 October 2021; pp. 1417–1422. [Google Scholar]
- Wang, J.; Du, H.; Liu, Y.; Sun, G.; Niyato, D.; Mao, S.; Kim, D.I.; Shen, X. Generative AI based Secure Wireless Sensing for ISAC Networks. arXiv 2024, arXiv:2408.11398. [Google Scholar]
- Lin, Y.; Gao, Z.; Du, H.; Niyato, D.; Kang, J.; Xiong, Z.; Zheng, Z. Blockchain-based Efficient and Trustworthy AIGC Services in Metaverse. IEEE Trans. Serv. Comput. 2024, 17, 2067–2079. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).