Deep Reinforcement Learning for Energy-Efficient 6G V2X Networks

Abstract

The deployment of 6G vehicle-to-everything (V2X) networks is a challenging task given the 6G requirements of ultra-high data rates along with ultra-low latency levels. For intelligent transportation systems (ITSs), V2X communications involve a high density of user equipment (UE), vehicles, and next-generation Node-B (gNB). Therefore, optimal management of the current network infrastructure plays a key role in minimizing energy and latency. Optimal resource allocation using linear programming methods cannot be scaled to the required scenarios of 6G V2X communications and is not suitable for online allocation. To overcome these limitations, deep reinforcement learning (DRL) is a promising approach given its properties of direct integration with online allocation models. In this work, we investigate the problem of optimal resource allocation in 6G V2X networks, where ITSs are deployed to execute tasks offloaded by vehicles subject to data rate and latency requirements. We apply a policy optimization-based DRL to jointly reduce the number of active gNBs and the latency concerning the offloaded tasks going on in the vehicle. The model is analyzed for several ITS scenarios to investigate the performance observed and the advantages of the proposed policy optimization allocation for 6G V2X networks. Our evaluation results illustrate that the proposed DRL-based algorithm produces dynamic solutions that approximate the optimal ones at reasonable rates of energy consumption. Our numerical results indicate that DRL-based solutions are distinguished by equivalently balanced energy consumption under different scenarios.

1. Introduction

In the coming years, fifth-generation (5G) networks may face a drawback in meeting the desired quality of service (QoS) for vehicle-to-everything (V2X) communications, for example, due to limitations in resources, enormous traffic volume, and advanced digital devices and applications. In contrast, cutting-edge technologies are required to meet V2X QoS in terms of power consumption, latency-sensitive applications, achievable data rates, etc. [1]. Sixth-generation (6G) communication networks are expected to support intelligent transportation systems (ITSs) by meeting the broad-range requirements of V2X communications [2]. As shown in Figure 1, V2X communications include vehicle-to-network (V2N), vehicle-to-infrastructure (V2I), vehicle-to-vehicle (V2V), and vehicle-to-pedestrian (V2P) communications, including communications with vulnerable road users (VRUs) [3]. An example of a V2I link is a vehicle-to-roadside unit (RSU), where the RSU is a device that facilitates communications between vehicles and the transportation infrastructure in ITSs.

Figure 1. Types of V2X communications.

Sixth-generation V2X communications require ultra-high data rates (in Gbps) and reliability (99.999%), extremely low latencies (1 millisecond), high mobility, and ubiquitous connectivity. To fulfill these requirements, technological advancements are needed, including artificial intelligence (AI) and machine learning (ML) techniques, intelligent edge, terahertz communications, lower wavelengths, and higher frequencies [4]. The open radio access network (Open RAN) is a promising architecture to enhance and optimize the implementation of future 6G V2X networks. The open RAN deployment is based on disaggregated, virtualized, and software-based units, connected by open interfaces between multiple vendors [5]. The next-generation Node-B (gNB) functionality in Open RAN is disaggregated into a central unit (CU), a distributed unit (DU), and a radio unit (RU), connected via open interfaces to intelligent controllers that manage the network at near-real-time (10 milliseconds to 1 s) and non-real-time (longer than 1 s) time scales [6].

The deployment of multi-access edge computing (MAEC) at the Open RAN edge and close to the V2X user equipment (UE), that is, the vehicle, provides network capabilities for end users that deploy computing and storage services with minimal latency and reduced energy consumption [7]. Due to constrained MAEC servers, such as RSUs, resource management is considered one of the key challenges that play a role in addressing the energy-efficient and ultra-low latency requirements of 6G V2X applications [8]. Traditional optimization takes a long convergence time to optimize the energy consumption because of the extensive searching when the action space is huge. An ML approach is considered a promising technique for resource management optimization due to its ability to map any input to the required output and make a suboptimal decision without waiting for the optimal one [9].

Classical ML techniques include supervised and unsupervised learning. Supervised learning requires a well-labeled data set to train its model, while in unsupervised learning, there is no such requirement to label the data. An alternative technique is reinforcement learning (RL), where agents can learn the best strategy by interacting with the environment based on its feedback represented as an immediate reward [10]. Deep reinforcement learning (DRL) is favored for V2X communication tasks in complex scenarios due to its efficacy in rapid decision making, overcoming the difficulties associated with labeled data in dynamic environments [9].

To satisfy the aforementioned challenges, appropriate assignments must be performed between vehicles and RSUs, taking into consideration the management of signal-to-noise-to-interference ratio (SINR) and intercell interference (ICI). Furthermore, to optimize resource allocation and save energy, RSUs can be turned on or off depending on the traffic demand of the vehicles [11]. The CU control plane of the RSU should take decisions quickly, in the order of seconds, to determine the appropriate assignments and activation, which lead to minimizing the energy consumption while satisfying the QoS requirements in terms of ultra-low latency and available radio resource, i.e., resource blocks (RBs).

To this end, in this study, we investigate the problem of how to allocate the resources efficiently in MAEC to optimize resource management and save energy while meeting the QoS requirements for 6G V2X Open RAN. In particular, given the number of RSUs with available RBs and the number of vehicles with required RBs for sending tasks, we need to find an optimal vehicle-to-RSU association and a state of each RSU to minimize the number of active RSUs and energy consumption while satisfying the constraints on the number of required RBs, data rates, allowed latency, and available resources.

The main contributions of this work are summarized as follows:

• We formulate the resource allocation problem as an integer linear programming (ILP) optimization problem to minimize energy consumption and the number of active RSUs by determining the best vehicle-to-RSU association and whether to turn the RSU on or off.
• We reduce the number of RSUs that are active and minimize energy consumption while satisfying the constraints on the number of RBs, data rates, SINR, and latency.
• We use a CPLEX implementation [12] to find the optimal solutions to our optimization problem and evaluate our proposed model.
• We transform the aforementioned problem into an equivalent DRL environment and subsequently propose a proximal policy optimization (PPO) algorithm to solve it.
• We perform a comprehensive comparison between optimal and approximate solutions to assess the effectiveness of the DRL environment and the performance of our proposed model.
• We examine the performance of our proposed model in 6G V2X Open RANs for different scenarios with various vehicle densities and RSUs.

The remainder of this paper is organized as follows: Section 2 reviews previous works on energy efficiency for MAEC networks. Section 3 describes the system model and the formulation of the optimization problem, including the DRL environment and the proposed PPO algorithm. Section 4 presents the performance of the model and the numerical results. Section 5 concludes the article and points out future work.

2. Related Work

This section presents a concise review of current work on optimizing energy efficiency for MAEC V2X networks. Several ML and traditional optimization techniques have been used for task offloading and resource allocation to minimize energy consumption, reduce latency, or maximize average throughput and data rates. We highlight the contributions, limitations, and differences from our work. Table 1 compiles the objectives, constraints, and solutions introduced in the reviewed literature. We categorize the reviewed literature into the following aspects:

Table 1. Comparison of research publications.

Lit.	Objectives	Constraints	Solutions
[11]	Minimize energy consumption	Resources	Optimal ILP and heuristic algorithms
[13]		Latency and energy	DRL-TCOA
[14]		Energy and resources	PPO-based
[15]		Energy	Convex optimization, DDQN, and DDPG
[16]		Latency and resources	SCA and MADDPG
[17]		Latency and resources	Double-iteration joint optimization
[18]		Transmission rate	DDPG-based
[19]		Latency	TD3
[20]	Minimize energy consumption and latency	Latency and resources	Game theory and ED3QN
[21]		Resources	DAG-based and DRL-based ODCO
[22]		Latency and resources	MAPPO
[23]		Latency and resources	SPSO and PERDDQN
[24]		Latency and resources	DRL and matching theory
[25]		Latency, energy, and resources	DQN-based
[26]		Latency and energy	PPO and asynchronous FL
[27]		Latency and resources	Distributed collaborative computing
[28]		Resources	GA and PSO
[29]		Energy	Decentralized and probability-based
[30]		Latency	Lagrange multipliers
[31]	Minimize latency	Resources	MADDPG
[32]		Latency and resources	Clustering algorithm and DDQN
[33]		Throughput	DDPG and DQN
[34]		Latency and reliability	DDQN
[35]		Energy and resources	DMARL
[36]		URLLC	SNC and Lyapunov-guided DRL
[37]		Energy and resources	A2C-based
[38]		Latency and energy	Lyapunov optimization and JCORA
[39]		Latency	SA and TD3
Ours	Minimize energy consumption	Latency and resources	Optimal ILP and PPO

• DRL-based approaches to minimize energy consumption;
• DRL-based approaches to jointly minimize energy consumption and latency;
• DRL-based approaches to minimize latency;
• Traditional optimization approaches to minimize energy consumption and latency.

As shown in Table 1, most of the reviewed studies did not jointly consider optimal and approximate solutions. In contrast, the comparison of optimal and approximate solutions is a key feature of this work. Some important elements that are partially included or absent in the reviewed work are real-time resource allocation, evaluation of complex real-world environments, and efficient allocation of edge resources while considering service fairness.

2.1. DRL-Based Approaches to Minimize Energy Consumption

Several studies proposed DRL-based algorithms to solve the resource allocation problem of minimizing the energy consumption. Yan et al. [13] proposed a joint optimization problem to minimize the cost of age-of-information (AoI), energy consumption, and rental price for computation offloading in unmanned aerial vehicle (UAV)-assisted vehicular edge computing networks. They developed a solution using a DRL-based joint trajectory control and offloading allocation algorithm (DRL-TCOA) to solve the proposed computation offloading problem. Song et al. [14] introduced energy harvesting (EH) into a vehicular ad hoc network (VANET) and suggested a decentralized multi-agent DRL-based resource allocation algorithm to maximize energy efficiency. They composed power splitting and DRL to efficiently divide the harvested energy. They formulated the non-convex optimization problem as a Markov decision process (MDP) and used a PPO-based algorithm to solve it.

Zhijian et al. [17] designed a distributed edge computing-based task offloading scheme in a vehicular network. They proposed a joint optimization problem for the offloading strategy and resource allocation. They developed a double-iteration joint optimization algorithm to minimize energy consumption by optimizing the offloading strategy and bandwidth allocation.

Deep deterministic policy gradient (DDPG) and twin delayed DDPG (TD3) algorithms are employed to solve the resource scheduling problem and reduce energy consumption. Huang et al. [15] studied an intelligent reflecting surface (IRS)-enabled UAV edge computing to improve energy efficiency and formulated a joint optimization problem of IRS phase shift, UAV trajectory, and power allocation. The mixed-integer non-linear problem (MINLP) is decomposed into two subproblems and solved using convex optimization, double deep Q-network (DDQN), and DDPG algorithms. Yin et al. [18] proposed a joint optimization problem to determine user offloading strategies and UAV trajectories. They used a DDPG-based iterative optimization of the energy consumption algorithm to minimize vehicle energy consumption and determine optimal offloading while ensuring the maximization of the task transmission rate.

Gao et al. [16] considered a task offloading scenario in a hybrid UAV-assisted MEC network with the objective of minimizing system energy consumption subject to maximum tolerable latency and computing limitations. They proposed a DRL-combined successive convex approximation (SCA) algorithm to obtain a near-optimal solution with low complexity. The multiagent DDPG (MADDPG) algorithm is used to provide a suitable service assignment and task splitting, while the SCA algorithm solves trajectory planning and resource scheduling. Xie et al. [19] investigated the computation offloading and resource allocation in a satellite-terrestrial integrated network. They minimized energy consumption while guaranteeing latency tolerance by jointly optimizing the offloading decision and resource allocation. They formulated the minimization problem as an MDP and designed a TD3 algorithm to determine offloading decision and resource allocation mechanisms.

2.2. DRL-Based Approaches to Jointly Minimize Energy Consumption and Latency

DRL-based algorithms are used to minimize the weighted sum of energy consumption and latency under various constraints. Liu et al. [21] modeled a computation task offloading problem as a partially observable MDP to minimize energy consumption and latency in vehicular edge computing (VEC) networks. They introduced a subtask priority scheduling method based on a directed acyclic graph (DAG) structure to guarantee the priority order of subtasks. They also proposed a DRL-based optimized distributed computation offloading (ODCO) scheme to optimize resource allocation. They did not consider a complex real-world scenario for vehicular networks and focused only on minimizing the average latency and energy consumption of vehicles. Tang et al. [24] formulated an optimization problem to minimize energy consumption and task execution latency in a UAV-assisted mobile edge computing (MEC) system considering the device offloading priority. They used DRL for dynamic trajectory planning supported by matching theory to solve scheduling and computing resource allocation.

PPO and multi-agent PPO (MAPPO) algorithms are used to dynamically allocate resources. Ji et al. [22] proposed a semantic-aware multitask offloading network with the objective of maximizing the performance of the task execution of the semantic offloading system, leading to reduced task execution time and energy consumption. A MAPPO algorithm is used to perform resource allocation in a distributed manner with low computational complexity. Si et al. [26] introduced a new UAV-assisted task offloading framework in the MEC system and developed task dependency and priority models. They formulated an optimization problem to jointly minimize system latency and the energy consumption of computational tasks. They combined asynchronous federated learning (FL) and the PPO algorithm to solve the minimization problem. The PPO algorithm is used to determine dynamic offloading decisions, while an asynchronous federated learning mechanism is used to train models that ensure data privacy.

DRL-based deep Q-learning network (DQN) algorithms are employed to solve the resource allocation. Song et al. [20] introduced a scheme for heterogeneous multiserver computation offloading (HMSCO) assisted by UAVs in the MEC network. They formulated a minimization problem to reduce the system cost, which consists of a weighted sum of latency and energy consumption under the constraints of reliability requirements, maximum tolerable latency, computational resource limits, minimum communication rate, transmission power range, and interference threshold. They decomposed the minimization problem into two subproblems and solved it using game theory and a multi-agent enhanced dueling double deep Q-network (ED3QN) with centralized training and distributed execution.

Zeng et al. [23] designed a task offloading strategy to minimize task execution latency and energy consumption in a device-edge-cloud architecture. They first introduced a serial particle swarm optimization (SPSO) algorithm to find an optimal connected MEC node for each task. Then they designed a prioritized experience replay-based double deep Q-learning network (PERDDQN) to jointly optimize offloading ratio and resource allocation in the task offloading process. Shinde et al. [25] formulated an optimization problem to minimize latency and energy costs considering the appropriate time scales in the vehicle network enabled by VEC. They proposed a DQN-based multi-time scale MDP algorithm to jointly solve the service placement, network selection, and offloading problem.

2.3. DRL-Based Approaches to Minimize Latency

DRL-based algorithms are used to solve the resource allocation problem and minimize latency. Yahya et al. [39] presented a novel ratio-based offloading approach in a two-tier V2X network that covers both vertical and horizontal offloading. They used metaheuristic simulated annealing (SA) and TD3 algorithms to minimize system latency by optimizing offload ratios. Lin et al. [31] proposed a scheme in which each vehicle can select an appropriate RSU to offload its application. The computed application is delivered to the vehicle after being computed with the cooperation of the RSUs. A joint optimization problem is formulated to minimize latency and maximize reliability by determining the amount of uploading, computing, and result downloading. They transformed the non-convex weighted sum problem into an MDP and used the MADDPG algorithm to minimize the termination time and the probable delivery failure penalty.

Fu et al. [35] formulated a base station (BS) deployment optimization problem to maximize the communication coverage ratio of vehicular networks under the constraints of moving velocity, energy consumption, and communication coverage radius. They modeled the prolonged decision-making process with a dual-layered decision loop in a multi-UAV vehicular network scenario. To solve the optimization problem, they developed a dense multi-agent reinforcement learning (DMARL) algorithm based on a dual-layer nested decision-making structure, decentralized deployment, and centralized training. Wu et al. [36] formulated a resource allocation problem as an optimization problem to minimize the utility of the system under the constraint of ultra-reliable low-latency communications (URLLC). They considered a heterogeneous VEC with various communication technologies and multiple types of tasks. They modeled the URLLC constraint using the stochastic network calculus (SNC) and then introduced a Lyapunov-guided DRL approach to convert and solve the optimization problem. Their proposed method requires retraining the model as the types of tasks continue to grow.

DQN and advantage actor-critic (A2C)-based algorithms are used to determine the offloading decision and solve the resource allocation problem. Shen et al. [32] proposed a collaborative Internet of vehicles (IoV) architecture with integrated software-defined networking (SDN) based on cloud-edge clusters. They introduced a dynamic pricing model to deal with the complexity of the resource management problem and formulated a mathematical model with the objective of minimizing computation latency and maximizing the profits of edge service providers (ESPs). A clustering algorithm is used to determine offloading decisions and reduce the action space, while the DDQN algorithm is applied to achieve the optimal strategy for allocating computational resources. Zeinali et al. [33] introduced a joint BS assignment and resource allocation (JBSRA) framework for mobile V2X users considering co-existence schemes based on the flexible duty cycle (DC) mechanism for unlicensed bands. They formulated an optimization problem to maximize the average throughput of the V2X network while satisfying the throughput of WiFi users and used the DDPG and DQN algorithms to solve the resource allocation problem.

Aung et al. [34] investigated a simultaneously transmitting and reflecting re-configurable intelligent surface (STAR-RIS)-assisted V2X network and formulated an optimization problem to maximize the achievable data rate for V2I users while guaranteeing latency and the reliability of V2V pairs. The MINLP is decomposed into two subproblems and solved using DDQN with an attention mechanism and implementing a standard optimization-based approach. Ding et al. [37] formulated a joint task offloading and resource management problem to maximize computation efficiency in a MEC-enabled heterogeneous network. They proposed an advantage A2C-based joint task offloading and resource allocation algorithm to find the offloading strategy, transmit power, and computing frequencies under constraints of the maximum consumed energy, the offloading time, the computing frequencies, and the maximum transmit power.

2.4. Traditional Optimization Approaches to Minimize Energy Consumption and Latency

Traditional (conventional) optimization is employed to minimize energy consumption and latency in the resource allocation problem. Hwang et al. [11] formulated an ILP resource management problem to minimize the number of active remote radio heads (RRHs) subject to uplink data rate constraints and V2X QoS requirements. They solved the resource allocation problem using an optimal algorithm to appropriately associate vehicles with RRHs. They proposed heuristic algorithms to deal with the complexity of large-size scenarios. Ma et al. [27] proposed a novel low-complexity distributed algorithm to minimize average latency and energy consumption in a vehicular edge computing system. They used the alternating-direction method of multipliers for equal resource allocation using distributed latency-aware collaborative computing. They used distributed energy-aware collaborative computing to optimize the partial offloading ratio and the local computation resource allocation ratio.

Zhang et al. [28] proposed a two-tier task offloading structure for a multiuser multi-server edge Internet of things (IoT) system. They formulated an optimization problem to minimize task processing latency and energy consumption. They solved the minimization problem by combining a genetic algorithm (GA) and particle swarm optimization (PSO) computation offloading algorithms to perform global and local searches. Tan et al. [29] formulated a joint optimization problem to minimize total task response times and communication energy while satisfying computational energy constraints. They developed a decentralized convex optimization approach to decompose a holistic MINLP into a hierarchy of convex optimization problems. The optimization problem is decoupled into two subproblems: resource allocation and task offloading. To achieve a near-optimal solution, the resource allocation subproblem is solved in a decentralized manner, while task offloading is solved using a probability-based solution.

Yang et al. [30] proposed a traffic model based on a stochastic geometry framework to simulate a real traffic scenario of autonomous driving vehicles. They formulated an average-cost minimization problem to reduce the processing task cost in a distributed computation offloading environment based on MEC. The optimization problem is divided into several subproblems and is solved using Lagrange multipliers with Karush–Kuhn–Tucker (KKT) constraints. Liu et al. [38] introduced a joint computation offloading and resource allocation strategy to build green V2X networks with MEC and integrated sensing and communication (ISAC) technologies. They formulated an optimization problem to minimize the queuing latency of computing tasks while satisfying the constraints on latency and energy consumption constraints. The minimization problem is reformulated using the Lyapunov optimization method to transfer latency and energy constraints to queue stability problems. A joint computation offloading and resource allocation (JCORA) scheme is proposed to reduce energy consumption under the task latency constraint.

3. System Model and Problem Formulation

This section describes the architecture of the 6G V2X Open RAN, communication and computation models, problem formulation, and the DRL allocation framework. Table 2 summarizes the mathematical notation used in this paper.

Table 2. Mathematical notations used throughout this paper.

Symbol	Meaning
$P_v$	Transmission power of vehicle v
$d_{n,v}$	Distance between vehicle v and RSU n
$\alpha$	Attenuation factor: calculated from the COST 231–Hata Model [40]
$N_0$	Power spectral density of white noise source
$I_{\mathrm{tot}}$	Aggregated uplink ICI representing interference power level of RSUs
$I_i$	Mean value of uplink ICI for RSU i
C	RSU coverage (in kilometers)
$\kappa$	Distance between the vehicle and the interfering RSU (in kilometers)
$\rho$	Distance from transmitter to receiver (in kilometers)
$\vartheta$	Vehicle’s angle to direct line connecting target RSU to interfering RSU
N	Set of RSUs
V	Set of vehicles
$M_n$	Available uplink RBs per time slot for RSU n
$F_n$	Maximum available computation capacity of RSU n
${\mathcal{L}}_v$	Maximum allowed latency for vehicle v
$R_{n,v}$	Required RBs per time slot to send data
$H_{n,v}$	Threshold value for ${\Gamma }_{n,v}$
$U_{n,v}$	Required uplink data rate of vehicle v
${\mathcal{U}}_{n,v}$	Link capacity between vehicle v and RSU n
${\psi }_n^V$	Energy coefficient associated with chip architecture of RSU server
$x_n$	Decision variable to turn on/off RSU n
$y_n^v$	Decision variable indicating whether vehicle v is associated with RSU n or not
$z_v$	Decision variable indicating whether vehicle v is not allocated

3.1. Network Model

We consider a 6G V2X Open RAN computing infrastructure consisting of sets of vehicles and RSUs that provides new radio communication capabilities to the vehicles. RSUs are densely deployed closer to vehicles and provide computing and communication capabilities to end users. In our model of the system under study, as shown in Figure 2, vehicles need to upload their tasks to the RSUs for processing. In particular, we investigate a scenario consisting of a set of RSUs ($n=1, 2, \dots , N$) and a set of vehicles ($v=1, 2, \dots , V$). Each RSU n has a number of RBs available per time slot, indicated by $M_n$. Each vehicle v, if it is associated with RSU n, will require several RBs per time interval to send the sensing data, indicated by $R_{n,v}$. The required number of RBs depends on the SINR values and the uplink data rates.

Figure 2. A small example of V2X network topology.

3.2. Communication Model

Given the number of RSUs with available uplink RBs and the number of vehicles with RBs required to send data to RSUs, we need to decide whether to turn the RSU on or off and determine the optimal associations of vehicles with RSUs. Our goal aims at reducing the number of turned-on RSUs depending on the required tasks and subject to the uplink bandwidth constraints exemplified by ICI and SINR.

SINR can be expressed as the signal power divided by the noise power plus the interference power of other signals in the network. SINR can be calculated from the transmission power of the vehicle and the interference power level of other interferer RSUs in the network. SINR values for uplink transmission can be obtained as

$${\Gamma }_{n,v}=P_v d_{n,v}^{-\alpha } {\left(N_0+I_{\mathrm{tot}}\right)}^{-1},$$

(1)

where $P_v$ is the transmission power of the vehicle v; $d_{n,v}$ is the distance between the vehicle v and the center of the RSU n; $\alpha$ is the attenuation factor, that is, the path loss, calculated from the COST 231–Hata Model [40]; $N_0$ is the power spectral density of a white noise source; and $I_{\mathrm{tot}}$ is the aggregated uplink ICI.

Assuming that the network model is fully loaded with traffic, omnidirectional antennas are used, and the regular coverage pattern occurs, we could approximate the uplink ICI from the RSU n with a log-normal distribution by analytically determining the statistical parameters [41]. Therefore, the aggregated uplink ICI, $I_{\mathrm{tot}}$, is approximated with another log-normal distribution and calculated according to

$$I_{\mathrm{tot}}=\sum _{i=1,i\ne n}^N{I}_i,$$

(2)

where $I_i$ is the mean value of the uplink ICI of the interfering RSU i, and for each RSU, only a single interference source is considered since only one vehicle is scheduled per RB. $I_i$ is computed as (in this paper, we focus on the optimization problem rather than on the interference and SINR; for further details, we refer the reader to [41])

$$I_i={\displaystyle \frac{1}{\pi }}{\int }_0^C{\int }_0^{2\pi }{P}_v{C}^{-2}{\rho }^{1+\alpha }{({\kappa }^2+{\rho }^2+2\kappa \rho cos\vartheta )}^{-{\displaystyle \frac{\alpha }{2}}} d\rho d\vartheta ,$$

(3)

where C is the coverage of the RSU in kilometers, $\kappa$ is the distance between the vehicle and the interferer RSU in kilometers, $\rho$ is the distance from the transmitter to the receiver in kilometers, $\vartheta$ is the angle of the vehicle to the directed line connecting the target RSU to the interferer RSU, and ${({\kappa }^2+{\rho }^2+2\kappa \rho cos\vartheta )}^{1/2}$ denotes the Euclidean distance between the target RSU and the interferer RSU [41].

After calculating the SINR values for each vehicle, we need to calculate the RB data rate according to the SINR value, channel quality indicator (CQI) index and efficiency from the mapping table that determines various CQI indices based on different modulation orders, SINR ranges, and efficiencies [42]. We use this mapping to obtain the number of necessary RBs. For the sake of simplicity, we consider both vehicles and RSUs forming the network working in single-input-single-output (SISO) mode [42]. The CQI index is calculated in the vehicle and reported to the RSU. We use the CQI to determine the efficiency and calculate the data rate of an RB. An RB per time slot of 0.25 milliseconds consists of 12 subcarriers of 60 kHz wide in frequency, and each subcarrier consists of 14 symbols. Accordingly, the data rate of an RB (bits/milliseconds) is calculated as

$${dr}_{RB}=12\times 14\times \mathrm{efficiency}.$$

(4)

After calculating the data rates of the RBs, we can determine the number of RBs ($R_{n,v}$) requested by each vehicle to execute its uplink task. $R_{n,v}$ depends on the uplink and RB’s data rates, i.e., $U_{n,v}$ and ${dr}_{RB}$. We use the following formula:

$$R_{n,v}={\displaystyle \frac{U_{n,v}}{{dr}_{RB}}}.$$

(5)

3.3. Computation Model

In our model, the tasks of the vehicles are offloaded to RSUs equipped with computational capabilities to process traffic volumes. The computation task is related to both energy consumption (in joules) and processing (in seconds). There are three stages to accomplish task computation: (i) task uploading, (ii) task computing, and (iii) task downloading. Depending on the computation and communication demands, the vehicles will experience latencies influenced by the computing and communication capacities of the RSUs. The uplink and downlink bandwidths influence the communication latency. We neglect the downloading latency due to the small size of the computed tasks and the high data rates of the RSUs. The task of vehicle v is represented by the communication demand $D_v$ (in bits) and the computation demand ${\Phi }_v$ (in CPU cycles per bit). We denote the task offloading time by $L_{n,v}$, which includes the uploading time ${\mathcal{l}}_{n,v}^u$ and the processing time ${\mathcal{l}}_{n,v}^p$. We calculate $L_{n,v}$ as

$$L_{n,v}={\mathcal{l}}_{n,v}^u+{\mathcal{l}}_{n,v}^p,$$

(6)

where

$${\mathcal{l}}_{n,v}^u=D_v {\left(U_{n,v}\right)}^{-1},$$

(7)

and

$${\mathcal{l}}_{n,v}^p=D_v {\Phi }_v {\left(f_{n,v}\right)}^{-1}.$$

(8)

$U_{n,v}$ is the communication capacity (throughput or data transmission rate from vehicle v to RSU n in bits per second). $U_{n,v}$ is calculated from the SINR mapping table for the throughput of 5G New Radio (NR) with a bandwidth of 100 MHz and a subcarrier spacing of 60 kHz [43].

$f_{n,v}$ is the computing power assigned from RSU n to vehicle v in CPU cycles per second (computation capacity). The energy consumption of the computation task $E_{n,v}$ includes the consumptions resulting from offloading and execution. We denote the transmission energy consumption with $e_{n,v}^u$ and the processing energy consumption with $e_{n,v}^p$. We can calculate $E_{n,v}$ as

$$E_{n,v}=e_{n,v}^u+e_{n,v}^p,$$

(9)

where

$$e_{n,v}^u=P_v D_v {\left({\mathcal{U}}_{n,v}\right)}^{-1},$$

(10)

and

$$e_{n,v}^p={\psi }_n^V D_v {\Phi }_v {\left(f_{n,v}\right)}^2.$$

(11)

$P_v$ is the transmit power of vehicles v. ${\psi }_n^V$ is the energy coefficient associated with the chip architecture of the RSU server (effective capacitance coefficient for each CPU cycle of the RSU).

3.4. Optimization Model

Considering N RSUs with a number of available uplink RBs (namely, ${\mathit{M}}_n$) and V vehicles with a number of required RBs per time slot for sending the sensing data from vehicle v to the RSU n (namely, $R_{n,v}$), we need to determine $y_{n,v}$, which denotes whether the vehicle v is associated with RSU n or not; $x_n$, which indicates whether to turn the RSU n on or off; and $z_v$, which determines whether a vehicle is not allocated. The whole optimization problem minimizes the number of active RSUs and the energy consumption while satisfying the constraints on maximum allowed latency and the available resources. We formulate it as follows:

$$\begin{array}{c}\hfill min {\omega }_1\sum _{n\in N}{x}_n + {\omega }_2\sum _{n\in N}\sum _{v\in V}{E}_{n,v} y_{n,v} + {\omega }_3\sum _{v\in V}{z}_v\end{array}$$

(12)

$$\begin{array}{c}\hfill \mathrm{s}.\mathrm{t}. \sum _{v\in V}{R}_{n,v} y_{n,v}\le M_n, n\in N,\end{array}$$

(13)

$$\begin{array}{c}\hfill \sum _{v\in V}{\Gamma }_{n,v} y_{n,v}\ge H_{n,v}, n\in N,\end{array}$$

(14)

$$\begin{array}{c}\hfill \sum _{v\in V}{f}_{n,v} y_{n,v}\le F_n, n\in N,\end{array}$$

(15)

$$\begin{array}{c}\hfill \sum _{n\in N}{L}_{n,v} y_{n,v}\le {\mathcal{L}}_v, v\in V,\end{array}$$

(16)

$$\begin{array}{c}\hfill \sum _{n\in N}{y}_{n,v} + z_v=1, v\in V,\end{array}$$

(17)

$$\begin{array}{c}\hfill x_n\ge y_{n,v}, n\in N,v\in V,\end{array}$$

(18)

$$\begin{array}{c}\hfill x_n,z_v, y_{n,v}\in \{0,1\}, n\in N,v\in V.\end{array}$$

(19)

Our objective (12) is to jointly minimize the weighted sum of active RSUs and overall energy consumption. The above-mentioned objective function is subject to the following requirements: constraint (13) ensures that the number of required RBs per time slot to uplink data from vehicle v to the RSU n should not exceed the number of available uplink RBs at the RSU n, constraint (14) indicates that vehicle v can be assigned to RSU n if the predicted SINR is larger than the assumed threshold H, constraint (15) guarantees that the computational capacity assigned from RSU n to vehicle v should not exceed the maximum available computational capacity of RSU n, constraint (16) ensures that the task offloading time from vehicle v to RSU n should not exceed the maximum allowed latency for vehicle v, constraint (17) states that each allocated vehicle v should be associated with one and only one RSU, constraint (18) ensures that vehicle v can be connected to RSU n only if RSU n is turned on, and constraint (19) indicates the lower and the upper bounds of the binary decision variables.

In complex real-world V2X environments, rapid solutions are required for the combinatorial optimization model presented in (12)–(19). Therefore, approximate solutions are used for real-time allocation. We implement a DRL environment to provide online allocation, where we consider a snapshot of vehicle locations instead of mobility to reduce the complexity of the model. As we focus on uplink in 6G V2X Open RAN, the effect of mobility can be neglected.

3.5. Energy-Efficient Deep Reinforcement Learning Allocation Framework

We formulate the problem of (12) as an MDP and leverage DRL to solve it. In a DRL-based algorithm, an agent can make decisions in real time by interacting with the environment without the need for prior data sets. The agent reviews and updates its policy using a trial-and-error method. A correct description of the underlying process can be advantageous for a successful implementation of DRL-based algorithms, for example, when considering control strategies in wireless communications [44] or nonlinear power systems [45].

A classical MDP is mathematically characterized by the tuple $\left\{\mathcal{S},\mathcal{A},\mathcal{P},\Gamma ,\mathcal{R}\right\}$. $\mathcal{S}$ represents the state space, $\mathcal{A}$ represents the action space, $\mathcal{P}$ represents the transition probability from the current state s to the next state $s^{\prime }$, $\Gamma$ represents the discount factor to achieve trade-off between the current reward and the future reward, and $\mathcal{R}$ represents the reward function.

We formulate the contexts of a state, an action, and a reward within the framework of V2X with the RSUs network based on the PPO algorithm. Figure 3 illustrates the structure of the PPO-based allocation, consisting of a V2X environment and an agent. The agent uses system information states s, such as computation and communication capacity, to determine the optimal allocation decision a, resulting in a high reward r (indicative of low energy consumption), thus altering the condition of the system to $s^{\prime }$. The V2X environment includes the connections to gNB, where the DRL framework is implemented. The DRL framework covers an area composed of several RSUs.

Figure 3. PPO-based resource allocation framework.

In our 6G V2X Open RAN topology, vehicles are assigned to the infrastructure such as RSUs to process their tasks. The RSUs receive vehicle traffic and decide the amount of resources to be allocated to the vehicle to process its task and minimize energy consumption. The system control plane, which serves as the assignment agent, makes the assignment and allocation decisions. The assignment agent is deployed within an RSU. This learning agent requires environmental information and trains using prior experience to determine the best action. The prior experience has the form of state, action, next-state, and reward $(s,a,s^{\prime },r)$. The agent will learn to take the best action during the state of a particular environment.

3.5.1. State

The state represents the status of the current system, which can be determined by monitoring system parameters such as uplink data rates, link capacity, communication capacity, computation capacity, latency, and system energy consumption. The action will transit the state from s to $s^{\prime }$ with larger or smaller energy consumption. The optimal action minimizes system energy consumption and is positively rewarded. The following states constitute the 6G V2X Open RAN system information: uplink data rate ($U_{n,v}$), uplink capacity (${\mathcal{U}}_{n,v}$), uplink RBs ($M_n$), computing resources ($F_n$), and tolerable latency (${\mathcal{L}}_v$). The state space of the assignment agent at time t can be defined as

$$s_t=\{U_t, F_t, L_t\},$$

(20)

where $U_t$ denotes communication resources, $F_t$ denotes computing resources, and $L_t$ denotes allowed latency.

3.5.2. Action

The action space represents the allocation status of all vehicles. The action space of the assignment agent at time t can be expressed as

$$a_t=\{a_t^x, a_t^y, a_t^z\},$$

(21)

where $a_t^x$ denotes the action of turning on/off the RSU, $a_t^y$ denotes the action of associating the vehicle with the RSU, and $a_t^z$ denotes the action that determines whether the vehicle is not allocated. The action space is restricted to include only feasible actions, which ensures that constraints (13)–(19) are satisfied.

3.5.3. Reward

The reward function is formed corresponding to the objective in (12). Since our objective is to minimize energy consumption as much as possible, computational tasks with higher energy consumption in time t ($E_t$) should be assigned a smaller reward value. The objective of DRL is to maximize the reward function for an action made in time t, which can be expressed as

$$r_t={\displaystyle \frac{1}{E_t}}.$$

(22)

3.5.4. PPO Algorithm

Our proposed PPO-based algorithm uses an artificial neural network (NN) with an actor-critic framework. The PPO algorithm is selected for its stability and efficiency as a policy-based RL algorithm. The training process of the proposed algorithm is illustrated in Algorithm 1. The critic NN is based on a value function, where the state of the environment changes when the actor NN takes an action $a_t$. The critic NN takes the state $s_t$ as input and returns the state-value function as

$$V^{\pi }\left(s_t\right)={\mathbb{E}}_{\pi }\left[\sum _{\tau =0}^{\infty }\gamma · r_{\tau }(s_{\tau },a_{\tau })\mid s_0=s_t\right]={\mathbb{E}}_{\pi }\left[r_t(s_t,a_t)+\gamma · V^{\pi }\left(s_{t+1}\right)\mid s_o=s_t\right],$$

(23)

where ${\mathbb{E}}_{\pi }$ is the estimator of the policy $\pi$ and $\gamma$ is the discount factor. The critic NN returns the state-action value as

$$Q^{\pi }(s_t,a_t)={\mathbb{E}}_{\pi }\left[\sum _{\tau =0}^{\infty }\gamma · r_{\tau }(s_{\tau },a_{\tau })\mid s_0=s_t, a_0=a_t\right].$$

(24)

The advantage function that represents the difference between the current Q value and the average can be calculated as

$$A^{\pi }(s_t,a_t)=Q^{\pi }(s_t,a_t)-V^{\pi }(s_t,a_t).$$

(25)

The actor network is updated using PPO by the ratio of the new policy and the old policy to ensure stability. The loss function of the actor network can be determined as

$$L\left(\theta \right)={\widehat{\mathbb{E}}}_t\left[{\displaystyle \frac{{\pi }_{\theta }(a_t\mid s_t)}{{\pi }_{{\theta }_{old}}(a_t\mid s_t)}} {\widehat{A}}_t-\beta \mathrm{clip}\left[{\pi }_{{\theta }_{old}}(· \mid s_t), {\pi }_{\theta }( · \mid s_t)\right]\right],$$

(26)

where ${\pi }_{\theta }$ is a random policy function, $\beta$ is a penalty coefficient, and ${\widehat{A}}_t$ is an estimator of the advantage function at time t.    

Algorithm 1:Resource Allocation Algorithm Based on PPO

4. Simulations and Results

This section analyzes the performance of our proposed model by comparing optimal and DRL energy-efficient solutions for 6G V2X systems. In particular, we define different scenarios with a maximum number of RSUs, number of vehicles, and deployment area per scenario, as shown in Table 3, where the density of RSUs is 126 RSUs per km², the density of vehicles is 1000 vehicles per km², and the maximum allowed latency values range from 50 to 20 ms.

Table 3. Configuration of scenarios.

Scenario	1	2	3	4	5	6	7	8	9
Max. number of RSUs	4	6	8	10	12	14	16	18	20
Number of vehicles	32	48	63	79	95	111	127	143	159
Side (km)	0.178	0.218	0.252	0.282	0.309	0.333	0.356	0.378	0.398
Area (km2)	0.032	0.048	0.064	0.079	0.095	0.111	0.127	0.143	0.159

4.1. Simulation Environment

The simulation environment is written in Python 3.11 and is carried out on a Core i9 13th gen processor, 64 GB RAM, and an RTX 4080 GPU. Table 4 lists the parameter values that are used in the calculations and evaluations. The values are assumed according to the service requirements for 6G V2X services and to guarantee the QoS requirements of the communications system [46].

Table 4. Parameter values used in the evaluation.

Parameter	Value	Parameter	Value
$\alpha$	4	$N_0$	−174 dBm/Hz
C	0.2 km	${\mathcal{P}}_v$	23–33 dBm
$M_n$	135 RBs	$H_{n,v}$	−7 dB
$F_n$	20 GHz	$U_{n,v}$	50–100 Mbps
${\mathcal{L}}_v$	50–20 ms	$D_v$	10–60 kbit

To compute the optimal solutions of the problem (12)–(19) for the scenarios presented in Table 3, we use the CPLEX optimizer [12]. For the DRL implementation, we use the Python libraries Gymnasium [47] and Stable-Baselines3 [48]. In order to compare the optimal solution with the proposed DRL solution, we conduct 96 repetitions for the scenarios under consideration.

4.2. Implementation of the DRL Framework

In this work, we consider the Open RAN architecture, where critical tasks like 6G V2X allocation can be performed in a near-real-time computing environment. Support operations, such as ML training, are performed in a distinct, non-real-time computing environment [6].

In Table 5, we collect important details for the deployment of the DRL framework. For each scenario in Table 3, we performed several training runs, considering a variety of learning rates and training timesteps for the PPO algorithm. The range of train durations spans 1.67 min for 32 vehicles to 224.5 min for 159 vehicles. These durations were selected to achieve good optimal performance in the optimization task after policy stabilization.

Table 5. DRL training details.

Scenario	Learning Rate	Training Timesteps (k Step)	Train Duration (min)	Step Duration (ms)	Model Size (MiB)
1	$5.1\times {10}^{-4}$	$10.2$–$64.5$	1.67	2.2	1.43
	$1.9\times {10}^{-4}$	$128.6$–$200.7$	3.79	1.5
2	$1.2\times {10}^{-3}$	$10.8$–$64.5$	2.08	2.9	2.22
	$9.9\times {10}^{-4}$	$124.4$–$202.8$	7.29	2.4
3	$3.0\times {10}^{-4}$	$45.7$–$64.5$	7.09	7.1	3.13
	3.0 × 10 −5	201.6	14.9	4.4
4	3.0 × 10 −4	65.7	17.23	15.7	4.17
	3.0 × 10 −5	202.2	28.61	8.5
5	3.0 × 10 −4	66.9–103.4	24.85	20.9	5.33
	3.0 × 10 −5	200.6	42.02	12.6
6	3.0 × 10 −4	67.5	52.99	47.1	6.60
	3.0 × 10 −5	206.0	122.08	35.6
7	3.0 × 10 −4	32.5–65.0	42.51	53.1	7.99
	3.0 × 10 −5	203.2	105.88	31.3
8	3.0 × 10 −5	201.3	283.52	84.5	9.50
9	3.0 × 10 −5	203.5	224.53	66.2	11.12

After the initial training is performed, the resulting DRL model can be re-trained online in the non-real-time computing environment to adapt to the variations of live V2X network environments. To address critical aspects of real-world 6G V2X communications, including sudden network congestion, operational interference, and seasonal or time-of-day variations, quick model retraining is essential. As the DRL model is already in an operational state, a short number of training timesteps are required to accommodate the new environmental conditions.

In Table 5, we can appreciate that the step duration ranges from 1.5 ms to 84.5 ms, allowing for a model retraining rate of 1.4 k steps per minute for a mid-range training step duration of 43 ms. The last column of the aforementioned Table 5 presents the size of the model in MiB for each scenario, the largest size being 11.12 MiB. The small footprint of the DRL models makes them suitable for deployment in the near-real-time computation environment of an Open RAN 6G V2X communication system.

4.3. Results Evaluation

The experiment results are organized to compare the optimal versus DRL solutions. We obtained the optimal solutions by solving the resource allocation problem (12)–(19) using the CPLEX optimizer [12] and the DRL solutions by implementing the PPO-based Algorithm 1. We explore the impact of the number of vehicles on the following aspects:

• Number of active RSUs;
• System energy consumption;
• Energy consumption per active RSU;
• Proportion of active RSUs.

Figure 4 shows the impact of the number of vehicles on the number of RSUs to be turned on for different allowed latencies. The number of active RSUs represents a partial goal of our objective function in (12). The number of activated RSUs depended on the association of the vehicle with the RSUs and RBs required to perform vehicle tasks. Intuitively, as the number of vehicles increased, so did the number of active RSUs. We noticed that the number of active RSUs according to optimal solutions ranged between 2 and 6 to serve 32 to 159 vehicles. We also observed that the number of RSUs turned on according to the DRL solutions ranged from 2.5 to 10 RSUs to serve vehicles ranging from 32 to 159. The number of vehicles increased 5 times, while the number of active RSUs increased 3 and 4 times, implying that optimal and DRL allocations led to a reduction in the number of RSUs that must be turned on and save energy.

Figure 4. Number of vehicles vs. number of active RSUs.

Figure 5 shows the impact of the number of vehicles on the energy consumption for the maximum tolerable latency range of 20 to 50 ms. The energy consumption of the system represents a partial goal of the objective function in (12). The energy consumed depended on the number of vehicles and their associations with active RSUs. Intuitively, as the number of vehicles increased, so did the energy consumption. We observed that, to process the tasks of 32 vehicles, the average energy consumption according to optimal and DRL solutions was 2.5 and 3.5 millijoules, respectively. We also noticed that, to process the tasks of 159 vehicles, the average energy consumed according to optimal and DRL solutions was 6.3 and 11.9 millijoules, respectively. The percentage of energy added with the proposed DRL solution ranged between 40% and 88% in the scenarios of 32 and 159 vehicles, respectively. When the number of vehicles increased 5 times, the energy consumption increased 2.5 and 3.5 times for the optimal and DRL solution, respectively. This implies that optimal and DRL associations of vehicles with serving RSUs led to efficient resource utilization, minimization of energy consumption, and energy savings.

Figure 5. Number of vehicles vs. energy consumption.

Figure 6 shows the energy consumed per each active RSU for a different number of vehicles at various values of the maximum tolerable latency ranging from 50 to 20 milliseconds. The energy consumed per active RSU is an observed output, and it is calculated from the optimal solution of our objective function in (12). We noticed that the optimal solution showed a high increase in energy consumption per RSU when the latency level decreased. In contrast, the DRL solution is characterized by an equally balanced energy consumption per RSU regardless of the choice of latency level. We also observed that the average energy consumed per each active RSU according to optimal and DRL solutions was 1.06 and 1.09 millijoules, respectively. The maximum allowed latency decreased 2.5 times, while the energy consumption increased 1.2 times. This implies that the resource allocation of optimal and DRL solutions led to minimized energy consumption.

Figure 6. Number of vehicles vs. energy consumption per active RSU.

Figure 7 shows the percentage of the number of active RSUs for various numbers of vehicles with different values for the maximum allowed latency. We observed that, to serve 32 vehicles, the percentage of activated RSUs was 50 and 60 for optimal and DRL associations, respectively. We also noticed that, to serve the number of vehicles ranging from 48 to 159, the percentage of activated RSUs was 35 and 50 for optimal and DRL associations, respectively. The number of vehicles increased 1.5 to 5 times, while the percentage of activated RSUs decreased 1.2 to 1.4 times, implying that the optimal and DRL assignments of the vehicles to the RSUs led to a reduction in energy consumption.

Figure 7. Number of vehicles vs. proportion of active RSUs.

5. Conclusions

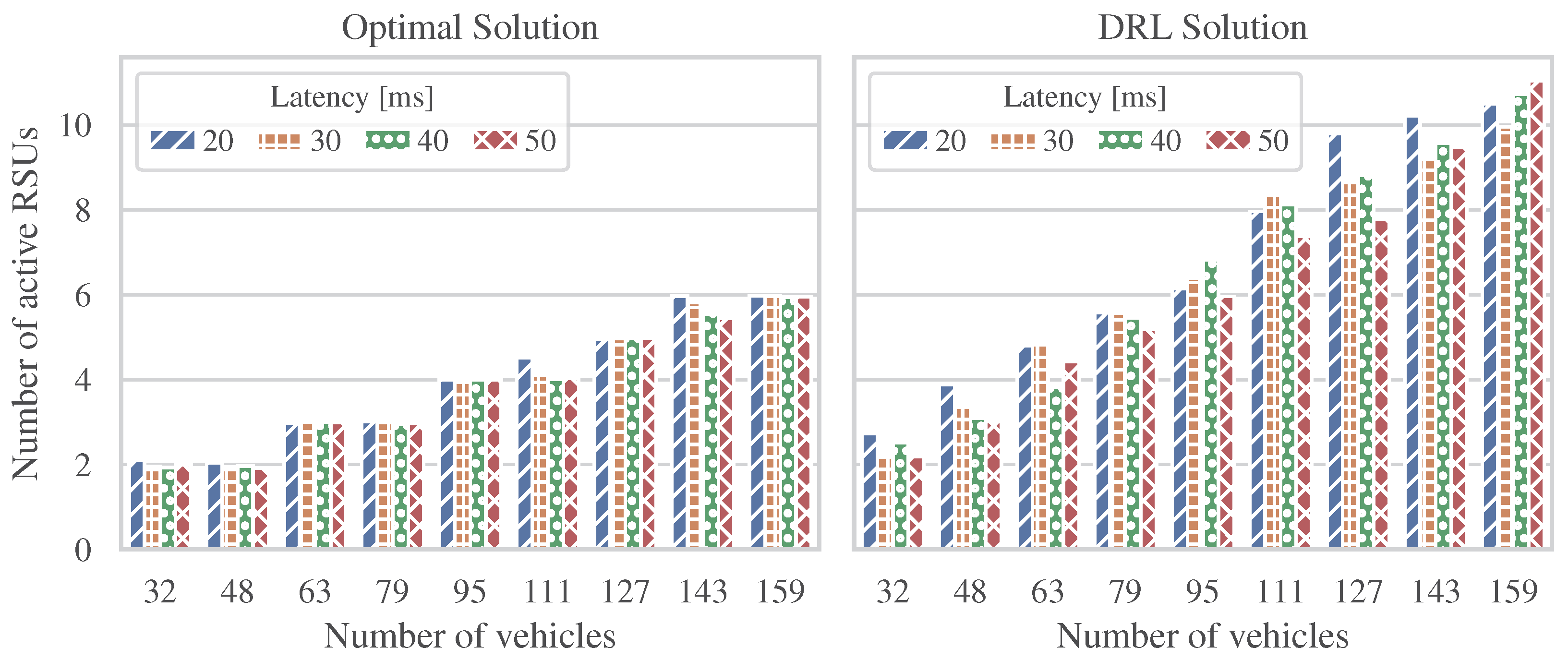
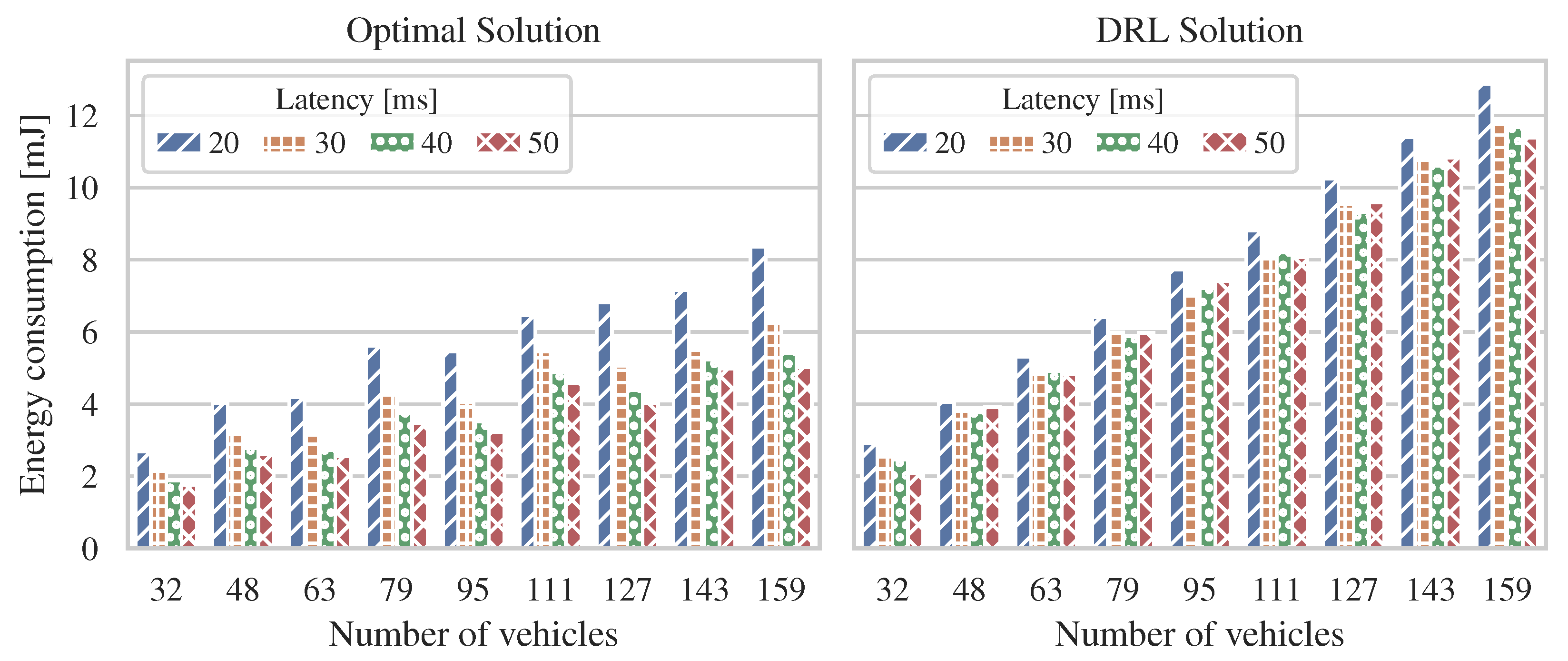
We investigated energy efficiency in 6G V2X communication systems and formulated an ILP-based optimization problem to reduce the energy consumption of the system. We obtained the optimal solutions using the CPLEX solver and implemented a DRL framework using the PPO algorithm. Under various simulated conditions, our research evaluated the DRL-PPO-derived allocation decisions against optimal centralized solutions.

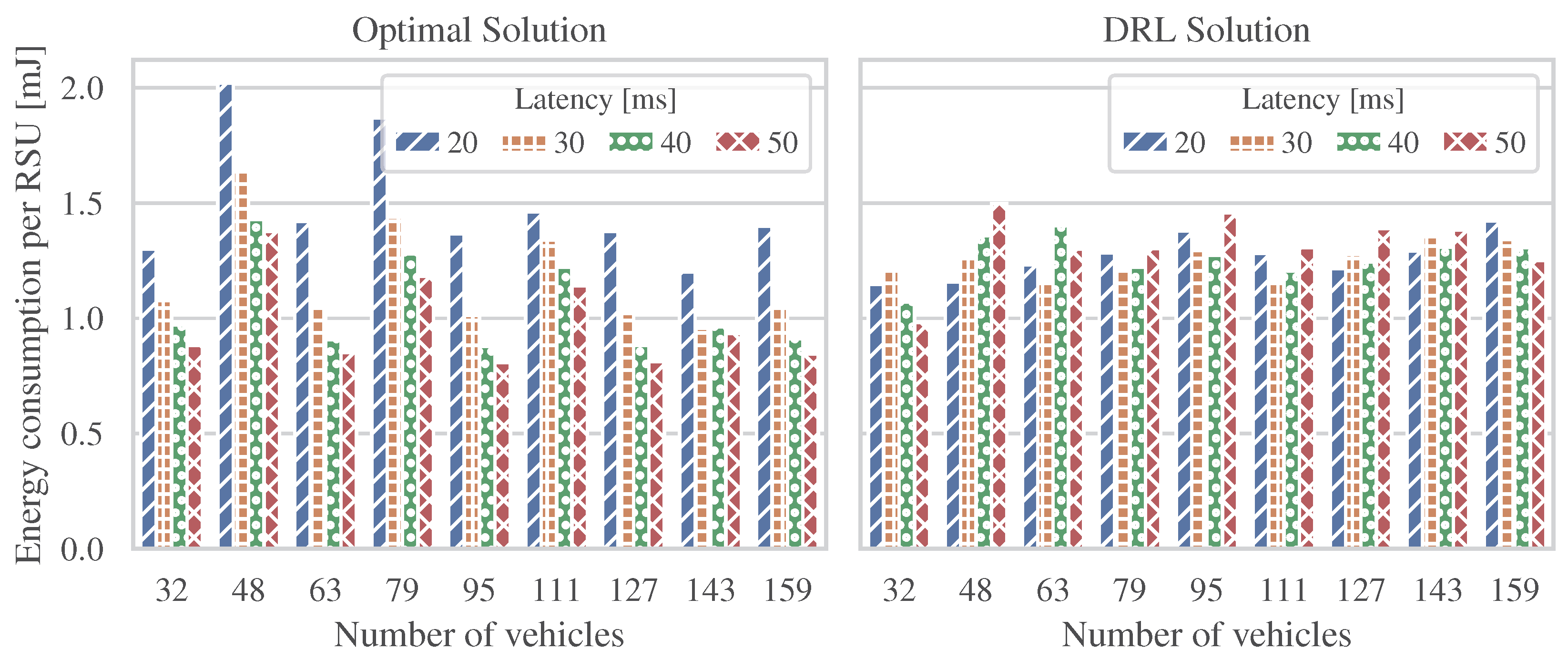
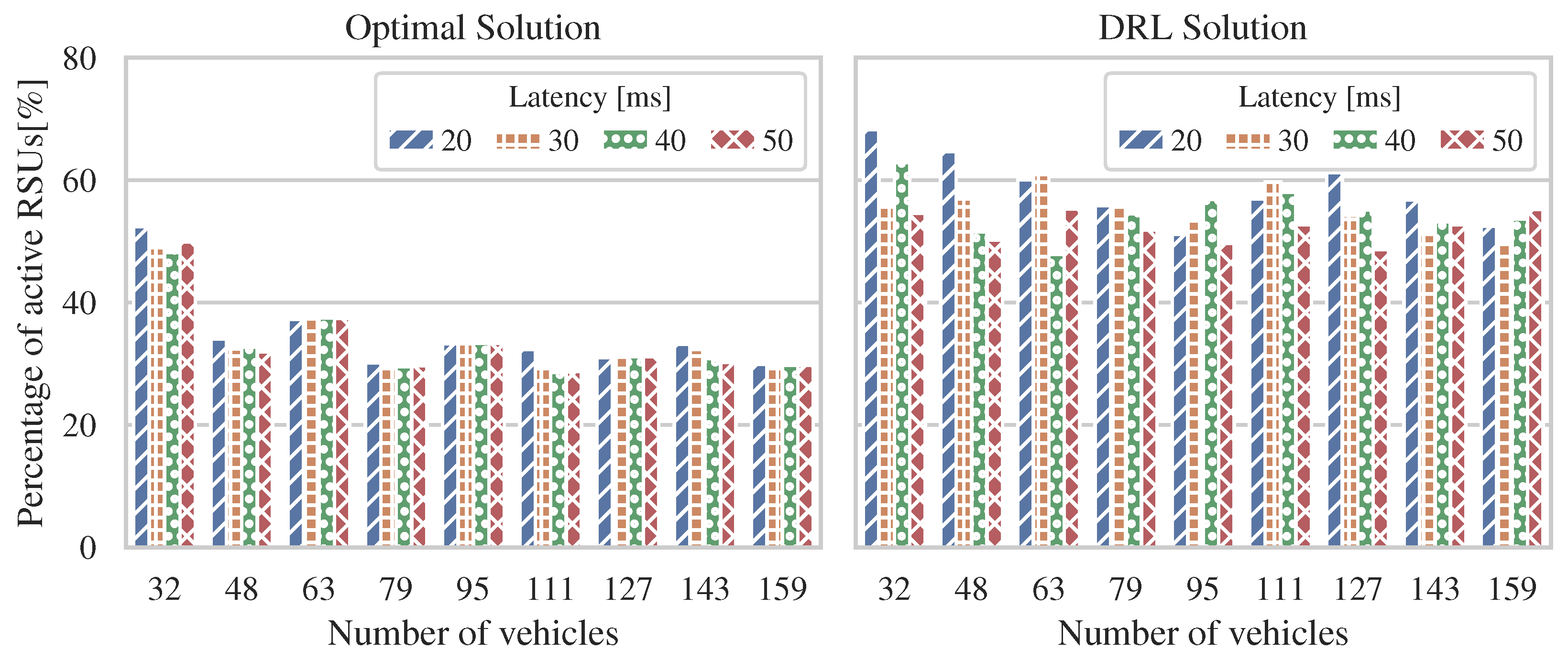
The energy consumption linearly increased with respect to the problem scale in both ILP-based and DRL-based solutions. The proposed DRL approach ran efficiently in the range of scenarios studied and produced dynamic decisions that approximated the optimal ones at acceptable energy consumption levels. An important aspect of the DRL-based solution is that even when different latency levels were studied, the calculated energy consumption per RSU remained stable in different scenarios.

Our numerical results illustrated that the proposed approach is appropriate for energy-saving operation in 6G V2X networks. The system model under study allowed us to minimize the energy consumption while satisfying the allowed latency levels to ensure 6G V2X communications.

For further research and future work, we plan to consider additional constraints (e.g., vehicle mobility), formulate multi-objective optimization models, and investigate the impact of different factors on the performance of the proposed model. We also plan to perform a comparative analysis between our PPO-based algorithm and alternative DRL approaches. In addition, we plan to address security and reliability concerns by validating the proposed model through real testbed experiments to assess its robustness and resilience.