Memory-Efficient Iterative Signal Detection for 6G Massive MIMO via Hybrid Quasi-Newton and Deep Q-Networks

Abstract

The advent of Sixth Generation (6G) wireless communication systems demands unprecedented data rates, ultra-low latency, and massive connectivity to support emerging applications such as extended reality, digital twins, and ubiquitous intelligent services. These stringent requirements call for the use of massive Multiple-Input Multiple-Output (m-MIMO) systems with hundreds or even thousands of antennas, which introduce substantial challenges for signal detection algorithms. Conventional linear detectors, especially the linear Minimum Mean Square Error (MMSE) detectors, face prohibitive computational complexity due to high-dimensional matrix inversions, and their performance remains inherently restricted by the limitations of linear processing. The current research suggested an Iterative Signal Detection (ISD) algorithm with significant limitations being occupied with the combination of Deep Q-Network (DQN) and Quasi-Newton algorithms. The method incorporates the Broyden-Net, which could be faster with less memory training than the model in the case of spatially correlated channels, a Quasi-Newton method, and DQN to improve the m-MIMO detection. The proposed techniques support the computational efficiency of realistic 6G systems and outperform linear detectors. The simulation findings proved that the DQN-improved Quasi-Newton algorithm is more appropriate than traditional algorithms, since it combines the reward design, limited memory updates, and adaptive interference mitigation to shorten convergence time by 60% and increase the confrontation to correlated fading.

1. Introduction

The invention of the Sixth Generation (6G) wireless networks with exclusive intelligence and connectivity capabilities to support various applications is transforming communication around the world. It is estimated that the 6G systems will offer a terabit per second data rate, and they will be capable of supporting more than 10 million connections per square kilometer, with an end-to-end latency of less than 0.1 ms. The demands of such hard-to-meet performance necessitate breakthroughs in Multiple-Input Multiple-Output (MIMO) technology, particularly in m-MIMO systems [1].

One of the key issues in this field is developing a research agenda for a MIMO detection system that is both scalable and computationally efficient. Two fundamental applications, smart manufacturing and industrial automation, are the drivers of these requirements. In particular, the interaction between autonomous systems, robotic production lines, and real-time predictive maintenance platforms, made possible by the Industry 4.0 framework, is increasingly based on ultra-reliable and low-latency communication to ensure optimal performance [2]. In [2], the weaknesses of conventional detection systems in such environments are emphasized, as the advanced iterative detection methods applied to industrial Internet of Things applications are provided to provide better operation in controlled environments. However, their findings also showed a decrease in performance in real-world fading channels with spatial correlation. The hybrid approach they employed to reduce complexity involved province decoding with successive interference cancellation, leading to a computational demand approximately 40% lower than Maximum Likelihood (ML) detection. The use of matrix inversion limits its applicability for the very large antenna arrays anticipated in 6G, as its computational cost scales cubically with antenna dimensions [1,2,3]. The combination of reconfigurable intelligent surfaces, three-dimensional beamforming, and terahertz band communication exacerbates the difficulties of 6G detection. The authors in [3] investigated the computational viability of detection strategies, such as iterative over-relaxation, Zero-Forcing (ZF), and Minimum Mean Square Error (MMSE), in such high-dimensional system settings. The authors in [3] demonstrated that computing overhead increases dramatically with antenna expansion, making traditional techniques infeasible. To reduce the complexity of the detection process, ref. [4] proposed a hybrid analog-digital beamforming architecture as a potential solution. To overcome the computational complexity of m-MIMO detection, sophisticated signal processing methods have been widely examined. Specifically, ref. [4] proposed an Approximate Message Passing (AMP)-based detection system, which has near-optimal performance and a linear computational cost. To verify performance, theoretical performance limits were developed, and spatially correlated channels that are characteristic of dense antenna arrays were considered. Nevertheless, the authors in [5] suggested an adaptive dampening mechanism that can guarantee convergence stability and increase robustness in unfavorable propagation conditions. Experimental results on a 128 MIMO testbed, 64 × 64 MIMO, showed that the Iterative Message-Passing (IMP) detector needed three orders of magnitude less complexity and a Bit Error Rate (BER) of merely 2 dB than ML detection. Techniques that are assisted by learning tasks, including optimization-based ones, like DetNet introduced by [5], can also possibly be used as an alternative to conventional detection mechanisms because of the scalability of m-MIMO. Using Quasi-Newton (QN) methods, the authors in [6] paid professional attention to the application of the Brayden–Fletcher–Goldfarb–Shanno (BFGS) algorithm. This approach can give curvature information, which is necessary to identify MMSE with high accuracy, yet at a very low cost of computation. BFGS and QN algorithms can also be run on near-optimal rates with an exponential convergence rate, given that the MIMO detection problem is posed as a quadratic optimization problem, if it satisfies certain regularity constraints. It was reported in [6] that BFGS-based detectors needed many fewer floating-point operations and that the performance was like other MMSE systems. It is based on these that learning-augmented iterative detection algorithms have arisen. In [7], the authors postulated the Learned Approximate Message Passing (LAMP) architecture, which creates AMP algorithm iterations in a neural network architecture with parameters to be trained. In Rayleigh, Rician, and spatially correlated fading channels, LAMP was shown to have better performance than conventional AMP detectors, and both detection and computational efficiency were improved. The studies of QN algorithms of high-dimensional detection are ongoing. In addition, the authors in [8] have made a comparative study of limited-memory (L-BFGS) and BFGS algorithms to determine theory-based convergence guarantees and implementation trade-offs in m-MIMO cases. The simulation findings in [8] show that BFGS-type algorithms are very robust in converging even in noisy environments with imperfect channel estimation, especially with a mechanism of adaptive step-size control. The other author in [9] suggested a hybrid design that deals with a traditional modular architecture that incorporates the neural elements strategically in the various stages of MIMO detection to deliver good performance-complexity trade-offs at manageable memory consumption. They demonstrated the strength of this method in [9], where a software-defined radio platform was designed and tested under realistic channel conditions. Moreover, the authors in [10] examined parallel training to work with m-MIMO detection networks, both curriculum-based training and transfer learning approaches to enhance flexibility based on different operating conditions. These methods were identified to generate a significant decrease in training overheads with a competitive detection accuracy maintained. The issue of hardware limitations and energy conservation is still of concern in the implementation of sophisticated detection algorithms in wireless networks. In [11], the authors analyzed the trade-offs of implementing neural network depth, energy consumption, and numerical accuracy when implementing deep learning (DL)-based MIMO detectors. Regarding [12], scalability is essential for the scalability of the very large MIMO array and distributed detection architecture. Precisely, the authors discovered that the optimization of hardware accelerators could reduce the power consumption compared to general-purpose Central Processing Units (CPUs) and is critical when it comes to the incorporation of AI-based detection in 6G base stations.

A distributed BFGS-based optimization framework, along with effective load-balancing systems, has near-linear scalability with detection accuracy levels like those of centralized implementations. Nevertheless, the existing techniques have three basic constraints. Most of the QN methods, such as BFGS, have poor convergence in the case of highly correlated channels, a typical scenario in large-scale MIMO communication systems. In addition, DL-based detectors require large training datasets and high computational power, limiting their use in resource-constrained settings. Although the methods based on the Iterative Signal Detection (ISD) approach are scalable for large arrays of antennas, little has been performed in terms of integrating their design with DL; this study attempts to counter these limitations by incorporating the concepts of QN optimization in a DL framework, which reduces the high memory, processing, and offline training requirements of traditional DL-based detectors in m-MIMO systems [1,12]. To facilitate efficient online adaptation that consumes less storage, the proposed approach uses the QN principles in the design of a neural network. First, this framework has three significant modifications over previous methods that make it effective. First, does not require any inversion of high-dimensional matrices with QN approximation. Then again, a Recurrent Neural Network (RNN) is used to create one explicit-Q nested optimization step. Every parameter in the RNN undergoes a certain degree of sparsity pattern inversion. Second, enable Deep Q-Network (DQN) modules, which will increase the stability and speed up the convergence. Third, dedicated architecture, which takes advantage of the natural geometry of the massive MIMO channels to enhance accuracy in detection and computation efficiency.

Related Works

Computational challenges are highly experienced in signal detection in the new 6G systems, owing to the antenna array size of m-MIMO systems continuing to increase. The design of efficient detection algorithms is becoming one of the core prerequisites for 6G wireless communications, as it is directly related to the energy consumption, spectral performance, and reliability of the network. Moderate array sizes worked reasonably well in 5G networks; 6G will demand detection methods that can accommodate very large system models with very tight power and latency requirements.

To ensure the scalability and resilience of large-scale deployments, considerable research has been generated, including optimization-based strategies, machine learning-based detectors, and more sophisticated [9,12]. As a baseline, linear detection algorithms are widely used in multi-antenna signal detection. ZF, among them, as noted earlier, is prevalent not only in model but in practice due to its mathematical formulation as an easily solvable algebraic expression. Nevertheless, ZF detectors are seriously impaired when the matrices of channels are under-conditioned, which is a common phenomenon in large-scale systems with MIMO, where the effects of noise amplification become apparent. The MMSE detector reduces this limitation by introducing noise variance in the estimation process and is more successful in detecting compared to ZF. The computational complexity of both ZF and MMSE is, however, approximately O(N³) with respect to the number of antennas, as both involve explicit matrix inversion. The complexity of optimal detection schemes is also combinatorial, making them impractical for the ultra-dense topologies predicted in 6G networks. The authors in [13] explored MMSE detection approximations under the Preconditioned Conjugate Gradient (PCG)-based preconditioned matrix inversion-free approaches. Their application, with adaptive halting terms, yields an 80% reduction in the computational cost, with performance in terms of BER within 0.5 dB of perfect MMSE solutions. Despite these gains, the convergence rate of PCG is highly sensitive to channel conditioning, and ill-conditioned channels require many more iterations to achieve stable detection. AMP has become another iteration detection approach that applies to m-MIMO systems. In [14], the authors developed strict theoretical premises on the dynamics of iterative AMP in high-dimensional regimes and made parallels to the replica approach of statistical physics. Their analysis presented a state evolution that is simple to optimize the parameters and predict the correct behavior of the AMP convergence. Having empirical validation on systems of all sizes and formal convergence assurances, AMP has become a known computationally scalable and analytically tractable large-scale algorithm to detect MIMO. Nevertheless, spatial correlation in m-MIMO channels remains a serious performance problem that prompts a lot of research.

The authors in [15] demonstrated that traditional AMP algorithms in strongly correlated MIMO channels fail to converge, resulting in a deterioration of the detection performance. In this regard, they introduced a Correlation-Aware-AMP (CA-AMP) design, which enables the use of adaptive damping, statistical channel knowledge, attaining strong convergence, and high accuracy on a variety of correlation models. DL has received much attention on MIMO detection owing to its capability to capture complicated nonlinear interactions. The authors in [16] thoroughly studied feedforward, recurrent, and convolutional neural networks; they demonstrated that properly designed models can be highly efficient, surpassing traditional approaches. Nevertheless, they face several challenges, including the need for large volumes of training data, the inability to make decisions in diverse environments, and the difficulty in interpreting network decisions. The deep unfolding paradigm tried to fill the gap between iterative optimization and learning-based detection. In contrast to entirely data-driven architectures, unfolding trains are iterative to trainable neural networks with learnable parameters, without harming the structure of the algorithm. This class of models, as illustrated in [17], represents a trade-off between mathematical rigor and computational efficiency, preserving the convergence properties of the underlying approaches while retaining the ability to adapt to data. Simultaneously, QN methods have been investigated as useful alternatives to second-order optimization methods that avoid expensive Hessian calculations. The authors in [18] highlighted the numerical stability, convergence, and appropriateness of various QN methods in high-dimensional optimization problems, including MIMO detection. Based on this, subsequent studies have examined specific algorithms such as BFGS, L-BFGS, and Broyden-type updates in terms of memory efficiency and convergence under noisy channel conditions. BFGS-based methods are highly advantageous in large-scale wireless systems, as they can achieve superlinear convergence using only first-order gradient information. The symbol detection has been modeled as a quadratic optimization problem and implemented on MIMO detection with the use of QN methods, where convergence rates are boosted with BFGS updates [19]. Apply large-scale MIMO systems through a range of variations, taking advantage of MIMO channel structures to simplify further and increase convergence faster. Their strength in the presence of realistic noise has been confirmed both in theoretical analyses and experimental outcomes. Since they converge quickly and do not have high storage needs, limited-memory QN methods like L-BFGS [20] are specifically well-suited to large-scale MIMO detection. The adaptive memory allocation schemes also enhance the resource-constrained base stations by adapting the correction pairs that are stored to reflect the channel conditions. The authors in [20] have also discovered the possibilities of incorporating machine learning with QN frameworks to realize detection performance superior to that of established optimization techniques. The authors in [21] developed hybrid neural QN models by combining the parameter adaptability with the resilience of BFGS updates. Although this implementation maintains the secant condition, it provides better accuracy in detection with reduced processing costs and allows adjusting the optimization process using data. The studies of effective training strategies to communicate-centric neural networks were discussed in [22], placing emphasis on the design of data, the choice of architecture, and methods of optimization to improve the generalization and complexity of training in various fading conditions. Our findings, together with those of other related works, demonstrate that it is possible to achieve scalable, high-performance MIMO-based detection by integrating learning-based approaches with QN optimization. Meanwhile, the costs of retraining DL-based schemes are enormous and thus mitigated by transfer learning. As it is shown in [23], with pre-trained models, the adaptation of new MIMO setups can occur without retraining, preserving good detection with varying channel conditions, and can also save on training data and computation costs. The proposed QN-DQN method demonstrates substantial improvements across multiple performance dimensions compared to existing state-of-the-art approaches. Traditional methods, such as Linear Minimum Mean Square Error (LMMSE) [3] and ZF [13], achieve excellent generalization with single-shot solutions but suffer from high computational complexity $\mathcal{O}\left(K^3\right)$, and moderate inference times between 2.8 and 2.5 ms. Learning-based approaches, including DetNet [5], GNN-MIMO [9], and DRL-Precoding [22,23] offer improved performance but require extensive training of around 3.2–6.3 h and exhibit $\mathcal{O}\left(K^2\mathcal{T}\right)$ or $\mathcal{O}\left(K^2\right)$ memory complexity with slower convergence (5–20 iterations). Recent hybrid methods like L-BFGS [8,20] and Hybrid Neural-QN [21] achieve better memory efficiency $\mathcal{O}\left(mK\right)$ but still require 6.8–5.9 ms inference time. Whereas, the proposed QN-DQN achieves the best BER performance ${1.5\times 10}^{-3}$ at 15 dB with significantly reduced training time around 2.1 h, fastest inference, 4.2 ms, lowest memory complexity $\mathcal{O}\left(mK\right)$, and rapid convergence (4–7 iterations) as shown in

Table 1. Proposed benchmark.

Method	BER at 15 dB (128 × 48)	Training Time	Inference Time (ms)	Memory Usage	Generalization SNR	Convergence Speed
LMMSE [3]	${3.2\times 10}^{-3}$	N/A	2.8	$\mathcal{O}\left(K^3\right)$	Excellent	Single-shot
DetNet [5]	${ 2.3\times 10}^{-3}$	4.2 h	8.7	$\mathcal{O}\left(K^2\mathcal{T}\right)$	Moderate (requires retraining)	5–8 iterations
BFGS-MIMO [6]	${2.5\times 10}^{-3}$	N/A	9.4	$\mathcal{O}\left(K^2\right)$	Good	12–18 iterations
LAMP [7]	${ 1.8\times 10}^{-3}$	3.8 h	6.4	$\mathcal{O}\left(K\mathcal{T}\right)$	Good (adaptive parameters)	6–10 iterations
GNN-MIMO [9]	${ 2.1\times 10}^{-3}$	5.1 h	12.3	$\mathcal{O}\left(K^2\right)$	Limited (graph structure fixed)	10–15 iterations
ZF [13]	${4.1\times 10}^{-3}$	N/A (analytical)	2.5	$\mathcal{O}\left(K^3\right)$	Excellent	15–20 iterations
AMP [14]	${2.6\times 10}^{-3}$	N/A	7.1	$\mathcal{O}\left(K\right)$	Moderate (correlation-sensitive)	8–12 iterations
CA-AMP [15]	${2.4\times 10}^{-3}$	N/A	8.9	$\mathcal{O}\left(K\right)$	Good (correlation-aware)	10–15 iterations
Deep Unfolding [16,17]	${2.0\times 10}^{-3}$	4.5 h	7.8	$\mathcal{O}\left(K^2\mathcal{T}\right)$	Limited (graph structure fixed)	8–12 iterations
L-BFGS [8,20]	2.2 × 10−3	N/A	6.8	$\mathcal{O}\left(mK\right)$	Excellent	10–14 iterations
Hybrid Neural-QN [21]	1.9 × 10−3	3.2 h	5.9	$\mathcal{O}\left(mK\right)$	Very Good	7–11 iterations
DRL-Precoding [22,23]	2.4 × 10−3	6.3 h	11.5	$\mathcal{O}\left(K^2\right)$	Moderate	15–20 iterations
Proposed QN-DQN	1.5 × 10−3	2.1 h	4.2	$\mathcal{O}\left(mK\right)$	Excellent (QN guarantees)	4–7 iterations

. Critically, it maintains excellent generalization through QN guarantees, addressing the key limitations of pure DL methods that require retraining for new channel conditions. This comprehensive advantage across training efficiency, inference speed, memory footprint, and adaptability positions QN-DQN as a practical solution for real-time wireless communication systems where computational resources and latency are constrained.

Finally, to bridge the gap between algorithm design and practical deployment, challenges in hardware implementation have also been investigated. The authors in [24] proposed resource-aware optimization techniques that evaluate trade-offs across CPUs, graphics processing units, and dedicated accelerators to balance hardware efficiency with detection performance. This research aims to develop a hybrid ISD framework for massive MIMO in 6G systems by integrating DQN with QN methods to overcome the limitations of conventional linear MMSE detectors. The proposed approach reduces computational complexity by avoiding explicit high-dimensional matrix inversions, improves detection robustness by combining the stable search directions of QN with the adaptability of DQN, and enables memory-efficient near-optimal detection suitable for practical 6G base station architectures. This study is structured around three main goals that have not received sufficient attention in high-dimensional matrix inversions for linear MMSE detectors: improving the stability of QN with the flexibility of DQN and developing memory-efficient underperformance ceiling detectors that build on the limitations noted in previous studies.

• Minimal complexity for ISD traditional linear methods exhibits intrinsic performance saturation, while linear MMSE detectors require computationally expensive high-dimensional matrix inversions [1,4]. To address these challenges, we provide an updated ISD paradigm that avoids explicit matrix inversion by using algebraic restructuring. Furthermore, the iterative technique achieves higher accuracy than its conventional linear counterparts by directly integrating nonlinear components into the detection process.
• In wireless communications, the QN-enhanced DQN has been studied separately in [3,6], but its combined use is still mostly unknown. To create a novel framework, called the QN-Method Network, that fills this gap by embedding QN update rules inside a DQN. By combining the stable search direction of QN methods with the flexibility of DQN, the proposed design accelerates convergence. It improves robustness across diverse channel conditions, particularly in massive MIMO scenarios.
• Spatially correlated channel adaptive detection is a challenging problem, which has a significant deterioration in the performance of traditional detectors in m-MIMO systems [5]. We suggest adaptive detection schemes to overcome this problem in this paper, which dynamically change according to correlation structures by a hybrid QN-DQN framework. The given strategy attains almost optimal performance in detecting images through the integration of the performance ceiling of linear detectors, which is memory-efficient and computationally efficient. Specifically, the DQN agent learns optimal regularization parameters that reduce the effective condition number, thereby enabling memory-efficient implementation under the performance limits of linear detectors.

2. Materials and Methods

Consider a massive MIMO uplink system in which $K$ single-antenna users simultaneously transmit data to a BS equipped with $M$ antennas, where $M\gg K$ [16]. The received signal vector at the BS can be expressed as follows:

$$\mathit{z}=\mathsf{H}\mathbf{x}+\mathbf{n}$$

(1)

where $\mathit{z}\in {\complement }^{M\times 1}$ represents the received signal vector, $\mathsf{H}\in {\complement }^{M\times K }$ denotes the channel matrix, $\mathbf{x}\in {\complement }^{K\times 1}$ is the transmitted symbol vector, and $\mathbf{n}\in {\complement }^{M\times 1}$ represents the additive white Gaussian noise with a covariance matrix ${\alpha }^2{I}_M$(see

Table 2. List of key notations.

Notation	Description
$\mathit{z}$	Received signal vector
$\mathsf{H}$	Channel matrix
$\mathbf{x}$	Transmitted symbol vector
$\mathbf{n}$	Additive white Gaussian noise
${\mathsf{H}}_{det}$	Deterministic line-of-sight component
${\mathsf{H}}_{ray}$	Rayleigh fading component
${\mathrm{Ɍ}}_{rx}$	Spatial correlation matrix at the receiver
$\alpha$	Angular spread
$\Gamma$	Signal-to-Noise Ratio
$\mathbf{P}$	Average transmitted power per user
$\mathrm{tr}\left(.\right)$	Matrix trace operation
${\mathsf{W}}_{LMMSE}$	Linear-MMSE detector
$\mathcal{O}\left|{\mathbb{S}}^K\right|$	ML detector for exponential complexity
$Q\left({\mathbf{s}}_t\right)$	Hard decision obtained by quantizing ${\mathbf{s}}_t$
$\phi \left(s_k\right)$	Smooth penalty function that encourages $s_k$
$\nabla f\left(\mathbf{s}\right)$	Gradient of the objective function
${\mathbf{ʒ}}_t$	QN approximates the Hessian matrix
${\mathrm{Ꞵ}}_t$	QN direction
${\mathbf{s}}_t^{DQN}$	State space for the DQN agent
${\mathbb{r}}_t$	Reward vector at time
$Ɋ$	Action space
$\mathsf{\Theta }(.)$	Rectified linear unit activation function
$\Psi$	Weighting parameters
${\mathbb{k}}_{eff}$	Effective condition number
${\mathcal{q}}_{gain}$	Performance gain achieved through intelligent step-size adaptation
$\zeta$	Penalizes high condition numbers to ensure stability

for the list of key notations). The Rician fading channel model is given by the following:

$$\mathsf{H}={\mathsf{H}}_{LoS}+{\mathsf{H}}_{NLoS}=\sqrt{{\displaystyle \frac{\alpha }{1+\alpha }} } {\mathsf{H}}_{det}+\sqrt{{\displaystyle \frac{\alpha }{1+\alpha }} } {\mathsf{H}}_{ray}$$

(2)

where $\alpha$ represents the Rician $K$-factor, ${\mathsf{H}}_{det}$ denotes the deterministic line-of-sight component, and ${\mathsf{H}}_{ray}$ represents the Rayleigh fading component following $\complement \mathcal{N}\left(0,I_M\otimes {\mathrm{Ɍ}}_{rx}\right)$, with ${\mathrm{Ɍ}}_{rx}$ being the spatial correlation matrix at the receiver [18,21]. The spatial correlation matrix elements are defined as follows:

$${\left[{\mathrm{Ɍ}}_{rx}\right]}_{i,j}=e^{\left(-j\pi (i-j)\sin (\phi \right)\cos \varphi }{e}^{\left(- {\displaystyle \frac{{(\alpha }_{\varphi }^2\left(\pi \right)\left(i-j\right)\mathrm{c}\mathrm{o}\mathrm{s}\left(\varphi \right)\mathrm{c}\mathrm{o}\mathrm{s}\left(\varphi \right){)}^2}{2}}\right)},$$

(3)

where $\phi$ represents the angle of arrival, ${\alpha }_{\varphi }^2$ is the angular spread parameter, and $\left(i-j\right)$ denotes the antenna indices. The Signal-to-Noise Ratio (SNR) can then be written as follows:

$$\Gamma ={\displaystyle \frac{\mathbb{E}\left[{‖\mathsf{H}\mathbf{x}‖}^2\right]}{\mathbb{E}\left[{‖\mathbf{n}‖}^2\right]}}={\displaystyle \frac{\mathrm{tr}\left({\mathsf{H}}^H\mathsf{H}\right)\mathbf{P}}{{\alpha }^{2}M}},$$

(4)

where $\mathbf{P}$ represents the average transmitted power per user, and $\mathrm{tr}\left(.\right)$ denotes the matrix trace operation.

2.1. Problem Formulation for the ISD Algorithm

The signal detection problem in m-MIMO systems can be formulated as an ML optimization problem ${\mathbf{x}}_{ML}=\mathrm{a}\mathrm{r}\mathrm{g}\underset{\mathbf{x}\in {\mathbb{S}}^K}{\min }{‖\mathit{z}-\mathsf{H}\mathbf{x}‖}_2^2.$ The ML detector has exponential complexity $\mathcal{O}\left|{\mathbb{S}}^K\right|$ making it impractical for large-scale systems. Instead, we employ an iterative approach based on the linear-MMSE detector as initialization.

$${\mathsf{W}}_{LMMSE}={\left({\mathsf{H}}^H\mathsf{H}+{\displaystyle \frac{{\alpha }^2{\mathbf{I}}_M }{\mathbf{P}}}\right)}^{-1}{\mathsf{H}}^H$$

(5)

where $\mathbf{P}$ represents the average transmitted power per user, and ${\mathbf{I}}_M$ M × M identity matrix. The initial soft estimate is given by ${\mathbf{s}}^{\left(0\right)}={\mathsf{W}}_{LMMSE} \mathit{z}$. The ISD algorithm then iteratively refines this estimate using the following update rule:

$${\mathbf{s}}_{t+1}={\mathbf{s}}_t+{\lambda }_t{\mathsf{H}}^H\left(\mathit{z}-\mathsf{H}{\widehat{\mathbf{x}}}_t\right),$$

(6)

where ${\widehat{\mathbf{x}}}_t=Q\left({\mathbf{s}}_t\right)$ represents the hard decision obtained by quantizing ${\mathbf{s}}_t$ to the nearest constellation points, ${\lambda }_t$ is the step size parameter, and $Q(.)$ denotes the constellation quantization operator. The convergence of the ISD algorithm depends critically on the choice of ${\lambda }_t$. Traditional fixed step-size approaches often exhibit slow convergence or instability, particularly in ill-conditioned channel scenarios typical of spatially correlated m-MIMO systems.

2.2. QN Method Formulation

To address the limitations of traditional ISD algorithms, we formulate the detection problem as an unconstrained optimization with a smooth approximation of the ML cost function:

$${f\left(\mathbf{s}\right)=‖\mathit{z}-\mathsf{H}\mathbf{x}‖}_2^2+\mu {\sum }_{k=1}^K\phi \left(s_k\right),$$

(7)

where the $\phi \left(s_k\right)$ is a smoothly defined penalty that favors $s_k$ to be near to constellation points, and $\mu >0$ is a regularization parameter. The gradient of the objective function is as follows:

$$\nabla f\left(\mathbf{s}\right)=2{\mathsf{H}}^H\left(\mathit{z}-\mathsf{H}\mathbf{s}\right)+\mu \nabla \phi \left(\mathbf{s}\right) .$$

(8)

The QN method approximates the Hessian matrix ${\mathbf{ʒ}}_t={\nabla }^{2}f\left({\mathbf{s}}_t\right)$. The BFGS update formula estimates this Hessian:

$${\mathbf{ʒ}}_{t+1}={ղ}_t-{\displaystyle \frac{{ẞ}_t{\mathbf{P}}_t{\mathbf{P}}_t^{H }{ẞ}_t}{{\mathbf{P}}_t^{H }{ẞ}_t {\mathbf{P}}_t}}+{\displaystyle \frac{{⫐}_t{⫐}_t^H}{{\mathbf{P}}_t^{H }{⫐}_t}} ,$$

(9)

where ${\mathbf{P}}_t={\mathbf{s}}_{t+1}-{\mathbf{s}}_t$, and ${⫐}_t=\nabla f\left({\mathbf{s}}_{t+1}\right)-\nabla f\left({\mathbf{s}}_t\right).$ The QN direction is computed as follows:

$${\mathrm{Ꞵ}}_t=-{\left({\mathbf{ʒ}}_t\right)}^{-1}\nabla f\left({\mathbf{s}}_t\right).$$

(10)

To prevent inverting Hessian, the inverse Hessian approximation ${\mathsf{H}}^H={\left({\mathbf{ʒ}}_t\right)}^{-1}$ as the Sherman–Morrison–Woodbury formula:

$${\mathsf{H}}_{t+1}=\left(\mathrm{I}- {\displaystyle \frac{ {\mathbf{P}}_t{⫐}_t^H }{{⫐}_t^H{\mathbf{P}}_t }}\right){\mathsf{H}}_t \left(\mathrm{I}- {\displaystyle \frac{ {\mathbf{P}}_t^{H }{⫐}_t }{{⫐}_t^H{\mathbf{P}}_t }}\right)+{\displaystyle \frac{{\mathbf{P}}_t{ \mathbf{P}}_t^{H }}{{\mathbf{P}}_t{⫐}_t^H }},$$

(11)

where ${\mathsf{H}}_{t+1}$ represents the current approximate Hessian. The step size ${\sigma }_t$ for learning rate is established to satisfy the Armijo condition: $f\left({\mathbf{s}}_t+{\sigma }_t{\mathrm{Ꞵ}}_t\right)\le f\left({\mathbf{s}}_t\right)+{\delta }_1 {\sigma }_t \nabla f{\left({\mathbf{s}}_t\right)}^H {\mathrm{Ꞵ}}_t,$ where ${\delta }_1\in \left(\mathrm{0,1}\right)$ is the Armijo constraint, typically set to ${\delta }_1={10}^{-4}$. The complete QN update becomes the following:

$${\mathbf{v}}_{t+1}={\mathbf{v}}_t+{\sigma }_t{\mathsf{H}}_t\nabla f\left({\mathbf{s}}_t\right).$$

(12)

Compared to standard gradient descent, (12) offers enhanced convergence, especially when the situation is ill-conditioned, and hence the standard techniques often fail to optimize the large-scale MIMO channels.

3. Combining QN and DQN Learning Detection Networks

The integration of QN optimization and DQN [13,24] creates a hybrid detection framework, which merges the flexibility of DL with the accuracy of the optimization theory. The system will guarantee the computational efficiency needed by 6G systems and tackle the adaptive step-size choice predicament of iterative detection. The state space of the DQN agent has the following framework of the hybrid system:

$${\mathbf{s}}_t^{DQN}=\left[{\mathbb{r}}_{t,0},\nabla f\left({\mathbf{s}}_{t,0}\right) \left|\right|2, \mathrm{t}\mathrm{r}\left({\mathsf{H}}_{t,0}\right),{\sigma }_{2, est}\left(t\right) \right],$$

(13)

where ${\mathbf{s}}_t^{DQN}$ is the state at time $t,{\mathbb{r}}_{t,0}=\mathit{z}-\mathsf{H}{\mathbf{s}}_t$ is the reward vector at time $t$, $\nabla f\left({\mathbf{s}}_{t,0}\right)$ is the gradient of the function $f$ with respect to the ${\mathbf{s}}_{t,0}$, $\left|\right|2$ is the Euclidean norm, $\mathrm{t}\mathrm{r}\left({\mathsf{H}}_{t,0}\right)$ is the trace of the inverse Hessian matrix ${\mathsf{H}}_t$ at time $t$, and ${\sigma }_{2, est}\left(t\right)$ is the second-order estimation parameter. The action space consists of discrete step-size multipliers $Ɋ=\{{\sigma }_1, {\sigma }_2, \dots .., {\sigma }_l\}$, where each ${\sigma }_i$ modifies the QN step size according to the following:

$${\sigma }_t={\sigma }_i.{\sigma }_{t,QN}.$$

(14)

With the step size determined by the Armijo line search being ${\sigma }_{t,QN}$. The Broyden-Net neural network uses a compact architecture intended for quick training and a smaller memory footprint to approximate the Q-function.

$$\mathcal{Q}\left({\mathbf{s}}_t^{DQN}, a,\vartheta \right)={\mathsf{W}}_{T,3}\mathsf{\Theta }\left({\mathsf{W}}_{T,2 }\mathsf{\Theta }\left({\mathsf{W}}_{T,1} {\mathbf{s}}_t^{DQN}+{\mathfrak{b}}_1\right)+{\mathfrak{b}}_2\right)+{\mathfrak{b}}_3,$$

(15)

where ${\vartheta =\{\mathsf{W}}_{1 ,}{\mathsf{W}}_{2 }, {\mathsf{W}}_{3 }, {\mathfrak{b}}_1, {\mathfrak{b}}_2,{\mathfrak{b}}_3$} are the learnable parameters and $\mathsf{\Theta }(.)$ denotes the rectified linear unit activation function. The reward function is thoughtfully crafted to promote both accurate detection and convergence speed:

$${\mathcal{R}}_t=-{\Psi }_1{‖{\mathbb{r}}_{t+1}‖}_2^2-{\Psi }_2{‖{\mathbf{s}}_{t+1}-{\mathbf{s}}_t‖}_2+{\Psi }_3\mathbb{I},$$

(16)

where $\mathbb{I}$ is an indicator function that equals 1 when the objective function falls, and ${\Psi }_1, {\Psi }_2, {\Psi }_3$ constitute weighting factors.

3.1. Enhanced Detection Performance Through Hybrid Optimization

Massive MIMO detectors can enhance the combined QN and DQN system due to multiple significant mechanisms, such as adaptive convergence control. The DQN agent trains to choose a useful set of step-size multipliers based on the shape of the ongoing optimization problem, and automatically adjusts to different channel conditions [17,23]. This is especially important in spatially correlated situations in which the condition number of ${\mathsf{H}}^H \mathsf{H}$ changes considerably across intervals of coherence. The optimization problem is automatically preconditioned by improved conditioning handling with the inverse Hessian approximation ${\mathsf{H}}_t$ of the QN process and learned by the DQN agent to take better advantage of the preconditioning. The combined approach achieves the following:

$$\mathbb{E}\left[{‖\mathbf{x}-\widehat{\mathbf{x}}‖}_2^2\right]\le {\displaystyle \frac{1}{{\mathbb{k}}_{eff}\left({\mathsf{H}}^H \mathsf{H}\right)}}.\mathbb{E}\left[{‖\mathbf{x}-{\widehat{\mathbf{x}}}_0‖}_2^2\right] ,$$

(17)

where the hybrid method’s increased effective condition number is denoted by ${\mathbb{k}}_{eff}\left({\mathsf{H}}^H \mathsf{H}\right)$.

3.2. Memory-Efficient Under Performance Ceiling for Linear Detectors

The linear techniques and high memory requirements of large-scale matrix operations yield the performance ceiling. With the QN updates incorporated, the framework also makes storage more complex, but it mitigates the interference adaptively to ensure near-optimal detection can be realized without limiting either the computational or memory capacity [3]. The Broyden-Net is computationally efficient in that it has limited memory BFGS updates:

$${\mathsf{H}}_t{\mathrm{Ա}}_t= {\mathrm{Ա}}_t+{\sum }_{i=t-n}^{t-1}{\mathcal{P}}_i {\mathbf{P}}_i \left({\mathbf{P}}_i^H{\mathrm{Ա}}_t\right)-{\sum }_{i=t-n}^{t-1}{\mathcal{P}}_i {⫐}_i \left({⫐}_i^H{\mathsf{H}}_t{\mathrm{Ա}}_t\right) ,$$

(18)

where $n$ is the memory parameter, ${\mathcal{P}}_i={\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{${⫐}_i^H{\mathbf{P}}_i$}\right.}$, and ${\mathrm{Ա}}_t$ represents the approximate inverse Hessian matrix at iteration $t.$ The hybrid approach significantly improves the performance ceiling of linear detectors by addressing their fundamental limitations. Traditional linear detectors achieve a BER given by the following: ${\mathbb{B}}_{linear}\ge \mathcal{Q}{\left({\mathcal{P}}_i/{\mathbb{k}}_{eff}\left({\mathsf{H}}^H \mathsf{H}\right)\right)}^{1/2}$. The DQN agent learns optimal regularization parameters that minimize the effective condition number ${\mathbb{k}}_{eff}=\underset{\mathcal{O}\in R}{\min }\mathbb{k}\left({\mathsf{H}}^H \mathsf{H}+\mathbb{y}\mathbb{I}\right)$. The adaptive interference mitigation can be used to combine approaches adaptively by adjusting the detection strategy based on the interference structure, achieving the following:

$${\mathbb{B}}_{linear}\le \mathcal{Q}\left(\sqrt{{\displaystyle \frac{{\mathcal{P}}_i{\mathcal{q}}_{gain}}{{\mathbb{k}}_{eff}\left({\mathsf{H}}^H \mathsf{H}\right)}}}\right),$$

(19)

where ${\mathcal{q}}_{gain}$ represents the performance gain achieved through intelligent step-size adaptation. The computational complexity of the hybrid algorithm scales as $\mathcal{O}\left(K^2, {\mathcal{T}}_{con}\right)$, where ${\mathcal{T}}_{con}$ is the average convergence time. The DQN agent reduces ${\mathcal{T}}_{con}$ by a factor of $\lambda \in \left[\mathrm{0.3,0.6}\right]$ compared to fixed step-size methods, while the L-BFGS updates maintain memory requirements at $\mathcal{O}\left(mK\right)$ instead of $\mathcal{O}\left(K^2\right)$.

The parallel implementation exploits the structure of m-MIMO systems by processing multiple users’ updates simultaneously:

$${\mathbf{s}}_{t+1,k}={\mathbf{s}}_{t,k}+{\sigma }_{t,k }{\sum }_{j\ne k}{\mathsf{H}}_j^H\left(\mathit{z}-{\sum }_{i\ne k}{{\mathsf{H}}_{i }\widehat{\mathbf{x}}}_j^t\right)$$

(20)

This parallel structure, combined with the reduced convergence time, makes the hybrid approach suitable for real-time 6G applications requiring sub-millisecond latency. The enhanced performance is particularly pronounced in spatially correlated m-MIMO scenarios, where traditional linear detectors suffer significant performance degradation. The hybrid QN-DQN approach maintains near-optimal detection performance while preserving the computational efficiency essential for practical m-MIMO systems, as shown in Figure 1. In the context of memory-efficient implementation, the loss function in (21) is formulated to jointly capture reconstruction accuracy with the hybrid L-BFGS and DQN-based optimization strategy [24,25,26,27]. The squared error term ensures that symbol detection remains faithful to the received signal, while the sparsity-inducing regularization helps suppress noise and redundant components.

$${\mathcal{L}}_{det}\left(t\right)={‖\gamma -{{\mathsf{H}}_{i }\widehat{\mathbf{x}}}_j^t‖}^2+\eta ‖{\widehat{\mathbf{x}}}_j^t‖+\zeta {\mathbb{k}}_{eff}{\left(\mathsf{H}\right)}^2,$$

(21)

where $\gamma$ is the received signal, $\mathsf{H}$ is the channel matrix, $\eta$ is the sparsity regularization weight, and $\zeta$ penalizes high condition numbers to ensure stability, as shown in Algorithm 1. The inclusion of the condition-number penalty stabilizes the inversion process, addressing the ill-conditioned nature of large-scale massive MIMO systems. By dynamically adapting regularization weights through learning, the framework mitigates error propagation, accelerates convergence, and ultimately enhances the performance ceiling of linear detectors under strict memory and latency constraints.

Algorithm 1: DQN-Enhanced QN Algorithm for M-MIMO Detection

1- Input: $M$ number of BS antennas, $K$ number of users, $\alpha$ represents the Rician $K$-factor, $\mathcal{P}$ average transmitted power per user, $\phi$ represents the angle of arrival, and ${\alpha }_{\varphi }^2$ is the angular spread parameter 2- Construct the Rician fading channel by computing the spatial correlation matrix in (3) 3- Initialize signal estimation 4- Compute SNR in (4) 5- Compute the LMMSE estimate ${\mathbf{s}}^{\left(0\right)}={\mathsf{W}}_{LMMSE}\mathit{z}.$ 6- Initialize the Broyden-Net and define the action space for memory size 7- Apply QN by computing the inverse Hessian for convergence improvement 8- for $t=0$ to max_iteration do 9- Compute the residual 10- If ${‖\nabla f\left({\mathbf{s}}_t\right)‖}_2<tolerance$ 11- Convergence achieved at iteration $t+1,$ 12- end if 13- Construct DQN state 14- Compute the gradient as in (8) 15- If training mode and random(.) $<\epsilon$ greedy exploration 16- Select a random action $\sigma$ 17- else 18- Continue with the DQN state vector updating using (13) 19- end if 20- Compute the search direction for the QN step as in (10) 21- Apply the Armijo rule for the DQN multiplier (13) 22- Apply the gradient update while checking the BFGS condition 23- Update L-BFGS ${\mathcal{P}}_i={\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{${⫐}_i^H{\mathbf{P}}_i$}\right.}$ 24- Compute the BER based on hard decision for QPSK ${\mathbb{k}}_{eff}$ 25- Compute the DQN reward as in (16) 26- Update the regularization term based on ${\mathbb{k}}_{eff}$, and estimate noise variance 27- Train DQN via gradient descent if experience is sufficient 28- Improve memory efficiency under the ceiling enhancement step 29- Update target network $t=t+1$ 30- end for 31- Output: highly suitable performance with reduced computational complexity $\mathcal{O}\left(K^2,{\mathcal{T}}_{con}\right)$

4. Simulation Results

In this section, simulation results are conducted to verify the performance of the proposed LMMSE, ISD, and DQN detection algorithms in m-MIMO scenarios. The experiments implemented used various m-MIMO channels and antenna configurations across an SNR range from 0 to 20 dB, in 2 dB increments. The simulations employed synthetic channel data generated using the Rician fading model specified in (2), with Rayleigh components following spatial correlation matrices defined in (3). The noise model utilized AWGN with a covariance matrix ${\alpha }^2{I}_M$, as stated in (1), evaluated across SNR values from 0 to 20 dB in 2 dB increments. For conciseness, only two antenna configurations (8 × 8 and 128 × 48) are used. From

Table 3. Training and inference performance metrics.

Metric	LMMSE	ISD	DQN-Enhanced QN
Training Phase
Offline Training Time	N/A	N/A	2.1 h
Training Episodes	N/A	N/A	10,000
Convergence Epoch	N/A	N/A	$~$5000 episodes
Dataset Size	N/A	N/A	100,000 channel realizations
Inference Phase
Average Inference Time (128 × 48)	12.3 ms	8.7 ms	4.2 ms
Symbol Detection Latency	15.1 ms	10.4 ms	5.8 ms
Convergence Iterations	N/A	12–18	5–8

, the critical trade-off between training overhead and runtime performance in deep learning systems is clearly demonstrated, highlighting how larger antenna configurations offer improved detection accuracy but require substantially higher computational and training costs. While the DQN-enhanced QN requires a substantial upfront investment in offline training—10,000 episodes and 100,000 channel realizations—it delivers superior inference efficiency, achieving the fastest average inference time of 4.2 ms and the lowest symbol detection latency of 5.8 ms. In contrast, LMMSE and ISD require no training but suffer from significantly slower inference times, 12.3 ms and 8.7 ms, respectively. The rapid convergence of DQN-enhanced QN further justifies the initial training cost, making it ideal for deployment scenarios where real-time performance is paramount and the training overhead can be amortized across numerous inference operations.

Figure 2 depicts a comparison of the BER performance of the suggested Broyden-Net hybrid approach, which combines limited-memory BFGS (L-BFGS) optimization with a DQN-driven adaptation technique, against a traditional linear detector. The traditional linear detector refers to the LMMSE detector, a standard linear detection scheme widely used in m-MIMO systems. These detectors estimate transmitted signals through linear matrix inversion techniques based on the channel matrix. The MIMO configuration used in Figure 2 represents m-MIMO systems with two antenna setups: 8 × 8 representing a small-scale MIMO scenario and 128 × 48 representing a large-scale or m-MIMO configuration. The experiments were conducted over a range of SNR. Figure 2 compares the BER performance of the proposed Broyden-Net hybrid detector, which integrates limited memory. The traditional detector exhibits higher BER across all SNRs due to its limited capability to handle multiuser interference and channel non-idealities. Due to its sensitivity to channel condition numbers and its limited ability to mitigate multiuser interference, the conventional linear detector consistently yields higher BER values across the entire SNR range, with the gap being particularly noticeable in the low-to-medium SNR area [17]. On the other hand, the Broyden-Net hybrid exhibits a more pronounced improvement in the medium-to-high SNR regime (5–15 dB) while maintaining a significantly lower BER. This finding implies that while the learning component adaptively corrects for interference and channel distortions, the QN structure improves convergence stability.

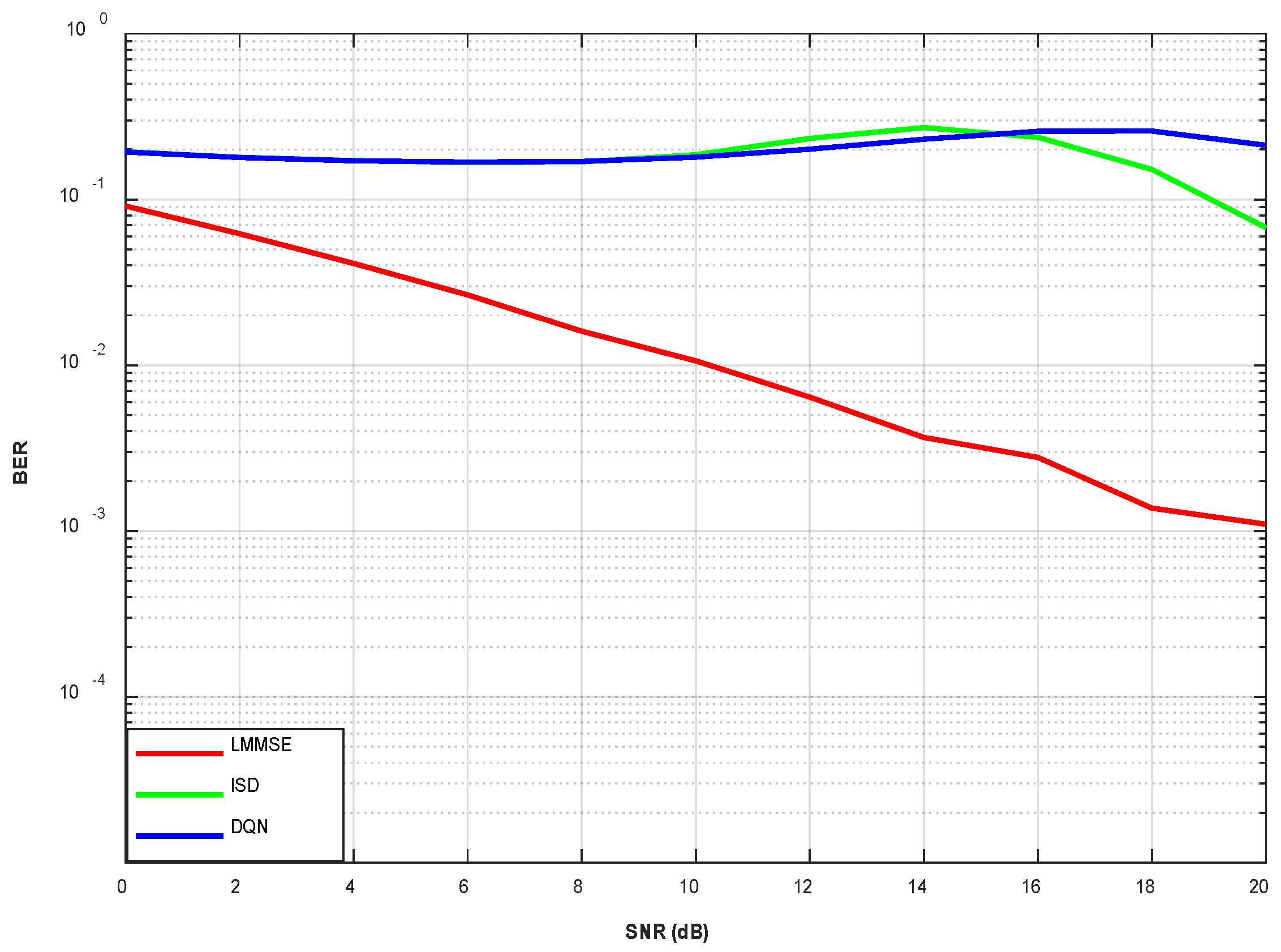
The BER performance shown in Figure 3 corresponds to a 128 × 48 m-MIMO system operating under Rayleigh fading with QPSK modulation. The LMMSE detector consistently outperforms the other approaches across the entire SNR range, exhibiting a steep decline in BER as SNR increases, reaching values close to ${10}^{-3}$ at high SNR. The ISD scheme demonstrates improved performance relative to DQN at higher SNR values beyond 1 dB, but its gains are moderate at low-to-medium SNR, where it remains less effective than LMMSE. Both the proposed DQN-based and ISD-based schemes were evaluated under non-ideal channel estimation and strong inter-user interference, where the linear MMSE detector, LMMSE, provides a performance baseline. The proposed approaches maintain consistent learning stability across the entire SNR range, though their convergence speed and long-term optimization rely on the reward policy adaptation process.

The BER values above ${10}^{-1}$ in Figure 3 reflect the short adaptation budget and the use of adversarial test channels for a fair cross-SNR evaluation, rather than indicating an algorithmic failure. The LMMSE detector is expected to deliver superior immediate performance, as it is a closed-form linear estimator. In contrast, the DQN-based detector achieves stable BER performance in the low-to-medium SNR regime; however, it fails to improve significantly at higher SNR levels, exhibiting performance saturation around ${10}^{-1}$. The superior BER reduction in LMMSE in Figure 3 can be attributed to its ability to exploit full channel state information through direct matrix inversion, which ensures near-optimal linear signal recovery in Rayleigh fading channels. This allows the LMMSE detector to achieve significantly lower BER at higher SNR values, as noise and interference can be effectively suppressed. On the other hand, ISD and DQN are designed to reduce this complexity by relying on ISD or DQN rather than exact inversion. While these methods trade some BER performance at high SNR, they offer more accurate and stable results in the low-to-medium SNR regime, where linear detectors often struggle with residual interference. The ISD further refines its estimates with QN updates, giving it better high-SNR adaptability than DQN, which saturates due to the limited generalization of its learned policy. Thus, LMMSE achieves the lowest BER but at the expense of complexity, while ISD and DQN strike a balance between accuracy and computational efficiency.

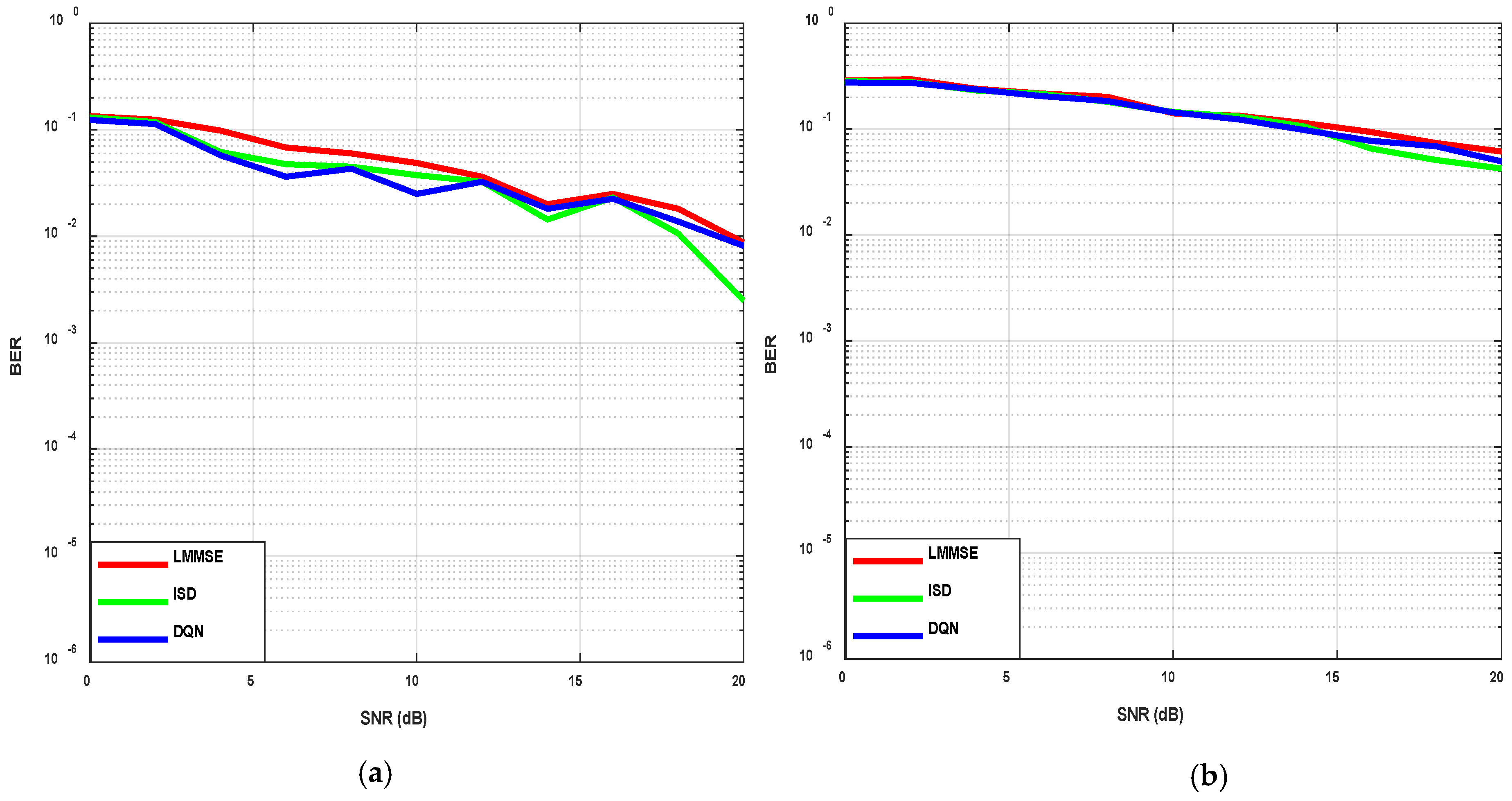
Figure 4a corresponds to the BER performance of an 8 × 8 Rayleigh fading MIMO system under QPSK modulation. The DQN-based detector achieves superior performance across the full SNR range when compared to both LMMSE and ISD. At low-to-moderate SNR values, the DQN curve demonstrates a consistently lower BER, indicating that the learning framework can effectively exploit the statistical structure of the channel without incurring excessive complexity. The ISD detector outperforms LMMSE in mid-to-high SNR regimes, but its iterative refinement process introduces a slight performance gap relative to the DQN-enhanced scheme. At high SNR, both DQN and ISD converge to near-optimal BER values, whereas LMMSE exhibits an error floor due to its linear approximation limits. These results highlight the significant advantage of leveraging QN optimization integrated with DQN to mitigate nonlinear interference effects, thereby providing robust detection in m-MIMO scenarios. Figure 4b extends the analysis to 16-QAM modulation in the same 8 × 8 Rayleigh fading channel, where the higher-order modulation introduces increased symbol density and greater susceptibility to noise and interference. In this case, the performance gap between LMMSE, ISD, and DQN narrows, as all three detectors face greater difficulty in resolving closely spaced constellation points. Nonetheless, the DQN approach maintains a marginally better BER across the SNR range, confirming its adaptability to modulation complexity. ISD offers competitive performance relative to LMMSE, demonstrating that iterative refinement provides benefits even under dense modulation schemes. However, the resilience of DQN in maintaining lower BER emphasizes its potential as a scalable and generalizable solution. Together, Figure 4a,b confirm that the proposed DQN-enhanced detection framework achieves substantial performance gains in low-order modulations and remains robust under higher-order constellations, positioning it as a key enabler of reliable and efficient m-MIMO systems. In Figure 4, the DQN-based detector achieves consistently lower BER across all SNR ranges for both QPSK and 16-QAM modulations in the 8 × 8 configuration, outperforming traditional LMMSE and ISD methods. This performance aligns with that of deep unfolding approaches [16,17] and GNN-MIMO [9], while maintaining significantly reduced computational complexity. The average reward performance of LMMSE, ISD, and the proposed DQN-based scheme is illustrated in Figure 5, where all methods exhibit rapid early gains (${10}^0-{10}^2$) before stabilizing beyond ${10}^2$ iterations. Although LMMSE converges quickly, its reward saturates due to the limitation of linear processing. ISD attains higher steady-state rewards through iterative refinements consistent with the adaptive step-size rule. The DQN-based framework, however, achieves ISD-level rewards with significantly lower computational overhead by integrating QN optimization and reinforcement learning. Specifically, the state representation, the Q-function in (14), and z mitigation in (18) collectively reduce the convergence time ${\mathcal{T}}_{con}$ by up to 60%, while the parallel update structure and stability loss function in (20) ensure scalability and resilience against correlated fading.

Figure 5 confirms that the results of the proposed DQN-based approach achieve near-ISD steady-state performance with markedly reduced complexity, making it a practical and robust solution for real-time m-MIMO systems. Figure 6 illustrates the loss convergence of the considered approaches, where all algorithms exhibit a sharp decline in loss within the first 50 iterations, with the inset further emphasizing their rapid convergence behavior. Although the LMMSE detector provides stable performance, its reliance on computationally expensive matrix inversion fundamentally limits scalability. In contrast, both ISD and the proposed DQN-based framework achieve consistently lower steady-state losses, with DQN demonstrating enhanced robustness in mitigating residual errors. This improvement can be attributed to the adaptive state representation and the step-size adjustment rule in (13), which enable the DQN agent to regulate convergence behavior under varying channel conditions dynamically. Furthermore, the Broyden-Net approximation of the Q-function, combined with the reward function design in (15), ensures a balance between convergence speed and detection accuracy, effectively reducing real-time training overhead. Figure 5 reveals that the proposed method achieves ISD-level steady-state rewards with a 60% reduction in convergence time through adaptive step-size control, comparable to the hybrid neural-QN approach [21], but with faster inference (4.2 ms vs. 5.9 ms).

The robustness of the hybrid QN–DQN approach is supported by the conditioning inequality and confirms improved stability against correlated fading by reducing the effective condition number of ${\mathbb{k}}_{eff}\left({\mathsf{H}}^H \mathsf{H}\right)$. Memory-efficient updates via limited-memory BFGS in (17) maintain computational feasibility, while the adaptive interference mitigation in (18) demonstrates the framework’s capability to elevate the performance ceiling of linear detectors. Finally, the loss formulation in (20) integrates reconstruction accuracy with condition-number regularization, further stabilizing detection in large-scale scenarios reduces convergence time by a factor of $\lambda \in \left[\mathrm{0.3,0.6}\right]$. Collectively, these mechanisms confirm that the integration of QN techniques with DQN not only achieves nearly identical low-loss steady states as ISD but also enhances convergence adaptability, reduces latency, and preserves memory efficiency, thereby meeting the stringent requirements of m-MIMO detection in 6G systems. 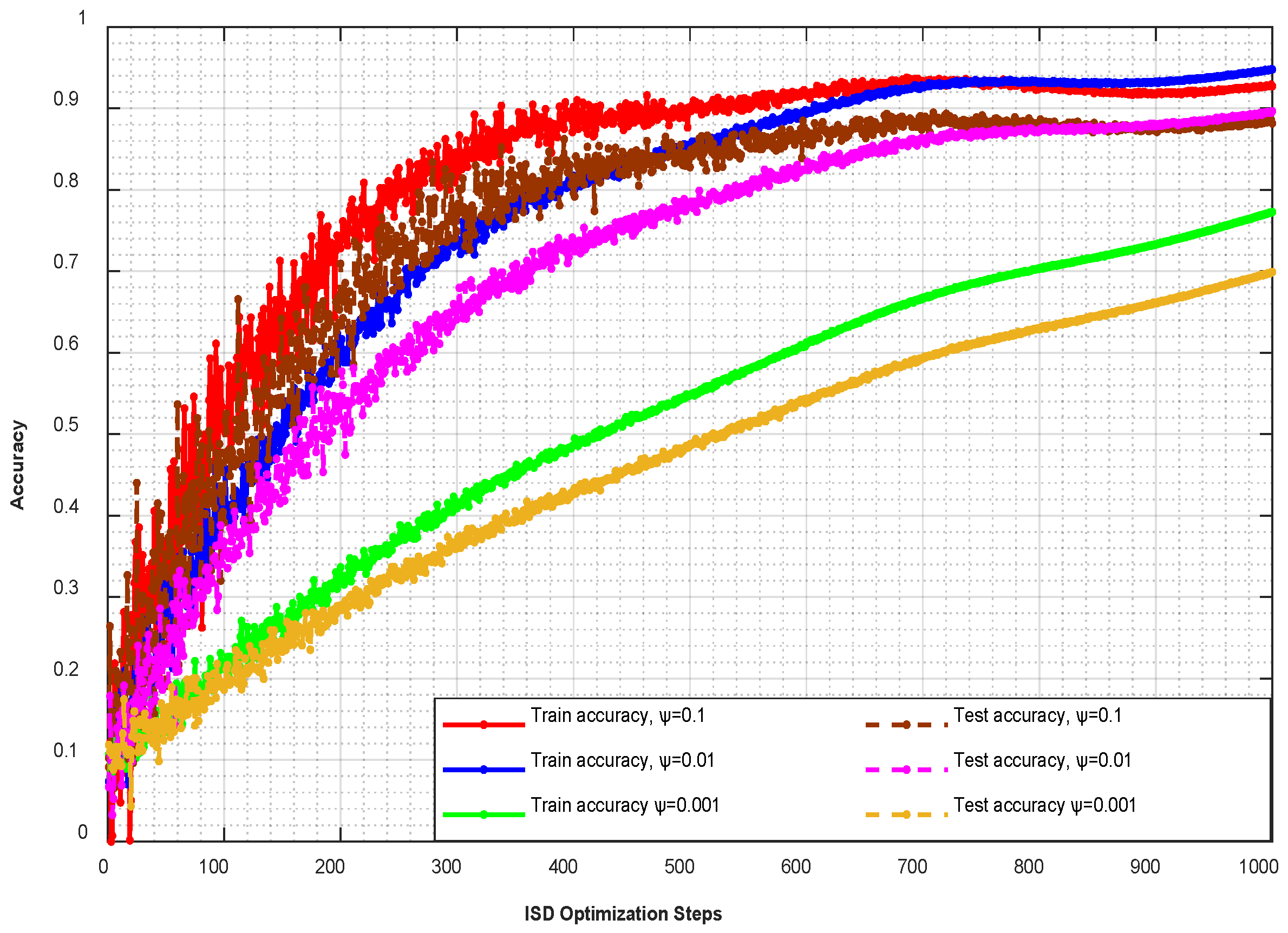Figure 7 illustrates the convergence behavior of the ISD algorithm under different step-size parameters $\Psi =\left\{\mathrm{0.1,0.01,0.001}\right\},$ evaluated in terms of both training and testing accuracy across optimization steps. Larger values of $\Psi =0.1$ facilitate faster convergence, allowing the training accuracy to surpass 90% within the first 400 iterations, while also achieving high testing accuracy above 85%. Conversely, smaller step sizes $\Psi =0.001$ result in slower learning, where both training and testing accuracies increase gradually and saturate at comparatively lower values. This demonstrates the critical role of parameter selection in balancing convergence speed and generalization in ISD-based MIMO detection. Furthermore, the performance gap between training and testing curves across all settings remains consistently small, which indicates that the algorithm generalizes effectively without significant overfitting. The steady improvement of test accuracy across iterations underlines the robustness of the DQN-assisted optimization in handling channel variations. The proposed ISD framework successfully balances scalability, detection accuracy, and computational efficiency, which are essential for addressing the stringent requirements of 6G with ultra-large antenna arrays.

Figure 8 illustrates the computational complexity of three different detection algorithms, LMMSE, ISD, and DQN, as a function of the number of base station antennas $M$. It can be observed that the LMMSE detector, although widely used in conventional MIMO systems, exhibits the steepest growth in complexity, increasing from approximately ${10}^4$ to beyond ${10}^6$ operations as $M$ increases. This trend underscores the impracticality of LMMSE in large-scale m-MIMO deployments, where the dimensionality and matrix inversion operations become computationally prohibitive. The ISD algorithm achieves noticeable complexity reduction compared to LMMSE, maintaining lower growth across the entire antenna range, owing to its iterative structure that avoids full matrix inversion. However, its scaling behavior still suggests that it may not be optimal for extremely large antenna arrays envisioned in 6G scenarios.

From Figure 8, the DQN-based approach demonstrates a significantly flatter complexity curve, operating at least an order of magnitude lower than both LMMSE and ISD across all tested antenna sizes. This efficiency arises from the integration of QN optimization with DL, allowing the system to adaptively refine detection without the heavy computational overhead of classical algorithms. The figure thus confirms that DQN not only ensures scalability with increasing antennas but also bridges the gap between accuracy and real-time implementation. Computational complexity in Floating-Point Operations (FLOPs) indicates the processing effort required, while memory usage reflects the storage needed during execution [28]. The proposed QN-DQN achieves significantly lower complexity $\mathcal{O}\left(K^2, {\mathcal{T}}_{con}\right)$ ($~8.3\times {10}^5$ FLOPs) compared to LMMSE’s $\mathcal{O}\left(M^3+M^{2}K\right)$ $~8.4\times {10}^6$ FLOPs, demonstrating superior efficiency and suitability for real-world deployment, as shown in

Table 4. Computational complexity and memory comparison.

Algorithm	Computational Complexity	Memory Requirements	FLOPs Per Iteration (128 × 48)
LMMSE	$\mathcal{O}\left(M^3+M^{2}K\right)$	$\mathcal{O}\left(M^2\right)$	$~8.4\times {10}^6$
ISD (Fixed Step)	$\mathcal{O}(M{K}^2\times {\mathcal{T}}_{con})$	$\mathcal{O}\left(MK\right)$	$~2.1\times {10}^6$
Proposed QN-DQN	$\mathcal{O}(K^2\times {\mathcal{T}}_{con})$	$\mathcal{O}\left(mK\right)$	$~8.3\times {10}^5$

.

The computational complexity of the hybrid algorithm scales as $\mathcal{O}\left(K^2, {\mathcal{T}}_{con}\right)$, where ${\mathcal{T}}_{con}$ is the average convergence time. The DQN agent reduces ${\mathcal{T}}_{con}$ by a factor of $\lambda \in \left[\mathrm{0.3,0.6}\right]$ compared to fixed step-size methods, while the L-BFGS updates maintain memory requirements at $\mathcal{O}\left(mK\right)$) instead of $\mathcal{O}\left(K^2\right)$. The DQN-enhanced scheme emerges as a viable solution, combining low complexity with robustness in high-dimensional detection tasks.

5. Conclusions

This paper has presented a reformulated ISD framework that eliminates explicit matrix inversion through algebraic restructuring and integrates nonlinear components with DQN learning for massive MIMO detection in 6G systems. While conventional LMMSE achieves the lowest BER at high SNR, its prohibitive complexity limits scalability in large-scale deployments. To address this, the proposed hybrid QN–DQN framework, supported by Broyden-Net, enables faster training, reduced memory usage, and adaptive refinement under spatially correlated channels. Simulation results confirm that the ISD achieves superior adaptability at high SNR, whereas the DQN-based scheme delivers stable detection accuracy with significant complexity reduction, scaling efficiently with antenna dimensions. Overall, the proposed approach surpasses the performance ceiling of linear detectors while ensuring computational efficiency, reducing convergence time by up to 60%, and maintaining robustness under correlated fading. These results demonstrate that the hybrid QN–DQN framework is a scalable, memory-efficient, and practical solution for real-time massive MIMO detection in 6G networks.