Fault Injection Tool for FPGA Reliability Testing: A Novel Method and Discovery of LUT-Specific Logical Redundancies
Abstract
1. Introduction
1.1. Problem of Interest
1.2. Fault Injection Literature Review
1.3. The Research Gap
1.4. Contribution and Scope of This Paper
1.5. Paper Organization
2. State of the Art
3. Proposed SEU Fault Models
- Incorrect logical functions generated by LUT, stored in the configuration memory;
- Faults stuck at the inputs and outputs of the LUT;
- Address decoders of memory and LUT faults.
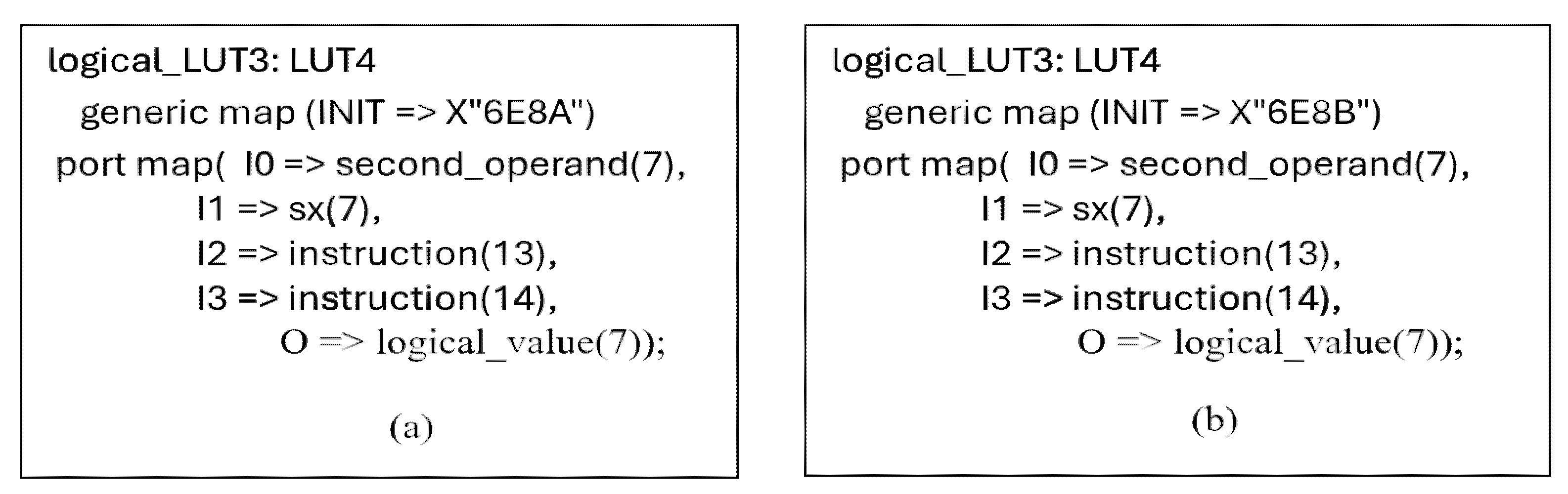
3.1. Example 1: Logic Group Fault Model
3.2. Example 2: Stuck-At Fault Model
3.3. Address Decoders of Memory and LUT Faults
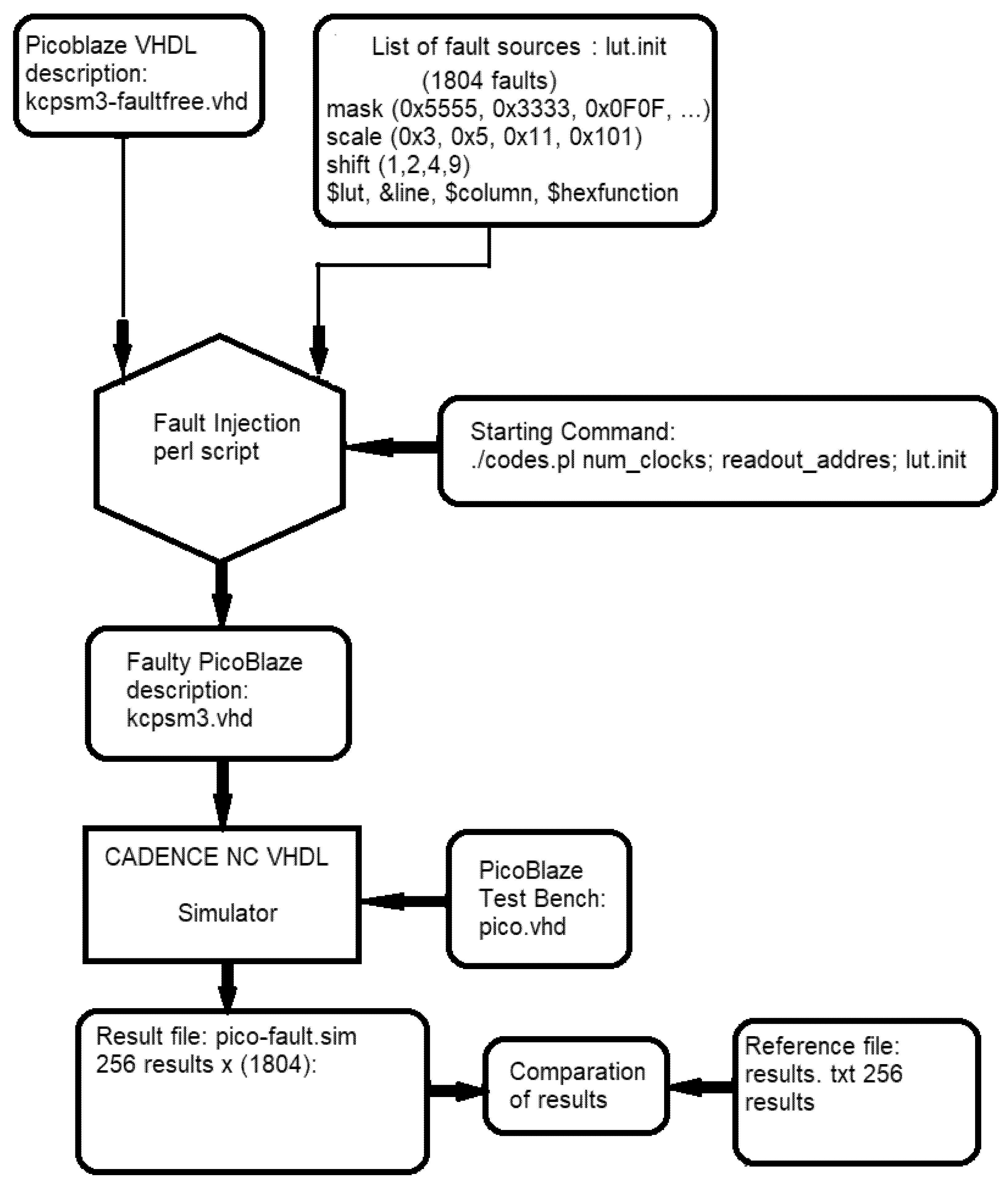
4. Proposed Fault Injection Tool and Environment Composition
4.1. Proposed Methodology of Fault Injection for the Specified FPGA
- Using the basic programming logical “and” operation between the parameter value and the consecutive bit mask, each parameter is modified one by one. These bit masks are also scaled (multiplied by a scale factor) and shifted to obtain all possible 1-bit changes in the parameters stored as hexadecimal numbers. This is also carried out to fit these masks to the number of bits in which a given parameter is stored (4, 8, or 16 bits). This depends on the number of inputs of the LUT described by a given parameter (LUT1—2; LUT3—3; or LUT4—4 inputs). For instance, if inputs I2 and I3 are not used, the mask makes it possible to inject faults merely in the last four bits into the LUT.
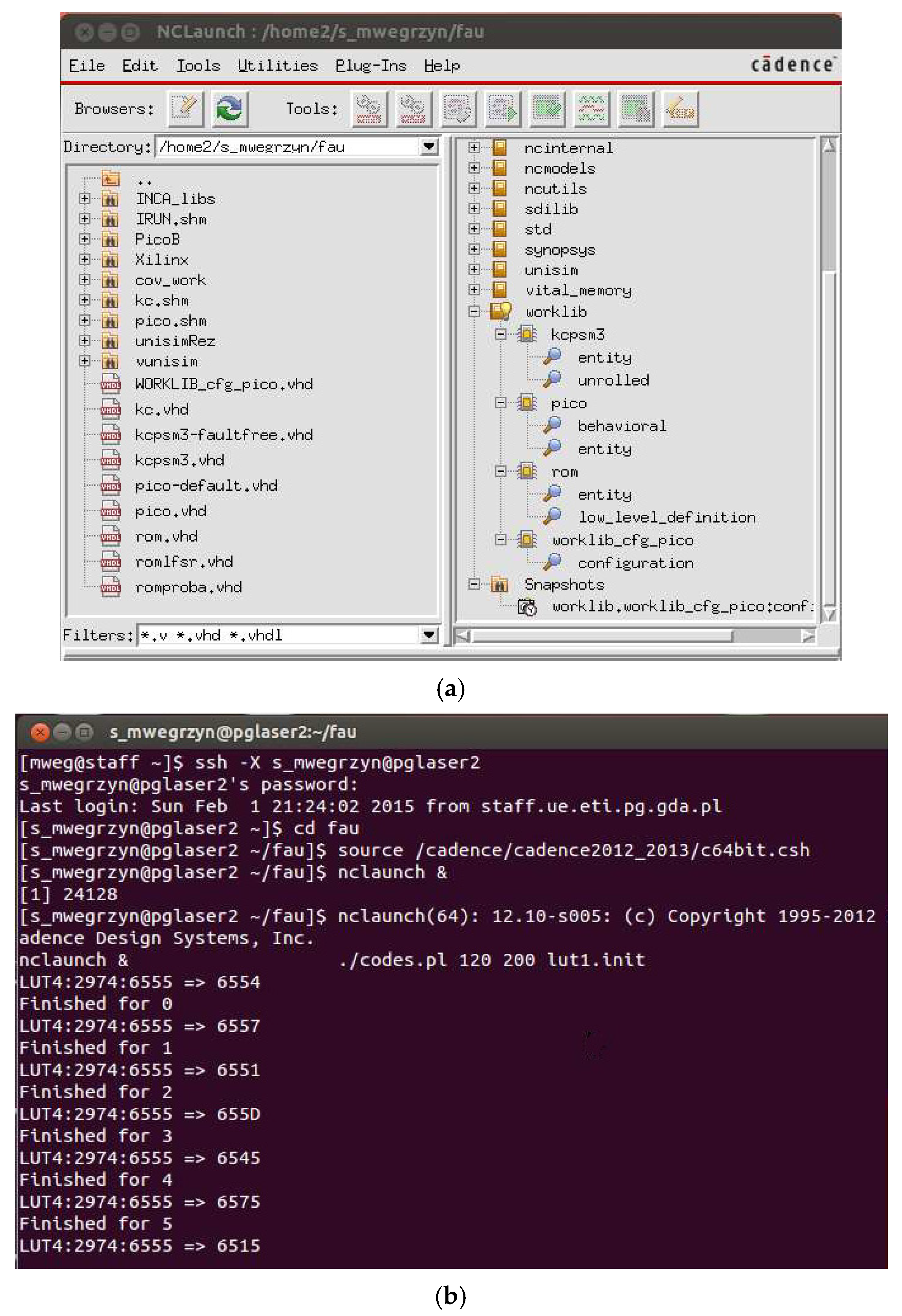
- The Perl script opens the kcpsm.vhd file and writes new faulty values of the INIT parameter in the line and column indicated in the lut.init file.
- The Perl script automatically runs the simulator 1804 times using the CADENCE command. This means that the script will be executed until the entire list of fault sources is exhausted and all possible masking operations are completed.
- The script takes input parameters such as a number of clock cycles required to complete the SEU simulation, an address of the last assembler instruction to read the results of the test program execution, and the lut.init file. The first two parameters depend on the number of instructions that make up the test program. These were frequently modified during the development phase of our test program, and obviously, they may vary depending on the individual user’s test programs. Thus, we made it possible to enter them from the command line when starting the script.
- Parameters, such as the readout address, are passed to the VHDL test bench, which opens the simulation output file and writes the SEU simulation results from the addressed assembler instruction.
- The VHDL Testbench writes an “XX” string in the case where the PicoBlaze operation was stopped by an injected fault in the PicoBlaze control logic.
- The simulation stop conditions are also set inside the test bench.
- The test sequence of the assembler program is executed with 256 unique input test patterns (8-bit numbers) on a fault-free PicoBlaze, and the output results were saved as a reference for comparison purposes.
- The CADENCE simulator generates a file of 256 output results for each fault injected in PicoBlaze. For any 8-bit processor, the number of different generated results is 256, each for a different input test vector. Then, these results are compared to the results contained in the reference file. The entire operation is repeated 1804 times for each injected fault one by one. This generates 461,824 (256 × 1804) results. Finally, the pico-fault.sim result file was compared with the reference file results.txt, which contains 256 correct results. If any result inside the frame of 256 results is wrong, the fault is detected. It should be emphasized that this version of the script modifies the LUT functions by introducing a single bit-flip. According to this rule, 1108 faults can be injected into the description of PicoBlaze. The remaining 883 faults were of the stuck-at type. This resulted in a total of 1804 faults. This is the exhaustive set of single bit-flip faults for PicoBlaze. If necessary, the script can also inject multi-bit flip faults. The above-described Perl script flowchart is shown in Figure 7.
4.2. PicoBlaze Microcontroller Case Study
4.3. Fault Coverage Results
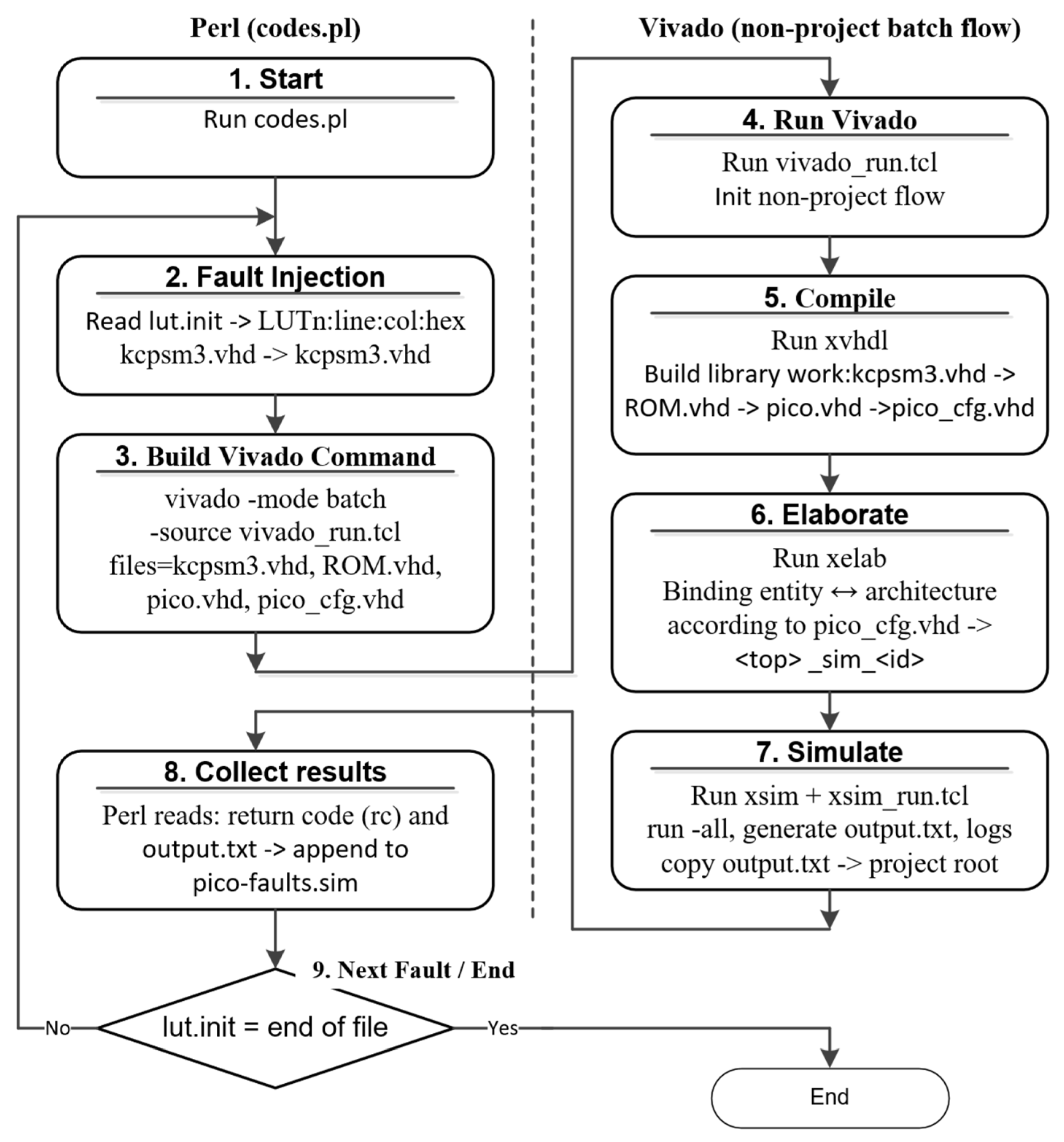
4.4. Integrating the Perl Script into the Xilinx Vivado Environment
5. Investigation of the Fault-Masking Mechanism
- Redundant term(s) (of logic sum): Its logical value is equal to “0” for all possible input data. Therefore, such an additional component of logical sum is not capable of causing any detectable difference in results;
- Redundant variables of terms;
- Reduced term(s);
- Reduced variables constituting the logic terms. Also, reduced terms and variables in logical sums cannot, in every case, change the final logical values of the logical expression;
- Changed one or more variables constituting the terms (of a logic sum).
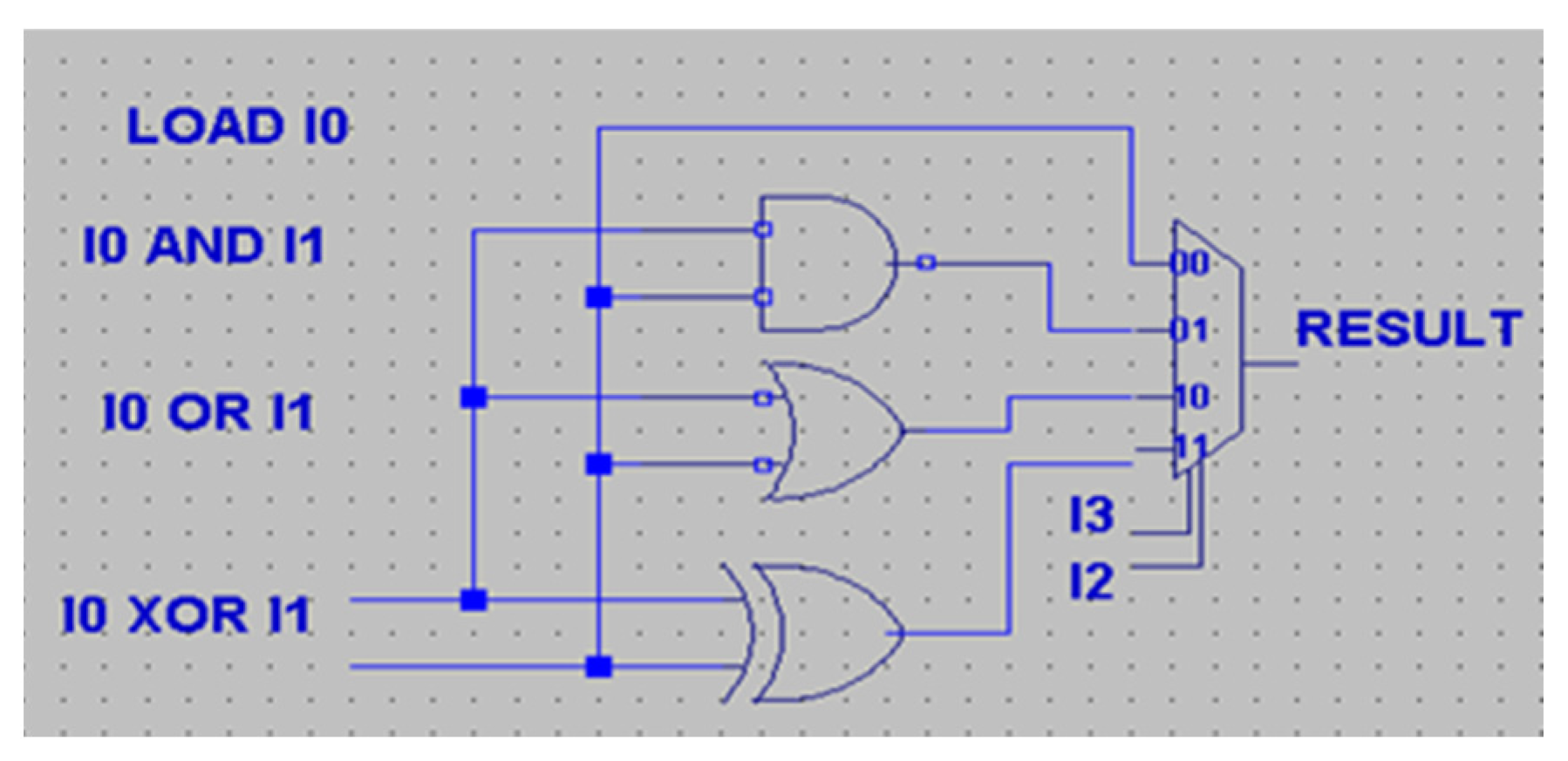
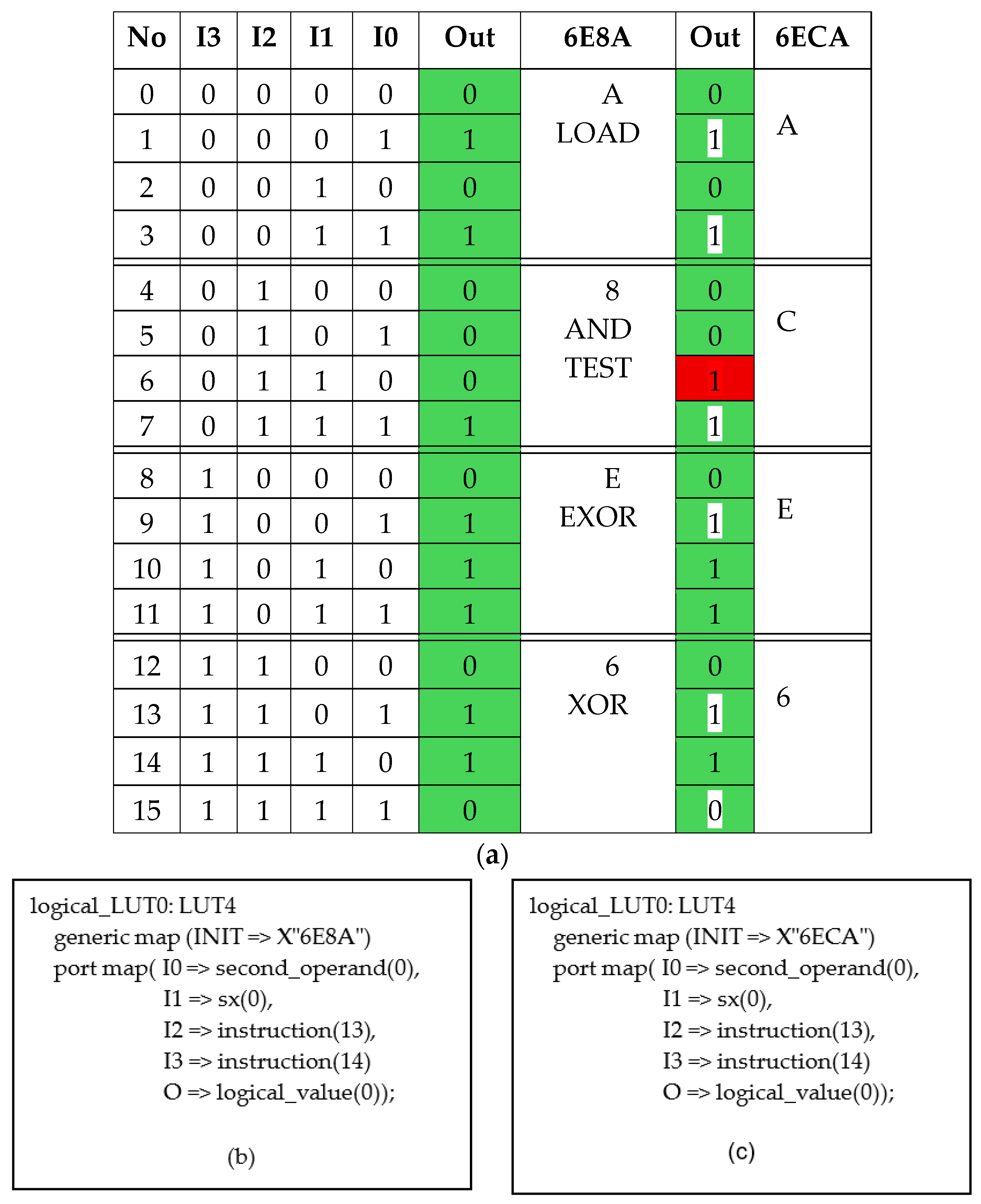
5.1. The Case of the Redundant Term Located in Logical Operations—Block (No. 5)
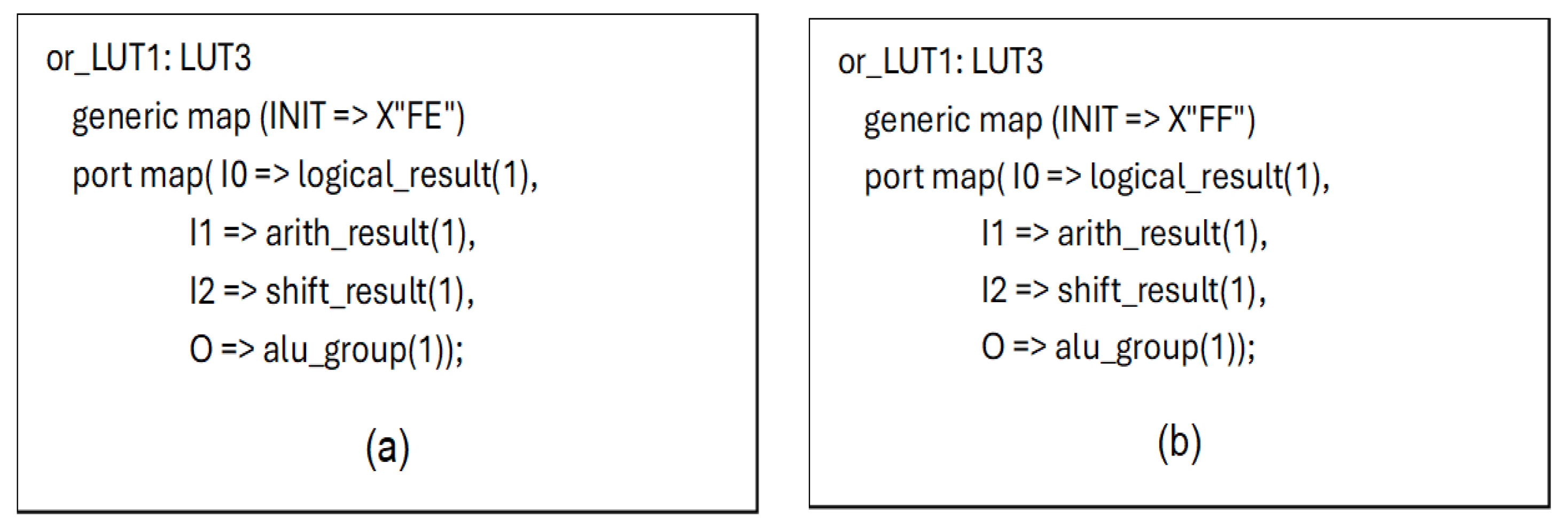
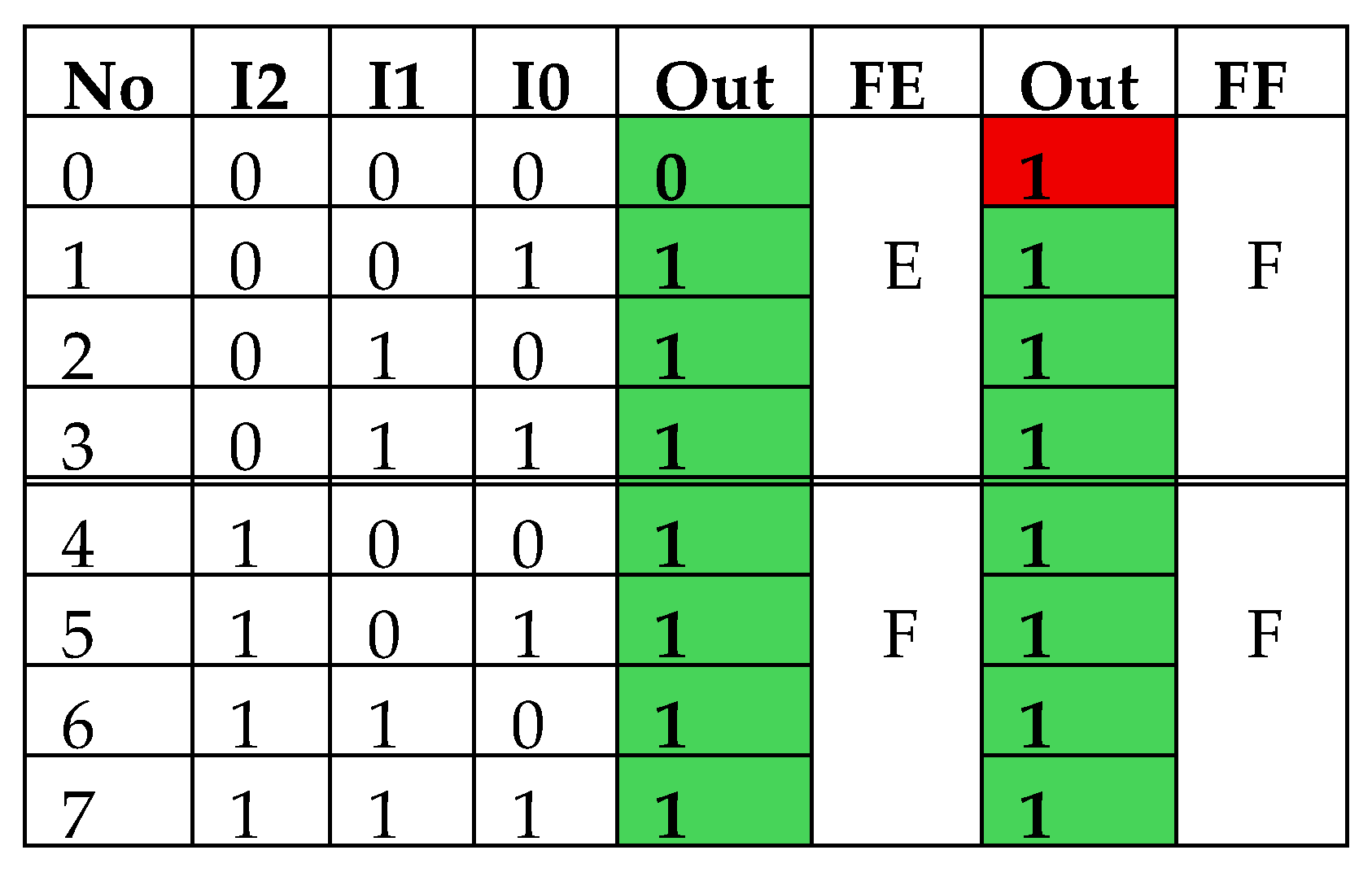
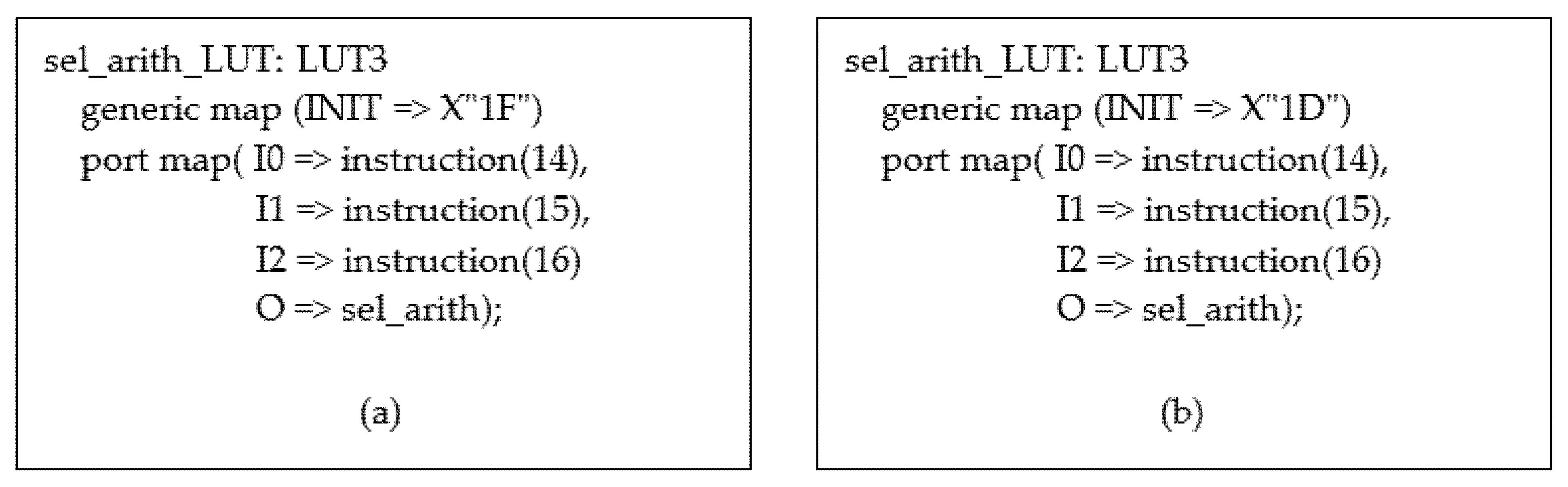
5.2. The Case of the Redundant Variables of the Logical Term Located in the Block of Arithmetic Operations—(No. 7)
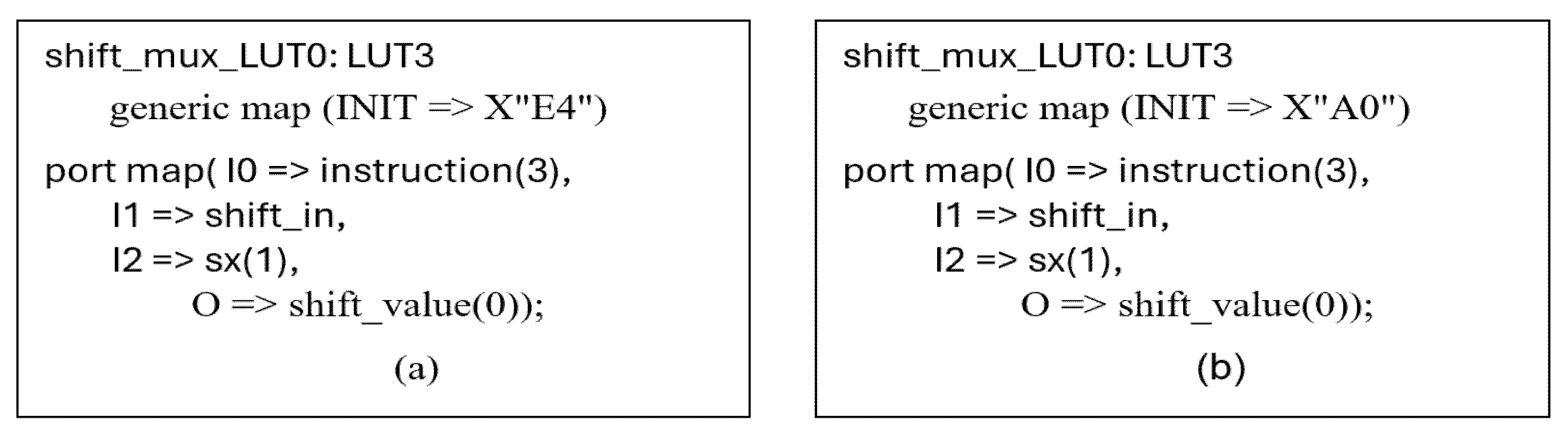
5.3. The Example of the Reduced Term in SHIFT and ROTATE Operations—Block (No. 6)
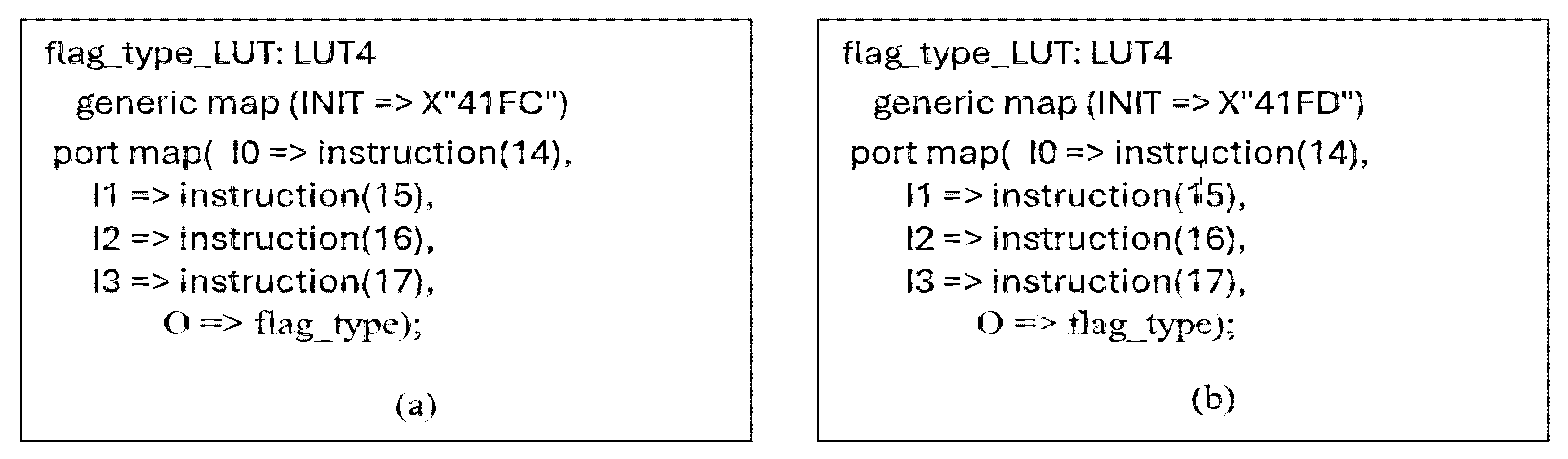
5.4. The Case of the Reduced Variables of ONE Term in ZERO and CARRY Flags—Block No. 3
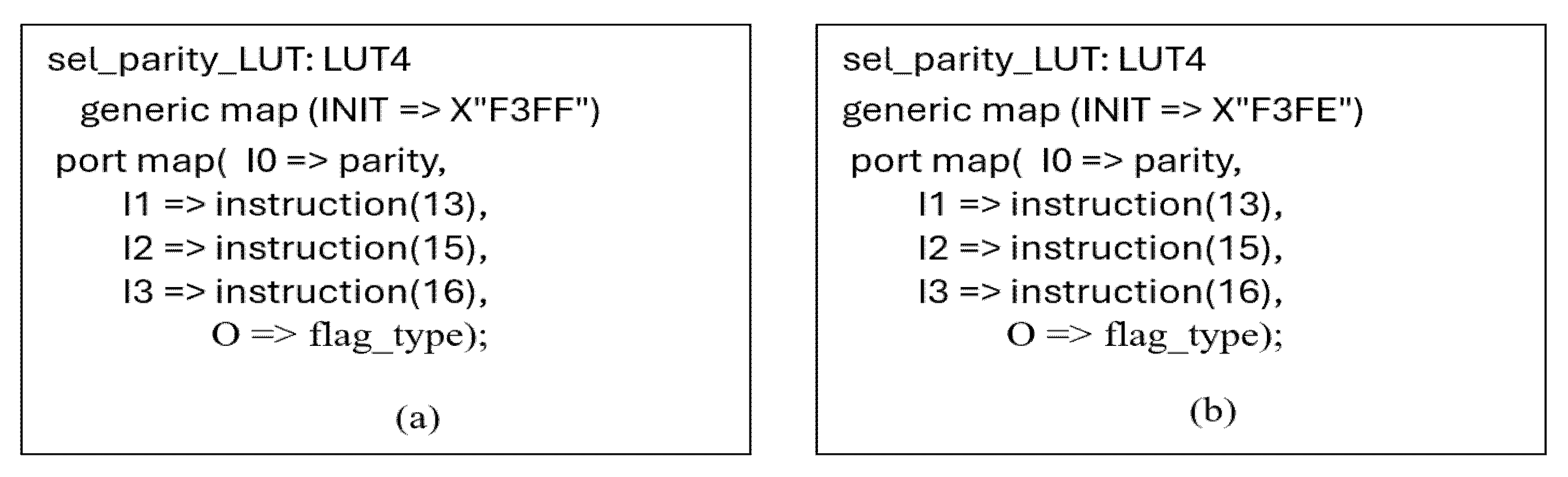
5.5. Example of Changes in Variables of the Logical Term in ZERO and CARRY Flags—Block No. 3
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, R.; Xiao, L.; Li, J.; Cao, X.; Qi, C. A Fault Injection Platform Supporting Both SEU and Multiple SEUs for SRAM-Based FPGA. IEEE Trans. Device Mater. Reliab. 2018, 18, 599–605. [Google Scholar] [CrossRef]
- Gao, Z.; Feng, J.; Gao, S.; Liu, Q.; Ge, G.; Wang, Y.; Reviriego, P. Modeling the Effect of SEUs on the Configuration Memory of SRAM-FPGA-Based CNN Accelerators. IEEE J. Emerg. Sel. Top. Circuits Syst. 2024, 14, 799–810. [Google Scholar] [CrossRef]
- He, W.; Li, J.; Zhou, Y.; Lin, J. Study on an Estimation Method of On-orbit Single Event Upset Rate Based on Historical Data. In Proceedings of the 2021 IEEE 4th International Conference on Electronics Technology (ICET), Chengdu, China, 7–10 May 2021; pp. 1342–1346. [Google Scholar] [CrossRef]
- Węgrzyn, M.; Jamro, E.; Dąbrowska-Boruch, A.; Wiatr, K. Optimal Reduction in the Number of Test Vectors for Soft Processor Cores Implemented in FPGA. Electronics 2021, 10, 2505. [Google Scholar] [CrossRef]
- Masar, F.; Mrazek, V.; Sekanina, L. Late Breaking Result: FPGA-Based Emulation and Fault Injection for CNN Inference Accelerators. In Proceedings of the 2025 Design, Automation & Test in Europe Conference (DATE), Lyon, France, 31 March–2 April 2025; pp. 1–2. [Google Scholar] [CrossRef]
- Wang, W.; Li, X.; Chen, L.; Sun, H.; Zhang, F. A Review on Soft Error Correcting Techniques of Aerospace-Grade Static RAM-Based Field-Programmable Gate Arrays. Sensors 2024, 24, 5356. [Google Scholar] [CrossRef]
- Malagón, D.; Torrens, G.; Segura, J.; Bota, S.A. Single Event Upsets characterization of 65 nm CMOS 6T and 8T SRAM cells for ground level environment. Microelectron. Reliab. 2020, 110, 113696. [Google Scholar] [CrossRef]
- Węgrzyn, M.; Sosnowski, J. Tracing fault effects in FPGA systems. Int. J. Electron. Telecommun. 2014, 60, 103–108. [Google Scholar] [CrossRef]
- Ruano, Ó.; García-Herrero, F.; Aranda, L.A.; Sánchez-Macián, A.; Rodriguez, L.; Maestro, J.A. Fault Injection Emulation for Systems in FPGAs: Tools, Techniques and Methodology, a Tutorial. Sensors 2021, 21, 1392. [Google Scholar] [CrossRef] [PubMed]
- Paiva, D.; Duarte, J.M.; Lima, R.; Carvalho, M.; Mattiello-Francisco, F.; Madeira, H. Fault injection platform for affordable verification and validation of CubeSats software. In Proceedings of the 2021 10th Latin-American Symposium on Dependable Computing (LADC), Florianópolis, Brazil, 22–26 November 2021; pp. 1–11. [Google Scholar] [CrossRef]
- Pitchaimani, B.; Sridharan, M. A novel emulation method to assess the effects of cosmic radiation for avionics SoC using the GA based fault injection hardware. Sadhana 2022, 47, 61. [Google Scholar] [CrossRef]
- Eslami, M.; Ghavami, B.; Raji, M.; Mahani, A. A survey on fault injection methods of digital integrated circuits. Integration 2020, 71, 154–163. [Google Scholar] [CrossRef]
- de Oliveira, A.B.; Tambara, L.A.; Benevenuti, F.; Benites, L.A.C.; Added, N.; Aguiar, V.A.P.; Medina, N.H.; Silveira, M.A.G.; Kastensmidt, F.L. Evaluating Soft Core RISC-V Processor in SRAM-Based FPGA Under Radiation Effects. IEEE Trans. Nucl. Sci. 2020, 67, 1503–1510. [Google Scholar] [CrossRef]
- Muñoz-Quijada, M.; Sanz, L.; Guzman-Miranda, H. A Virtual Device for Simulation-Based Fault Injection. Electronics 2020, 9, 1989. [Google Scholar] [CrossRef]
- Monopoli, M.; Biondi, M.; Nannipieri, P.; Moranti, S.; Fanucci, L. RADSAFiE: A Netlist-Level Fault Injection User Interface Application for FPGA-Based Digital Systems. IEEE Access 2025, 13, 28809–28823. [Google Scholar] [CrossRef]
- Ferlini, F.; Viel, F.; Seman, L.O.; Pettenghi, H.; Bezerra, E.A.; Leithardt, V.R.Q. A Methodology for Accelerating FPGA Fault Injection Campaign Using ICAP. Electronics 2023, 12, 807. [Google Scholar] [CrossRef]
- Pensec, W.; Lapôtre, V.; Gogniat, G. Scripting the Unpredictable: Automate Fault Injection in RTL Simulation for Vulnerability Assessment. In Proceedings of the 2024 27th Euromicro Conference on Digital System Design (DSD), Paris, France, 28–30 August 2024; pp. 369–376. [Google Scholar] [CrossRef]
- Feng, H.; Li, W.; Chen, L.; Wang, S.; Zhou, J.; Tian, C.; Zhang, Y. Precise Fault Injection and Fault Location System for SRAM-based FPGAs. In Proceedings of the 2022 IEEE 10th Joint International Information Technology and Artificial Intelligence Conference (ITAIC), Chongqing, China, 17–19 June 2022; pp. 2371–2376. [Google Scholar] [CrossRef]
- Liu, Y.; Yao, L.; Zhang, W.; Wang, Y.; Jiang, X.; Li, F.; Xu, Q. SEU Fault Injection Strategy for SRAM-based FPGA User Memory Based on Dual-Circuit Model. J. Electron. Test. 2025, 41, 75–84. [Google Scholar] [CrossRef]
- Vacca, E.; Buccellato, F. POSTER: Hardware-Aware Software-Based Fault Injection Platform for DNN Accelerators. In Proceedings of the 22nd ACM International Conference on Computing Frontiers (CF’25), Cagliari, Italy, 28–30 May 2025; Cagliari Association for Computing Machinery: New York, NY, USA, 2025; pp. 220–221. [Google Scholar] [CrossRef]
- Alhayan, F.; Kaur, G.; Alanazi, S.; Rehman, M.B.; Mansouri, W.; Albalawneh, D.; Alqazzaz, A.; Alkhudhayr, H. DA-FIS: A high-speed dynamic adaptive fault injection server framework for reliable FPGA-based embedded systems. PeerJ Comput. Sci. 2025, 11, e2996. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Siecha, R.T.; Alemu, G.; Prinzie, J.; Leroux, P. Analysis of the SEU Tolerance of an FPGA-Based Time-to-Digital Converter Using Emulation-Based Fault Injection. Electronics 2025, 14, 2176. [Google Scholar] [CrossRef]
- Tuzov, I.; de Andrés, D.; Ruiz, J.-C.; Hernández, C. BAFFI: A bit-accurate fault injector for improved dependability assessment of FPGA prototypes. In Proceedings of the 2023 Design, Automation & Test in Europe Conference & Exhibition (DATE), Antwerp, Belgium, 17–19 April 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Brömer, F.; Kenny, P.; Lund, A.; Gremzow, C.; Lüdtke, D. FPGA-Based Fault Injector for SEU-Robustness Analysis of ScOSA; Deutsche Gesellschaft für Luft- und Raumfahrt—Lilienthal-Oberth e.V.: Bonn, Germany, 2023. [Google Scholar] [CrossRef]
- Alderighi, M.; Casini, F.; D’Angelo, S.; Mancini, M.; Codinachs, D.M.; Pastore, S.; Poivey, C.; Sechi, G.R.; Weigand, G.S.R. Experimental validation of fault injection analyses by the FLIPPER tool. In Proceedings of the 2009 European Conference on Radiation and Its Effects on Components and Systems, Brugge, Belgium, 14–18 September 2009; Volume 57, pp. 544–548. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, L.; Wang, S.; Zhou, J.; Tian, C.; Feng, H. Research on agile FPGA fault injection system. In Proceedings of the 2021 International Conference on Microelectronics (ICM), New Cairo City, Egypt, 19–22 December 2021; pp. 57–61. [Google Scholar] [CrossRef]
- Aponte-Moreno, A.; Isaza-González, J.; Serrano-Cases, A.; Martínez-Álvarez, A.; Cuenca-Asensi, S.; Restrepo-Calle, F. Evaluation of fault injection tools for reliability estimation of microprocessor-based embedded systems. Microprocess. Microsyst. 2022, 96, 104723. [Google Scholar] [CrossRef]
- Muñoz-Quijada, M.; Sanchez-Barea, S.; Vela-Calderon, D.; Guzman-Miranda, H. Fine-grain circuit hardening through VHDL datatype substitution. Electronics 2018, 8, 24. [Google Scholar] [CrossRef]
- Altera Corporation. SEU Mitigation User Guide; Intel Altera: Santa Clara, CA, USA, 2024. [Google Scholar]
- European Space Agency. Space Engineering. In Engineering Techniques for Radiation Effects Mitigation in ASICs and FPGAs Handbook; European Space Agency: Paris, France, 2023. [Google Scholar]
- Dutton, B.; Ali, M.; Sunwoo, J.; Stroud, C. Embedded Processor Based Fault Injection and SEU Emulation for FPGAs. In Proceedings of the International Conference on Embedded Systems and Applications, Las Vegas, NV, USA, 14 July 2009; pp. 183–189. [Google Scholar]
- Wilson, A.E.; Wirthlin, M. Fault Injection of TMR Open Source RISC-V Processors using Dynamic Partial Reconfiguration on SRAM-based FPGAs. In Proceedings of the 2021 IEEE Space Computing Conference (SCC), Laurel, MD, USA, 23–27 August 2021; pp. 1–8. [Google Scholar] [CrossRef]
- Sari, A.; Psarakis, M. A fault injection platform for the analysis of soft error effects in FPGA soft processors. In Proceedings of the 2016 IEEE 19th International Symposium on Design and Diagnostics of Electronic Circuits & Systems (DDECS), Kosice, Slovakia, 20–22 April 2016; pp. 1–6. [Google Scholar] [CrossRef]
- de Andres, D.; Ruiz, J.C.; Gil, D.; Gil, P. Fault emulation for dependability evaluation of vlsi systems. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2008, 16, 422–431. [Google Scholar] [CrossRef]
- Choi, S.; Yoo, H. Fast Logic Function Extraction of LUT from Bitstream in Xilinx FPGA. Electronics 2020, 9, 1132. [Google Scholar] [CrossRef]
- Barbirotta, M.; Angioli, M.; Mastrandrea, A.; Menichelli, F.; Cheikh, A.; Olivieri, M. Special Session: SE-UVM, an Integrated Simulation Environment for Single Event Induced Failures Characterization and its Application to the CV32E40P Processor. In Proceedings of the 2024 IEEE International Symposium on Defect and Fault Tolerance in VLSI and Nanotechnology Systems (DFT), Didcot, UK, 8–10 October 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Serrano, F.; Alaminos, V.; Clemente, J.; Mecha, H.; Liu, S. NESSY: Una Plataforma de Inyección de Errores para una FPGA Virtex-5. JCRA. 2012. Available online: https://jornadassarteco.org (accessed on 25 December 2022).
- Ramos, A.; Maestro, J.A.; Reviriego, P. Characterizing a RISC-V SRAM-based FPGA implementation against Single Event Upsets using fault injection. Microelectron. Reliab. 2017, 78, 205–211. [Google Scholar] [CrossRef]
- Lavin, C.; Kaviani, A. Rapidwright: Enabling custom crafted implementations for fpgas. In Proceedings of the 2018 IEEE 26th Annual International Symposium on Field-Programmable Custom Computing Machines (FCCM), Boulder, CO, USA, 29 April–1 May 2018; pp. 133–140. [Google Scholar] [CrossRef]
- Le, R. Soft Error Mitigation Using Prioritized Essential Bits. 2012. Available online: http://www.xilinx.com/support/documentation/application_notes/xapp538-soft-error-mitigationessential-bits.pdf (accessed on 8 June 2025).
- Siemens Verification Academy. Universal Verification Methodology Cookbook. Available online: https://verificationacademy.com/cookbook/uvm-universal-verification-methodology/ (accessed on 8 June 2025).
- Gear, K.W.; Sánchez-Macián, A.; Maestro, J.A. An analysis of FPGA configuration memory SEU accumulation and a preventative scrubbing technique. Microprocess. Microsyst. 2022, 90, 104467, ISSN 0141-9331. [Google Scholar] [CrossRef]
- Chapman K. Xilinx 2011. PicoBlaze 8-Bit Embedded Microcontroller User Guide. Available online: https://docs.amd.com/v/u/en-US/ug129 (accessed on 12 November 2025).
- Xilinx. Spartan-3 Libraries Guide for HDL Designs; Xilinx: San Jose, CA, USA, 2013. [Google Scholar]
- Moroz, L.; Samotyy, V.; Gepner, P.; Węgrzyn, M.; Nowakowski, G. Power Function Algorithms Implemented in Microcontrollers and FPGAs. Electronics 2023, 12, 3399. [Google Scholar] [CrossRef]


| Method | Publication | Precision | Time | Advantage | Requirements | Costs | Disadvantage | FC | SEU Mod |
|---|---|---|---|---|---|---|---|---|---|
| Hardware-Based Radiation Experiment | [3,6,7,9,10,13,25,27,28,29,30] | Very low | Medium | Realistic results | Specific equipment | Very high | Uncontrollable fault locations, potentially destructive | Low | Physical |
| Laser-Based | [11,12] | High | Long | Realistic results | Laser equipment | Medium/high | Limited no. of results, potentially destructive | Medium/low | Physical |
| Emulation-Based | [1,2,3,4,5,6,7,8,9,16,18,20,21,23,26,31,32,33,34,35] | Up to 83% Conf. frame-dependent | Low: several dozen [ms] | Reduced execution time | FPGA board, host computer | High | Intrusive approach, complex | Low | Bitstream modification |
| Simulation-Based Sim. Commands | [4,8,9,17,27,36] | Up to 100% Application-dependent | Long: several dozen hours | Early analysis, full control of injections | Computer, simulator SW | Low | Long sim. time, high computing resources not compatible with others simulators | High | HDL code modification |
| Simulation-Based Saboteurs | [9,14,15,19,24] | Both application- and no. of saboteur-dependent | Long: several dozen hours | Compatible with all simulators | Computer, simulator SW | Low | Changed HW and timings | High | HDL code modification |
| Test Program | Fault Coverage [%] | |
|---|---|---|
| Stuck-at | Total | |
| 883 faults | 1804 faults | |
| Fibonacci number generator | 49.9 | 33.8 |
| Fibonacci (recursion) | 56.0 | 43.3 |
| Random instruction order | 62.7 | 46.8 |
| MM1 | 63.6 | 49.9 |
| MM2 | 64.4 | 51.2 |
| MM3 | 66.4 | 53.1 |
| Data-sensitive path without full bijective property | 72.6 | 62.9 |
| Data-sensitive path with full bijectivity | 88.1 | 76.6 |
| Full bijective property with LFSR block for SHIFTs | 90.3 | 84.2 |
| PicoBlaze Functional Block | # CLB | # LUTs | # Injected Faults | Number of Undetected Faults | Undetected Faults [%] |
|---|---|---|---|---|---|
| Basic control | 1 | 1 | 2 | 0 | 0 |
| Interrupt logic | 2 | 3 | 47 | 38 | 80.86 |
| Dec. control PC CALL/RETURN stack | 3 | 6 | 104 | 37 | 35.6 |
| ZERO/CARRY flags | 6 | 11 | 179 | 32 | 17.9 |
| Program Counter | 10 | 20 | 320 | 11 (extended PC), 61 (LFSR solution) | 3.4/19.1 |
| Registers and 2nd operand select. | 5 | 10 | 157 | 0 | 0 |
| Memory storing function | 5 | 2 | 35 | 0 | 0 |
| Logical op. | 5 | 9 | 233 | 1 | 0 |
| Shift/Rotate op. | 6 | 11 | 176 | 14 | 8 |
| Arithmetical op. | 6 | 11 | 156 | 4 | 2.6 |
| ALU MUX | 9 | 17 | 217 | 84 (inputs) | 38.7 |
| R/W strobes | 2 | 3 | 52 | 43 (in/out) | 82.7 |
| CALL/RETURN stack control | 6 | 5 | 126 | 22 (stack extended) /60 (for LFSR) | 17.9/48.8 |
| SUM | 73 | 115 | 1804 | x 286 (with in/out) or 84 without (in/out) | 15.8/5.24 |
| Redundancy Type | No. Undetected Faults | Redundant Terms | Redundant Variables of Terms | Reduced Logical Terms | Reduced Variables in Terms | Changed Variables in Terms | |
|---|---|---|---|---|---|---|---|
| Processor Block | |||||||
| 1. Interrupts logic | 37 | 19 | 8 | 2 | 8 | 0 | |
| 2. Decoder for control PC, CALL /RETURN STACK | 38 | 14 | 9 | 3 | 6 | 6 | |
| 3. ZERO and CARRY flags | 31 | 7 | 4 | 6 | 6 | 8 | |
| 4. Program counter | 12 | 1 | 3 | 2 | 4 | 2 | |
| 5. Logical operations | 1 | 1 | 0 | 0 | 0 | 0 | |
| 6. Shift and rotate operations | 15 | 3 | 2 | 3 | 4 | 3 | |
| 7. Arithmetical operations | 4 | 1 | 1 | 1 | 1 | 0 | |
| 8. ALU multiplexer | 83 | 16 | 29 | 5 | 12 | 21 | |
| 9. Read and write strobes | 42 | 29 | 0 | 0 | 12 | 1 | |
| 10. CALL/RETURN stack | 23 | 4 | 2 | 8 | 7 | 2 | |
| SUM | 286 | 95 | 58 | 30 | 60 | 43 | |
| Publication | Year | Method | DUT | No. Injected Faults | FC [%] |
|---|---|---|---|---|---|
| Munoz [14] | 2020 | Sim. | Counter | 1000 | 98.5 |
| Wegrzyn [4] | 2021 | Sim. | PicoBlaze | 1804 | 94.75 |
| Ferlini [16] | 2023 | Emul. | Leon3 | 5425 | 72 |
| Zhang [26] | 2021 | Emul. | FIR | 299,520 | 15.5 |
| Feng [18] | 2022 | Emul. | FFT | 544,123 | 11.18 |
| Zhang [1] | 2018 | Emul. | c5315 | 53,783 | 3.7 |
| Pensec [17] | 2024 | Simul. | RISC-V | 48,006 | 2.93 |
| Wilson [32] | 2021 | Emul. | PicoBlaze | 318,348 | 1.13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Węgrzyn, M.; Kochan, O.; Maikiv, I. Fault Injection Tool for FPGA Reliability Testing: A Novel Method and Discovery of LUT-Specific Logical Redundancies. Electronics 2025, 14, 4600. https://doi.org/10.3390/electronics14234600
Węgrzyn M, Kochan O, Maikiv I. Fault Injection Tool for FPGA Reliability Testing: A Novel Method and Discovery of LUT-Specific Logical Redundancies. Electronics. 2025; 14(23):4600. https://doi.org/10.3390/electronics14234600
Chicago/Turabian StyleWęgrzyn, Mariusz, Orest Kochan, and Ihor Maikiv. 2025. "Fault Injection Tool for FPGA Reliability Testing: A Novel Method and Discovery of LUT-Specific Logical Redundancies" Electronics 14, no. 23: 4600. https://doi.org/10.3390/electronics14234600
APA StyleWęgrzyn, M., Kochan, O., & Maikiv, I. (2025). Fault Injection Tool for FPGA Reliability Testing: A Novel Method and Discovery of LUT-Specific Logical Redundancies. Electronics, 14(23), 4600. https://doi.org/10.3390/electronics14234600







