Zone-Based Simplification of Fuzzy Logic Controllers for Switched Reluctance Motor Drives
Abstract
1. Introduction
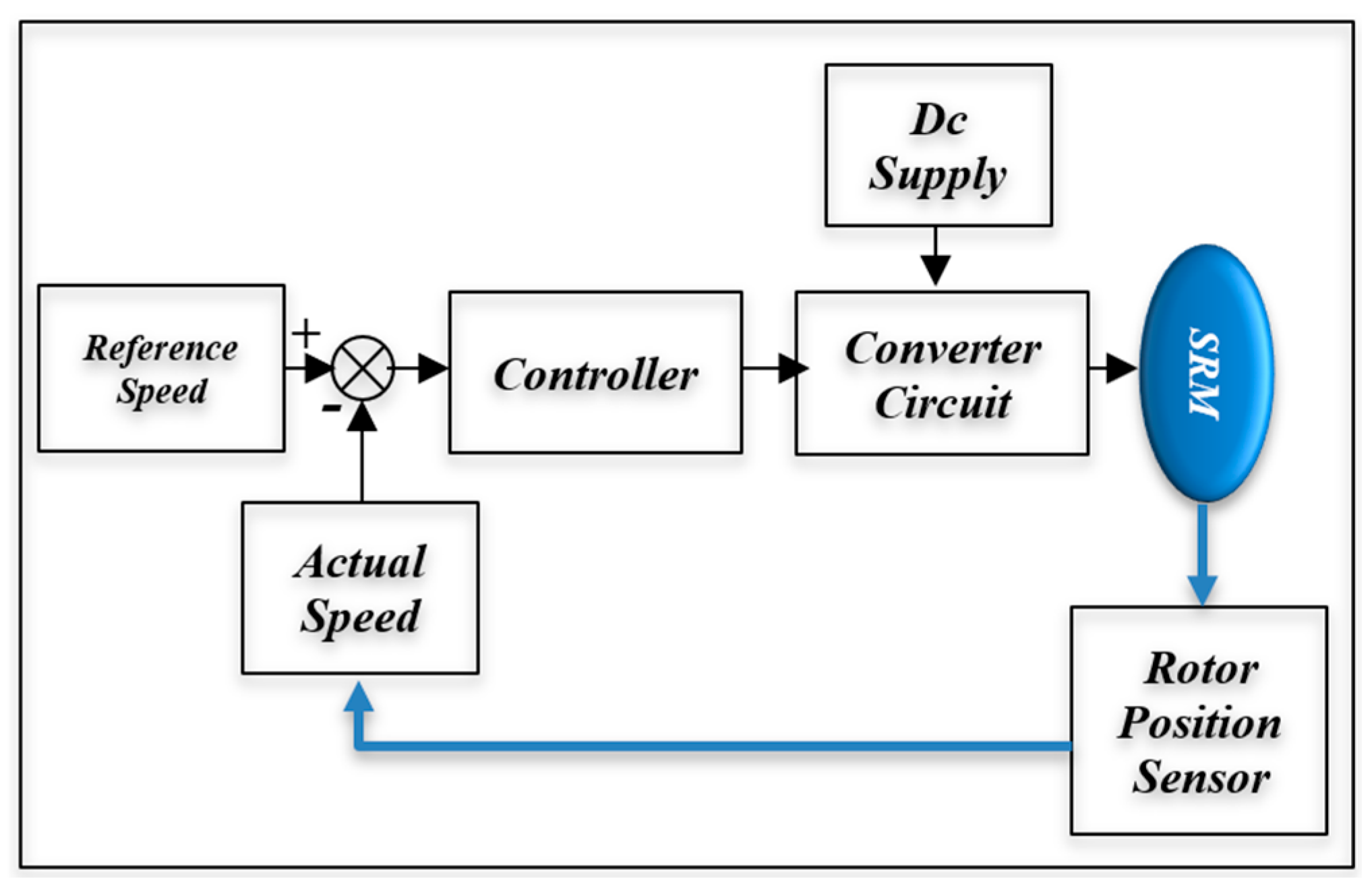
2. Mathematical Modeling of SRM

3. Speed Controller Design
3.1. Speed Regulation of a Switched Reluctance Motor with a Proportional–Integral–Derivative Controller
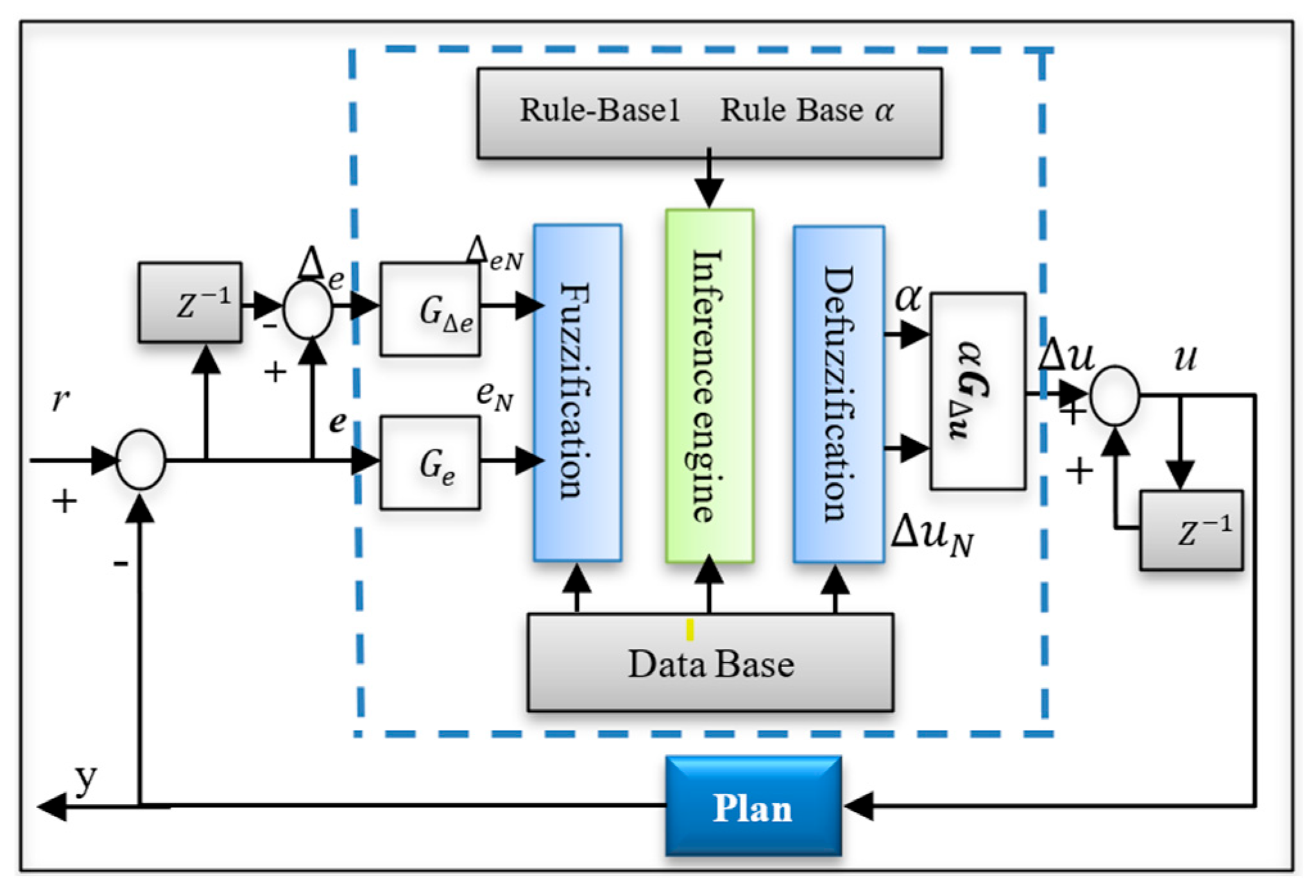
3.2. Speed Regulation of a Switched Reluctance Motor with a Fuzzy Logic Controller
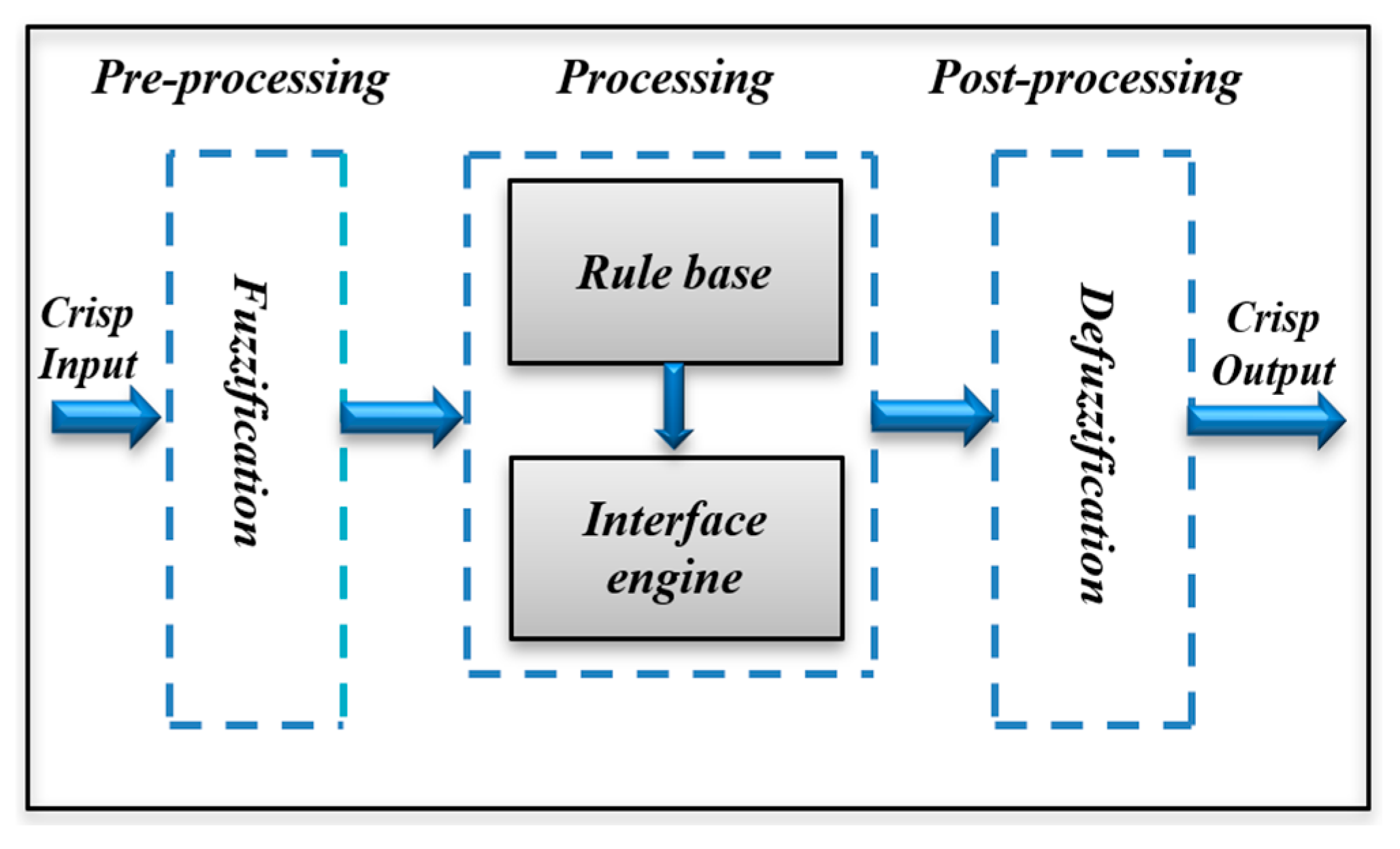
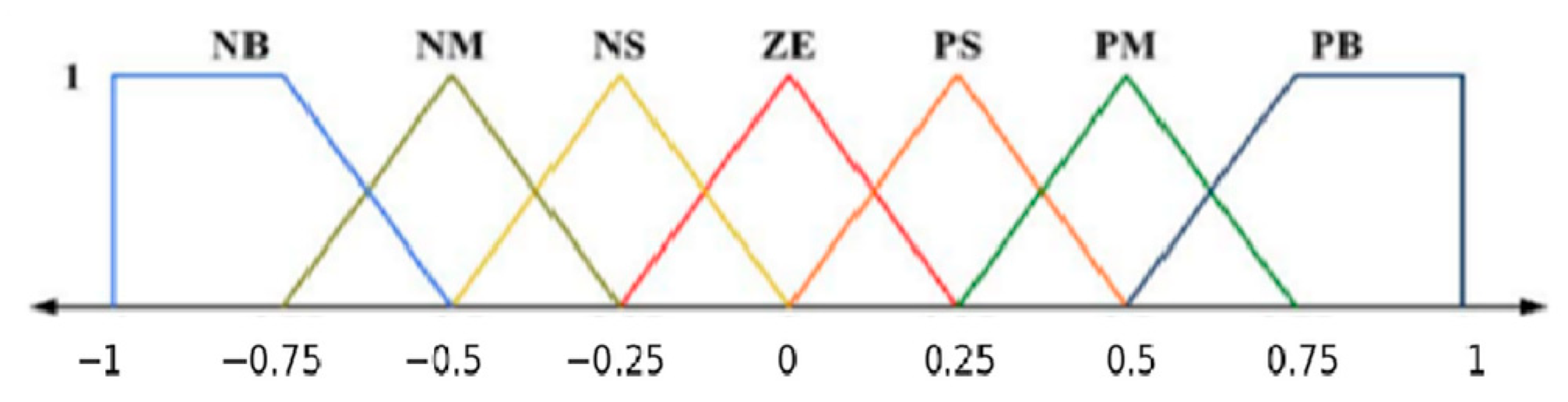
4. Standard FLC Design
5. Review on Simplification Techniques for Fuzzy Logic Speed Control
5.1. Rule Base Reduction
5.2. Membership Function Simplification
5.3. Hybrid and Adaptive Simplification
5.4. Zone-Based and Behavioral Simplification
5.5. Simplified Fuzzy Logic Design Using Zone-Based Simplification
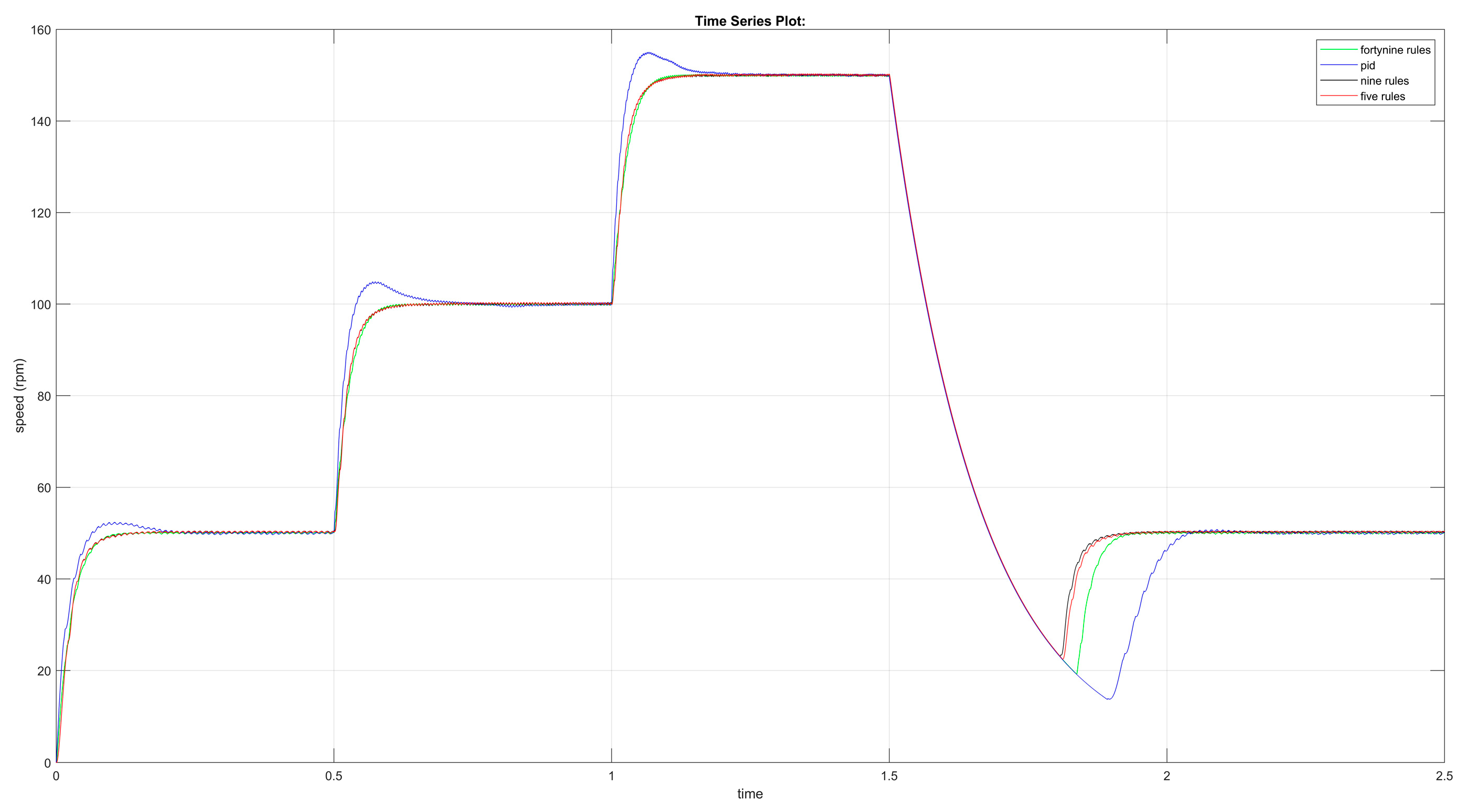
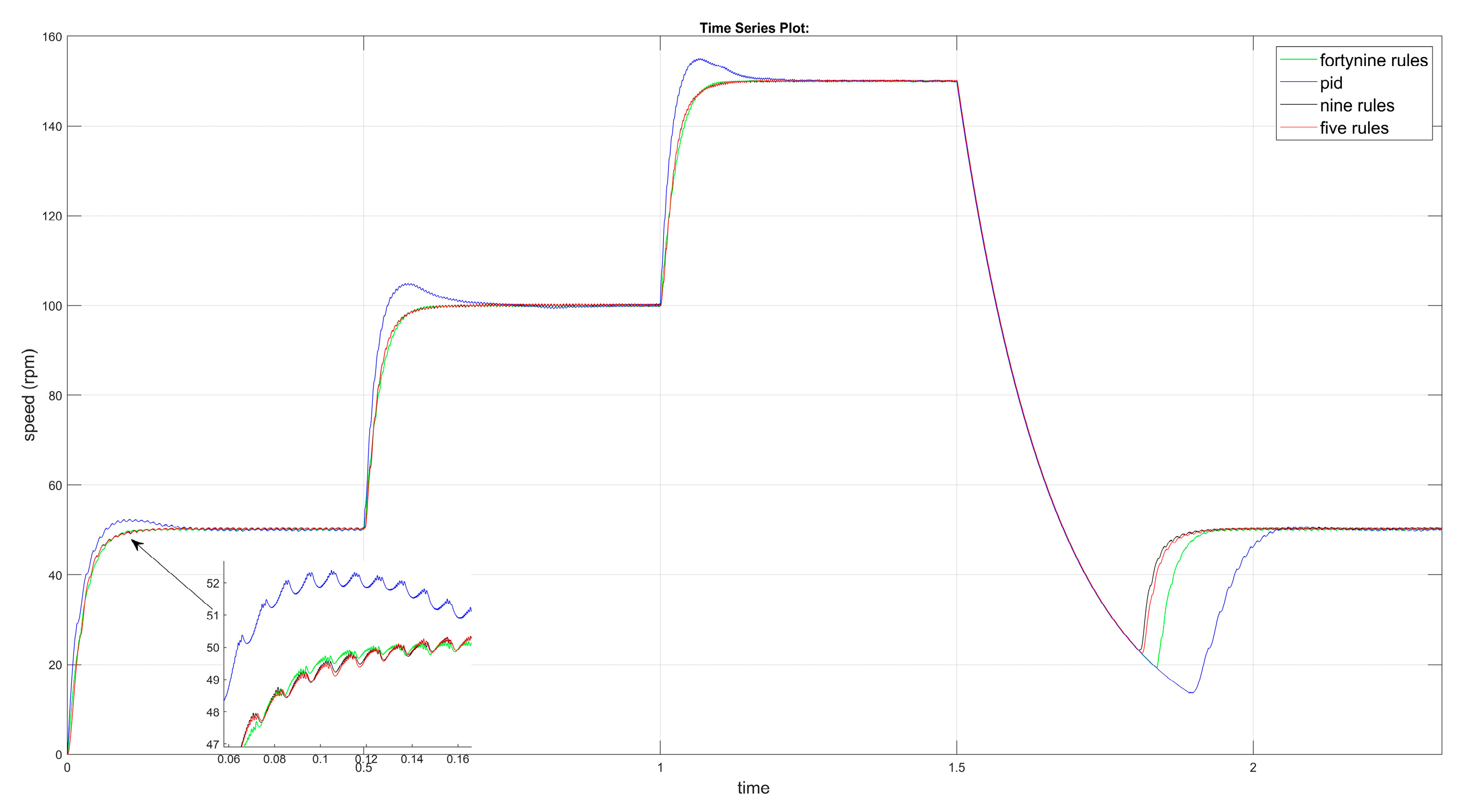
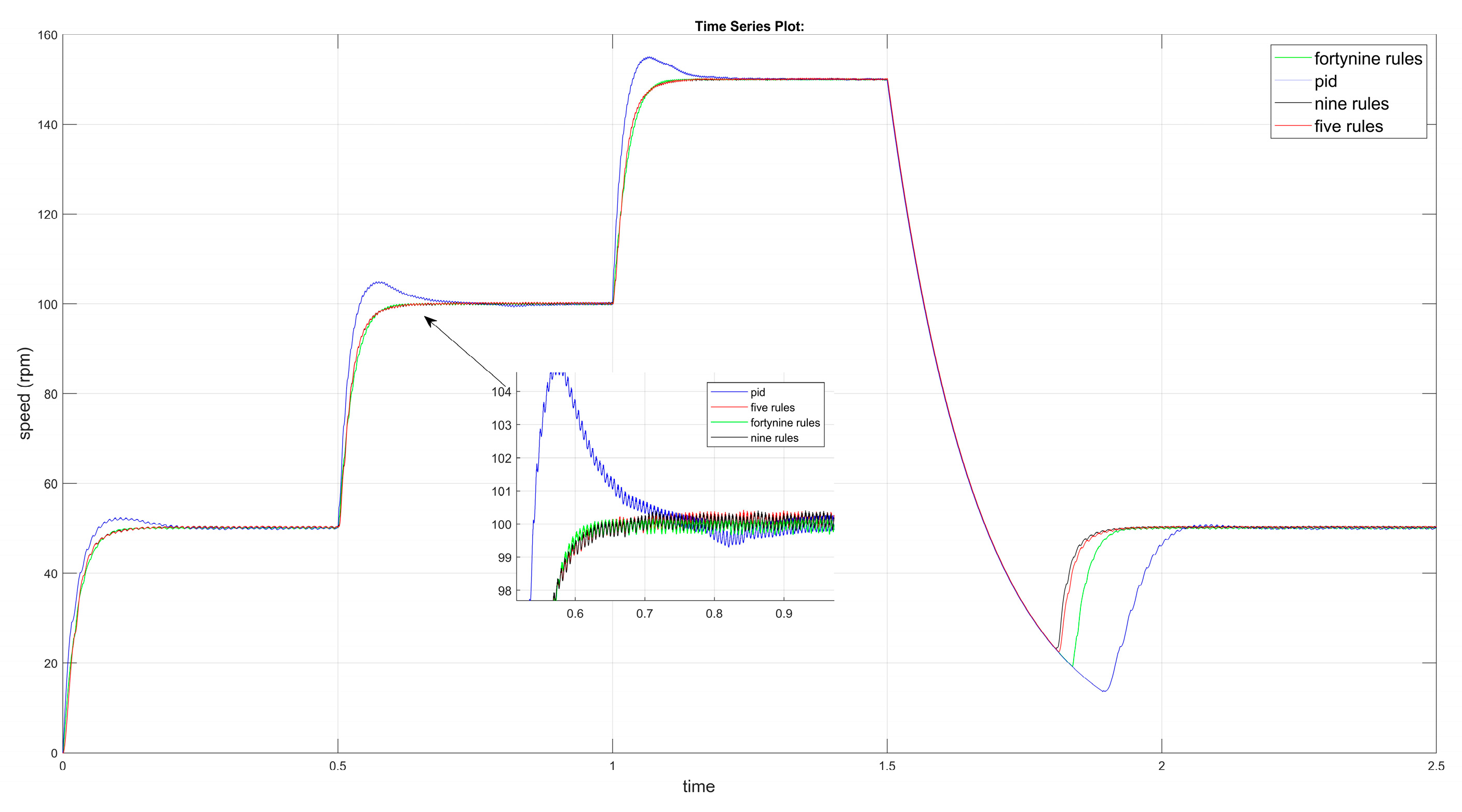
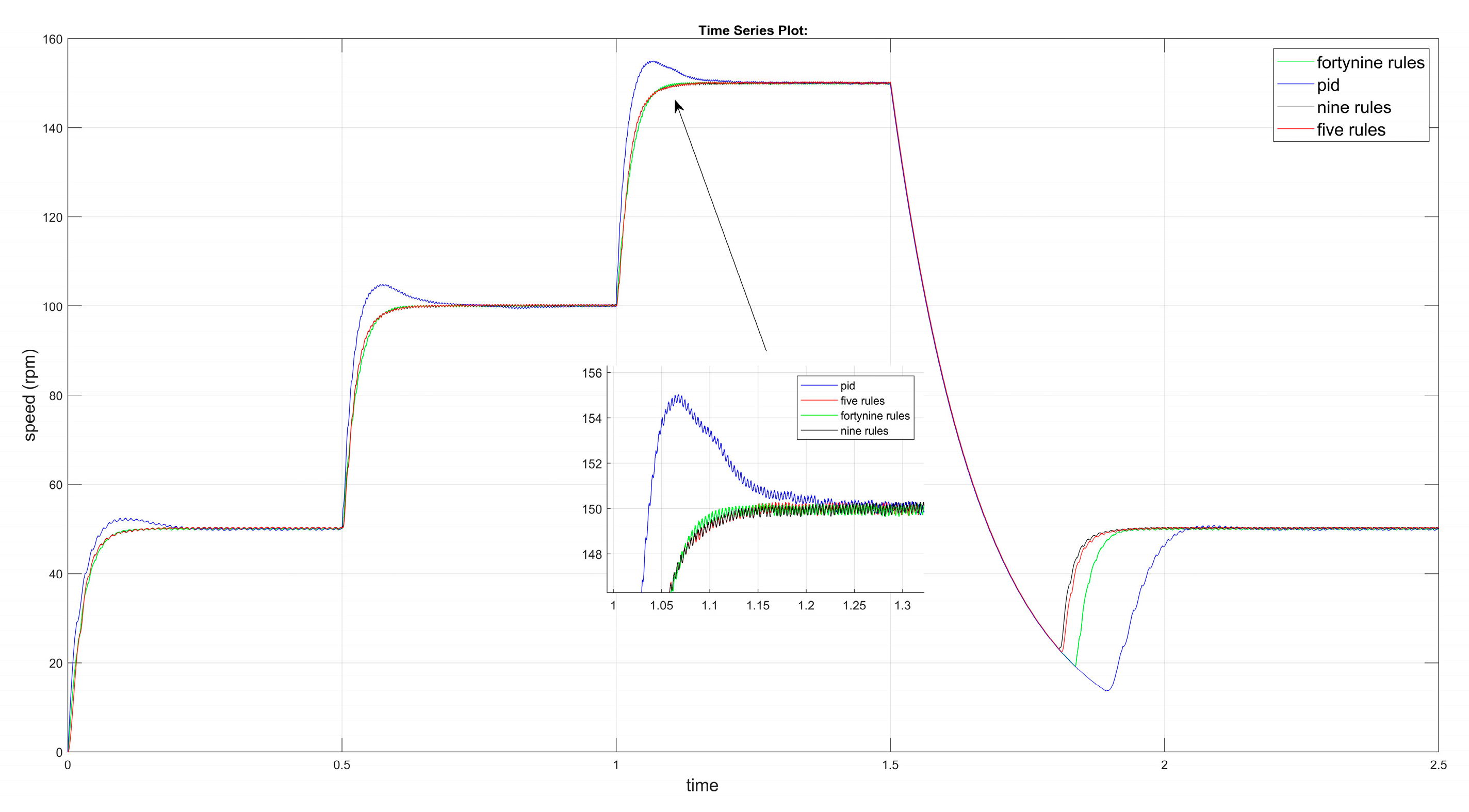
6. Results and Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SRM | Switched Reluctance Motor |
| FLC | Fuzzy Logic Controller |
| SFLC | Simplified Fuzzy Logic Controller |
| PID | Proportional–Integral–Derivative |
| ANN | Artificial Neural Network |
| ANFIS | Adaptive Neuro-Fuzzy Inference System |
| SMC | Sliding Mode Controller |
| ZE | Zero Error |
| MF | Membership Function |
| UOD | Universe of Discourse |
| DTC | Direct Torque Control |
| PI | Proportional–Integral |
| PMSM | Permanent Magnet Synchronous Motor |
| AI | Artificial Intelligence |
References
- Maksoud, H.A. Torque Ripple Minimization of a Switched Reluctance Motor using a Torque Sharing Function based on the Overlap Control Technique. Eng. Technol. Appl. Sci. Res. 2020, 10, 5371–5376. [Google Scholar] [CrossRef]
- Saleh, A.L.; Al-Amyal, F.; Számel, L. Control techniques of switched reluctance motors in electric vehicle applications: A review on torque ripple reduction strategies. AIMS Electron. Electr. Eng. 2024, 8, 104–145. [Google Scholar] [CrossRef]
- García-Amorós, J.; Andrada, P.; Blanqué, B. Assessment of Linear Switched Reluctance Motor’s Design Parameters for Optimal Performance. Electr. Power Compon. Syst. 2015, 43, 810–819. [Google Scholar] [CrossRef]
- Desai, P.; Krishnamurthy, M.; Schofield, N.; Emadi, A. Novel Switched Reluctance Machine Configuration with Higher Number of Rotor Poles Than Stator Poles: Concept to Implementation. IEEE Trans. Ind. Electron. 2010, 57, 649–659. [Google Scholar] [CrossRef]
- Corda, J.; Jamil, S.M. Experimental Determination of Equivalent-Circuit Parameters of a Tubular Switched Reluctance Machine With Solid-Steel Magnetic Core. IEEE Trans. Ind. Electron. 2010, 57, 304–310. [Google Scholar] [CrossRef]
- Zhang, B.; Han, J.; Ma, R. Adaptive fuzzy control of nonlinear aeroelastic system with measurement noise. J. Vibroeng. 2021, 23, 1184–1195. [Google Scholar] [CrossRef]
- Talib, M.H.N.; Ibrahim, Z.; Rahim, N.A.; Zulhani, R.; Nordin, N.; Farah, N.; Razali, A. An improved simplified rules Fuzzy Logic Speed Controller method applied for induction motor drive. ISA Trans. 2020, 105, 230–239. [Google Scholar] [CrossRef]
- Ismail, M.Z.; Talib, M.H.N.; Ibrahim, Z.; Lazi, J.M.; Rasin, Z. Experimental simplified rule of self tuning fuzzy logic-model reference adaptive speed controller for induction motor drive. Indones. J. Electr. Eng. Comput. Sci. 2020, 20, 1653. [Google Scholar] [CrossRef]
- Shi, J.; Mi, Q.; Cao, W.; Zhou, L. Optimizing BLDC motor drive performance using particle swarm algorithm-tuned fuzzy logic controller. SN Appl. Sci. 2022, 4, 293. [Google Scholar] [CrossRef]
- Ma, M.; Ling, F.; Li, F.; Liu, F. Torque ripple suppression of switched reluctance motor by segmented harmonic currents injection based on adaptive fuzzy logic control. IET Electr. Power Appl. 2020, 14, 325–335. [Google Scholar] [CrossRef]
- Song, B.; Xiao, Y.; Xu, L. Design of fuzzy PI controller for brushless DC motor based on PSO–GSA algorithm. Syst. Sci. Control Eng. 2020, 8, 67–77. [Google Scholar] [CrossRef]
- Hai, T.; Zhou, J.; Furukawa, N. Performance enhancement of fuzzy-PID controller for MPPT of PV system to extract maximum power under different conditions. Soft Comput 2024, 28, 2035–2054. [Google Scholar] [CrossRef]
- Mahjoub, S.; Labdai, S.; Chrifi-Alaoui, L.; Drid, S.; Derbel, N. Design and implementation of a Fuzzy logic supervisory based on SMC controller for a Dual Input-Single Output converter. Int. J. Electr. Power Energy Syst. 2023, 150, 109053. [Google Scholar] [CrossRef]
- Abdel-Aziz, A.; Elgenedy, M.; Williams, B. Review of Switched Reluctance Motor Converters and Torque Ripple Minimisation Techniques for Electric Vehicle Applications. Energies 2024, 17, 3263. [Google Scholar] [CrossRef]
- Bechaouech, H.; Van den Bossche, A.; Ibrahim, M. Switched reluctance machine configurations with higher number of rotor poles. In Proceedings of the ICCEE’18 International Conference on Communications and Electrical Engineering, Tokyo, Japan, 12–14 October 2018. [Google Scholar]
- Miron, A.; Cziker, A.C.; Beleiu, H.G. Fuzzy Control Systems for Power Quality Improvement—A Systematic Review Exploring Their Efficacy and Efficiency. Appl. Sci. 2024, 14, 4468. [Google Scholar] [CrossRef]
- Vidal-Martínez, R.; García-Martínez, J.R.; Rojas-Galván, R.; Álvarez-Alvarado, J.M.; Gozález-Lee, M.; Rodríguez-Reséndiz, J. A Review of Mamdani, Takagi–Sugeno, and Type-2 Fuzzy Controllers for MPPT and Power Management in Photovoltaic Systems. Technologies 2025, 13, 422. [Google Scholar] [CrossRef]
- Shill, P.C.; Akhand, M.A.H.; Asaduzzaman, M.D.; Murase, K. Optimization of Fuzzy Logic Controllers with Rule Base Size Reduction using Genetic Algorithms. Int. J. Inf. Technol. Decis. Mak. 2015, 14, 1063–1092. [Google Scholar] [CrossRef]
- Dombi, J.; Rigó, P.R. The construction of multidimensional membership functions and its application to feasibility problems. Fuzzy Sets Syst. 2023, 469, 108634. [Google Scholar] [CrossRef]
- Hassani, H.; Zarei, J. Interval Type-2 fuzzy logic controller design for the speed control of DC motors. Syst. Sci. Control. Eng. 2015, 3, 266–273. [Google Scholar] [CrossRef]
- Cordon, O.; Herrera, F. A proposal for improving the accuracy of linguistic modeling. IEEE Trans. Fuzzy Syst. 2000, 8, 335–344. [Google Scholar] [CrossRef]
- Goswami, R.; Joshi, D. Performance Review of Fuzzy Logic Based Controllers Employed in Brushless DC Motor. Procedia Comput. Sci. 2018, 132, 623–631. [Google Scholar] [CrossRef]
- Cerruto, E.; Consoli, A.; Raciti, A.; Testa, A. Fuzzy Adaptive Vector Control of Induction Motor Drive. Power Electronics. IEEE Trans. Power Electron. 1997, 12, 1028–1040. [Google Scholar] [CrossRef]
- Lima, J.F.; Patiño-León, A.; Orellana, M.; Zambrano-Martinez, J.L. Evaluating the Impact of Membership Functions and Defuzzification Methods in a Fuzzy System: Case of Air Quality Levels. Appl. Sci. 2025, 15, 1934. [Google Scholar] [CrossRef]
- Tarbosh, Q.A.; Aydogdu, O.; Farah, N.; Talib, H.N.; Salh, A.; Cankaya, N.; Omar, F.A.; Durdu, A. Review and Investigation of Simplified Rules Fuzzy Logic Speed Controller of High Performance Induction Motor Drives. IEEE Access 2020, 8, 49377–49394. [Google Scholar] [CrossRef]
- Yilmaz, B.M.; Tatlicioglu, E.; Savran, A.; Alci, M. Adaptive fuzzy logic with self-tuned membership functions based repetitive learning control of robotic manipulators. Appl. Soft Comput. 2021, 104, 107183. [Google Scholar] [CrossRef]
- Tatlicioglu, E.; Yilmaz, B.M.; Savran, A.; Alci, M. Adaptive fuzzy logic with self-adjusting membership functions based tracking control of surface vessels. Ocean. Eng. 2022, 253, 111129. [Google Scholar] [CrossRef]
- Mitra, P.; Dey, C.; Mudi, R.K. Fuzzy rule-based set point weighting for fuzzy PID controller. SN Appl. Sci. 2021, 3, 651. [Google Scholar] [CrossRef]
- Zhao, Z.; Wang, T.; Yu, J.; Basin, M.V. Bilateral Cooperative Control of Nonlinear Multiagent Systems with State and Output Quantification. IEEE Trans. Cybern. 2025, 55, 2949–2957. [Google Scholar] [CrossRef]
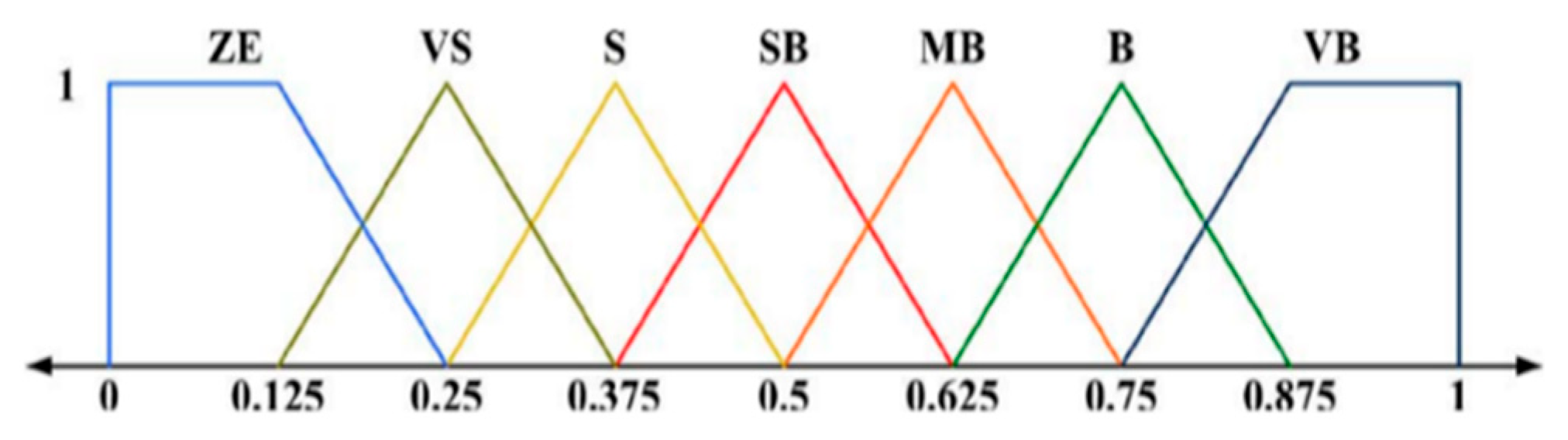
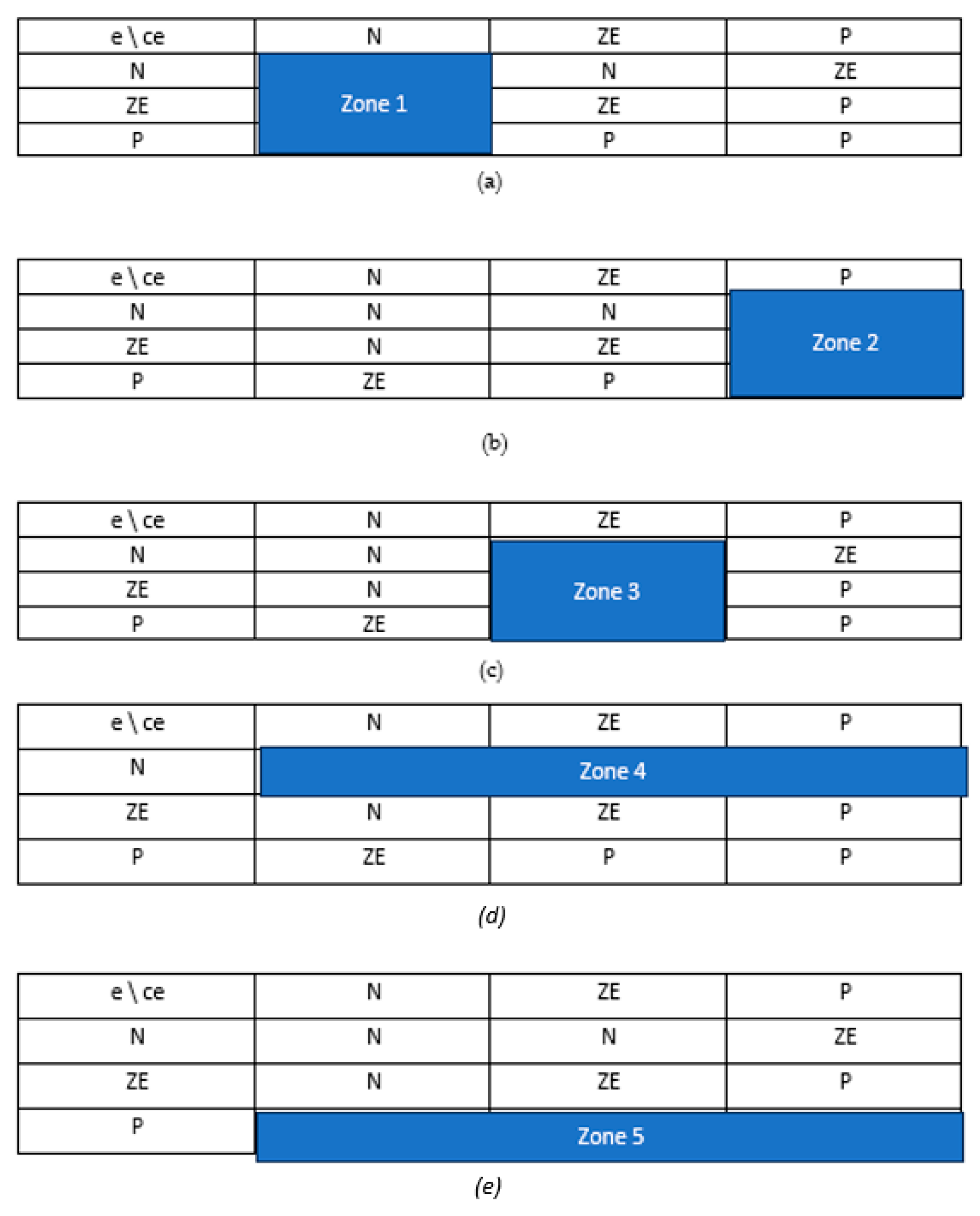
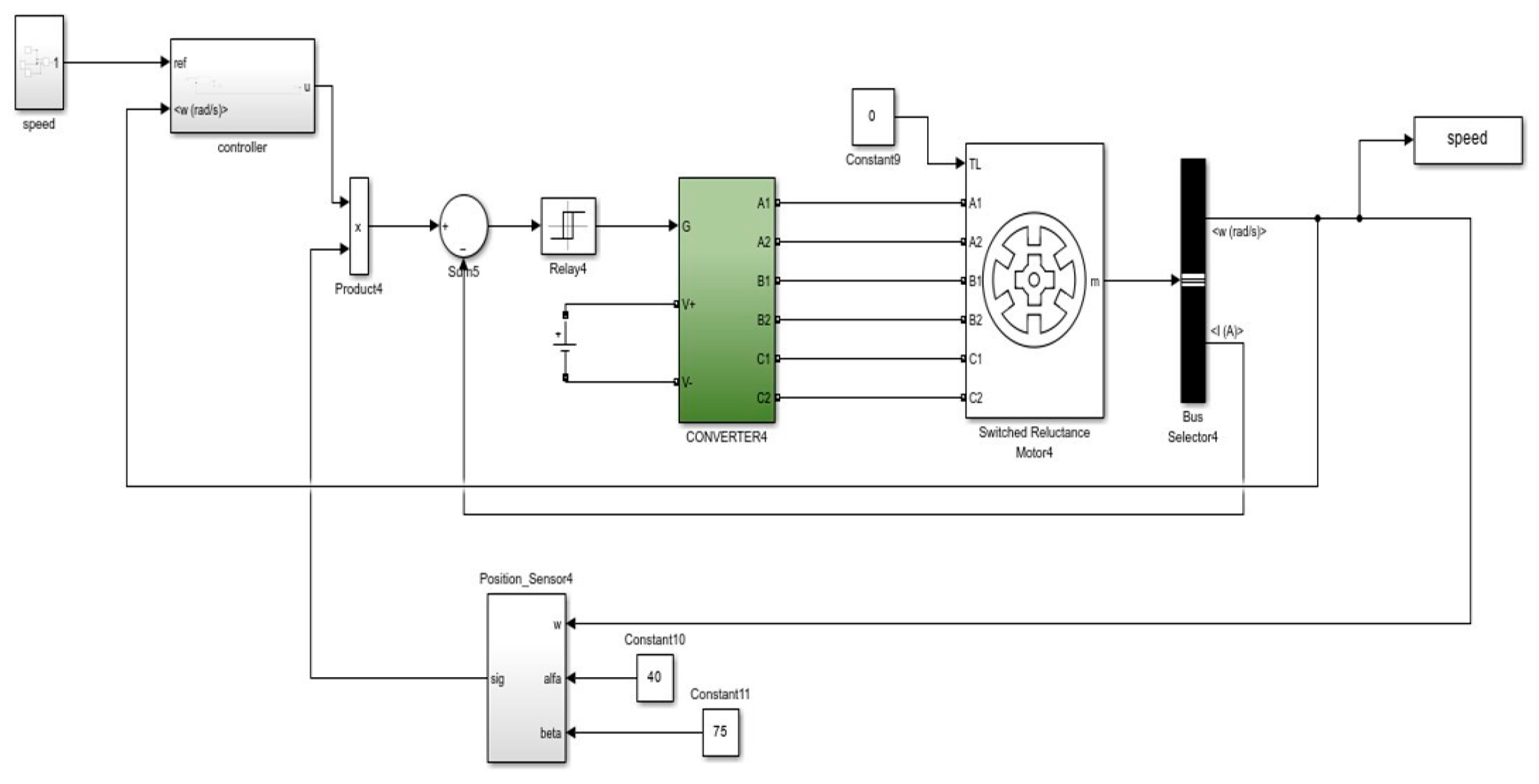
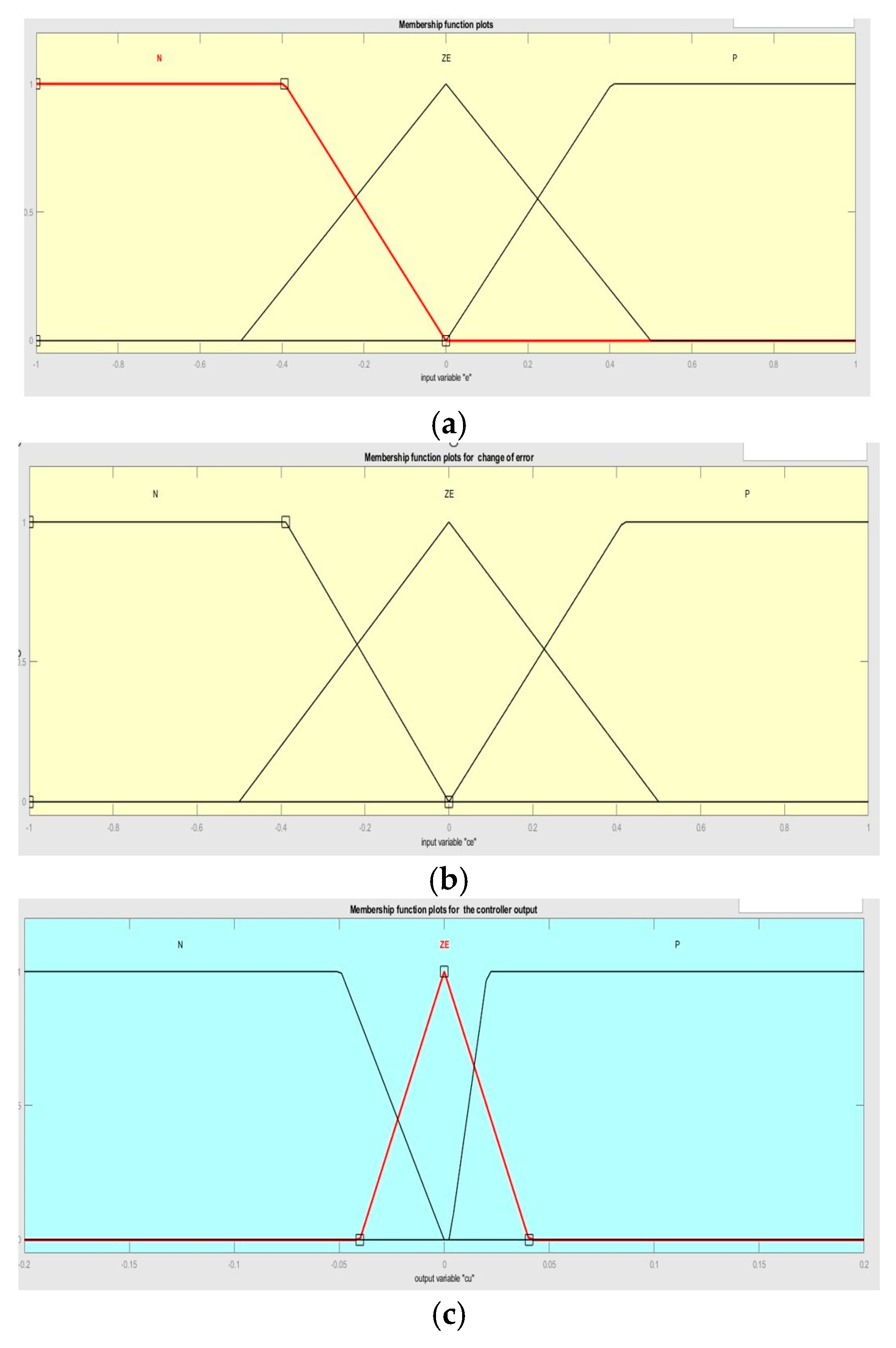
| ΔE\E | NG | NM | NP | ZE | PP | PM | PG |
| NG | NG | NG | NG | NG | NM | NP | ZE |
| NM | NM | NM | NP | NP | NM | ZE | PP |
| NP | NG | NG | NM | NP | ZE | PP | PM |
| ZE | NG | NM | NP | ZE | PP | PM | PG |
| PP | NM | NP | ZE | PP | PM | PG | PG |
| PM | NP | ZE | PP | PM | PG | PG | PG |
| PG | ZE | PP | PM | PG | PG | PG | PG |
| ΔE\E | NG | NM | NP | ZE | PP | PM | PG |
| NG | Zone 1 | Zone 2 | Zone 3 | ||||
| NM | |||||||
| NP | Zone 4 | Zone 5 | Zone 6 | ||||
| ZE | |||||||
| PP | |||||||
| PM | Zone 7 | Zone 8 | Zone 9 | ||||
| PG | |||||||
| e\ce | N | ZE | P |
| N | N | N | ZE |
| ZE | N | ZE | P |
| P | ZE | P | P |
| e\ce | N | ZE | P |
| N | N | ||
| ZE | N | ZE | P |
| P | P |
| Parameter | Value | Unit |
|---|---|---|
| Motor type | 6/4 | - |
| Stator resistance | 0.01 | Ohm |
| Unaligned inductance | 0.67 × 10−3 | H |
| Aligned inductance | 23.6 × 10−3 | H |
| Saturated aligned inductance | 0.15 × 10−3 | H |
| Inertia | 0.0082 | kg·m2 |
| Friction | 0.05 | N·m·s |
| Maximum current | 450 | A |
| Maximum flux linkage | 0.486 | V·s |
| Reference Step | PID | 49-Rule FLC | 9-Rule FLC | 5-Rule FLC |
|---|---|---|---|---|
| 1st step (~50 rpm) | noticeable (~10%) | minimal (~2–3%) | minimal | minimal |
| 2nd step (~100 rpm) | high (~7–10%) | slight (~2%) | negligible | negligible |
| 3rd step (~150 rpm) | highest (~8–10%) | moderate (~3%) | very low | very low |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Uğurenver, A.; Khudhur, A.I.K. Zone-Based Simplification of Fuzzy Logic Controllers for Switched Reluctance Motor Drives. Electronics 2025, 14, 4248. https://doi.org/10.3390/electronics14214248
Uğurenver A, Khudhur AIK. Zone-Based Simplification of Fuzzy Logic Controllers for Switched Reluctance Motor Drives. Electronics. 2025; 14(21):4248. https://doi.org/10.3390/electronics14214248
Chicago/Turabian StyleUğurenver, Abbas, and Ahmed Ibrahim Khudhur Khudhur. 2025. "Zone-Based Simplification of Fuzzy Logic Controllers for Switched Reluctance Motor Drives" Electronics 14, no. 21: 4248. https://doi.org/10.3390/electronics14214248
APA StyleUğurenver, A., & Khudhur, A. I. K. (2025). Zone-Based Simplification of Fuzzy Logic Controllers for Switched Reluctance Motor Drives. Electronics, 14(21), 4248. https://doi.org/10.3390/electronics14214248






