Abstract
The need for unpredictable sequences of bits is common in many important security applications. These sequences can only be generated by true random number generators (TRNGs). Apart from the natural analog domain for TRNGs, this type of generator is also required as a digital-based solution, particularly leveraging field-programmable gate array (FPGA) platforms. Despite the number of existing FPGA-based implementations, new solutions that use different types of entropy sources, utilize fewer FPGA resources, or ensure higher throughput are still being sought. This paper presents an architecture of a simple TRNG targeted for implementation in FPGAs. As a source of entropy, the TRNG exploits jitter in capacitive oscillators and metastability in flip-flops. The capacitive oscillators, in turn, use the input–output cells of an FPGA chip and unconnected external pins and cyclically charge and discharge the parasitic capacitance associated with these pins. The TRNG needs a small number of FPGA resources, namely 13 look-up tables (LUTs), 12 flip-flops, and 3 unused pins. Its throughput is approximately 12.5 Mbit/s for AMD/Xilinx Artix-7 FPGA family chips. The presented TRNG passes all the NIST statistical tests for a wide range of operating conditions.
1. Introduction
True random number generators (TRNGs) have broad applications in areas requiring unpredictable randomness, such as cryptography, Monte Carlo simulations, machine learning, probabilistic computing, gaming, and others. They constitute essential components, particularly for generating strong cryptographic keys and secure communication protocols [1,2]. Unlike pseudo-random number generators, TRNGs exploit physical processes as a source of randomness. These processes include, for example, thermal noise [3], clock jitter [4], metastable states [5], random telegraph noise [6], quantum phenomena [7], vacuum fluctuations [8], bistability of nanopillar magnetic tunnel junctions [9], and others.
Field-programmable gate arrays (FPGAs) constitute a relevant platform for the fast prototyping and implementation of digital systems, including cryptographic systems and their essential components. Thus, continuous interest in TRNG implementation in FPGAs can be observed in research publications. For example, a TRNG exploiting the jitter of ring oscillators as well as the metastability of D-Latches and requiring very few FPGA resources is portrayed in [5]. The random jitter of free-running oscillators that incorporate programmable delay lines is utilized as a source of randomness in [10]. A TRNG that exploits the runtime capability of the digital clock manager (DCM) hardware primitives in Xilinx FPGAs to tune the phase shift between two clock signals is presented in [11]. In [12], a TRNG is presented, for which randomness comes from the combined effect of waveform interaction and device noise, enhanced by a chaotic evolution process. A chaos-based hybrid function integrated with the El-Gamal algorithm has been proposed to design a TRNG in [13]. A TRNG based on a physical, unclonable function dedicated to FPGAs is proposed in [14]. The mutual influence between ring oscillators used as sources of randomness for a TRNG implemented in an FPGA is considered in [15]. A modified nonlinear Fibonacci Galois ring oscillator model, introduced in [16], was leveraged to build a TRNG in [17]. The dual entropy source (i.e., clock jitter and metastability) TRNG architecture based on an FPGA is proposed in [18]. The TRNG portrayed in [19] generates random numbers based on race hazard and jitter from braided and cross-coupled combinational logic gates. In [20], FPGAs and field-programmable analog arrays (FPAAs) are used to generate true random numbers. The FPAA amplifies the analog noise generated by the thermistor, while the FPGA digitizes and processes the signal using Von Neumann whitening. In [2], the TRNG architecture is presented using a dynamic hybrid entropy source called a self-feedback multiplexer, consisting of four high-frequency independent ring oscillators, four MUXs, four DFFs, and one XOR gate. The TRNG with entropy sources involving random telegraph noise and ring oscillator jitter is proposed in [21]. The TRNG also utilizes a direct digital synthesizer to realize phase control and frequency control for generating random sequences. The authors of [22] propose a TRNG based on a dynamic hybrid entropy unit exploiting both jitter and metastability, enhanced by coupling and feedback strategies. Another TRNG based on jitter and metastability is proposed in [23]. This TRNG uses a dual cross-coupled XOR gate unit to generate a random output sequence. A TRNG entropy source based on an autonomous Boolean network circuit with imbalanced node oscillation rings is described in [24]. The study [25] demonstrates a TRNG whose randomness is generated by the oscillation of self-timed rings and accurately extracted by a jitter-latch structure. A TRNG based on the principle of beat frequency detection, dedicated to Xilinx FPGAs, is presented in [26].
Taking into account this very concise review, it can be observed that a number of approaches have been applied so far to implement true random number generators in FPGAs. The approaches differ in the nature of the entropy source and the randomness extraction circuits, which are essential factors allowing unpredictable sequences of bits to be obtained. These factors also strongly influence the utilization of FPGA resources and the throughput achieved. Solutions for which post-processing circuits are not needed, those requiring a low number of resources, and those achieving high throughput are particularly sought after. Another important factor is that the randomness quality and unpredictability of the output sequence of TRNGs should not be disturbed by temperature variations or supply voltage changes. Meeting all these requirements is always difficult. Thus, new implementation solutions are still emerging.
In a previous work of the author [27], a preliminary investigation of the TRNG architecture involving a novel source of entropy based on a jitter in capacitive oscillators was reported. These oscillators utilized the unused pins of an FPGA chip. The disadvantages of the proposed TRNG were a relatively high FPGA resource requirement, low utilization of FPGA components within a single slice, and the need for a resource-intensive post-processing circuit, which also decreased the overall throughput.
In this paper, a significantly improved and simplified architecture of the TRNG, which was initially introduced in [27], is presented. The improved TRNG, which passes all NIST statistical tests within a wide range of the die temperatures and supply voltages of I/O cells without a post-processing circuit, requires 5 times fewer FPGA slices, 2.5 times fewer look-up tables (LUTs), and 3.9 times fewer flip-flops (FFs). Due to the fact that the post-processing circuit is not needed, it also allows slightly higher throughput to be achieved. Compared to [27], the presented TRNG employs a different architecture of capacitive oscillators, freely discharging parasitic capacitance associated with an FPGA pin. Furthermore, this TRNG includes more LUTs with feedback paths instead of some D-type FFs and D-latches, which allows for a denser deployment of components within a single FPGA slice.
The improved and simplified architecture of the TRNG also introduces a specific shift register, clocked by a locally generated clock signal, for which there is a relatively high probability of hold time violation. This violation, which leads to metastability, additionally increases the randomness of the proposed TRNG and eliminates the need for any external post-processing circuit.
Unlike most published solutions, this paper reveals all the details of the FPGA implementation of the TRNG. It provides a complete schematic of the TRNG, involving standard library components, which makes it very easy and straightforward to replicate using a structural description in Verilog or VHDL hardware description languages.
The remainder of this paper is organized as follows. In Section 2, the architecture of capacitive oscillators is presented. The essential Section 3 describes the true number generator circuit, while Section 4 shows statistical test results, including voltage and temperature changes, of the proposed TRNG. Section 5 discusses the results obtained in reference to other published solutions. Finally, Section 6 concludes the paper.
2. Capacitive Oscillator
The capacitive oscillator exploits the parasitic capacitance associated with the unconnected external pin of an FPGA chip. This capacitance is cyclically charged and discharged using a specifically connected input/output buffer (IOBUF) of an I/O cell of an FPGA. Figure 1 shows two versions of the capacitive oscillator architecture. Apart from the IOBUF, the first version (Figure 1a), which was applied in [27], requires the PULLUP component and an additional NOT gate (a LUT configured to negate the signal), while the second one (Figure 1b) needs only a PULLDOWN resistor.

Figure 1.
Two versions of the capacitive oscillator: (a) with a PULLUP resistor; (b) with a PULLDOWN resistor.
The IOBUF component consists of an input buffer, shown in the top part of the IOBUF in Figure 1, and a three-state output buffer, located in the bottom part. The output of the three-state buffer is in a high impedance state when the control signal (T) is in a high logic state. When the voltage at the input buffer of the IOBUF exceeds the threshold value for the high (Figure 1a) or low (Figure 1b) levels, then, by appropriately driving the three-state buffer control signal, this buffer will force the voltage at the external FPGA pin to be low (Figure 1a) or high (Figure 1b), respectively. This causes fast discharging (Figure 1a) or charging (Figure 1b) of the parasitic capacitance. After that, the three-state buffer goes to a high impedance state, and the parasitic capacitance is relatively slowly charged or discharged by the PULLUP (Figure 1a) or PULLDOWN (Figure 1b) resistor, respectively. Then the entire process is repeated, causing oscillations. Since the charging process of the parasitic capacitance for the oscillator with a PULLUP resistor takes much longer than the discharging, the oscillation waveform contains a series of very short pulses with an active high logic state separated by long gaps with a low logic state. For the oscillator with a PULLDOWN resistor, the output waveform is negated—there is a series of very short pulses with a low logic state and long gaps with a high logic state. It is also worth noting that the PULLUP and PULLDOWN components are, in fact, a weak current source or current sink, respectively. Thus, the voltage waveform on the FPGA pin with a parasitic capacitance has a sawtooth-like character.
Figure 2 shows oscilloscope waveforms acquired from the oscillator output, connected to the FPGA I/O pin, and measured on the crucial FPGA pin, which is part of the capacitive oscillator. To illustrate fluctuations in the output phase as well as the voltage level on the crucial FPGA pin, the oscilloscope persistence time was set to 6 s. These fluctuations are shown as some fuzziness of the waveforms in Figure 2. The waveforms were measured using the Digilent Nexys-Video evaluation board (Digilent Co., Austin, TX, USA) with an AMD/Xilinx Artix-7 FPGA chip (AMD, Santa Clara, CA, USA). The LVCMOS33 I/O standard was chosen for both the oscillator output and the crucial pin with parasitic capacitance. As can be noted, the output frequency of the capacitive oscillators is relatively low, around 3 MHz. However, the parasitic capacitance for these measurements was increased by the capacitances of the PCB board trace, board header, and oscilloscope probe (11 pf in this case). The other measurements showed that, apart from the parasitic capacitance, the oscillator frequency firmly depends on the applied I/O standard and the actual IOBUF supply voltage (VCCO). For example, for the crucial pin connected nowhere (even without any PCB trace leading to this pin) and the LVCMOS12/LVCMOS18 I/O standard applied with the nominal voltage value of the VCCO, the frequency reaches a 13 MHz level for Artix-7 FPGA chips.

Figure 2.
Oscilloscope waveforms acquired with 6 s of persistence time for two versions of capacitive oscillators: (a) version with a PULLUP resistor; (b) version with a PULLDOWN resistor. The upper waveform in blue represents the output of the oscillator, whereas the lower waveform shows the voltage change on the FPGA pin with parasitic capacitance.
Although the waveforms in Figure 2 indicate that the capacitive oscillator output has a noticeable jitter, the jitter itself does not seem to be high, even for a relatively long persistence time applied for measurements. However, it has been observed that the jitter can be substantially increased when an additional high-frequency ring oscillator is connected to the input (I) of the three-state buffer of the IOBUF for the oscillator in Figure 1b instead of a constant high logic state. The high-frequency ring oscillator, in turn, can be built using a series connection of two LUTs (one LUT configured to negate a signal and the other acting as a simple buffer) with a feedback path. The oscilloscope waveforms for this case are shown in Figure 3.
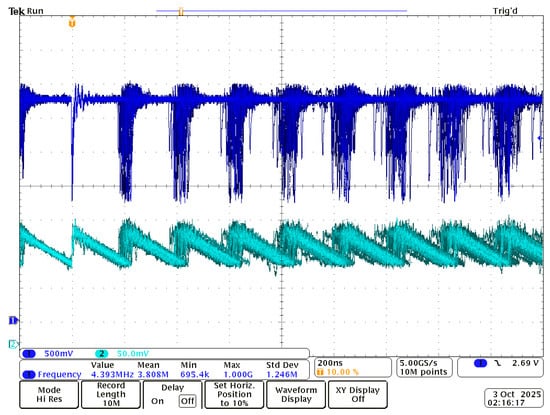
Figure 3.
Waveforms acquired with 6 s of persistence time for the capacitive oscillator with a PULLDOWN resistor (Figure 1b) and the input of the three-state buffer connected to a high-frequency ring oscillator instead of a constant high logic state.
The waveforms in Figure 3 confirm that the jitter level for the modified capacitive oscillator with a PULLDOWN resistor is significantly higher than for the basic oscillator architecture from Figure 1b. This is an important finding of this work. It is also worth noting that applying a high-frequency ring oscillator to the architecture of the capacitive oscillator with a PULLUP resistor (Figure 1b) does not seem to bring a positive effect. Despite several trials and experiments with different frequencies of the ring oscillator, the capacitive oscillator failed to generate oscillations. Thus, the modified architecture of the capacitive oscillator with a PULLDOWN resistor was applied as a pivotal component of the proposed TRNG.
3. Architecture of the Proposed True Random Number Generator
A complete schematic of the TRNG is presented in Figure 4. The schematic uses AMD/Xilinx Artix-7 standard library components [28]. Basic components, such as D-type flip-flops (FDCEs) and 5-input look-up tables (LUT5), are deployed within 5 slices of an FPGA, depicted in Figure 4 as regions with a non-continuous line. The relative location of these slices, given in the top right corner (e.g., SLICE X1Y3), was applied for experiments presented in Section 3 using the RLOC attribute in the Verilog HDL description.
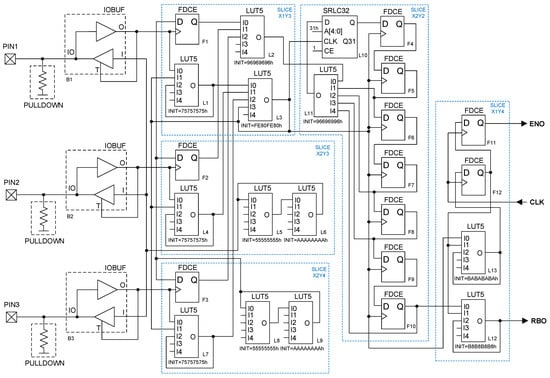
Figure 4.
Complete schematic of the TRNG.
The main source of entropy of the TRNG comes from the jitter of three capacitive oscillators with PULLDOWN resistors, as described in the previous section. These oscillators implement the modification of the basic architecture presented in Figure 1b, which causes the charging process of the parasitic capacitance to be modulated by a high-frequency signal of the ring oscillator involving L5 and L6 LUTs (SLICE X2Y3). The L5 LUT performs a negation operation, whereas the L6 acts as a simple buffer passing the signal without any changes. It is worth noting that capacitive oscillators, even for their basic structure without modification, seem to exhibit higher jitter than typically applied ring oscillators. Thus, a significantly lower number of this type of oscillators can be used to obtain a reliable source of entropy. It is also worth noting that in [27], only the basic architecture of the capacitive oscillator with a PULLUP resistor (Figure 1a) was applied.
The outputs of the three aforementioned capacitive oscillators are connected to the clock inputs of the corresponding D-type flip-flops F1–F3. The data inputs of these flip-flops are shorted and connected to the output of the second ring oscillator located in SLICE X2Y4 (LUTs L8 and L9). Thus, the basic idea behind random bit extraction is based on an already established technique of sampling a high-frequency signal (a ring oscillator, in this case) by a much lower-frequency signal (the capacitive oscillator output). The LUTs L1, L4, and L7 are configured to perform a set–reset function. The outputs of these LUTs go to a high logic state when a short pulse from the corresponding capacitive oscillator takes place and is maintained until the L3 LUT generates a positive pulse. This LUT performs a Müller C-element function. Thus, the output of L3 is set when the L1, L4, and L7 LUTs are in a high logic state, and then the output is reset when the outputs of all these LUTs return to a low logic state.
The Muller gate L3 serves as a local clock frequency source for the remaining part of the TRNG circuit, namely the shift register (the L10 LUT configured as a simple 32-bit shift register and the F4–F10 flip-flops) and the synchronization circuit (the F11, F12 flip-flops and L12, L13 LUTs). As the Xilinx Vivado implementation tool reports, such a connection of a local clock signal might lead to a large hold time violation for the involved flip-flops, including the SRLC32 shift register. A hold time violation causing metastability constitutes an auxiliary source of entropy for the TRNG. Additionally, the shift register has an architecture similar to that of the Fibonacci linear feedback shift register. The L11 LUT, performing a 5-input XOR function, takes signals from the F5, F7, F8, and F10 FFs, and the output of the L2 LUT and delivers it to the serial input of the shift register. This also improves the statistical features in cases where the hold time violation does not occur or does not have an essential impact on the state of the shift register. L2 in turn performs another 3-input XOR function for the signal originating from the outputs of F1–F3 FFs that capture signals from capacitive oscillators.
The last part of the TRNG is the synchronization circuit. The signal taken from the output of the last flip-flop (F10) of the shift register was passed to the L12 LUT, performing a D-latch function. The I0 input of the L12 LUT acts as the data input of the D-latch, whereas the I1 input performs the gate function of the D-latch. The output of the L12 LUT also constitutes the RBO output of the TRNG. This output can only be altered when the F12 FF is in a high logic state (the gate input of the D-latch is active). This, in turn, takes place only when the output of the L13 LUT is set and the rising edge of the external clock signal (CLK) occurs, causing activation of the F12 FF. The L13 LUT performs another set–reset function. The output is set when the local clock pulse is generated by the L3 Müller gate and is maintained until the F12 toggles to a high logic state. Since the L3 LUT generates a very short pulse determined by the time in which the outputs of all L1, L4, and L7 LUTs will go to a low logic state, and the moment of occurrence of this pulse is asynchronous to the external CLK clock signal, the L13 LUT stores the information, indicating that the local clock pulse was generated until a positive edge of the CLK signal takes place. The F11 FF filters out potential metastability from the F12 FF and provides a one clock period delay for the signal indicating that a new random bit has just been generated by the TRNG. This signal is available on the ENO output of the TRNG. The ENO is active for exactly one clock period of the CLK.
The TRNG from Figure 4 was specified using a structural description in Verilog HDL. The parameter values of the IOBUF cells, namely IBUF_LOW_PWR, SLEW, and DRIVE, were set to FALSE, FAST, and 4, respectively. The properties allowing combinatorial loops for nets involving outputs of LUTs with feedback paths were also specified as user constraints. Adding any timing constraints or changing the implementation parameters of the synthesis tool was not necessary.
4. Experimental Results
The TRNG was tested using the system presented in Figure 5 and implemented on the Digilent Nexys-Video board with an AMD/Xilinx Artix-7 FPGA chip. The test system employs a MicroBlaze microcontroller attached with peripherals (i.e., AXI bus controllers, DDR3 memory controller, etc.) and two custom IP blocks: the random number generator and the SPI slave module. The former block includes the TRNG (Figure 4) as well as the 32-bit shift register (SR) and a simple ring counter (RC). The SR block converts the serial bit stream into 32-bit words, while the 32-bit RC block indicates when a packet of 32 random bits is fully shifted into the SR register.
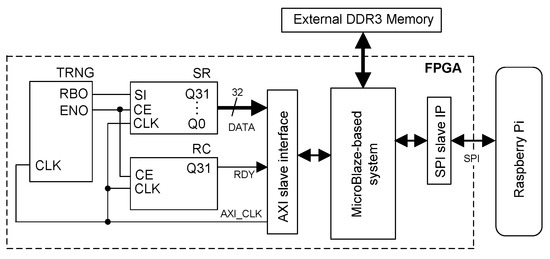
Figure 5.
Block diagram of the test system for the TRNG.
The capacitive oscillators of the TRNG exploit the unused package pins (connected nowhere) of the FPGA chip from the development board, namely E16, D16, and D20. The LVCMOS12 I/O standard was applied for these pins. Experiments show that, contrary to [27], this standard delivers the highest frequencies of capacitive oscillators with the architecture presented in Figure 1b. This enables the highest possible TRNG throughput to be achieved.
The basic task of the test system presented in Figure 5 is to harvest 1 G bits (1 × 109) of random data generated by the TRNG block and transfer them through the SPI slave block to the Raspberry Pi (Cambridge, UK) single-board computer. The data collected by the Microblaze microcontroller are temporarily stored in the external DDR3 memory, which is available on the evaluation board. The resource utilization of the entire system depicted in Figure 5 is as follows: 11,596 LUTs (8.6% of available LUTs on the FPGA chip), 11,717 FFs (4.4%), and 54 BlockRAM blocks (14.8%). The TRNG block, in turn, needs only 13 LUTs and 12 FFs.
Table 1 and Table 2 show the results of the NIST SP800-22 statistical test [29] and TRNG throughput (TP) for different temperatures of the FPGA die and for a few arbitrarily chosen voltage supply values of the FPGA I/O buffer (VCCO). The range of VCCO changes considered was within the widest interval recommended by the FPGA manufacturer. The internal temperature sensor of the Artix-7 chip was used for temperature measurement. This measurement is accomplished by the SPI slave IP block, and the results are transferred to the Raspberry Pi.

Table 1.
Results of the NIST SP800-22 tests and throughput (TP) for different die temperatures (VCCO = 1.227 V).

Table 2.
Results of the NIST SP800-22 tests and throughput (TP) for different supply voltages of I/O cells (T = 44 °C).
Medical hot/cold packs were applied to cool the chip below 45 °C, whereas a hot air soldering station was used to warm the chip above 50 °C. Two hot/cold packs, cooled to approximately −10 °C, were used to maintain a temperature of 15 °C for the FPGA die. One pack was placed at the bottom of the evaluation board, whereas the second was lightly pressed to the FPGA case. The temperature was maintained within the set value by manually controlling the pressing force (and position) of the second pack. Special care was taken to ensure that temperature fluctuations did not exceed +/−0.25 °C within the set value during the data collection process. For temperatures higher than 15 °C, only one cold pack (the second one) was used to maintain a particular value. In the case of heating the FPGA chip above 55 °C, the temperature of the hot air soldering station was properly adjusted (as well as the distance to the FPGA case) to obtain a stable temperature of the FPGA die.
The throughput values given in Table 1 and Table 2 are calculated by measuring the time period necessary to collect 1 × 106 random bits. To carry out tests that involve changes in the I/O voltage supply, a minor modification of the Nexys-Video evaluation board was made. That is, the VADJ voltage section, which delivers the voltage to the I/O bank in which the capacitive oscillators operate, was disconnected from the internal regulator and connected to the external laboratory power supply. For the results presented in Table 2, the temperature of the FPGA chip was naturally stable at approximately 44 °C.
As an option for the NIST SP800-22 tests, a thousand streams consisting of 1 × 106 bits were chosen. For particular tests that report more than one value (e.g., the results for the NonOverlappingTemplate and RandomExcursionsVariant tests appear 148 and 18 times, respectively), only the smallest p-value and lowest pass rate value are listed in the table. Therefore, the table includes the worst-case results. The default parameters for the NIST test were not altered. Thus, the pass threshold for the p-value for all tests and the pass rate value for the tests, excluding the RandomExcursions, amounted to 1 × 10−4 and 0.980, respectively. The minimum pass rate for the RandomExcursion and RandomExcursionVariant tests varied slightly depending on the sample size indicated in the final analysis report file generated by the test suite. For example, for the case where the die temperature was 75 °C, the pass rate amounted to 587 for a sample size of 601 binary sequences. This gives a 0.977 pass threshold value. In other cases, the pass rate value and the sample size value were slightly different. However, the resulting threshold still oscillated within a narrow range of 0.977–0.978. More details on the NIST test used can be found in [29].
As the data show, the TRNG passes all the NIST SP800-22 tests for the range of temperatures and I/O supply voltages considered. It is important to note that the die temperature noticeably affects the TRNG throughput. The colder the die, the higher the throughput. The VCCO changes also slightly affect the throughput. However, the highest throughput can be achieved within a relatively narrow interval close to the nominal value for the selected I/O standard (1.2 V in this case). Outside this interval, throughput deteriorates slightly.
Other statistical tests that were also conducted for all data collected include NIST SP800-90B [30]. The option involving the Independent and Identically Distributed (IID) track was applied for these tests. It is worth highlighting that the NIST SP800-90B tests were also passed by the presented TRNG. The minimum and maximum initial estimate of the entropy per sample (a byte entropy in this case), reported by the C++ test application of NIST SP800-90B, were 7.9637 (T = 35 °C, VCCO = 1.227 V) and 7.9726 (T = 44 °C, VCCO = 1.011 V), respectively.
The test system from Figure 5 was also implemented on another development board, namely the Digilent Gensys-2 with a Kintex-7 FPGA chip. In this case, no relative location (RLOC) attributes were applied to the structural Verilog description of the TRNG. All NIST SP800-22 tests were also passed by this implementation of the TRNG. Additionally, throughput was noticeably higher, reaching approximately 14 Mbit/s for the nominal I/O supply voltage (1.2 V).
5. Comparison with Other Solutions
Table 3 shows a comparison of the presented TRNG with similar works (other comparisons can be found, e.g., in [2,5,10]). Apart from the number of FPGA look-up tables (LUTs), flip-flops (FFs), and slices (for works reporting this parameter), the throughput (TP) is also listed in Table 3. Additional FPGA resources, such as digital clock managers for [26] or I/O buffers for this work, are in turn not included. The data for the previous work of the author [27] relate to the true random number generator, including the post-processing circuit, which was needed to pass all NIST tests.

Table 3.
Comparison table of the proposed TRGN with other similar solutions.
As the results indicate, the proposed TRNG requires a low number of LUTs compared to other solutions. It is also worth noting that the most LUT-saving solution listed in Table 3, namely [5], does not specify the resources required for a control circuit (a finite state machine), which is necessary for random bit generation. On the other hand, the proposed TRNG circuit also includes the synchronization block, which is not encountered in other solutions and additionally utilizes 2 LUTs and 2 FFs (1 slice). Since for contemporary AMD/Xilinx FPGAs, a single slice contains 2 times more FFs than LUTs (e.g., four 6-input LUTs and eight FFs for 7-series FPGAs), keeping the utilization of LUTs as low as possible is an important factor for resource-efficient implementations.
The other crucial issue is how many LUTs and FFs contained in a digital circuit specification can be deployed within a single slice, which has a direct impact on the overall slice utilization. For example, only flip-flops that share the same set of control signals, such as the clock or asynchronous reset, can be used inside a single slice. The proposed TRNG also seems to exhibit good efficiency in this regard. In particular, the number of slices required was significantly reduced (5 times) compared to the initial work [27].
Unfortunately, the obvious drawback of the proposed TRNG is its relatively low throughput, which is caused by the physical limitation of the maximum clock frequency generated by capacitive oscillators. This frequency is determined, in turn, by a relatively weak internal pulldown resistor.
6. Conclusions
The proposed TRNG leverages capacitive oscillators that exploit I/O buffers and unused package pins of FPGAs as essential components of the true random number generator. With the exception of the previous work of the author [27], similar solutions have not been reported in the literature to date.
The presented TRNG has a simple architecture, requires a low number of FPGA resources, and passes all NIST statistical tests for a wide range of operating conditions. Passing all statistical tests without a post-processing circuit, for different temperatures and supply voltages, is an essential difficulty for the implementation of true random number generators in FPGAs. The author did not achieve this result in the previous work.
The number of utilized resources was significantly reduced and the architecture was substantially simplified compared to the initial work [27]. Due to the internal synchronization circuit, the TRNG can be directly integrated with a digital system clocked at any frequency. Usually encountered solutions do not include such a feature, and they are validated only for passing statistical tests for a specific sampling frequency related to the reported throughput. Using a different sampling frequency should entail the need for revalidation of the statistical features of the TRNG involved. This need does not exist in the case of the presented TRNG.
Compared to other state-of-the-art solutions, the proposed TRNG is characterized by a relatively low throughput. However, the throughput slightly exceeding 10 Mbits/s might still be enough for many applications, including cryptographic and safety systems, machine learning systems, evolutionary algorithm implementations, and others.
It is also worth noting that since the proposed TRNG uses external FPGA pins, it may be susceptible to environmental factors, such as humidity and surface contaminants. However, using a BGA-type case for the FPGA chip to hide crucial pins inside the array, away from the edges, and ensuring that these pins are not connected anywhere can significantly mitigate the problem.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Serrano, R.; Duran, C.; Sarmiento, M.; Hoang, T.T.; Tsukamoto, A.; Suzaki, K. A robust and healthy against PVT variations TRNG based on frequency collapse. IEEE Access 2022, 10, 41852–41862. [Google Scholar] [CrossRef]
- Wang, J.; Huang, Z.; Chen, Y.; Liu, J.; Zhou, L.; Jiang, X.; Zhou, J.; Wang, Q. An Ultrahigh-Throughput and FPGA-Compatible TRNG Based on Dynamic Hybrid Metastability and Jitter Entropy Cells. IEEE Trans. Circuits Syst. I Regul. Pap. 2025, 72, 2202–2215. [Google Scholar] [CrossRef]
- Bucci, M.; Germani, L.; Luzzi, R.; Trifiletti, A.; Varanonuovo, M. A high-speed oscillator-based truly random number source for cryptographic applications on a smart card IC. IEEE Trans. Comput. 2003, 52, 403–409. [Google Scholar] [CrossRef]
- Cui, J.; Yi, M.; Cao, D.; Yao, L.; Wang, X.; Liang, H. Design of true random number generator based on multistage feedback ring oscillator. IEEE Trans. Circuits Syst. II Exp. Briefs 2022, 69, 1752–1756. [Google Scholar] [CrossRef]
- Della Sala, R.; Bellizia, D.; Scotti, G. A novel ultra-compact FPGA compatible TRNG architecture exploiting latched ring oscillators. IEEE Trans. Circuits Syst. II Exp. Briefs 2022, 69, 1672–1676. [Google Scholar] [CrossRef]
- Zanotti, T.; Ranjan, A.; O’Shea, S.J.; Raghavan, N.; Thamankar, R.; Pey, K.L.; Puglisi, F.M. Guidelines for the Design of Random Telegraph Noise-Based True Random Number Generators. IEEE Trans. Device Mater. Reliab. 2024, 24, 184–193. [Google Scholar] [CrossRef]
- McCabe, H.; Koziol, S.M.; Snider, G.L.; Blair, E.P. Tunable, Hardware-Based Quantum Random Number Generation Using Coupled Quantum Dots. IEEE Trans. Nanotechnol. 2020, 19, 292–296. [Google Scholar] [CrossRef]
- Sajal, M.S.; Dandin, M. True Random Number Generation Using Dark Noise Modulation of a Single-Photon Avalanche Diode. IEEE Trans. Circuits Syst. II Exp. Briefs 2024, 71, 1586–1591. [Google Scholar] [CrossRef]
- Dubovskiy, A.; Criss, T.; El Valli, A.S.; Rehm, L.; Kent, A.D.; Haas, A. One Trillion True Random Bits Generated with a Field-Programmable Gate Array Actuated Magnetic Tunnel Junction. IEEE Magn. Lett. 2024, 15, 4500304. [Google Scholar] [CrossRef]
- Anandakumar, N.N.; Sanadhya, S.K.; Hashmi, M.S. FPGA based true random number generation using programmable delays in oscillator-rings. IEEE Trans. Circuits Syst. II Exp. Briefs 2020, 67, 570–574. [Google Scholar] [CrossRef]
- Frustaci, F.; Spagnolo, F.; Perri, S.; Corsonello, P. A High-Speed FPGA-Based True Random Number Generator Using Metastability with Clock Managers. IEEE Trans. Circuits Syst. II Exp. Briefs 2023, 70, 756–760. [Google Scholar] [CrossRef]
- Wei, X.; Xiu, L.; Cai, Y. A Perspective of Using Frequency-Mixing as Entropy in Random Number Generation for Portable Hardware Cybersecurity IP. IEEE Trans. Inf. Forensics Secur. 2024, 19, 320–333. [Google Scholar] [CrossRef]
- Liao, T.L.; Wan, P.Y.; Yan, J.J. Design and Synchronization of Chaos-Based True Random Number Generators and Its FPGA implementation. IEEE Access 2021, 10, 8279–8286. [Google Scholar] [CrossRef]
- Rojas-Muñoz, L.F.; Sánchez-Solano, S.; Martínez-Rodríguez, M.C.; Brox, P. True Random Number Generation Capability of a Ring Oscillator PUF for Reconfigurable Devices. Electronics 2022, 11, 4028. [Google Scholar] [CrossRef]
- Delolme, E.; Fischer, V.; Bernard, F.; Bochard, N.; Pelcat, M. Beyond Total Locking: Demonstrating and Measuring Mutual Influence on a RO-Based True Random Number Generator on an FPGA. In Proceedings of the 2024 IEEE 37th International System-on-Chip Conference (SOCC), Dresden, Germany, 16–19 September 2024. [Google Scholar] [CrossRef]
- Tao, S.; Yu, Y.; Dubrova, E. FPGA Based True Random Number Generators Using Non-Linear Feedback Ring Oscillators. In Proceedings of the 2018 16th IEEE International New Circuits and Systems Conference (NEWCAS), Montreal, QC, Canada, 24–27 June 2018. [Google Scholar] [CrossRef]
- Magyari, A.; Chen, Y. Integrating Lorenz Hyperchaotic Encryption with Ring Oscillator Physically Unclonable Functions (RO-PUFs) for High-Throughput Internet of Things (IoT) Applications. Electronics 2023, 12, 4929. [Google Scholar] [CrossRef]
- Chen, Y.; Liang, H.; Zhang, L.; Yao, L.; Lu, Y. High throughput dynamic dual entropy source true random number generator based on FPGA. Microelectron. J. 2024, 145, 106113. [Google Scholar] [CrossRef]
- Ahmed, H.O.; Kim, D.; Buchanan, W.J. A True Random Number Generator Based on Race Hazard and Jitter of Braided and Cross-Coupled Logic Gates Using FPGA. IEEE Access 2024, 12, 182943–182955. [Google Scholar] [CrossRef]
- El-Hadedy, M.; Abelian, A.; Lee, K.; Cheng, B.N.; Hwu, W.M. ANUBIS: Hybrid FPAA–FPGA Architecture for Entropy-Based True Random Number Generation in Secure UAV Communication. IEEE Embed. Syst. Lett. 2025, 17, 164–167. [Google Scholar] [CrossRef]
- Liu, Y.; Wu, Y.; Chen, B.; Sang, P.; Wu, J.; Wei, X.; Zhan, X.; Chen, J. High-Speed True Random Number Generator with Multiple Entropy Sources: Ring Oscillator Jitter and Random Telegraph Noise. IEEE Embed. Syst. Lett. 2025. Early Access. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhong, K.; Zhang, J. High Throughput and Compact FPGA TRNGs Based on Hybrid Entropy, Reinforcement Strategies, and Automated Exploration. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2025. Early Access. [Google Scholar] [CrossRef]
- Yang, S.; Liang, H.; Hu, R.; Yao, L.; Huang, Z.; Yi, M.; Lu, Y. Lightweight Hybrid Entropy Source True Random Number Generator Based on Jitter and Metastability. IEEE Trans. Circuits Syst. II Exp. Briefs 2024, 71, 3513–3518. [Google Scholar] [CrossRef]
- Yi, M.; Liu, Z.; Miao, Z.; Lu, Y.; Liang, H.; Ma, L. A true random number generator based on autonomous Boolean network with imbalanced node oscillation rings. Microelectron. J. 2025, 160, 106694. [Google Scholar] [CrossRef]
- Wang, X.; Liang, H.; Wang, Y.; Yao, L.; Guo, Y.; Yi, M. High-throughput portable true random number generator based on jitter-latch structure. IEEE Trans. Circuits Syst. I Reg. Pap. 2021, 68, 741–750. [Google Scholar] [CrossRef]
- Johnson, A.P.; Chakraborty, R.S.; Mukhopadyay, D. An improved DCM-based tunable true random number generator for xilinx FPGA. IEEE Trans. Circuits Syst. II Exp. Briefs 2017, 64, 452–456. [Google Scholar] [CrossRef]
- Hajduk, Z. Field programmable gate arrays-based true random number generator using capacitive oscillators. Electronics 2024, 13, 4819. [Google Scholar] [CrossRef]
- AMD Technical Information Portal. Vivado Design Suite 7 Series FPGA and Zynq 7000 SoC Libraries Guide (UG953); AMD: Santa Clara, CA, USA, 2025. [Google Scholar]
- Bassham, L.E.; Rukhin, A.L.; Soto, J.; Nechvatal, J.R.; Smid, M.E.; Leigh, S.D.; Levenson, M.; Vangel, M.; Heckert, N.A.; Banks, D.L. A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2010. [Google Scholar]
- Turan, M.S.; Barker, E.; Kelsey, J.; McKay, K.A.; Baish, M.L.; Boyle, M. Recommendation for the Entropy Sources Used for Random Bit Generation; NIST Special Publication 800-90B; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2018. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).