Dynamic Resource Allocation in Full-Duplex Integrated Sensing and Communication: A Multi-Objective Memetic Grey Wolf Optimizer Approach
Abstract
1. Introduction
- The proposed AM-MOGWO utilizes a problem-driven fusion of diverse strategies—including Lévy Flight, an adaptive hybrid search, and Memetic Computing—enabling it to exhibit superior global exploration capabilities and efficient convergence performance when solving complex NP-hard problems such as ISAC resource allocation. To ensure a rigorous and effective evaluation of the proposed optimization algorithms, this paper first establishes a high-fidelity system model for an ISAC network.
- This paper constructs a comprehensive ISAC system model that simulates a realistic operational environment by incorporating key physical factors—including 3GPP-standardized channels, the Doppler effect, environmental clutter, and bidirectional self-interference—thereby situating the resource allocation problem within a challenging and practical scenario for validation.
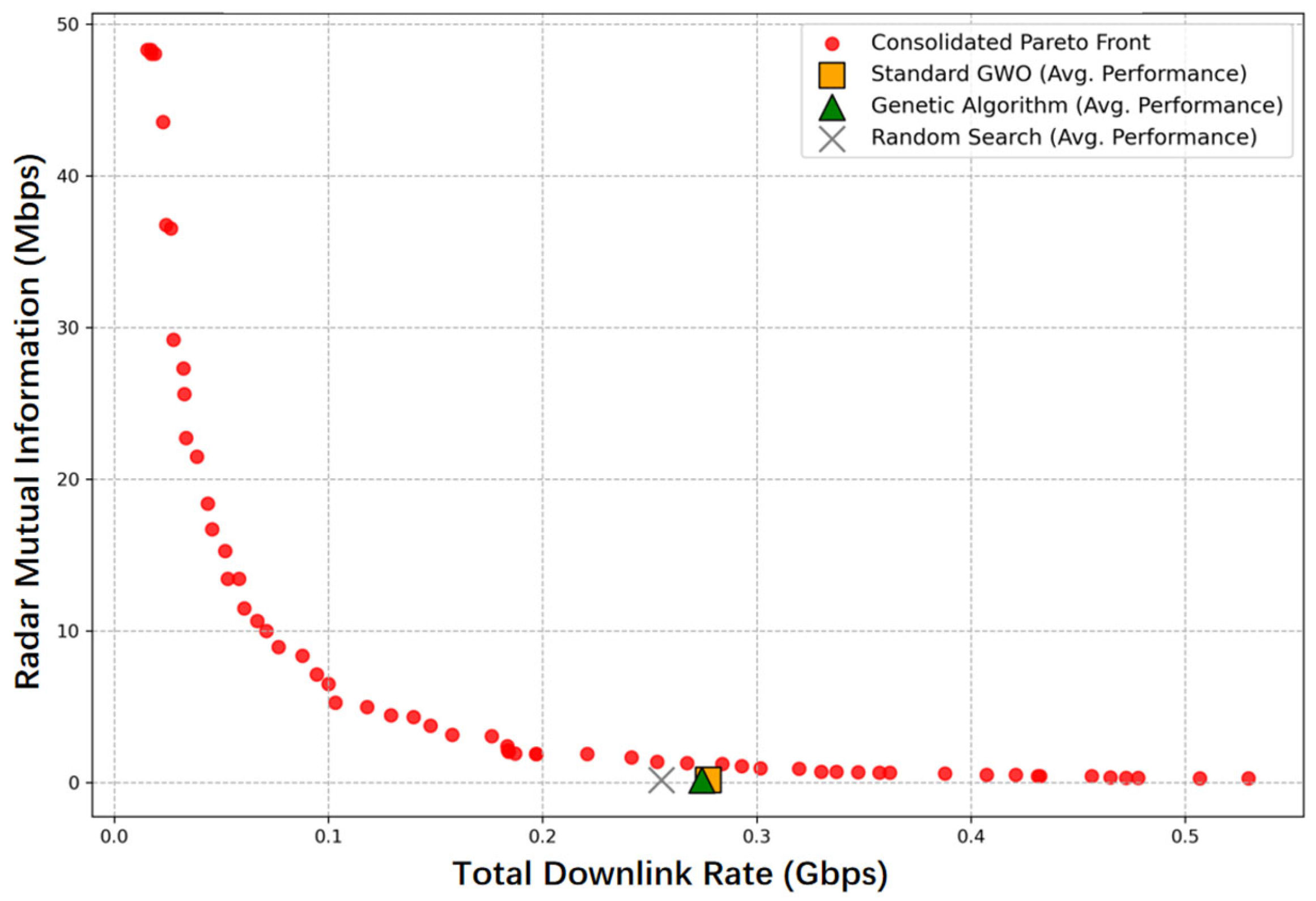
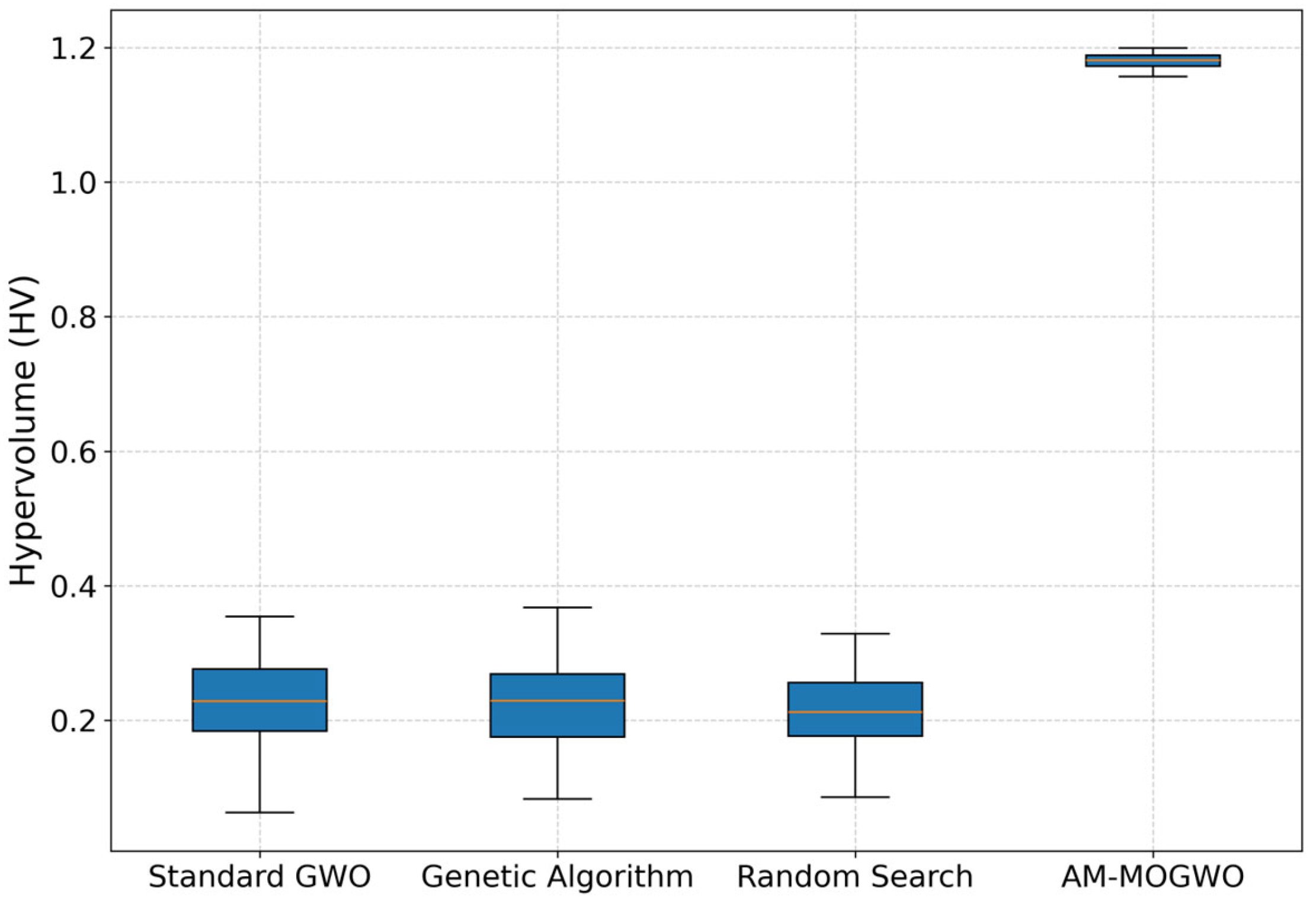
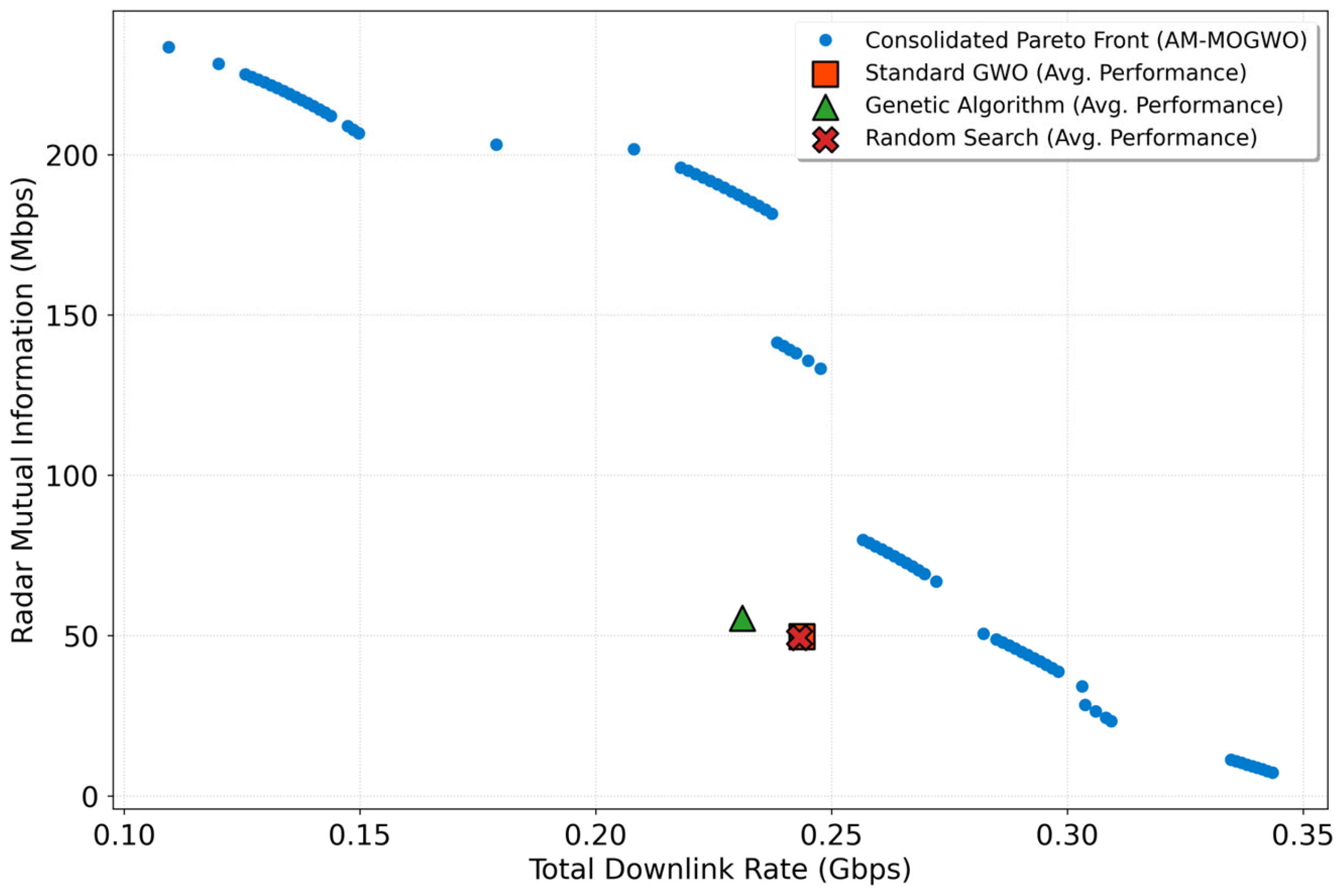
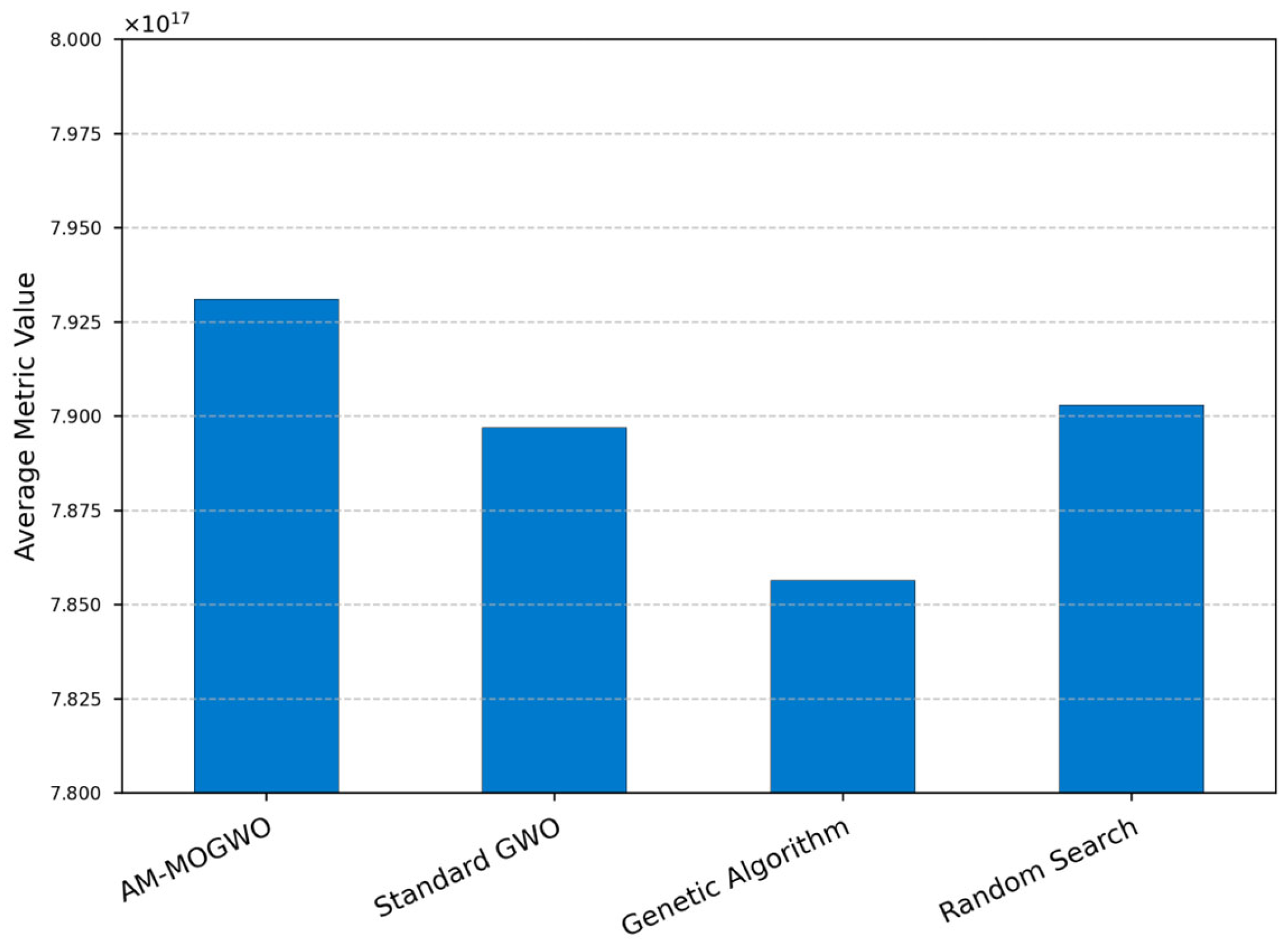
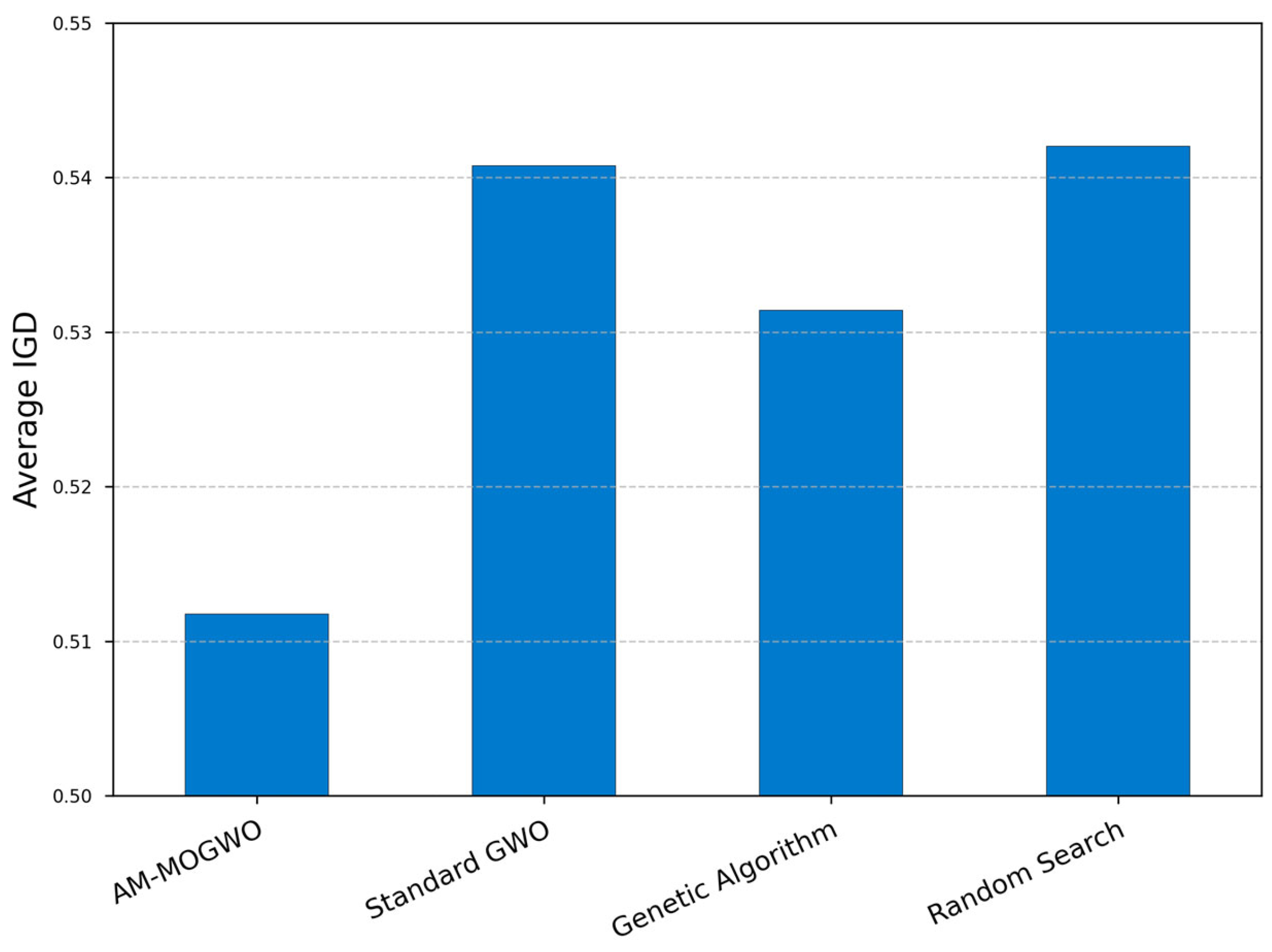
- The proposed algorithm’s performance is comprehensively evaluated in both a foundational single-cell environment and a more challenging, realistic multi-cell interference scenario. In both settings, the superiority of AM-MOGWO over baseline methods is systematically demonstrated through visual Pareto front dominance and quantitative metrics, yielding critical insights for the practical design and deployment of ISAC systems.
2. Materials and Methods
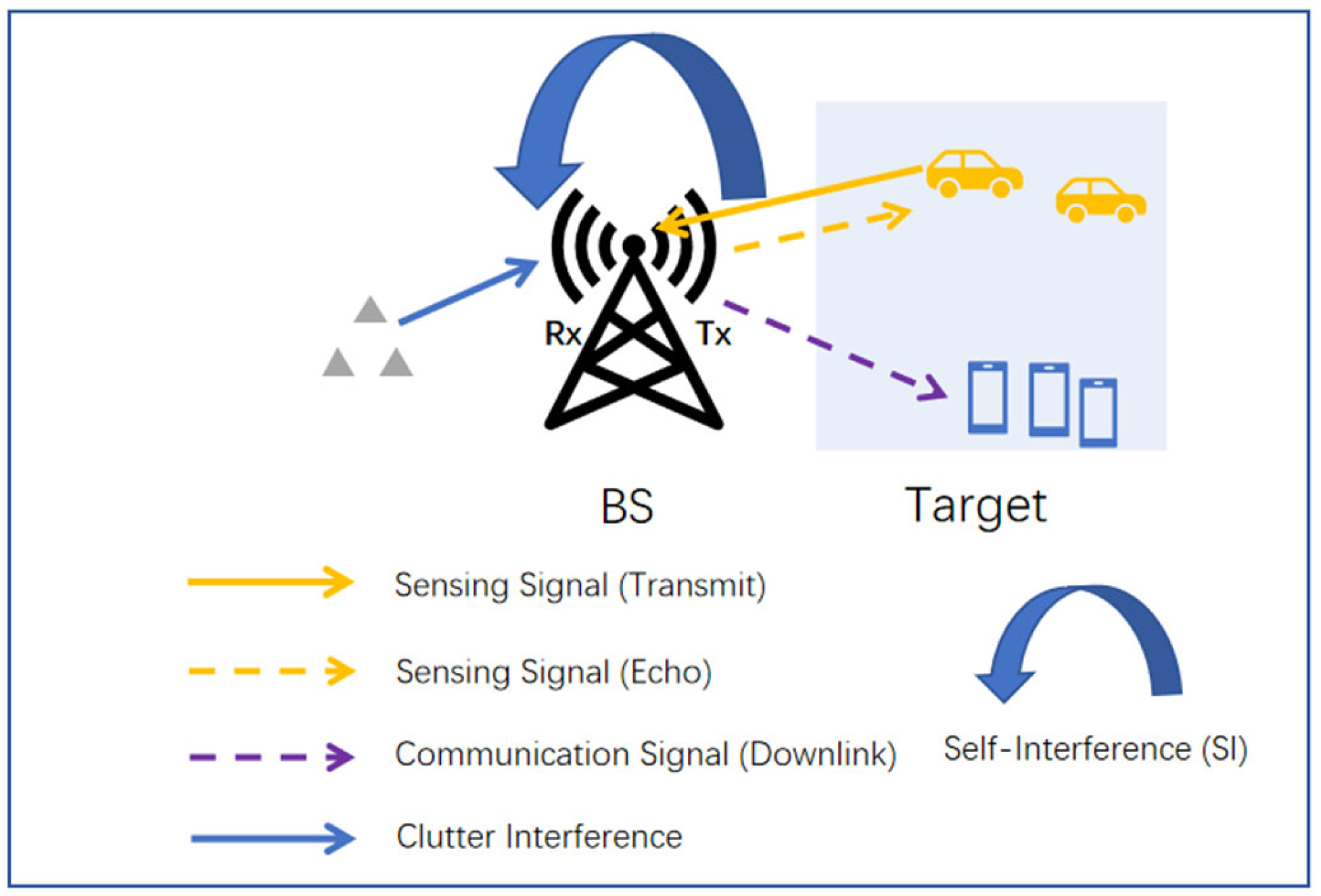
2.1. Scenario Description
2.1.1. A Foundational Single-Cell Scenario
2.1.2. A More Challenging Multi-Cell Interference Scenario
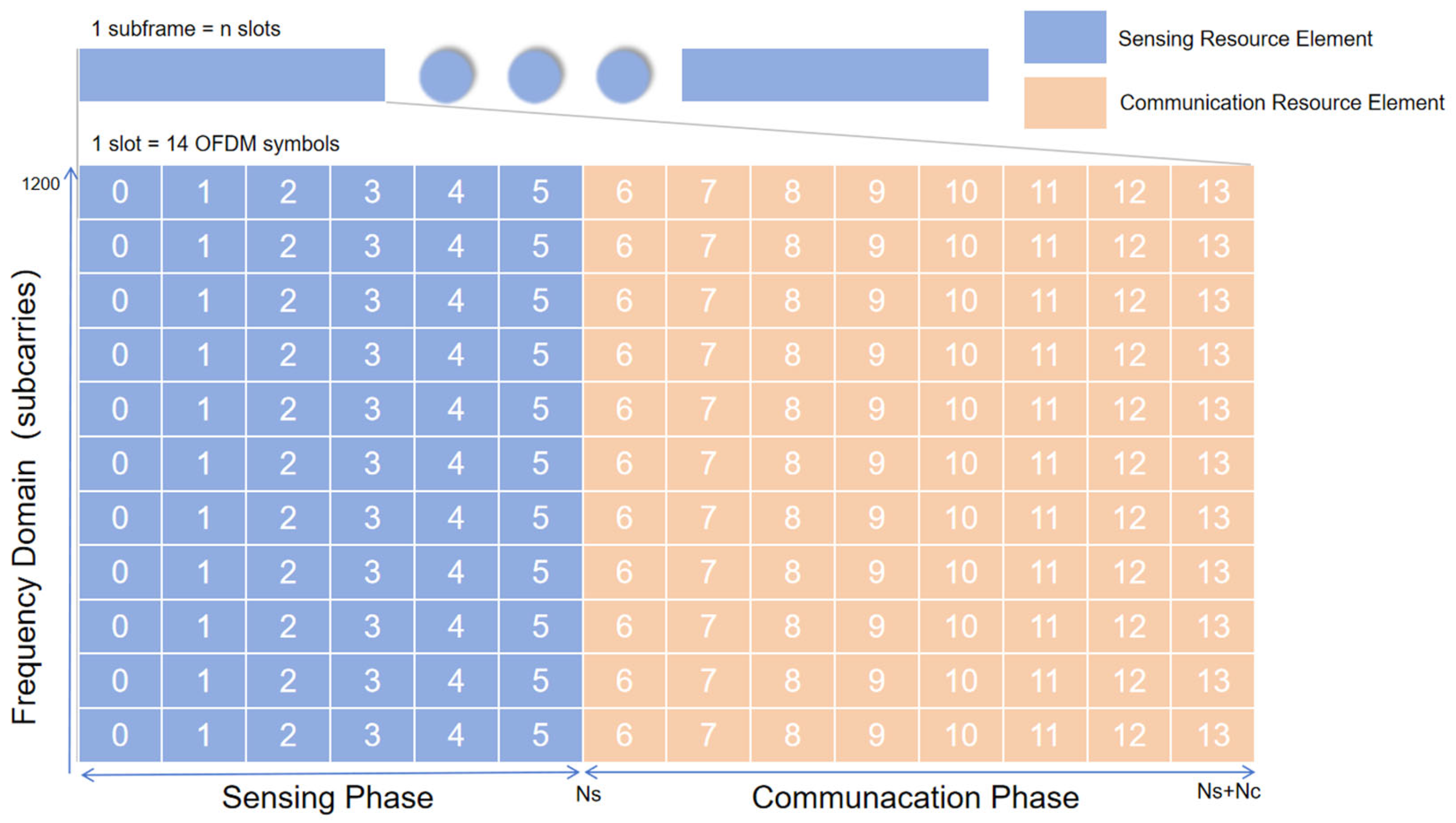
2.2. Dynamic TDM Frame
2.3. Channel Model
2.3.1. Large-Scale Fading
2.3.2. Small-Scale Fading
2.4. System Performance Evaluation Indicators
2.4.1. Radar Metric
2.4.2. Communication Metric
2.5. System Modeling
2.5.1. Modeling in the Single-Cell Scenario
2.5.2. Modeling Extension for the Multi-Cell Scenario
2.6. Multi-Objective Problem Formulation
3. A Grey Wolf Optimizer for Dynamic Resource Allocation
3.1. Standard GWO
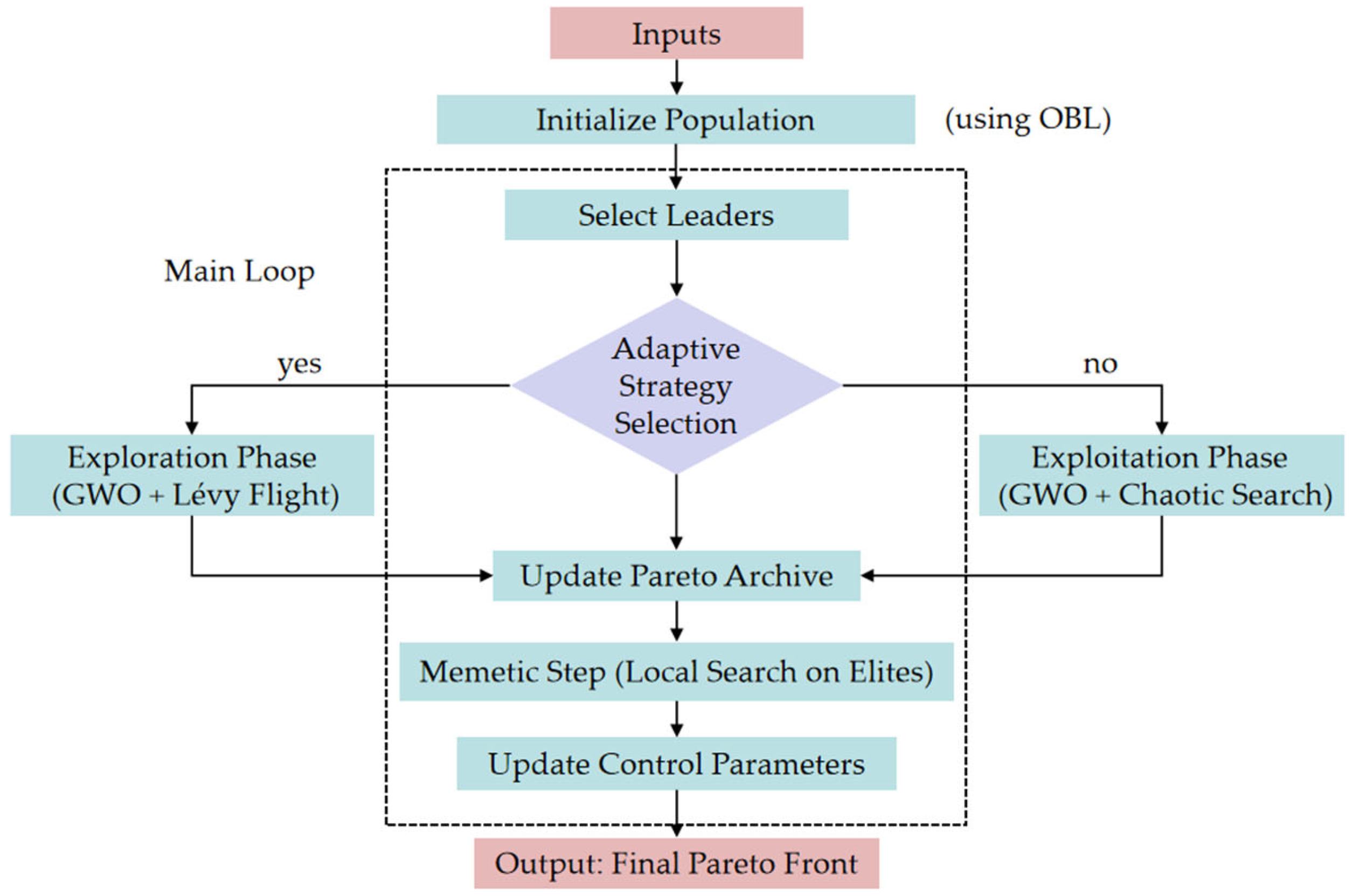
3.2. AM-MOGWO
| Algorithm 1 The Proposed AM-MOGWO Framework |
| (Search bounds) |
| (The Pareto front) |
| ) |
| 4: Repeat |
| ) |
| 7: // Adaptive Hybrid Position Update Rule |
| 9: end for |
| . |
| ) |
| 13: // Memetic Step |
| )). |
| ) |
| . |
4. Results
4.1. Performance Analysis in the Single-Cell Scenario
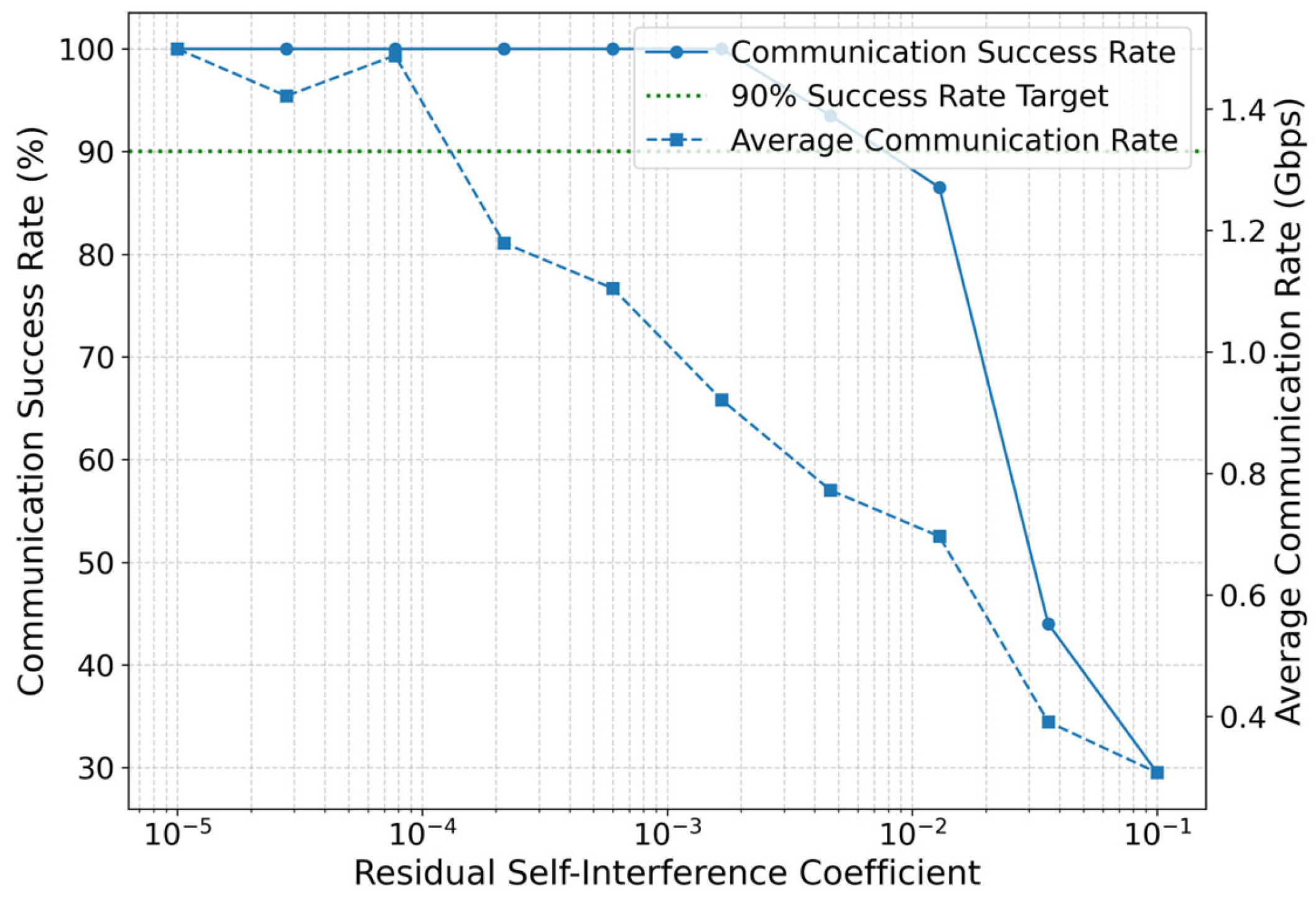
4.2. Robustness Validation in the Multi-Cell Interference Scenario
5. Conclusions
6. Future Works and Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FD | Full-duplex |
| ISAC | Integrated sensing and communication |
| SI | Self-interference |
| MOP | Multi-objective optimization problem |
| AM-MOGWO | Adaptive Hybrid Memetic Multi-Objective Grey Wolf Optimizer |
| GWO | Grey wolf optimizer |
| RS | Random search |
| GA | Genetic algorithm |
| HV | Hyper volume |
| TDD | Time division duplexing |
| SDR | Semidefinite relaxation |
| NOMA | Non-orthogonal multiple access |
| MOEAs | Multi-objective evolutionary algorithms |
| DRL | Deep reinforcement learning |
| SIC | Self-interference cancelation |
| QoS | Quality-of-service |
| BS | Base station |
| UEs | User equipments |
| RCS | Radar cross-section |
| NR | 5G new radio |
| SCS | Sub-carrier spacing |
| TDM | Time-division multiplexing |
| DoF | Degree of freedom |
| UMa | Urban macro |
| LOS | Line-of-sight |
| NLOS | Non-line-of-sight |
| 2D | Two-dimensional |
| PL | Path loss |
| 3D | Three-dimensional |
| mmWave | Millimeter-wave |
| CSCG | Circularly symmetric complex Gaussian |
| SCNR | Signal-to-clutter-plus-Interference-plus-noise ratio |
| ICI | Inter-Carrier Interference |
| MI | Mutual information |
| MINLP | Mixed-integer non-linear programming |
| OBL | Opposition-based learning |
| IGD | Inverted generational distance |
| CDF | Cumulative distribution function |
| CoMP | Coordinated multi-point |
| ICIC | Inter-cell interference coordination |
References
- Liu, F.; Cui, Y.; Masouros, C.; Xu, J.; Han, T.X.; Eldar, Y.C. Integrated Sensing and Communications: Toward Dual-Functional Wireless Networks for 6G and Beyond. IEEE J. Sel. Areas Commun. 2022, 40, 1728–1767. [Google Scholar] [CrossRef]
- Chiriyath, A.R.; Paul, B.; Bliss, D.W.; Rock, S.M. Radar-Communications Convergence: Coexistence, Cooperation, and Co-Design. IEEE Trans. Cogn. Commun. Netw. 2017, 3, 1–12. [Google Scholar] [CrossRef]
- Zhang, J.A.; Liu, F.; Eldar, Y.C.; Li, G.Y.; Guo, Y.J.; Hanzo, L. Enabling Joint Communication and Radar Sensing in Mobile Networks—A Survey. IEEE Commun. Surv. Tutor. 2022, 24, 306–345. [Google Scholar] [CrossRef]
- Roh, W.; Seol, J.-Y.; Park, J.; Lee, B.; Lee, J.; Kim, Y.; Cho, J.; Cheun, K.; Aryanfar, F. Millimeter-Wave Beamforming as an Enabling Technology for 5G Cellular Communications: Theoretical Feasibility and Prototype Results. IEEE Commun. Mag. 2014, 52, 106–113. [Google Scholar] [CrossRef]
- Xiao, Z.; Liu, R.; He, Z.-Q.; Zhu, Y.; Schober, R.; Kumar, P.V. On the Performance-Cost Tradeoff in Integrated Sensing and Communication Systems. IEEE Trans. Wirel. Commun. 2023, 22, 9170–9184. [Google Scholar]
- Liu, F.; Masouros, C.; Petropulu, A.P.; Griffiths, H.; Hanzo, L. Joint Radar and Communication Design: Applications, State-of-the-Art, and the Road Ahead. IEEE Trans. Commun. 2020, 68, 3834–3862. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, X.; Li, Z.; Wei, Z. Design and Performance Evaluation of Joint Sensing and Communication Integrated System for 5G mmWave Enabled CAVs. IEEE J. Sel. Top. Signal Process. 2021, 15, 1500–1514. [Google Scholar] [CrossRef]
- Zhang, Q.; Sun, H.; Gao, X.; Wang, X.; Feng, Z. Time-Division ISAC Enabled Connected Automated Vehicles Cooperation Algorithm Design and Performance Evaluation. IEEE J. Sel. Areas Commun. 2022, 40, 2206–2218. [Google Scholar] [CrossRef]
- Zhang, J.A.; Cantoni, A.; Huang, X.; Guo, Y.J.; Heath, R.W. Framework for an Innovative Perceptive Mobile Network Using Joint Communication and Sensing. In Proceedings of the IEEE 85th Vehicular Technology Conference (VTC2017-Spring), Sydney, Australia, 4–7 June 2017; pp. 1–5. [Google Scholar]
- Han, L.; Wu, K. Joint Wireless Communication and Radar Sensing Systems—State of the Art and Future Prospects. IET Microw. Antennas Propag. 2013, 11, 876–885. [Google Scholar] [CrossRef]
- Sabharwal, A.; Schniter, P.; Guo, D.; Bliss, D.W.; Rangarajan, S.; Wichman, R. In-Band Full-Duplex Wireless: Challenges and Opportunities. IEEE J. Sel. Areas Commun. 2014, 32, 1637–1652. [Google Scholar] [CrossRef]
- Kolodziej, K.E.; Perry, B.T.; Herd, J.S. In-Band Full-Duplex Technology: Techniques and Systems Survey. IEEE Trans. Microw. Theory Techn. 2019, 67, 3025–3041. [Google Scholar] [CrossRef]
- Liu, F.; Liu, Y.-F.; Li, A.; Masouros, C.; Eldar, Y.C. Cramér–Rao Bound Optimization for Joint Radar-Communication Beamforming. IEEE Trans. Signal Process. 2022, 70, 240–253. [Google Scholar] [CrossRef]
- Wang, X.; Fei, Z.; Zhang, J.A.; Huang, J. Sensing-Assisted Secure Uplink Communications with Full-Duplex Base Station. IEEE Commun. Lett. 2022, 26, 249–253. [Google Scholar] [CrossRef]
- Babu, N.; Masouros, C.; Papadias, C.B.; Eldar, Y.C. Precoding for Multi-Cell ISAC: From Coordinated Beamforming to Coordinated Multipoint and Bi-Static Sensing. IEEE Trans. Wirel. Commun. 2024, 23, 14637–14651. [Google Scholar] [CrossRef]
- Rahman, M.L.; Zhang, J.-A.; Chen, X.; Saaifan, K.K.; Kouzayha, N.; Alkhateeb, A. Integrated Sensing and Communication: A Review. IEEE Open J. Commun. Soc. 2023, 4, 2381–2443. [Google Scholar]
- Hua, H.; Xu, J.; Han, T.X. Rate-Splitting Multiple Access for ISAC: A Novel Framework for Transmit Beamforming and Subcarrier Allocation. IEEE Trans. Veh. Technol. 2023, 72, 10588–10603. [Google Scholar] [CrossRef]
- Chen, J.; Wu, K.; Niu, J.; Li, Y.; Xu, P.; Zhang, J.A. Spectral and Energy Efficient Waveform Design for RIS-Assisted ISAC. IEEE Trans. Commun. 2025, 73, 158–172. [Google Scholar] [CrossRef]
- Dou, C.; Huang, N.; Wu, Y.; Qian, L.; Quek, T.Q.S. Sensing-Efficient NOMA-Aided Integrated Sensing and Communication: A Joint Sensing Scheduling and Beamforming Optimization. IEEE Trans. Veh. Technol. 2023, 72, 13591–13603. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, Y.; Mu, X.; Ding, Z.; Dobre, O.A. NOMA Empowered Integrated Sensing and Communication. IEEE Commun. Lett. 2022, 26, 677–681. [Google Scholar] [CrossRef]
- Liu, S.; Hu, J.; Tie, Z.; Shi, J. Joint Subcarrier and Power Allocation for OTFS Based Integrated Sensing and Communication System. In Proceedings of the 2023 International Conference on Ubiquitous Communication (Ucom), Xi’an, China, 15–17 December 2023; pp. 350–355. [Google Scholar]
- Gong, J.; Gao, D.; Tian, R.; Liu, X.; Peng, M. Frame Structure Design and Task Scheduling in 5G NR for ISAC Systems: A Deep Reinforcement Learning Approach. IEEE Trans. Veh. Technol. 2025. Early Access. [Google Scholar] [CrossRef]
- Deb, K. Multi-Objective Optimization Using Evolutionary Algorithms; John Wiley & Sons: Chichester, UK, 2001. [Google Scholar]
- 3GPP. Study on Channel Model for Frequencies from 0.5 to 100 GHz; Technical Report TR 38.901, V16.1.0; 3rd Generation Partnership Project (3GPP): Valbonne, France, 2020. [Google Scholar]
- Vassaki, S.; Poulakis, M.I.; Panagopoulos, A.D.; Constantinou, P. Power Allocation in Cognitive Satellite Terrestrial Networks with QoS Constraints. IEEE Commun. Lett. 2013, 17, 1344–1347. [Google Scholar] [CrossRef]
- Huang, E.; DeLude, C.; Romberg, J.; Mukhopadhyay, S.; Swaminathan, M. Anisotropic Scatterer Models for Representing RCS of Complex Objects. In Proceedings of the 2021 IEEE Radar Conference (RadarConf21), Atlanta, GA, USA, 7–21 May 2021; pp. 1–6. [Google Scholar]
- Technical Specification TS 38.211; NR; Physical Channels and Modulation; V16.7.0; 3rd Generation Partnership Project (3GPP): Valbonne, France, 2021.
- Rappaport, T.S. Wireless Communications: Principles and Practice, 2nd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2002; pp. 175–190. [Google Scholar]
- Proakis, J.G.; Salehi, M. Digital Communications, 5th ed.; McGraw-Hill: New York, NY, USA, 2008. [Google Scholar]
- Bell, M.R. Information Theory and Radar: Mutual Information and the Design and Analysis of Radar Waveforms and Systems. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 1988. [Google Scholar]
- Tang, B.; Li, J. Spectrally Constrained MIMO Radar Waveform Design Based on Mutual Information. IEEE Trans. Signal Process. 2019, 67, 821–834. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Yang, X.-S. Nature-Inspired Metaheuristic Algorithms, 2nd ed.; Luniver Press: Frome, UK, 2010. [Google Scholar]
- Tizhoosh, H.R. Opposition-Based Learning: A New Scheme for Machine Intelligence. In Proceedings of the International Conference on Computational Intelligence for Modelling, Control and Automation and International Conference on Intelligent Agents, Web Technologies and Internet Commerce (CIMCA-IAWTIC’05), Vienna, Austria, 28–30 November 2005; pp. 695–701. [Google Scholar]
- Li, B.; Jiang, W.S. A new class of chaotic optimization algorithms. Control Decis. 1997, 12, 537–541. [Google Scholar]
- Moscato, P. On Evolution, Search, Optimization, Genetic Algorithms and Martial Arts: Towards Memetic Algorithms; Technical Report C3P Report 826; California Institute of Technology: Pasadena, CA, USA, 1989. [Google Scholar]
- May, R.M. Simple mathematical models with very complicated dynamics. Nature 1976, 261, 459–467. [Google Scholar] [CrossRef] [PubMed]


| Parameter | Value |
|---|---|
| Network Layout | Hexagonal Grid |
| Number of Cells | 7 |
| Inter-Site Distance | 100 m |
| 28 GHz [4] | |
| 144 MHz [27] | |
| 10 [19] | |
| Channel Model | 3GPP UMa and Rician [24] |
| Rician K-factor K | 0.1 |
| 40 W (46 dBm) [24] | |
| ) | 25 dBi/5 dBi [24] |
| −174 dBm/Hz [28] | |
| 0.5 m2 [26] | |
| Residual Self-Interference Coeff. | 0.01 [11] |
| 140 [27] | |
| 0.4 Gbps | |
| 80 | |
| 200 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, X.; Wang, J.; Sun, L.; Zhang, C.; Wang, T. Dynamic Resource Allocation in Full-Duplex Integrated Sensing and Communication: A Multi-Objective Memetic Grey Wolf Optimizer Approach. Electronics 2025, 14, 3763. https://doi.org/10.3390/electronics14193763
Feng X, Wang J, Sun L, Zhang C, Wang T. Dynamic Resource Allocation in Full-Duplex Integrated Sensing and Communication: A Multi-Objective Memetic Grey Wolf Optimizer Approach. Electronics. 2025; 14(19):3763. https://doi.org/10.3390/electronics14193763
Chicago/Turabian StyleFeng, Xu, Jianquan Wang, Lei Sun, Chaoyi Zhang, and Teng Wang. 2025. "Dynamic Resource Allocation in Full-Duplex Integrated Sensing and Communication: A Multi-Objective Memetic Grey Wolf Optimizer Approach" Electronics 14, no. 19: 3763. https://doi.org/10.3390/electronics14193763
APA StyleFeng, X., Wang, J., Sun, L., Zhang, C., & Wang, T. (2025). Dynamic Resource Allocation in Full-Duplex Integrated Sensing and Communication: A Multi-Objective Memetic Grey Wolf Optimizer Approach. Electronics, 14(19), 3763. https://doi.org/10.3390/electronics14193763






