An Exhaustive Method of TOA-Based Positioning in Mixed LOS/NLOS Environments

Abstract

This paper studies the problem of locating wireless sensor networks (WSNs) based on time-of-arrival (TOA) measurements in mixed line of sight/non-line-of-sight (LOS/NLOS) environments. To mitigate the impacts of NLOS and improve performance both in positioning accuracy and computation time, we hereby propose an exhaustive method (i.e., EM). The EM method mainly consists of two processes. In the first process, all BSs are arranged into various combinations. For each combination, a solution and its corresponding residual vector can be obtained. For each combination, all BSs can be divided into two categories: BSs that participate in positioning and BSs that do not. Therefore, the above residual vector can also be divided into two categories in each group. In the second process, combining the comparison results of two residual vectors and the characteristics of NLOS errors, we propose a new criterion to find out solutions with only LOS-BSs. Then the final solution can be obtained by further processing these solutions. This method does not require any prior information regarding NLOS status, NLOS amplitude, or noise variance, and only needs three LOS-BSs. Numerical simulation results shows that our method greatly improves the accuracy and reduces the computation time compared to state-of-art methods.

1. Introduction

Recently, WSN positioning systems based on TOA have attracted a lot of attention from the academic and industrial fields [1,2,3,4,5,6]. They have been applied in many fields, such as monitoring workers in high-voltage power plants with irregularities and locating workers’ positions in mines for rescue operations [7,8,9,10]. However, in complicated industrial environments, the receiver cannot directly receive the signals due to various obstructions. Therefore, the NLOS error is introduced and inaccurate observation values are obtained, which degrades the positioning performance and can cause a positioning failure [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29]. Therefore, it is crucial to mitigate the effects of NLOS errors.

To improve the localization performance by mitigating the impacts of NLOS errors, a conventional method is to firstly identify the NLOS paths then subsequently use all the LOS BSs for positioning [11]. However, it is unscientific to determine the NLOS status from only the residual size. The residual is defined as the difference between the estimated distance and the observed distance, where the estimated distance refers to the euclidean distance between the positioning coordinates and the base station. This method has a high probability of misidentification, which limits its application.

Another conventional method to deal with the problem of NLOS errors is to arrange all the BSs in various combinations to obtain multiple solutions: in [12], the final positioning solution is obtained by weighting and summing all the solutions. It gives a high positioning accuracy under the environment with few NLOS-BSs. However, the positioning performance degrades significantly with many NLOS-BSs; In [13], a residual test (RT) based on the central Chi-Square distribution is proposed. It can calculate the number of LOS-BSs and identify the LOS-BSs. But this method needs to estimate the threshold value in advance and has a certain probability of incorrect LOS BSs identification.

Currently, a class of convex optimization techniques can obtain accurate positioning results with prior information on NLOS status, NLOS amplitudes, and noise variances [3,14]. Unfortunately, in practice it is very hard to effectively identify the NLOS status and estimate the NLOS bias. Thus, it is of great value to develop a new method to improve the positioning accuracy without any prior information on NLOS status. Moreover, with the advancement of artificial intelligence technologies, deep learning has been increasingly leveraged in research domains encompassing NLOS path detection and high-precision positioning [24,25,29].

Thus, we propose an exhaustive method to systematically solve this problem with a minimum of three LOS-BSs. In step 1, a residual weighting algorithm (RWGH) [12] or residual test method (RT) [13] is utilized to arrange all the BSs in various combinations to obtain the solution for each combination. In step 2, the solution of each combination is substituted into the basic positioning equation to obtain the vector, which consists of distance estimates. And then the difference between the distance vector and the original observations is calculated to acquire the residual vector of each combination. Finally, in step 3, a new criterion and a refinement procedure are applied to select the final positioning solution with only the LOS-BSs from all solutions. The simulation results verify the effectiveness of our algorithm both in accuracy improvement and computation time reduction.

2. Problem Statement and Algorithm Development

We assume that the total number of BSs with known coordinates is N, and there is only one moving station (MS) to be located. Under the two-dimensional (2-D) positioning scenario, $(x_i,y_i)$ and $(x,y)$ represent the coordinates of the ith BS and MS, respectively. The TOA positioning system transforms the time signal into observed distance by multiplying the collected time signal with the signal transmission speed. The signal propagation paths are split into LOS and NLOS according to the presence of obstacles blocking signal transmission. Therefore, the distance observation between the ith BS and MS can be expressed as [12,19]

$$d_i=\sqrt{{\left(x_i-x\right)}^2+{\left(y_i-y\right)}^2}+{\eta }_i+\left\{\begin{array}{c}0,i\in {\mathsf{\Psi }}_{LOS}\hfill \\ {\epsilon }_i,i\in {\mathsf{\Psi }}_{NLOS}\hfill \end{array},\right.$$

(1)

where $d_i$ denotes the observation value of the distance between the ith BS and MS, ${\eta }_i$ and ${\epsilon }_i$, respectively, denote the white Gaussian noise with the mean zero and NLOS error, and ${\mathsf{\Psi }}_{LOS}$ and ${\mathsf{\Psi }}_{NLOS}$, respectively, represent the LOS sets and NLOS sets. Generally speaking, ${\epsilon }_i$ is a positive number and has the following relationship with ${\eta }_i$ [2]:

$${\displaystyle \frac{{\epsilon }_i}{\left|{\eta }_i\right|}}\gg 1.$$

(2)

We firstly square both sides of (1), then move the unknown variables to the left side of the equation to obtain

$$\begin{array}{c}2x_{i}x+2y_{i}y-x^2-y^2=x_i^2+y_i^2-d_i^2\hfill \\ +{\eta }_i^2+2{\eta }_i{R}_i+\left\{\begin{array}{c}0,i\in {\mathsf{\Psi }}_{LOS}\hfill \\ {\epsilon }_i^2+2{\epsilon }_i\left(R_i+{\eta }_i\right),i\in {\mathsf{\Psi }}_{NLOS}\hfill \end{array}\right.\hfill \end{array},$$

(3)

where $R_i=\sqrt{{\left(x_i-x\right)}^2+{\left(y_i-y\right)}^2}$ represents the true distance from MS to the ith BS.

To briefly illustrate our algorithm, we use the least squares (LS) algorithm to solve the equation. Thus, (3) can be equivalently expressed as a standard linear mode

$$\mathbf{A}\mathbf{x}=\mathbf{b}+\mathbf{e},$$

(4)

where

$$\mathbf{A}=\left[\begin{array}{ccc}2x_1& 2y_1& 1\\ ⋮& ⋮& ⋮\\ 2x_N& 2y_N& 1\end{array}\right],\mathbf{x}=\left[\begin{array}{c}x\\ y\\ x^2+y^2\end{array}\right],$$

(5)

$$\mathbf{b}=\left[\begin{array}{c}{x}_1^2+y_1^2-d_1^2\\ ⋮\\ x_N^2+y_N^2-d_N^2\end{array}\right],\mathbf{e}=\left[\begin{array}{c}{e}_1\\ ⋮\\ e_N\end{array}\right],$$

(6)

$$e_i={\eta }_i^2+2{\eta }_i{R}_i+\left\{\begin{array}{c}0,i\in {\mathsf{\Psi }}_{LOS}\hfill \\ {\epsilon }_i^2+2{\epsilon }_i\left(R_i+{\eta }_i\right),i\in {\mathsf{\Psi }}_{NLOS}\hfill \end{array}.\right.$$

(7)

The core principle of the algorithm in this study is to firstly arrange all the BSs to obtain various combinations and their corresponding solutions. Then, we select some localization solutions as the new set according to our criterion. Finally, the X and Y coordinates of all solutions in this new set are sorted in order separately, and the intermediate value of each coordinate vector is selected to compose the final positioning solution.

Then, we arrange all the BSs in various combinations to form a new set $\mathbf{\Phi }$. The jth subset ${\mathbf{\Phi }}_j$ is composed of different BSs, and the total number of subsets is

$$\mathsf{\Gamma }=\sum _{K=3}^{N-1}{C}_N^K,$$

(8)

where

$$C_N^K={\displaystyle \frac{N\left(N-1\right)\dots (N-K+1)}{K\left(K-1\right)\dots 1}},$$

(9)

where K represents the number of BSs involved in positioning. Under a 2-D positioning environment, we need at least three LOS paths. Hence, the minimum value of K is 3. In addition, under mixed LOS/NLOS conditions, the maximum of K is $N-1$. $C_N^K$ is the number of combinations of K BSs randomly selected from N BSs. Now, we define the subset of BSs that are not selected as ${\mathbf{\Omega }}_{\mathbf{j}}$, where the relationship between ${\mathbf{\Phi }}_{\mathbf{j}}$ and ${\mathbf{\Omega }}_{\mathbf{j}}$ is

$${\mathbf{\Phi }}_{\mathbf{j}}\cup {\mathbf{\Omega }}_{\mathbf{j}}=\left\{1,2,\dots ,N\right\},$$

(10)

$${\mathbf{\Phi }}_{\mathbf{j}}\cap {\mathbf{\Omega }}_{\mathbf{j}}=\varphi ,$$

(11)

where ∪ means union, ∩ means intersect, and $\varphi$ means empty set. Formula (10) means that ${\mathbf{\Phi }}_{\mathbf{j}}$ and ${\mathbf{\Omega }}_{\mathbf{j}}$ constitute all the BSs, and formula (11) means that there is no same BS between them. Note that ${\mathbf{\Phi }}_{\mathbf{j}}$ is assumed to be a subset composed of LOS-BSs, and ${\mathbf{\Omega }}_{\mathbf{j}}$ is assumed to be a subset composed of NLOS-BSs.

Considering the case that N is equal to 5, K can be 3 or 4. Therefore, the total number of subsets of $\mathbf{\Phi }$ is equal to $\mathsf{\Gamma }={\displaystyle \sum _{K=3}^4}{C}_5^K=15$, and $\mathbf{\Phi }$ can be represented as

$$\begin{array}{cc}\hfill \mathbf{\Phi }& =\left\{{\mathbf{\Phi }}_{\mathbf{1}},{\mathbf{\Phi }}_{\mathbf{2}},\dots ,{\mathbf{\Phi }}_j,\dots ,{\mathbf{\Phi }}_{\mathbf{15}}\right\}\hfill \\ \hfill & =\left\{\right\{1,2,3\},\{1,2,4\},\{1,2,5\},\{1,3,4\},\{1,3,5\},\hfill \\ \hfill & =\{1,4,5\},\{2,3,4\},\{2,3,5\},\{2,4,5\},\{3,4,5\},\hfill \\ \hfill & =\{1,2,3,4\},\{1,2,3,5\},\{1,2,4,5\},\{1,3,4,5\},\hfill \\ \hfill & =\{2,3,4,5\}\}\hfill \end{array}$$

(12)

Based on Formulas (10) and (11), the $\mathbf{\Omega }$ that corresponds to $\mathbf{\Phi }$ can be denoted as

$$\begin{array}{cc}\hfill \mathbf{\Omega }& =\left\{{\mathbf{\Omega }}_1,{\mathbf{\Omega }}_2,\dots ,{\mathbf{\Omega }}_j,\dots ,{\mathbf{\Omega }}_{15}\right\}\hfill \\ \hfill & =\left\{\right\{4,5\},\{3,5\},\{3,4\},\{2,5\},\{2,4\},\{2,3\},\hfill \\ \hfill & =\{1,5\},\{1,4\},\{1,3\},\{1,2\},\left\{5\right\},\left\{4\right\},\left\{3\right\},\hfill \\ \hfill & =\left\{2\right\},\left\{1\right\}\}\hfill \end{array}$$

(13)

Then, combining (4), (8), and (10), we get

$${\mathbf{A}}_{{\mathbf{\Phi }}_{\mathbf{j}}}{\mathbf{x}}_{{\mathbf{\Phi }}_{\mathbf{j}}}={\mathbf{b}}_{{\mathbf{\Phi }}_{\mathbf{j}}}+{\mathbf{e}}_{{\mathbf{\Phi }}_{\mathbf{j}}},\left(j=1,2,\dots ,\mathsf{\Gamma })\right.$$

(14)

where ${\mathbf{A}}_{{\mathbf{\Phi }}_{\mathbf{j}}}$ is obtained by taking K rows from the matrix $\mathbf{A}$, K denotes the total number of elements in ${\mathbf{\Phi }}_{\mathbf{j}}$, and each element of ${\mathbf{\Phi }}_{\mathbf{j}}$ represents the row number of matrix $\mathbf{A}$, ${\mathbf{b}}_{{\mathbf{\Phi }}_{\mathbf{j}}}$, is made in the same manner from matrix $\mathbf{b}$ using ${\mathbf{\Phi }}_{\mathbf{j}}$ as the row number vector, and ${\mathbf{x}}_{{\mathbf{\Phi }}_{\mathbf{j}}}$ and ${\mathbf{e}}_{{\mathbf{\Phi }}_{\mathbf{j}}}$, respectively, denote the solution and residual vector corresponding to ${\mathbf{\Phi }}_{\mathbf{j}}$.

Applying the LS method, we obtain

$${\mathbf{x}}_{{\mathbf{\Phi }}_{\mathbf{j}}}={\left({\mathbf{A}}_{{\mathbf{\Phi }}_{\mathbf{j}}}^T{\mathbf{A}}_{{\mathbf{\Phi }}_{\mathbf{j}}}\right)}^{-1}{\mathbf{A}}_{{\mathbf{\Phi }}_{\mathbf{j}}}^T{\mathbf{b}}_{{\mathbf{\Phi }}_{\mathbf{j}}}.$$

(15)

By substituting solution (15) into (1), the distance estimates can be obtained:

$$\widetilde{d_{j,i}}=\sqrt{{\left(x_i-{\mathbf{x}}_{{\mathbf{\Phi }}_{\mathbf{j}}}\left(1\right)\right)}^2+{\left(y_i-{\mathbf{x}}_{{\mathbf{\Phi }}_{\mathbf{j}}}\left(2\right)\right)}^2}.$$

(16)

Then, we calculate the difference between (16) and the original observation:

$$\widetilde{e_{j,i}}=\widetilde{d_{j,i}}-d_i,(i=1,\dots ,N).$$

(17)

If BSs corresponding to ${\mathbf{\Phi }}_{\mathbf{j}}$ are all LOS-BSs, (17) can be further written as

$$\widetilde{e_{j,i}}=\left\{\begin{array}{c}-{\eta }_i,i\in {\mathbf{\Phi }}_{\mathbf{j}}\hfill \\ -{\eta }_i-{\epsilon }_i,i\in {\mathbf{\Omega }}_{\mathbf{j}}\hfill \end{array}.\right.$$

(18)

We express $\widetilde{e_{j,i}},(i=1,\dots ,N)$ as $\widetilde{{\mathbf{e}}_j}$, the residuals corresponding to ${\mathbf{\Phi }}_{\mathbf{j}}$ as $\tilde{{\mathbf{e}}_{{\mathbf{\Phi }}_{\mathbf{j}}}}$, and the residuals corresponding to ${\mathbf{\Omega }}_{\mathbf{j}}$ as $\tilde{{\mathbf{e}}_{{\mathbf{\Omega }}_{\mathbf{j}}}}$; then, $\tilde{{\mathbf{e}}_{{\mathbf{\Phi }}_{\mathbf{j}}}}\cup \tilde{{\mathbf{e}}_{{\mathbf{\Omega }}_{\mathbf{j}}}}=\widetilde{{\mathbf{e}}_j}$.

Combining (4), (14) and (18), the criterion we use to select the solutions of LOS-BSs can be described as

$$\left\{\begin{array}{c}\tilde{e_{{\mathsf{\Omega }}_{j,k}}}<0\hfill \\ \left|\tilde{e_{{\mathsf{\Omega }}_{j,k}}}\right|>max\left(\left|\tilde{{\mathbf{e}}_{{\mathbf{\Phi }}_{\mathbf{j}}}}\right|\right)\hfill \end{array},\right.$$

(19)

where $\tilde{e_{{\mathsf{\Omega }}_{j,k}}}$ denotes the kth element in vector $\tilde{{\mathbf{e}}_{{\mathbf{\Omega }}_{\mathbf{j}}}}$, $max\left(\left|\tilde{{\mathbf{e}}_{{\mathbf{\Phi }}_{\mathbf{j}}}}\right|\right)$, and denotes the maximum absolute value of the vector $\tilde{{\mathbf{e}}_{{\mathbf{\Phi }}_{\mathbf{j}}}}$. Therefore, (19) means that the residuals corresponding to BSs that do not participate in positioning are all less than 0, and their magnitudes are all greater than the maximum absolute values of $\tilde{{\mathbf{e}}_{{\mathbf{\Phi }}_{\mathbf{j}}}}$ corresponding to BSs that participate in positioning.

When (19) is satisfied, ${\mathbf{\Phi }}_{\mathbf{j}}$ can be regarded as a combination which is composed of only LOS-BSs, and ${\mathbf{x}}_{{\mathsf{\Phi }}_j}$ can be considered as the solution obtained from only these LOS-BSs. Otherwise, the vector ${\mathbf{\Phi }}_{\mathbf{j}}$ contains NLOS-BS, and ${\mathbf{x}}_{{\mathsf{\Phi }}_j}$ is not the solution we need.

We substitute all the subsets of $\mathbf{\Phi }$ into Formula (14) to obtain the corresponding solutions. Then, for each solution, the corresponding residual vector is obtained through Formula (16) and Formula (17). Then, Formula (19) is applied to select te solutions we need. Finally, all solutions that satisfy condition (19) will form a new set $\mathbf{\Theta }$, and we assume that there are M solutions in $\mathbf{\Theta }$.

If M is equal to 1, the final positioning solution ${\mathbf{x}}^{*}$ is

$${\mathbf{x}}^{*}={\mathbf{x}}_{{\mathbf{\Theta }}_{\mathbf{1}}}$$

(20)

If M is not equal to 1, we assume that ${\mathbf{x}}_{{\mathbf{\Theta }}_{\mathbf{c}}}$ represents the cth solution in set $\mathbf{\Theta }$. And let $x_{{\mathbf{\Theta }}_{\mathbf{c}}}$ and $y_{{\mathbf{\Theta }}_{\mathbf{c}}}$ denote the X coordinate and Y coordinate in the solution ${\mathbf{x}}_{{\mathbf{\Theta }}_{\mathbf{c}}}$, respectively. Now sort $x_{{\mathbf{\Theta }}_{\mathbf{c}}},(c=1,\dots ,M)$ and $y_{{\mathbf{\Theta }}_{\mathbf{c}}},(c=1,\dots ,M)$ in order, so that the solution composed of two intermediate values can be used as the final positioning solution, i.e.,

$${\mathbf{x}}^{*}={\left[x_{{\mathbf{\Theta }}_{in}},y_{{\mathbf{\Theta }}_{in}}\right]}^T,$$

(21)

where $x_{{\mathbf{\Theta }}_{in}}$ and $y_{{\mathbf{\Theta }}_{in}}$ denote the intermediate value of vector $x_{{\mathbf{\Theta }}_{\mathbf{c}}},(c=1,\dots ,M)$ and vector $y_{{\mathbf{\Theta }}_{\mathbf{c}}},(c=1,\dots ,M)$, respectively.

In this paper, we use the LS algorithm in order to introduce the principle and calculation process of our method in detail. Indeed, our method can be applied to other positioning algorithms as well.

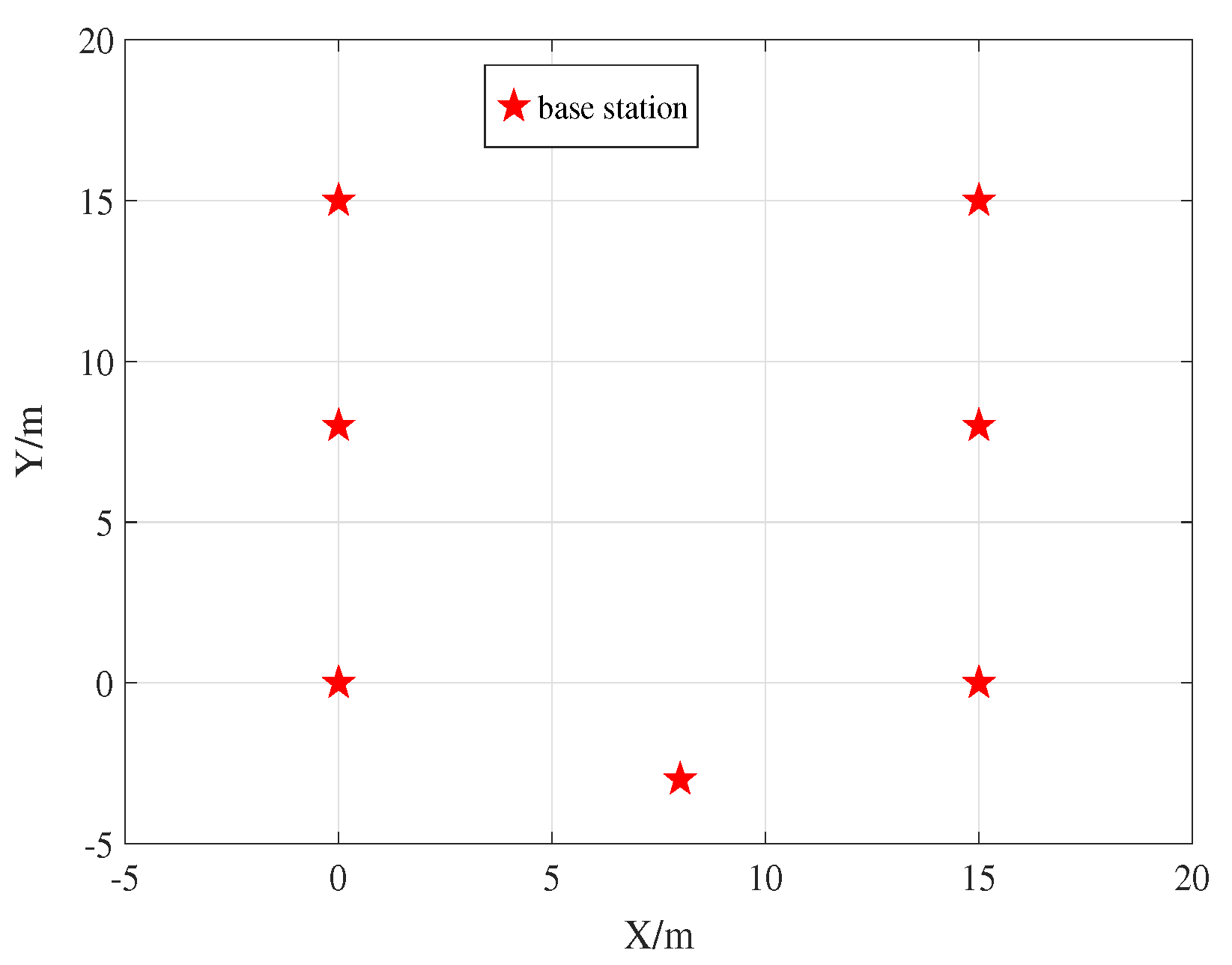
3. Numerical Results

In this section, we use four simulation examples to test the positioning performance of various methods. In each case, the variance of white Gaussian noise ${\eta }_i$ can be expressed as ${\sigma }_i^2$ and the number of Monte Carlo (MC) simulations is set at $M=300$. To ensure that the NLOS error is included in each MC simulation, we set the range of the NLOS error from $6\ast max\left(\left|{\eta }_i\right|\right)$ to $15\ast max\left(\left|{\eta }_i\right|\right)$. Therefore, to demonstrate the advantages of our EM method, we compare it with the SDR [3], SOCR [3], CWLS [30], and RSDP-New [14] algorithms. Note that the RSDP-New algorithm assumes that the NLOS status, NLOS amplitudes, and corresponding noise variances are all known in advance. In both the methods, the RMSE is used as an index to evaluate the positioning performance, using $\mathrm{RMSE}=\sqrt{{\displaystyle \frac{1}{\mathrm{M}}}{\displaystyle \sum _{i=1}^M}{\left({\mathbf{x}}_i-{\mathbf{x}}_i^{*}\right)}^2}$, where ${\mathbf{x}}_i$ and ${\mathbf{x}}_i^{*}$ denote the estimated position and true coordinates of MS in the ith simulation, respectively.

Example 1. 

We use seven BSs with coordinates (0, 0), (15, 0), (15, 15), (0, 15), (15, 8), (8, −3), and (0, 8), respectively. And their layout is shown in Figure 1. The true positions of MS are randomly generated in the areas surrounded by these seven BSs. Furthermore, the proposed algorithm can be applied to any mixed LOS/NLOS environment, with a minimum of three LOS BSs. As the total number of BSs is seven in our simulations, the maximum number of NLOS paths is four. Therefore, we, respectively, set the number of NLOS paths from 1 to 4, and corresponding results are shown, respectively, in Figure 2, Figure 3, Figure 4 and Figure 5. Each figure is the comparison of the RMSE among our method and the other 4 methods mentioned above. Then, we can draw the following conclusions:

(1)

From Figure 2, Figure 3 and Figure 4, we can conclude that our algorithm is significantly better than the SDR, SOCR, RSDP-New, and CWLS methods, indicating that the criterion proposed in this study can select the LOS BSs and obtain good positioning solutions.

(2)

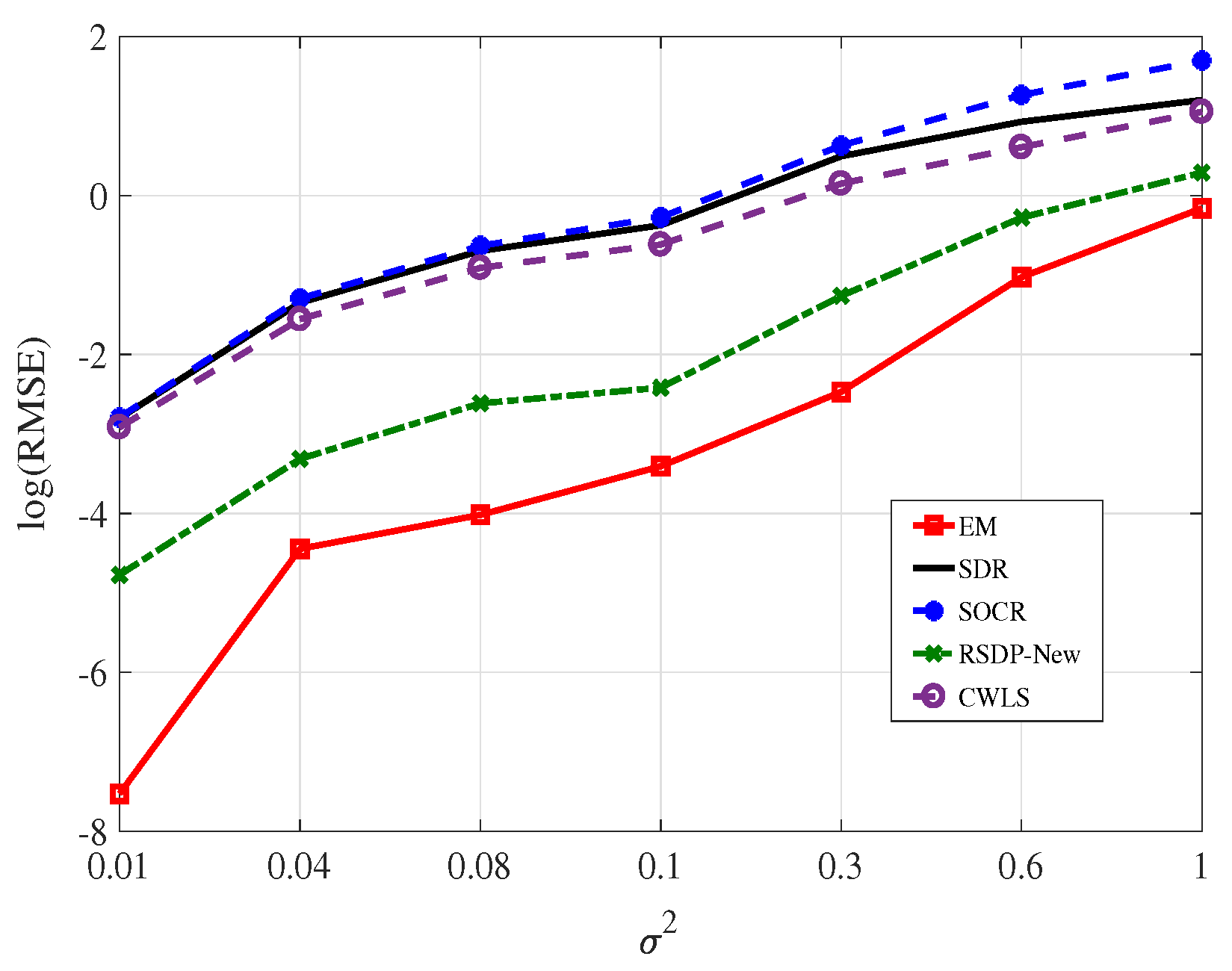
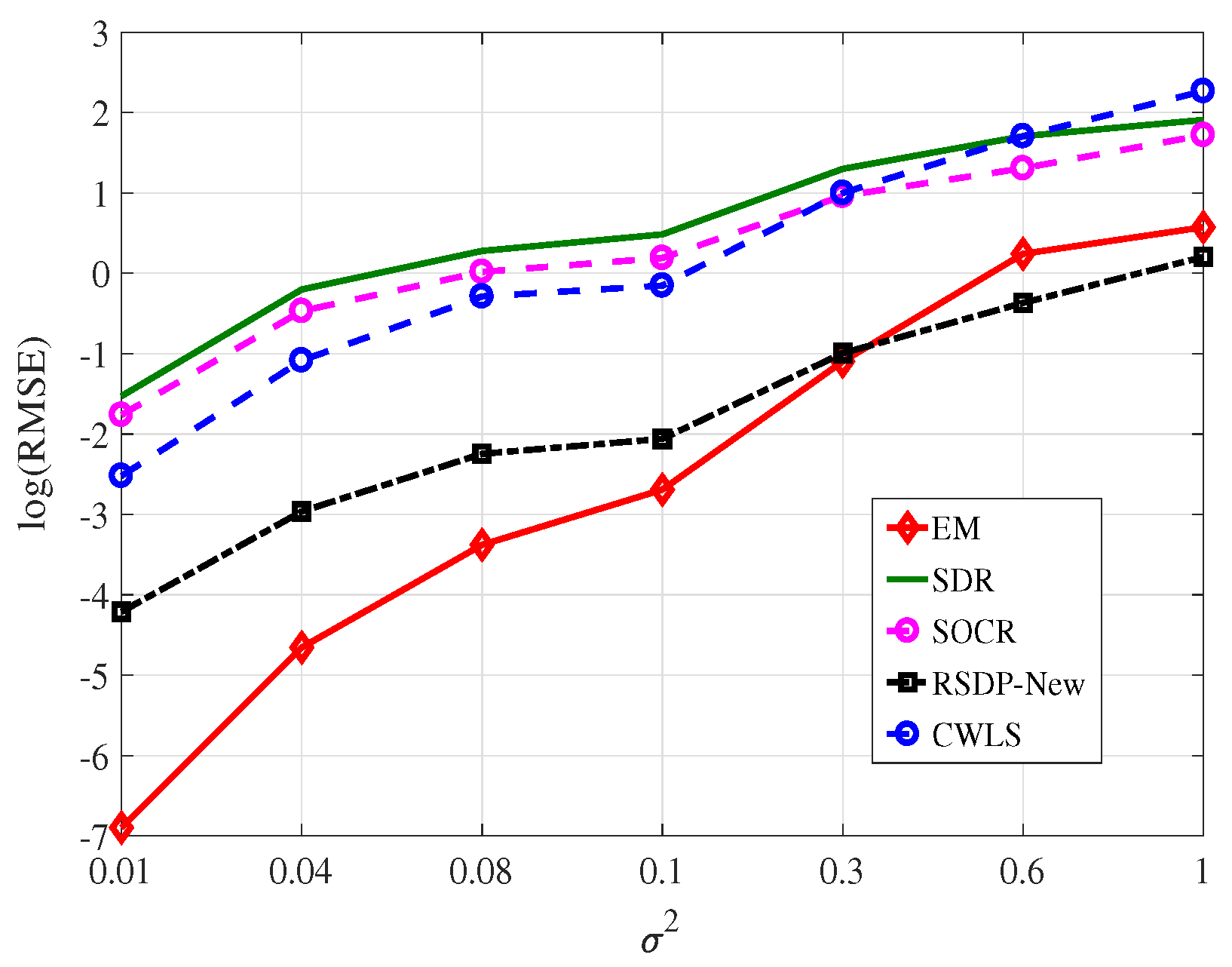
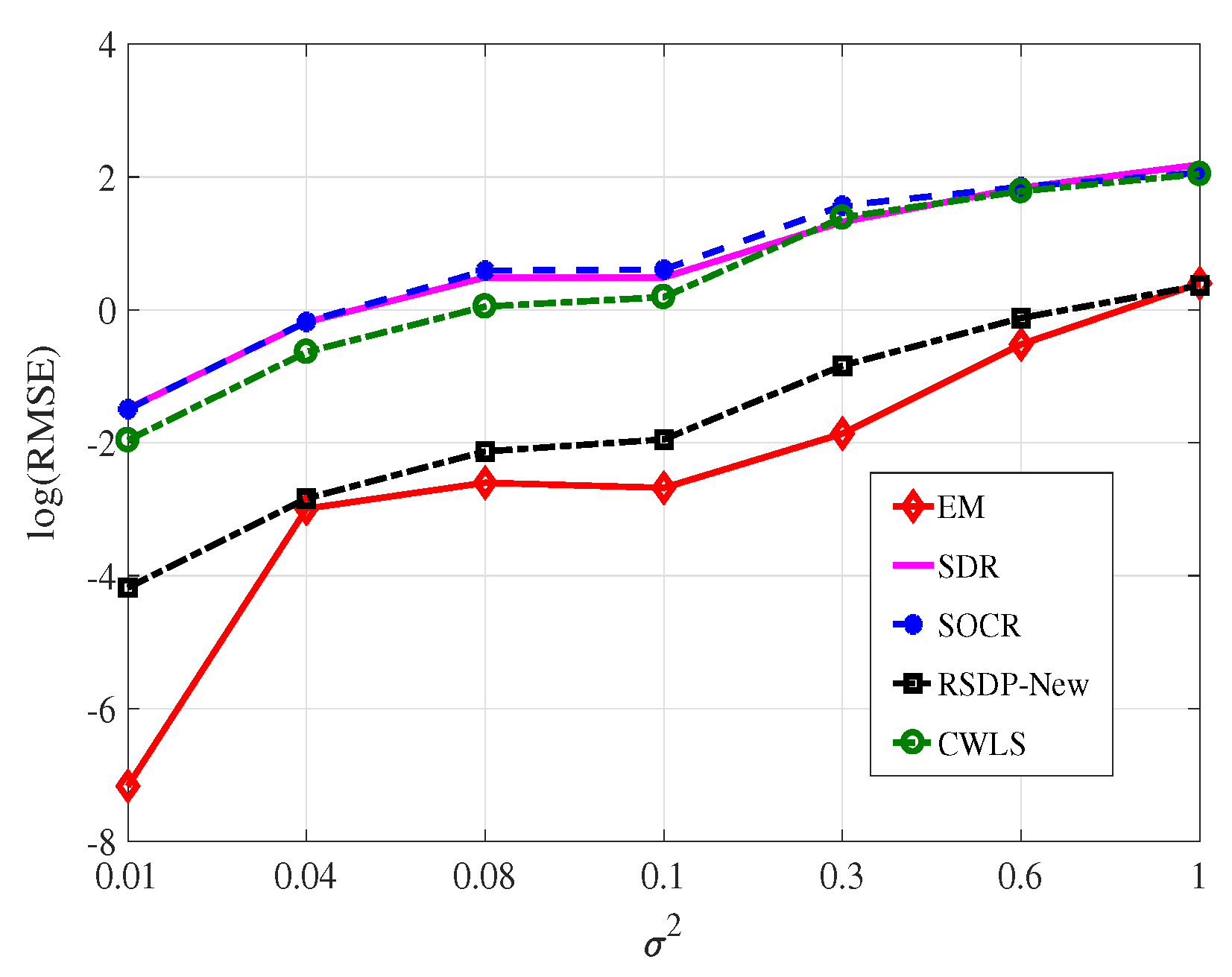
Figure 5 shows that our EM method performs significantly better than SDR, SOCR, and CWLS. Compared to the RSDP-New method, when ${\sigma }^2\ge 0.1$, the RMSE produced by our method is slightly higher. This is due to the fact that the RSDP-New method applies prior information about NLOS paths, but we do not. In the case that ${\sigma }^2<0.1$, obviously, our method produces a much lower RMSE without any prior ’information about NLOS paths.

(3)

On the whole, the proposed method is superior to the RSDP-New method in positioning accuracy. This indicates that the proposed criterion can find out the LOS-BSs.

Example 2. 

In general, the probability of four BSs participating in positioning is relatively large in an industrial environment. Therefore, this experiment uses four BSs to locate the MS, and their coordinates are (0, 0), (15, 0), (15, 15), and (0, 15), respectively. And their layout is shown in Figure 6. The coordinates of MS are randomly generated in the area surrounded by these BSs. Since the minimum number of LOS BSs is three, the number of NLOS BSs can only be one in this example. Other conditions are consistent with Example 1, and the corresponding results are shown in Figure 7.

Based on Figure 7, we can draw some conclusions: (1) When the variance in noise is less than or equal to 0.3, our EM method performs much better than the other four algorithms. (2) When the variance in noise is greater than 0.3, our EM method performs significantly better than SDR, SOCR, and CWLS methods and slightly inferior to the RSDP-New method. (3) The performance curves of the SDR, SOCR, and CWLS methods are basically consistent.

Example 3. 

To test the performance of the five methods under the scenario where MS is outside the area surrounded by all BSs, we set the coordinates of MS at (−2,−2), and other conditions are consistent with Example 2. The simulation result is shown in Figure 8.

Based on Figure 8, our EM method performs better than the RSDP-New method and much better than the SDR, SOCR, and CWLS algorithms.

Example 4. 

To further test the computation speed of all the five methods, we set the number of NLOS paths and MC simulations to 3 and 1000, respectively. The other conditions are similar to those in Example 1. Corresponding results are shown in

Table 1. Average computation time (in seconds) of five algorithms.

Method	Average Time
EM	0.0084
SDR	0.83
SOCP	0.67
RSDP-New	0.94
CWLS	0.3

. The computation times of the EM, SDP, SOCP, RSDP-New, and CWLS methods are 0.0084, 0.83, 0.67, 0.94, and 0.3 s, respectively. This indicates that our method is the fastest in terms of calculation speed.

In this study, we choose the TOA positioning mode, but our method can be applied to other modes, such as the angle-of-arrival (AOA), time-difference-of-arrival (TDOA), and phase-difference-of-arrival (PDOA) modes. Because although these modes differ in observed data, they can all use the principle idea of our method to find out the number of LOS paths under the mixed LOS/NLOS scenarios to improve the accuracy of positioning. That is, each positioning mode has its own characteristics of NLOS errors, and a specific criterion can be designed to distinguish LOS and NLOS paths.

In contrast to algorithms proposed in previous studies, our algorithm significantly improves the positioning accuracy without the need to identify the NLOS status and estimate the NLOS bias. Moreover, it performs well both in terms of positioning performance and calculation speed.

The proposed approach performs well in scenarios where the number of LOS-BSs is greater than or equal to three. The method’s performance in scenarios where the number of LOS-BSs is less than three should be studied in future work.

4. Conclusions

In recent decades, more and more studies have focused on improving positioning accuracy by reducing the impacts of NLOS errors under mixed LOS/NLOS conditions. However, it is very hard to find a solution which can obtain good performance both in positioning accuracy and computation time. To solve this problem, this paper presents an EM method and a criterion that can be used to select LOS BSs and their corresponding localization solutions from all combinations. Simulation results show that compared to other methods, the proposed algorithm presents better performance in positioning accuracy and computation time. In our future work, we will focus on improving the positioning performance of the system under extreme environments.