Abstract
Orthogonal frequency division multiplexing (OFDM) has been regarded as an attractive waveform for integrated sensing and communication (ISAC). However, suffering from its high peak-to-average power ratio (PAPR), sensitivity to phase noise (PN), and spectral efficiency saturation, the performance of OFDM in ISAC is limited. Against this background, this paper proposes a constellation-optimized index-modulated OFDM (CO-IM-OFDM) framework that leverages neural networks to design a constellation suitable for subcarrier activation patterns. A correlation model between index modulation and constellation is established, enabling adaptive constellation mapping in IM-OFDM. Then, Adam optimizer is employed to train the constellation tailored for ISAC, enhancing spectral efficiency under PN and PAPR constraints. Furthermore, a weighting factor is defined to characterize the joint communication–sensing performance, thus optimizing the overall system performance. Simulation results demonstrate that the proposed method can achieve improvements in bit error rate (BER) by over 4 dB and in Cramér–Rao bound (CRB) by 2% to 8% compared to traditional IM-OFDM constellation mapping. It overcomes fixed constellation constraints of conventional IM-OFDM systems, offering theoretical innovation waveform design for low-power communication–sensing systems in highly dynamic environments.
1. Introduction
Integrated sensing and communication (ISAC) technology has witnessed rapid development and found increasingly extensive applications in the sixth generation (6G) networks, intelligent transportation systems, and internet of things (IoT) [1,2]. Given the precious and scarce broadband resources, researchers are actively investigating efficient spectrum utilization strategies. Consequently, dual-functional waveforms that integrate wireless communication and sensing capabilities have emerged as a critical frontier in 6G [3,4]. How to design efficient and channel-adaptive dual-functional waveforms has become a pivotal challenge demanding urgent resolution, particularly under dynamic channel conditions.
Thanks to its high spectral efficiency and multipath interference resistance, conventional OFDM dominates fifth generation (5G) implementations. However, the high peak-to-average power ratio (PAPR) and acute sensitivity to phase noise (PN) of OFDM typically limit its practical implementation [5,6,7,8]. In contrast, index-modulated orthogonal frequency division multiplexing (IM-OFDM), which represents a dual-functional waveform technology, has shown emerging potential for ISAC applications [9,10]. In particular, benefiting from its dynamic activation of the subcarrier, IM-OFDM enables low-power transmission [11]. IM-OFDM encodes information not only through conventional quadrature amplitude modulation (QAM) symbols, but also through the indices of activated subcarriers in the frequency domain [12,13]. While index modulation grants IM-OFDM advantages, including superior energy efficiency, reduced PAPR, and robustness against inter-carrier interference (ICI), the selective subcarrier activation procedure introduces inherent spectral efficiency compromises compared to traditional OFDM [14].
Adaptive constellation design for IM-OFDM can effectively enhance spectral efficiency. For example, the authors in [15] proposed dual-mode OFDM-IM (DM-OFDM-IM), which partitions subcarriers within subblocks into two groups and employs different constellation mappings for each group to improve transmission rates. However, conventional constellations exemplified by phase shift keying (PSK) and QAM induce significant power penalty due to the increased PAPR. To tackle this problem, the authors in [16,17] proposed distinct constellation pairs to reduce pairwise error probability (PEP) and bit error rate (BER) in DM-OFDM-IM systems. The authors in [18] introduced transmit diversity in IM-OFDM through silent subcarriers and multi-signal constellations, which further improved power efficiency. Nevertheless, existing IM-OFDM constellation designs predominantly employ conventional constellation combinations, which achieve a mild throughput improvement while fundamentally suffering critical limitations of PAPR and PN [19,20].
Recently, artificial intelligence (AI) has shown significant potential in adaptive constellation generation tailored to IM-OFDM under stringent constraints [21,22,23,24]. In contrast to conventional constellation designs, which are based on the assumptions of ideal Gaussian channels while ignoring the effect of hardware impairments such as nonlinearities of the power amplifier (PA) [25], the AI-enabled constellation design shows the ability to adapt to such impairments. More specifically, with the help of neural networks, the transceiver of wireless communication systems is represented as a specialized neural network capable of learning symbol mapping processes and channel characteristics, thus reconstructing signals with minimal distortion at the receiver [26,27,28]. Ref. [20] proposes an OFDM modulation recognition (MR) architecture based on a scattering transform MR-network, considering constraints of radio frequency nonlinear distortion. Ref. [29] employs a blind channel equalization strategy to mitigate the effects of fading channels. Ref. [30] classifies OFDM symbol modulation based on convolutional neural networks. Implementing constellation mapping through the neural network structure enables the discovery of optimal symbol constellations that balance spectral efficiency, power efficiency, and PN robustness [31,32].
Against this background, this paper proposes a neural network-empowered constellation-optimized IM-OFDM (CO-IM-OFDM) architecture, which can derive optimal constellations for index-modulated subcarriers under dual constraints of low PAPR and PN resilience. The framework jointly optimizes communication and sensing performance through weighted metric training. The main contributions are summarized as follows:
- A neural network-based CO-IM-OFDM framework is proposed, which jointly optimizes subcarrier indices and constellation diagrams. By incorporating PAPR constraints, the trained constellations are suitable for IM-OFDM systems.
- A neural network tailored for IM-OFDM constellations in ISAC systems is proposed. Using Adam optimizer, the network generates constellations considering PN robustness and PA nonlinearity constraints, which jointly optimize spectral efficiency and ranging accuracy.
- We analyze constellation designs and performance metrics under varying trade-off weights via numerical simulations. With bit error rate (BER) and Cramér–Rao bound (CRB) as performance metrics, a weighting factor is defined to characterize joint performance, enabling maximization of the overall system efficiency.
2. Fundamentals
2.1. IM-OFDM Module
The block diagram of the considered IM-OFDM system is presented in Figure 1. Let the total available subcarriers be M with subcarrier spacing and symbol duration . For implementation convenience, these subcarriers are divided into G groups, each containing subcarriers. Since each subblock undergoes identical procedures, it suffices to consider the -th subblock (). Within each group, there are subcarriers with indices , where is the index of the n-th subcarrier in each subblock.
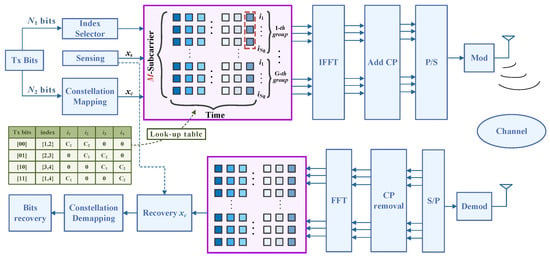
Figure 1.
The framework of the IM-OFDM system.
In the IM-OFDM system, k subcarriers in each subblock are activated to transmit modulated symbols, where the indices of the activated subcarriers are stored in the set , and the complex modulated symbol set is . An example look-up table with a subblock of with symbols is shown in Figure 1. Assume the input bitstream of N bits is partitioned into and bits, which are given by
where denotes the binomial coefficient representing the number of k-element combinations from n elements, and Q is the modulation order defined by the constellation diagram. bits determine indices of activated subcarriers, and the remaining bits form the information sequence , which is mapped via constellation modulation to generate the symbol sequence , where .
Subsequently, during the j-th OFDM symbol (), where is the length of the OFDM symbol, its communication-oriented signal is expressed as
where if ; otherwise, . The total number of information bits per symbol is given by bits.
Different from conventional approaches to realizing sensing functionality, which insert communication and sensing signals into separate subcarriers or superimpose both onto index-modulated subcarriers [13], the sensing signal in our considered scheme employs pseudo-random sequences with superior auto-correlation properties. The sequences satisfy , indicating statistical orthogonality between communication and sensing signals. Through the power allocation factor , we linearly combine them to maintain consistent transmission power, yielding the transmitted signal , where , which can guarantee both communication and sensing functionalities.
By performing inverse fast Fourier transform (IFFT) on the frequency-domain samples , the time-domain OFDM symbol is given by
where is the element of the OFDM symbol matrix . After IFFT operation, a cyclic prefix (CP) of length C is appended to the beginning of the OFDM symbol, given by
where . Then, a parallel-to-serial (P/S) conversion is performed to sequentially concatenate IM-OFDM symbols, forming the transmitted signal . Subsequently, the baseband discrete signal undergoes digital-to-analog conversion (DAC) and is upconverted to radio frequency (RF) band before transmission. The passband analog signal can be expressed as
where and are the carrier frequency and initial phase of transmitted signal, respectively. Then, the signal is sent via the Gaussian fading channel.
2.2. Operation of IM-OFDM Receiver
At the IM-OFDM receiver, the received signal is processed to achieve both target sensing and communication decoding. We consider one frame of OFDM data; the received signal in the frequency domain after passing through the channel can be expressed as
where , , and are the received signal, channel fading coefficient, and noise sample in the frequency domain, respectively. is additive white Gaussian noise (AWGN) with zero mean and variance . Regarding target sensing, we can handle and separately thanks to the statistical orthogonality between them. Considering time delay and Doppler shift , the channel function can be expressed as , where is the attenuation due to the pass loss, scattering and radar cross-section. By correlating with at the estimated value, the estimate of is identified as the peak of range power spectrum.
For bit decoding, we analyze received signal by subtracting the sensing component. The indices of activated subcarriers and their corresponding information symbols can be detected. In this process, we employ detection algorithms for IM-OFDM, specifically using the Log-Likelihood Ratio (LLR) detector. The posterior probability ratio of frequency-domain symbols being non-zero versus zero provides information about the activation status of index m, which is given by
where . A higher value indicates a greater likelihood of index m being activated by the transmitter’s index selector. Based on Bayes’ theorem, we get
where is the noise variance in the frequency domain. With higher-order modulations, we can define
where .
After computing M LLR values, the receiver selects k indices with maximum LLR values per subblock. The detected indices are then passed to an index demapper to estimate bits, followed by standard constellation demodulation.
3. Proposed Method
3.1. Framework of Constellation Optimization via Neural Network
Reliable transmission in IM-OFDM systems requires the consideration of PN and PA nonlinearity constraints. Therefore, this subsection integrates the IM-OFDM transmission system with mapping optimization and loss function, presenting a neural network-based constellation optimization system architecture for IM-OFDM.
In traditional communication systems, constellation design typically follows predefined rules, where constellations such as QAM and PSK are adopted. These constellation designs usually rely on theoretical assumptions of ideal Gaussian channels, thus making them ill-suited to dynamic channel environments and nonlinear PA constraints. In contrast, deep learning can autonomously learn the correlation between channel characteristics and transmission objectives through input–output architectures. More importantly, modeling the constellation mapping process as a trainable neural network layer enables end-to-end optimal mapping training [33]. To be noticed, such a neural network-empowered communication system can learn robust message representations associated with channel impairments during symbol mapping, thereby facilitating the recovery of transmitted messages with minimal error probability.
As shown in Figure 2, only the mapper and demapper modules contain trainable parameters, which are shared between the two. As this system is optimized jointly in an end-to-end manner, the training data are not part of a conventional pre-prepared dataset but are dynamically generated during the training process. At the start of each training iteration, a sufficiently long bit stream is randomly generated. In the mapper, the input random bit stream is first utilized to generate constellation-point symbol labels based on the modulation order (for instance, the 16-QAM modulation labels such as ‘0110’, ‘0010’, etc.). Subsequently, these labels are used to select the corresponding points from the constellation generated by trainable weight parameters, completing the constellation mapping. In the demapper, we implement the demapping by calculating the LLR. The LLR estimates the probability of each transmitted bit being 0 or 1 from the received signal and outputs the LLR. After performing a forward propagation through an end-to-end system, we obtain the communication and sensing performance losses. These losses are combined into a joint loss function. Subsequently, the Adam optimization algorithm is employed to update the trainable weight parameters, modifying the mapping relationship of the real and imaginary parts of the constellation diagram, ultimately achieving constellation optimization.
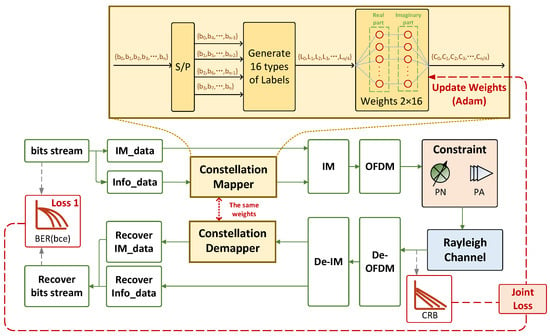
Figure 2.
The framework of constellation optimization via neural network.
3.2. Constrained Channel Module
During the neural network training process, PN and PA nonlinearity constraints are explicitly incorporated into the channel model to construct an impairment-augmented-equivalent channel. This drives the network to learn robust constellation diagrams with nonlinear predistortion compensation capabilities.
To depict the nonlinear characteristics of PA, a modified Rapp model is considered, which models the amplitude and phase amplitude distortion as [34,35]
where A is the input signal amplitude, is the PA saturation level, s is the smoothness parameter for the amplitude compression curve, and are parameters, respectively.
The Gaussian PN model is adopted for its analytical tractability in deriving key performance metrics like BER and CRB. Gaussian assumption also simplifies gradient computation for signal design optimization, such as constellation shaping and power allocation. The received signal under PN and AWGN is expressed as , where is the transmitted symbol, . is the phase noise sample reflecting oscillator stability, and is the complex AWGN with , where B and denote the channel bandwidth and noise power spectral density, respectively.
This approach achieves adaptive constellation mapping tailored for IM-OFDM systems. By integrating channel-state information and nonlinear distortion characteristics into neural network training, the mapping scheme dynamically optimizes symbol distribution based on actual channel conditions. By incorporating PA nonlinear and PN into an equivalent channel model, the neural network is driven to train robust constellation diagrams with nonlinear predistortion compensation capabilities, resulting in spiral-like phase-dimensional distributions that suppress phase rotation interference while ensuring PAPR compliance with system transmission requirements.
3.3. Loss Function
To evaluate the communication performance while considering the impact of symbol confidence on system robustness, cross-entropy is selected as a refined communication performance metric [36], given by
where is the true probability distribution of transmitted symbols and is the predicted probability distribution from the receiver. The cross-entropy loss penalizes low-confidence correct classifications by assigning higher loss values and encourages output distributions closer to ground truth through gradient updates. Under dynamic channel conditions, this metric effectively quantifies receiver sensitivity to channel impairments.
The core objective of sensing systems lies in high-precision parameter estimation, such as range, velocity, and angle. The CRB, serving as the theoretical performance lower bound, characterizes the minimum mean square error (MSE) of unbiased estimators and evaluates the optimal achievable estimation accuracy. When the estimation parameter is , we obtain , where denotes the Fisher information matrix (FIM), yielding
where is the element of matrix . corresponds to and . Then, is a matrix whose elements are as follows:
where
Then, the CRB function of parameters and is given by
To achieve a dynamic balance between communication and sensing performance, a weighted joint loss function is constructed. For the joint performance of the communication–sensing system, the weighting factor is employed to combine communication performance and sensing performance, yielding
where the weighting factor controls the priority between communication and sensing objectives, enabling adaptive constellation design for different scenarios. In communication-priority mode (), high-density irregular constellation mappings are adopted to maximize BER. In sensing-priority mode (), regular sparse constellation mappings are designed to minimize CRB. The weighting factor can be dynamically adjusted based on real-time channel conditions, i.e., increase to prioritize ranging accuracy in high-Doppler-shift scenarios and reduce to optimize the system in low-SNR environments. Then, the framework essentially finds the optimal constellation , where denotes all possible constellation mappings.
3.4. Optimal Training Method Based on Adam
Considering that gradient-directed search is more suitable for constellation optimization in terms of complexity and real-time performance, we select an appropriate gradient descent algorithm. For constellation optimization design, the real and imaginary parts of constellation points can be set as network weights to optimize the constellation through loss minimization. When the loss function represents system performance, this essentially identifies the constellation that maximizes communication–sensing system performance.
Stochastic Gradient Descent (SGD) is a gradient-based optimization algorithm that minimizes loss functions by updating parameters using gradients computed from randomly sampled data batches. Define the constellation mapping function as , where is the set of all possible constellation mapping relationships. For constellation diagram optimization, the real and imaginary parts of constellation points are directly parameterized as network weights, where , and M is the modulation order.
Compared to SGD, which only considers the first moment estimate and is prone to becoming trapped in local optima, Adam combines momentum gradients with adaptive learning rates, taking into account both first- and second-moment estimates. This allows for adaptive adjustment of the learning rate, enabling faster escape from local optima, resulting in more accurate and efficient convergence. The process is depicted as Algorithm 1. The parameter settings for Adam include the learning rate, exponential decay rate (EDR) for the first-moment estimates, EDR for the second-moment estimates, and a small constant for numerical stability.
| Algorithm 1 End-to-End Constellation Optimization Algorithm Based on Adam |
Require: Random bitstream , The set of network weights of neural network .
|
4. Experiments
In this paper, we present experiments that were conducted on the proposed CO-IM-OFDM system, comparing it with existing traditional constellation mappings, including 16APSK, 16spiral, and 16QAM. The training employed the Keras deep learning framework for network model construction, with the open-source library Sionna serving as the backend engine for link-level simulations. We also investigated the impact of different loss function weighting factors on the proposed scheme. The simulation configurations for the neural network-empowered constellation optimization design are shown in Table 1.

Table 1.
Simulation parameters for constellation optimization.
Considering the CO-IM-OFDM system, index modulation corresponds to and , and the other simulation parameters for CO-IM-OFDM are shown in Table 2.

Table 2.
Simulation parameter configuration for CO-IM-OFDM.
Figure 3 demonstrates the training results under different weighting factors. It can be observed that when communication performance is optimized (), the constellation exhibits a spiral-like structure to counteract signal-rotation-induced PN. Simultaneously, the inner and outermost constellation points maintain sufficient separation to preserve Euclidean distance uniformity under PA nonlinear distortion. Conversely, when sensing performance is prioritized (), the constellation approximates a constant-envelope structure where the signal’s constant modulus property ensures stable sensing capabilities. However, this sensing-optimal configuration sacrifices amplitude diversity, a critical degree of freedom for information encoding, leading to degraded communication performance. This demonstrates an inherent deterministic–stochastic trade-off between communication and sensing objectives: communication-driven design requires maximized signal randomness to enhance information capacity, and sensing-driven design demands deterministic signal features to guarantee sensing reliability.
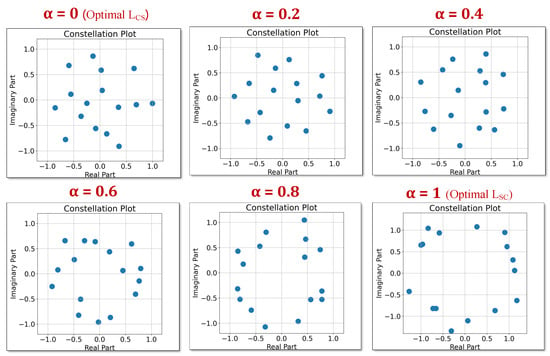
Figure 3.
The constellation under different weighting factors.
Figure 4 illustrates the results of balancing communication and sensing performance through weighting factor adjustment. The allocation of a weighting factor essentially represents a resource allocation trade-off, which is adjusted according to specific application scenarios. Through varying the weighting factor, we establish a constellation design framework and obtain the joint CRB-BER boundary for IM-OFDM under constellation optimization. Curve A represents the ideal state of the ISAC system, where both communication and sensing maintain optimal performance without mutual interference. However, this state is known to be unattainable. Curve B depicts the current baseline ISAC system state, which compromises partial communication performance to achieve sensing. This approach provides no additional performance gain and consequently causes performance degradation in the other objectives. The closed region formed by Curves A and B represents the achievable integrated performance area, with the research goal being to approach the performance upper limit (Curve A). Curve C shows performance obtained through continuous weighting factor adjustment and the proposed end-to-end training. It can be observed that BER increases with , while CRB decreases with . The trained constellation diagram demonstrates performance gains compared to Curve B, approaching the theoretical upper limit.
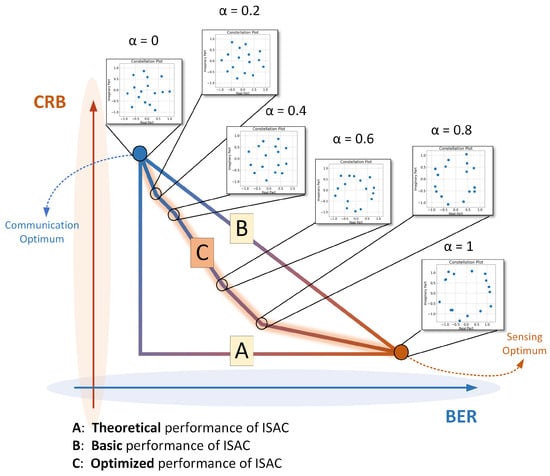
Figure 4.
The CRB-BER joint performance of ISAC.
In practical scenarios, selecting an appropriate value yields a constellation tailored to the dominant system requirement. In detail, for applications predominantly considering sensing performance, such as autonomous driving, would be set; for prioritizing communication performance, such as end-to-end video transmission, would be set. This resource allocation problem depends heavily on the specific application context. We acknowledge that a more detailed investigation into optimal selection strategies would be a valuable point of focus for future research.
Then, we provide simulation results under Gaussian channels and Rayleigh fading channels with different numbers of paths. By varying the number of multipath components as 1, 10, 20, and PN level as 0.01, 0.1, we simulated in different channel conditions.
As shown in Figure 5, we simulated the CRB-BER joint performance under Rayleigh and AWGN channel conditions. It can be observed that all simulation curves exhibit a concave characteristic. This phenomenon indicates that in the trade-off between BER and CRB, the system achieves a significant improvement in communication reliability by sacrificing a small amount of sensing accuracy, thus obtaining performance gains. This concave trend is consistently present across all simulated channel conditions. In addition, as PN increases, the system performance deteriorates, with both endpoints of the curve, optimal communication and optimal sensing points, shifting back. This fully demonstrates that the proposed neural network architecture can adapt to different channel conditions and effectively achieve performance optimization in joint communication and sensing design.
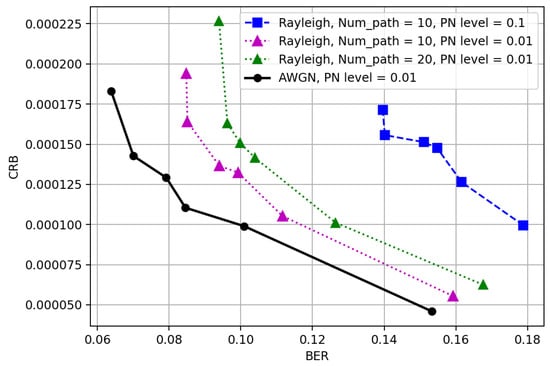
Figure 5.
The CRB-BER joint performance in different channel conditions.
Next, the performance indicators, including BER, throughput, and CRB under various weight factors, as well as their variations with respect to SNR, are compared. The benchmark for comparison is based on traditional 16QAM modulation.
Figure 6 illustrates the BER performance curves under varying and weight factors. For the traditional 16QAM baseline, the BER decreases slowly at high SNR, remaining as high as at . With the proposed algorithm, performance improves significantly as decreases. Specifically, when communication performance () is prioritized, BER outperforms the baseline by approximately 10 dB under the same conditions, exhibiting a steep decline in high-SNR regions. Conversely, yields the worst BER due to the enforced constant-envelope constraint, demonstrating the limitation of deterministic signals on communication reliability.
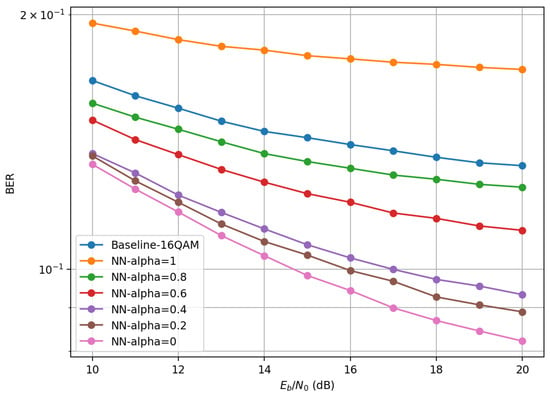
Figure 6.
BER of CO-IM-OFDM under different weighting factors.
Figure 7 shows the CRB curves under varying and weight factors. As SNR increases, the CRB decreases. When prioritizing communication performance, the proposed algorithm slightly underperforms compared to 16QAM. However, in sensing-priority mode (), the CRB decreases by 2∼8% as the weight factor increases, indicating optimized parameter estimation accuracy through deterministic signal structures.
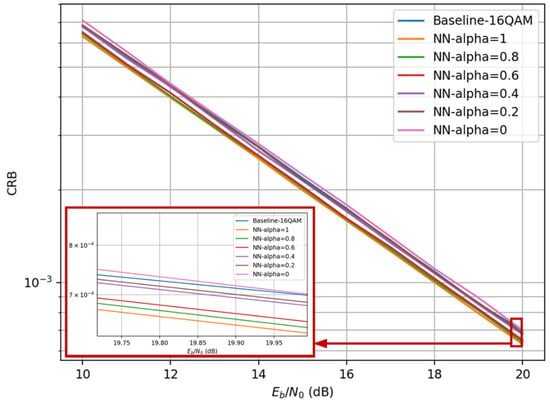
Figure 7.
CRB of CO-IM-OFDM under different weighting factors.
Next, the performance of the constellation adapted for IM-OFDM via neural networks is compared with the existing constellations. We select 16APSK, 16QAM, and 16spiral as algorithms for comparison. Their constellation diagrams are shown in Figure 8. Among them, the amplitude of 16APSK satisfies the constant envelope characteristic, enabling it to combat nonlinear channels and making it suitable for power-constrained scenarios. The constellation points of 16QAM are evenly distributed, offering high-frequency utilization, but it cannot effectively resist nonlinear distortion. The 16spiral constellation exhibits a spiral structure, possessing excellent PN resistance properties. These constellation diagrams cannot simultaneously satisfy the requirements of resisting PN, PA nonlinearity, and ensuring communication and sensing performance.
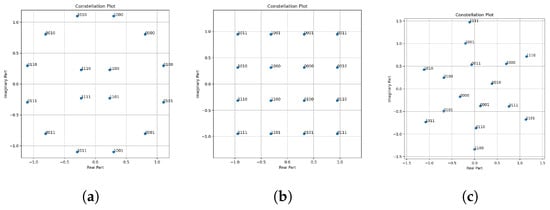
Figure 8.
The constellation: (a) 16APSK; (b) 16QAM; (c) 16spiral.
Figure 9 illustrates BER performance curves of the proposed constellation and classical constellations when applied to IM-OFDM systems. When sensing performance is prioritized (), the proposed scheme exhibits degraded BER performance, even underperforming 16QAM and 16APSK. However, for , the proposed constellation achieves remarkable BER improvements. For instance, at , it attains a 5 dB gain over 16QAM under the same BER conditions, demonstrating its adaptability to channel constraints and system requirements. Furthermore, smaller values correlate with better BER performance, with optimization effects becoming more pronounced in high-SNR regions (). These results confirm that the proposed algorithm dynamically balances signal randomness and deterministic structures to enhance demodulation robustness.
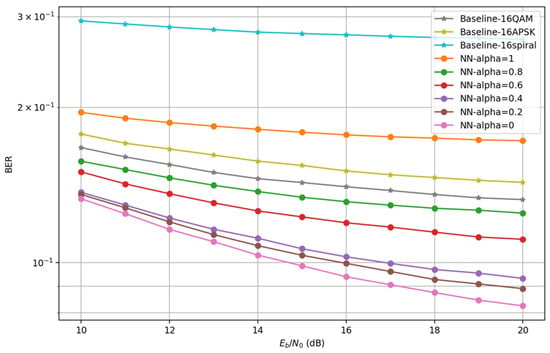
Figure 9.
The comparison results of BER under different weighting factors.
Figure 10 illustrates throughput performance for different training results. The simulation results indicate that, in terms of throughput performance, all the values of , except for 1, significantly outperformed the traditional 16QAM and 16APSK. It is noteworthy that the result for showed a decrease in throughput compared to the baseline scheme. Under full sensing conditions, the training process solely maximizes the sensing performance without considering the communication performance. Consequently, the network parameters under this mode cannot effectively support efficient data transmission, leading to lower communication throughput than the baseline scheme that balances both communication and sensing. The significant improvement in throughput performance observed at other values of fully demonstrates that the proposed joint optimization architecture can effectively achieve performance gains in terms of throughput.
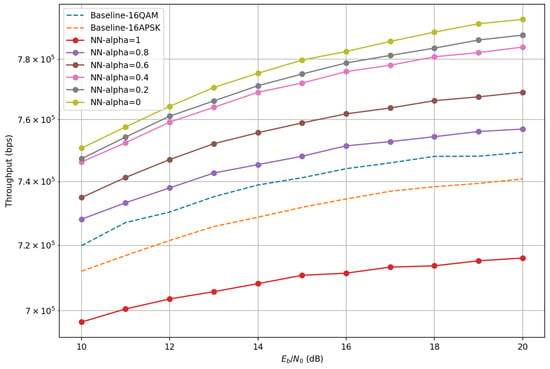
Figure 10.
The comparison results of throughput under different weighting factors.
Figure 11 depicts CRB performance curves of the proposed constellation and benchmark constellations in IM-OFDM systems. When communication performance is prioritized (), the CRB degrades significantly due to the signal’s high randomness, which introduces amplitude fluctuations detrimental to parameter estimation accuracy. However, as increases within , the CRB decreases, reaching its minimum at . This trend aligns with the theoretical trade-off between deterministic signal structures and stochastic modulation diversity in ISAC systems. The joint analysis of BER and CRB performance reveals that, except for the communication-optimal () and sensing-optimal () configurations, all trained constellations achieve significant performance gains compared to conventional 16QAM, 16APSK, and 16spiral schemes.
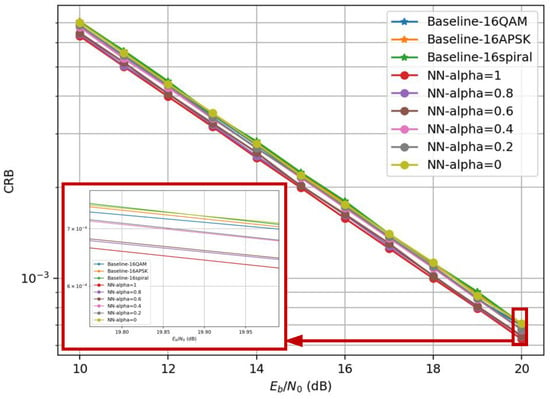
Figure 11.
The comparison results of CRB under different weighting factors.
5. Conclusions
In this paper, we proposed a CO-IM-OFDM framework that integrates neural network-trained constellation mappings with index modulation techniques. We designed optimized constellations adaptive to dynamic subcarrier activation patterns in IM-OFDM systems, aiming to maximize spectral efficiency while adhering to PAPR and PN constraints. Furthermore, the communication–sensing joint performance was defined as the primary optimization objective, where the Adam optimizer is employed to train the constellation design. Simulation results demonstrated that the proposed method achieves BER performance gains exceeding 4 dB and CRB improvements of 2–8%, substantially outperforming conventional fixed-constellation IM-OFDM systems in terms of both communication and sensing capabilities.
Author Contributions
Conceptualization, L.L., J.L. (Jiying Lin), J.L. (Jianguo Li) and X.B.; methodology, L.L., J.L. (Jiying Lin) and J.L. (Jianguo Li); software, L.L. and J.L. (Jiying Lin); validation, L.L., J.L. (Jiying Lin) and J.L. (Jianguo Li); formal analysis, L.L. and J.L. (Jiying Lin); investigation, L.L. and J.L. (Jiying Lin); resources, X.B.; data curation, L.L. and J.L. (Jiying Lin); writing—original draft preparation, L.L. and J.L. (Jiying Lin); writing—review and editing, J.L. (Jianguo Li) and X.B.; visualization, L.L. and J.L. (Jiying Lin); supervision, J.L. (Jianguo Li); project administration, J.L. (Jianguo Li); funding acquisition, X.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Liu, A.; Huang, Z.; Li, M.; Wan, Y.; Li, W.; Han, T.X.; Chetty, K. A survey on fundamental limits of integrated sensing and communication. IEEE Commun. Surv. Tutor. 2022, 24, 994–1034. [Google Scholar] [CrossRef]
- Liu, F.; Cui, Y.; Masouros, C.; Xu, J.; Han, T.X.; Eldar, Y.C.; Buzzi, S. Integrated sensing and communications: Toward dual-functional wireless networks for 6G and beyond. IEEE J. Sel. Areas Commun. 2022, 40, 1728–1767. [Google Scholar] [CrossRef]
- He, Y.; Yu, G.; Tang, Z.; Wang, J.; Luo, H. A dual-functional sensing-communication waveform design based on OFDM. IEEE Trans. Wirel. Commun. 2024, 23, 16962–16975. [Google Scholar] [CrossRef]
- Yang, T.; He, D.; Hou, H.; Wang, H.; Yin, H.; Huang, Y.; Wang, Z.; Quek, T. A unified tensor-based joint AUD and ISAC parameter estimation with large-scale user access. IEEE Trans. Cogn. Commun. Netw. 2025; in press. [Google Scholar]
- Leshem, A.; Yemini, M. Phase noise compensation for OFDM systems. IEEE Trans. Signal Process. 2017, 65, 5675–5686. [Google Scholar] [CrossRef]
- Jawhar, Y.A.; Audah, L.; Taher, M.A.; Ramli, K.N.; Shah, N.S.M.; Musa, M.; Ahmed, M.S. A review of partial transmit sequence for PAPR reduction in OFDM systems. IEEE Access 2019, 7, 18021–18041. [Google Scholar] [CrossRef]
- Wang, P.; Ye, N.; Wang, A.; Liu, J.; Yuan, W.; Nallanathan, A. Delay-Doppler domain spectral shaping multiple access (SSMA) for satellite communications: A unified multi-branch framework. IEEE Trans. Wirel. Commun. 2025, 24, 3546–3560. [Google Scholar] [CrossRef]
- Chen, Y.; He, D.; Lu, Z.; Yuan, M.; Wang, H. Design of Precoded Waveform with Low PAPR for High Mobility Communication Systems. IEEE Wirel. Commun. Lett. 2025, 28, 2156–2160. [Google Scholar]
- Şahin, M.M.; Gurol, I.E.; Arslan, E.; Basar, E.; Arslan, H. OFDM-IM for joint communication and radar-sensing: A promising waveform for dual functionality. Front. Commun. Netw. 2021, 2, 715944. [Google Scholar] [CrossRef]
- Başar, E.; Aygölü, Ü.; Panayırcı, E.; Poor, H.V. Orthogonal frequency division multiplexing with index modulation. IEEE Trans. Signal Process. 2013, 61, 5536–5549. [Google Scholar] [CrossRef]
- Hawkins, H.; Xu, C.; Yang, L.L.; Hanzo, L. IM-OFDM ISAC outperforms OFDM ISAC by combining multiple sensing observations. IEEE Open J. Veh. Technol. 2024, 5, 312–329. [Google Scholar] [CrossRef]
- Li, Q.; Wen, M.; Basar, E.; Chen, F. Index modulated OFDM spread spectrum. IEEE Trans. Wirel. Commun. 2018, 17, 2360–2374. [Google Scholar] [CrossRef]
- Yang, Z.; Gao, S.; Cheng, X.; Yang, L. Superposed IM-OFDM (S-IM-OFDM): An enhanced OFDM for integrated sensing and communications. IEEE Trans. Veh. Technol. 2024, 73, 15832–15836. [Google Scholar] [CrossRef]
- Wen, M.; Ye, B.; Basar, E.; Li, Q.; Ji, F. Enhanced orthogonal frequency division multiplexing with index modulation. IEEE Trans. Wirel. Commun. 2017, 16, 4786–4801. [Google Scholar] [CrossRef]
- Mao, T.; Wang, Z.; Wang, Q.; Chen, S.; Hanzo, L. Dual-mode index modulation aided OFDM. IEEE Access 2016, 5, 50–60. [Google Scholar] [CrossRef]
- Kim, K.H. New constellation design and bit mapping for dual-mode OFDM-IM. arXiv 2019, arXiv:1902.00936. [Google Scholar] [CrossRef]
- Sridhar, S.; Latha, S.; Thakre, A. Constellation design for dual-mode OFDM-IM. In Proceedings of the 2020 Fourth International Conference on Computing Methodologies and Communication (ICCMC), Erode, India, 11–13 March 2020; pp. 808–814. [Google Scholar]
- Zheng, J.; Chen, R. Achieving transmit diversity in OFDM-IM by utilizing multiple signal constellations. IEEE Access 2017, 5, 8978–8988. [Google Scholar] [CrossRef]
- Başar, E. OFDM with index modulation using coordinate interleaving. IEEE Wirel. Commun. Lett. 2015, 4, 381–384. [Google Scholar] [CrossRef]
- An, Z.; Xu, Y.; Tahir, A.; Wang, J.; Ma, B.; Pedersen, G.; Shen, M. Physics-Informed Scattering Transform Network for Modulation Recognition in 5G Industrial Cognitive Communications Considering Nonlinear Impairments in Active Phased Arrays. IEEE Trans. Ind. Inform. 2025, 21, 425–434. [Google Scholar] [CrossRef]
- Wang, D.; Zhang, M.; Li, J.; Li, Z.; Li, J.; Song, C.; Chen, X. Intelligent constellation diagram analyzer using convolutional neural network-based deep learning. Opt. Express 2017, 25, 17150–17166. [Google Scholar] [CrossRef] [PubMed]
- Pan, J.; Ye, N.; Yu, H.; Hong, T.; Al-Rubaye, S.; Mumtaz, S.; Chih-Lin, I. AI-driven blind signature classification for IoT connectivity: A deep learning approach. IEEE Trans. Wirel. Commun. 2022, 21, 6033–6047. [Google Scholar] [CrossRef]
- Zhang, Y.; Ding, X.; Li, G.; Zhang, Z.; Yang, K. Offline real-world wireless interference signal classification algorithm utilizing denoising diffusion probability model. IEEE Signal Process. Lett. 2023, 30, 1132–1136. [Google Scholar] [CrossRef]
- Ye, N.; Li, X.; Yu, H.; Zhao, L.; Liu, W.; Hou, X. DeepNOMA: A unified framework for NOMA using deep multi-task learning. IEEE Trans. Wirel. Commun. 2020, 19, 2208–2225. [Google Scholar] [CrossRef]
- Li, J.; Han, C.; Ye, N.; Pan, J.; Yang, K.; An, J. Instant Positioning by Single Satellite: Delay-Doppler Analysis Method Enhanced by Beam-Hopping. IEEE Trans. Veh. Technol. 2025; in press. [Google Scholar] [CrossRef]
- Huang, Z.; He, D.; Chen, J.; Wang, Z.; Chen, S. Autoencoder with fitting network for Terahertz wireless communications: A deep learning approach. IEEE China Commun. 2022, 19, 172–180. [Google Scholar] [CrossRef]
- Zhou, S.; Liu, B.; Ren, J.; Mao, Y.; Wu, X.; Guo, Z.; Li, Y. A high-security probabilistic constellation shaping transmission scheme based on recurrent neural networks. Photonics 2023, 10, 1078. [Google Scholar] [CrossRef]
- Ding, X.; Zhou, K.; Li, G.; Yang, K.; Gao, X.; Yuan, J.; An, J. Customized joint blind frame synchronization and decoding methods for analog LDPC decoder. IEEE Trans. Commun. 2023, 72, 756–770. [Google Scholar] [CrossRef]
- Wang, Y.; Gui, J.; Yin, Y.; Wang, J.; Sun, J.; Gui, G.; Gacanin, H.; Sari, H.; Adachi, F. Automatic modulation classification for MIMO systems via deep learning and zero-forcing equalization. IEEE Trans. Veh. Technol. 2020, 69, 1611–1620. [Google Scholar] [CrossRef]
- Kim, B.; Mecklenbräuker, C.; Gerstoft, P. Deep Learning-based Modulation Classification of Practical OFDM Signals for Spectrum Sensing. In Proceedings of the IEEE INFOCOM 2024—IEEE Conference on Computer Communications, Vancouver, BC, Canada, 20–23 May 2024; Volume 69, pp. 5688–5692. [Google Scholar]
- Zou, Q.; Tarighat, A.; Sayed, A.H. Compensation of phase noise in OFDM wireless systems. IEEE Trans. Signal Process. 2007, 55, 5407–5424. [Google Scholar] [CrossRef]
- Wunder, G.; Fischer, R.F.; Boche, H.; Litsyn, S.; No, J.S. The PAPR problem in OFDM transmission: New directions for a long-lasting problem. IEEE Signal Process. Mag. 2013, 30, 130–144. [Google Scholar] [CrossRef]
- Cui, Q.; You, X.; Wei, N.; Nan, G.; Zhang, X.; Zhang, J.; Yuen, C. Overview of AI and communication for 6G network: Fundamentals, challenges, and future research opportunities. Sci. China Inf. Sci. 2025, 68, 171301. [Google Scholar] [CrossRef]
- Glock, S.; Rascher, J.; Sogl, B.; Ussmueller, T.; Mueller, J.E.; Fischer, G.; Weigel, R. A novel power amplifier behavioral model for improving the linearity-efficiency tradeoff. In Proceedings of the IEEE MTT-S International Microwave and RF Conference, New Delhi, India, 14–16 December 2013; pp. 1–4. [Google Scholar]
- He, D.; Zhang, Z.; Lin, Z.; Wu, H.; Huang, Z.; Wang, Z. Performance comparison of single-carrier and multi-carrier waveforms over Terahertz wireless channels. Digit. Commun. Netw. 2024, 10, 1297–1304. [Google Scholar] [CrossRef]
- Lee, K.C.; Wang, S.H.; Li, C.P.; Chang, H.H.; Li, H.J. Adaptive resource allocation algorithm based on cross-entropy method for OFDMA systems. IEEE Trans. Broadcast. 2014, 60, 524–531. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).