Design and Measurements of an Electrothermal Filter Using CMOS Technology †
Abstract
1. Introduction
2. Electrothermal Filter
2.1. Principles of Operation
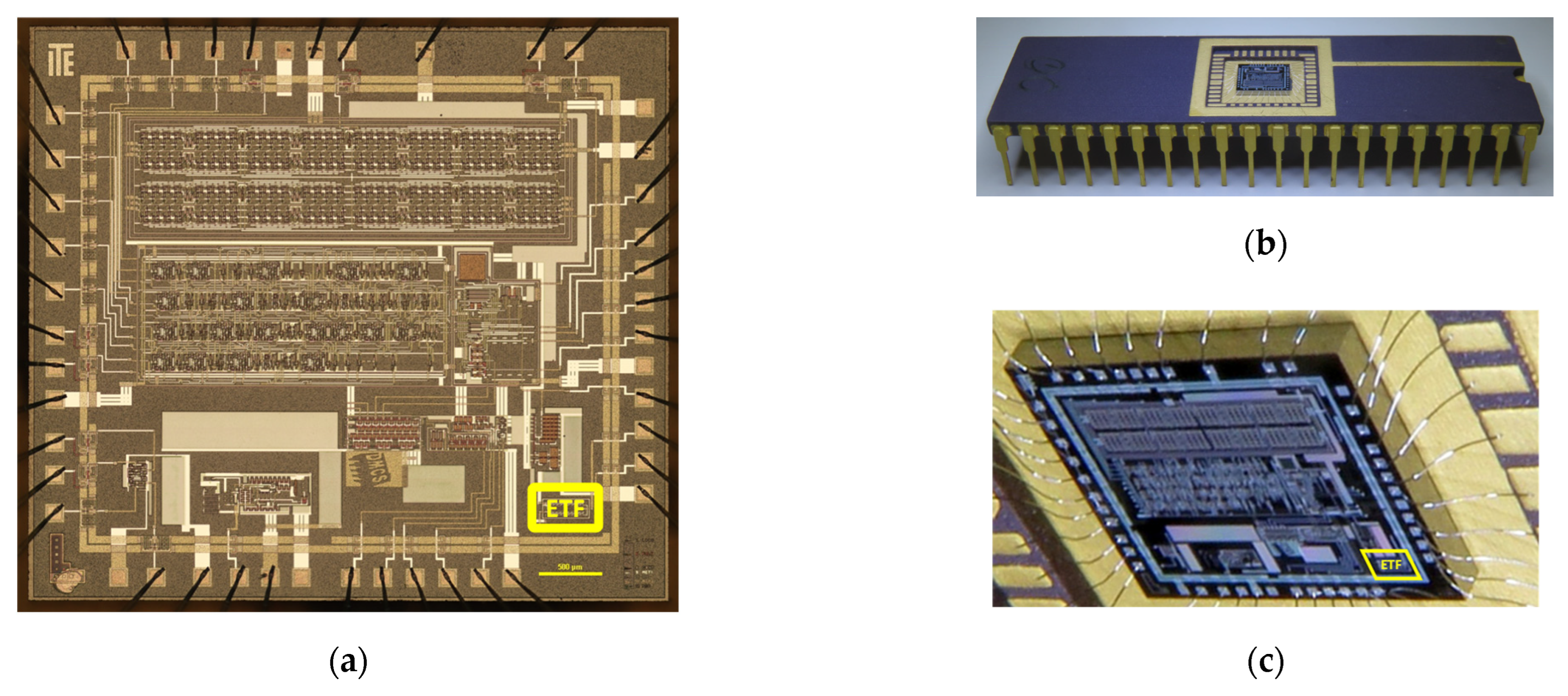
2.2. Practical Realization
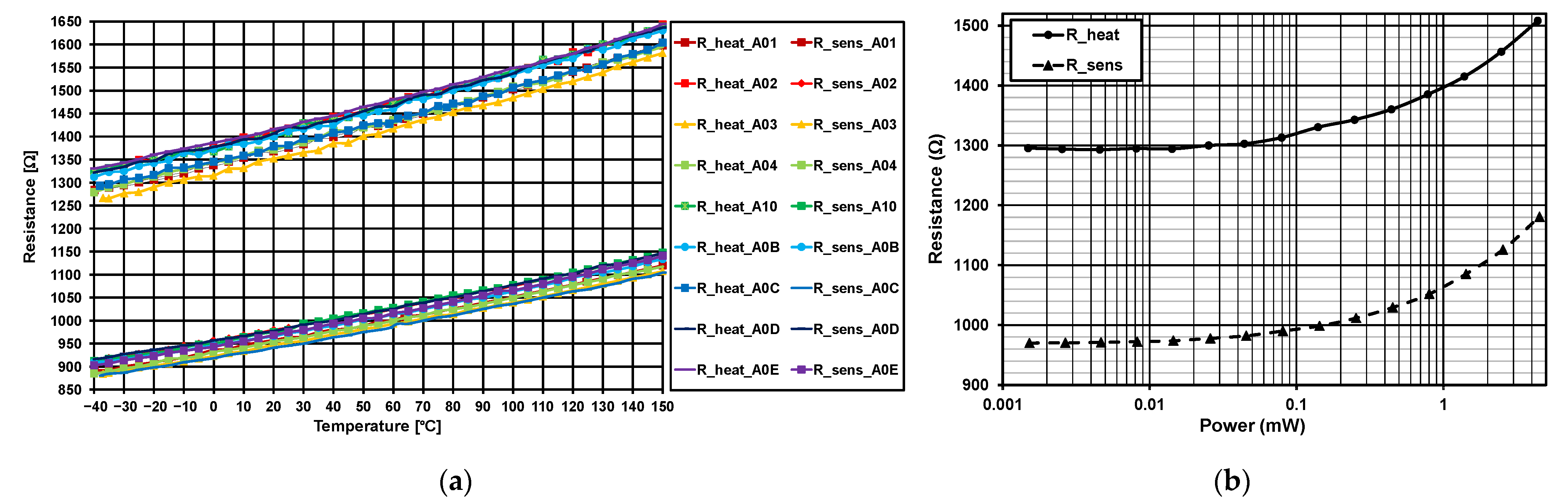
2.3. Preliminary Tests
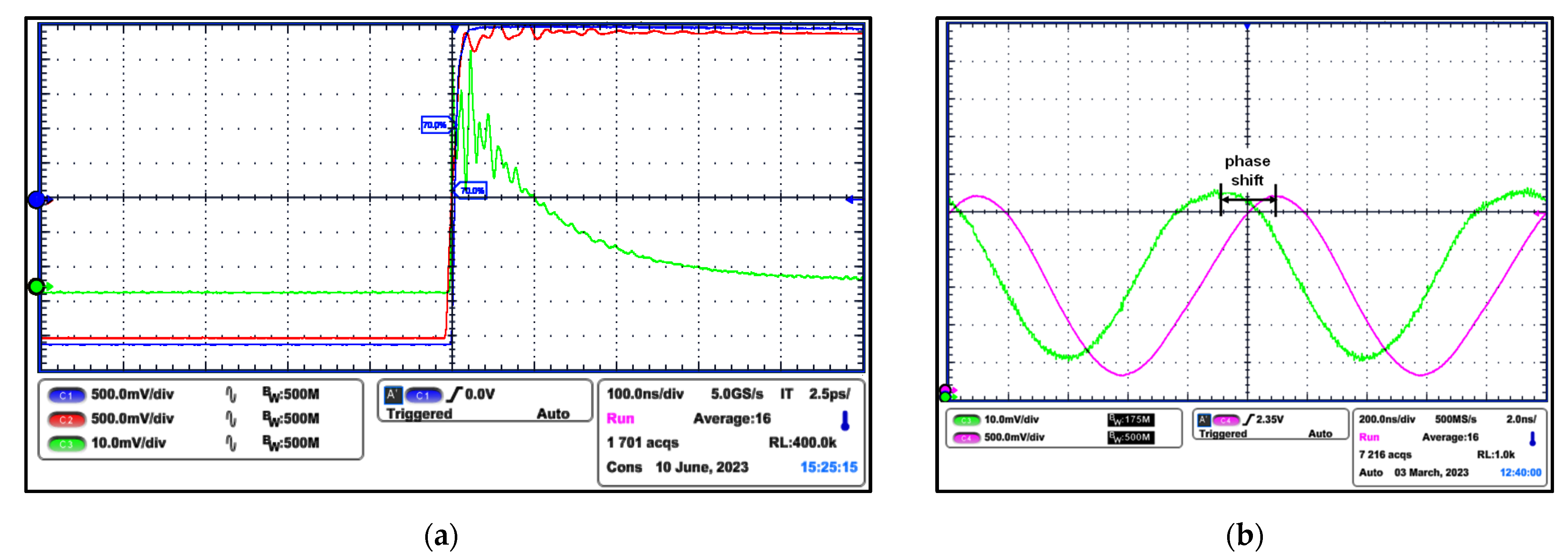
3. Measurement Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Krishnamoorthy, R.; Krishnan, K.; Chokkalingam, B.; Padmanaban, S.; Leonowicz, Z.; Holm-Nielsen, J.B.; Mitolo, M. Systematic Approach for State-of-the-Art Architectures and System-on-Chip Selection for Heterogeneous IoT Applications. IEEE Access 2021, 9, 25594–25622. [Google Scholar] [CrossRef]
- Sallehuddin, N.M.; Muhamad, M.; Hussin, H.; Halim, A.K.; Wahab, Y.A. Trade-offs and Optimization: Low Power Approaches for Area, Power Consumption, and Performance in Microprocessor Design. In Proceedings of the IEEE Regional Symposium on Micro and Nanoelectronics (RSM), Langkawi, Malaysia, 28–30 August 2023; pp. 102–105. [Google Scholar] [CrossRef]
- Peña-Fernández, M.; Verdasco, B.; Entrena, L.; Lindoso, A. Soft-Error Detection and Execution Observation for ARM Microprocessors. IEEE Trans. Nucl. Sci. 2025, 72, 1504–1512. [Google Scholar] [CrossRef]
- Hill, I.; Chanawala, P.; Singh, R.; Sheikholeslam, S.A.; Ivanov, A. CMOS Reliability From Past to Future: A Survey of Requirements, Trends, and Prediction Methods. IEEE Trans. Device Mater. Reliab. 2022, 22, 1–18. [Google Scholar] [CrossRef]
- Lasance, C. Ten years of BCI compact thermal modelling of electronic parts: A review. Heat Transf. Eng. 2007, 29, 149–168. [Google Scholar] [CrossRef]
- Szekely, V. Thermal monitoring of microelectronic structures. Microelectron. J. 1994, 25, 157–170. [Google Scholar] [CrossRef]
- Oshita, T.; Shor, J.; Duarte, D.E.; Kornfeld, A.; Zilberman, D. Compact BJT-based thermal sensor for processor applications in a 14 nm tri-gate CMOS process. IEEE J. Solid-State Circuits 2015, 50, 799–807. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, Y.; Zhang, W.; Zhang, J. The Study of Temperature Calibration Method for NTC Thermistor. In Proceedings of the 4th IEEE International Conference on Frontiers of Sensors Technologies (ICFST), Shanghai, China, 6–9 November 2020; pp. 50–53. [Google Scholar] [CrossRef]
- Ganwani, M.; Shaikh, B.; Sinha, S. Design and Investigation of MEMS-Based Thermopile Detector Arrays for Infrared Sensing Applications. In Proceedings of the IEEE Applied Sensing Conference (APSCON), Goa, India, 22–24 January 2024; pp. 1–4. [Google Scholar] [CrossRef]
- Elamaran, D.; Suzuki, Y.; Satoh, H.; Banerjee, A.; Hiromoto, N.; Inokawa, H. Performance Comparison of SOI-Based Temperature Sensors for Room-Temperature Terahertz Antenna-Coupled Bolometers: MOSFET, PN Junction Diode and Resistor. Micromachines 2020, 11, 718. [Google Scholar] [CrossRef] [PubMed]
- Shor, J.S.; Luria, K. Miniaturized BJT-based thermal sensor for microprocessors in 32- and 22-nm technologies. IEEE J. Solid-State Circuits 2013, 48, 2860–2867. [Google Scholar] [CrossRef]
- Rossi, C.; Aguirre, P. Ultra-low Power CMOS Cells for Temperature Sensors. In Proceedings of the SBCCI, Florianopolis, Brazil, 4–7 September 2005. [Google Scholar]
- Lee, T.J.; Tu, K.H. Wide Dynamic Range Temperature Sensor Using High Sensitivity PTAT Current Generator. In Proceedings of the 19th International SoC Design Conference, Gangneung-si, Republic of Korea, 19–22 October 2022; pp. 17–18. [Google Scholar] [CrossRef]
- Szermer, M.; Jankowski, M.; Janicki, M. Design, Fabrication, and Characterization of a PTAT Sensor Using CMOS Technology. Electronics 2024, 13, 429. [Google Scholar] [CrossRef]
- Bhargava, C.; Khanal, G.M. Basic CMOS VLSI Design. In Basic VLSI Design Technology: Technical Questions and Solutions; River Publishers: Gistrup, Denmark, 2020; pp. 113–152. [Google Scholar]
- Jacob Baker, R. CMOS Circuit Design, Layout, and Simulation, 4th ed.; Wiley-IEEE Press: Hoboken, NJ, USA, 2019; ISBN 978-1-119-48151-5. [Google Scholar]
- Meijer, G.C.; Wang, G.; Fruett, F. Temperature Sensors and Voltage References Implemented in CMOS Technology. IEEE Sens. J. 2001, 1, 225–234. [Google Scholar] [CrossRef]
- Makinwa, K.A.A.; Snoeij, M.F. A CMOS temperature-to-frequency converter with an inaccuracy of less than ±0.5 °C (3σ) from −40 °C to 105 °C. IEEE J. Solid-State Circuits 2006, 41, 2992–2997. [Google Scholar] [CrossRef]
- Zhang, C.; Makinwa, K.A.A. Interface electronics for a CMOS electrothermal frequency-locked-loop. IEEE J. Solid-State Circuits 2008, 43, 1603–1608. [Google Scholar] [CrossRef]
- Makinwa, K.A.; Witte, J.F. A temperature sensor based on a thermal oscillator. In Proceedings of the IEEE Sensors, Irvine, CA, USA, 30 October–3 November 2005; pp. 1149–1152. [Google Scholar] [CrossRef]
- Xia, S.; Makinwa, K.A. Design of an Optimized Electrothermal Filter for a Temperature-to-Frequency Converter. In Proceedings of the IEEE Sensors, Atlanta, GA, USA, 28–31 October 2007; pp. 1255–1258. [Google Scholar] [CrossRef]
- Kashmiri, S.M.; Xia, S.; Makinwa, K.A.A. A Temperature-to-Digital Converter Based on an Optimized Electrothermal Filter. In Proceedings of the 34th European Solid-State Circuits Conference ESSCIRC, Edinburgh, UK, 15–19 September 2008; pp. 74–77. [Google Scholar] [CrossRef]
- Vroonhoven, C.; van Makinwa, K.A. Thermal diffusivity sensing: A new temperature sensing paradigm. In Proceedings of the IEEE Custom Integrated Circuits Conference (CICC), San Jose, CA, USA, 19–21 September 2011. [Google Scholar] [CrossRef]
- Sönmez, U.; Sebastiano, F.; Makinwa, K.A. Compact Thermal-Diffusivity-Based Temperature Sensors in 40-nm CMOS for SoC Thermal Monitoring. IEEE J. Solid-State Circuits 2017, 52, 834–843. [Google Scholar] [CrossRef]
- Pedalà, L.; Sönmez, U.; Sebastiano, F.; Makinwa, K.A.; Nagaraj, K.; Park, J. An Oxide Electrothermal Filter in Standard CMOS. In Proceedings of the IEEE Sensors, Orlando, FL, USA, 30 October–3 November 2016; pp. 1–3. [Google Scholar] [CrossRef]
- Janicki, M.; Jankowski, M.; Szermer, M. Preliminary Characterization of An Electro-Thermal Converter. In Proceedings of the 30th International Conference on Mixed Design of Integrated Circuits and System (MIXDES), Kraków, Poland, 29–30 June 2023; pp. 160–163. [Google Scholar] [CrossRef]
- Jankowski, M.; Szermer, M. Simulation, Measurements and Analysis of the CMOS Temperature Sensor. In Proceedings of the 31st International Conference on Mixed Design of Integrated Circuits and System (MIXDES), Gdansk, Poland, 27–28 June 2024; pp. 138–143. [Google Scholar] [CrossRef]
- Turkes, P. An Ion-implanted Resistor as Thermal Transient Sensor for the Determination of the Thermal Diffusivity in Silicon. Phys. Stat. Sol. A 1983, 75, 519–523. [Google Scholar] [CrossRef]
- Łukasiewicz—Instytut Mikroelektroniki i Fotoniki, Warszawa, Poland. Available online: https://imif.lukasiewicz.gov.pl (accessed on 14 July 2025).
- Kosuge, A.; Sumi, H.; Shimamoto, N.; Ochiai, Y.; Inoue, Y.; Amano, H.; Mogami, T.; Mita, Y.; Ikeda, M.; Kuroda, T. Agile-X: A Structured-ASIC Created With a Mask-Less Lithography System Enabling Low-Cost and Agile Chip Fabrication. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2025, 33, 746–756. [Google Scholar] [CrossRef]
- Petrou, L.; Georgiou, J. An ASIC Architecture With Inter-Chip Networking for Individual Control of Adaptive-Metamaterial Cells. IEEE Access 2022, 10, 80234–80248. [Google Scholar] [CrossRef]
- Sayal, A.; Ajay, P.; McDermott, M.W.; Sreenivasan, S.V.; Kulkarni, J.P. M2A2: Microscale Modular Assembled ASICs for High-Mix, Low-Volume, Heterogeneously Integrated Designs. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2020, 39, 4760–4776. [Google Scholar] [CrossRef]
- Binder GmbH—Drying and Heating Chambers, Tuttlingen, Germany. Available online: https://www.binder-world.com (accessed on 14 July 2025).
- Test Equipment Solutions Ltd., Langley, UK. Available online: https://www.testequipmenthq.com/datasheets/TEKTRONIX-DPO5054-Datasheet.pdf (accessed on 25 July 2025).
- Gnidzińska, K.; Napieralski, A.; De Mey, G. Theoretical Investigation on Electrothermal Filters. In Proceedings of the 16th International Conference Mixed Design of Integrated Circuits & Systems MIXDES, Lodz, Poland, 25–27 June 2009; pp. 381–384. [Google Scholar]
- Szekely, V. Identification of RC networks by deconvolution: Chances and limits. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 1998, 45, 244–258. [Google Scholar] [CrossRef]


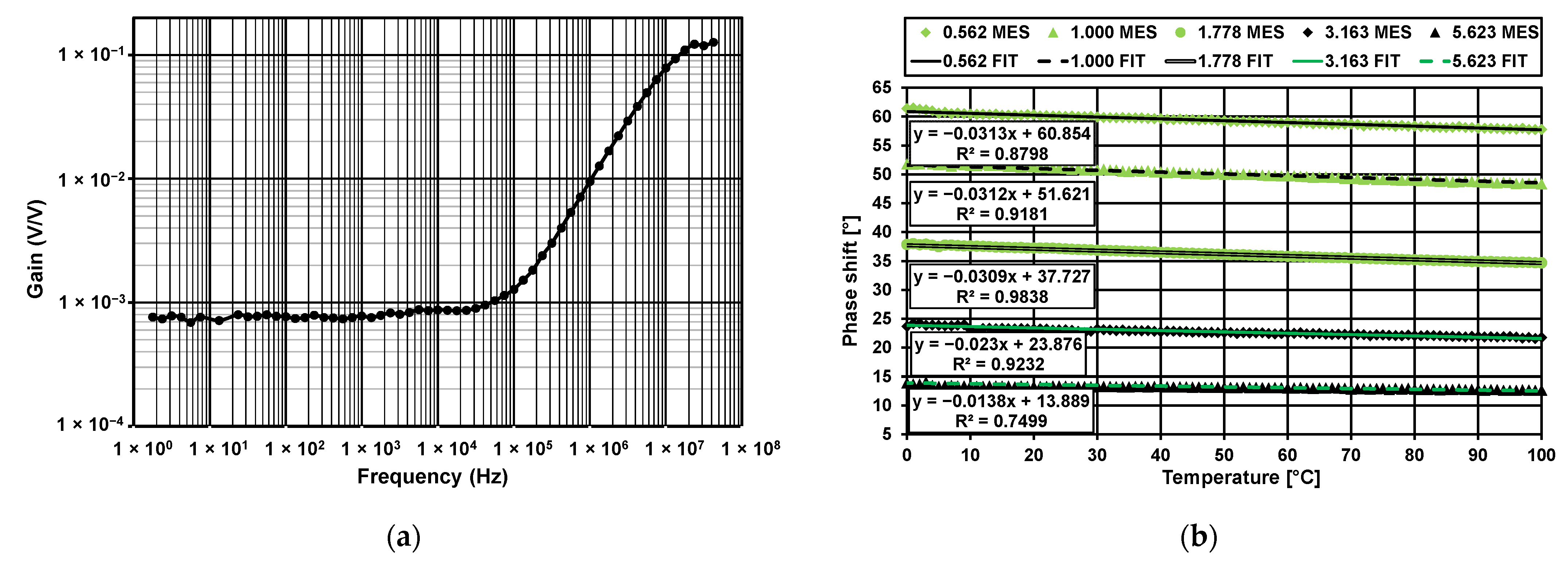
| Frequency [MHz] | Gain [mV/V] | Sensitivity [deg/K] |
|---|---|---|
| 0.562 | 5.987 | 0.0313 |
| 1.000 | 10.692 | 0.0312 |
| 1.778 | 17.453 | 0.0309 |
| 3.163 | 26.242 | 0.0230 |
| 5.623 | 33.210 | 0.0138 |
| 10.000 | 36.655 | 0.0025 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jankowski, M.; Szermer, M.; Janicki, M. Design and Measurements of an Electrothermal Filter Using CMOS Technology. Electronics 2025, 14, 3355. https://doi.org/10.3390/electronics14173355
Jankowski M, Szermer M, Janicki M. Design and Measurements of an Electrothermal Filter Using CMOS Technology. Electronics. 2025; 14(17):3355. https://doi.org/10.3390/electronics14173355
Chicago/Turabian StyleJankowski, Mariusz, Michał Szermer, and Marcin Janicki. 2025. "Design and Measurements of an Electrothermal Filter Using CMOS Technology" Electronics 14, no. 17: 3355. https://doi.org/10.3390/electronics14173355
APA StyleJankowski, M., Szermer, M., & Janicki, M. (2025). Design and Measurements of an Electrothermal Filter Using CMOS Technology. Electronics, 14(17), 3355. https://doi.org/10.3390/electronics14173355









