Design of a Brushless DC Motor Drive System Controller Integrating the Zebra Optimization Algorithm and Sliding Mode Theory
Abstract
1. Introduction
2. Brushless DC Motor Drive System
2.1. Field-Oriented Control Architecture
2.2. Proportional-Integral (P-I) Controller
3. Proposed Drive Control Based on the Novel Algorithm
3.1. Zebra Optimization Algorithm
3.1.1. Foraging Behavior
3.1.2. Defense Behavior
3.2. Sliding Mode Controller
3.2.1. State Variable Design
3.2.2. Sliding Mode Trajectory Design
3.2.3. Design of the Sliding Mode Reaching Law
- (1)
- Constant reaching law:
- (2)
- Exponential reaching law:where, denotes the constant speed reaching gain, represents the exponential reaching gain, and is the sign function, defined as shown in Equation (34).
3.2.4. Controller Output Design
3.3. Speed Control Based on a Sliding Mode Controller Optimized by the Zebra Optimization Algorithm
- Step 1:
- Set relevant parameters, including the number of zebras N, maximum number of iterations T, search space boundaries [], random number , population variation index I, strategy switching probability , constant R, and weight coefficients and .
- Step 2:
- Initialize the position X and fitness value F of each zebra.
- Step 3:
- Randomly select one zebra to serve as the pioneer zebra , and input its position coordinates directly into the ERLSMC. Then, the initial fitness value is calculated using the sum of squared error (SSE), which is based on the feedback speed error and the rate of change in speed error , according to the predefined weight coefficients and . These weights represent the relative importance of each feature. As shown in Equation (23), the sliding mode dynamic trajectory function exhibits a correction effect with respect to the speed error rate. Although both variables are important indicators for control performance, the speed error is considered more critical. Moreover, since the sliding mode controller already accounts for the error derivative when computing the sliding surface trajectory, the speed error is given a higher weight, while the error derivative is assigned a lower one. Therefore, the weights are set as and , with . The fitness value is then calculated using the SSE, as expressed in Equation (42).
- Step 4:
- Record the current position and fitness value of the selected pioneer zebra as the best solution found so far.
- Step 5:
- Use Equation (17) from the first-phase foraging behavior to compute the new position of the i-th zebra in the j-th dimension, along with its new fitness value. Then, apply Equation (18) to compare the newly obtained fitness value with the current best fitness value . If < , update the position of the i-th zebra to ; otherwise, retain its original position.
- Step 6:
- Record the newly calculated positions and fitness values of all zebras as their current positions and fitness values.
- Step 7:
- Use Equation (19) from the second-phase defense behavior to recalculate the position and fitness value of the i-th zebra in the j-th dimension. If the strategy switching probability , function (Strategy 1) is applied; otherwise, function (Strategy 2) is used. After computation, apply Equation (20) to compare the resulting fitness value with the current fitness value . If < , update the position of the i-th zebra to ; otherwise, retain the current position. Subsequently, the zebra with the lowest fitness value among all individuals, indicating a better solution than the current best, is designated as the new pioneer zebra .
- Step 8:
- Update the record of the best fitness value and corresponding position obtained so far. If the number of iterations has reached the predefined maximum, terminate the iteration process. The best position coordinates are then output as the optimized values for the three gain parameters of the ERLSMC. Finally, the output is determined using Equation (41).
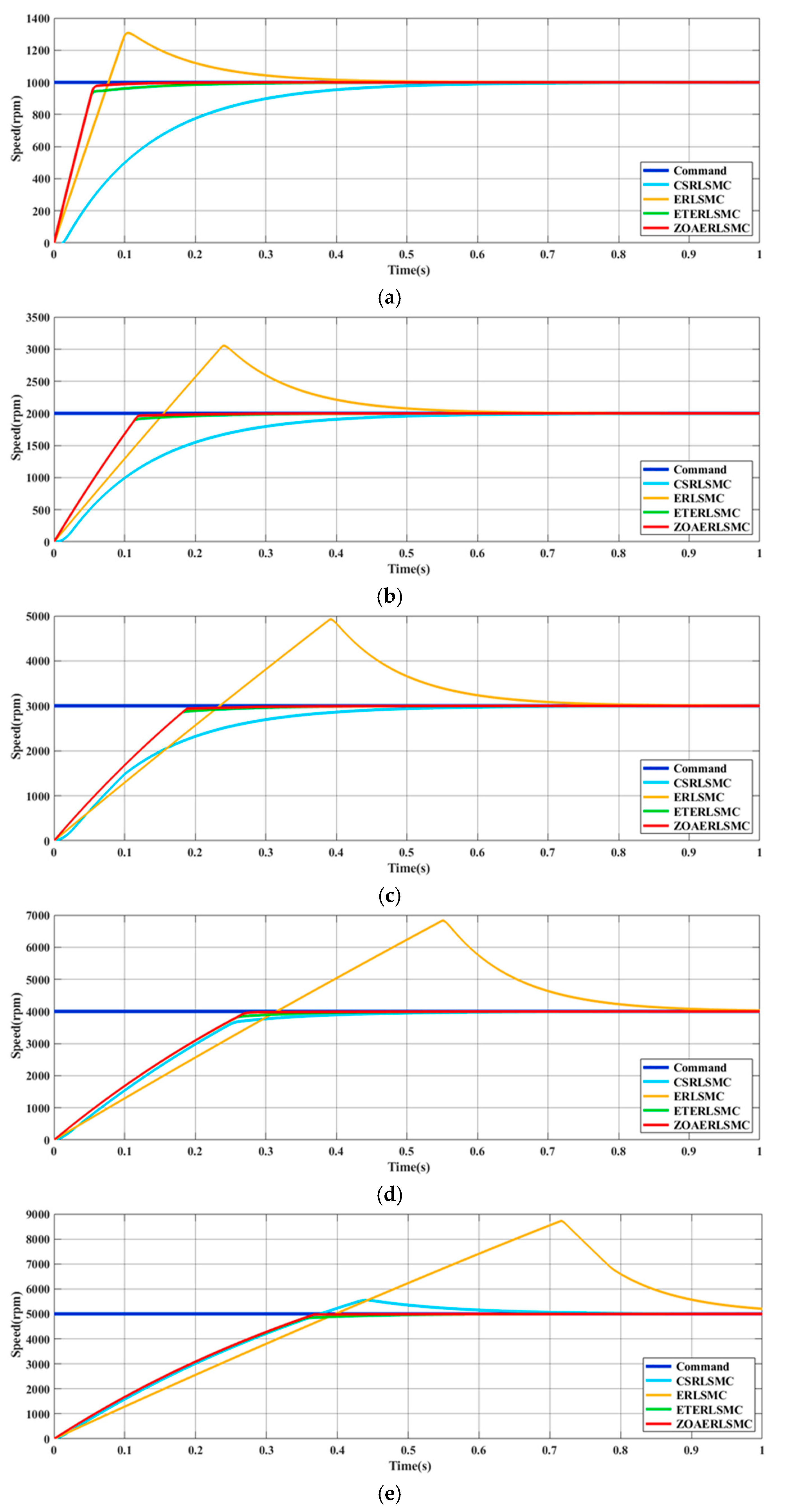
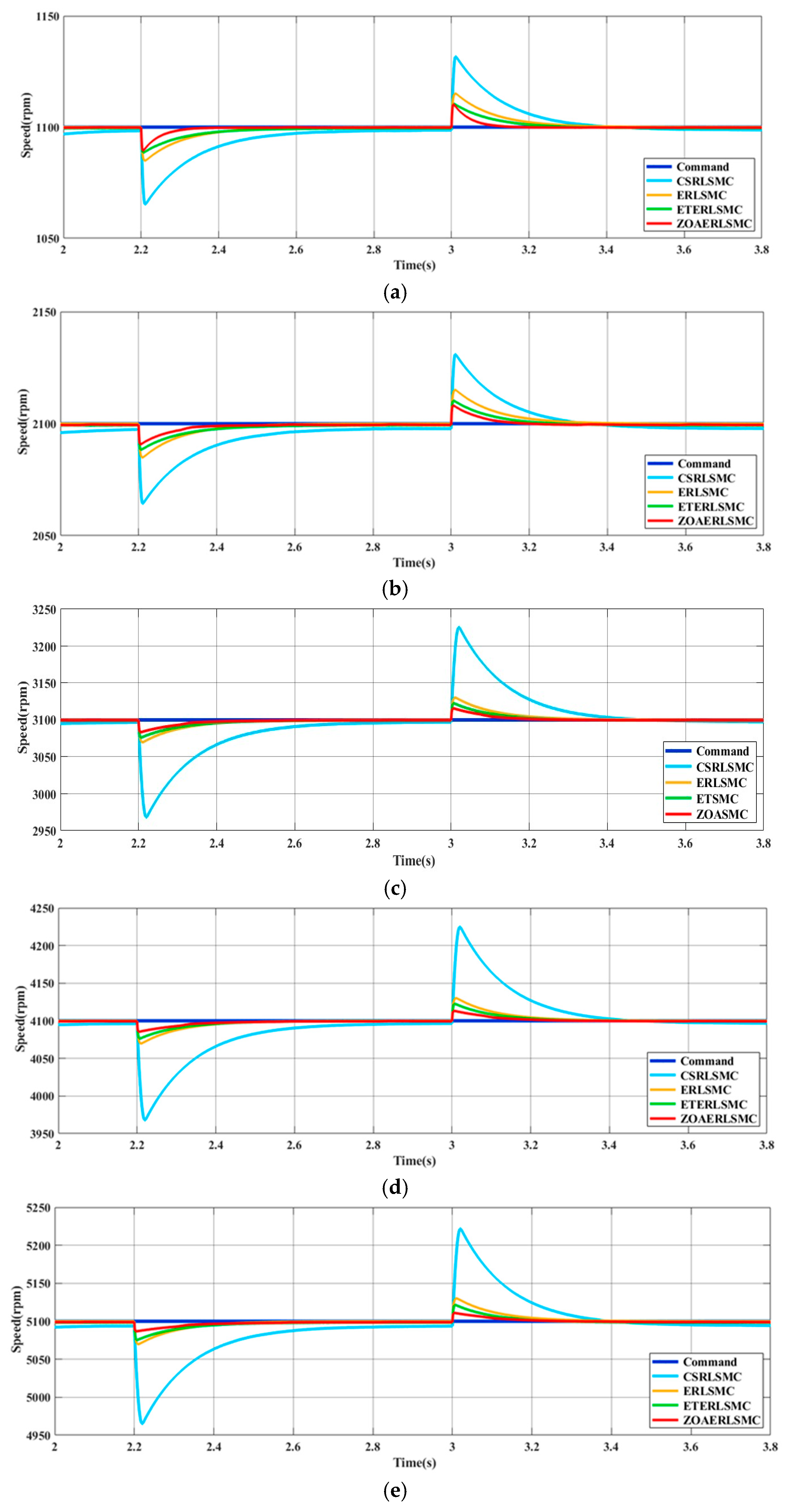
4. Simulation Results
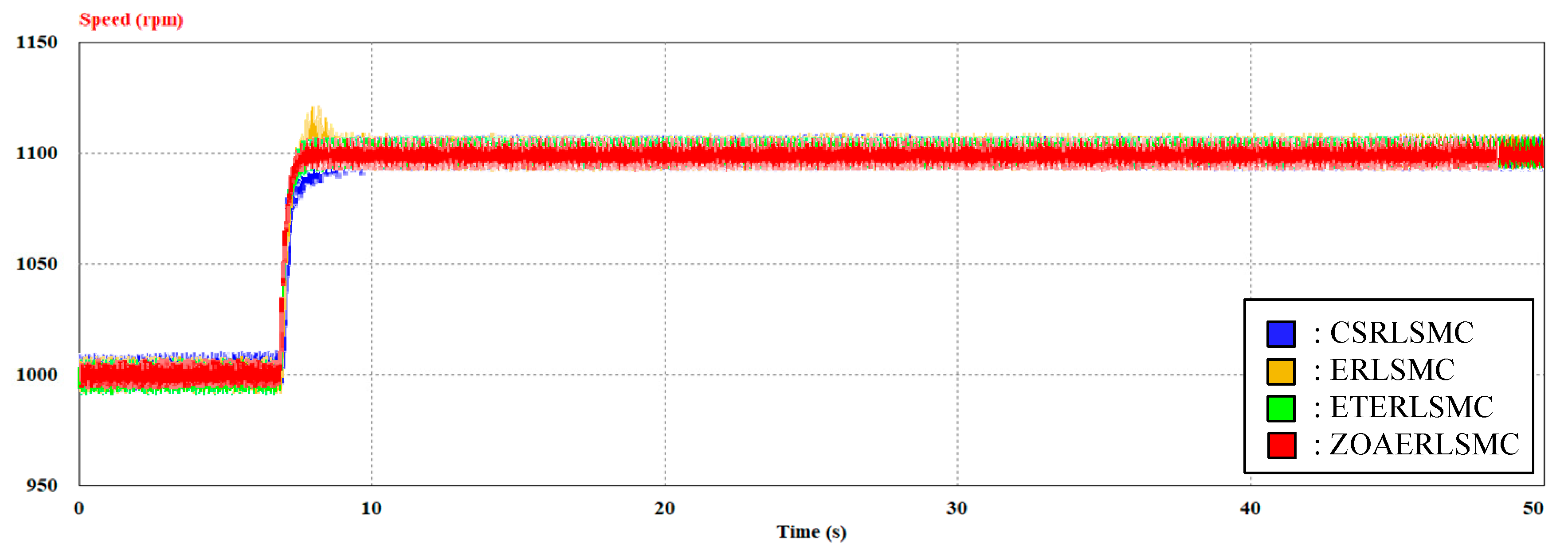
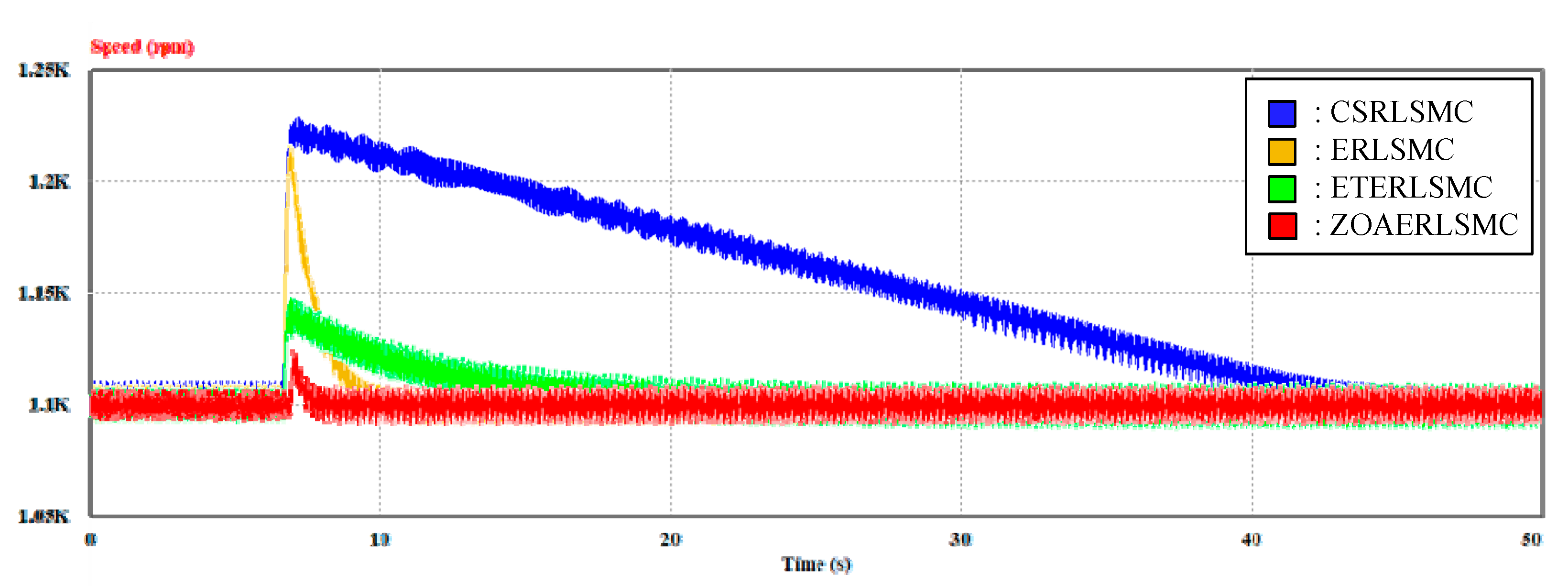
5. Experimental Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Acronyms | |
| BLDCM | brushless DC motors |
| FOC | field-oriented control |
| ZOA | zebra optimization algorithm |
| SMT | sliding mode theory |
| ERLSMC | exponential reaching law-based sliding mode controller |
| ET | extension theory |
| P-I | proportional-integral |
| SMC | sliding mode controller |
| 2DOFC | two-degree-of-freedom controller |
| PSO | particle swarm optimization |
| EFT2DOFC | extendable fuzzy theory with two-degree-of-freedom controller |
| PSOP-IC | particle swarm optimization algorithm combined with P-I controller |
| ETERLSMC | extension theory combined with exponential reaching law-based sliding mode controller |
| SVPWM | space vector pulse width modulation |
| ZOAERLSMC | zebra optimization algorithm combined with exponential reaching law-based sliding mode controller |
| CSRLSMC | constant speed reaching law-based sliding mode controller |
| Symbols | |
| stator fluxs of the d-axis and q-axis | |
| flux linkage | |
| stator voltages of the d-axis and q-axis | |
| stator resistance | |
| stator currents of the d-axis and q-axis | |
| electrical angular velocity of the motor | |
| stator inductances of the d-axis and q-axis | |
| electromagnetic torque | |
| number of poles | |
| moment of inertia | |
| mechanical angular velocity | |
| load torque | |
| viscous friction coefficient | |
| torque constant | |
| two-phase stationary coordinate | |
| two-phase synchronous rotating coordinate | |
| two-phase stationary coordinate voltage | |
| stator reference current of the q-axis | |
| position of the i-th zebra in the j-th dimension | |
| lower and upper bounds of the search space in the j-th dimension | |
| random number uniformly distributed in the range [0, 1] | |
| new position of the i-th zebra in the j-th dimension during the first-stage foraging behavior | |
| position of the pioneer zebra in the j-th dimension | |
| randomly selected value from the set {1,2} | |
| the current position of the i-th zebra | |
| the current fitness value of the i-th zebra | |
| the fitness value after the first-stage foraging | |
| two defensive strategies | |
| new position of the i-th zebra in the j-th dimension during the second-stage defensive behavior | |
| the fitness value after the second-stage foraging | |
| constant set to 0.01 | |
| the current iteration number | |
| the maximum number of iterations | |
| random probability value within [0, 1] that determines the type of predator encountered | |
| the position of the attacked zebra in the j-th dimension | |
| commanded rotor speed | |
| speed difference | |
| rate change of the speed difference | |
| sliding mode dynamic trajectory function | |
| sliding mode dynamic trajectory control gain | |
| control force function | |
| Lyapunov’s second stability criterion continuous function | |
| reaching law functions | |
| speed difference | |
| rate change of the speed difference | |
| weight values |
References
- Wang, M.; Chen, Z. Research on Permanent Magnet Structure of Permanent Magnet Synchronous Motor for Electric Vehicle. In Proceedings of the 2nd International Conference on Electrical Engineering and Control Science (IC2ECS), Nanjing, China, 16–18 December 2022; pp. 990–993. [Google Scholar]
- Lee, C.I.; Jang, G.H. Experimental Measurement and Simulated Verification of the Unbalanced Magnetic Force in Brushless DC Motors. IEEE Trans. Magn. 2008, 44, 4377–4380. [Google Scholar] [CrossRef]
- BV, P.; Balamurugan, A.; Selvathai, T.; Reginald, R.; Varadhan, J. Evaluation of Different Vector Control Methds for Electric Vehicle Application. In Proceedings of the 2nd International Conference on Power and Embedded Drive Control (ICPEDC), Chennai, India, 21–23 August 2019; pp. 273–278. [Google Scholar]
- Bhatti, S.A.; Malik, S.A.; Daraz, A. Comparison of P-I and I-P Controller by Using Ziegler-Nichols Tuning Method for Speed Control of DC Motor. In Proceedings of the International Conference on Intelligent Systems Engineering (ICISE), Islamabad, Pakistan, 15–17 January 2016; pp. 330–334. [Google Scholar]
- Murali, S.B.; Rao, P.M. Adaptive Sliding Mode Control of BLDC Motor Using Cuckoo Search Algorithm. In Proceedings of the 2nd International Conference on Inventive Systems and Control (ICISC), Coimbatore, India, 19–20 January 2018; pp. 989–993. [Google Scholar]
- Qi, C.; Xie, J.; Mao, H.; Xie, Q. Condition Assessment of Valve-side Bushing of Converter Transformer Based on Extension Theory. In Proceedings of the IEEE International Conference on High Voltage Engineering and Application (ICHVE), Beijing, China, 6–10 September 2020; pp. 1–4. [Google Scholar]
- Trojovská, E.; Dehghani, M.; Trojovský, P. Zebra Optimization Algorithm: A New Bio-inspired Optimization Algorithm for Solving Optimization Algorithm. IEEE Access 2022, 10, 49445–49473. [Google Scholar] [CrossRef]
- Chao, K.H.; Hsieh, C.T.; Chen, X.J. A Robust Controller Based on Extension Sliding Mode Theory for Brushless DC Motor Drives. Electronics 2024, 13, 4028. [Google Scholar] [CrossRef]
- Chao, K.H.; Chang, C.L. Design of a Robust Controller for Induction Motor Drive Systems Based on Extendable Fuzzy Theory. Mathematics 2024, 12, 3235. [Google Scholar] [CrossRef]
- Chen, G.Y.; Perng, J.W.; Ma, L.S. DSP Based BLDC Motor Controller Design with Auto Tuning PSO-PID Algorithm. In Proceedings of the IEEE/SICE International Symposium on System Integration (SII), Nagoya, Japan, 11–13 December 2015; pp. 766–770. [Google Scholar]
- Wang, J.; Ye, J.; Yan, R. The Magnetostatic Simulation and Determination of Magnetic Components for an External Ventricular Drainage Device. In Proceedings of the 40th Chinese Control Conference (CCC), Shanghai, China, 26–28 July 2021; pp. 6386–6391. [Google Scholar]
- Liu, C.H. AC Motor Control: Principles of Vector Control and Direct Torque Control, 4th ed.; Donghua Book Company: Taipei, Taiwan, 2007. [Google Scholar]
- Xie, T.; Kuai, Z.; Ye, X.; Zhu, L.; Guo, K.; Shi, S. Coordinate Conversions and Deviation Analysis in Multi-source Data Fusion. In Proceedings of the 2nd China International SAR Symposium (CISS), Shanghai, China, 3–5 November 2021; pp. 1–3. [Google Scholar]
- Kishore, N.; Shukla, K.; Gupta, N. A Novel Three-Phase Multilevel Inverter Cascaded by Three-Phase Two-Level Inverter and Two Single-Phase Boosted H-Bridge Inverters. In Proceedings of the IEEE PES Innovative Smart Grid Technologies-Asia (ISGT Asia), Singapore, 1–5 November 2022; pp. 330–334. [Google Scholar]
- Butt, C.; Hoque, M.A.; Rahman, M.A. Simplified Fuzzy Logic Based MTPA Speed Control of IPMSM Drive. IEEE Trans. Ind. Appl. 2004, 40, 1529–1535. [Google Scholar] [CrossRef]
- Luo, N.; Zhang, L. Chaos Driven Development for Software Robustness Enhancement. In Proceedings of the 9th International Conference on Dependable Systems and Their Applications (DSA), Wulumuqi, China, 4–5 August 2022; pp. 1029–1034. [Google Scholar]
- Song, H.; Zhang, M.; Shi, Q. Capacity Optimization of Hybrid Energy Storage System Based on Improved Zebra Optimization Algorithm. In Proceedings of the 2024 IEEE 7th Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), Chongqing, China, 20–22 September 2024; pp. 1390–1394. [Google Scholar]
- Lebedev, A.; Filaretov, V. Adaptive Variable Structure System with the Sliding Surfaces Adjustment for the Control of Nonstationary Linear Object. In Proceedings of the 2008 IEEE International Conference on Mechatronics and Automation, Takamatsu, Japan, 5–8 August 2008; pp. 684–689. [Google Scholar]
- Zhang, J.; Liu, B.; Jiang, Z.; Hu, H. The Application of Sliding Mode Control with Improved Approaching Law in Manipulator Control. In Proceedings of the 13th IEEE Conference on Industrial Electronics and Applications (ICIEA), Wuhan, China, 31 May–2 June 2018; pp. 807–812. [Google Scholar]
- Bodur, F.; Kaplan, O. A Novel Sliding Mode Control Based on Super Twisting Reaching Law for PMSM Speed Controller with Fixed-Time Disturbance Observer. In Proceedings of the 12th International Conference on Renewable Energy Research and Applications (ICRERA), Oshawa, ON, Canada, 29 August–1 September 2023; pp. 1–6. [Google Scholar]
- AM2200H BLDC Motor. Available online: https://www.adlee.com/zh-tw/product-552515/%E5%B7%A5%E6%A5%AD%E7%94%A8%E7%9B%B4%E6%B5%81%E7%84%A1%E5%88%B7%E9%A6%AC%E9%81%94.html (accessed on 8 May 2024).






| Parameters | Value |
|---|---|
| The number of zebras (N) | 5 |
| Maximum number of iterations (T) | 30 |
| ] | [350, 7000] |
| ] | [0.1, 3.5] |
| ] | [0.1, 1] |
| The range of random number (r) | [0, 1] |
| Population variation index (I) | {1, 2} |
| The range of random number of strategy switching probability (Ps) | [0, 1] |
| Constant (R) | 0.01 |
| ) | 0.7 |
| ) | 0.3 |
| Electrical Specifications | Value |
|---|---|
| Three-phase rated voltage | AC 220 V |
| Three-phase rated current | AC 9.8 A |
| Rated apparent power | 2156 VA |
| Rated speed | 6000 rpm |
| Operating frequency range | 0 ~ 200 Hz |
| Number of poles | 4 |
| Stator resistance | 1.5 × 10−1 Ω |
| Stator inductance | 1.235 × 10−3 H |
| Flux linkage | 1.26 × 10−1 Wb |
| Moment of inertia | 1.45 × 10−3 () |
| Viscous friction coefficient | 2.38 × 10−3 () |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chao, K.-H.; Huang, K.-H.; Guo, Y.-H. Design of a Brushless DC Motor Drive System Controller Integrating the Zebra Optimization Algorithm and Sliding Mode Theory. Electronics 2025, 14, 3353. https://doi.org/10.3390/electronics14173353
Chao K-H, Huang K-H, Guo Y-H. Design of a Brushless DC Motor Drive System Controller Integrating the Zebra Optimization Algorithm and Sliding Mode Theory. Electronics. 2025; 14(17):3353. https://doi.org/10.3390/electronics14173353
Chicago/Turabian StyleChao, Kuei-Hsiang, Kuo-Hua Huang, and Yu-Hong Guo. 2025. "Design of a Brushless DC Motor Drive System Controller Integrating the Zebra Optimization Algorithm and Sliding Mode Theory" Electronics 14, no. 17: 3353. https://doi.org/10.3390/electronics14173353
APA StyleChao, K.-H., Huang, K.-H., & Guo, Y.-H. (2025). Design of a Brushless DC Motor Drive System Controller Integrating the Zebra Optimization Algorithm and Sliding Mode Theory. Electronics, 14(17), 3353. https://doi.org/10.3390/electronics14173353







