Privacy Protection Anomaly Detection in Smart Grids Based on Combined PHE and TFHE Homomorphic Encryption

Abstract

With the growing scale and complexity of smart grids, ensuring both effective anomaly detection and robust privacy protection has become increasingly critical. This paper proposes a ciphertext-based anomaly detection model built upon a collaborative architecture between edge computing and public cloud, integrating a hybrid homomorphic encryption scheme that combines partial homomorphic encryption (PHE) and fully homomorphic encryption over torus (TFHE). The encryption method is selected based on the task type: TFHE is used for complex anomaly detection tasks requiring encrypted computation in the cloud, while PHE is applied to cross-regional data aggregation tasks for secure homomorphic addition. Edge nodes handle low-latency, lightweight tasks locally, whereas complex encrypted tasks are processed in the cloud using an enhanced Isolation Forest model adapted for homomorphic computation. Extensive experiments on three benchmark datasets demonstrate that the proposed model achieves anomaly detection performance comparable to plaintext-based models, while significantly outperforming existing homomorphic encryption-based methods in terms of accuracy and ROC-AUC. This work provides a scalable and practical solution for secure and efficient anomaly detection in smart grids.

1. Introduction

With the continuous rise in global energy demand, power systems—the critical infrastructure of modern society—are undergoing profound transformations. As a cornerstone of next-generation power systems, the smart grid [1] integrates advanced sensors, communication networks, and computing platforms to improve electricity resource management and scheduling. However, the rapid development of smart grids has also raised unprecedented challenges related to data security. The real-time transmission and processing of massive data volumes expose the system to security threats, turning data privacy breaches into a major concern for grid stability [2]. Despite the vital role smart grids play in improving the stability, efficiency, and sustainability of electricity systems, the security challenges they face are becoming increasingly severe [3]. According to the latest report published by Omdia in March 2024 [4], the global smart grid market reached USD 25.2 billion, with hardware components—such as smart meters, communication modules, and IoT sensors—comprising over one-third of the market. Meanwhile, data security risks are growing at an exponential rate.

As the scale of smart grids continues to expand, user privacy is increasingly at risk. With the widespread integration of IoT and smart home devices, modern power systems continuously monitor electricity usage. This includes appliance-level consumption patterns, frequency, and timing. Such information often contains highly personal attributes that can reveal residents’ daily routines and even infer sensitive details such as user identities and activity patterns, thereby posing potential risks of data misuse.

Meanwhile, the increasing distribution and complexity of modern smart grids have significantly heightened the challenges of anomaly detection. Unlike traditional power systems that operate under centralized control, smart grids comprise tens of thousands of distributed energy resources, storage units, and end-user terminals, forming a large-scale, dynamic, and heterogeneous network. While this decentralized architecture enhances system resilience and operational flexibility, it also introduces new security vulnerabilities. In practice, anomalies may stem from various sources, including equipment malfunctions, cyberattacks, communication failures, or data tampering—each of which can severely compromise system reliability. According to public reports, more than one billion data records were stolen or exposed in 2024 alone, highlighting the growing fragility of digital infrastructures. This alarming trend underscores the urgent necessity of developing robust, secure, and efficient anomaly detection mechanisms tailored to the unique characteristics of smart grids.

To address the pressing challenges of user privacy, researchers have proposed various privacy-preserving techniques, which can be broadly categorized into the following approaches: One approach is based on anonymization [5,6], which removes or replaces user-identifiable information, such as IP addresses and usernames, to achieve data de-identification. This method is simple to implement and incurs low overhead, and can effectively reduce the risk of privacy leakage in certain scenarios. However, it lacks adaptability in dynamic environments or with frequently changing data streams, and may increase system management and maintenance complexity in smart grids that require real-time response. Another approach is based on perturbation, which introduces random noise or distortions into the original data to obscure user behavior and protect privacy [7]. While such methods preserve some statistical characteristics and allow for basic anomaly detection, the intensity of perturbation must be carefully balanced between privacy and data utility. In particular, when dealing with high-dimensional, large-scale, or complex data, the added noise may significantly impair detection accuracy and system responsiveness. A further approach is based on encryption [8,9], particularly homomorphic encryption (HE), which enables computations to be performed directly on encrypted data without decryption. This allows for privacy-preserving anomaly detection while maintaining functional completeness. Although encryption-based methods offer strong security guarantees, they still face considerable challenges in terms of processing efficiency and computational overhead, especially when applied to large volumes of data.

To address the challenges of privacy-preserving anomaly detection in cloud environments, this paper proposes a hybrid encryption mechanism that combines partial homomorphic encryption (PHE) and fully homomorphic encryption over the torus (TFHE) to enable efficient and secure data processing. Compared to traditional anonymization and perturbation techniques—which, while capable of offering some level of privacy protection, often result in substantial information loss when balancing data utility and confidentiality—homomorphic encryption allows for direct computation on encrypted data without compromising privacy. In particular, fully homomorphic encryption (FHE) supports arbitrary operations on ciphertexts, effectively eliminating the risk of privacy leakage during data transmission and analysis. However, FHE is typically hindered by high computational complexity and ciphertext noise accumulation, especially when applied to the large-scale data produced by smart grid systems. To mitigate these limitations, this work adopts the TFHE scheme, which leverages fast gate bootstrapping to perform real-time noise refreshing during encrypted computation, thereby enhancing both computational efficiency and ciphertext usability. Additionally, for multi-source tasks such as cross-regional data aggregation, the Paillier encryption scheme is employed to enable homomorphic addition and statistical analysis, ensuring privacy protection while preserving system responsiveness. In recent years, edge computing has been widely adopted in collaborative networked systems to address challenges related to latency and privacy [10], and considering the enormous storage and computational overhead introduced by thousands of distributed resources in smart grids, this paper introduces an edge computing–public cloud collaborative framework. By performing data preprocessing and partial encryption at the edge nodes, the framework reduces transmission latency and bandwidth consumption, while complex anomaly detection tasks are offloaded to the public cloud, fully leveraging its high computational and storage capabilities. By combining an improved Isolation Forest anomaly detection algorithm with an adaptive dynamic encryption strategy, this work achieves efficient anomaly detection in encrypted environments while ensuring the privacy of smart grid data.

In summary, this paper proposes a privacy-preserving ciphertext anomaly detection model based on an edge computing and public cloud collaborative architecture. It innovatively introduces a combined homomorphic encryption mechanism of PHE and TFHE, as well as an adaptive dynamic encryption strategy, aiming to protect data privacy while encrypting electricity data. This enables data mining through encrypted data and leverages cloud servers to perform computations on ciphertext. The main contributions of this paper include the following:

• This paper proposes a novel edge computing–public cloud collaborative framework tailored for anomaly detection in smart grids, which achieves a dynamic balance between detection accuracy and response speed. Unlike traditional solutions that rely solely on either cloud or edge computing, the proposed framework supports local detection of lightweight and latency-sensitive tasks at the edge, while offloading complex ciphertext computations to the cloud. This hybrid architecture significantly reduces bandwidth consumption and enhances overall system responsiveness, offering a previously underexplored, yet crucial, solution for privacy-sensitive and delay-critical scenarios in smart grids;
• This work introduces an innovative anomaly detection model based on hybrid homomorphic encryption, combining partial homomorphic encryption (PHE) with fully homomorphic encryption over the torus (TFHE). This model provides reliable encryption protection for smart grid systems, preventing privacy leaks during data communication and processing. The model integrates an improved Isolation Forest anomaly detection method to enable fast and effective deep learning on encrypted data. Furthermore, the model leverages cloud server collaboration for anomaly detection, enhancing detection efficiency;
• Comprehensive experiments and security analyses are conducted on multiple publicly available benchmark datasets. The results demonstrate that the proposed method achieves anomaly detection performance comparable to plaintext models while ensuring data privacy. Compared with existing ciphertext-based anomaly detection methods, our approach achieves superior performance in terms of accuracy and AUC, indicating its broad applicability and practical value in real-world smart grid applications.

2. Related Works

Machine learning and deep learning techniques have been widely applied to smart grid anomaly detection to enhance system security and reliability. Zhao et al. [11] proposed a weight-based improved k-prototype algorithm, optimizing anomaly detection efficiency by unifying measurement methods for categorical and numerical attributes. Barua et al. [12] implemented real-time anomaly detection using a hierarchical temporal memory (HTM) architecture for PMU data, demonstrating performance comparable to mainstream algorithms. To address cyberattack threats, Qi et al. [13] developed an attack detection model combining semi-supervised learning with deep representation learning, while Jithish et al. [14] introduced a federated learning approach for distributed anomaly detection. Researchers have explored diverse technical directions: Dai et al. [15] trained models using power consumption side-channel features to detect operational anomalies; Saraswat et al. [16] designed the AnSMart scheme based on Support Vector Machines (SVM) to predict data deviations; in 2024, Duan et al. [17] proposed the Transformer-GAN model, which integrates the Transformer architecture with GAN techniques. Its self-attention mechanism and generative capabilities endow it with exceptional adaptability and robustness when handling dynamic power data patterns and previously unseen anomalies, and Park et al. [18] integrated sliding windows with LightGBM models for load forecasting and anomaly repair. While existing methods have advanced detection accuracy and real-time performance, most studies inadequately address data privacy protection, necessitating further exploration of privacy-preserving mechanisms for high-efficiency detection.

To mitigate data privacy risks and model parameter leakage in smart grids, researchers have integrated homomorphic encryption (HE) into anomaly detection frameworks. Lee et al. [19] designed an encrypted deep neural network using the RNS-CKKS algorithm, improving ciphertext operation efficiency through parallel computing, but noise accumulation compromises decryption accuracy. Sanskruti Joshi et al. [20] proposed an additive homomorphic scheme based on elliptic curve cryptography, achieving smaller key sizes and faster computation than traditional CKKS approaches. Rakesh Shrestha et al. [21] incorporated the Paillier algorithm into federated learning scenarios to protect LSTM and autoencoder training processes. However, these solutions only support single homomorphic addition or multiplication operations, limiting their scalability in complex computational environments. In 2023, Kumar et al. [22] proposed a privacy chain-based homomorphic encryption scheme combined with statistical methods to protect and analyze users’ sensitive data. This approach enables data mining in the encrypted domain while enhancing the traceability of access control. However, the method relies heavily on encrypted computation resources, which may introduce performance bottlenecks in practical deployment, especially when handling large-scale data. Current HE schemes face trade-offs between computational efficiency, functional extensibility, and storage demands, highlighting the need for more flexible and efficient hybrid encryption architectures to address smart grids’ complex requirements. To provide a clearer understanding of how our approach compares with existing privacy-preserving anomaly detection methods,

Table 1. Comparison of encrypted anomaly detection methods.

Method	Privacy Protection	Detection Accuracy	Computation Efficiency	Scalability/Performance Gap
Lee et al. [19]	Strong	Medium	Low	Poor (cloud-only, heavy computation)
Joshi et al. [20]	Strong	Low	High	Poor (addition-only operations)
Shrestha et al. [21]	Moderate	Medium	Moderate	Moderate (training only, no encrypted inference)
Kumar et al. [22]	Strong	Low	Low	Poor (statistical model, limited generality)
Our Method	Strong (end-to-end)	High	High	Excellent (close to plaintext, flexible deployment)

presents a side-by-side comparison across several critical dimensions, including privacy protection, detection accuracy, computational efficiency, and system scalability.

3. System Architecture and Security Model

3.1. Overview of the System Model

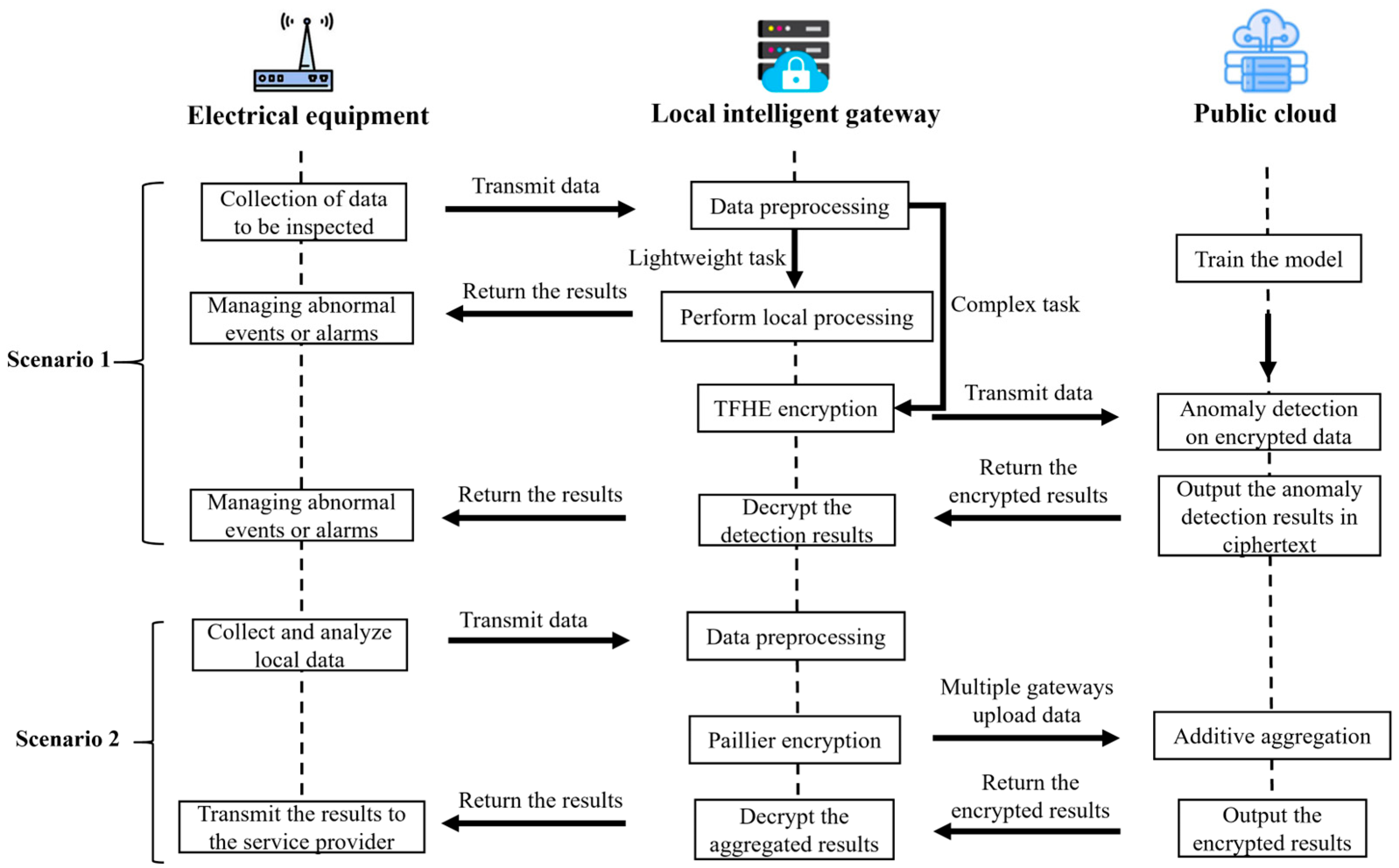
The proposed homomorphic encryption-based anomaly detection scheme for the smart grid consists of three main entities: power devices, edge computing nodes (implemented by local intelligent gateways), and the public cloud. The system’s design framework is illustrated in Figure 1.

In the smart grid system, sensors are responsible for collecting data generated during the operation of electrical equipment, such as the temperature of devices and cables, the voltage and current in transmission lines, and the physical vibrations of transformers or generators. The system analyzes the collected data to promptly detect anomalies and ensure stable operation of the system.

As an edge computing node, the local intelligent gateway directly interacts with electrical equipment, and is responsible for the preprocessing and homomorphic encryption of sensor data. The tasks of electrical equipment can be roughly divided into two categories: one is anomaly detection, which involves processing and analyzing the uploaded data to identify potential attacks and equipment failures; the other is cross-regional multi-device data aggregation, where operators aggregate multi-source data and perform statistical analysis to gain a comprehensive understanding of equipment operating status and optimize detection models deployed on cloud servers, thereby improving overall detection efficiency and system responsiveness.

To align task complexity with system capabilities, the proposed architecture categorizes anomaly detection into two types:

(1) Simple anomaly detection tasks—such as threshold-based alerts and basic equipment fault identification—are directly processed by edge nodes. This allows for fast response with minimal latency, ensuring real-time system operation.

(2) Complex or sensitive anomaly detection tasks—including deep anomaly pattern recognition and multi-device fault prediction—involve high computational demand and privacy concerns. In such cases, edge nodes first encrypt the data using the TFHE fully homomorphic encryption scheme and then upload the ciphertext to the public cloud. The cloud server, equipped with powerful computing and storage resources, performs encrypted inference and statistical analysis directly on the ciphertext. This enables accurate anomaly detection while maintaining end-to-end privacy protection. Furthermore, the cloud can dynamically optimize task scheduling and resource allocation based on system conditions and edge feedback, thereby ensuring scalable, efficient, and privacy-aware system operation.

When tasks involve data aggregation across multiple devices in different regions, each intelligent gateway first preprocesses the local data and encrypts it using the Paillier encryption algorithm. The encrypted data is then uploaded to the public cloud server. The public cloud server performs homomorphic addition on the encrypted data from multiple sources and conducts statistical analysis. Finally, the encrypted results are returned to the operator. Based on the analysis results, the operator can optimize the anomaly detection models deployed on both the local intelligent gateways and the public cloud servers, thereby enhancing the overall detection performance and response efficiency of the system.

For example, in a regional substation scenario, electrical equipment such as transformers and circuit breakers are equipped with sensors to collect critical operational data in real time (e.g., voltage, current, temperature, and vibration). This data is transmitted to the local intelligent gateway, which performs preliminary analysis. For simple threshold-based alert tasks, the gateway can handle detection locally. For more complex tasks—such as pattern recognition and fault prediction—the gateway encrypts the sensitive data using the TFHE homomorphic encryption scheme and uploads the ciphertext to the public cloud for encrypted deep analysis.

Moreover, in multi-substation or cross-regional grid monitoring scenarios, each intelligent gateway encrypts its locally collected data using the Paillier scheme before uploading it to the cloud. The cloud server then performs homomorphic addition over the aggregated ciphertexts and conducts statistical analysis across multiple sources to support global model optimization.

3.2. Threat Model

The privacy protection issue addressed in this paper is the risk of data leakage during the outsourcing of anomaly detection services to cloud servers. In the proposed threat model, the system comprises three components: power equipment, local intelligent gateways, and public cloud servers. The public cloud server is assumed to follow a semi-honest model, meaning that it executes tasks strictly according to predefined protocols but may attempt to infer additional private information during the anomaly detection process. This is a widely adopted assumption in homomorphic encryption-based systems, especially in cloud computing scenarios [8]. In contrast, the power equipment and local intelligent gateways are considered secure, with no risk of internal data leakage, as the power equipment is managed by power operators, and the local intelligent gateways are also deployed and maintained by the operators themselves.

Within this framework, the threat model identifies three potential security risks:

• Malicious inference or data leakage by the public cloud server: the public cloud server can correctly follow the predefined algorithms and protocols and execute tasks in an orderly manner. However, during execution, it may attempt to learn and extract additional information about user data and the trained anomaly detection model.
• Parameter inference by power equipment users: in scenarios where the cloud provides a trained model and the equipment uploads data for anomaly detection, the equipment strictly adheres to predefined protocols and executes tasks in an orderly manner. However, during execution, users may attempt to infer or recover model parameters or other sensitive information provided by the cloud.
• External attackers’ malicious data theft: at any stage of the system model, external attackers may attempt to steal or compromise private data through malicious attacks.

3.3. Design Objectives

Based on the system model and threat model, the design objectives focus on two key aspects: security and efficiency.

Security: since the public cloud server in the system model operates under a semi-honest assumption, it is essential to ensure that data is not transmitted in plaintext to prevent potential interception by attackers. Additionally, it is necessary to prevent the cloud server from accessing the original device data and anomaly detection results during the entire processing procedure, thereby effectively safeguarding user privacy.

Efficiency: given the limited computational and communication capabilities of power devices, and the inability of edge computing centers to handle overly complex computations or encryption tasks, the system should minimize the computational and communication burden on these components during the anomaly detection process. On the one hand, the encryption algorithm used by edge nodes should have low computational complexity to ensure efficient data encryption without causing performance bottlenecks. On the other hand, the system should allow user devices to remain offline after uploading data, without participating in the computation of anomaly detection results, and only receive the final results once detection is complete.

4. Proposed Privacy-Preserving Anomaly Detection Method

4.1. Data Localization for Anomaly Detection

In the context of smart grids, the system must continuously monitor the operational status of power equipment to prevent faults and anomalies. Current solutions primarily rely on cloud servers for anomaly detection. However, this approach presents several issues:

• Data privacy and security: uploading and storing large amounts of plaintext data on cloud servers poses a risk of user privacy leakage.
• Network resource waste: transmitting vast amounts of redundant and invalid data consumes limited network resources.
• Real-time detection requirement: some sensor data in smart grids demand real-time anomaly detection to swiftly identify anomalies and promptly issue warnings and decisions.

To address the need for efficient and timely anomaly detection, this paper proposes an edge computing-based approach for handling small-scale or latency-sensitive detection tasks by offloading them to terminal devices. As illustrated in Figure 1, operational data are collected by power equipment via sensors and transmitted to corresponding local intelligent gateways for processing. Given that intelligent gateways possess higher computational capabilities compared to the equipment itself, an AutoEncoder-based anomaly detection method is employed at the gateway level to perform low-latency and resource-efficient preliminary screening. The specific process of the AutoEncoder is as follows:

• Let the dimensionality of the power data be $d$, and each input sample be represented as a vector $x\in {\mathbb{R}}^d$. To enhance the training performance and stability of the model, all input features are first normalized:

  $$x^{\prime }={\displaystyle \frac{x-\mu }{\sigma }},$$

  (1)

  where $\mu$ and $\sigma$ represent the mean and standard deviation of each feature dimension, respectively.
• A symmetric AutoEncoder network is constructed, consisting of an encoder $f_{\theta }$ and a decoder $g_{\varphi }$, with the objective of minimizing the reconstruction error between the input and the reconstructed data:

  $$\widehat{x}=g_{\varphi }\left(f_{\theta }\right(x^{\prime }\left)\right)$$

  (2)
• The mean squared error (MSE) is used as the loss function, and the training objective is defined as:

  $$L\left(\theta ,\varphi \right)={\displaystyle \frac{1}{n}}\sum _{i=1}^n{‖x^{\left(i\right)}{-\widehat{x}}^{\left(i\right)}‖}^2$$

  (3)
• During the inference phase, the trained model is used to reconstruct new input samples, and their reconstruction errors are computed as:

  $$e_i={‖x^{\left(i\right)}-{\widehat{x}}^{\left(i\right)}‖}_2^2$$

  (4)
• The reconstruction errors of all samples are collected, and a threshold $\tau$ is set:

  $$Anomaly if e_i>\tau$$
• Finally, labels are assigned: if the reconstruction error of a sample exceeds the predefined threshold $t$, the sample is classified as anomalous.

Through this anomaly detection method, this paper achieves the localized processing of power equipment data. By leveraging edge computing devices, small, simple, or real-time tasks can be completed, overcoming the latency issues caused by data transmission to the cloud and the limitations of the power equipment’s insufficient computing power. Additionally, the lightweight anomaly detection algorithm, such as the fuzzy AutoEncoder algorithm, is selected to meet the requirements of routine monitoring tasks in the smart grid.

At the same time, the overhead of the edge computing–public cloud framework is analyzed in comparison with direct data upload to the public cloud. Using time as the standard, the computational overhead $t_{e-c}$ of this framework is:

$$t_{e-c}=max\{t_e,t_c\}$$

(5)

where $t_e$ and $t_c$ represent the data processing time at the edge computing node and the public cloud, respectively. Clearly, $t_{e-c}$ is less than the processing time for direct data upload to the cloud server. Similarly, in terms of communication overhead, the data uploaded to the public cloud server is reduced after filtering through the edge computing node, compared to the direct upload model.

4.2. Encrypted Data Aggregation Task

This section corresponds to Scenario 2 in Figure 1, which depicts the process wherein multiple intelligent gateways encrypt locally collected data and upload it to the public cloud for secure aggregation and analysis. To address the task of cross-regional data aggregation among multiple gateways, this paper adopts a partially homomorphic encryption (PHE) approach. Such tasks are typically characterized by low computational complexity but high data sensitivity, often involving statistical analysis of critical indicators such as regional electricity consumption and power load. To achieve a balance between data privacy and computational efficiency, the Paillier additive homomorphic encryption scheme is employed to encrypt the data collected by local gateways. The Paillier scheme inherently supports additive operations over ciphertexts, enabling the cloud server to perform summation and aggregation directly on encrypted data without requiring decryption. This mechanism facilitates collaborative processing and global analysis of multi-source data while preserving the privacy of each gateway’s local dataset, thereby laying a solid foundation for subsequent operations such as load scheduling and anomaly detection. Figure 2 illustrates the encrypted data aggregation workflow based on the Paillier encryption scheme.

This section presents the Paillier scheme adopted in this paper.

• Key generation: select two large prime numbers $p$ and $q$ such that $\gcd \left(pq,\left(p-1\right)\left(q-1\right)\right)=1$, and compute:

  $$n=p·q, \lambda =lcm(p-1,q-1)$$

  (6)

  where $lcm\left(\right)$ denotes the least common multiple, i.e., the smallest positive integer divisible by both $p-1$ and $q-1$.
  chose $g\in {\mathbb{Z}}_{n^2}^{*}$ such that:

  $$L\left(g^{\lambda }mod n^2\right), \mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e} L\left(u\right)={\displaystyle \frac{u-1}{n}}$$

  (7)

  compute:

  $$\mu ={\left[L\right(g^{\lambda }mod n^2\left)\right]}^{-1}mod n$$

  (8)
  The public key is $(n,g)$, and the private key is $(\lambda ,\mu )$.
• Encryption: to encrypt a message $m \in {\mathbb{Z}}_n$, select a random $r\in {\mathbb{Z}}_n^{*}$, then compute the ciphertext:

  $$c=g^m·r^{n}mod n^2$$

  (9)
  This ensures semantic security due to the randomization introduced by $r$.
• Decryption: given a ciphertext $c\in {\mathbb{Z}}_{n^2}$, compute:

  $$m={\displaystyle \frac{L(c^{\lambda }mod n^2)}{n}}mod n, \mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e} L\left(u\right)={\displaystyle \frac{u-1}{n}}$$

  (10)
• Homomorphic addition of two ciphertexts:

  $$Enc\left(m_1\right)·\mathrm{E}\mathrm{n}\mathrm{c}\left(m_2\right)\mathrm{m}\mathrm{o}\mathrm{d}{n}^2=Enc(m_1+m_{2}mod n)$$

  (11)

4.3. Data Encryption Privacy Protection

For tasks that are both complex and privacy-sensitive, this paper delegates the processing to an anomaly detection model deployed on the public cloud server. To prevent data leakage during transmission and to ensure that encrypted data remains usable for anomaly detection, the proposed framework adopts the TFHE fully homomorphic encryption scheme [23]. This approach not only ensures that plaintext data is never exposed during transmission, but also enables the cloud server to perform anomaly detection computations directly in the encrypted domain. Specifically, the power equipment transmits raw data to the edge aggregation node, where the data is encrypted using the TFHE scheme. The encrypted data is then uploaded to the public cloud for further analysis.

This paper elaborates on the TFHE (fully homomorphic encryption over the torus) algorithm used in the study. Let $R$ denote the real numbers, $Z$ the set of integers, and the real number torus $\mathbb{T}=\mathbb{R}/\mathbb{Z}=\mathbb{R}\mathrm{m}\mathrm{o}\mathrm{d}1$. Let $B$ represent the set $\left\{\mathrm{0,1}\right\}$, and ${\mathbb{Z}}_N\left[X\right]$ denote the polynomial ring. $k$ represents a positive integer greater than or equal to 0.

• Key generation: the user generates a secret vector $s\in {\mathbb{B}}^k$ as the key, where $k$ represents the length of the key.
• Data encryption: first, sample a noise value $e\in {\mathbb{Z}}_N$ from a Gaussian distribution with mean 0 and standard deviation $\sigma ={\mathbb{R}}^{+}$, and add it to the plaintext $m$ to obtain an intermediate value $b=m+e$. Then, sample a random vector $a\in {\mathbb{Z}}_N^k$ and compute the dot product with the secret vector s. Finally, add the intermediate value to the dot product to obtain the final result: $b=a\cdot s+m+e$. The ciphertext $c=(a,b)$ is the output.
• Data decryption: for the ciphertext $c=(a,b)$, compute the dot product of the secret vector $s$ and $a$ to obtain $⟨a\cdot s⟩$. Then, calculate $x=b-⟨a\cdot s⟩$, which results in the decrypted value with noise. Finally, determine the output based on the sign of $x$: if $x>0$, output 1; if $x<0$, output 0. This gives the decryption result for a single-bit data.
• Homomorphic analysis: two ciphertexts, $c_1=(a_1,b_1)$ and $c_2=(a_2,b_2)$, can be processed through logic gates. In addition to negation and the Max gate, the TFHE algorithm supports homomorphic computations for ten different binary logic gates.

4.4. Data Transformation for TFHE Encryption

For the aforementioned TFHE homomorphic encryption scheme, the uploaded data must be preprocessed. This is because the TFHE homomorphic encryption algorithm is a fully homomorphic encryption public-key cryptographic scheme based on the learning with errors (LWE) problem. It provides a Boolean data encryption FHE scheme, meaning that it encrypts single-bit data into a single ciphertext, with a plaintext space of {0,1}. However, the acquired power grid data is typically floating-point time-series data. Therefore, it needs to be transformed to be mapped into the plaintext space of the addition-based encryption algorithm.

Here, this paper proposes using the IEEE 754 standard [24] for data processing. The IEEE 754 standard provides a method for converting floating-point numbers into binary encoding. Let the floating-point data to be processed be $c$, and its corresponding IEEE 754 standard encoding be $F$. It occupies a 32-bit field (expandable to 64-bit), with different fields representing different meanings. The 0th field, denoted as $S$, is the sign bit. A value of 0 indicates a positive number, while a value of one indicates a negative number. The first to eighth fields, denoted as $E$, represent the exponent, where the stored value is 127 greater than the actual exponent. The 9th to 31st fields, denoted as $M$, represent the mantissa, which stores the fractional part of the number, excluding the leading one in the normalized representation. $F$ can be expressed as:

$$F=(-1{)}^S\times 2^{E-127}\times (1+M)$$

(12)

4.5. Encrypted Anomaly Detection Model

As illustrated in Figure 1, in scenarios requiring complex tasks or deep anomaly detection, data is first generated at the device end and transmitted to the edge node for preprocessing. The edge node employs an adaptive dynamic encryption strategy, dynamically selecting the encryption method based on data sensitivity and task complexity. For lightweight tasks, partially homomorphic encryption (PHE) is used for fast processing. For deep anomaly detection tasks, TFHE fully homomorphic encryption (FHE) is applied. After encryption, the processed data is uploaded to the cloud for further analysis.

In the cloud, this paper proposes an improved Isolation Forest anomaly detection model. Isolation Forest is an unsupervised anomaly detection method based on decision trees, which trains and predicts anomalies by constructing multiple isolation trees. The core idea of Isolation Forest is to randomly select features and split points within their value ranges to iteratively partition the dataset into smaller subsets. Since anomalous data points are typically more distant from normal data points in the feature space, they tend to be isolated earlier in the tree structure, resulting in shorter path lengths. By computing the path length of each data point within the isolation trees, Isolation Forest can effectively identify outliers that significantly differ from the majority of the dataset.

The key aspect of this model lies in constructing TFHE homomorphic ciphertext operations and a bootstrap-based tree network for encrypted decision-making. This paper employs a quantization approach in the construction process. Before anomaly detection, input data is preprocessed and converted into binary encoding. The decision threshold also needs to be quantized, following the quantization formula given in Equation (13).

$$processWeight(\omega ,\theta )=\theta \cdot ⌊{\displaystyle \frac{\omega }{\theta }}⌋$$

(13)

In Equation (13), $\omega$ denotes the original real-valued weight to be quantized, and $\theta$ represents the quantization step size. The quantization function discretizes $\omega$ into uniformly spaced levels separated by $\theta$. The floor operation maps the input value to the nearest lower quantized level, and multiplying by $\theta$ restores the quantized result back to the original scale. This ensures that the weight values are compatible with integer-based encrypted computation while preserving approximate numerical meaning.

The purpose of quantizing the above parameters is to ensure compatibility with fully homomorphic ciphertext operations. Encoding data in binary format effectively controls the ciphertext space, while the quantization process improves anomaly detection efficiency at the cost of a slight loss in precision.

Moreover, since the TFHE computing environment does not support control flow and the Paillier homomorphic encryption algorithm only supports additive homomorphism, the traditional tree traversal logic of Isolation Forest cannot be directly applied to ciphertext data. To address this, the tree traversal process is transformed into tensor operations. By leveraging matrix operations, the node selection and leaf node classification are represented as matrix computations, enabling the tree structure to be executed efficiently through matrix operations rather than explicit traversal. Specifically, each decision node did_idi in an isolation tree can be represented as a binary comparison matrix $M_i$, where the input ciphertext vector $\mathrm{x}$ is compared against a quantized threshold ${\sigma }_i$, The comparison logic is implemented using homomorphic logical gates such as MUX or NAND under the TFHE scheme. The decision path from root to leaf is encoded as a sequence of such binary operations, which can be evaluated in parallel across trees using matrix multiplications and logical conjunctions. This transformation eliminates the need for control flow by converting branching logic into a linear algebraic format compatible with ciphertext computation.

The improved Isolation Forest algorithm follows these steps:

• Random feature and split point generation: the cloud server generates multiple Isolation Trees with predefined features and split points, which are then distributed to edge nodes. The edge nodes preprocess and encrypt local data based on the selected encryption scheme before uploading the ciphertext to the cloud.
• Constructing the hybrid ciphertext trees: for TFHE-encrypted data, it utilizes gate bootstrapping techniques to refresh noise and perform logical operations. For Paillier-encrypted data, the path length is directly accumulated through homomorphic addition.
• Computing path length and identifying anomalies: the isolation path length of each data point is determined by averaging its path lengths across all Isolation Trees. For a given data point $x$, its average path length $h\left(x\right)$ can be computed using Equation (9):

  $$h(x)={\displaystyle \frac{1}{T}}\sum _{t=1}^T h_t(x)$$

  (14)

Here, $h\left(x\right)$ represents the path length of data point $x$ in the t-th Isolation Tree, and $T$ denotes the total number of trees.

The Isolation Forest algorithm uses the average path length of a data point to determine whether it is anomalous. Normal points typically require longer paths to be isolated, while anomalous points are isolated earlier due to their distinctive features. The anomaly score can be calculated using Equation (10):

$$s(x)=2^{-{\displaystyle \frac{h\left(x\right)}{c\left(n\right)}}}$$

(15)

where $c\left(n\right)$ is a constant used to normalize the path length, which can be calculated using Equation (16):

$$c(n)={\displaystyle \frac{2(n-1)}{n}}$$

(16)

Here, $n$ is the number of samples in the dataset.

To further clarify the operational logic of the proposed encrypted Isolation Forest under the TFHE scheme, we summarize the complete anomaly detection process in Algorithm 1.

Algorithm 1. Encrypted Isolation Forest for TFHE

Input: Preprocessed and quantized binary feature set $X$, number of trees $T$, subsample size $\psi$ Output: Anomaly scores $S$ for each input data point For $t=1 to T$: Randomly sample a subset $X_t\subset X$, size $\psi$ Randomly select a feature $f$ and split value $s$ Build a binary decision node with condition $x_f<s$ Repeat recursively to build a tree until max depth or node size = 1 end for Quantize all split values sss using Equation (13) Encrypt binary-encoded data $X$ using TFHE scheme For each encrypted sample $x\in X$: Traverse all $T$ trees in parallel using matrix logic evaluation Compute encrypted path length $h\left(x\right)$ Use Equations (15) and (16) to calculate anomaly score $S\left(x\right)$ end for Return anomaly score list $S$

While the adoption of TFHE introduces additional computational overhead—particularly due to the use of bootstrapping operations—we emphasize that such costs are acceptable within our targeted application scenarios. Specifically, encrypted anomaly detection is performed on the cloud side, where computational resources are scalable and not subject to strict real-time constraints. Moreover, we adopt a quantized model and binary preprocessing to reduce ciphertext size and minimize the number of gate-level operations. Compared to prior fully homomorphic schemes, our method offers a favorable trade-off between privacy preservation and efficiency.

5. Experiments and Analysis

The experimental setup consists of an Intel(R) Core(TM) i7-12700 CPU @ 2.90 GHz with 32 GB of RAM, manufactured by Intel Corporation (Santa Clara, CA, USA). The TFHE library, developed in C++, is used for encrypting the dataset and performing homomorphic computations. In the experiments, several commonly used datasets are selected, as detailed in

Table 2. The information of datasets.

Dataset	Total Samples	Anomaly Ratio	Original Features	Processed Features
Annthyroid [25]	7200	534 (7.4%)	6	4
ForestCover [26]	286,048	2747 (0.9%)	10	6
Shuttle [27]	49,097	3511 (7%)	9	8

. The accuracy of the proposed model is verified by comparing the anomaly detection performance on plaintext data with that on ciphertext data. For the Isolation Forest anomaly detection, the same parameters $t$ and $\psi$ are applied to both the plaintext and ciphertext datasets:

• $t=100$: number of isolation trees;
• $\psi =256$: number of subsampled data points per tree.

5.1. Experimental Data Preprocessing

Based on the proposed improved Isolation Forest anomaly detection model, which integrates PHE and TFHE encryption mechanisms, encrypted preprocessed data must be uploaded during the anomaly detection phase. In this experiment, the data preprocessing procedure is designed as follows:

• Feature selection: a statistical analysis is performed on the power grid dataset to filter out features that follow a normal distribution and exhibit strong discriminative properties. These selected features enhance the model’s sensitivity to anomalies while reducing computational redundancy caused by irrelevant features during homomorphic encryption.
• Dimensionality reduction: Principal Component Analysis (PCA) is applied to reduce the dimensionality of the dataset. This step helps to preserve essential information from the original data while removing noise and redundant features, thereby preventing potential leakage of sensitive attributes.
• Binary transformation: as described in Section 4.4, all floating-point data are converted into binary representations following the IEEE 754 standard.

The processed feature set is presented in Table 2. For model training and evaluation, the dataset is divided into training, validation, and test sets, with proportions of 65%, 15%, and 20%, respectively. To ensure that the proportion of normal and anomalous samples remains consistent across all subsets, stratified sampling is used for data partitioning.

5.2. Evaluation Metrics

Since the proposed model is based on the Isolation Forest algorithm for encrypted anomaly detection, it is compared with the plaintext Isolation Forest, as well as state-of-the-art encrypted anomaly detection models. Specifically, we compare our method with two existing encrypted anomaly detection algorithms: BGV-FCM proposed by Alabdulatif et al. [28], and CKKS-KNN proposed by Behera et al. [29]. By conducting these comparisons, we aim to evaluate the effectiveness of our model in detecting anomalies while ensuring data privacy. The primary goal of this experiment is to demonstrate that our model achieves detection performance comparable to the plaintext Isolation Forest while improving efficiency and accuracy in identifying anomalies. That is, our model should enable efficient and privacy-preserving anomaly detection without compromising detection effectiveness.

To assess the performance of different methods, we utilize two key evaluation metrics: accuracy and ROC-AUC (area under the ROC curve). Accuracy measures the correctness of anomaly detection and is computed using Equation (17):

$$\mathrm{A}\mathrm{c}\mathrm{c}\mathrm{u}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{y}={\displaystyle \frac{TP+TN}{TP+FP+TN+FN}}$$

(17)

ROC-AUC represents the area under the ROC curve, which is determined by two parameters: true-positive rate (TPR) and false-positive rate (FPR). These parameters define the shape and size of the ROC curve and are computed using Equation (18):

$$TPR={\displaystyle \frac{TP}{TP+FN}}, FPR={\displaystyle \frac{FP}{FP+TN}}$$

(18)

Here, TP (true-positive) represents correctly identified anomalies, FP (false-positive) represents normal instances incorrectly classified as anomalies, TN (true-negative) represents correctly identified normal instances, and FN (false-negative) represents anomalies incorrectly classified as normal. The ROC curve is plotted with FPR on the x-axis and TPR on the y-axis. ROC-AUC is particularly useful for evaluating the model’s performance across different classification thresholds. A higher AUC (closer to 1) indicates a more accurate anomaly detection model, while an AUC close to 0.5 suggests the model performs no better than random classification.

5.3. Result Analysis

The experiments first validated the correctness and effectiveness of the proposed model. As shown in

Table 3. Performance of accuracy for each model on different datasets.

Model	Annthyroid	ForestCover	Shuttle
Our model	0.8823	0.9811	0.9563
Iforest	0.8950	0.9950	0.9944
BGV-FCM	0.8563	0.9705	0.8859
CKKS-KNN	0.8430	0.9809	0.8963

, the model achieves high accuracy across the Annthyroid, ForestCover, and Shuttle datasets, with values of 0.8823, 0.9811, and 0.9563, respectively. Correspondingly,

Table 4. Performance of ROC-AUC for each model on different datasets.

Model	Annthyroid	ForestCover	Shuttle
Our model	0.8059	0.8510	0.9592
IForest	0.8216	0.9084	0.9974
BGV-FCM	0.6350	0.7543	0.6178
CKKS-KNN	0.7262	0.7597	0.8993

reports the ROC-AUC scores of 0.8059, 0.8510, and 0.9592 on the same datasets. On the Annthyroid dataset, the proposed method achieves a ROC-AUC of 0.8059, representing a 27.0% improvement over BGV-FCM (0.6350) and a 10.9% improvement over CKKS-KNN (0.7262). For the ForestCover dataset, our model improves the ROC-AUC by 12.8% compared to BGV-FCM and by 12.0% compared to CKKS-KNN. On the Shuttle dataset, the improvements reach 55.2% and 6.7% over BGV-FCM and CKKS-KNN, respectively. Figure 3, Figure 4 and Figure 5 illustrate the ROC curves for the evaluated methods. Compared with existing homomorphic encryption-based anomaly detection models such as BGV-FCM and CKKS-KNN, the proposed method consistently demonstrates superior performance in both accuracy and ROC-AUC, while achieving results comparable to those of the plaintext-based Isolation Forest model.

The neural network architecture proposed in this paper is designed to support efficient computation under TFHE ciphertext, thereby achieving anomaly detection performance comparable to plaintext models. Experimental results demonstrate that the proposed model consistently outperforms existing encrypted anomaly detection algorithms—such as BGV-FCM and CKKS-KNN—across all datasets, exhibiting superior detection accuracy and significant advantages in multiple performance metrics. These findings confirm that the model can achieve efficient and accurate anomaly detection while ensuring data privacy and security.

5.4. Detection Efficiency Evaluation

To further evaluate the practical applicability of the proposed model, we investigate its runtime efficiency compared with both plaintext and ciphertext-based anomaly detection schemes. In particular, we compare the average inference time per sample across three benchmark datasets: Annthyroid, ForestCover, and Shuttle. The runtime was measured on an Intel i7-12700 CPU with 32 GB RAM (manufactured by Intel Corporation, Santa Clara, CA, USA) using a consistent experimental setup. The results are shown in

Table 5. Comparison of average detection time per sample on different datasets.

Model	Annthyroid (ms/Sample)	ForestCover (ms/Sample)	Shuttle (ms/Sample)
IForest	6.5	6.8	5.9
BGV-FCM	45.2	57.1	49.8
CKKS-KNN	38.7	43.5	40.1
Our Model	17.5	21.0	18.3

.

While the proposed model incurs additional computational overhead due to ciphertext operations—particularly from TFHE’s bootstrapping process—several optimization strategies have been implemented to mitigate performance degradation. These include data quantization, matrix-based tree evaluation, and offloading of intensive computations to cloud servers with scalable resources. As a result, although the runtime increases by approximately 2.5× compared to plaintext models in our experiments, the proposed method still demonstrates significantly better efficiency than other homomorphic encryption-based schemes such as BGV-FCM and CKKS-KNN. Specifically, our method reduces the per-sample inference time by over 50% compared to these models, while achieving superior detection accuracy. This confirms that the proposed approach offers a practical trade-off between detection performance, computational efficiency, and privacy protection, making it well-suited for real-world smart grid applications.

6. Conclusions

To address the challenges of low detection speed, limited accuracy, and data privacy risks in smart grid anomaly detection, this paper proposes a hybrid homomorphic encryption model based on partial homomorphic encryption (PHE) and fully homomorphic encryption over the torus (TFHE) for ciphertext-based anomaly detection in an edge–cloud collaborative architecture. By leveraging the synergy between edge computing and public cloud computing, the proposed model enables lightweight tasks to be executed at edge devices, while offloading complex computations to the cloud, thereby significantly improving system responsiveness and detection efficiency. Experimental results demonstrate that the proposed model achieves anomaly detection performance comparable to plaintext-based models, while outperforming existing homomorphic encryption-based and traditional detection methods. Moreover, the model ensures accurate anomaly detection while maintaining strong data security and privacy guarantees.

Although this work primarily targets smart grid applications, the proposed edge–cloud collaborative framework and ciphertext-based anomaly detection model exhibit strong generalizability. Similar requirements—such as low-latency response, constrained edge-side computation, stringent privacy protection, and secure task offloading—are also prevalent in other domains, including unmanned aerial vehicle (UAV) networks, the industrial Internet of Things (IIoT), and smart healthcare systems. These scenarios represent promising directions for future research and adaptation of the proposed methodology.

Despite the promising results, this study has several limitations that warrant further investigation. First, the current encryption scheme is primarily evaluated on structured datasets with a focus on anomaly detection; its performance on unstructured or multimodal data (e.g., images, text) remains to be explored. Second, the computation overhead introduced by TFHE bootstrapping, while acceptable in our setting, may still pose challenges in large-scale or resource-constrained deployments. Third, while the current framework assumes a semi-honest threat model, more robust mechanisms will be needed to address fully malicious adversaries.

In future work, we plan to further optimize the encrypted inference pipeline, explore lightweight ciphertext representations to reduce latency, and investigate broader deployment scenarios such as real-time grid protection and collaborative encrypted learning across edge nodes.