Signal Processing to Characterize and Evaluate Nonlinear Acoustic Signals Applied to Underwater Communications
Abstract
1. Introduction
- The first study involves three methods of acoustic signal analysis for estimating the ToA: the threshold method, the power variation method (Pvar), and the cross-correlation method. For each of these methods, the accuracy and advantages relative to the Signal-to-Noise Ratio (SNR) for this type of modulation are evaluated.
- Once the ToA has been estimated, the amplitude of the received signals is evaluated through a comprehensive analysis using time-domain, frequency-domain, and cross-correlation signal processing techniques. For each of these techniques, relevant parameters, such as voltage, are extracted for the proposed modulations.
2. Methods for Estimation the Time of Arrival of Acoustic Signals
2.1. Threshold Method
2.2. Power Variation Method (Pvar)
2.2.1. Cumulative Power Variation ()
2.2.2. Saw Pvar ()
2.3. Cross-Correlation Method
3. Amplitude Analysis of the Received Signal
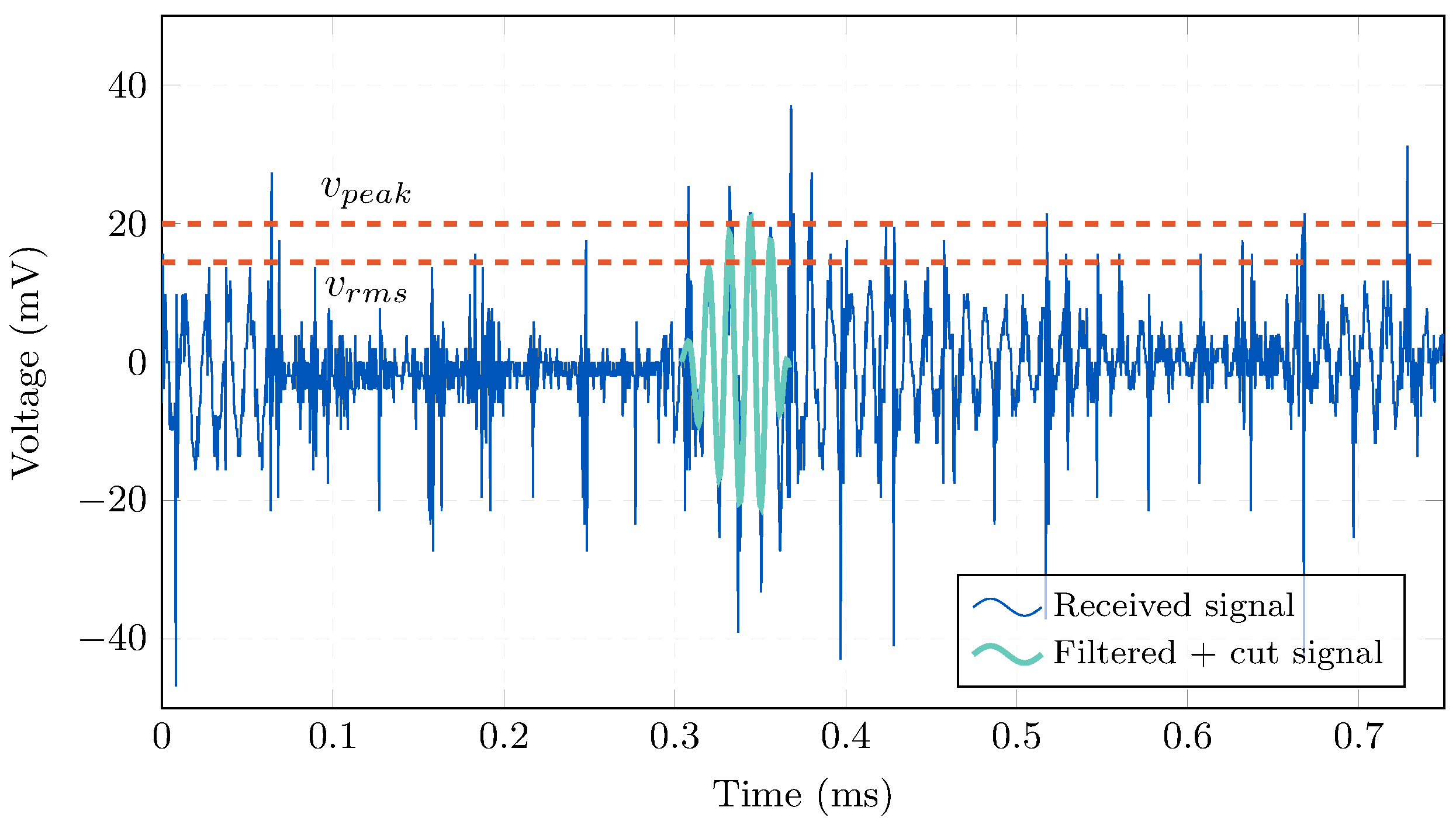
3.1. Time Parameterization
- To remove unwanted noise from the received signals, specifically filtering out frequency components outside the desired range.
- To analyze information across different frequency bands within the target frequency range.
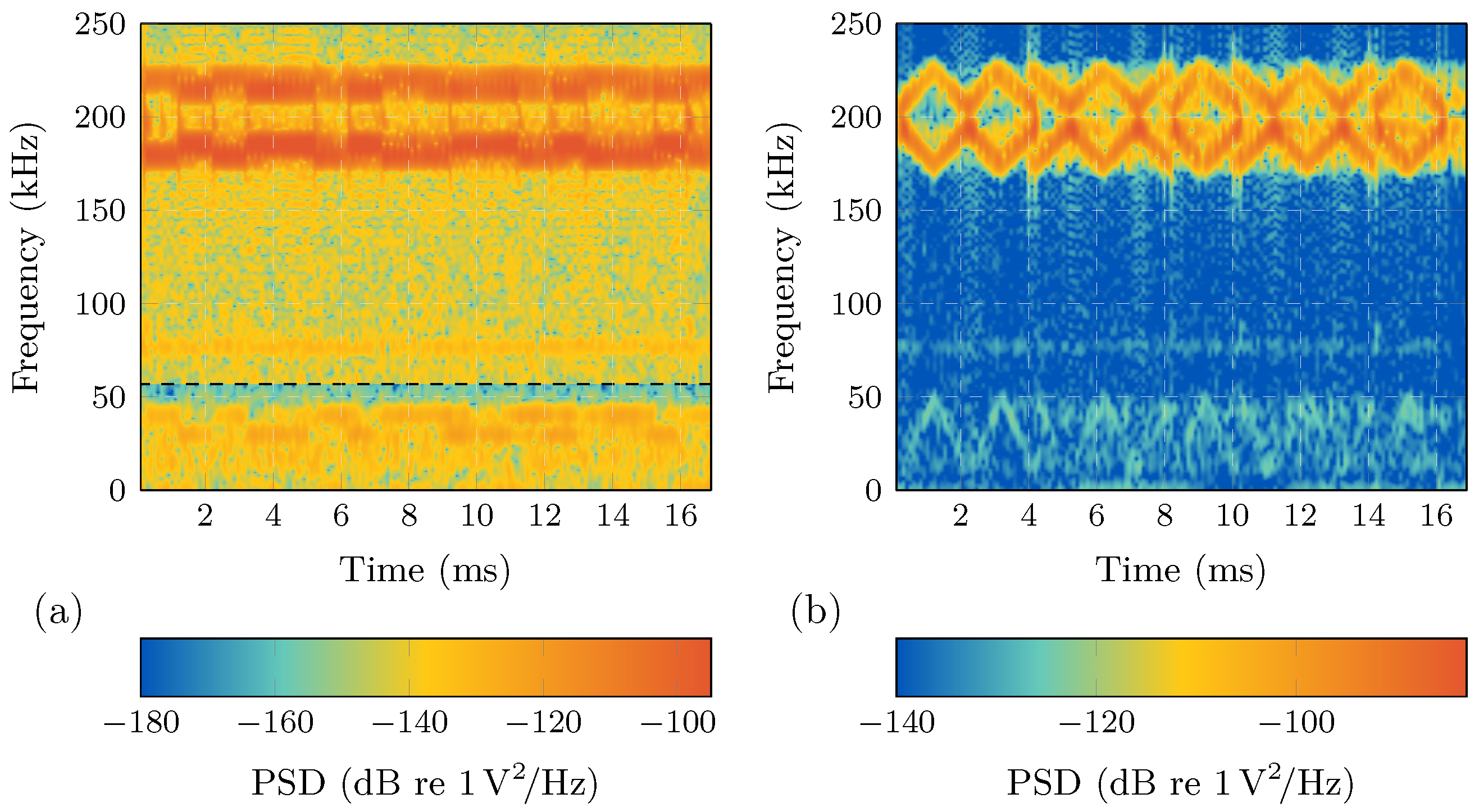
3.2. Frequency Parameterization
3.3. Cross-Correlation Parameterization
4. Experimental Set-Up
5. Analysis and Results of the Nonlinear Modulated Signals
5.1. Frequency-Shift Keying (FSK) Modulation
5.2. Sine-Sweep Modulation
5.3. Signal Processing for ToA Estimation
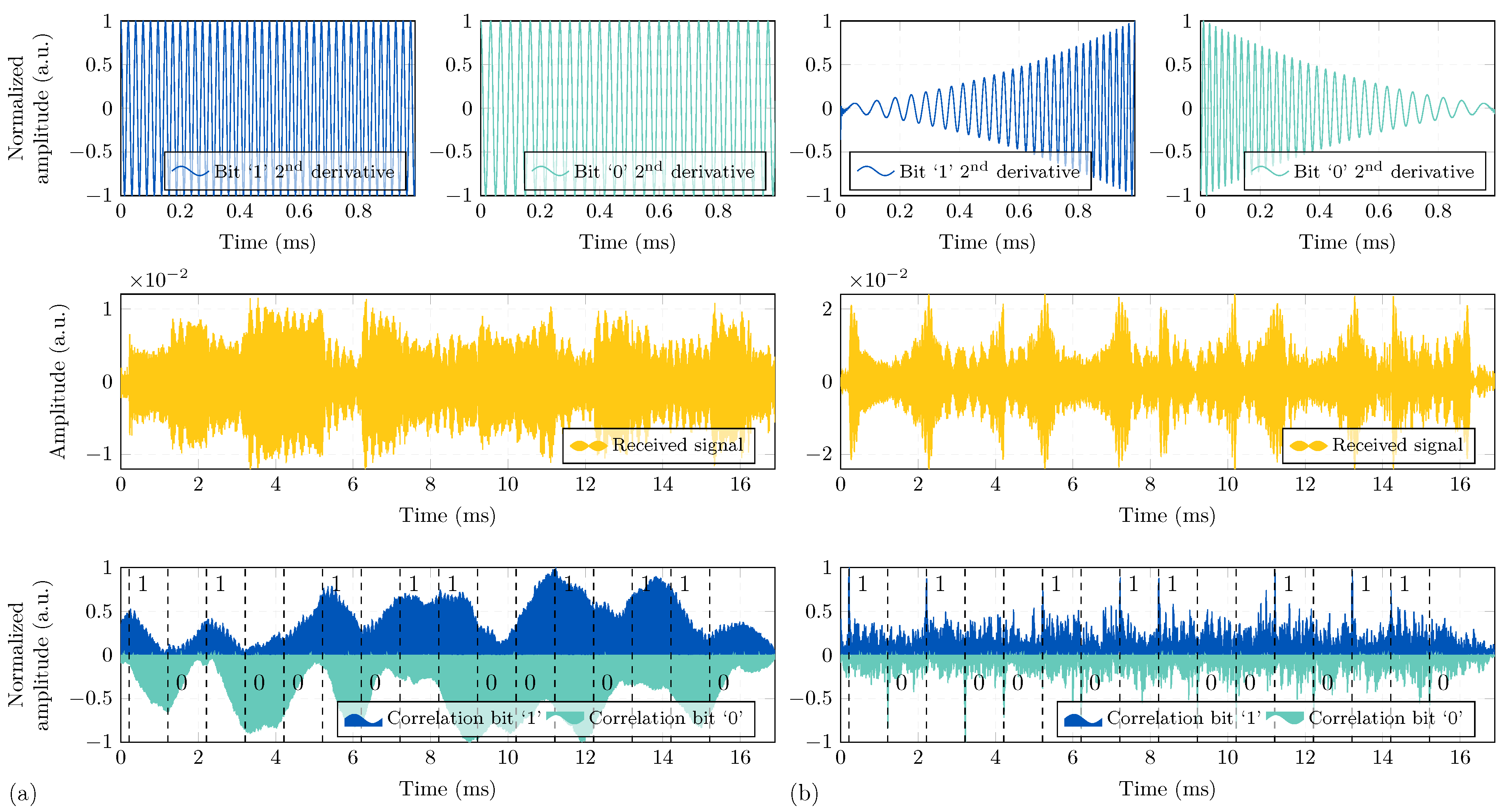
5.4. Amplitude Parameterization and Bit Detection of the Proposed Modulations
Bit Detection for Parametric Modulations: FSK and Sine-Sweep
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

Appendix B
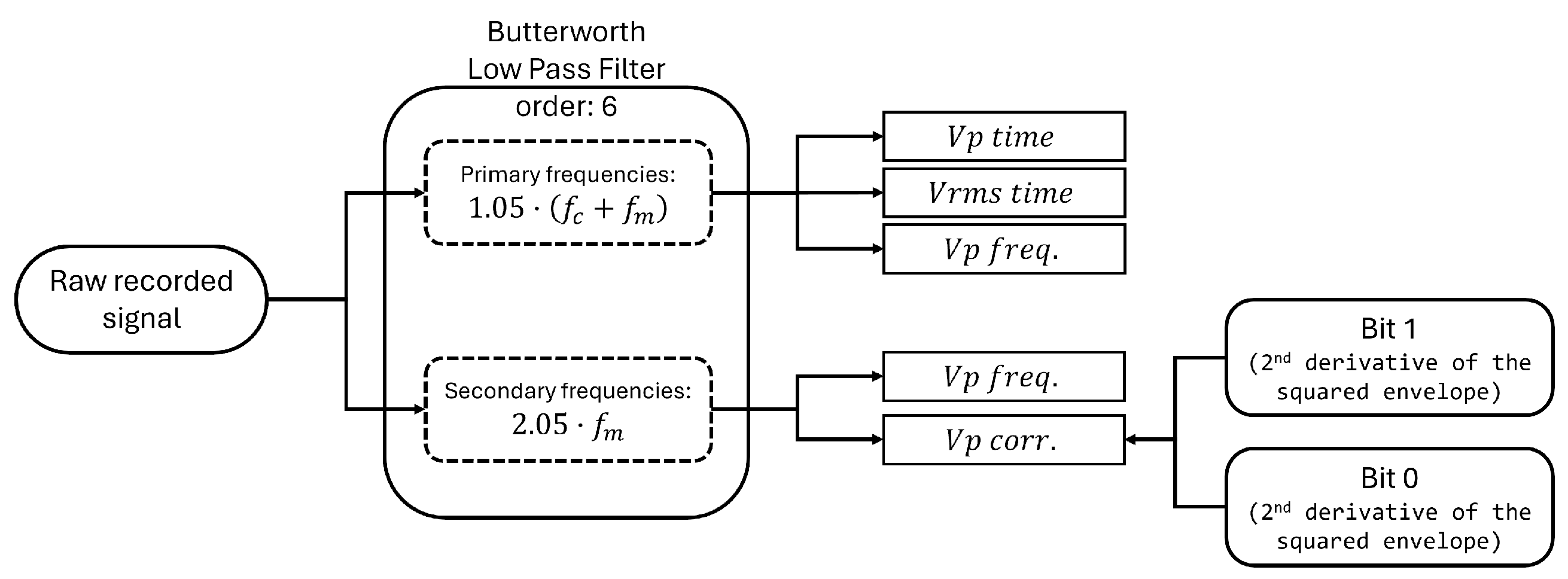
Appendix C
- Signal input: The function takes as input the raw signal, the , the duration of the evaluation window , and the power parameter n for the Pvar method. These inputs help define the scope and resolution of the ToA analysis.
- Pvar transform: The function computes the Pvar-transform of the signal, which is essentially the cumulative sum of the absolute value of the signal raised to the power n. This operation helps to smooth the signal and highlight key variations.
- Slope calculation: The function then fits linear segments (slopes) to portions of the transformed signal within the time window. These slopes represent the changes in signal intensity over time and are essential for detecting the ToA.
- Slope intersection and ToA estimation: Once the slopes are determined, the function calculates the intersection between them. This intersection corresponds to the estimated ToA, as it represents a significant change in the signal’s behavior, likely caused by the arrival of the transmitted signal.
- Noise simplification (optional): if enabled, the function includes a noise simplification step to handle noisy signals, improving the robustness of the ToA estimation in low SNR environments.
- Parallel processing: for large datasets, the function can utilize parallel processing (via the parforMode parameter) to speed up the Pvar-transform calculations, making the function scalable for more complex scenarios.
- Visualization: If required, the function can generate plots to visualize the signal, the Pvar-transform, and the detected ToA points. This feature can be enabled with the plotter parameter, helping to visually validate the accuracy of the ToA estimation.
References
- Lu, J.; Zhang, H.; Li, S.; Wu, P.; Huang, W. Enhancing Few-Shot Prediction of Ocean Sound Speed Profiles through Hierarchical Long Short-Term Memory Transfer Learning. J. Mar. Sci. Eng. 2024, 12, 1041. [Google Scholar] [CrossRef]
- Khan, M.S.; Petroni, A.; Biagi, M. Cooperative Communication Based Protocols for Underwater Wireless Sensors Networks: A Review. Sensors 2024, 24, 4248. [Google Scholar] [CrossRef] [PubMed]
- Janowski, Ł.; Wróblewski, R. Application and Evaluation of the AI-Powered Segment Anything Model (SAM) in Seafloor Mapping: A Case Study from Puck Lagoon, Poland. Remote Sens. 2024, 16, 2638. [Google Scholar] [CrossRef]
- Campo-Valera, M.; Asorey-Cacheda, R.; Rodríguez-Rodríguez, I.; Villó-Pérez, I. Characterization of a piezoelectric acoustic sensor fabricated for low-frequency applications: A comparative study of three methods. Sensors 2023, 23, 2742. [Google Scholar] [CrossRef]
- Tang, N.; Zeng, Q.; Luo, D.; Xu, Q.; Hu, H. Research on development and application of underwater acoustic communication system. J. Phys. Conf. Ser. Iop Publ. 2020, 1617, 012036. [Google Scholar] [CrossRef]
- Felis-Enguix, I.; Otero-Vega, J.; Campo-Valera, M.; Villó-Pérez, I.; Gómez-Tornero, J. Practical aspects of acoustic leaky-wave antennas applied to underwater direction finding. Eng. Proc. 2020, 2, 93. [Google Scholar] [CrossRef]
- Hwang, Y.; Ahn, H.; Nguyen, D.N.; Kim, W.; Moon, W. An underwater parametric array source transducer composed of PZT/thin-polymer composite. Sens. Actuators A Phys. 2018, 279, 601–616. [Google Scholar] [CrossRef]
- Bjørnø, L.; Neighbors, T.; Bradley, D. Applied Underwater Acoustics; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Murad, M.; Sheikh, A.A.; Manzoor, M.A.; Felemban, E.; Qaisar, S. A survey on current underwater acoustic sensor network applications. Int. J. Comput. Theory Eng. 2015, 7, 51. [Google Scholar] [CrossRef]
- Westervelt, P.J. Scattering of Sound by Sound. J. Acoust. Soc. Am. 1957, 29, 199–203. [Google Scholar] [CrossRef]
- Westervelt, P.J. Parametric Acoustic Array. J. Acoust. Soc. Am. 1963, 35, 535–537. [Google Scholar] [CrossRef]
- Berktay, H. Possible exploitation of non-linear acoustics in underwater transmitting applications. J. Sound Vib. 1965, 2, 435–461. [Google Scholar] [CrossRef]
- Berktay, H.; Leahy, D. Farfield performance of parametric transmitters. J. Acoust. Soc. Am. 1974, 55, 539–546. [Google Scholar] [CrossRef]
- Villó-Pérez, I.; Alcover-Garau, P.M.; Campo-Valera, M.; Toledo-Moreo, R. A novel 1D-FDTD scheme to solve the nonlinear second-order thermoviscous hydrodynamic model. Commun. Nonlinear Sci. Numer. Simul. 2022, 118, 107015. [Google Scholar] [CrossRef]
- Yu, S.; Liu, B.; Yu, K.; Yang, Z.; Kan, G.; Zong, L. Application of a parametric array over a mid-frequency band (4–10 kHz) –measurements of bottom backscattering strength. Ocean. Eng. 2023, 280, 114914. [Google Scholar] [CrossRef]
- Campo-Valera, M.; Felis-Enguix, I.; Villó-Pérez, I. Signal Processing for Parametric Acoustic Sources Applied to Underwater Communication. Sensors 2020, 20, 5878. [Google Scholar] [CrossRef] [PubMed]
- Campo-Valera, M.; Felis, I. Underwater acoustic communication for the marine environment’s monitoring. Proceedings 2019, 42, 51. [Google Scholar] [CrossRef]
- Campo-Valera, M.; Ardid, M.; Tortosa, D.D.; Felis, I.; Martínez-Mora, J.A.; Llorens, C.D.; Cervantes, P. Acoustic parametric signal generation for underwater communication. Sensors 2018, 18, 2149. [Google Scholar] [CrossRef]
- Campo Valera, M.M.; Felis Enguix, I. Propiedades y Aplicaciones del Efecto Paramétrico en Aire y Agua. IV Jornadas JAAS Acústica, Audio y Sonido 2018. Universidad Tres de Febrero, Buenos Aires, Argentina. 2018. Available online: https://www.jaas.untref.edu.ar/uploads/documents/IV_JAAS-Memorias.pdf (accessed on 23 October 2024).
- An, J.; Ra, H.; Youn, C.; Kim, K. Experimental results of underwater acoustic communication with nonlinear frequency modulation waveform. Sensors 2021, 21, 7194. [Google Scholar] [CrossRef]
- Zhou, H.; Huang, S.; Li, W. Parametric acoustic array and its application in underwater acoustic engineering. Sensors 2020, 20, 2148. [Google Scholar] [CrossRef]
- Cheng, Y.; Zhao, A.; Hui, J.; An, T.; Zhou, B. Parametric underwater transmission based on pattern time delay shift coding system. Math. Probl. Eng. 2018, 2018, 8249245. [Google Scholar] [CrossRef]
- Ardid, M.; Campo-Valera, M.D.; Tortosa, D.; Felis, I.; Llorens, C.D.; Martínez-Mora, J.A. Underwater communication using acoustic parametric arrays. Proceedings 2018, 2, 139. [Google Scholar] [CrossRef]
- Schneider von Deimling, J.; Held, P.; Feldens, P.; Wilken, D. Effects of using inclined parametric echosounding on sub-bottom acoustic imaging and advances in buried object detection. Geo-Mar. Lett. 2016, 36, 113–119. [Google Scholar] [CrossRef]
- Tan, H.P.; Diamant, R.; Seah, W.K.; Waldmeyer, M. A survey of techniques and challenges in underwater localization. Ocean. Eng. 2011, 38, 1663–1676. [Google Scholar] [CrossRef]
- Wang, C.; Zhu, G.; Tang, S.; Yin, J.; Guo, L.; Sheng, X.; Li, M. Directional bionic underwater communication method using a parametric acoustic array and recursive filtering. Appl. Acoust. 2022, 191, 108665. [Google Scholar] [CrossRef]
- Ortuño-Sáez, G.; Sánchez-Ricart, L. Aliasing Reduction with a 6th Order Space-Time Variational Formulation. Acta Acust. United Acust. 2016, 102, 1045–1060. [Google Scholar] [CrossRef]
- Serrano, E.P.; Fabio, M.; Figliola, A. Métodos tiempo-frecuencia basados en la transformada wavelet. Rev. Math. Teor. Apl. 2012, 19, 157–168. [Google Scholar] [CrossRef]
- Cervenka, P.; Alais, P. Fourier formalism for describing nonlinear self-demodulation of a primary narrow ultrasonic beam. J. Acoust. Soc. Am. 1990, 88, 473–481. [Google Scholar] [CrossRef]
- Diamant, R. Clustering approach for detection and time of arrival estimation of hydroacoustic signals. IEEE Sens. J. 2016, 16, 5308–5318. [Google Scholar] [CrossRef]
- Gezici, S. A Survey on Wireless Position Estimation. Wirel. Pers. Commun. 2007, 44, 263–282. [Google Scholar] [CrossRef]
- Chen, J.; Benesty, J.; Huang, Y. Time Delay Estimation in Room Acoustic Environments: An Overview. EURASIP J. Adv. Signal Process. 2006, 2006, 26503. [Google Scholar] [CrossRef]
- Ash, J.N.; Moses, R.L. Acoustic time delay estimation and sensor network self-localization: Experimental results. J. Acoust. Soc. Am. 2005, 118, 841–850. [Google Scholar] [CrossRef]
- McCrady, D.; Doyle, L.; Forstrom, H.; Dempsey, T.; Martorana, M. Mobile ranging using low-accuracy clocks. IEEE Trans. Microw. Theory Tech. 2000, 48, 951–958. [Google Scholar] [CrossRef]
- Pallas, M.A.; Jourdain, G. Active high resolution time delay estimation for large BT signals. IEEE Trans. Signal Process. 1991, 39, 781–788. [Google Scholar] [CrossRef]
- Cheng, L.; Liu, Y.; Zhang, B.; Hu, Z.; Zhu, H.; Luo, B. Direction of Arrival Joint Prediction of Underwater Acoustic Communication Signals Using Faster R-CNN and Frequency–Azimuth Spectrum. Remote Sens. 2024, 16, 2563. [Google Scholar] [CrossRef]
- Zhang, Y.; Huang, Y.; Tao, J.; Tang, S.; So, H.C.; Hong, W. A Two-Stage Multi-Layer Perceptron for High-Resolution DOA Estimation. IEEE Trans. Veh. Technol. 2024, 73, 9616–9631. [Google Scholar] [CrossRef]
- Feintuch, S.; Tabrikian, J.; Bilik, I.; Permuter, H. Neural-Network-Based DOA Estimation in the Presence of Non-Gaussian Interference. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 119–132. [Google Scholar] [CrossRef]
- Guo, Y.; Zhang, Z.; Huang, Y. Dual Class Token Vision Transformer for Direction of Arrival Estimation in Low SNR. IEEE Signal Process. Lett. 2024, 31, 76–80. [Google Scholar] [CrossRef]
- Papageorgiou, G.; Sellathurai, M.; Eldar, Y. Deep Networks for Direction-of-Arrival Estimation in Low SNR. IEEE Trans. Signal Process. 2021, 69, 3714–3729. [Google Scholar] [CrossRef]
- Zheng, S.; Yang, Z.; Shen, W.; Zhang, L.; Zhu, J.; Zhao, Z.; Yang, X. Deep Learning-Based DOA Estimation. IEEE Trans. Cogn. Commun. Netw. 2024, 10, 819–835. [Google Scholar] [CrossRef]
- Merkofer, J.P.; Revach, G.; Shlezinger, N.; Routtenberg, T.; van Sloun, R.J.G. DA-MUSIC: Data-Driven DoA Estimation via Deep Augmented MUSIC Algorithm. IEEE Trans. Veh. Technol. 2024, 73, 2771–2785. [Google Scholar] [CrossRef]
- Bell, C.J.; Adhikari, K.; Freeman, L.A. Convolutional Neural Network-Based Regression for Direction of Arrival Estimation. In Proceedings of the 2023 IEEE 14th Annual Ubiquitous Computing, Electronics & Mobile Communication Conference (UEMCON), New York, NY, USA, 12–14 October 2023; IEEE: Piscataway, NJ, USA, 2023; Volume I, pp. 0373–0379. [Google Scholar] [CrossRef]
- Campo-Valera, M.; Villó-Pérez, I.; Fernández-Garrido, A.; Rodríguez-Rodríguez, I.; Asorey-Cacheda, R. Exploring the Parametric Effect in Nonlinear Acoustic Waves. IEEE Access 2023, 11, 97221–97238. [Google Scholar] [CrossRef]
- Oppenheim, A.V.; Schafer, R.W. Tratamiento de señales en Tiempo Discreto; Prentice Hall: Old Tappan, NJ, USA, 2011. [Google Scholar]
- Youn, D.; Mathews, V. Adaptive realizations of the maximum likelihood processor for time delay estimation. IEEE Trans. Acoust. Speech Signal Process. 1984, 32, 938–940. [Google Scholar] [CrossRef]
- Knapp, C.; Carter, G. The generalized correlation method for estimation of time delay. IEEE Trans. Acoust. Speech Signal Process. 1976, 24, 320–327. [Google Scholar] [CrossRef]
- Cabot, R. A note on the application of the Hilbert transform to time delay estimation. IEEE Trans. Acoust. Speech Signal Process. 1981, 29, 607–609. [Google Scholar] [CrossRef]
- Choi, H.I.; Williams, W. Improved time-frequency representation of multicomponent signals using exponential kernels. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 862–871. [Google Scholar] [CrossRef]
- Serrano, E.G.F.; Cardona i Foix, S.; Nebot, L.J. Análisis en tiempo y frecuencia de señales de vibración tomadas al pie del carril durante el paso de un tren. Sci. Tech. 2007, 13, 243–247. [Google Scholar]
- Calleja, B.; del Río, L.; San Emeterio, J.L. Procesado digital de señales ultrasónicas para la determinación de constantes elásticas dinámicas en materiales rocosos. In Acustica 2008: V Congreso Ibérico de Acústica, XXXIX Congreso Español de Acústica TecniAcustica 2008, Acoustics European Symposium, ExpoAcustica 2008; Sociedad Española de Acústica (SEA): Coimbra, Portugal, 2008; pp. 1–12. [Google Scholar]
- Adrián-Martínez, S.; Bou-Cabo, M.; Felis, I.; Llorens, C.D.; Martínez-Mora, J.A.; Saldaña, M.; Ardid, M. Acoustic Signal Detection Through the Cross-Correlation Method in Experiments with Different Signal to Noise Ratio and Reverberation Conditions. In Ad-Hoc Networks and Wireless; Garcia Pineda, M., Lloret, J., Papavassiliou, S., Ruehrup, S., Westphall, C.B., Eds.; Springer: Berlin/Heidelberg, Germany, 2015; pp. 66–79. [Google Scholar] [CrossRef]
- Campo-Valera, M.; Rodríguez-Rodríguez, I.; Rodríguez, J.V.; Herrera-Fernández, L.J. Proof of Concept of the Use of the Parametric Effect in Two Media with Application to Underwater Acoustic Communications. Electronics 2023, 12, 3459. [Google Scholar] [CrossRef]
- Campo-Valera, M.; Diego-Tortosa, D.; Asorey-Cacheda, R.; Gómez-Tornero, J.; Herrera-Fernández, L. A Novel Modulation Approach Based on Nonlinear Acoustic Signals for Underwater Communications. In Proceedings of the 10th Convention of the European Acoustics Association Forum Acusticum 2023, Torino, Italy, 11–15 September 2023; European Acoustics Association: Torino, Italy, 2023; pp. 5065–5070. [Google Scholar] [CrossRef]
- Enflo, B.O.; Hedberg, C.M. Theory of Nonlinear Acoustics in Fluids, 2002nd ed.; Fluid Mechanics and Its Applications; Springer: New York, NY, USA, 2002. [Google Scholar]
- Tjo/tta, J.N.; Tjo/tta, S. Nonlinear equations of acoustics, with application to parametric acoustic arrays. J. Acoust. Soc. Am. 1981, 69, 1644–1652. [Google Scholar] [CrossRef]
- Kinsler, L.E.; Frey, A.R.; Coppens, A.B.; Sanders, J.V. Fundamentals of Acoustics, 4th ed.; John Wiley & Sons: Nashville, TN, USA, 1999. [Google Scholar]
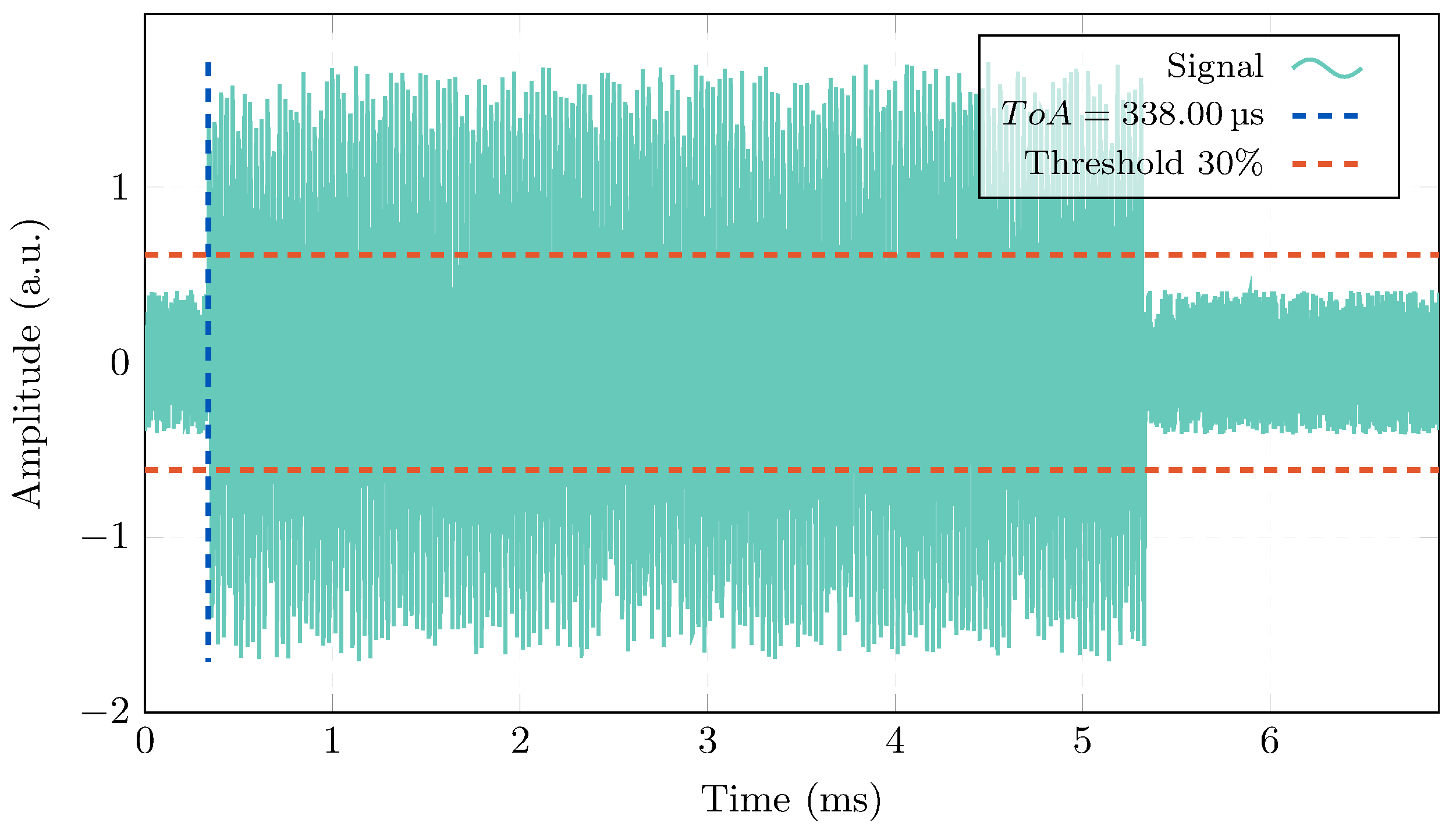

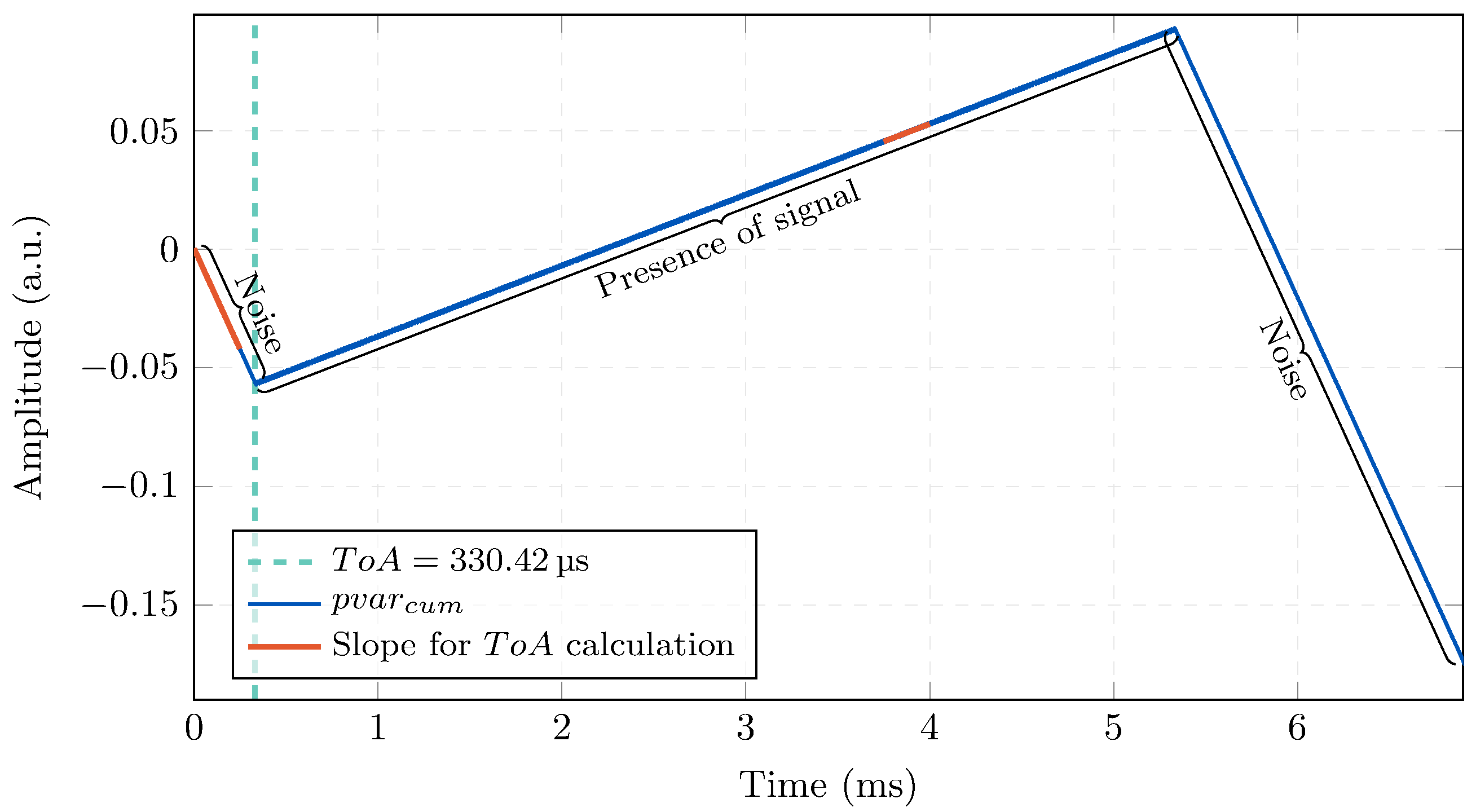
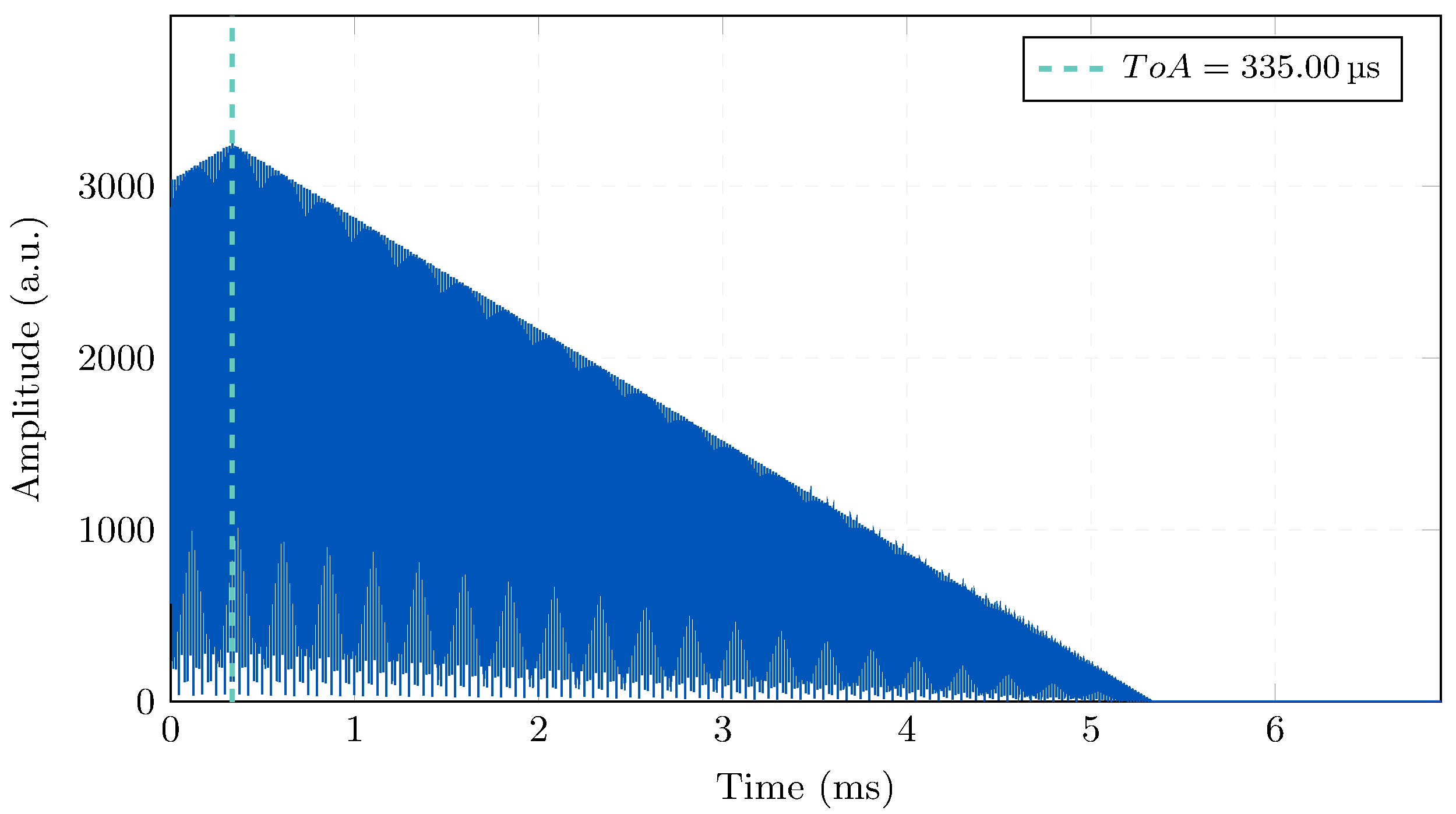





| ToA Estimation Methods | FSK Modulation | Sine-Sweep Modulation |
|---|---|---|
| Mean | Mean | |
| Threshold | (218.43 ) μs | (232.6 ) μs |
| (219.31 ) μs | (241.32 ) μs | |
| (219.31 ) μs | (241.43 ) μs | |
| Cross-correlation | (220.23 ) μs | (229.35 ) μs |
| Bit String | FSK Modulation | Sine-Sweep Modulation | ||||
|---|---|---|---|---|---|---|
| Bit ‘1’ (μV) | Bit ‘0’ (μV) | Diff Factor | Bit ‘1’ (μV) | Bit ‘0’ (μV) | Diff Factor | |
| 1 | 21.1 | 11.3 | 1.9 | 67.3 | 21.9 | 3.07 |
| 0 | 35.4 | 68.2 | 19.2 | 12.7 | 68.9 | 5.4 |
| 1 | 16.5 | 12.1 | 1.35 | 58.8 | 15.2 | 3.8 |
| 0 | 2.7 | 91.3 | 33.4 | 16.8 | 83.2 | 4.9 |
| 0 | 8.3 | 73.6 | 8.8 | 18.7 | 59.4 | 3.2 |
| 1 | 31.8 | 15.4 | 2.05 | 52.3 | 31.4 | 1.6 |
| 0 | 12.5 | 84.5 | 6.74 | 14.4 | 70.3 | 4.8 |
| 1 | 27.6 | 27.6 | 1.00 | 58.5 | 20.3 | 2.8 |
| 1 | 30.3 | 39.8 | 0.76 | 58.9 | 26.2 | 2.2 |
| 0 | 15.8 | 101.8 | 6.4 | 13.9 | 65.9 | 4.7 |
| 0 | 14.5 | 87.4 | 6.02 | 16.3 | 69.9 | 4.3 |
| 1 | 42.3 | 65.2 | 0.6 | 62.9 | 15.7 | 4.0 |
| 0 | 25.6 | 89.6 | 3.5 | 25.4 | 65.8 | 2.6 |
| 1 | 29.1 | 36.1 | 0.8 | 64.3 | 16.9 | 3.8 |
| 1 | 32.0 | 48.8 | 0.6 | 49.6 | 14.0 | 3.5 |
| 0 | 99.3 | 70.8 | 7.1 | 15.2 | 47.8 | 3.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Campo-Valera, M.; Diego-Tortosa, D.; Rodríguez-Rodríguez, I.; Useche-Ramírez, J.; Asorey-Cacheda, R. Signal Processing to Characterize and Evaluate Nonlinear Acoustic Signals Applied to Underwater Communications. Electronics 2024, 13, 4192. https://doi.org/10.3390/electronics13214192
Campo-Valera M, Diego-Tortosa D, Rodríguez-Rodríguez I, Useche-Ramírez J, Asorey-Cacheda R. Signal Processing to Characterize and Evaluate Nonlinear Acoustic Signals Applied to Underwater Communications. Electronics. 2024; 13(21):4192. https://doi.org/10.3390/electronics13214192
Chicago/Turabian StyleCampo-Valera, María, Dídac Diego-Tortosa, Ignacio Rodríguez-Rodríguez, Jorge Useche-Ramírez, and Rafael Asorey-Cacheda. 2024. "Signal Processing to Characterize and Evaluate Nonlinear Acoustic Signals Applied to Underwater Communications" Electronics 13, no. 21: 4192. https://doi.org/10.3390/electronics13214192
APA StyleCampo-Valera, M., Diego-Tortosa, D., Rodríguez-Rodríguez, I., Useche-Ramírez, J., & Asorey-Cacheda, R. (2024). Signal Processing to Characterize and Evaluate Nonlinear Acoustic Signals Applied to Underwater Communications. Electronics, 13(21), 4192. https://doi.org/10.3390/electronics13214192








