Abstract
Subgraph matching stands as a fundamental issue within the research realm of graph analysis. In this paper, we investigate a novel combinatorial problem that encompasses both multigraph matching and subgraph matching. The objective of this investigation is to identify all data graphs within a larger graph that are isomorphic to the given query graphs. Firstly, multiple query graphs are collaborated through the design of a categorical graph, which aggregates similar query graphs into a single cluster. Following this, these similarity-clustered query graphs are integrated into a unified categorical graph. Secondly, a minimal isomorphic data graph is derived from a larger data graph, guided by the categorical graph. Additionally, an analysis of the inclusive and equivalence relationships among query nodes is conducted, with the aim of minimizing redundant matching computations. Simultaneously, all subgraph isomorphic mappings of the categorical graph onto the data graph are performed. Extensive empirical evaluations, conducted on both real and synthetic datasets, demonstrate that the proposed methods surpass the state-of-the-art algorithms in performance.
1. Introduction
Subgraph matching has garnered considerable attention from a multitude of researchers across diverse fields, including question answering [1], semantic search [2], and community detection [3]. These challenges, which fall within the purview of multigraph matching and subgraph matching, have been pivotal in highlighting the significance and broad applicability of subgraph matching techniques. The problem of graph matching is defined as identifying node correspondences across two or more graphs, relying on affinity information between nodes, edges [4], or hyper-edges [5,6] within query graphs. Conversely, the problem of subgraph matching involves searching for all possible subgraphs within a data graph that are isomorphic to a given query graph. Building upon these two foundational problems, a combinatorial problem encompassing multigraph matching and subgraph matching, named as the multi-query graph matching problem, is examined. This study aims to formally define the multi-answer requirement in domains such as question answering [7,8], semantic search [9,10], and community detection [11,12].
The problem of graph matching can be categorized into two-graph matching and multigraph matching. Two-graph matching aims to determine the maximal similarity between two graphs and serves as a foundational basis for studying multigraph matching. In contrast, multigraph matching seeks to balance the local optimal similarity between individual graph pairs with the global similarity across the entire set of graphs. A widely recognized formal representation of two-graph matching is formulated as the quadratic assignment programming (QAP) problem, as introduced by Lawler [13]. QAP aims to obtain a minimized consistency cost function between the vertices and edges of query graphs, shown in Formula (1).
In Formula (1), a minimized consistency cost function J is derived from the query graphs and . The consistency of query graphs can be expressed by node-to-node and edge-to-edge correspondence. Herein, the permutation matrix denotes the node correspondence between graphs and , is a vector arranged by rows in matrix and the affinity matrix corresponds to the node-to-node and edge-to-edge affinity information to the diagonal elements and off-diagonal ones, respectively. Result is a quantified score of similarity between graphs and .
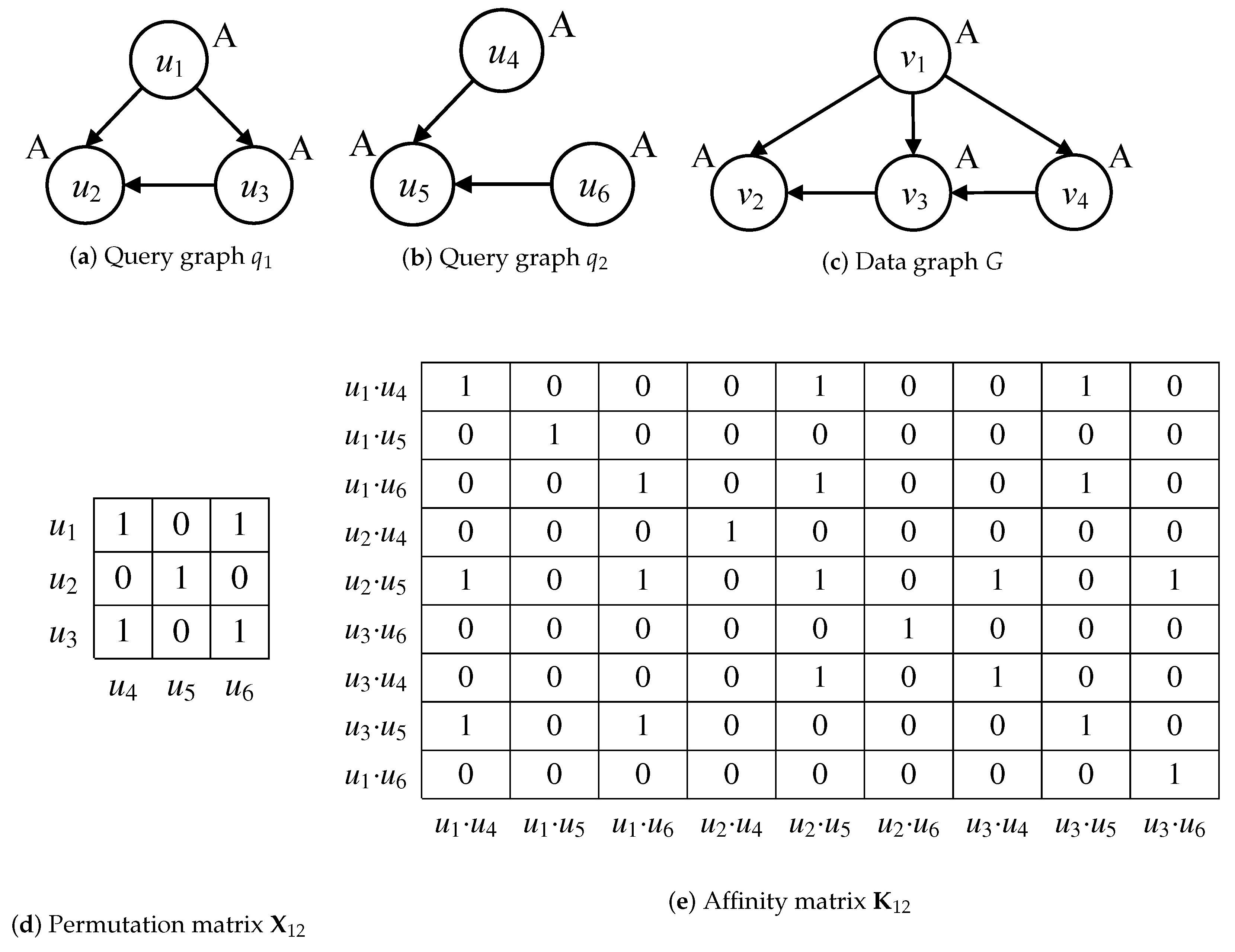
Considering the graphs and , the node correspondence and affinity information of node-to-node and edge-to-edge are shown as matrices in Figure 1d,e. The node correspondence denotes the label consistency of node and its neighbors. Regarding the query nodes in Figure 1a,b, the node correspondence is satisfied by and , because label A of and its out-edge neighbor correspond to the ones of and its out-edge neighbor or . The node correspondence is not satisfied by and , because it cannot find an out-edge of that corresponds to the one of . The node correspondence and non-correspondence are quantified as values 1 and 0 of the permutation matrix in Figure 1d. The affinity information is to verify the node-to-node and edge-to-edge correspondences in the quadratic assignment programming (QAP) problem. Assume that · and · satisfy the positive node-to-node correspondences of nodes , and nodes , in Figure 1e. If the edge-to-edge correspondence is satisfied by the verification of consistency between edges (, ) and (, ), then the value is set to 1 in affinity matrix . In Formula (1), the matching of graphs and is quantified as a result score = 11, which is used to specify the similarity between query graphs.
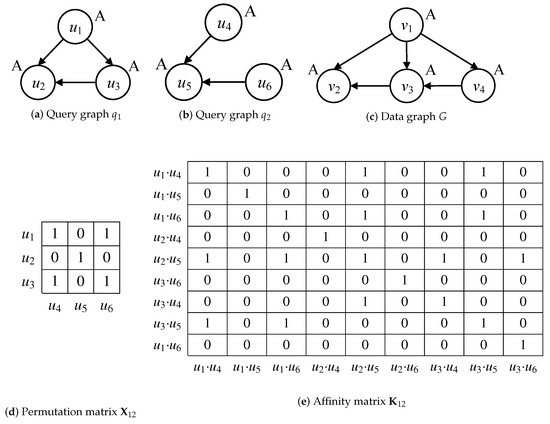
Figure 1.
Examples of graph matching, subgraph matching and multi-query graph matching.
Different from the quantization of graph matching, subgraph matching is defined as the problem of subgraph isomorphism, whose results are represented as the subgraph isomorphic mappings. Considering the directed query and data graphs in Figure 1a,c, is a subgraph isomorphic to G since there exists a subgraph isomorphic mapping M{⟨, ⟩, ⟨, ⟩, ⟨, ⟩}. The difference between subgraph matching and multi-query graph matching lies in the goal of solving the problem of subgraph isomorphism. The solution goal of subgraph matching only focuses on finding all possible subgraph isomorphic mappings of on G, such as the other one M{⟨, ⟩, ⟨, ⟩, ⟨, ⟩}. However, the solution goal of multi-query graph matching is to synchronously conduct the subgraph isomorphic mappings within a possible minimal cost of overlapped isomorphic computation over multi-query graphs on data graphs. Regarding query graphs and , satisfying that contains , then the subgraph isomorphic mappings M{⟨, ⟩, ⟨, ⟩, ⟨, ⟩} and M{⟨, ⟩, ⟨, ⟩, ⟨, ⟩} of are also the results of . Therefore, the problem of multi-query graph matching is more complicated, due to the involvement of minimal overlapped isomorphic computation cost over multi-query graphs.
Most existing studies [14,15] define multi-query graph matching as an expansion problem of subgraph matching. These studies were devoted to reducing the time consumption in matching multiple query graphs, and hypothesized that the optimal way is to cluster query graphs based on multigraph matching. Their solutions are to synchronously respond to the multi-answers for dependent queries based on the query-decomposed subgraph-constructed hyper-tree or hyper-graph, where each hyper-node denotes a query-decomposed subgraph and a hyper-edge represents the residual edges between two query-decomposed subgraphs. However, these solutions based on the decomposition of query graphs destroyed the consistency of edges; thus, it needed to pay a high time-cost to construct the hyper-structure of multiple query graphs and maintain the destroyed consistency of multiple query-decomposed subgraphs.
The research motivation of this paper is to use a categorical graph composed of multiple similar query graphs, such that the redundant calculations of identical substructures can be reduced. Therefore, a potential near-optimal solution of multi-query graph matching is first analyzed, and then a category-driven method is given to identify the identical substructures of multiple similar query graphs and reduce the redundant calculations of query–data node pairs. The main contributions are shown as follows.
- A potential near-optimal solution for a multi-query graph matching problem is analyzed based on the maximal correspondence of query graphs and minimal isomorphic data graphs (Section 3).
- A category-driven method is proposed to solve the problem of multi-query graph matching. Firstly, the query graphs are gathered into one category graph, based on the score of node-to-node and edge-to-edge correspondences. Secondly, a minimal isomorphic data graph is constructed from the data graph induced by the category graph. Finally, the functors are employed to analyze the inclusive and equivalence relationships of query nodes (Section 4).
- A synchronous algorithm is designed to respond to the multi-answers of multi-query graphs within a minimum time-cost (Section 5).
- Extensive empirical studies on real and synthetic graphs demonstrate that our techniques outperform the state-of-the-art algorithms (Section 6).
The rest of this paper is organized as follows. Section 2 introduces the problem definition of subgraph matching and related works on subgraph matching and multi-query graph matching. Section 3 describes the problem analysis and our framework. Section 4 presents the category of multi-query graphs, including categorical graphs of multi-query graphs, functors, and minimal isomorphic data graphs. A subgraph matching algorithm of category-driven multi-query graphs on a data graph is constructed in Section 5. Experimental results are reported in Section 6, and concluding remarks are given in Section 7.
2. Problem Definition and Related Works
In this section, the formal introductions of subgraph matching, multigraph matching, and multi-query graph matching are given first, and then related research is introduced after.
2.1. Problem Definition
In this paper, we focus on a directed labeled graph G(V, E), where V is a set of vertices and E ⊆ V × V is a set of directed edges. A labeling function L is defined to assign a label to each node in a directed labeled graph. The problem of graph matching is defined to find the node correspondence over two or more multiple edges, based on the affinity information between nodes, edges, or hyper-edges over query graphs Q = {, , ⋯, }. The detailed notations and their meanings are illustrated in Table 1.

Table 1.
Notations and meanings.
Graph matching is divided into two-graph matching and multigraph matching based on the number of involved graphs, which are quantified as matching degrees of two-graph and multigraph. The matching degrees denote the similarities of two-graph and multigraph, respectively. A general form of a two-graph matching degree involving graphs and is defined as the quadratic assignment programming (QAP) problem [13], shown in Formula (1). Given a set of query graph Q = and affinity matrix for each pairwise query graph and , the QAP problem of multi-query graph matching is defined in Formula (2).
where = indicates the node correspondence for each pairwise query graph. Further, the multigraph matching degree can be defined as to represent the maximal relevance degree of multiple query graphs.
The problem of subgraph matching is to search all possible subgraphs of data graph D that are isomorphic to query graph q. In this paper, both q ∈ Q and D are the directed labeled graphs, defined as D(V, E) and q(, ), respectively. Subgraph matching is formally defined as a problem of subgraph isomorphism [16,17], as shown in Definition 1.
Definition 1
(Subgraph Isomorphism). Given a data graph D(V, E) and a query graph q(, ), q is a subgraph isomorphic to D if and only if there exists a bijective mapping M from to V such that ∀u ∈ , ∃ ∈ V: ⊆ and ∀ ∈ , ∃(u, ) ∈ :, ∈ E.
A query graph q is a subgraph isomorphic to a data graph G if there exists a subgraph isomorphic mapping (subgraph mapping for short) of q on G. If query graph q(, ) is a subgraph of data graph G(V, E), it should satisfy that ⊆ V and ⊆ E. Considering the directed query and data graphs in Figure 1a,c, A is a label node, and is a subgraph isomorphic to G since there exists a subgraph isomorphic mapping M{⟨, ⟩, ⟨, ⟩, ⟨, ⟩}.
Multi-query graph matching is a combinatorial problem of subgraph matching and multigraph matching that focuses on the synchronous matching way to conduct all subgraph mapping in a global minimal matching time consumption of query graphs, denoted in Definition 2.
Definition 2
(Multi-Query Graph Matching). Given a data graph G(V, E) and query graphs Q = , the problem of multi-query graph matching is to synchronously conduct all subgraph mappings of D on Q, such that each query graph of D satisfies the constraint of subgraph isomorphism.
Most research on multi-query graph matching has been devoted to reducing the time consumption in matching multiple query graphs and hypothesized that the optimal way is to cluster query graphs based on multigraph matching. Furthermore, the redundant matching calculations resulting from identical substructures across multiple query graphs pose a significant challenge that cannot be ignored.
The calculations of subgraph matching show that the results of a data graph matched a query graph in an iterative manner, continuously calculating and connecting query–data node pairs to form a data graph isomorphic to the query graph. However, in the realm of multi-query subgraph matching, the presence of identical substructures across multiple query graphs can lead to redundant calculations of query–data node pairs. The research motivation of this paper is to use a categorical graph composed of multiple similar query graphs, so that the redundant calculations of identical substructures can be reduced. Therefore, a potential near-optimal solution of multi-query graph matching is first analyzed, and then a category-driven method is given to identify the identical substructures of multiple similar query graphs and reduce the redundant calculations of query–data node pairs.
2.2. Related Works
In this section, we introduce related works on multigraph matching, subgraph matching, and multi-query graph matching.
Multigraph Matching: Most research formed the problem of multigraph matching as a regularization model, which has become famous through cycle consistency. The mechanism of cycle consistency is that the node correspondence between and shall be consistent with a derived two-step matching through an intermediate graph , formed as = . Obviously, the consistency is so important that it is widely employed in many popular solutions of multigraph matching.
The first group used the affinity of two-graph matching to optimize the cycle consistency. Benefiting from a central reference graph , a unified method [18] strictly employed a strict cycle consistency regularizer, which is a set of basis , to encode the two-graph matching, such that the pairwise graph could be modeled by the cycle = . A soft cycle consistency regularizer was adopted by a distributed method [19] that used a jointly objective function of affinity score and consistency to optimize the integrated two-graph matchings . A state-of-the-art approach [20] formulated a pairwise matching as a shortest path on the super-graph, where a super-node denotes a graph and an edge represents the node correspondence of two-graph matching.
The second group separated affinity to recover the cycle consistency based on matching and post-smoothing on each pairwise graph. Spectral techniques [21,22,23] have been developed to extract the consistent matches by the spectrum of node and edge correspondences calculated from pairwise graphs. The underlying rationale is that the problem can be formulated as quadratic integer programming which can be converted into a generalized Rayleigh problem [21]. Huang et al. [22] presented a convex relaxation method for estimating cycle-consistent matchings to find the nearest positive semi-definite matrix that is stacked by all initial matchings. Recently, the message-passing algorithm [23] has been employed to solve the multigraph matching problem, which accounts for first-order/second-order affinity as well as cycle consistency.
Subgraph Matching: Subgraph matching has been studied extensively since 1976. Ullmann [24] first proposed a backtracking-based subgraph matching algorithm that iteratively mapped node pairs guided by a matching order of query graphs. However, iterative backtracking-based subgraph matching should result in a significant amount of redundant calculations. VF2 [25] proposed the reduction rules of partial connectivity that could verify the partial subgraph isomorphism with one selected data node and pruned the negative candidate data earlier. However, the verification of partial subgraph isomorphism with a selected data node was only to verify the consistency of candidate nodes in the range of a one-hop node. Benefiting from the structural characteristics, more studies devoted their resources to eliminating redundant calculations by indexing multi-hop nodes. Spath [26] proposed a multi-hop adjacent index to divide the paths with similar labels and depths. However, the index needed a huge space consumption, because data nodes with the same label are stored repeatedly in paths with different depths. To reduce the search space, the static and dynamic equivalences of vertices were employed to plan an efficient matching order and remove the redundancies in the search space [27]. Circinus [28] proposed a new compression-based backtracking method that generated compressed groups of partially matched groups so that computation could be shared within each group. GraphZero [29] optimized query compiler to completely address these limitations through symmetry breaking based on group theory.
More efficient multi-hop indexes were designed to reduce the redundant storage of data nodes. TurboISO [30] proposed an index of adjacent multi-regions, which was constructed by the parent–child relationships of a spanning tree on a query graph. However, those common candidates were still stored repeatedly in different regions. CFLMatch [31] proposes a compact multi-path index that is induced by a spanning tree on a query graph, and it is composed of multiple clusters and inter-cluster relationships that can reduce the overlapping candidates and reduce the negative candidates of an upper-lever cluster. Because the relaxed GPM models have emerged as they yield interesting results in a polynomial time, distributed Graph Pattern Matching in Massive Graphs is also a research hotspot [32]. BENU [33] divided a subgraph enumeration task into a group of local search tasks that only queries the necessary edges of the data graph and avoids shuffling partial matching results. The sketch tree [34] integrated the advantages of both join-based and exploration-based paradigms that can reduce invalid intermediate results and avoid duplicate computation. An index-based incremental subgraph matching method [35] was proposed to maintain tight partial matchings by properly encapsulating the structure and temporal information.
Multi-Query Graph Matching: Most existing works of multi-query graph matching proceed in two steps: clustering and query combination. Le et al. [36] incorporated an efficient algorithm to discover the common sub-structures of multiple query graphs and an effective cost model to compare candidate execution plans. MQO [14] identified the common query subgraphs and cached the intermediate results to execute the general algorithm of subgraph matching for multi-query graph matching, whose experimental evaluation of matching time employed the algorithm of TurboISo. vMSQ [15] proposed a scheduling algorithm for processing multiple queries in parallel, considering the load balance and maximum possible sharing of computation. A distributed system for online multi-GPM [37] optimized query plans by maximizing computation sharing among multiple queries and minimizing intermediate matching results.
In this paper, a category-driven method is designed to solve the problem of multi-query graph matching. The multiple query graphs are clustered into categorical graphs, which can guide the data graph to reduce the redundant data and construct a minimal isomorphic data graph. Additionally, the functors of a categorical graph are mined to identify the inclusive and equivalence relationships of query nodes. Benefiting from the auxiliary of categorical graph, the time-effectiveness of conducting subgraph mappings can be accelerated.
3. Problem Analysis and Our Framework
This section first analyzes a near-optimal solution for multi-query graph matching that is constrained by two factors: the maximal related relevance of multiple query graphs and the minimal isomorphic data graph of query graphs. Then, we introduce our framework of category-driven multi-query graph matching on labeled graphs.
3.1. Problem Analysis
Most existing research defines multi-query graph matching as an expansion problem of subgraph matching. Their solutions synchronously respond to the multi-answers for dependent queries based on the query-decomposed hyper-tree or hyper-graph. However, these solutions based on the decomposition of query graphs destroyed the consistency of edges; thus, they need to pay a high time-cost for constructing the hyper-structure of multiple query graph and maintaining the destroyed consistency of multiple query-decomposed subgraphs.
The problem of multi-query subgraph matching is to find all data graphs isomorphic to any one of query graphs Q = on a data graph D with minimal time consumption, as shown in Formula (3).
In Formula (3), Q is a set of query graphs with size n, satisfying Q = , denotes a set of data graphs isomorphic to any query graph Q on a data graph D, and represents the time consumption of the entire matching period of Q on D.
The multigraph matching problem with minimal time consumption is constrained by two factors: the maximal related relevance of multiple query graphs and the minimal isomorphic data graph of query graphs.
In order to more intuitively explain the maximal related factor of multiple query graphs, the multigraph matching problem with maximal time consumption is used to disprove the constraints of this maximal related factor, given in Formula (4).
The multi-query graph matching with maximal time consumption is interpreted as sequentially conducting the subgraph matching of each query graph in Q on the data graph D, on the premise that all query graphs are unrelated and independent. As the multi-query graphs are dependent, the multigraph matching problem with minimal time consumption should acquire the maximal related relevance of multiple query graphs to reuse the common intermediate results for the multiple closely related query graphs in the process of subgraph matching. The related relevance of multiple query graphs is defined as the affinity in research on the multiple graph matching problem.
Given a set of query graphs Q = and an affinity matrix for each pairwise query graph and , the QAP problem of multi-query graph matching is defined in Formula (5).
In Formula (5), = indicates the node correspondence for each pairwise query graph, and Result is a quantified score of similarity between graphs and . Further, the multi-graph affinity degree can be defined as to represent the maximal relevance degree of multiple query graphs, which represents the global optimal value with the highest similarity among multiple query graphs.
Then, the multigraph matching problem with minimal time consumption is dominated by the maximal related relevance of multiple query graphs, formed as ≺ . Herein, is a set of matrices about node correspondence for each pairwise query graph.
The minimal isomorphic data graph of a query graph is used to evaluate the minimal redundant candidates of query graph q on data graph D. Given a data graph G(V, E) and a query graph q(, ), D is a minimal isomorphic data graph of query graph q, formed as = , if and only if it satisfies the following conditions: ∀v ∈ V, ∃u ∈ : = and ∀ ∈ V, ∃(v, ) ∈ E, , ∈ : = and = . Note that it does not mean that the matching time consumption on this minimal isomorphic data graph is completely free of redundant matching computations, because the acquisition of the data graph without redundant matching computations is an NP-Hard problem [38], proved by our previous work, but this minimal isomorphic data graph is still able to intuitively express the nature of the multigraph matching problem. Compared to the unprocessed data graph, this minimal isomorphic data graph prunes all the non-candidate nodes and edges that are non-isomorphic to the ones of query graph. Then, the multigraph matching problem with minimal time consumption is still dominated by the minimal data graph of query graphs Q, formed as ≺ .
Therefore, a near-optimal solution of multi-query subgraph matching can be found by the maximal related relevance of multiple query graphs and the minimal isomorphic data graph of query graphs, formed as ≺ . Given a set of query graphs Q = {, , ⋯, } and a larger data graph D, multi-query subgraph matching synchronously obtains all the isomorphic subgraphs of data graph D on multiple query graphs Q, formed as = . Then, a near-optimal solution for multi-query subgraph matching is constrained by the maximal related relevance of multiple query graphs and the minimal isomorphic data graph of query graphs, formed as ≺ , where = indicates the node correspondence for each pairwise query graph in Q and = .
Through Formula (5), the maximal related relevance of multiple query graphs Q can be acquired, and the minimal isomorphic data graph is equivalent to the (=), denoted in Theorem 1.
Theorem 1
(Minimal Isomorphic Data Graph). Given a larger data graph D, a set of multiple query graphs Q = {, , ⋯, } and its maximal related relevance , the minimal isomorphic data graph (=) of D is equivalent to the (=).
Proof.
The determination of maximal related relevance, denoted as , involves two key steps in the context of query graphs Q. The process can be outlined as follows:
For any alternative related relevance set , if it satisfies the condition < , then the metric must be greater than . Here, represents a measure that quantifies the quality of the node correspondence relationships within the set relative to some dataset D.
The reason for > when < is that contains a significantly higher number of node in-correspondence relationships compared to . This implies that, while represents the optimal set of correspondences in terms of similarity, may capture more nuanced differences that are reflected in the higher metric value. □
Thus, this paper is devoted to designing an optimal solution for multi-query graph matching on the following three steps. The first step is to calculate the maximal related relevance of multiple query graphs Q, and correspond to categorical graphs. The second step is to find the minimal isomorphic data graph based on the maximal related relevance . The third step is to conduct all the subgraph isomorphic mappings of data graphs on category graphs, synchronously.
3.2. Our Framework of Multi-Query Graph Matching
A view representation of our framework is first given to express our design intention purely. Then, the strategies of categorical graphs on multi-query graphs and subgraph matching of a larger data graph on categorical graphs are detailed introduced in Section 4 and Section 5, respectively.
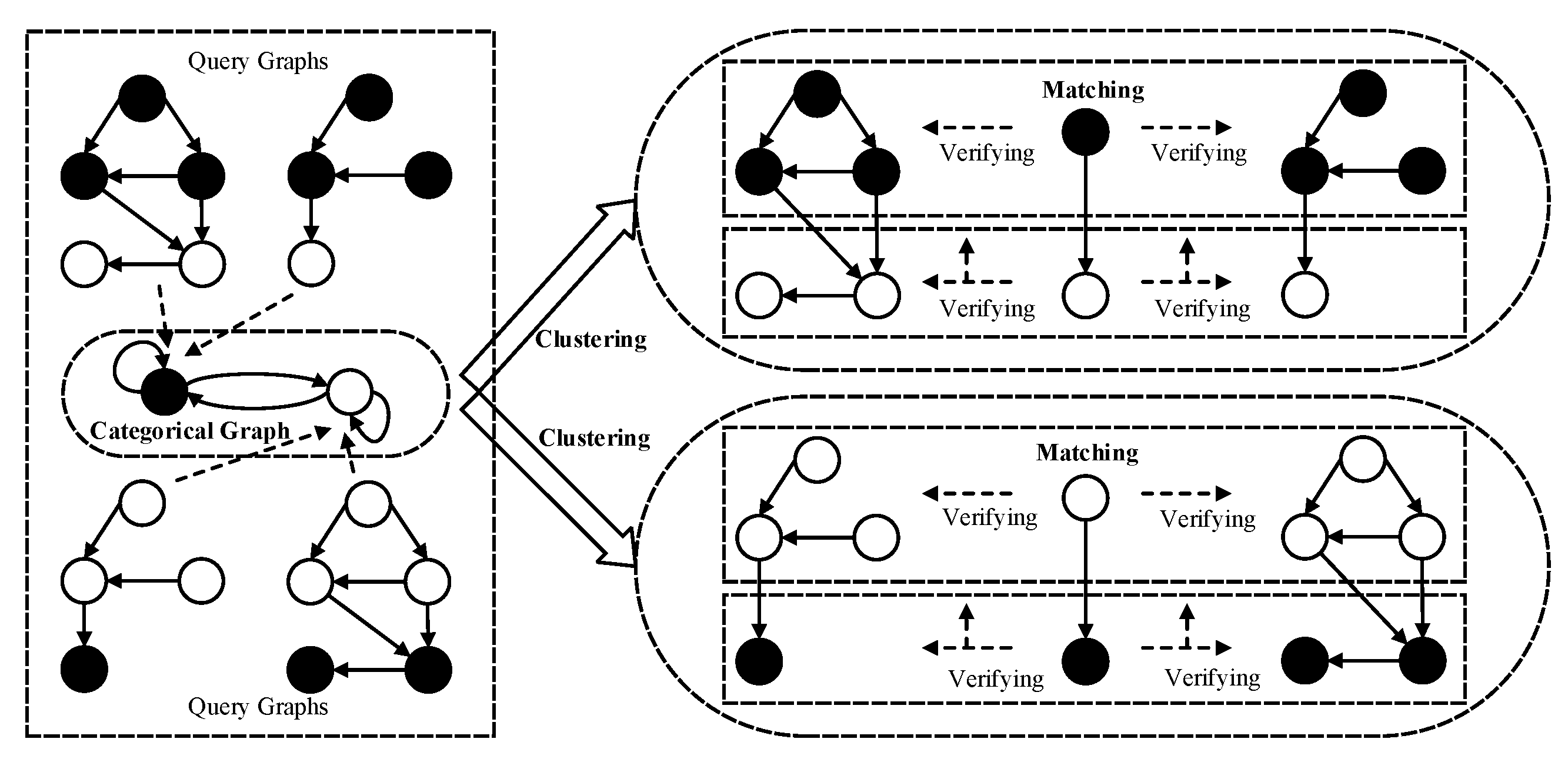
Our framework of category-driven multi-subgraph matching on labeled graphs is shown in Figure 2, which includes two processes: clustering of query graphs and subgraph matching of multi-query graphs on a larger data graph.
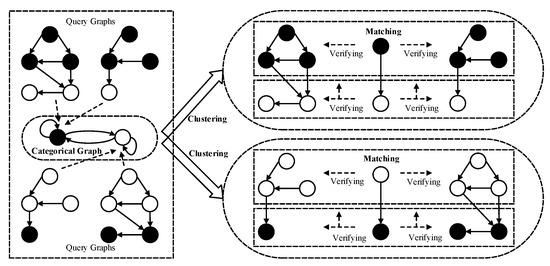
Figure 2.
The framework of category-driven multi-subgraph matching on labeled graphs.
The first process involving the clustering of query graphs is specifically dedicated to segmenting multiple similar query graphs into a single cluster. Each resultant cluster corresponds to a categorical graph, where the multiple query graphs within a cluster are homomorphic to their respective categorical graph. The categorical graph is represented as a directed graph, in which each categorical node corresponds to a query subgraph comprising homogeneous query nodes sharing the same label. Furthermore, each categorical edge denotes the relationship between multiple non-homogeneous query nodes.
The second process involving the subgraph matching of multi-query graphs is to synchronously create the isomorphic data subgraphs of multiple query graphs on a larger data graph, which is guided by a matching order of categorical nodes in the categorical graph. The consistency verifications of subgraph isomorphism are classified as horizontal and vertical verification. The horizontal verification is used to verify the subgraph isomorphism between the query subgraphs of homogeneous query nodes and the larger data graph. The vertical verification is used to verify the edge consistency of non-homogeneous query nodes on the larger data graph. For example, in Figure 2, the hollow and solid circles represent two categorical nodes or two query node labels, which encapsulate the subgraphs of the same query node labels in the multiple query graphs, respectively, and the horizontal and vertical verifications are represented by the horizontal and vertical arrows.
4. Categorical Graph Abstracted from Multi-Query Graphs
The categorical graph models the correlation of objects, and pays attention to the inter-object relationships. It employs the inter-object relationships to analyze the complex connotation of objects, and it is not limited to the constraints of a specific computing environment.
This section introduces the category of multi-query graphs. Firstly, it constructs the categorical graph abstracted from the multi-query graphs. Secondly, it mines the inter-object relationships in this categorical graphs to identify the reused intermediate results in the process of multi-query graph matching.
4.1. Category of Multi-Query Graphs
The construction of categorical graphs is based on the correspondence analysis between categories and multi-query graphs. It is used to ensure the consistency of edge directions and node labels.
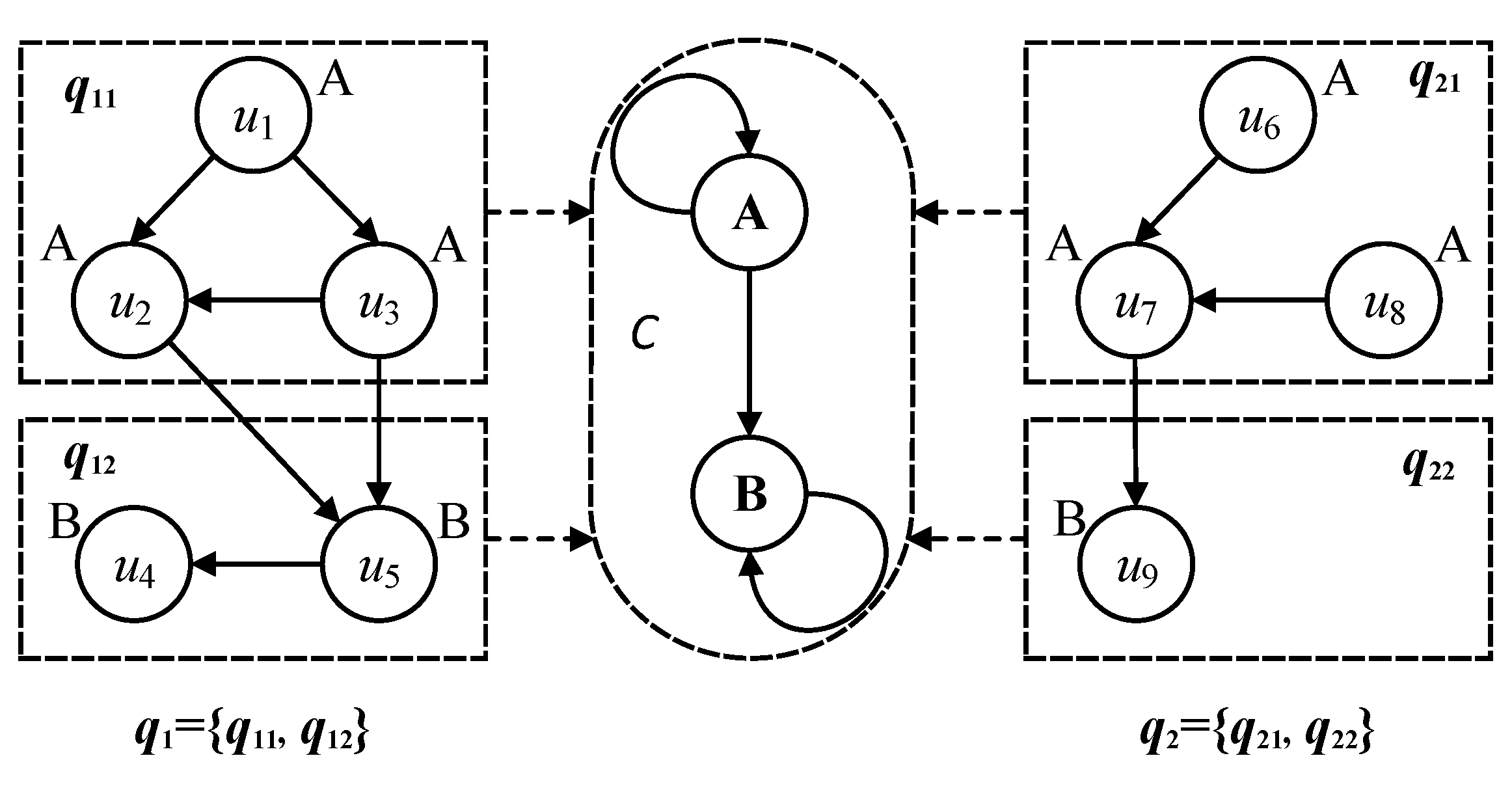
In the construction of the categorical graph, the nodes of same labels are gathered into the same categories. The edges in the query graph correspond to self-connected edges of the categories. Considering query graphs and in Figure 3, each of them can be classified into two categories by the different node labels A and B, that is = {, } and = {, }, then query subgraphs and are gathered into category A, and query subgraphs and are gathered into category B. The self-connected edges of categories A and B represent the inner edges of , and , , respectively. The directed edges between and and the directed edges between and are extracted as one directed edge between categories A and B. From the above illustration in Figure 3, it can be found that the category abstracts the different research objects with the same semantic labels and their relationships into a unified category, which can be constructed as a reference graph corresponding to the all query graphs.
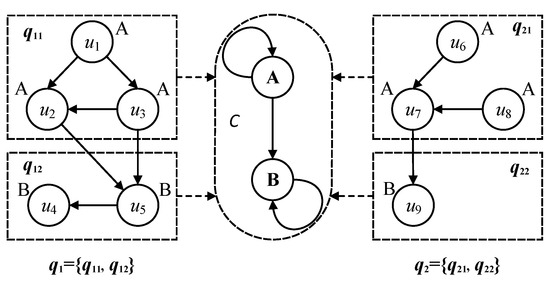
Figure 3.
Correspondence between categories and multi-query graphs.
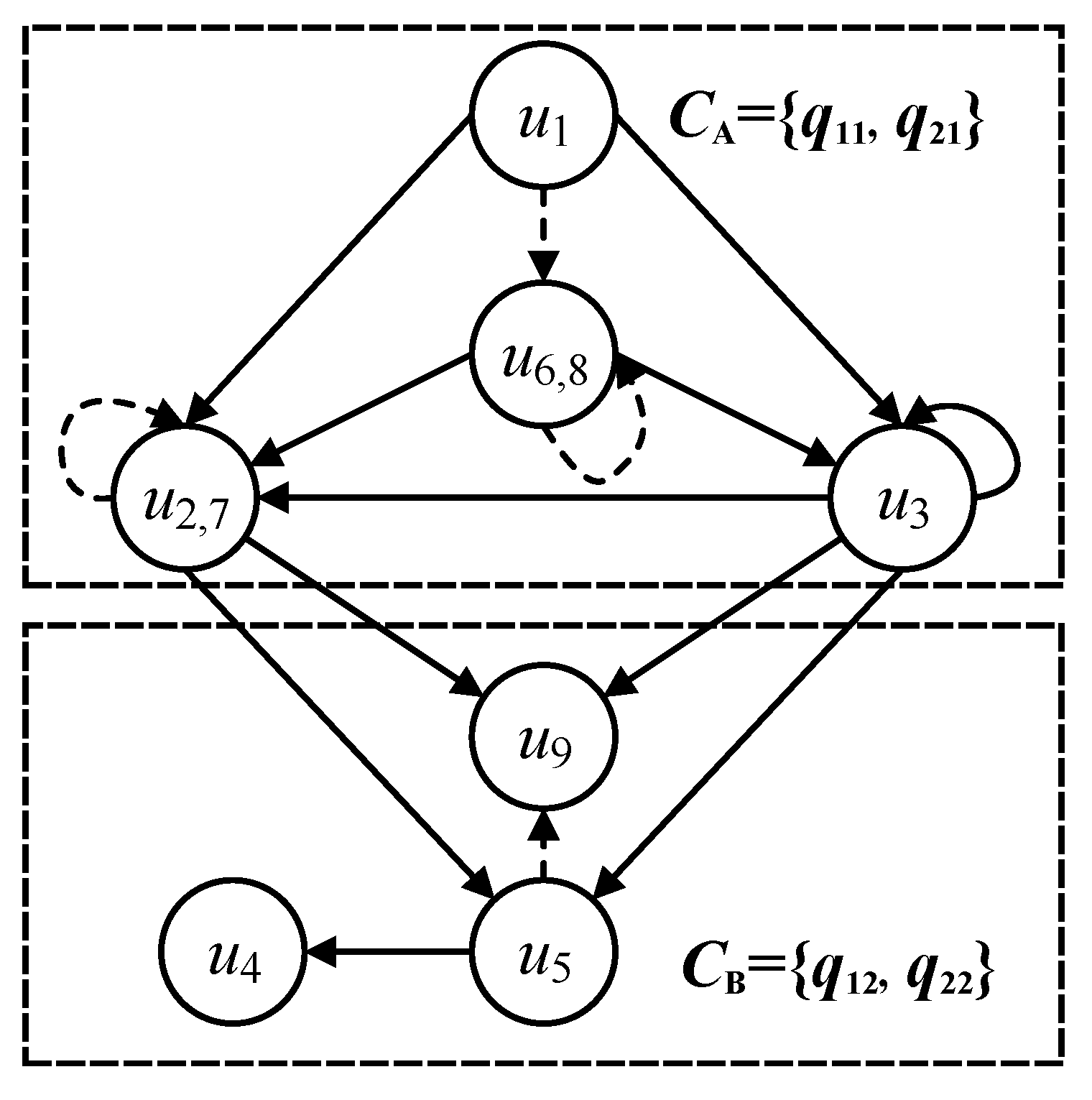
Categories gather the multi-query graphs into a reference graph, which includes all the nodes and directed edges of multi-query graphs. To distinguish the category and its graph structure, the graph structure of the category is renamed as a categorical graph. A category gathers the nodes of same labels into the same categorical graph and corresponds to the directed edges in multi-query graphs. Considering the query graphs and in Figure 3, the gathered categories are illustrated in Figure 4, where the categorical nodes are the query nodes and the solid lines represent the edges between categorical nodes in the multi-query graphs.
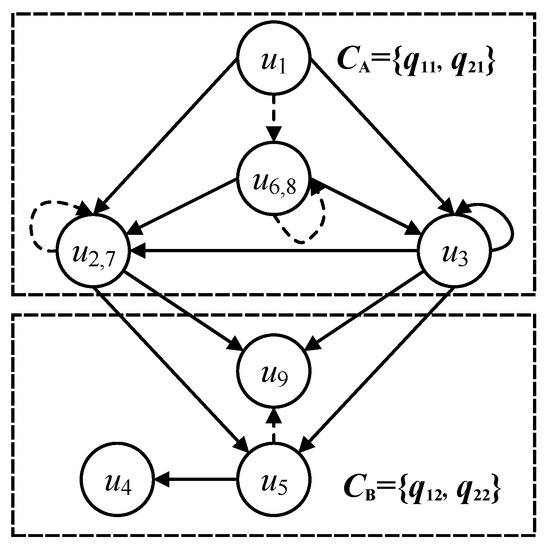
Figure 4.
Categorical graph on multi-query graphs.
Each categorical node is parsed into two features: input and output. The input of a categorical node receives the in-edges of some categories, and the output of a categorical node sends the out-edges of some categories.
Considering the query node of in Figure 3, the input of the transformed categorical node should receive the in-edges of category A, and the output of sends the out-edges of categories A and B in Figure 3. Then, the transformed categorical node should receive all the nodes that can send the out-edges of category A, including categorical nodes , , and . Meanwhile, the transformed categorical node should send all the nodes that can receive the in-edges of categories A and B, including , , of category A and , of category B. Note that query nodes and can be transformed into one categorical node, because they contain the equivalent in-edges and out-edges in the query graph and . Similarly, the query nodes and are also transformed into one categorical node. Some query nodes are explained by the equivalent functors of categorical nodes in detail in Section 4.2.
The category of multi-query graphs ensures that all edges of categorical nodes can be calculated by the composition operator ∘. Regarding categorical nodes u, and , if ∃ f:u → , g: → ∈ , then f ∘ g:u → ∈ . The proof is shown as follows: the edges f:u → and g: → indicate that categorical node u can send the out-edge of category and can receive the in-edge of category . Thus, there must be an edge u → of category .
4.2. Functors
The inclusive and equivalence operators of categorical nodes are employed to identify the reused intermediate results in the process of multi-query graph matching. Before the inclusive and equivalence operators of categorical nodes are introduced, a mapping functor is given to represent the inter-node relationships of the categorical graph
The mapping functor F is used to identify the similar categorical nodes of the different local sub-categories in the same category. A local sub-category denotes a categorical node and all its neighbors and adjacent edges. Regarding the categorical node in Figure 4, the local sub-category is constructed by , its neighbors and , and its adjacent edges (f: → , : → and : → ). The local sub-category collects the minimum semantic structure of one categorical node that provides the basic calculated unit for categorical functor operations. Similar to , the local sub-category is constructed by , its neighbors (, ) and its adjacent edges (g: → , : → and : → ). The inclusive functor F: → is defined because categorical node is similar to categorical node , as they have the same node label A, contain similar out-edges ((, ), (, ), (, ), and (, ), and their end-nodes , , , and also have the same node label A). Thus, all isomorphic constraints of local sub-categories and can be satisfied on the premise of the inclusive relationships between and .
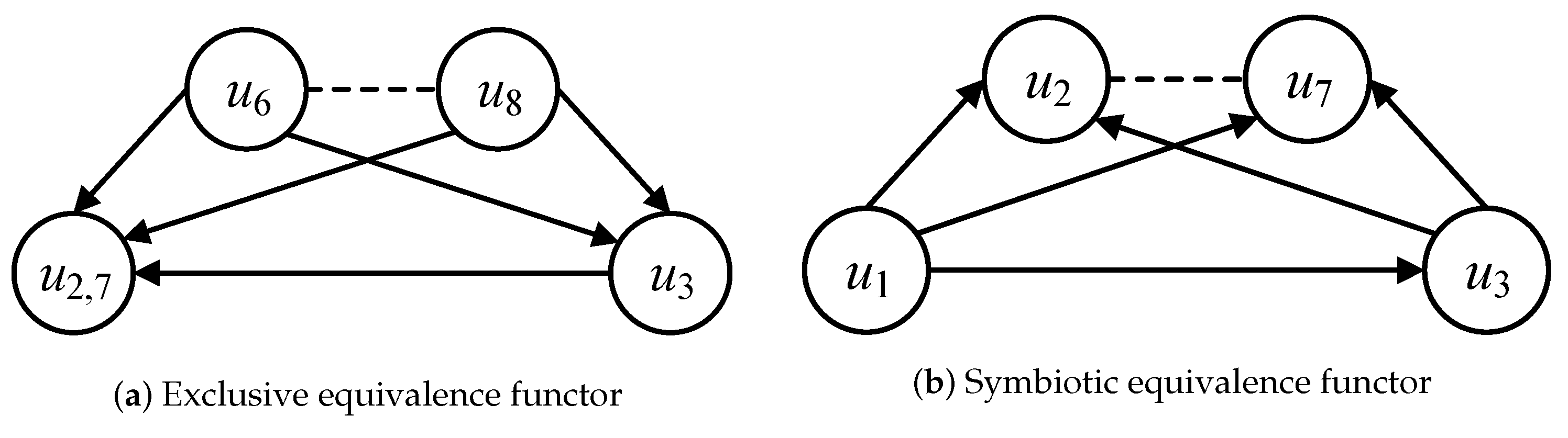
The equivalence functor of categorical nodes can be classified as exclusive and symbiotic equivalence functor by different dominated query graphs. Regarding the local sub-categories and in Figure 5a, the exclusive equivalence functor can be defined as F: , because the local sub-categories and satisfy the constraints of graph isomorphism and their categorical nodes and are included in the same query graph . Regarding the local sub-categories and in Figure 5b, the symbiotic equivalence functor can be defined as F: , because the local sub-categories and satisfy the constraints of graph isomorphism and their categorical nodes and are included in the different query graphs and , respectively. The classified exclusive and symbiotic equivalence functors are employed to identify the reused intermediate results in the process of multi-query graph matching.
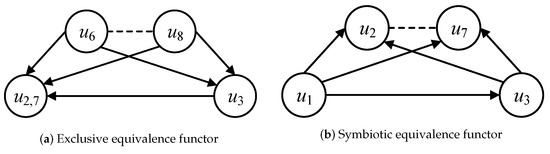
Figure 5.
Equivalence functors.
4.3. Minimal Isomorphic Data Graph
The minimal isomorphic data graph prunes all the non-candidate nodes and edges that are non-isomorphic to the query nodes. The pruned non-candidate nodes are verified by candidate verification of data on query nodes, formed in Definition 3.
Definition 3
(Candidate Verification). A data node v is the candidate of query node u, if and only if it satisfies the following constraints: (1) L(u) = L(v), ∀ ∈ , ∃, ∈ : = and , ∈ E.
In Definition 3, denotes a labeling function that assigns a label to node u, indicates a bijective mapping function from u to data nodes of G, and , represents an edge between u and . Note that the directionality of , and , should be consistent. The candidate set of query node u is denoted as . If data node v satisfies the candidate verification of query node u, v is a candidate data node of u, and it is denoted as , where denotes the candidate set of u.
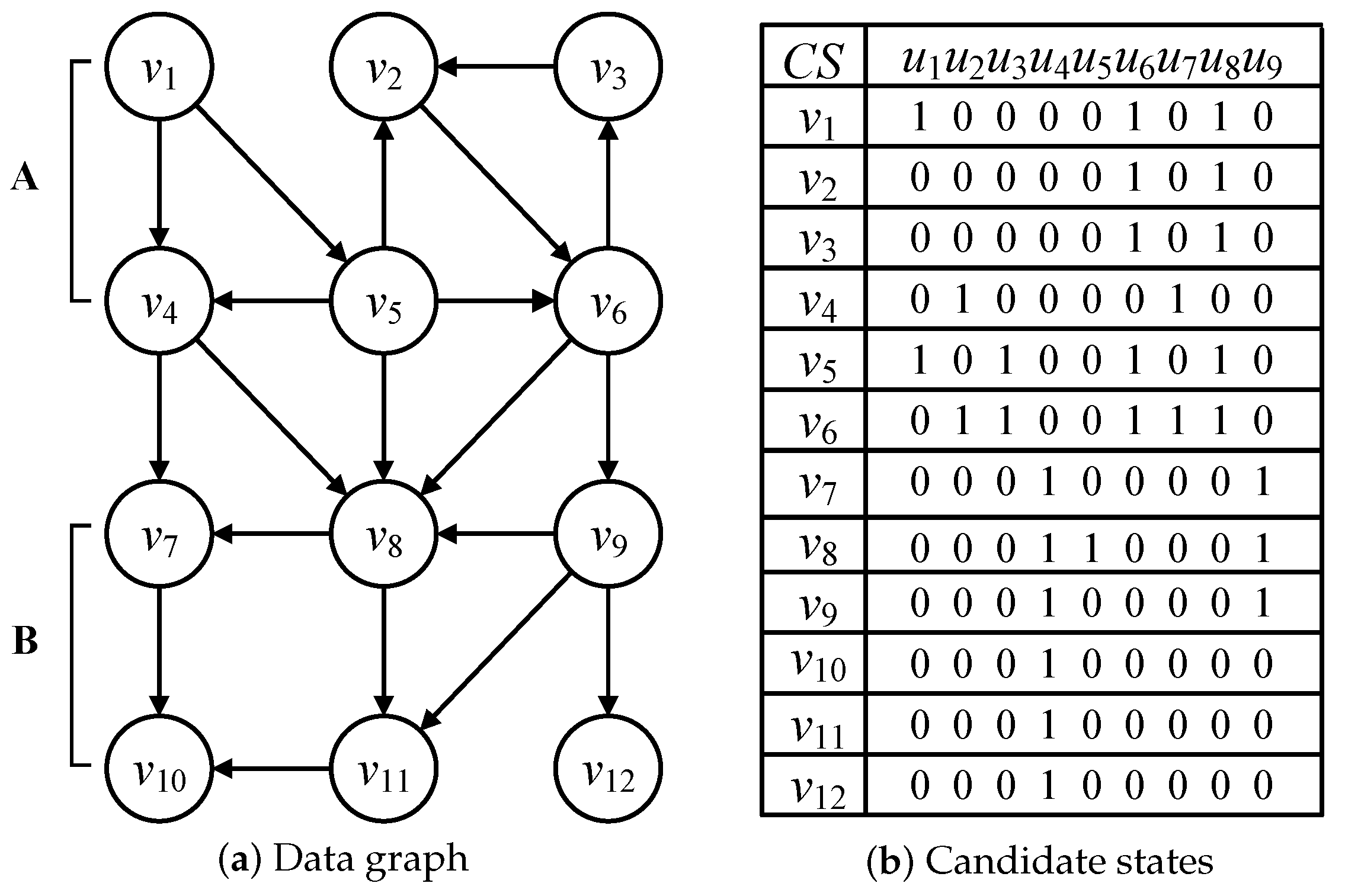
Considering query graphs in Figure 3 and the data graph in Figure 6a, the candidate relationships between data and query nodes are illustrated in Figure 6b and are represented by candidate state CS and verified by Definition 3. Regarding the candidate states CS() = , each candidate state denotes the candidate verification of one query graph. If a candidate state CS(, ) = 1, is a candidate data node of query node . Otherwise, if the candidate state CS(, ) = 0, is a non-candidate data node of . According to Figure 6b, all the data nodes in Figure 6a are included in the minimal isomorphic data graph, because any a data node must be a candidate of one query node according to the candidate verification in Definition 3.
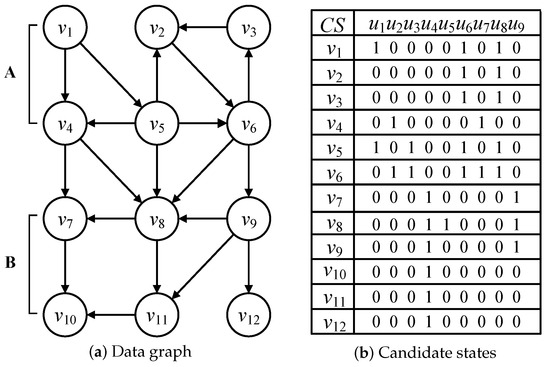
Figure 6.
Data graph and candidate states.
The candidate states also disprove the functors of the categorical graph. According to the candidate states CS() = , is the candidate data node of multiple query nodes , and . Thus, the relationships among query nodes , and may be calculated by the inclusive or equivalence functors. Additionally, the main function of the functor is used to assign the reused candidate data node to similar query nodes in the process of multi-query graph matching that is introduced in detail in Section 5.
5. Subgraph Matching Algorithm of Categorical Multi-Query Graphs on a Larger Data Graph
Multi-query graph matching is employed to synchronously find all the possible subgraph isomorphic mappings (subgraph mappings for short) between multi-query graphs and a larger data graph that can be transformed as the traversal of the categorical graph on the minimal isomorphic data graph and given in Theorem 2.
Theorem 2.
All subgraph mappings of Q on D can be obtained through the traversal of the categorical graph C on the minimal isomorphic data graph .
Proof.
Consider a subgraph mapping M = , , , , ⋯, , which is composed of multiple node pairs, and each node pair contains a query node and its candidate data node , 1 ≤ i ≤ n.
The proof for Theorem 2 can be given as the following three steps:
Step 1: All the query nodes and directed edges of Q are included in the categorical nodes and edges of C. A categorical graph gathers the multi-query graphs into a reference graph that includes all the nodes and directed edges of multi-query graphs. Regarding a directed query edge (, ), the transformed categorical node of must send an out-edge, and that of must receive an in-edge of one categorical node. Thus, there must be an edge from to .
Step 2: All the candidate data nodes can be found in the minimal isomorphic data graph . The minimal isomorphic data graph prunes all the non-candidate nodes and edges that are non-isomorphic to the query nodes through the candidate verification in Definition 3. Thus, all the candidate data nodes of D can be preserved losslessly in .
Step 3: All subgraph mappings of Q on D correspond to the ones of C on . Considering subgraph mappings M = , , , , ⋯, , if there exist node pairs , and , in M, satisfying the edge relationships (, ) and (, ), then C must contain an edge from to and data edge (, ) cannot be destroyed in , proven by Steps 1 and 2. Thus, the subgraph mappings of C on still correspond to the ones of Q on D. □
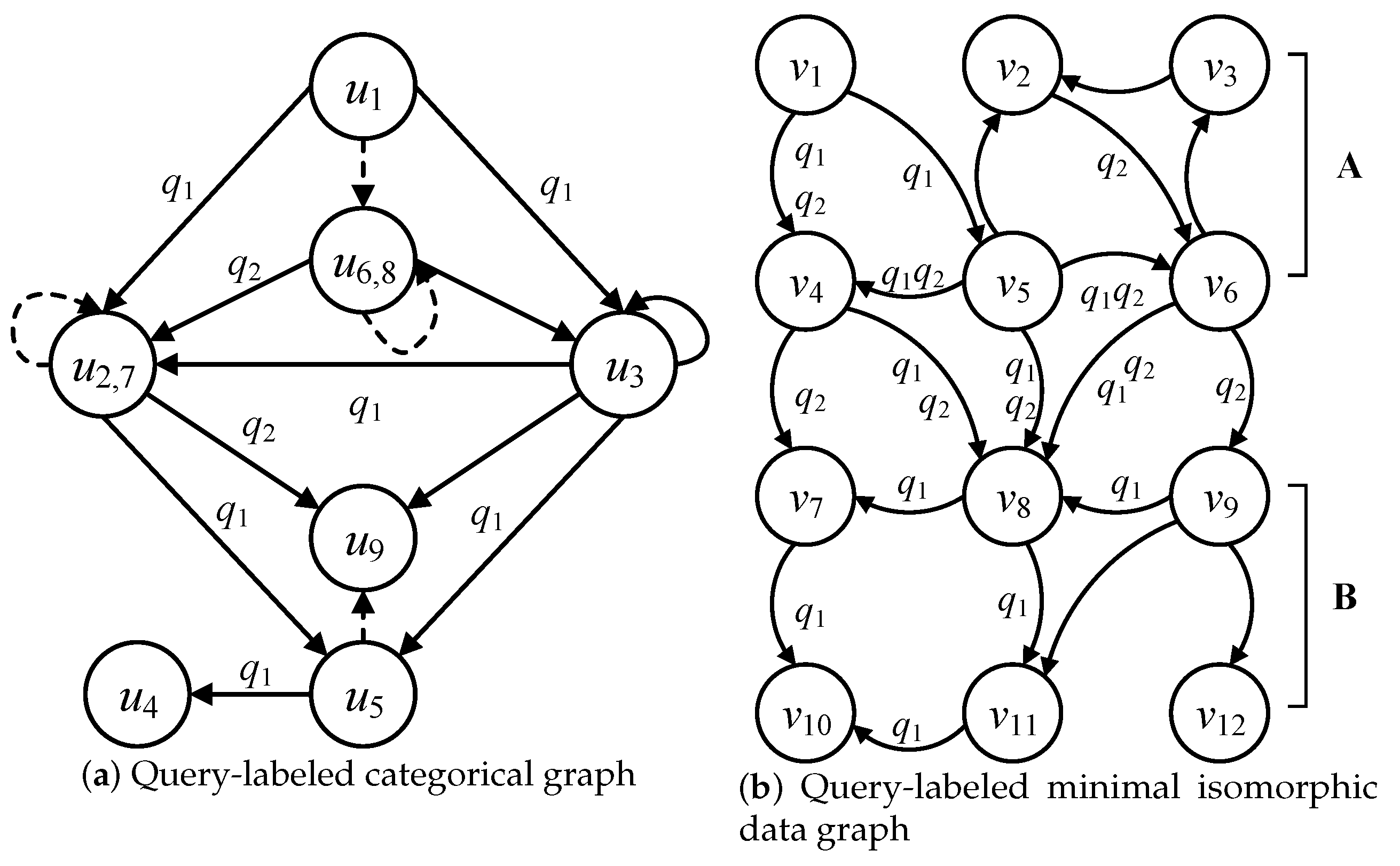
The query labels are attached to the edges of the categorical graph and minimal isomorphic data graph, which is used to reduce the redundant edges in C and the redundant data edges and data nodes in . Considering the categorical graph in Figure 3 and the data graph in Figure 5a, the query-labeled categorical graph and minimal isomorphic data graph are illustrated in Figure 6a,b, respectively. The query-labeled categorical graph attaches the query labels to the edges that correspond to the query edges in the multi-query graph. Regarding the edge f: → in Figure 3, the query edge (, ) of corresponds to f; thus, f is labeled by . Regarding the edge f: → in Figure 3, a query edge cannot be found in both and that corresponds to f; thus, f cannot marked by any query label.
Then, the query-labeled categorical graph induces and labels the minimal isomorphic data graph, which can further reduce the redundant data edges and data nodes. The query-labeled minimal isomorphic data graph corresponds to the consistent relationships with edges in the categorical graph. The consistent relationship is reflected in the following two aspects: label consistency and connectivity consistency. Label consistency refers to the fact that the node labels and edge labels between the query graph and data graph are the same. Connectivity consistency refers to the directional consistency between the edges of query nodes and those of candidate data nodes.
Considering the edge e: → in Figure 7a, and candidate data nodes of and of in Figure 6a, the data edge (, ) satisfies the consistent relationships with edge e; thus, the data edge (, ) is also labeled by , where the direction from to is consistent with the one from to .
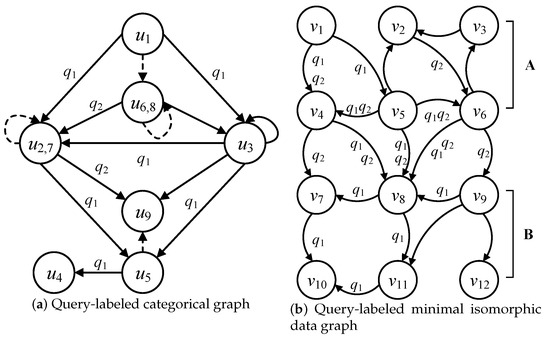
Figure 7.
Query-labeled categorical graph and minimal isomorphic data graph.
Additionally, the consistent constraints of a categorical graph can further the negative candidates in the minimal isomorphic data graph. The reductions of negative data edges and data nodes are denoted in Lemmas 1 and 2, respectively.
Lemma 1
(Reduction of negative data edges). Given a candidate data node of , edge e: → labeled by q and data edge (, ); if is a non-candidate data node of , then (, ) is a negative data edge in q.
Lemma 2
(Reduction of negative data nodes). Given a candidate data node v of u and its out-edge e labeled by q, if an out-edge labeled by q cannot be found, then v is a negative data node of u in q.
Proof.
For Lemmas 1 and 2: According to the subgraph isomorphism in Definition 1, given a data graph G(V, E) and a query graph q(, ), q is a subgraph isomorphic to G if and only if there exists a bijective mapping M from to V such that ∀u ∈ , ∃ ∈ V: ⊆ and ∀ ∈ , ∃(u, ) ∈ :, ∈ E and u, = , . It can be found that the negative data edges and data nodes cannot satisfy the consistent constraint of edge relationships. □
The detailed illustration of Lemmas 1 and 2 is shown in Figure 7. Considering the data edges (, ) and (, ), and are the candidate data nodes of and is a non-candidate data node of , then the data edges (, ) and (, ) cannot be consistent with the edge e: → ; thus, (, ) and (, ) are the negative data edges by Lemma 1. Considering the candidate data nodes of , an out-edge labeled by cannot be found; thus, is a negative data node of in by Lemma 2.
Based on Theorem 1, all subgraph mappings of Q on D can be obtained through the traversal of the categorical graph C on the minimal isomorphic data graph , and the algorithm of multi-query graph matching is shown in Algorithm 1. The inputs are the multi-query graphs Q and data graph D, and the output is the set of subgraph mappings . The clustering algorithm of multi-query graphs first gathers the similar query graphs into a common group and constructs the categorical graph C for each group (Line 1). Then, the traversal on the minimal isomorphic data graph is executed for each categorical graph (Line 2). The minimal isomorphic data graph-constructing algorithm is used to establish a network of candidate data nodes and reduce the negative candidates of data nodes and data edges (Line 3). The category-driven subgraph matching algorithm conducts all the subgraph mappings of the categorical graph on the minimal isomorphic data graph (Line 4).
| Algorithm 1: Multi-query graph matching algorithm |
 |
5.1. Clustering Algorithm of Multi-Query Graphs
The clustering algorithm of multi-query graphs first gathers the similar query graphs into a common group, and then constructs the categorical graph C for each group, as shown in Algorithm 2. The input is a set of multi-query graphs and the output is a set of categorical graphs .
| Algorithm 2: Multi-query graph clustering algorithm |
 |
The QAP solution gathers the similar query graphs into a common group through the strategy of hypergraph-based optimal path selection (Line 1), which is a mature solution and has been studied by many researchers. Then, the categorical graph is established for each group and each group c collects the highly similar query graphs (Lines 2–9). For a query graph q of each group c, the query labels are employed to assign the query nodes into different categories (Line 4), and query edges into the in-edges E− and out-edges E+ (Line 5). Then, the categorical graph is constructed from the categorical nodes Obj C, in-edges E−, out-edges E+ and query label q (Line 6). Finally, the functors are analyzed for each pairwise categorical nodes, and collected into C (Lines 7–9).
5.2. Constructing Algorithm of Minimal Isomorphic Data Graph
The constructing algorithm of the minimal isomorphic data graph is used to establish the network of candidate data nodes and reduce the negative candidates of data nodes and data edges, as shown in Algorithm 3. The inputs are the data graph D and a categorical graph C, and the output is the minimal isomorphic data graph D(C)(V(C), E(C)).
| Algorithm 3: Minimal isomorphic data graph-constructing algorithm |
 |
The construction process of the minimal isomorphic data graph is classified into two subroutines. The first subroutine acquires all the candidate data nodes of categorical nodes (Lines 1–4). Regarding a data node v ∈ V and u ∈ ObjC, if v is a candidate data node of u, the candidate state v.CS(u) of v under u is set as 1 (Line 1), and collected into the candidate set Candidate(u) of u and set V(C) of categorical nodes, non-repeatedly (Line 2). The second subroutine verifies the consistent constraints between data edges and edges, and attaches the consistent query label to edges in E(C) (Lines 5–17). If one data in-edge or out-edge satisfies the consistent relationships with an edge, the query label of this edge is assigned to in-edge or out-edge, and collected into the set E(C) of edges (Lines 7–9 and Lines 13–15). The reductions of data edges and data nodes re-modify the candidate states of data nodes (Lines 10–11 and Lines 16–17), which is a lightweight strategy and does not reduce the negative data edges and data nodes in the minimal isomorphic data graph D(C). The advantage of the lightweight strategy is to avoid the high consumption of reconstructing the minimal isomorphic data graph and does not affect the time-efficiency of multi-query graph matching, because the candidate relationships of queries on data nodes have been marked in the candidate states CS.
5.3. Category-Driven Subgraph Matching Algorithm
The category-driven subgraph matching algorithm is used to iteratively conduct all the subgraph mappings of the categorical graph on the minimal isomorphic data graph, as shown in Algorithm 4. The inputs are the minimal isomorphic data graph D(C) and a categorical graph C and the output is a set of subgraph mappings .
| Algorithm 4: Category-driven subgraph matching algorithm (CSMA( )) |
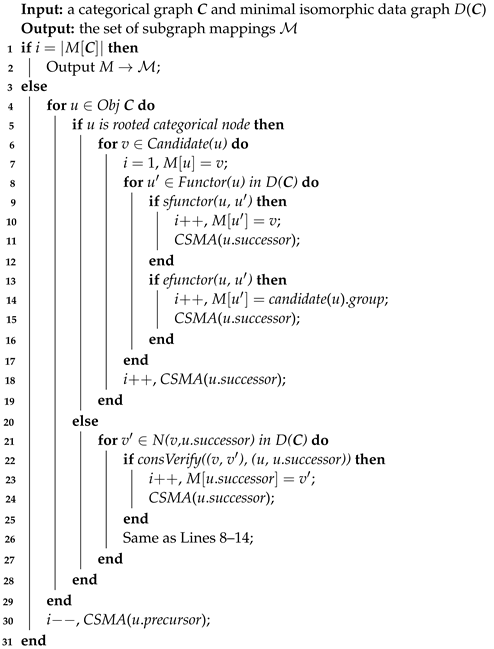 |
A number i is used to count the number of matching node pairs. If the number i is equivalent to the quantity of categorical nodes, subgraph mappings output a subgraph result into (Lines 1–2). The subgraph mappings are recorded as an array [] of size |obj C|, and stores a candidate of query node u. In actuality, each categorical node of C still corresponds to the original query node information of query graphs. Thus, when a categorical node is matched by a candidate data node, the matched query nodes corresponding to this categorical node are synchronously counted in statistical machines of each query graph. Considering categorical node in Figure 7, if is matched by a candidate data node, query nodes and are also matched, then the statistical machines of and increment the number of recording matched query–data node pairs by 1. When the number of recorded matched query–data node pairs is equivalent to the number of query nodes in one query graph, a subgraph mapping of this query graph is conducted.
The process of multi-query graph matching is classified into expanding and backtracking stages. The expanding process expands the positive candidate data nodes in the sequential forward process of categorical nodes; if a candidate data node is positive by the verification of consistency relationships, an iterative processing of the successor categorical node is executed (Lines 17–20). During the sequential backward traversal of categorical nodes, the backtracking process removes the negative candidate data node. If the candidates of a categorical node are deemed negative after verifying consistency relationships, an iterative processing of the preceding categorical node is initiated (Line 22). All the candidates of the rooted categorical node are positive without the involvement of edges; thus, a new iterative processing is executed for all candidates (Lines 7 and 15).
sFunctor and eFunctor employ the different grouping strategies to assign the candidate data nodes to symbiotic and exclusive categorical nodes (Lines 8–14). The main goal of grouping strategies is to avoid the overlapped calculation of consistency verification. If a categorical node u is matched by a candidate data node v, v is also assigned to all symbiotic categorical nodes of u. If a categorical node u is matched by a candidate data node v, an exclusive categorical node of u should calculate the consistency verification with other candidate data nodes except matched candidate v; then, the exclusive categorical nodes are sequentially matched by other un-matched candidates.
Note that the strategy of finding an optimal matching tree-based order of categorical nodes is not given in this paper, because a similar strategy has been designed in previous works [39,40]. u.successor and u.precursor denote the child and parent of categorical node u.
The methodology presented in this study comprises three primary steps: clustering of query graphs, generation of the minimal isomorphic data graph, and synchronous subgraph isomorphic mappings. The following analysis delineates the complexity in terms of both time and space within our method:
(1) Clustering of Query Graphs: The complexity of this step hinges on the clustering algorithm employed to discern similar query graphs. In our research, we adopt hierarchical clustering based on node and edge similarity, exhibiting a complexity of , where Q denotes the number of query graphs. The space complexity incurred by storing node and edge attributes, along with the similarity matrices, is . The memory usage for clustered categorical graphs scales proportionally to both the number and size of the query graphs, reflecting the necessity for storing comprehensive similarity information and cluster metadata.
(2) Generation of Minimal Isomorphic Data Graph: Subgraph isomorphism is recognized as an NP-complete problem. The fundamental complexity for isomorphism matching utilizing algorithms such as Ullmann’s is , where and signify the number of nodes in the data graph and query graph, respectively. The storage requirement for the minimal isomorphic data graph is proportional to the number of nodes () and edges () in the data graph. Utilizing an adjacency list representation, the space complexity can be expressed as , efficiently accommodating the sparse nature of real-world graphs.
(3) Synchronous Subgraph Isomorphic Mappings: For the synchronous matching of multiple query graphs, the complexity is , where denotes the time required for subgraph matching. Our synchronous algorithm further optimizes computational costs by sharing results and minimizing redundant calculations. During synchronous matching, a caching mechanism is employed to store partial matching results. The memory demands of this cache are contingent upon the number and size of the query graphs. Our caching strategy is specifically designed to minimize redundant storage by leveraging efficient data structures and algorithms, ensuring that only necessary information is retained in memory.
6. Experiments
This section conducts the experimental evaluation about the matching time, the scale and construction time of candidate over four real and synthetic datasets. Experiments were conducted on a machine with an Intel i7 3.20 GHz CPU and 64 GB memory.
6.1. Experiment Settings
Our method has been evaluated on a diverse array of both real-world and synthetic datasets, encompassing a broad spectrum of graph types. Our experiments included testing on social networks, citation networks, and biological datasets. These graphs exhibit significant variations in size, density, and degree distribution. For example, social networks typically possess small-world properties, high clustering coefficients, and scale-free degree distributions. Our method, which leverages categorical graph clustering, demonstrates robust adaptability by efficiently grouping similar substructures, thereby minimizing redundant calculations.
Experiment settings include three parts: compared algorithms, data and query sets.
Datasets: Experimental evaluation is conducted on one larger data graph and three small ones.
DBpedia 2016 (https://wiki.dbpedia.org/ (accessed on accessed on 3 July 2023)) is an open-domain knowledge base, which is constructed by the structural information from Wikipedia. It contains 5,040,948 vertices, 61,481,483 edges, 244 unique type labels and 650 unique relation labels.
Yeast and YeastH (https://chrsmrrs.github.io/datasets/docs/datasets (accessed on 3 July 2023)) are protein networks that contain 19,601 small graphs. The average numbers of nodes and edges are 21.54 and 22.84 in the Yeast dataset and 39.44 and 40.74 in the YeastH dataset, respectively.
DBLP_ct12 is a DBLP dataset, which is a collection of paper information. DBLP_ct1 contains 755 small graphs whose average numbers of nodes and edges are 52.85 and 320.09, respectively.
Graphs originating from different domains frequently exhibit significant variations in label distributions (e.g., node labels in biological networks contrast with those in social networks). Our method leverages these labels during the graph matching process.
By exploiting label information, we efficiently narrow down the search space within large graphs. For datasets characterized by diverse label sets, the algorithm promptly identifies and focuses on relevant candidate subgraphs. Conversely, in datasets with uniform labels, our method shifts its emphasis to structural properties, demonstrating versatility in handling both scenarios effectively. This dual focus on label information and structural properties enhances the robustness and adaptability of our graph matching approach.
QuerySet: The five dimensions of query graph size are extracted from the above four datasets, denoted as , , , and . The query set of collects one hundred query graphs, and each query graph contains three query nodes. The meanings of , , and are similar to . A metagraph is constructed to generate query graphs of different sizes from each dataset. Firstly, the top 10 instance types are generated randomly from datasets. Secondly, the edges of the top 10 instance types are constructed and correspond to one dataset. Finally, the metagraph is constructed by the top 10 instance types and their edges. Then, the query graphs can be generated under the guide of this metagraph. Note that the metagraph contains the self-connected edges of one node; thus, the query node can be of the same type.
Compared Algorithms: A large number of classic algorithms have been replicated and compared. The performance of eight representative in-memory subgraph matching algorithms was evaluated by different aspects [41]. In this paper, the compared methods include a basic line (VF2 algorithm [25]) and the optimized algorithm of multi-query graph matching (MQO algorithm [14]). The algorithm of VF2 [25] proposed the reduction rules of partial connectivity, which could verify the partial subgraph isomorphism with one selected data node and prune the negative candidate data earlier. The scale of reduced data nodes can be a benchmark to evaluate the reducing performance of redundant data by different algorithms. The MQO algorithm detects the common query subgraphs and caches the intermediate results to execute the general algorithm of subgraph matching for multi-query graph matching, whose experimental evaluation of matching time employs the algorithm of TurboISo.
Experiments evaluate the different scales of query graphs on four datasets, which focus on three aspects: scale of intermediate results, time of total matching and subgraph matching. The scale evaluation of intermediate results is used to verify the reducing performance of redundant data on different algorithms. The time evaluation of subgraph matching counts the matching time without the construction of a data index and clusters of multiple query graphs, and the time evaluation of total matching counts the time of the entire matching process.
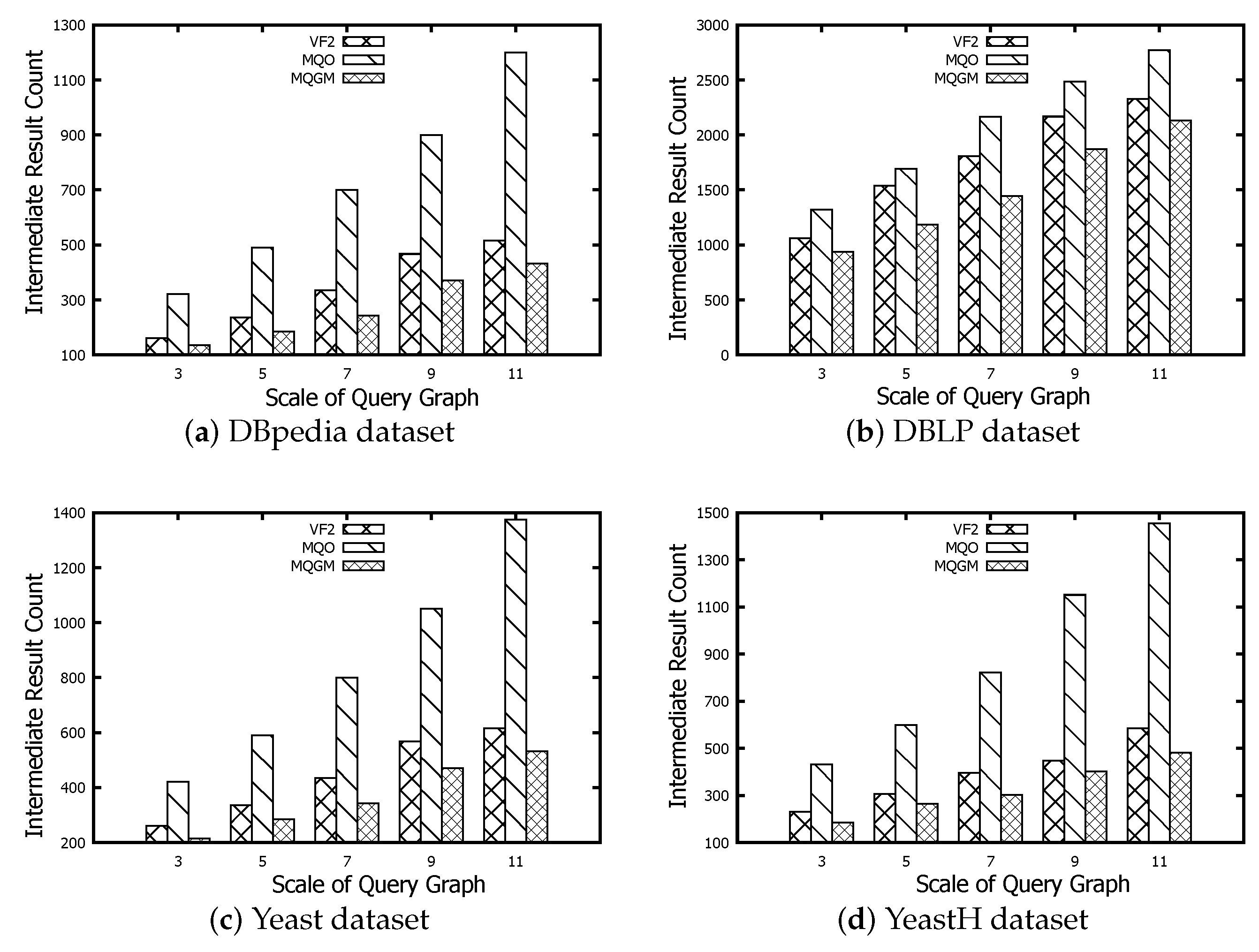
6.2. Scale Evaluation of Intermediate Results
The scale evaluation of intermediate results is used to verify the reducing performance of redundant data for different algorithms. VF2 employed the reduction rules of adjacent connectivity, similar to the candidate verification in Definition 3. MQO designed a depth-bounded tree-like partition of a data graph to cache the intermediate results limited by a fixed length. Our MQGM encapsulates the information of a categorical graph into a data-centric subgraph index, which adds the supplementary information (candidate relationships between data and query nodes, the dominating relationship between data nodes and query graphs) and does not destroy the structure of the original data graph. Meanwhile, the reduction lemmas of negative data nodes and edges are employed to further reduce the scale of redundant data.
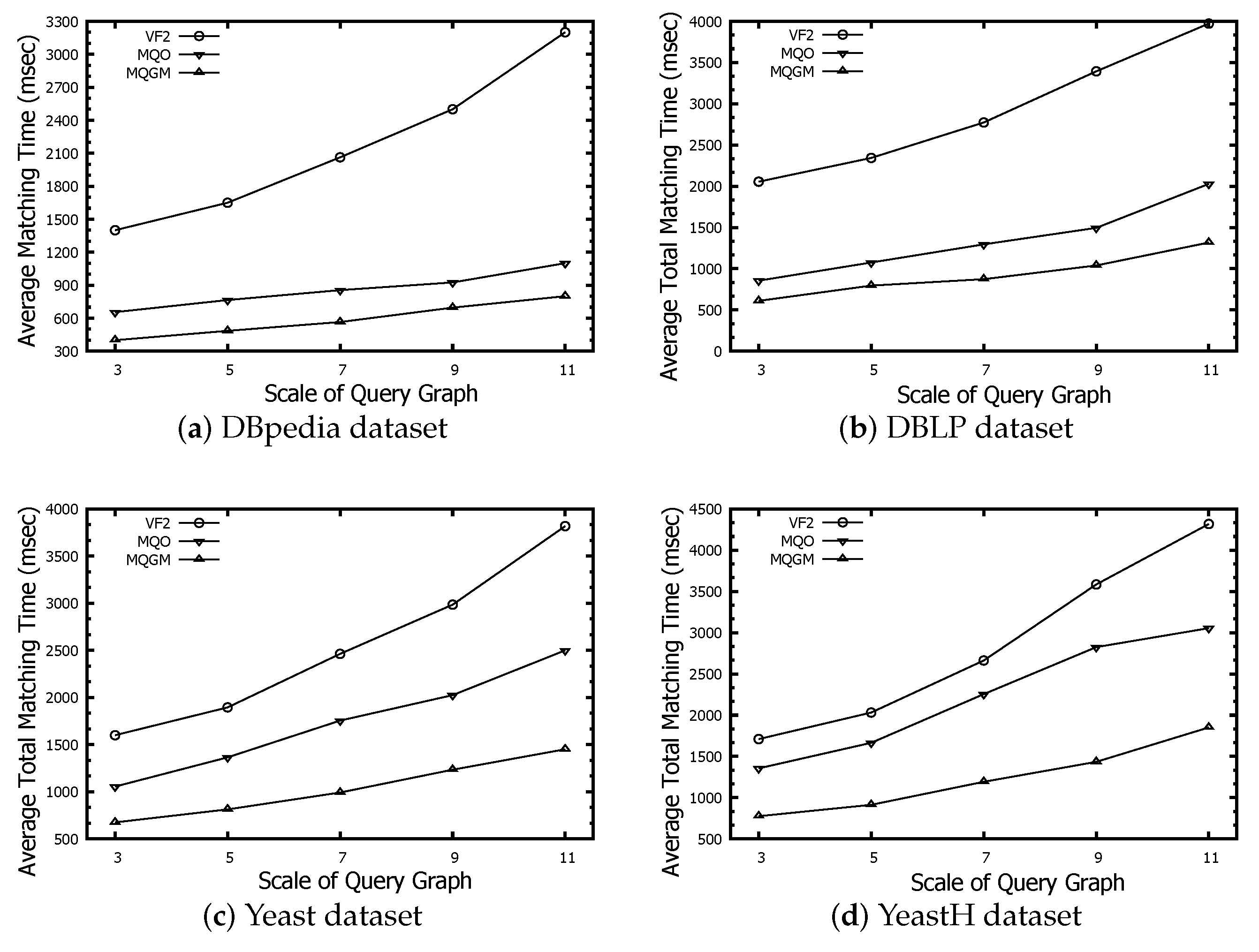
Figure 8 represents the scale evaluation of intermediate results regarding the algorithms of VF2, MQO and our MQGM on the DBpedia, DBLP, Yeast and YeastH datasets, respectively. The scale of intermediate results reflects the memory usage before subgraph matching starts executing, which indicates the number of candidate data nodes. The scale of intermediate results on VF2 can be a benchmark to evaluate the real candidate number of different queries on data graphs. The scales of intermediate results on MQO are more than real candidate numbers on VF2, because MQO should cache the common data node into different data partitions. Our MQGM can further reduce the redundant data by the reduction lemmas of negative data nodes and edges; thus, its scales of intermediate results are smaller than the real candidate number on VF2 and MQO. As the query graph size increases, so does the scale of intermediate results. The DBpedia dataset contains 244 type labels; thus, the data nodes matched to query nodes are relatively more sparse than the original data scale. The DBLP dataset has the smallest number of node types compared to the other three datasets; thus, many more data nodes can be matched to query nodes, so its scale of intermediate results is the greatest.The Yeast and YeastH datasets differ in terms of edge-to-node density. When using the VF2 method and our MQGM approach, the scale of intermediate results is smaller for YeastH compared to Yeast. The MQO method yields an opposite result due to the significant number of edges causing more overlapping data nodes to be cached across different data partitions.
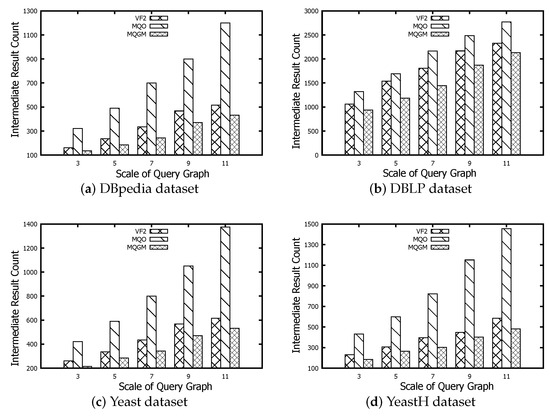
Figure 8.
Scale evaluation of intermediate results.
MQGM reduces the memory usage and efficient processing. Compared to VF2 and MQO, MQGM generates smaller intermediate results by minimizing redundant data through reduction lemmas. This results in lower memory usage before subgraph matching begins. MQGM also demonstrates versatility across diverse datasets, handling various node types and edge densities efficiently. As query graph size increases, MQGM scales well, maintaining lower intermediate result sizes compared to other methods.
6.3. Time Evaluation of Total Matching
The time evaluation of total matching counts the time of the entire matching process, including the construction of the data index and the clustering of multiple query graphs.
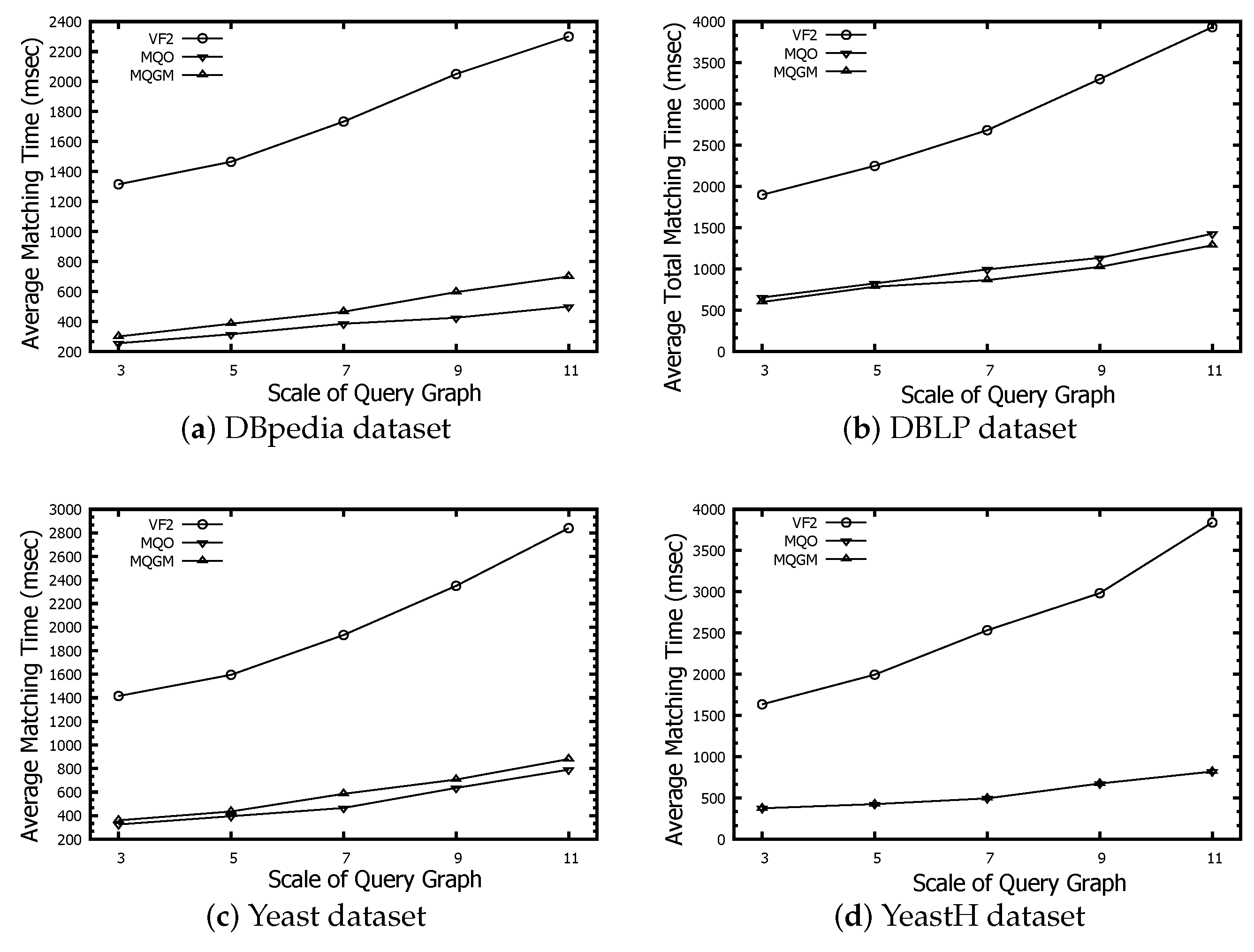
Figure 9 denotes the time evaluation of total matching regarding the VF2, MQO and MQGM algorithms on the DBpedia, DBLP, Yeast and YeastH datasets, respectively. The time-effectiveness of our MQGM is better than that of VF2 and MQO. The advantage of our MQGM is mainly reflected in the following two aspects. One aspect is that our MQGM employed a lightweight clustering strategy of multiple query graphs, based on the calculated model of Lawler quadratic assignment programming. The other aspect is that our MQGM designs a reduced verification to deeply reduce the redundant data and a subgraph index to cache the candidate nodes. Thus, the smaller scale of reserved candidates and lightweight clustering of multi-query graphs make our algorithm more efficient.
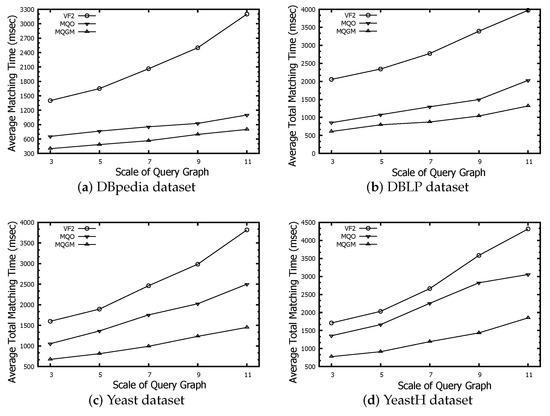
Figure 9.
Time evaluation of total matching.
MQGM demonstrates a superior level of time-effectiveness in comparison to both VF2 and MQO. Its efficiency stems from a lightweight clustering strategy for multiple query graphs, based on Lawler quadratic assignment programming, and a reduced verification process to minimize redundant data. MQGM also uses a subgraph index to cache candidate nodes, resulting in a smaller scale of reserved candidates. These features collectively enhance MQGM’s performance, making it more efficient.
6.4. Time Evaluation of Subgraph Matching
The time evaluation of subgraph matching only counts the matching time, without the construction of data index and the cluster of multiple query graph.
Figure 10 represents the time evaluation of subgraph matching regarding the VF2, MQO and MQGM algorithms on the DBpedia, DBLP, Yeast and YeastH datasets, respectively. Both MQO and MQGM identify the common subgraph of multiple query graphs and design the reduction rules/partitions of redundant data; thus, MQO and MQGM have a better matching time performance than VF2, benefiting from the reduction of redundant data. MQO caches a lot of intermediate results to accelerate the subgraph matching, resulting in the time-effectiveness of MQO being better than that of our MQGM on the DBpedia, Yeast and YeastH datasets. However, the time-effectiveness of total matching on our MQGM has a better advantage than that of MQO, because MQO requires high time consumption to construct the data partitions of intermediate results. Additionally, the time-effectiveness of MQO is less than that of our MQGM on the DBLP dataset.The DBLP dataset exhibits the densest edge-to-node relationships, leading MQO to frequently place common nodes into various data partitions. Consequently, searching within these extensive data partitions becomes time-consuming.
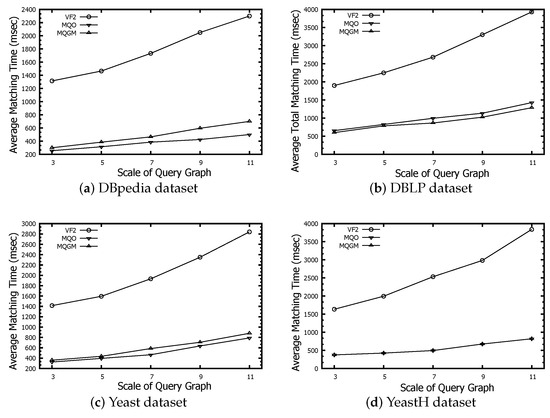
Figure 10.
Time evaluation of subgraph matching.
MQGM exhibits superior total matching time-effectiveness in comparison to MQO, particularly when dealing with datasets characterized by dense edge-to-node relationships, such as DBLP. MQGM reduces redundant data through common subgraph identification and partitioning, leading to better performance than VF2. While MQO caches intermediate results for faster subgraph matching, it consumes significant time when constructing data partitions, making MQGM more efficient in total matching. MQGM’s performance is also better than MQO on DBLP due to reduced searching time in large data partitions.
In summary, extensive empirical studies on four datasets demonstrate that our MQGM technique outperforms MQO by up to 5 times in terms of total matching time-efficiency, and VF2 by up to 6 times in terms of space complexity.
One of the core innovations of our method lies in the introduction of categorical graphs, which cluster similar query graphs together. This innovation enables substantial reductions in redundant calculations by processing shared substructures just once, a feature that is not present in other contemporary techniques.
Unlike other methods that address queries in isolation, our algorithm employs synchronous subgraph matching, enabling the simultaneous processing of multiple queries. This capability is particularly advantageous in scenarios such as question-answering systems or semantic search engines, where efficient handling of multiple similar queries is imperative.
Furthermore, our methodology introduces the generation of a minimal isomorphic data graph. This graph focuses solely on the pertinent sections of the data graph that are most likely to contain the query subgraphs, thereby further minimizing unnecessary computations.
7. Conclusions
This paper studies a novel combinatorial problem of multigraph matching and subgraph matching, named the multi-query graph matching problem. Then, a category-driven method is designed to solve the problem of multi-query graph matching.
Firstly, it gathers similar query graphs into one cluster, and then employs the edges of node labels to construct the clustered similar query graphs into one categorical graph. A potential near-optimal solution for the multi-query graph matching problem is analyzed based on the maximal correspondence of query graphs and minimal isomorphic data graphs. Then, a category-driven method is proposed to solve the problem of multi-query graph matching that gathers the query graphs into one category graph, based on the score of node-to-node and edge-to-edge correspondences. Secondly, it generates a minimal isomorphic data graph from the data graph induced by the categorical graph. The lemmas of negative data nodes and edges are proposed to reduce the redundant candidate in the matching algorithm. Finally, it employs the functors to analyze the inclusive and equivalence relationships of query nodes, and then conducts all the subgraph isomorphic mappings of data graph on the category graph synchronously. Extensive empirical studies on real and synthetic datasets demonstrate that our techniques outperform the state-of-the-art algorithms.
Author Contributions
Conceptualization: Y.S.; Methodology: B.N.; Validation: R.Q.; Software: X.C.; Writing—Original Draft Preparation: Y.S; Writing—Review & Editing: R.Q. and Y.S.; Supervision: R.Q. and H.C.; Funding Acquisition: R.Q., H.C. and Y.S. All authors have read and agreed to the published version of the manuscript. Authorship is limited to those who have made substantial contributions to the reported work.
Funding
This work was supported by the Liaoning Provincial Natural Science Foundation (No. 2022-BS-338, No. 2024-MS-174), the Basic Research Foundation of Liaoning Province (No. LJKQZ20222436, No. 2022JH2/101300270) and the General Project of the Humanities and Social Sciences Planning Fund of the Ministry of Education (No. 23YJAZH109).
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Ye, Y.; Lian, X.; Chen, M. Efficient Exact Subgraph Matching via GNN-based Path Dominance Embedding. Proc. VLDB Endow. 2024, 17, 1628–1641. [Google Scholar] [CrossRef]
- Yang, Q.; Yu, D.; Chen, X.; Xu, Y.; Yan, W.; Hu, B. Feature envy detection based on cross-graph local semantics matching. Inf. Softw. Technol. 2024, 174, 107515. [Google Scholar] [CrossRef]
- Lou, Y.; Wang, C. A Generalized Community-Structure-Aware Optimization Framework for Efficient Subgraph Matching in Social Network Analysis. IEEE Trans. Comput. Soc. Syst. 2024, 11, 2545–2557. [Google Scholar] [CrossRef]
- Cho, M.; Lee, J.; Lee, K.M. Reweighted Random Walks for Graph Matching. In Proceedings of the 11th European Conference on Computer Vision, Heraklion, Crete, Greece, 5–11 September 2010; pp. 492–505. [Google Scholar]
- Wang, T.; Jiang, Z.; Yan, J. Clustering-Aware Multiple Graph Matching via Decayed Pairwise Matching Composition. In Proceedings of the Thirty-Fourth AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; pp. 1660–1667. [Google Scholar]
- Yang, Z.; Zhang, W.; Lin, X.; Zhang, Y.; Li, S. HGMatch: A Match-by-Hyperedge Approach for Subgraph Matching on Hypergraphs. In Proceedings of the 39th IEEE International Conference on Data Engineering, Anaheim, CA, USA, 3–7 April 2023; pp. 2063–2076. [Google Scholar]
- Hu, S.; Zou, L.; Yu, J.X.; Wang, H.; Zhao, D. Answering Natural Language Questions by Subgraph Matching over Knowledge Graphs. IEEE Trans. Knowl. Data Eng. 2018, 30, 824–837. [Google Scholar] [CrossRef]
- Wang, X.; Chai, L.; Xu, Q.; Yang, Y.; Li, J.; Wang, J.; Chai, Y. Efficient Subgraph Matching on Large RDF Graphs Using MapReduce. Data Sci. Eng. 2019, 4, 24–43. [Google Scholar] [CrossRef]
- Li, F.; Zou, Z. Subgraph matching on temporal graphs. Inf. Sci. 2021, 578, 539–558. [Google Scholar] [CrossRef]
- Zheng, W.; Zou, L.; Peng, W.; Yan, X.; Song, S.; Zhao, D. Semantic sparql similarity search over rdf knowledge graphs. Proc. VLDB Endow. 2016, 9, 840–851. [Google Scholar] [CrossRef]
- Cai, T.; Li, J.; Mian, A.S.; Li, R.; Yu, J.X. Target-aware holistic influence maximization in spatial social networks. IEEE Trans. Knowl. Data Eng. 2020, 34, 1993–2007. [Google Scholar] [CrossRef]
- Li, J.; Cai, T.; Deng, K.; Wang, X.; Sellis, T.; Xia, F. Community-diversified influence maximization in social networks. Inf. Syst. 2020, 92, 101522. [Google Scholar] [CrossRef]
- Lawler, E.L. The Quadratic Assignment Problem. Manag. Sci. 1963, 9, 586–599. [Google Scholar] [CrossRef]
- Ren, X.; Wang, J. Multi-Query Optimization for Subgraph Isomorphism Search. Proc. VLDB Endow. 2016, 10, 121–132. [Google Scholar] [CrossRef]
- Hao, K.; Lai, L. Towards the Scheduling of Vertex-constrained Multi Subgraph Matching Query. In Proceedings of the 2020 International Conference on Management of Data, Portland, OR, USA, 14–19 June 2020; pp. 2857–2859. [Google Scholar]
- He, H.; Singh, A.K. Graphs-at-a-time: Query language and accessmethods for graph databases. In Proceedings of the ACM SIGMOD international Conference on Management of Data, Vancouver, BC, Canada,, 9–12 June 2008; pp. 405–418. [Google Scholar]
- Kim, K.; Seo, I.; Han, W.-S.; Lee, J.-W.; Hong, S.; Chafi, H.; Shin, H.; Jeong, G. Turboflux: A fast continuous subgraph matching system for streaming graph data. In Proceedings of the ACM SIGMOD International Conference on Management of Data, Vancouver, BC, Canada,, 9–12 June 2018; pp. 411–426. [Google Scholar]
- Yan, J.; Wang, J.; Zha, H.; Yang, X.; Chu, S.M. Consistency-Driven Alternating Optimization for Multigraph Matching: A Unified Approach. IEEE Trans. Image Process. 2015, 24, 994–1009. [Google Scholar] [CrossRef] [PubMed]
- Yan, J.; Cho, M.; Zha, H.; Yang, X.; Chu, S.M. Multi-Graph Matching via Affinity Optimization with Graduated Consistency Regularization. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 1228–1242. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Z.; Wang, T.; Yan, J. Unifying Offline and Online Multi-Graph Matching via Finding Shortest Paths on Supergraph. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 3648–3663. [Google Scholar] [CrossRef]
- Pachauri, D.; Kondor, R.; Singh, V. Solving the multi-way matching problem by permutation synchronization. In Proceedings of the 26th International Conference on Neural Information Processing Systems, Lake Tahoe, NV, USA, 5–10 December 2013; pp. 1860–1868. [Google Scholar]
- Huang, Q.-X.; Guibas, L.J. Consistent Shape Maps via Semidefinite Programming. Comput. Graph. Forum 2013, 32, 177–186. [Google Scholar] [CrossRef]
- Swoboda, P.; Kainmüller, D.; Mokarian, A.; Theobalt, C.; Bernard, F. A Convex Relaxation for Multi-Graph Matching. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 11156–11165. [Google Scholar]
- Ullmann, J.R. An algorithm for subgraph isomorphism. J. ACM 1976, 23, 31–42. [Google Scholar] [CrossRef]
- Cordella, L.P.; Foggia, P.; Sansone, C.; Vento, M. A (sub)graph isomorphism algorithm for matching large graphs. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 1367–1372. [Google Scholar] [CrossRef]
- Zhao, P.; Han, J. On graph query optimization in large networks. Proc. VLDB Endow. 2010, 3, 340–351. [Google Scholar] [CrossRef]
- Kim, H.; Choim, Y.; Park, K.; Lin, X.; Hong, S.-H.; Han, W.-S. Versatile Equivalences: Speeding up Subgraph Query Processing and Subgraph Matching. In Proceedings of the SIGMOD’21: International Conference on Management of Data, Virtual Event, China, 20–25 June 2021; pp. 925–937. [Google Scholar]
- Jin, T.; Li, B.; Li, Y.; Zhou, Q.; Ma, Q.; Zhao, Y.; Chen, H.; Cheng, J. Circinus: Fast Redundancy-Reduced Subgraph Matching. Proc. ACM Manag. Data 2023, 1, 12:1–12:26. [Google Scholar] [CrossRef]
- Mawhirter, D.; Reinehr, S.; Holmes, C.; Liu, T.; Wu, B. GraphZero: A High-Performance Subgraph Matching System. ACM SIGOPS Oper. Syst. Rev. 2021, 55, 21–37. [Google Scholar] [CrossRef]
- Han, W.-S.; Lee, J.; Lee, J.-H. Turboiso: Towards ultrafast and robust subgraph isomorphism search in large graph databases. In Proceedings of the ACM SIGMOD International Conference on Management of Data, New York, NY, USA, 22–27 June 2013; pp. 337–348. [Google Scholar]
- Bi, F.; Chang, L.; Lin, X.; Qin, L.; Zhang, W. Efficient subgraph matching by postponing cartesian products. In Proceedings of the ACM SIGMOD International Conference on Management of Data, San Francisco, CA, USA, 26 June–1 July 2016; pp. 1199–1214. [Google Scholar]
- Bouhenni, S.; Yahiaoui, S.; Nouali-Taboudjemat, N.; Kheddouci, H. A Survey on Distributed Graph Pattern Matching in Massive Graphs. ACM Comput. Surv. 2022, 54, 36:1–36:35. [Google Scholar] [CrossRef]
- Wang, Z.; Gu, R.; Hu, W.; Yuan, C.; Huang, Y. BENU: Distributed Subgraph Enumeration with Backtracking-Based Framework. In Proceedings of the 2019 IEEE 35th International Conference on Data Engineering (ICDE), Macao, China, 8–11 April 2019; pp. 136–147. [Google Scholar]
- Zhang, Y.; Zheng, W.; Zhang, Z.; Peng, P.; Zhang, X. Hybrid Subgraph Matching Framework Powered by Sketch Tree for Distributed Systems. In Proceedings of the 2022 IEEE 38th International Conference on Data Engineering (ICDE), Kuala Lumpur, Malaysia, 9–12 May 2022; pp. 1031–1043. [Google Scholar]
- Yang, J.; Fang, S.; Gu, Z.; Ma, Z.; Lin, X.; Tian, Z. TC-Match: Fast Time-constrained Continuous Subgraph Matching. Proc. VLDB Endow. 2024, 17, 2791–2804. [Google Scholar] [CrossRef]
- Le, W.; Kementsietsidis, A.; Duan, S.; Li, F. Scalable Multi-query Optimization for SPARQL. In Proceedings of the 2012 IEEE 28th International Conference on Data Engineering, Arlington, VA, USA, 1–5 April 2012; pp. 666–677. [Google Scholar]
- Jiang, G.; Zhao, Y.; Li, Y.; Liu, Z. Wings: Efficient Online Multiple Graph Pattern Matching. In Proceedings of the 2024 IEEE 40th International Conference on Data Engineering (ICDE), Utrecht, The Netherlands, 13–16 May 2024; pp. 3013–3027. [Google Scholar] [CrossRef]
- Garey, M.R.; Johnson, D.S. Computers and Intractability: A Guide to the Theory of NP-Completeness; W. H. Freeman: New York, NY, USA, 1979. [Google Scholar]
- Sun, Y.; Jiang, W.; Liu, S.; Li, G.; Ning, B. Accelerating Subgraph Matching by Anchored Relationship on Labeled Graph. Knowl.-Based Syst. 2021, 232, 107502. [Google Scholar] [CrossRef]
- Sun, Y.; Li, G.; Du, J.; Ning, B.; Chen, H. A Subgraph Matching Algorithm Based on Subgraph Index for Knowledge Graph. Front. Comput. Sci. 2022, 16, 163606. [Google Scholar] [CrossRef]
- Sun, S.; Luo, Q. In-Memory Subgraph Matching: An In-depth Study. In Proceedings of the 2020 ACM SIGMOD International Conference on Management of Data, Portland, OR, USA, 14–19 June 2020; pp. 1083–1098. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).