Abstract
The proliferation of edge devices and advancements in Internet of Things technology have created a vast array of distributed data sources, necessitating machine learning models that can operate closer to the point of data generation. Traditional centralized machine learning approaches often struggle with real-time big data applications, such as climate prediction and traffic simulation, owing to high communication costs. In this study, we introduce random node entropy pairing, a novel distributed learning method for artificial neural networks tailored to distributed computing environments. This method reduces communication overhead and addresses data imbalance by enabling nodes to exchange only the weights of their local models with randomly selected peers during each communication round, rather than sharing the entire dataset. Our findings indicate that this approach significantly reduces communication costs while maintaining accuracy, even when learning from non-IID local data. Furthermore, we explored additional learning strategies that enhance system accuracy by leveraging the characteristics of this method. The results demonstrate that random node entropy pairing is an effective and efficient solution for distributed learning in environments where communication costs and data distribution present significant challenges.
1. Introduction
The growing utilization and advancement of artificial intelligence (AI) across various applications have sparked significant interest in using AI to process large datasets [1,2]. However, managing big data that exceed the processing capabilities of current systems presents substantial challenges for machine learning (ML) and data mining techniques [3]. This is particularly evident in fields such as climate prediction, earthquake simulation, and traffic simulation, where real-time processing of vast, continuously collected datasets is crucial [4,5,6,7]. To overcome these challenges, research efforts have increasingly leveraged the exceptional scalability of distributed computing. Distributed big data processing technologies, such as Hadoop MapReduce and Spark, have been successfully implemented in cloud computing environments. However, exchanging large volumes of data generated by emerging big data technologies, including AI, can significantly strain existing communication networks [8,9,10,11].
These methods [12,13,14,15] still rely on broadcasting, which increases dependency on a central server, making the overall system performance highly dependent on the server’s capabilities. In addition, addressing issues at the hardware switch level can lead to compatibility issues with various applications and raise concerns regarding communication costs in a server-centric centralized approach [16]. Many large-scale communication models, including the federated learning models, use the message passing interface (MPI). Different communication types incur varying costs depending on the communication model. However, broadcasting incurs significantly higher communication costs than other types of communication [17,18]. Adopting a peer-to-peer (P2P) communication approach for data transmission can alleviate network traffic problems and mitigate issues associated with bottlenecks [19].
Moreover, even with the reduction in communication costs, the overall learning efficacy in a decentralized system may still be compromised due to imbalances in non-independent and identically distributed (non-IID) data held by individual nodes [20]. To address the global imbalances in the data used for distributed training, a data augmentation strategy was introduced in [21]. However, excessive reliance on data augmentation may add computational overhead on the local nodes, potentially contributing to noise in the learning process. Moreover, when dealing with non-IID data, the overall accuracy of the system can be significantly affected by the batch size. This is because variations in data distribution across different mini-batches may lead to fluctuations in the statistical estimates that are critical for batch normalization [22,23]. In the presence of non-IID data, such fluctuations can reduce the effectiveness of batch normalization.
In this paper, we propose a novel method for training artificial neural networks (ANNs) within a decentralized distributed computing system. Our approach aims to reduce communication costs while maintaining accuracy through weight sharing via random node pairing based on node entropy. This technique enables each local node to effectively utilize its local data. Periodically, after a local node completes a training cycle, its model-weighted parameters are shared and updated with a randomly selected local node. This pairing approach enables all the nodes in a distributed computing system to probabilistically update their models, thereby gaining access to global data information.
We compared the proposed random node entropy pairing (RNEP) method with existing techniques, such as applying global weights to local node models. Our method facilitates parameter exchange without extensive data transmission, thereby reducing the communication costs. Furthermore, in scenarios where local nodes encounter challenges due to imbalanced data or data scarcity, exchanging weights with other nodes allows local nodes to learn global features. This approach minimizes accuracy loss in local nodes while maintaining high accuracy for locally abundant data.
The RNEP method is well suited to diverse industry use cases, providing distinct advantages. In heterogeneous IoT networks, RNEP effectively mitigates challenges associated with non-IID data distributions, enhancing model accuracy and fairness. In healthcare, where collaborative machine learning must contend with data privacy and varied data distributions, RNEP’s entropy regularization allows secure cooperation among institutions, leading to more generalizable models. Additionally, RNEP demonstrates utility in local sensor network environments such as wildfire monitoring systems, where low-power devices operate independently [24]. By enabling efficient operation on these low-power devices, RNEP facilitates continuous monitoring and real-time data analysis, which are critical for timely response in wildfire detection and prevention.
The second chapter provides an in-depth exploration of decentralized distributed computing, focusing on updates to the weight parameters of node models and a comparison of communication costs, followed by a discussion of related work. In the third chapter, we compare our experimental results with existing methods, detail the experimental setup, and summarize our findings. The fourth chapter concludes the paper with research discussions and a strategic outlook.
2. Related Works
Owing to the substantial parameter size of state-of-the-art artificial intelligence (AI) algorithms based on deep learning, a significant exchange of intermediate data between nodes is often required. The approach presented in [12] addresses this challenge by partitioning a large dataset at the server level and transmitting only the necessary feature vectors to the nodes for overall training, thus eliminating the need to divide the data across local nodes. In [13], an asynchronous global weight update (AGWU) mechanism was introduced to reduce synchronization time between nodes and enhance the efficiency of distributed training. The method in [14] focused on a decentralized approach in which each node trains solely on its local dataset, computes local output weights, and updates the global model using a decentralized average consensus (DAC) method. In addition, the authors of [15] proposed a technique in which multiple training steps are conducted locally before the parameters are updated on the server, thereby further optimizing the communication overhead in distributed training scenarios.
The authors of [14] proposed a distributed learning algorithm for random vector functional link (RVFL) networks, designed to operate in a decentralized manner without reliance on a centralized server in a distributed ML environment. The algorithm functions in a fully distributed manner, utilizing a DAC and an alternating direction method of multipliers (ADMM). It computes a common learner model for local datasets and optimizes overall system performance. However, in [14], uniformly classified training data were distributed to all nodes without investigating the performance of the local nodes using unbalanced class data.
The bi-layered parallel training (BPT-CNN) method in [13] introduced a structure that utilizes multiple processors for the parallel processing of large-scale training by partitioning the convolutional layers and local weights of the CNN model. Utilizing a separate parameter server, this approach reduces the computation time by calculating global weights using locally computed weights from local processors. However, data transmission to each processor is necessary during task allocation based on processor capabilities using task management at the main server, resulting in relatively higher communication costs compared to cases where only parameters or class feature vectors are transmitted.
In federated learning approaches, computations are typically performed by local clients with only the parameters aggregated by a central server. Although this decentralized approach avoids the need to centralize large datasets and enables pattern estimation, it is susceptible to imbalanced data or non-IID distributions. FedAvg [25] addresses some of these challenges by introducing parameter averaging. However, these techniques may still suffer from significant communication overhead and accuracy degradation in non-IID settings.
In [12], a method was proposed for normalizing local training processors using globally averaged feature vectors without transmitting local data from regional hospitals for COVID-19 detection purposes. Instead of transmitting the model parameters, globally averaged feature vectors for each class on the local node are transmitted, thus reducing communication load. However, when deriving globally averaged feature vectors using the local feature vectors for each class, issues may arise if the data available to the local node are unbalanced, leading to either insufficient or excessive influence on the global model. Additionally, sending parameters to a central server and broadcasting updates to clients increase communication costs. Ongoing research focuses on addressing these challenges by quantifying the uncertainty or randomness of random variables using entropy [26,27,28,29].
FedEntropy [30] is an efficient federated learning approach designed to improve classification accuracy in non-IID scenarios. By employing a maximum entropy judgment method, FedEntropy selects and aggregates local models that maximize the overall entropy, thereby enhancing the global model accuracy and reducing communication overhead. However, this approach relies on a central server for computations and client updates. In contrast, our proposed method, RNEP, minimizes communication requirements by leveraging a random node pairing mechanism, which maintains accuracy even with non-IID data distributions. This approach not only complements federated learning by providing a robust alternative for decentralized learning but also enhances its applicability in scenarios where data heterogeneity is prevalent.
In the distributed computing environment of an ANN, communication cost is another important performance metric. Communication cost is expressed in terms of time complexity, which refers to the maximum time taken by any local node in the system to execute an algorithm and communicate the results. In cases involving asynchronous communication between nodes, it is defined as the interval between the time slots when the algorithm starts and ends within the overall algorithm time slot [31]. In the context of communication costs, a single time slot represents either a transmission or reception message. Each node calculates this cost based on its own clock and does not usually declare a communication cost dependent on synchronous timing [32].
Communication costs can significantly increase with the growth of nodes and data when using broadcasting methods. Recent research indicates that compared to the time slots required by each node in the broadcast approach, P2P communication incurs a communication cost of time slots when messages are sent directly to recipients on arbitrary labeled nodes [31,32,33]. Here, m denotes the aggregate number of support vectors across all local models. Considering the relationship between the node’s neighbor count , node count , and the total number of support vectors , the complexity of the broadcast method may exceed . While responds logarithmically, and with a squared logarithmic term to and , reacts directly to the node’s neighbor count. As a result, the complexity of the broadcast method can increase more rapidly than that of the P2P method as the value rises. These empirical findings underscore the advantages of P2P communication over traditional broadcast methodologies. The broadcast scheme requires each node to disseminate messages to all the participating nodes, resulting in significant communication overhead [34].
By contrast, P2P communication facilitates the direct messaging of designated nodes, thereby reducing communication costs. Although communication costs escalate when each node in the entire group broadcasts, exchanging information through P2P communication results in remarkably lower communication costs than broadcasting. Even as the total number of nodes increases, the difference remains significantly smaller, underscoring the efficiency of P2P communication in minimizing communication costs.
Centralized distributed computing systems, such as distributed cloud computing, involve a central server or controller that manages the overall data processing and tasks and mediates communication among all system nodes. This approach mitigates bias in the overall data and allows control over the learning volume based on node learning speeds [35]. However, it relies heavily on a central server, and its performance significantly impacts the entire system’s learning. Performance degradation due to bottlenecks remains a concern [36]. By contrast, decentralized computing enables individual nodes to manage learning and data, thereby enabling local data processing. It offers high scalability, facilitates easy addition or removal of nodes, lowers communication costs, and enables fast data processing in real time. However, data biases may arise at the node level, and evaluating the reliability of the weight information for an objective function at the system level can be challenging [37].
The Canadian Institute for Advanced Research-10 (CIFAR-10) dataset [38] consists of 60,000 32 × 32 color images and is commonly used as a benchmark to evaluate model performance in image classification. The dataset comprises 10 image classes. Despite its relatively low resolution, the CIFAR-10 dataset includes a wide variety of objects and scenes with distinct features. This diversity makes the dataset suitable for assessing general model performance.
Imagenette [39] is a subset of 10 easily classified classes from the ImageNet dataset. We used full-size images, cropped them to 90 × 90 pixels, and used the data for our experiments. This selection offers a simpler benchmark for model evaluation than the full ImageNet dataset, enabling efficient model performance testing. The 90 × 90 cropping ensured a uniform input size, which reduced computational overhead and accelerated the training process.
ResNet-18 [40], a deep neural network model introduced by He et al. in 2015, has become the cornerstone of image classification and recognition tasks. As a part of the ResNet series, this model employs residual learning to effectively address the vanishing gradient problem that often occurs in deep networks. Comprising 18 weight layers, ResNet-18 features residual blocks that enable direct connections between inputs and outputs. This architecture has proven highly effective across a range of computer vision tasks and is frequently used in experiments owing to its reliability.
3. Proposed Methodology
We conducted experiments aimed at reducing node-specific losses while incorporating global weight updates. Our method, called random node entropy pairing (RNEP), randomly pairs the nodes within a cluster to exchange and update weights. The exchange process is guided by the model weights and entropy values of the local data at each node. By considering entropy, the updates are more reflective of the diversity of data across nodes, ensuring the unique characteristics of the local datasets are preserved.
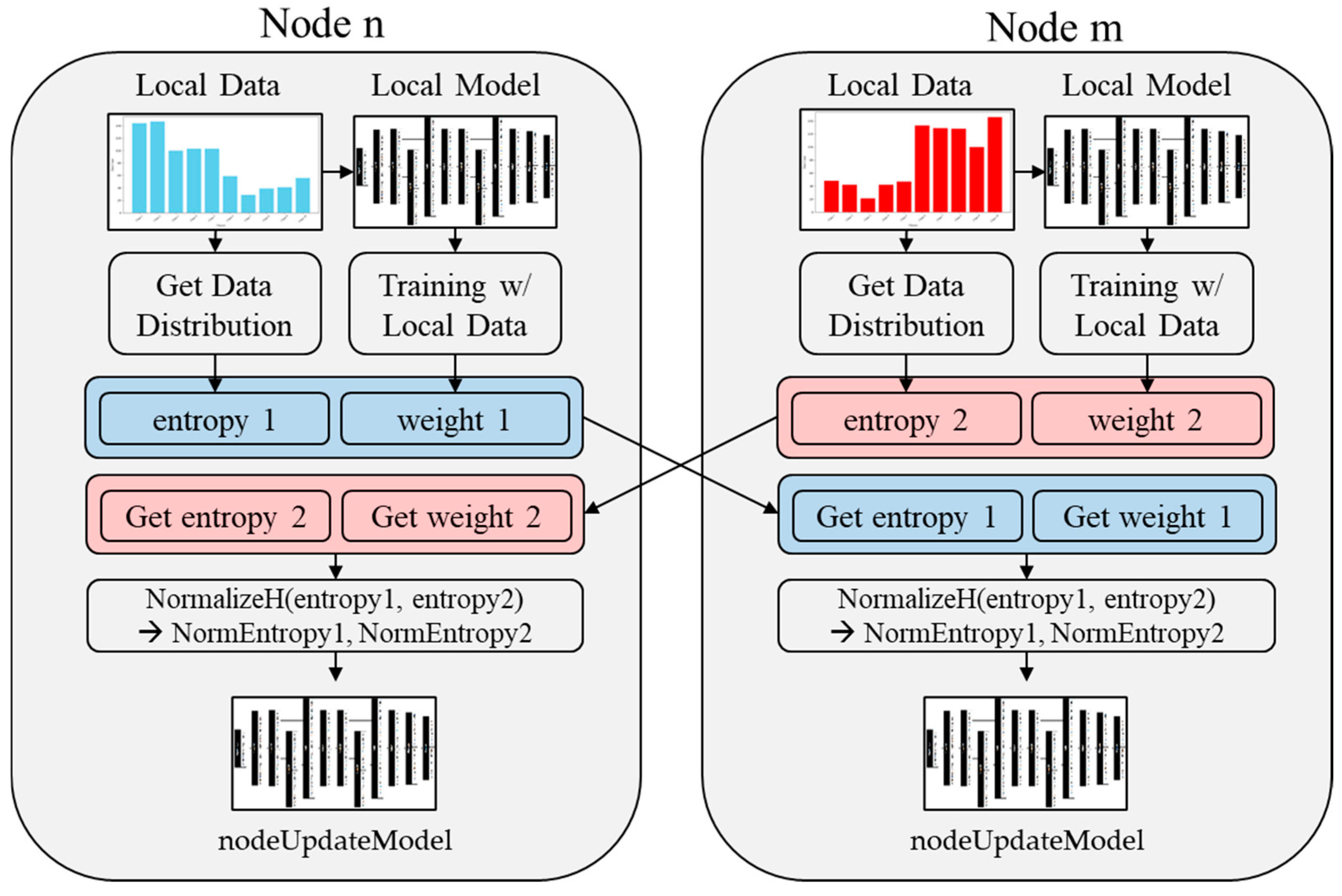
Figure 1 illustrates the RNEP system process. Each node operates independently with its local data and model, calculating entropy based on the data distribution and updating model weights accordingly. When nodes are paired, they exchange entropy values and model weights, which are then normalized to maintain consistency. The normalized weights are used to update the local models, gradually aligning them with the global model distribution. This repeated interaction ensures that all nodes contribute to and benefit from the shared learning process, achieving convergence over successive communication rounds.
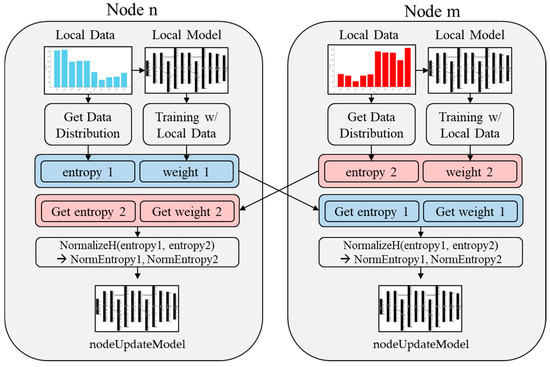
Figure 1.
RNEP system pair node process.
This approach strikes a balance between preserving the local model performance and achieving global consistency, addressing the challenges posed by non-IID data. Consequently, the learning process becomes more adaptive and equitable, improving the overall model accuracy while effectively reducing node-specific losses.
3.1. Random Node Pairing
In this decentralized distributed system, multiple edge devices serve as nodes, each with its own local data and corresponding model weights. In each communication round, two nodes are randomly selected and paired. The paired nodes exchange the model weights and share the entropy of their local data distribution. This random pairing and exchange process in each round helps the model weights across all the nodes converge gradually. As nodes repeatedly interact and share information, the local model weights at each node begin approximating the global weight distribution. Ultimately, despite the decentralized and distributed setup, each node increasingly reflects the global model as the communication rounds progress.
3.2. Weight and Entropy Exchange
Entropy was used to adjust the weight updates between nodes. The entropy calculation method is as follows:
where represents the entropy of data distribution X, and is the probability of occurrence of the value in the local dataset. By implementing RNEP, we aim to maintain the diversity and specific features of local datasets, thereby improving the overall performance of the global model.
Entropy acts as an indicator of the non-IID nature of the data at each node. Higher entropy reflects a more diverse local dataset, making it closer to the IID and more representative of the global distribution. In contrast, lower entropy indicates a more skewed or biased dataset, signifying a higher degree of non-IID data.
The PairingExchange procedure in Algorithm 1 enables the exchange of entropy values and model weights between two pairs of nodes. The current node’s weight and entropy are stored as weight1 and entropy1, while the paired node’s weight and entropy are received using the ReceiveWeight and ReceiveH functions. The functions ReceiveWeight and ReceiveH facilitate data exchange between paired nodes. These functions are implemented using the MPI communication primitives provided by the mpi4py library, which is built on OpenMPI. Specifically, comm.recv(source = dest_rank) is used to receive data from a designated source node, allowing each node to efficiently obtain entropy and weight values from its paired node.
| Algorithm 1 PairingExchange: Paired Node Exchange in RNEP |
|
The pairing-exchange allows each node to adjust its model weights based on its own data diversity and that of the paired node. Entropy values play a key role in this process; nodes with lower entropy (indicating more biased data distributions) have less influence on the weight updates of other nodes, helping maintain a balanced and consistent global model across the network.
Before updating the weights, the NormalizeH procedure in Algorithm 2 normalizes the entropy values exchanged between two nodes such that their sum is one. This ensures that each node’s data diversity has a balanced influence on the final weight update. Adjusting the weights based on entropy effectively handled non-IID data and promoted fair learning across the nodes. Nodes with lower entropy, indicating biased data, reduce the influence of external weights to avoid overfitting, while higher-entropy nodes, reflecting diverse data, prioritize external contributions. This fosters data diversity, enhances generalization, and improves the accuracy of the global model, ensuring balanced predictions across all classes.
| Algorithm 2 NormalizeH: Entropy Normalization in RNEP |
|
3.3. Weight Update Based on Entropy
This method leverages high entropy values to guide weight updates, which not only preserves unique local data characteristics but also significantly reduces communication overhead. Additionally, the proposed RNEP method is expected to achieve accuracy comparable to existing techniques while offering improved global weight convergence and enhanced communication efficiency. This procedure updates the model at each node based on the exchanged weights and normalized entropy values.
The nodeUpdateModel procedure in Algorithm 3 updates the model of the current node (nodeIndex) by utilizing the weights and entropy from a randomly paired node (nodePairedIndex). First, the normalizeH function normalizes the entropy values of both nodes. The model weights are updated by calculating the weighted sum of the weights of the two nodes, with the contributions determined by the normalized entropy values. This ensures that the model adapts based on the diversity of data at each node. The updated model replaces the local model, balancing the influence of the data from both nodes. By dynamically adjusting weight updates based on entropy, this method effectively handles non-IID data and promotes balanced and fair learning across all nodes.
| Algorithm 3 nodeUpdateModel: updating weight in RNEP |
|
4. Experiment and Discussion
4.1. Experimental Setup
We established a simulation environment for decentralized distributed computing. The environment consisted of nodes specializing in edge AI computing, including 1 NVIDIA Xavier NX and 14 NVIDIA Jetson NANO devices, all connected to a single router. We configured 15 nodes to establish a communication environment aligning with the constraints imposed by the OpenMPI settings of the edge devices, as well as the experimental limitations inherent to each local node’s communication and data processing capacity. These devices are commonly used in edge computing experiments owing to their optimization for local GPU computing. They offer strong performance in GPU-intensive tasks on edge devices, particularly in model optimization for AI operations [41,42,43,44].
The open-source message passing interface (OpenMPI) environment was implemented using the Python mpi4py library, version 3.1.4. Open-source libraries, such as OpenMPI, enable users to easily configure systems and apply them efficiently to high-performance computer clusters. This mechanism provides reliable communication and synchronization across distributed nodes, which is crucial for ensuring consistency and scalability within our networked environment. Additionally, OpenMPI offers broad compatibility with a variety of communication environments, allowing researchers to replicate our setup on different hardware and network configurations. This flexibility enhances the reproducibility and accessibility of our model, making it easier for other researchers to replicate our experimental conditions.
We used Python version 3.6.9 and TensorFlow version 2.5.1. MPI is a technology that facilitates data communication between processors or nodes and is widely employed in distributed and parallel computing systems [45,46,47]. We configured the system to enable each edge device to perform independent learning of local data by leveraging its respective GPU.
We employed the ResNet-18 [40] architecture on edge devices to conduct classification tasks using two datasets, CIFAR-10 [38] and Imagenette [39], each comprising 10 classes. Figure 2 shows randomly sampled images from both datasets. Since Imagenette consists of images of various sizes, we resized them to 90 × 90 pixels for this experiment to facilitate testing on the edge device.

Figure 2.
Dataset images: (a) sample images from CIFAR-10, with original size of 32 × 32 pixels; (b) sample images from Imagenette, preprocessed to 90 × 90 pixels.
Although ResNet-18 has a relatively small parameter size, it is well suited for our experimental environment because of its ease of convergence and ability to produce clearly measurable accuracy. These characteristics make ResNet-18 an appropriate choice for classification tasks, allowing straightforward and meaningful comparisons between different algorithms. Considering the constraints of training and communication on edge devices, ResNet-18 presented a feasible model size that ensured dependable performance. While other larger networks might offer marginally higher accuracy at the cost of huge datasets to prevent overfitting, we anticipate that the impact on results would be minimal within the scope of local node-level training and updates conducted in our experiments.
Given the computational constraints inherent to edge devices with networks like ResNet-18, certain tasks require localized processing. To address these limitations, we initially experimented with 32 × 32 pixels images from CIFAR-10, followed by tests on larger image sizes. Specifically, we utilized Imagenette, containing more generalized features, to identify an optimal resolution for resource-constrained environments. Through these experiments on edge devices, we found that a 90 × 90 pixel resolution with Imagenette provides an ideal balance, enabling efficient processing and effective training of ResNet-18 on the Jetson Nano within the device’s operational capabilities.
4.2. FedAvg Method
In the context of decentralized computing, typical distributed computing scenarios involve the exchange of only weights, without transferring data. This approach, known as FedAvg [25], averages the weights from all local nodes after training, broadcasts the global weights to all nodes, and updates the local models. This process converts local weights into global weights using the broadcast method and can be mathematically represented as follows:
where is the total number of local nodes, is the model weight of the n-th node, and is the updated weight of each node after the averaging is applied. This global averaging can negatively affect performance in heterogeneous data environments, where the data distribution across nodes varies significantly. For instance, in scenarios where local nodes are tasked with weather predictions, features relevant to a specific region’s climate may be overshadowed by the global model’s emphasis on broader, less localized patterns in a specific geographic region, and the local model’s weights may reflect these region-specific features.
4.3. Comparing the Learning Performance with Cifar10
We compared the learning performances of the FedAvg [25] and RNEP algorithms across different batch sizes (BSs) using the Cifar10 dataset. Each node trains on 6000 randomly selected and IID local data samples from the entire dataset. To simulate a real-world scenario where each node gathers its own data, we applied data augmentation during each communication round. This allowed the nodes to train as if they were continuously collecting and processing fresh local data.
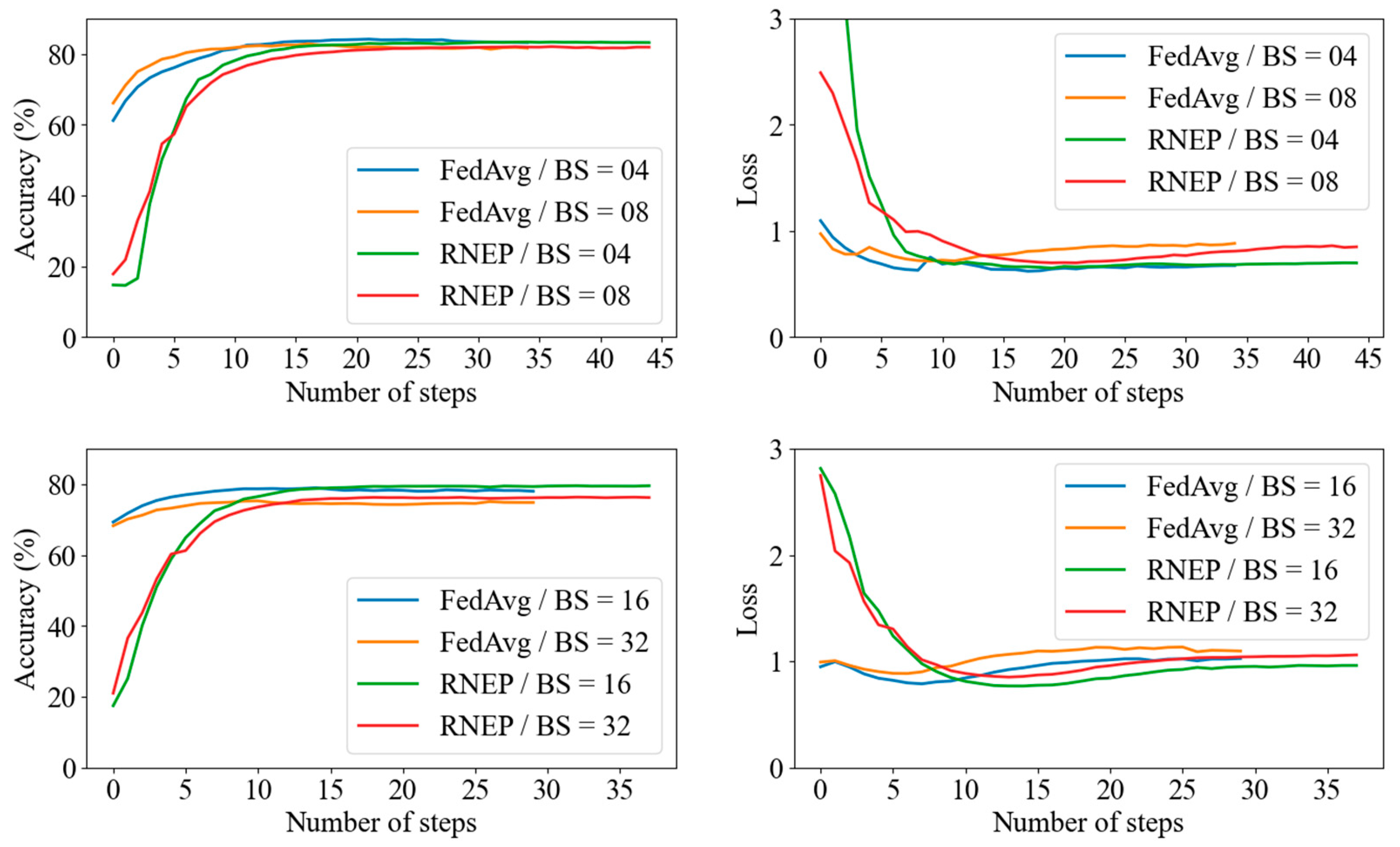
Figure 3 shows the accuracy trends for batch sizes of 4, 8, 16, and 32. The horizontal axis represents the number of communication steps after completing local epochs, with the local epoch set to 10. The results demonstrate that while FedAvg converges more quickly, RNEP consistently achieves a slightly higher accuracy across all batch sizes. Notably, RNEP’s performance is particularly strong at batch sizes of 16 and 32, suggesting that it may be more effective for learning with larger batch sizes. These findings indicate that RNEP offers comparable or slightly better efficiency and accuracy than FedAvg, particularly for larger batch sizes.
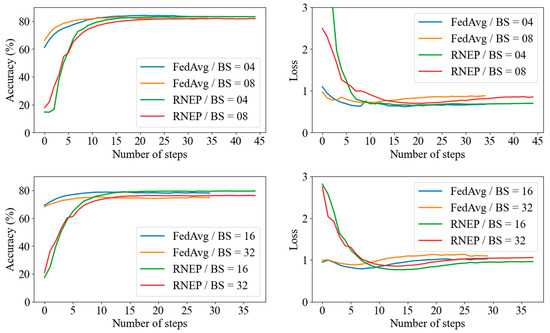
Figure 3.
Comparing FedAvg and RNEP for accuracy (left side) and loss (right side).
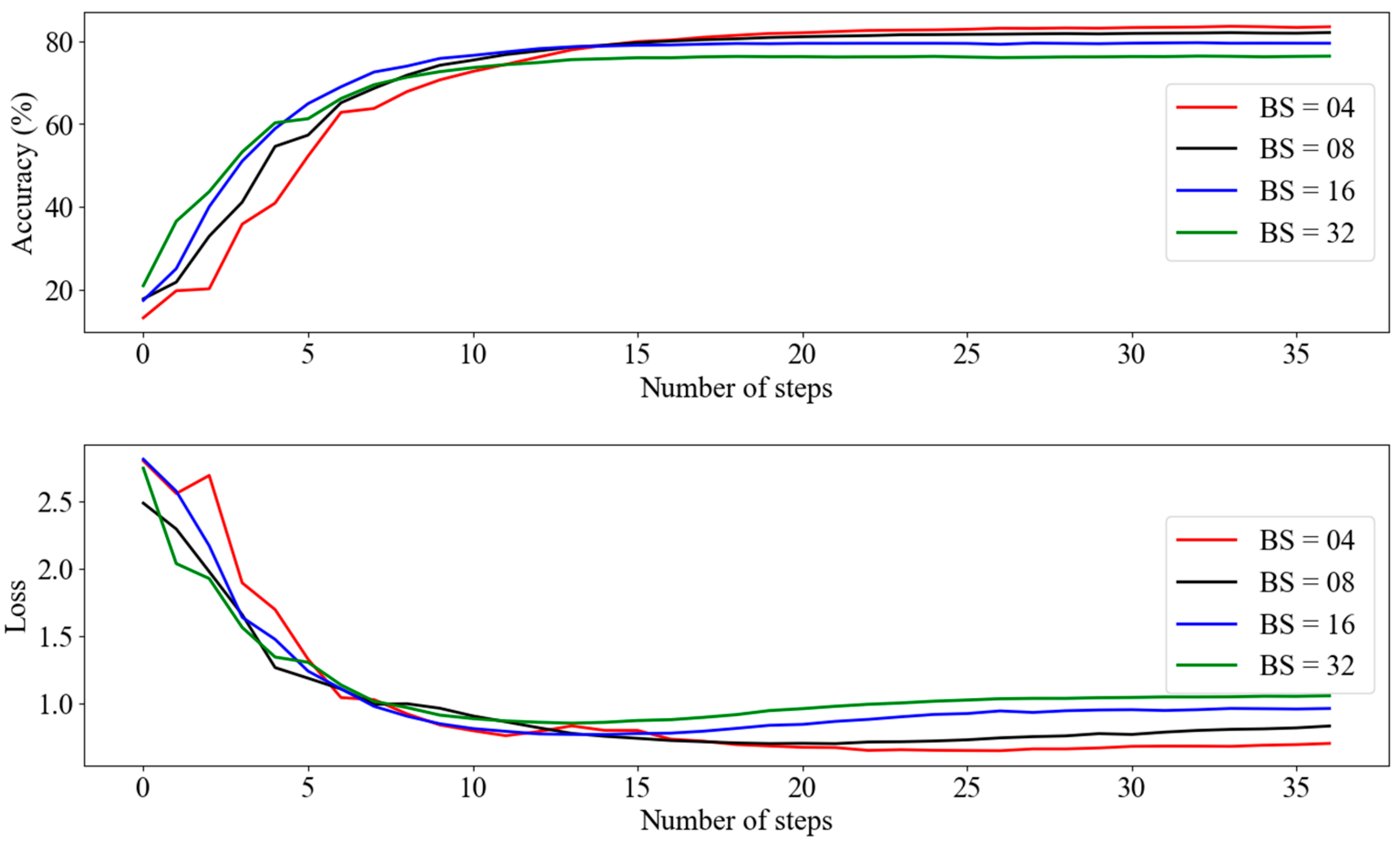
Figure 4 evaluates the learning performance of the RNEP method on edge devices with limited computational resources using varying batch sizes (BS = 04, 08, 16, and 32). Our results showed that smaller batch sizes (BS = 04 and 08) tend to achieve higher accuracy more rapidly in the initial stages of training. However, as training progressed, models trained with larger batch sizes (BS = 16 and 32) converged to similar accuracy levels.
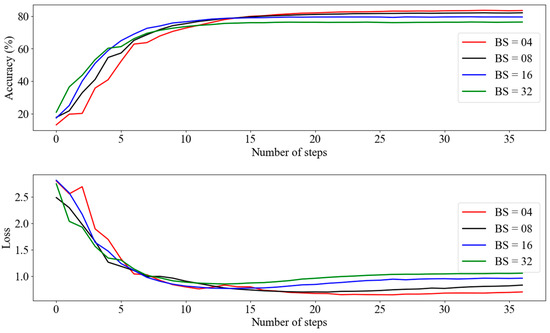
Figure 4.
RNEP accuracy and loss graph according to batch size.
While all batch sizes showed a rapid initial decrease in loss, indicating effective learning, smaller batch sizes (especially BS = 04) exhibit greater variability and higher variance in the loss curves. In contrast, larger batch sizes (BS = 16 and 32) produced smoother and more stable loss curves. Despite the slight increase in variability with smaller batch sizes, all configurations converged to comparable accuracy and loss levels by the end of the training. This demonstrates that, even with the constraints of edge devices, effective learning can be achieved with smaller batch sizes without significant performance loss.
The effects observed in our experiments are particularly relevant in decentralized distributed computing systems. Increasing the batch size at each local node can lead to a higher mean and variance across the system, potentially reducing model accuracy. This is particularly true in non-IID data scenarios, where the data distribution varies between nodes. Larger batch sizes may cause the model parameters to overfit specific local data distributions, rendering the global model less representative of the overall data. Consequently, the global model may become unstable with increased mean and variance, ultimately hindering performance.
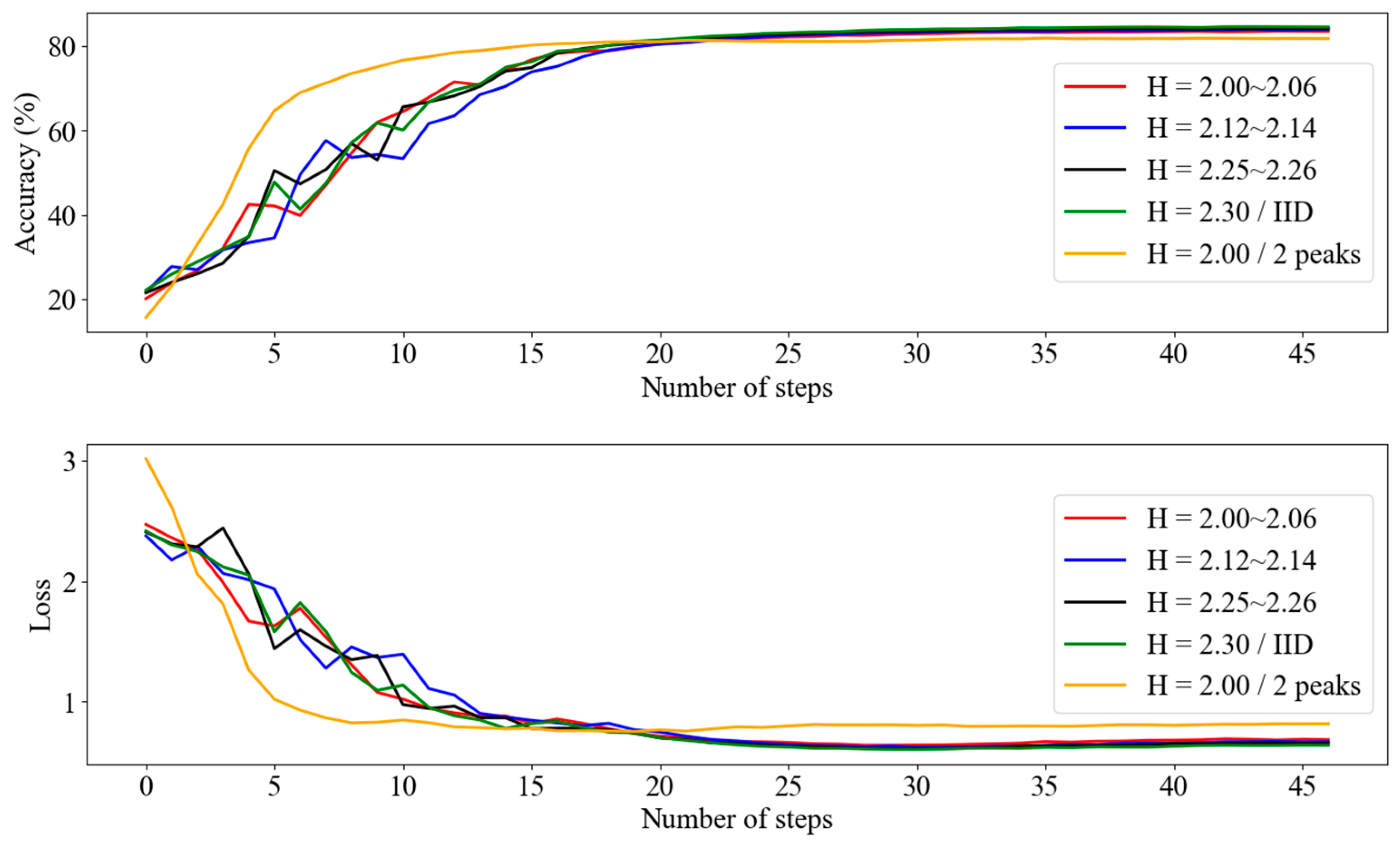
4.4. Effect of Entropy Variation
Figure 5 presents an analysis of learning performance in the RNEP experiment based on entropy (H) values. Each node trains on 6000 local data samples, either IID or non-IID, and is randomly selected from the full dataset. As in previous experiments, we applied data augmentation during each communication round to mimic a real-world scenario in which each node collects its own data. However, in this experiment, the entropy rate remained constant across all rounds.
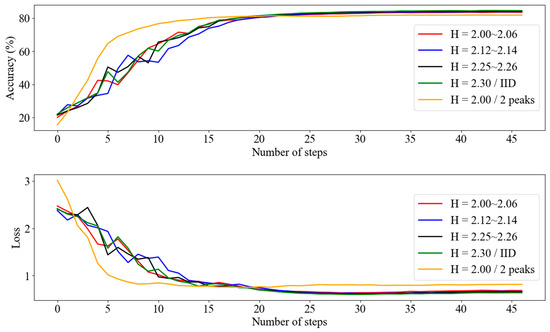
Figure 5.
RNEP accuracy and loss graph according to entropy.
The experiment was conducted using non-IID datasets in which each node contained data with varying entropy levels. Specifically, the datasets were configured with 10 classes, with one configuration featuring a single class with high entropy and the other configuration featuring 2 classes with high entropy (two peaks).
The results indicated that in datasets with lower entropy (H = 2.00/2 peaks), there was a rapid increase in accuracy and a rapid decrease in loss during the early stages of learning. However, despite this initial advantage, all datasets eventually converged to similar accuracy and loss levels as training progressed. Notably, stable learning performance was also observed in the non-IID dataset, suggesting that while entropy influences the initial learning dynamics, it does not lead to significant differences in the final learning outcomes.
These findings demonstrate that the models can effectively learn across various entropy conditions and highlight the practical implication that stable performance can be maintained even in non-IID datasets. This is particularly relevant in scenarios where learning is performed on multiple devices, as it suggests that local nodes, which are likely to collect data with diverse distributions, can still achieve consistent performance in non-IID data situations.
4.5. Convergence Speed for Various Local Epochs
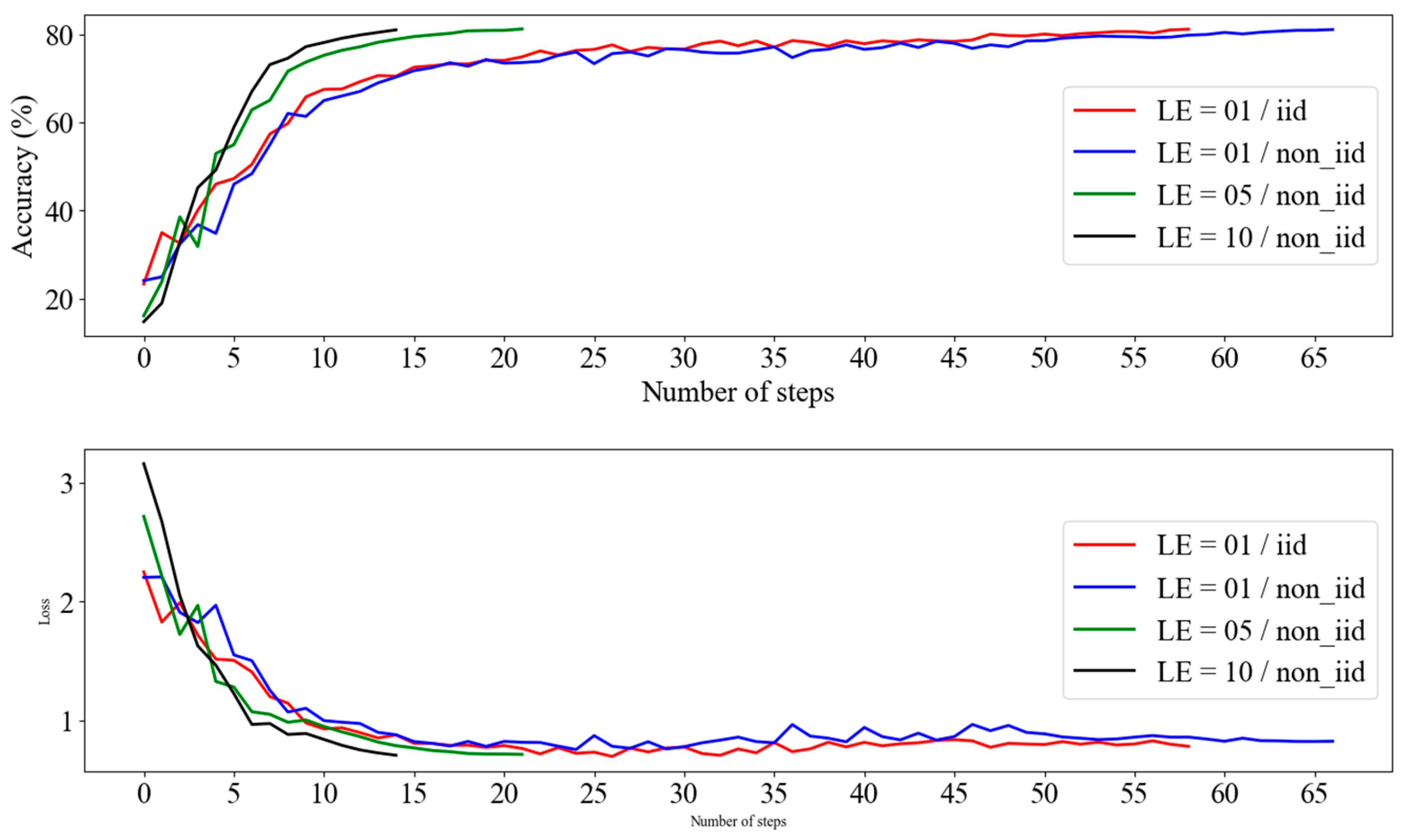
Figure 6 shows the analysis of the learning performance based on local epochs (LEs) and data distribution (IID and non-IID). Across all the experimental settings, the accuracy consistently increased with the number of learning steps, eventually converging to approximately 80%. In the non-IID settings with higher LE values (LE = 10/non-IID and LE = 05/non-IID), the accuracy increased more rapidly and converged earlier. By contrast, settings with lower LE values, such as LE = 01/IID and LE = 01/non-IID, exhibited a slower increase in accuracy and required more steps to achieve convergence.
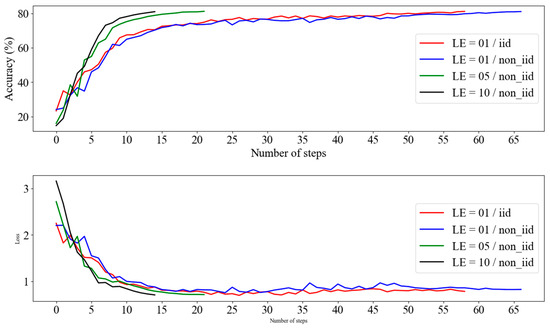
Figure 6.
RNEP performance according to local epochs and data distribution with entropy.
The findings indicated that in non-IID settings with high LE values (LE = 05, 10), the model achieved faster accuracy gains, quicker loss reduction, and earlier convergence during the initial learning stages. However, when the LE values are low, the reduced frequency of updates can lead to slower convergence because more steps are required to achieve a similar performance. Conversely, if LE values are excessively high, convergence may occur more quickly, and there is a risk that the model could be overfitted to the local node, potentially leading to a decline in the overall accuracy. Ultimately, despite these differences, all settings converged to similar levels of accuracy and loss, demonstrating no significant difference between IID and non-IID data distributions. These results suggest that stable and effective learning is possible even in non-IID data distributions, provided that LE is carefully managed to balance the speed of convergence with the risk of overfitting.
4.6. High-Resolution Experiments with Imagenette Dataset
Figure 7 compares the learning performances of the FedAvg and RNEP algorithms on the Imagenette dataset. Each node was trained on 2700 randomly selected IID local data samples from the entire dataset. As in the previous experiments, data augmentation was applied during each communication round to simulate a real-world scenario in which each node collects its own data. The dataset used in this experiment was larger and had relatively higher uncertainty in the images compared to CIFAR-10.
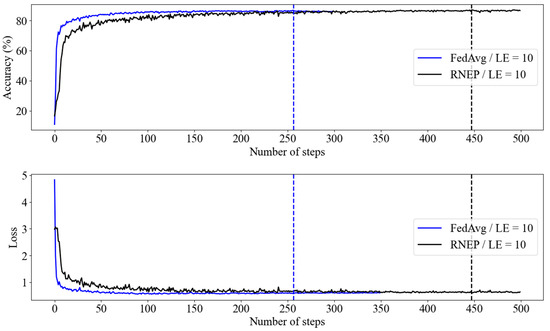
Figure 7.
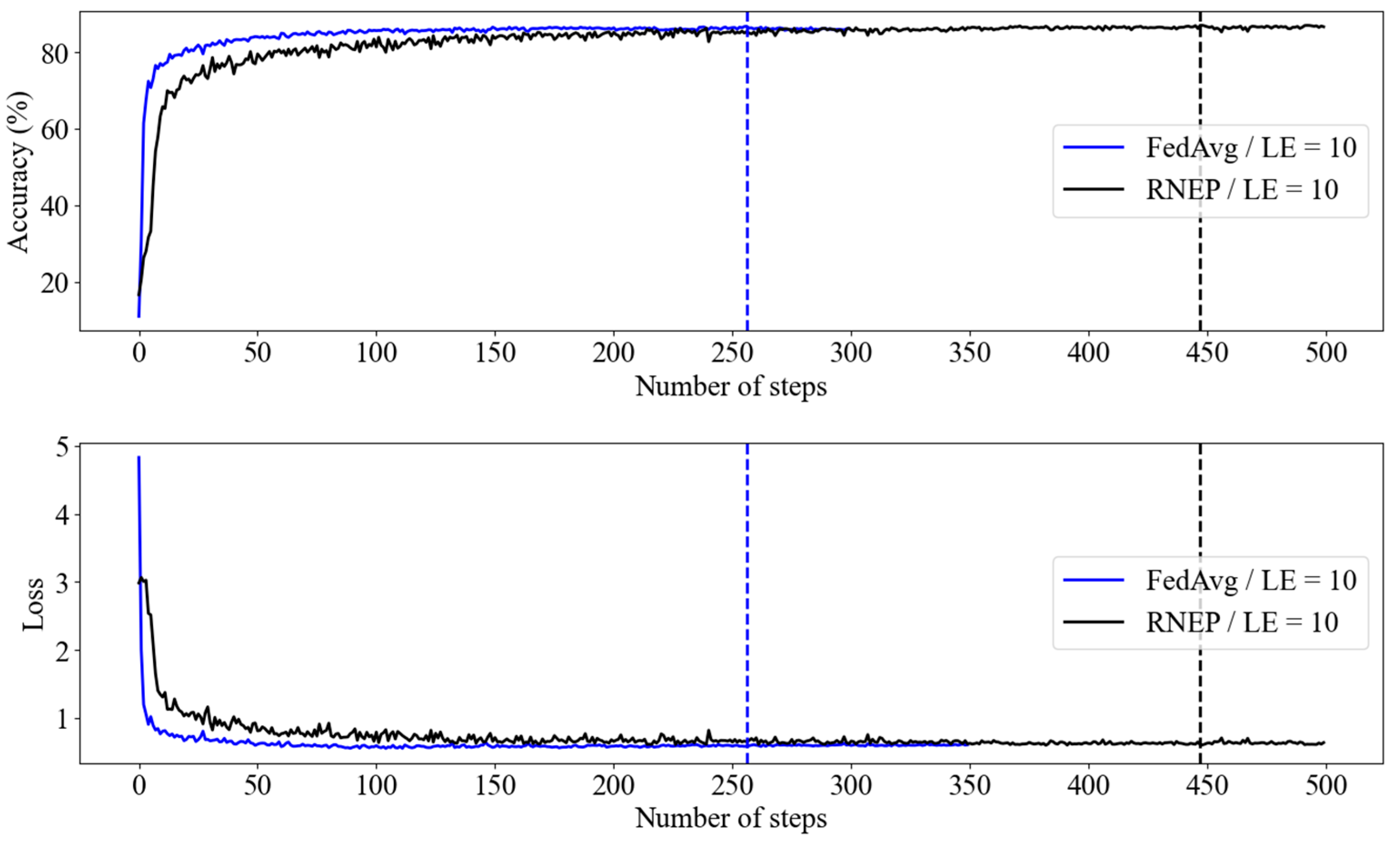
RNEP and FedAvg performance with Imagenette dataset (LE = 10).
The vertical lines indicate the convergence points of each algorithm. The FedAvg algorithm shows a rapid decline in loss and a swift increase in accuracy during the initial learning phase, achieving relatively quick stability. In contrast, the RNEP algorithm exhibited greater variability in the early stages, with the loss gradually decreasing. However, it eventually reached levels of accuracy and loss similar to those of FedAvg. Both algorithms converged to comparable points, with RNEP continuing to reduce loss over time despite initial fluctuations. These results suggest that RNEP can achieve performance stability on par with that of FedAvg.
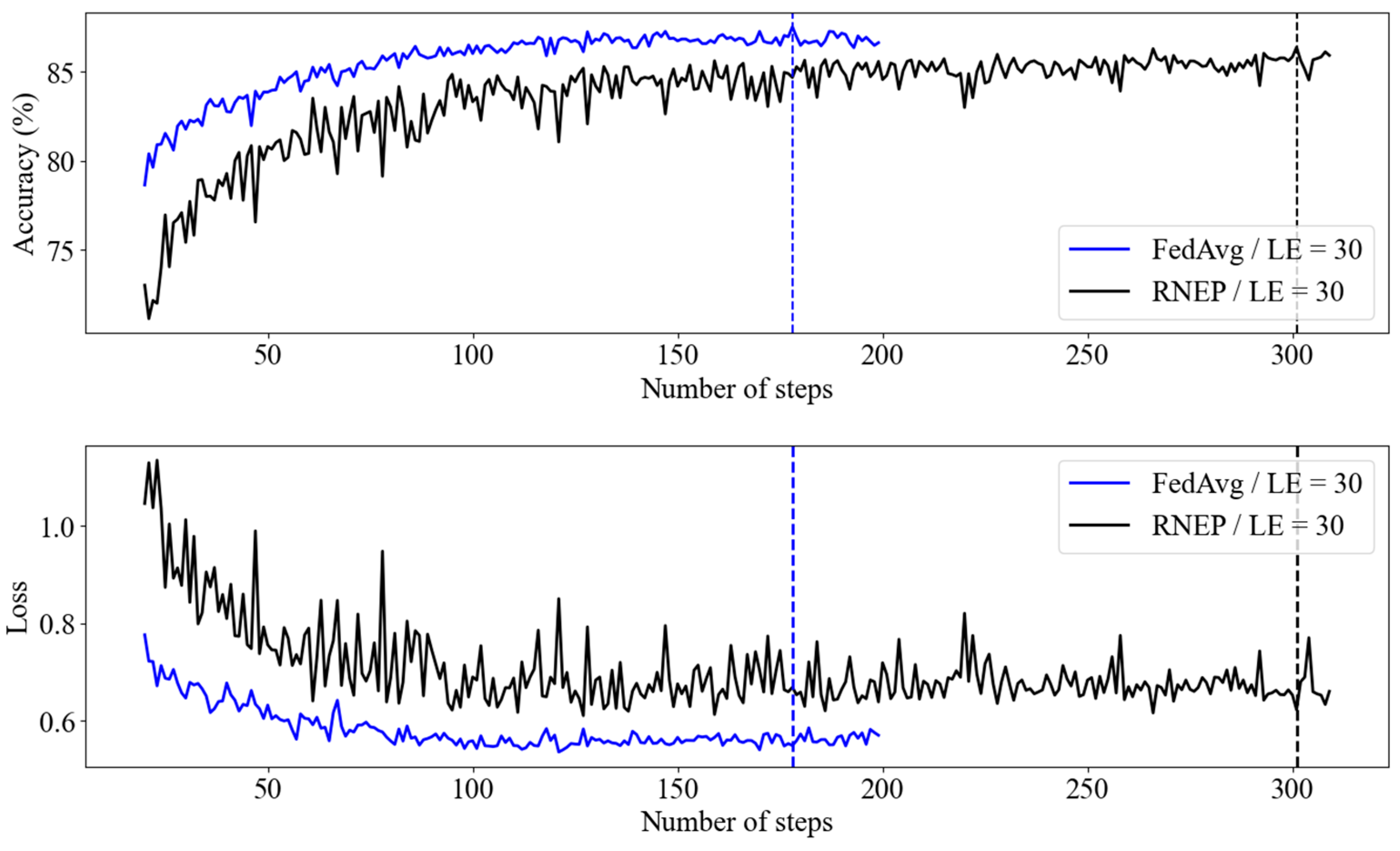
Figure 8 compares the learning performance of the FedAvg and RNEP algorithms with a local epoch (LE) value of 30. Similarly to Figure 7, the FedAvg algorithm continues to demonstrate quick convergence in both loss and accuracy, maintaining stable performance across different conditions.
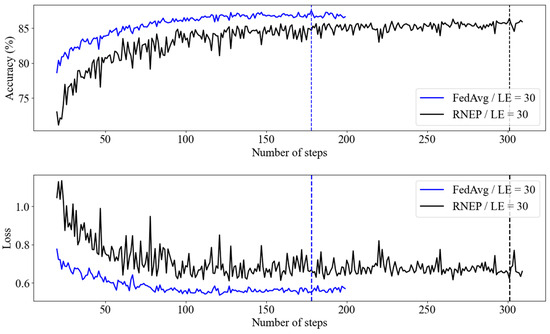
Figure 8.
RNEP and FedAvg performance with Imagenette dataset (LE = 30).
However, the RNEP algorithm showed increased variability and less stable convergence as the LE increased. However, both algorithms eventually achieved similar loss and accuracy levels. These findings indicate that while FedAvg offers a more consistent performance, RNEP is also capable of achieving effective learning outcomes over time. However, the increased variability in RNEP with higher LE values indicates that careful parameter tuning may be necessary to optimize its performance, particularly in more complex environments with higher image complexity and larger image sizes.
The experiment was conducted on an edge AI device that provided a constrained experimental environment. Furthermore, the Imagenette dataset used in this study, which has higher image complexity and larger image sizes than CIFAR-10, may have contributed to the observed performance variability and increased risk of local minima affecting local nodes.
It is also important to note that if a node becomes trapped at a local minimum, its weights can negatively affect the overall learning process when aggregated, potentially lowering the overall performance average. This risk is particularly significant in environments with high image complexity, such as the Imagenette dataset.
5. Conclusions
In this study, we introduce a novel approach called the RNEP method, which aims to improve both the efficiency and accuracy of distributed computing systems. By utilizing entropy-based weight sharing through random node pairing, RNEP effectively reduces communication costs while preserving model accuracy, even in environments with a non-IID data distribution. Our experimental results demonstrate that RNEP performs comparably to, or even surpasses, existing methods such as FedAvg, especially when managing larger batch sizes and non-IID data.
The results also highlight the importance of balancing local epochs and batch sizes to optimize convergence speed while minimizing the risk of overfitting. Experiments conducted using the Imagenette dataset further validated the robustness of the RNEP method, even in scenarios involving high image complexity.
In conclusion, the RNEP method provides an efficient and effective solution for distributed learning, particularly in contexts where communication overhead and data distribution imbalances present significant challenges. This approach not only reduces reliance on a central server but also preserves local data characteristics, thereby enhancing overall system performance.
Future research will focus on optimizing the RNEP method further, exploring its applicability across a broader range of machine learning models and real-world scenarios. To mitigate overfitting, we will explore regularization techniques, such as entropy regularization, to enhance model suitability in non-IID data environments. Additionally, we aim to verify RNEP’s accuracy under extended training periods by employing adaptive learning rates and early stopping mechanisms, thereby enhancing both robustness and generalizability.
Author Contributions
Conceptualization, J.-I.K. and S.-W.L.; methodology, J.-I.K. and S.-W.L.; software, J.-I.K.; validation, J.-I.K. and S.-W.L.; formal analysis, J.-I.K. and S.-W.L.; investigation, J.-I.K. and S.-W.L.; resources, J.-I.K. and S.-W.L.; data curation, J.-I.K.; writing—original draft preparation, J.-I.K.; writing—review and editing, S.-W.L.; visualization, J.-I.K.; supervision, S.-W.L.; project administration, S.-W.L.; funding acquisition, S.-W.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Technology Innovation Program (or Industrial Strategic Technology Development Program—High-quality human resources training for public-private joint investment semiconductors (R & D)) (RS-2024-00403397, BMS IC Development for Electric Vehicles Featuring Active Cell Balancing and Wireless Control) funded by the Ministry of Trade, Industry & Energy (MOTIE, Korea), by a Research Grant of Kwangwoon University in 2024, and by a National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (NRF-2021R1F1A1060183).
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Priadarsini, M.; Dharani, M.K. Distributed Inference Approach on Massive Datasets Using MapReduce. In Proceedings of the 2023 International Conference on Computer Communication and Informatics (ICCCI), Coimbatore, India, 23–25 January 2023. [Google Scholar]
- Ranftl, R.; Lasinger, K.; Hafner, D.; Schindler, K.; Koltun, V. Towards Robust Monocular Depth Estimation: Mixing Datasets for Zero-Shot Cross-Dataset Transfer. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 1623–1637. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Liu, X.; Matwin, S. A Distributed Instance-Weighted SVM Algorithm on Large-Scale Imbalanced Datasets. In Proceedings of the 2014 IEEE International Conference on Big Data (Big Data), Washington, DC, USA, 27–30 October 2014. [Google Scholar]
- Sinha, A.; Saini, T.; Srikanth, S.V. Distributed Computing Approach to Optimize Road Traffic Simulation. In Proceedings of the 2014 International Conference on Parallel, Distributed and Grid Computing, Solan, India, 11–13 December 2014. [Google Scholar]
- Deng, X.; Sun, T.; Liu, F.; Li, D. SignGD with Error Feedback Meets Lazily Aggregated Technique: Communication-Efficient Algorithms for Distributed Learning. Tsinghua Sci. Technol. 2022, 27, 174–185. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, Z.; Cai, Y.; Lu, H.; Wen, T.; Cai, B. Towards Ubiquitous Intelligent Computing: Heterogeneous Distributed Deep Neural Networks. IEEE Trans. Big Data 2022, 8, 644–657. [Google Scholar] [CrossRef]
- Darweesh, A.; Abouelfarag, A.; Kadry, R. Real-Time Adaptive Approach for Image Processing Using Mobile Nodes. In Proceedings of the 2018 6th International Conference on Future Internet of Things and Cloud Workshops (FiCloudW), Barcelona, Spain, 6–8 August 2018; IEEE: New York, NY, USA, 2018. [Google Scholar]
- Jayanthi, D.; Sumathi, G. Weather Data Analysis Using Spark—An In-Memory Computing Framework. In Proceedings of the 2017 Innovations in Power and Advanced Computing Technologies (i-PACT), Vellore, India, 21–22 April 2017. [Google Scholar]
- Hasan, M.; Goraya, M.S. A Framework for Priority-Based Task Execution in the Distributed Computing Environment. In Proceedings of the 2015 International Conference on Signal Processing, Computing and Control (ISPCC), Waknaghat, India, 24–26 September 2015. [Google Scholar]
- Yao, Y.; Liu, B.; Zhao, Y.; Shi, W. Towards Edge-Enabled Distributed Computing Framework for Heterogeneous Android-Based Devices. In Proceedings of the 2022 IEEE/ACM 7th Symposium on Edge Computing (SEC), Seattle, WA, USA, 12–14 December 2022. [Google Scholar]
- Zhang, Z.; Wang, C. SaPus: Self-Adaptive Parameter Update Strategy for DNN Training on Multi-GPU Clusters. IEEE Trans. Parallel Distrib. Syst. 2022, 33, 1569–1580. [Google Scholar] [CrossRef]
- Lai, W.; Yan, Q. Federated Learning for Detecting COVID-19 in Chest CT Images: A Lightweight Federated Learning Approach. In Proceedings of the 2022 4th International Conference on Frontiers Technology of Information and Computer (ICFTIC), Shanghai, China, 2–4 December 2022. [Google Scholar]
- Chen, J.; Li, K.; Bilal, K.; Zhou, X.; Li, K.; Yu, P.S. A Bi-Layered Parallel Training Architecture for Large-Scale Convolutional Neural Networks. IEEE Trans. Parallel Distrib. Syst. 2019, 30, 965–976. [Google Scholar] [CrossRef]
- Scardapane, S.; Wang, D.; Panella, M.; Uncini, A. Distributed Learning for Random Vector Functional-Link Networks. Inf. Sci. 2015, 301, 271–284. [Google Scholar] [CrossRef]
- Wang, S.-Y.; Kuo, N.-E. Using Programmable P4 Switches to Reduce Communication Costs of Parallel and Distributed Simulations. In Proceedings of the GLOBECOM 2022—2022 IEEE Global Communications Conference, Rio de Janeiro, Brazil, 4–8 December 2022; IEEE: New York, NY, USA, 2022. [Google Scholar]
- Wu, J.; Yang, T.; Wu, D.; Kalsi, K.; Johansson, K.H. Distributed Optimal Dispatch of Distributed Energy Resources Over Lossy Communication Networks. IEEE Trans. Smart Grid 2017, 8, 3125–3137. [Google Scholar] [CrossRef]
- Jang, H.; Kim, H.S. Hierarchical Broadcast Ring Architecture for High-Speed Ethernet Networks. In Proceedings of the IEEE INFOCOM 2006—25th IEEE International Conference on Computer Communications, Barcelona, Spain, 23–29 April 2006. [Google Scholar]
- Nurcahyani, I.; Laksono, F.F. Performance Analysis of Ad-Hoc On-Demand Distance Vector (AODV) and Dynamic Source Routing (DSR) Routing Protocols During Data Broadcast Storm Problem in Wireless Ad Hoc Network. In Proceedings of the 2019 International Seminar on Intelligent Technology and Its Applications (ISITIA), Surabaya, Indonesia, 29–30 August 2019. [Google Scholar]
- Markakis, E.; Skiannis, C.; Sideris, A.; Alexiou, G.; Palis, E. A Broadcast Aware P2P Mechanism for Improving BitTorrent Content Delivery. In Proceedings of the 2014 IEEE 19th International Workshop on Computer-Aided Modeling and Design of Communication Links and Networks (CAMAD), Athens, Greece, 1–3 December 2014. [Google Scholar]
- Zhai, J.-H.; Zhang, S.-F.; Wang, M.-H.; Li, Y. A Three-Stage Method for Classification of Binary Imbalanced Big Data. In Proceedings of the 2020 International Conference on Machine Learning and Cybernetics (ICMLC), Sanya, China, 6–9 December 2020. [Google Scholar]
- Duan, M.; Liu, D.; Chen, X.; Liu, R.; Tan, Y.; Liang, L. Self-Balancing Federated Learning with Global Imbalanced Data in Mobile Systems. IEEE Trans. Parallel Distrib. Syst. 2021, 32, 59–71. [Google Scholar] [CrossRef]
- Casella, B.; Esposito, R.; Sciarappa, A.; Cavazzoni, C.; Aldinucci, M. Experimenting with Normalization Layers in Federated Learning on Non-IID Scenarios. arXiv 2023, arXiv:2303.10630. [Google Scholar] [CrossRef]
- Wu, F.; Zhang, F.; Cai, Y.; Deng, T.; Su, M.; Tan, J. Efficient Online Edge Learning for UAV Object Detection via Adaptive Batch Size Fitting. In Proceedings of the 2023 9th International Conference on Big Data Computing and Communications (BigCom), Beijing, China, 4–6 August 2023. [Google Scholar]
- Choe, S.; Yoo, J.-H.; Tissera, P.S.S.; Kang, J.-I.; Yang, H.-K. Event Processing-based Low-Power Low-Cost Wireless Sensor Network for Real Time Wildfire Monitoring. Trans. Korean Inst. Electr. Eng. 2020, 69, 706–718. [Google Scholar] [CrossRef]
- McMahan, B.; Moore, E.; Ramage, D.; Hampson, S.; Arcas, B.A.y. Communication-Efficient Learning of Deep Networks from Decentralized Data. In Proceedings of the 20th International Conference on Artificial Intelligence and Statistics, Fort Lauderdale, FL, USA, 20–22 April 2017. [Google Scholar]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Orlandi, F.C.; Dos Anjos, J.C.S.; Leithardt, V.R.Q.; De Paz Santana, J.F.; Geyer, C.F.R. Entropy to Mitigate Non-IID Data Problem on Federated Learning for the Edge Intelligence Environment. IEEE Access 2023, 11, 78845–78857. [Google Scholar] [CrossRef]
- Ling, Z.; Yue, Z.; Xia, J.; Hu, M.; Wang, T.; Chen, M. FedEntropy: Efficient Device Grouping for Federated Learning Using Maximum Entropy Judgment. arXiv 2022, arXiv:2205.12038. [Google Scholar]
- Itahara, S.; Nishio, T.; Koda, Y.; Morikura, M.; Yamamoto, K. Distillation-Based Semi-Supervised Federated Learning for Communication-Efficient Collaborative Training with Non-IID Private Data. IEEE Trans. Mobile Comput. 2023, 22, 191–205. [Google Scholar] [CrossRef]
- Ling, Z.; Yue, Z.; Xia, J.; Wang, T.; Chen, M.; Lian, X. FedEntropy: Efficient Federated Learning for Non-IID Scenarios Using Maximum Entropy Judgment-Based Client Selection. In Proceedings of the 2023 IEEE International Conference on Parallel & Distributed Processing with Applications, Big Data & Cloud Computing, Sustainable Computing & Communications, Social Computing & Networking (ISPA/BDCloud/SocialCom/SustainCom), Melbourne, Australia, 21–23 December 2023. [Google Scholar]
- Yu, D.; Hua, Q.-S.; Wang, Y.; Lau, F.C.M. An O(log n) Distributed Approximation Algorithm for Local Broadcasting in Unstructured Wireless Networks. In Proceedings of the 2012 IEEE 8th International Conference on Distributed Computing in Sensor Systems, Hangzhou, China, 16–18 May 2012. [Google Scholar]
- Yu, D.; Wang, Y.; Hua, Q.-S.; Lau, F.C.M. Distributed (Δ + 1)-Coloring in the Physical Model. In Proceedings of the ALGOSENSORS 2011, Saarbrücken, Germany, 9–10 September 2011; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Jurdziński, T.; Stachowiak, G. Probabilistic Algorithms for the Wakeup Problem in Single-Hop Radio Networks. In Proceedings of the Algorithms and Computation, Kanazawa, Japan, 16–18 December 2002; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Ang, H.H.; Gopalkrishnan, V.; Ng, W.K.; Hoi, S. Communication-Efficient Classification in P2P Networks. In Proceedings of the Machine Learning and Knowledge Discovery in Databases, Bled, Slovenia, 7–11 September 2009; Springer: Berlin/Heidelberg, Germany, 2009; pp. 83–98. [Google Scholar]
- Zhang, B.; Xiong, Q.; Xu, Y.; Rao, H.; Mao, J. SNR-Based Adaptive Computing Resource Allocation in Centralized Baseband Pool. In Proceedings of the 2017 17th International Symposium on Communications and Information Technologies (ISCIT), Cairns, QLD, Australia, 25–27 September 2017. [Google Scholar]
- Al-Dmour, N.A.; Teahan, W.J. ParCop: A Decentralized Peer-to-Peer Computing System. In Proceedings of the 2004 IEEE Third International Symposium on Parallel and Distributed Computing/Third International Workshop on Algorithms, Models and Tools for Parallel Computing on Heterogeneous Networks, Cork, Ireland, 7 July 2004. [Google Scholar]
- Li, Z.; Chen, L. Communication-Efficient Decentralized Zeroth-Order Method on Heterogeneous Data. In Proceedings of the 2021 IEEE 13th International Conference on Wireless Communications and Signal Processing (WCSP), Hangzhou, China, 20–22 October 2021. [Google Scholar]
- Cifar10 Dataset. Available online: https://www.cs.toronto.edu/~kriz/cifar.html (accessed on 29 August 2024).
- Imagenette Datatset. Available online: https://www.tensorflow.org/datasets/catalog/imagenette (accessed on 29 August 2024).
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. arXiv 2015, arXiv:1512.03385. [Google Scholar]
- Naets, B.; Raes, W.; Deville, R.; Middag, C.; Stevens, N.; Minnaert, B. Artificial Intelligence for Smart Cities: Comparing Latency in Edge and Cloud Computing. In Proceedings of the 2022 IEEE European Technology and Engineering Management Summit (E-TEMS), Glasgow, UK, 9–11 March 2022. [Google Scholar]
- Biswas, S.; Muttangi, R.; Patel, H.; Prince, S. Edge AI Based Autonomous UAV for Emergency Network Deployment: A Study Towards Search and Rescue Missions. In Proceedings of the 2022 IEEE International Conference on Wireless Communications Signal Processing and Networking (WiSPNET), Chennai, India, 24–26 March 2022. [Google Scholar]
- Zhang, Z.; Cai, Y.; Lu, H.; Wen, T.; Cai, B. An Edge Computing-Enabled Track Obstacle Detection Method Based on YOLOv5. In Proceedings of the 2023 IEEE International Conference on Electromagnetics in Advanced Applications (ICEAA), Turin, Italy, 9–13 October 2023. [Google Scholar]
- Wasule, S.; Khadatkar, G.; Pendke, V.; Rane, P. Xavier Vision: Pioneering Autonomous Vehicle Perception with YOLO v8 on Jetson Xavier NX. In Proceedings of the 2023 IEEE Pune Section International Conference (PuneCon), Pune, India, 14–16 December 2023. [Google Scholar]
- Rahmat, R.F.; Saputra, T.; Hizriadi, A.; Lini, T.Z.; Nasution, M.K.M. Performance Test of Parallel Image Processing Using Open MPI on Raspberry PI Cluster Board. In Proceedings of the 2019 IEEE 3rd International Conference on Electrical, Telecommunication and Computer Engineering (ELTICOM), Medan, Indonesia, 19–21 September 2019. [Google Scholar]
- Graham, R.; Shipman, G.; Barrett, B.; Castain, R.; Bosilca, G.; Lumsdaine, A. Open MPI: A High-Performance, Heterogeneous MPI Implementation. In Proceedings of the 2006 IEEE International Conference on Parallel Processing (ICPP’06), Columbus, OH, USA, 14–18 August 2006. [Google Scholar]
- Strout, M.M.; Kreaseck, B.; Hovland, P.D. Data-Flow Analysis for MPI Programs. In Proceedings of the 2006 IEEE International Conference on Parallel Processing (ICPP’06), Columbus, OH, USA, 14–18 August 2006. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).