Abstract
The existing task assignment algorithms usually solve only a point-based model. This paper proposes a novel algorithm for task assignment in detection search tasks. Firstly, the optimal reconnaissance path is generated by considering the drone’s position and attitude information, as well as the type of heterogeneous targets present in the actual scene. Subsequently, an adaptive crowding distance calculation (ACD-NSGA-II) is proposed based on the relative position of solutions in space, taking into account the spatial distribution of parent solutions and constraints imposed by uncertain targets and terrain. Finally, comparative experiments using digital simulation are conducted under two different target probability scenarios. Moreover, the improved algorithm is further evaluated across 100 cases, and a comparison of the Pareto solution set with other algorithms is conducted to demonstrate the algorithm’s overall adaptability.
1. Introduction
In complex environments, single unmanned aerial vehicles (UAVs) struggle to efficiently complete tasks due to the types of payloads they carry [1]. The application style of UAV is evolving from singular to collective. Task assignment for multiple UAVs involves matching UAV payloads and target types, and assigning specific targets to each UAV. A well-executed assignment enhances task execution efficiency and reduces resource wastage. A multi-UAV task assignment problem (MUTAP) can be viewed as a multi-constraint optimization problem (MOP). However, the majority of MUTAPs are often treated as a multiple traveling salesman problem (TSP) or a vehicle routing problem (VRP) without considering the actual mission requirements of the UAVs [2].
Heuristic methods, as a type of artificial intelligence optimization technique, are widely applied to centralized MUTAPs. ShengGao et al. utilized a grouping ant colony algorithm to solve a heterogeneous multi-UAV task assignment problem [3]. To escape local optima, they proposed a mutation operator with a state transition format that enhances the algorithm’s stochastic search capability. LiJing et al. [4] improved the Grey Wolf Optimizer (GWO) using the Kent chaos algorithm, initializing the population and enhancing population diversity. The Non-Dominated Sorting Genetic Algorithm-II (NSGA-II) is a multi-objective optimization algorithm [5]. JieZhu et al. [6] proposed an improved NSGA-II algorithm for task assignment in UAV mobile edge computing systems. The algorithm includes a feasible solution generation method (FSGM) and genetic operations, such as crossover, mutation, and selection.
However, the NSGA-II algorithm does not consider the spatial distribution of solutions in its key step of crowding distance calculation, which may result in a lack of diversity in offspring solutions. In addition, traditional task allocation does not take into account the actual task requirements but merely follows a point-to-point VRP or TSP model. Therefore, the contributions of this paper are as follows:
- (1)
- We enhance the task assignment model by incorporating specific search and reconnaissance tasks in addition to the existing point-to-point tasks. We introduce Dubins curves to simulate the turning radius of UAVs, and consider that the reconnaissance tasks have heterogeneous objectives, with different targets requiring varying search methods.
- (2)
- We propose a method for adaptive crowding distance calculation (ACD), which calculates adaptively based on the relative spatial distribution of feasible parent solutions in the Pareto space, ensuring maximum diversity during selection. This method ensures that the distribution of Pareto solutions in space is uniform, which is advantageous for preserving population diversity.
2. Problem Description
2.1. Sensor Model
Here, we assume that the UAV is equipped with a fixed onboard sensor. If the sensor’s field of view completely covers the ground target area, the area is considered to be searched. To simplify the model, it is assumed that each UAV’s sensor reconnaissance range is fixed, as shown in Figure 1, and the field of view is not affected by the UAV’s maneuvers.
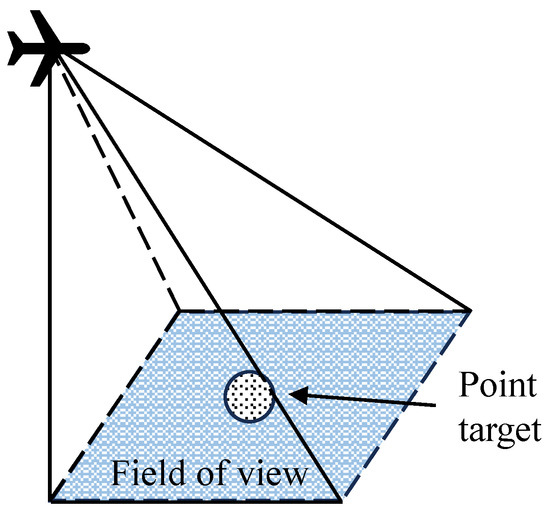
Figure 1.
Field of view of sensors.
2.2. Target Model
Area targets refer to whose length and width are both greater than the reconnaissance width of the UAV. Typical area targets include lakes, bases, plazas, and so on. To fully reconnaissance area targets, the UAV’s reconnaissance range needs to cover the target in a curved path, as shown in Figure 2, where represent the current position of UAV, which can be regarded as a directed particle. The UAV needs to determine whether to enter this area from or based on dynamic and cost constraints. In order to generate a reconnaissance path for area targets that takes into account the UAV’s maneuverability, a parallel pattern is adopted to generate the minimum length zigzag reconnaissance path.
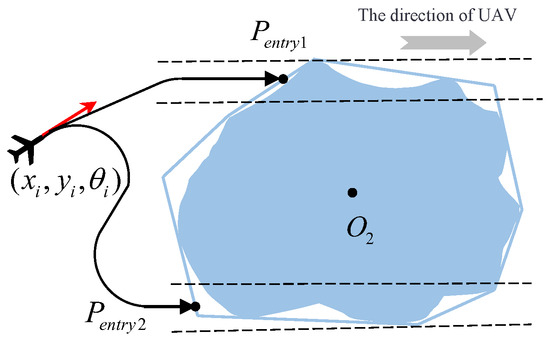
Figure 2.
Entry for area target.
2.3. Dubins Path Model
Dubins [7] curve demonstrates that a robot-like entity, with an initially specified heading, can reach the final position and heading via three path segments. Figure 3 illustrates four common configurations of Dubins paths composed of two curved segments and one straight segment, respectively are LSL, LSR, RSL, RSR, where R is the clockwise direction, L is the counterclockwise direction, and S is the straight line.
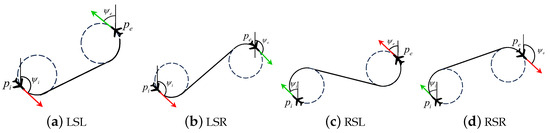
Figure 3.
Dubins shortest paths.
In this paper, we employed a Dubins path generator designed for fixed-wing unmanned aerial vehicles, targeting the simplified lateral dynamics of aircraft. It is assumed that all aircraft maintain constant altitude and velocity to avoid collisions. Dubins paths are utilized to generate new paths from the current aircraft position and direction to the desired position and direction.
2.4. Multi-UAV Task Assignment Model
The objective of a multi-UAV task assignment is to assign the most suitable mission objectives to each UAV. Given a set of N heterogeneous UAV groups , and M classes of targets , where N is the total number of UAVs and M is the total number of heterogeneous targets, the assignment is realized by constructing an assignment matrix between this multi-type UAV cluster and the targets. The elements within this matrix are defined as follows:
where i represents the ith UAV and j represents the jth target. There are three main objective functions to consider in the assignment problem of the process.
2.4.1. Objective Function 1
The reward of reconnaissance targets
where represents the importance level of the jth objective and denotes the probability of fully detecting the jth objective . The higher the importance of the target, the greater the benefits obtained, but tends to be relatively small.
2.4.2. Objective Function 2
The risk value of reconnaissance targets
where represents the value of the UAV; is the loss function of scouting by ; and is the path cost of scouting by . The risk value on the map determines the magnitude of and when a UAV flies over the path.
2.4.3. Objective Function 3
Time consumption for completing a task
where represents the speed of the UAV and represents the distance from the current pose to the pose after a full reconnaissance of heterogeneous targets .
3. Modified NGSA-II for MUTAP
In the NSGA-II, each individual represents a candidate solution. Addressing the issue of the original algorithm’s failure to consider the relative positions of solutions in space during crowding distance calculation [8], a method for adaptive crowding distance calculation (ACD-NSGA-II) is devised. The pseudocode for ACD-NSGA-II is depicted in Algorithm 1.
| Algorithm 1 ACD-NSGA-II |
|
3.1. Adaptive Crowding Distance
3.1.1. Crowding Distance
Crowding distance is used to estimate the diversity of individuals within the same Pareto front [9]. When comparing two different solutions on the same front, a solution with a larger crowding distance is considered to have better dispersion. Assuming that the crowding distance of individual i is . For each objective function and each Pareto rank set, the crowding distance of the member with the maximum and the minimum is set to . The crowding degree calculation formula for the remaining individuals is as follows:
where represents the objective function value of individual , k is the total number of individuals in the Pareto set, and N is the total number of objective functions. The algorithm prioritizes selecting individuals with larger crowding distance as the next generation when it iterates.
3.1.2. Adaptive Crowding Distance
According to (7), the crowding distance of individual i depends on the difference between and , without considering the position of the current target individual in the interval . The problem is that the previous individual and the next individual may be far apart, but the current individual i is very close to one of them.
If equals , then equals , but individual R and individual A are very close. The current crowding distance operator can ensure that the previous and next individuals are dispersed as much as possible, but it cannot guarantee that adjacent individuals are dispersed. If both individuals are preserved for the next generation, the offspring’s solutions will not be uniformly dispersed.
To address this issue, the adaptive crowding distance (ACD) calculation method is proposed based on the position of solutions in space. Optimizations to the crowding distance calculation method are made from the perspective of the geometric position of each individual. The calculation is as follows:
where is the radius weight coefficients. If the previous individual and the next individual are dispersed, and the target individual is far from the previous one but close to the next one, then the first equation can be used to calculate between the current individual and the previous one, greatly enhancing the dispersion of the solution set. As shown in Figure 4, if individual R is far from individuals D and B, and individual A is far from individuals D and R, then the solution set exhibits a significant distance of dispersion.
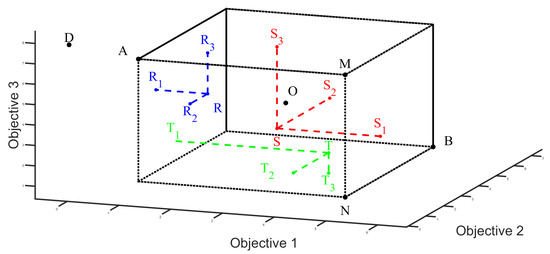
Figure 4.
The distribution of Pareto’s solution in space.
If the individual is close to the farthest vertex (N) of the largest cuboid formed by the previous and next individuals, then the solution has a large distance of dispersion.
As shown in Figure 4, if individual T is close to point N, then individual T is dispersed between individuals A and B. At this point, the crowding distance is calculated as
which ensures that it stays as far away from them as possible, resulting in a uniformly dispersed solution set.
In Figure 4, if individual S is close to the center O, then individual S is dispersed between individuals A and B. At this point, the crowding distance of the individual S is
which ensures that when the distance between the current individual and the next individual is large, the current individual is positioned close to the geometric center of the cuboid, leading to a uniformly dispersed solution set.
3.2. Analysis of Algorithm Complexity
The ACD-NSGA-II algorithm consists of two main components: non-dominated fast sort and adaptive crowding distance calculation. During the non-dominated sort in NSGA, each individual in a population of size N needs to compare M objective functions with n-1 individuals in the same population, resulting in a complexity of . Thus, the time complexity for each Pareto grading is . Secondly, during the adaptive crowding distance calculation, which involves sorting at most N solutions (when all individuals are in the first front), the first sorting algorithm requires operations. This process is repeated M times within an outer loop and at most N times within an inner loop, resulting in a total time complexity of . In fact, during the fast non-dominated sorting of R(t), sorting the entire population is unnecessary; only N solutions need to be found. Therefore, the overall time complexity for ACD-NSGA-II is .
4. Simulation
In this section, numerical simulation experiments were conducted to evaluate the effectiveness of the established model and proposed methods. The experiments were conducted on a personal computer equipped with an Intel(R) Core(TM) i7-13650HX 2.60 GHz CPU and 16 GB RAM, running in a Python 3.8 environment. The parameter design for the simulation experiments is as follows: The task area is confined to a square region of 100 × 100 units. The reconnaissance width for each drone is set to three units, with a minimum turning radius of three units. The probabilities of crossover and mutation are set to 0.6 and 0.05, respectively. The task targets are randomly generated, with each point on the map containing a normalized risk value ranging from 0 to 1.
4.1. Target Probability Map
In the simulation, the areas, airports, and vehicles that need reconnaissance are randomly generated, corresponding to area targets, line targets, and point targets, respectively, and the UAVs need to fully reconnaissance all targets, in turn, within the range allowed by the endurance. Firstly, a single UAV model with Dubins path kinematics is tested. A random region target (area1) and a point target (point1) are generated, as shown in Figure 5a. The area target requires a zigzag pattern for back-and-forth coverage, directly impacting the final evaluation function due to the constraints of minimum turning radius and search area, necessitating optimal decision-making by the algorithm. Furthermore, to validate the effectiveness and optimality of the proposed approach in solving multi-UAV task assignment and area search problems in complex scenarios, simulations are further conducted in randomly generated complex scenario 2. Figure 5b shows the best task assignment results and paths when using the improved algorithm for multi-UAV task assignment and search scenarios.
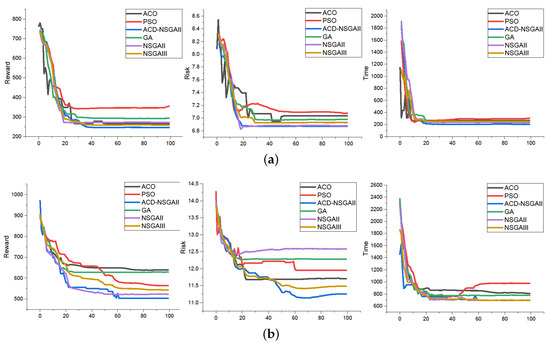
Figure 5.
Comparison of ACD-NSGA-II and other algorithms. (a) Scenario 1, (b) Scenario 2.
4.2. Optimization Results
The result of scenario 1 depicted in Figure 6 indicates that the proposed method generates the shortest search paths for all scenarios and ensures the minimization of all objective function values, and also provides a comparison between the proposed algorithm and NSGAII, GA, PSO, ACO, and NSGAIII algorithms. We conducted a reference experiment based on several comparison algorithms in [10], which summarized several algorithms for conventional multi-UAV task assignment, with all algorithms having 100 iterations. It can be observed that in simple scenarios, all algorithms converge quickly, but ACD-NSGAII outperforms the others in each objective function, demonstrating the effectiveness of the proposed improvement.
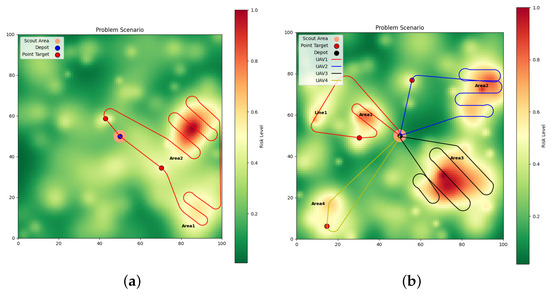
Figure 6.
Target probability map. (a) Scenario 1. (b) Scenario 2.
Figure 5 illustrates a performance comparison of ACD-NSGA-II with other algorithms in complex scenarios. As the complexity of the multi-objective optimization problem increases, a slower convergence speed can be observed in objective functions 1 and 2. At around 20 iterations, PSO, ACO, and GA algorithms begin to enter a state of local convergence. In contrast, ACD-NSGA-II maintains a uniform distribution of solutions in each generation’s crowding calculation, ensuring solution diversity and making it easier to escape local convergence. Around the 60th iteration, ACD-NSGA-II surpasses NSGA-II and eventually converges.
In complex scenarios, ACD-NSGAII outperforms GA, PSO, and NSGAII during the initial iteration stage by demonstrating superior exploration efficiency and early convergence characteristics. Furthermore, it achieves the lowest point in terms of optimizing objective function values at the end of iterations, which indicates its exceptional ability to effectively identify the Pareto front for multi-objective optimization problems. Multiple experiments confirm that ACD-NSGAII exhibits enhanced global search capability while successfully avoiding local optima.
4.3. Pareto Front Dominance Analysis
To demonstrate that ACD-NSGA-II outperforms other algorithms (e.g., PSO, ACO, NSGA-II, and GA) in common scenarios, independent experiments were conducted 100 times with random scenarios. The results were analyzed for each Pareto frontiers’ convergence shown in Figure 7. It represents a histogram of the number of times different scenes appear in the last generation.
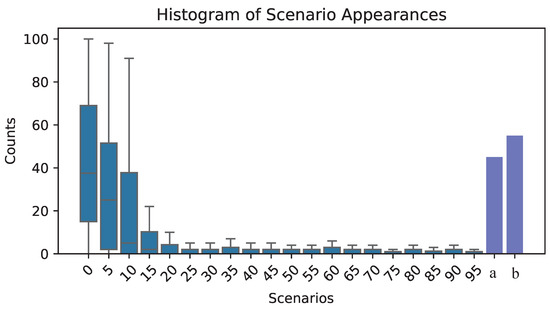
Figure 7.
A statistical box plot of 100 experiments, where ‘a’ represents the frequency of ACD-NSGA-II solutions on the Pareto front, and ‘b’ represents the frequency of ACD-NSGA-II dominating other algorithms. A lower median indicates that ACD-NSGA-II solutions are gradually gaining advantage.
The X-axis represents different scene types, and the results of each scene are derived by comparing the other algorithms (GA, PSO, and NSGA-II) and ACD-NSGA-II. Each scenario represents the dominant relationship between other algorithm solutions and ACD-NSGA-II solutions. Possible scenarios include the following:
- (1)
- Other solutions dominate one or more of the ACD-NSGA-II solutions.
- (2)
- The other solutions do not dominate any ACD-NSGA-II solutions, nor are they dominated by any ACD-NSGA-II solutions.
- (3)
- The other solutions are dominated by at least one ACD-NSGA-II solution.
The Y-axis represents the number of times each scenario appeared in all experiments. This value reflects the frequency of the dominant relationship between the other solutions and the ACD-NSGA-II solution over many experiments. In addition, the length of the error bar above each column reflects the range of fluctuations in the number of times this scenario occurs in different experiments. The longer the error bar, the greater the difference between the occurrence times of the scene in different experiments (that is, the greater the variability). The shorter the error bar, the more stable the occurrence of the scene in different experiments (i.e., less variability). By statistically analyzing the dominance relationships of the solutions from the 100 experiments, it can be observed that ACD-NSGA-II dominates other algorithms approximately 60 times, and its generated Pareto frontiers dominate about 50 times, proving that, in most scenarios, the performance of ACD-NSGA-II is superior to that of other algorithms.
5. Conclusions
This paper establishes a model for multi-UAV reconnaissance task assignments. Addressing the shortcomings of the original NSGA-II algorithm in crowding calculation, an improved adaptive crowding calculation method is proposed. The numerical simulation conducted demonstrates the effectiveness and optimality of the proposed method in most scenarios while also proving the dominance of the proposed algorithm over the original NSGA-II algorithm. In future work, we will consider how to enable collaborative reconnaissance task assignment among multiple UAVs, such as multiple UAVs collaborating to reconnoiter the same target. At the same time, we will also expand the path model to include obstacle or threat zones to better reflect real-word scenarios.
Author Contributions
Conceptualization and software, H.Z.; methodology, K.M.; formal analysis, H.Y.; writing—review and editing, Y.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| UAV | Unmanned aerial vehicle |
| MUTAP | Multi-UAV task assignment problem |
| ACD-NSGA-II | Adaptive Crowding Distance-Non-Dominated Sorting Genetic Algorithm-II |
References
- Xia, C.; Yongtai, L.; Liyuan, Y.; Lijie, Q. Cooperative Task Assignment and Track Planning For Multi-UAV Attack Mobile Targets. J. Intell. Robot. Syst. 2020, 100, 1383–1400. [Google Scholar] [CrossRef]
- Váňa, P.; Faigl, J. Optimal solution of the Generalized Dubins Interval Problem: Finding the shortest curvature-constrained path through a set of regions. Auton. Robot. 2020, 44, 1359–1376. [Google Scholar] [CrossRef]
- Gao, S.; Wu, J.; Ai, J. Multi-UAV reconnaissance task allocation for heterogeneous targets using grouping ant colony optimization algorithm. Soft Comput. 2021, 25, 7155–7167. [Google Scholar] [CrossRef]
- Li, J.; Yang, F. Task assignment strategy for multi-robot based on improved Grey Wolf Optimizer. J. Ambient. Intell. Humaniz. Comput. 2020, 11, 6319–6335. [Google Scholar] [CrossRef]
- Srinivas, N.; Deb, K. Muiltiobjective Optimization Using Nondominated Sorting in Genetic Algorithms. Evol. Comput. 1994, 2, 221–248. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, X.; Huang, H.; Cheng, S.; Wu, M. A NSGA-II Algorithm for Task Scheduling in UAV-Enabled MEC System. IEEE Trans. Intell. Transp. Syst. 2021, 23, 9414–9429. [Google Scholar] [CrossRef]
- Lugo, C.; Flores, S. Dubins path generation for a fixed wing UAV. In Proceedings of the 2014 International Conference on Unmanned Aircraft Systems (ICUAS), Orlando, FL, USA, 27–30 May 2014; pp. 339–346. [Google Scholar]
- Wu, X.; Chen, Z.; Liu, T.; Song, H.; Wang, Z.; Shi, W. Improved NSGA-II and its application in BIW structure optimization. Adv. Mech. Eng. 2023, 15, 16878132221150588. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, L.; Long, T.; Wen, Y. Multi-UAV reconnaissance task allocation for heterogeneous targets using an opposition-based genetic algorithm with double-chromosome encoding. Chin. J. Aeronaut. 2018, 31, 339–350. [Google Scholar] [CrossRef]
- Xiao, K.; Lu, J.; Nie, Y.; Ma, L.; Wang, X.; Wang, G. A Benchmark for Multi-UAV Task Assignment of an Extended Team Orienteering Problem. In Proceedings of the 2022 China Automation Congress (CAC), Xiamen, China, 25–27 November 2022; pp. 6966–6970. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).