Abstract
This paper analyzes the performance requirements that need to be met by a clock generator applied to a low-temperature quantum computer and analyzes the negative effects on the clock generator circuit under low-temperature conditions. In order to meet the performance requirements proposed in this paper and suppress the negative effects brought about by the low temperature, a clock generator for ultra-low-temperature quantum computing is designed. This clock generator is designed by using F-CLASS Voltage Controlled Oscillator (VCO), power filter, tail resistor, differential charge pump, and other techniques. And the noise characteristics of the clock generator are analyzed by Impulse Sensitive Function (ISF) and simulation results. After simulation tests, the average power consumption of the clock generator designed in this paper is 7 mW, the phase noise is −121 dBc/Hz@1 MHz, and the jitter is 62 fs. The performance of the clock generator meets the performance requirements proposed in this paper, and the reduction in the corner frequency proves that the circuit will have better performance at low temperatures.
1. Introduction
Quantum computing is a new computer system, with the special state and characteristics of quantum entanglement and superposition. Quantum computers can significantly reduce the overhead of some complex operations [1,2,3,4]. For example, quantum computing can complete the decomposition of large numbers in a very short period of time [2], which is almost impossible for traditional computers, and directly threatens the basis of the existence of existing cryptography and information security.
Existing quantum computers consist of several similar parts containing both a quantum processor and a classical electronic controller. In this case, the quantum processor consists of one or more quantum bits [5,6,7], which need to be at a very low temperature to exhibit quantum properties; usually this temperature is a few tens of millikelvin. But a quantum processor alone cannot work properly. Quantum processors need an external input control signal to make them rotate on a Bloch sphere, i.e., a quantum operation, and a set of circuits to read the result after the quantum operation. Therefore, a quantum computer needs a classical electronic controller to do the above work [8]. The existing classical electronic controllers for quantum computers are usually implemented by instruments at room temperature [9,10]. But as the number of quantum bits grows, controllers at room temperature cannot meet the demand for controlling large-scale quantum processors. So integrated circuit controllers based on cryogenic CMOS (Cryo-CMOS) circuits operating at temperatures below 4 Kelvin are proposed [11,12,13,14]. Controller circuits operating at ultra-low temperatures can provide larger system-on-a-chip integration to support higher numbers of quantum bits, significantly reducing the connection between low-temperature and room-temperature electronics. And the resulting high level of integration will pave the way for future practical quantum computers. The classical quantum computer architecture is shown in Figure 1, which can be divided into three parts based on temperature: a quantum processor part operating at a few tens of millikelvin, a quantum controller operating at 4 Kelvin, and a control device operating at room temperature to interact with the operator.
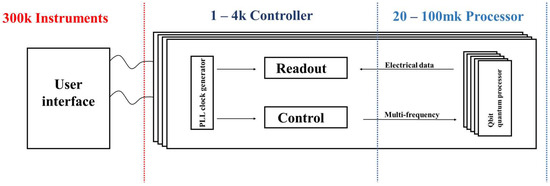
Figure 1.
Modern quantum computer scheme.
In quantum computers, clock signals generated by local clock sources are required for quantum controllers to operate quantum bits, and these signals are necessarily affected by noise. The impact of noise on quantum computers has been extensively analyzed in previous works, which partly focused on the different noise aspects of the control signals, which are usually RF signals whose noise is dominated by phase noise [15,16]. A part focuses on the effect of noise on the manipulation of quantum bits based on filtering function processing [17,18]. There are other different analyses [19,20,21,22,23,24] that address the effects of noise. All the above analyses show that the clock signal generated by the clock generator significantly affects the performance of the quantum computer. Therefore, a high-performance clock generator that can operate in an ultra-low-temperature environment is essential for quantum computers [25,26]. In order to design such a clock generator, this paper first analyzes the performance requirements of quantum computers for clock generators and accurately finds the values of the required target performance. Secondly, this paper analyzes the negative effects that CMOS circuits will be subjected to in low-temperature environments. And then this paper designs a clock generator for ultra-low-temperature quantum computing in response to the analyzed negative effects and analyzes its noise characteristics. After simulation tests, the average power consumption of the clock generator designed in this paper is 7 mW, the phase noise is −121 dBc/Hz@1 MHz, and the jitter is 62 fs, which meets the performance requirements of the clock generator proposed in this paper. Also, the reduction in the corner frequency proves that the circuit performs better at low temperatures.
Section 2 of this paper derives the performance requirements of quantum computers for clock generators. Section 3 analyzes the effects and negative effects of low-temperature environments on clock generators. Section 4 analyzes the design of the clock generator circuit and analyzes the principles of the key technologies applied in the circuit that affect the circuit. The present work is analyzed and discussed in Section 5, and Section 6 concludes the work of this paper.
2. Performance Requirements for Clock Generators Imposed by Quantum Computers
The process of quantum computing actually involves rotating the state vector on the Bloch sphere by injecting a suitable RF signal into the quantum processor. Different RF signal waveforms operate differently on the state vector, causing it to rotate at different angles.
Hamiltonian quantities are often used to evaluate the state evolution of quantum bits as a function of the RF signal input to the quantum processor. Thus, the describing the quantum operation can be expressed in terms of time-varying Hamiltonian quantities.
If the ideal quantum operation is denoted as , then the fidelity of the quantum computing process can be expressed by the degree of closeness of the actual quantum operation to the ideal quantum operation , and this degree of closeness can be denoted as [27,28].
For quantum computers, it is crucial to improve the quantum fidelity. And what affects the quantum fidelity is not only the characteristics of the quantum processor itself, but also the mismatch between the RF signal generated from the local clock source and the resonant frequency of the quantum bits. And the noise of the local clock source itself can have undesirable effects on the fidelity.
The non-fidelity caused by the non-ideal effects from the local clock source mentioned above can be expressed as
where is the phase noise of the clock source and is the frequency noise of the clock source. is the speed of the quantum spin and represents the sensitivity function of the quantum system to the noise, which is obtained according to [26]:
The transfer function has a low-pass characteristic, which illustrates that the quantum bits have different sensitivities to the phase noise of the clock source at different frequencies.
The phase noise of the clock source can be expressed as
where is a constant in and is the bandwidth of the clock source. For the phase-locked loop clock source, the in-band noise mainly comes from the divider, the discriminator, and the charge pump, and the out-of-band noise mainly comes from the oscillator.
For quantum operations, a fidelity higher than 99.9% is usually required. Therefore, the local clock source should have at least 99.999% fidelity to avoid the non-fidelity from the clock source limiting the inherent fidelity of the quantum bits. Considering a 1 MHz and 150 MHz reference frequency, the phase noise demand on the VCO is reduced by a larger bandwidth [25]. According to the above requirements, the phase-locked loop in-band noise should be below −120 dBc/Hz and the jitter should be within 63 fs.
3. Negative Effects of Circuits at Low Temperatures
3.1. Mismatch of Devices
One obvious negative effect of low-temperature circuits is the more severe device mismatch than at room temperature. CMOS device mismatch becomes more severe as the temperature decreases, and the device mismatch has a greater impact on the local clock source’s charge pump (CP) and Phase Frequency Detector (PFD), which introduces higher noise than at room temperature.
The mismatch of a circuit is usually analyzed by analyzing the mismatch of the drain current of a transistor pair by
where the superscript is the mean operator and the subscript indicates the first or second device in a pair. Mismatches in circuits usually include two types, systematic and random mismatches, with systematic mismatches arising from any asymmetry between a pair of devices and random mismatches mainly attributed to microscopic variations.
To be able to predict the device variability, the Croon model is used for drain current mismatch [29], where σ is the standard deviation operator and is the transconductance:
The well-known dependence of threshold voltage variability and current factor variability on area is described by Pelgrom’s law [30]:
where and are technology-related factors, and and are the width and length of the active device.
When the temperature is reduced from room temperature to the temperature at which the quantum computer operates, there is a significant increase in both and parameters. This increase indicates that and increase when the size of the device is constant. This means that the possibility of current mismatch between two devices in one transistor pair is increasing. At the same time, the size change due to low temperature also increases the mismatch of devices. Therefore, in order to reduce the noise introduced by mismatch in the circuit, it is necessary to introduce a design that can resist mismatch in the circuit design.
3.2. Noise at Low Temperature
The circuit noise performance changes significantly at low temperatures, and the flicker noise increases significantly while the thermal noise decreases significantly. Therefore, a special circuit structure needs to be introduced to suppress flicker noise [8].
4. Circuit Design and Noise Analysis
In order to overcome the negative effects of low temperature and design a local clock source for quantum computers, this paper designs a phase-locked loop circuit based on an F-Class VCO and a differential CP. The structure of the phase-locked loop (PLL) is shown in Figure 2. The phase-locked loop circuit adopts a typical integer N-division phase-locked loop structure and contains five parts: VCO, divider, discriminator, charge pump, and filter. In the design of the charge pump, a cross-current source is used to limit the mismatch of the circuit; in the design of the VCO, an on-chip transformer is used instead of an inductor to suppress flicker noise, and a tail resistor is introduced to reduce power consumption. The VCO noise is further reduced by introducing an Inductive Capacitance (LC) tank in the common-mode current path.
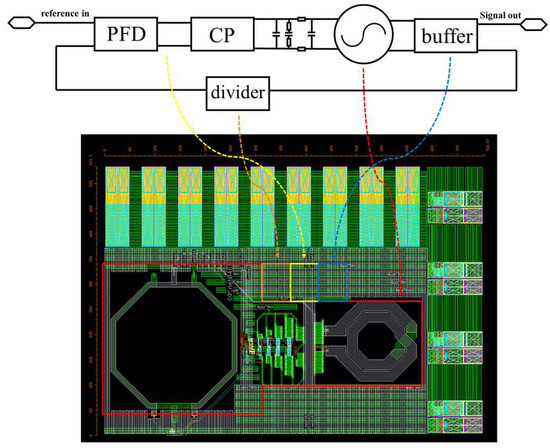
Figure 2.
Phase-locked loop structure.
The phase-locked loop is designed in a 28 nm process; the layout is shown in Figure 2, the area is 0.35 mm2, and the power consumption of the phase-locked loop is 7 mW. To compensate for the 20% frequency rise at low temperature, the phase-locked loop is locked at 10 GHz in the simulation. The phase noise is shown in Figure 3a as −121 dbc/Hz@1 MHz and the jitter is shown in Figure 3b as 62 fs.
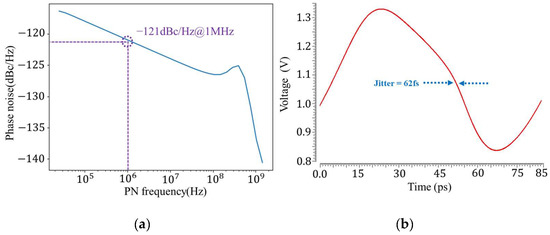
Figure 3.
(a) Phase noise of the PLL; (b) jitter of the PLL.
In order to analyze in detail the improvements and innovations made in this paper to improve the performance of the phase-locked loop, this section will focus on the structure and characteristics of the VCO and CP and analyze their noise performance.
4.1. F-Class VCO
4.1.1. Design of the Circuit
The noise of a phase-locked loop can be divided into in-band noise and out-of-band noise. The main source of out-of-band noise is the VCO, which is also the most important part of the PLL noise. So, it is important to design a high-performance VCO for designing phase-locked loops. According to the above analysis, flicker noise becomes an important noise source at low temperatures, so this paper constructs an F-Class VCO by using an on-chip transformer to suppress flicker noise.
According to the literature [31], the upconversion of flicker noise is a very important factor affecting the VCO noise performance. The modulation effect of the second harmonic with the VCO fundamental makes the oscillator waveform asymmetric, and this asymmetry affects the ISF of the oscillator, leading to the upconversion of flicker noise. And the auxiliary resonance at the third harmonic of the fundamental frequency is beneficial to improve the oscillator phase noise (PN) performance by creating a pseudo-square waveform. The VCO designed in this paper creates a resonance at the third harmonic of the fundamental frequency through a class F operation, which forms a pseudo-square waveform with the fundamental frequency, and the VCO structure is shown in Figure 4.
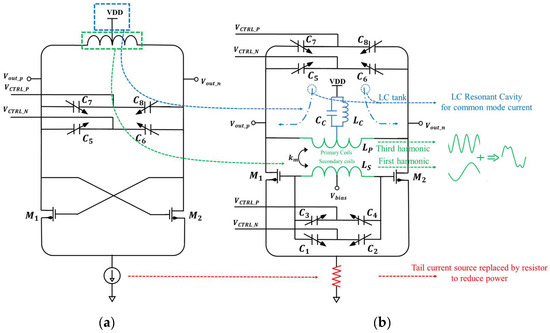
Figure 4.
(a) Conventional LC oscillator; (b) F-Class VCO proposed in this paper.
Compared to the conventional LC oscillator in Figure 4a, the F-CLASS VCO proposed in this paper is shown in Figure 4b, where the parts making improvements are marked by colored lines and analyzed in detail in the following.
In the transformer of the F-CLASS VCO, the primary coil is the top layer of thick metal and the secondary coil is the penultimate layer, located directly below the primary coil. This arrangement of the transformer allows for a higher quality factor (Q) value of the two coils [32]. According to electromagnetic simulations, the transformer has a Q value of 20 for the primary coil and 25 for the secondary coil, and the mutual inductance coefficient Km is 0.6. This VCO contains two sets of voltage-controlled capacitors, and all of these capacitors correspond to the resonant cavity formed by the primary and secondary coils of the transformer.
According to the conclusion of [33], in order to further suppress the second harmonic, the oscillator proposed in this paper also introduces an LC tank at the power supply input to provide an LC Resonant Cavity at the second harmonic and the common mode current. This LC tank is directly connected to the taps of the primary coil, which can effectively suppress the effect of the second harmonic. The third harmonic excited by the transformer and the second harmonic suppressed by the resonant cavity at the power supply result in a significant increase in the oscillator output spectrum at the fundamental and third harmonics and a significant suppression at the second harmonic, as shown in Figure 5.
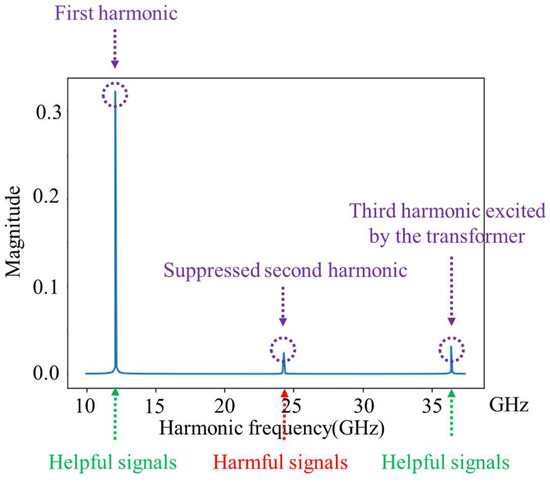
Figure 5.
DFT analysis of the oscillator output signal.
In a practical quantum computer system, the cooling device of the quantum computer has a cooling power limit. So, the lower the power of the controller, the more controllers and quantum processors can be integrated within the same quantum computer to achieve higher computational performance. The VCO also contributes most of the power consumption in the phase-locked loop, so it is crucial to reduce the oscillator power as much as possible. Therefore, in the circuit design, the tail current source is replaced with a resistor in this paper, and the oscillator power consumption is reduced from 30–40 mW to 3–4 mW.
In order to support the operation of as many quantum bits as possible, the quantum computer uses Frequency Division Multiple Access (FDMA) to control different qubits by means of different frequencies output from one controller, and there is usually a large frequency interval between each frequency of FDMA. Also, because the frequency of the VCO increases significantly at low temperatures, the VCO needs a large tuning range in order to balance the inaccuracy of the frequency at low temperatures with the bandwidth requirements of multiple qubits. To meet the requirement of frequency, the VCO in this paper uses multiple tuning capacitor arrays to expand the tuning range. The tuning range of the VCO is shown in Figure 6.
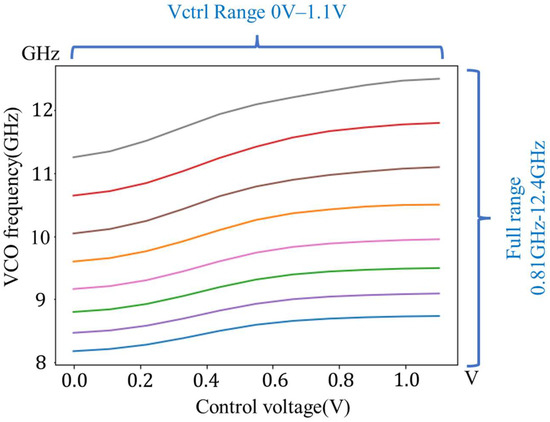
Figure 6.
The tuning range of the VCO.
4.1.2. Analysis of the Reasons Why This Circuit Can Reduce Noise
Since Hajimiri proposed the Impulse Sensitivity Function (ISF), the ISF has become a powerful tool for analyzing oscillator noise. The meaning of ISF is the response of the oscillator phase to an external injection pulse. So, if we analyze the noise as an external injection signal, the ISF can accurately describe the noise behavior of the oscillator.
According to [34,35], the phase noise contributed by the flicker noise can be written as in (9), where is the unnormalized ISF, is the flicker noise, and and are constants. According to the equation, we can conclude that, in addition to the flicker noise itself, the shape of the ISF significantly affects the phase noise contributed by the flicker noise. The phase noise is proportional to the integration of the product of ISF and flicker noise re-squared, so if you want to keep the oscillator phase noise as low as possible, a straightforward idea is to keep the ISF at zero as much as possible, so that the phase noise obtained from the integration will be as small as possible.
According to [31], in addition to the fundamental wave, the second and third harmonics are critical to the ISF. So, in order to analyze the effect of the circuit structure on the noise performance and to demonstrate that the structure proposed in this paper reduces the flicker noise, this paper firstly needs to investigate the effect of the higher harmonics on the circuit.
Firstly, we build a model for the resonant cavity of the oscillator to describe its behavior under the fundamental, second, and third harmonics, as shown in Figure 7.
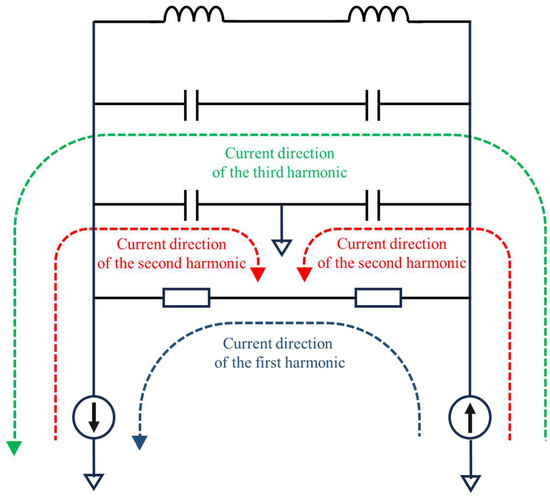
Figure 7.
Model for the resonant cavity of the oscillator.
Where the fundamental wave passes through the resistive path of the resonant cavity, the second and third harmonics pass through the capacitive path of the resonant cavity. According to the model, the voltage expression of the current generated by the second harmonic after flowing through the capacitive path can be written as
where is the capacitance on the second harmonic path, is the second harmonic current, is the fundamental frequency, is the phase overrun brought about by the harmonics, and is the phase lag brought about by the capacitive path. Therefore, the output signal of the oscillator at this point can be expressed as
An analysis of (5) shows that the effect of the second harmonic makes the synthesized signals of the fundamental and the second harmonic have different slopes on the falling and the rising edges, which leads to a significant increase in the ISF of the oscillator, as shown in Figure 8a. This, in turn, increases the effect of the conversion of the flicker noise to the phase noise of the oscillator and increases the oscillator noise.
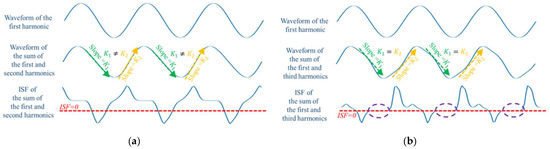
Figure 8.
(a) Fundamental waveforms, fundamental and second harmonic synthesized waveforms, ISF of synthesized waveforms. (b) Fundamental waveforms, fundamental and third harmonic synthesized waveforms, ISF of synthesized waveforms.
If only the fundamental and third harmonic cases are considered, the voltage signal of the third harmonic can be represented as
where is the capacitance on the second harmonic path, is the third harmonic current, is the fundamental frequency, and is the phase lag due to the capacitive path. Therefore, the output signal of the oscillator at this point can be expressed as
Analyzing (7), it can be concluded that the effect of the third harmonic does not cause the synthesized signals of the fundamental and the third harmonic to have different slopes at the falling and rising edges, so that the ISF has been kept small and a portion of it has been zero, as shown in Figure 8b. Such an ISF significantly suppresses the conversion of the flicker noise to the phase noise and reduces the oscillator noise.
Based on the above analysis, it can be concluded that the second harmonic is harmful to the oscillator, while the third harmonic is beneficial to the oscillator. Therefore, the on-chip transformer-based F-CLASS VCO designed in this paper suppresses the second harmonic by exciting the third harmonic of the oscillator to keep the oscillator ISF as much as possible in a state that suppresses the conversion of flicker noise to phase noise.
However, the analysis of the second harmonic on the oscillator ISF can be expanded. Assuming that we introduce a resonant cavity into the common mode path of the oscillator so that the capacitive path becomes a resistive path, the voltage expression for the second harmonic can be expressed as
The output signal of the oscillator at this point can be expressed as
The analysis of (9) shows that since the resistive path does not bring phase lag, the synthesis of the fundamental and the second harmonic does not bring the asymmetry of the slopes of the rising and falling edges, as shown in Figure 9, and, accordingly, it does not increase the conversion of the flicker noise to the phase noise. The resonant cavity that changes the common-mode path is the power filter used in this paper, which changes the nature of the common-mode path so that the second harmonic in the oscillator designed in this paper no longer enhances the conversion of flicker noise to phase noise.
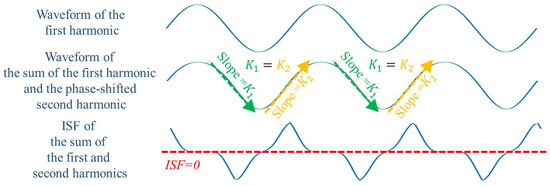
Figure 9.
Fundamental waveforms, fundamental and phase-shifted second harmonic synthesized waveforms, ISF of synthesized waveforms.
Through the derivation and analysis above, this paper explains the fundamentals of the designed oscillator to improve the phase noise by two methods: enhancing the third harmonic by F-CLASS VCO and changing the common-mode path by power supply filter. The ISF of the oscillator is also simulated in this paper, as shown in Figure 10. It can be seen that a relatively large portion of the ISF in the figure is 0, which does not enhance the flicker noise to phase noise. The corner frequency of the oscillator in this paper is shown in Figure 11a. It can be seen that the optimized corner frequency in this paper is about 200 KHz, which is significantly lower compared with the two unoptimized VCO structures in the paper [36], and the comparison of the corner frequencies of the three VCOs is shown in Table 1. In this paper, we have also simulated the oscillator with and without the power filter in the same oscillator structure. The phase noise of the oscillator with and without the power filter in the same oscillator structure is also simulated in this paper, as shown in Figure 11b. It can be seen that the phase noise of the oscillator with the power filter has a decrease of about 3 db. The above evidence shows that both the F-CLASS VCO structure and the power supply filter used in this paper can improve the noise performance of the oscillator very well.
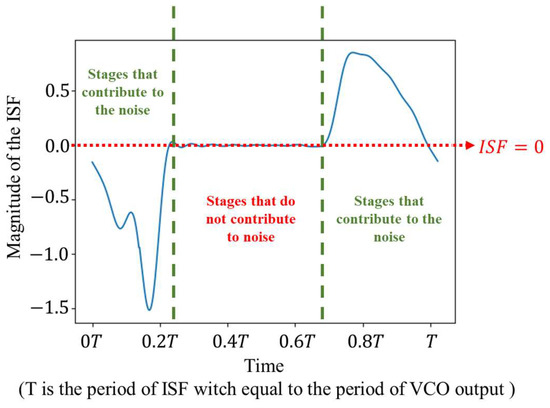
Figure 10.
ISF of the oscillator.
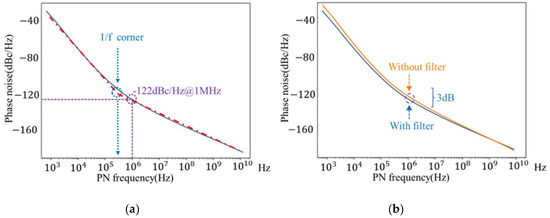
Figure 11.
(a) ISF; (b) VCO phase noise and corner frequency.

Table 1.
Comparison of the corner frequency of the three VCO structures.
4.2. Fully Differential Charge Pump
4.2.1. Design of the Fully Differential CP
The CP receives the output signal from the PFD and converts the phase error information into a current signal, which is then fed to the next stage of the filter. The classical charge pump structure is shown in Figure 12c. For charge pumps, device mismatches can have a significant impact on their performance. For a charge pump of the classic structure of Figure 12c, CMOS device mismatch will bring about a mismatch in the charge pump current, which in turn affects the performance of the phase-locked loop. And according to the analysis of the device mismatch under low temperature above, the device mismatch will be more serious under a low-temperature environment. In order to ameliorate the effects of device mismatch, a fully differential structure is used in this paper to mitigate the current mismatch.
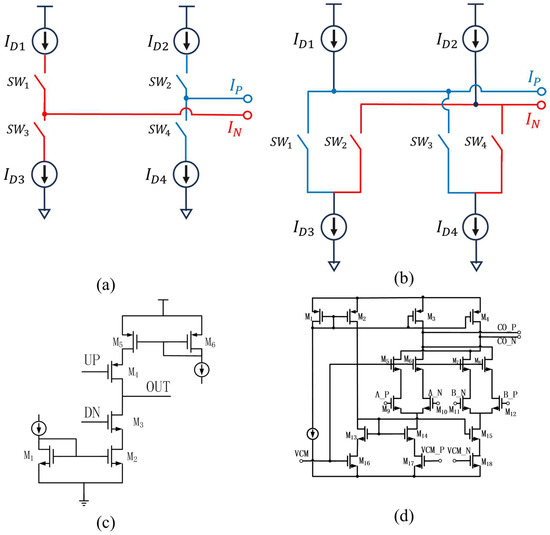
Figure 12.
(a) Simplified model of a classical structural charge pump. (b) Simplified model of a charge pump with fully differential structure. (c) Circuit structure of a classical charge pump. (d) Circuit structure of a fully differential charge pump.
The specific circuit is shown in Figure 12d. The charge pump is controlled by two pairs of switches (M9, M10, M11, M12), and the output of the switches suppresses the clock feedthrough through M5, M6, M7, M8. The charge pump is driven by four current sources, M3, M4, M14, M15. VCM_P, VCM_N are common mode voltage signals extracted from the filter and used to adjust the common mode point of the filter. When the common mode point of the filter deviates from the midpoint of the power supply and ground, the feedback loop adjusts the charge pump current to re-fix the common mode point at the midpoint of the power supply. In addition, the large size of M17 and M18 can reduce the high-frequency noise in the negative feedback loop.
4.2.2. Analysis of Device Mismatch
For a charge pump, its output current is the drain current of the MOS device that serves as the power supply. In order to analyze the effect of device mismatch on the current mismatch of the charge pump, we need to simplify the circuit of the charge pump to a logic structure that is only affected by the drain current. Figure 12c shows the differential charge pump composed of the classical charge pump structure, and Figure 12d shows the full differential charge pump structure proposed in this paper. In Figure 12a,b, correspond to the drain current of the MOS device which plays the role of current source in the circuit, and correspond to the four control switches of the charge pump, respectively. And correspond to the differential currents output from the charge pump. Each output current of the charge pump has three states, namely, pump-in current, pump-out current, and neither pump-in nor pump-out current. The charge pump dynamically pumps in or out current to adjust the control voltage of the VCO when the phase-locked loop is not locked. Its current mismatch is not significant in this process. When the phase-locked loop is locked, the discriminator no longer controls the charge pump; the charge pump at this time, in the ideal state, is neither pumped in nor pumped out current. But at this time, the charge pump current mismatch will cause continuous leakage, seriously affecting the stable state of the phase-locked loop. We can write out the classical charge pump structure and the full differential charge pump structure in the phase-locked loop locked when the charge pump is neither pumped in nor pumped out of the current mismatch.
From Table 2, it can be seen that for the classical charge pump, the current mismatch between the N and P paths is the mismatch between the two MOS devices corresponding to and the two MOS devices corresponding to . According to the Croon model and Pelgrom’s law in the third part of this paper, the mismatches of the two MOS devices corresponding to and the mismatches of the two MOS devices corresponding to are independently and identically distributed and can be described by the same one standard deviation operator σ.

Table 2.
Expressions for current mismatch of charge pumps with two structures.
However, for the fully differential charge pump, there are two possibilities in the state where it neither pumps in nor pumps out current. Taking the current in the N path as an example, half of its current mismatches are possible between , and the other half are possible between . Therefore, the current mismatch here should be the average of the mismatch between and the mismatch between . Because the mismatch between and the mismatch between also satisfy the independent and identical distribution, according to the Croon model and Pelgrom’s law, the total mismatch of the P-path current should be σ/√2. Therefore, we can conclude that the fully differential charge pump proposed in this paper can make the standard deviation operator describing the current mismatch decrease significantly and improve the mismatch phenomenon of the charge pump effectively. And this method is not affected by temperature; even if σ increases at low temperature, we can still reduce its mismatch by means of full differential charge pumping.
In this paper, the accuracy of the above proof is verified by Monte Carlo simulation, as shown in Figure 13. The mismatch simulation results of the classical charge pump are fitted as in Figure 13a. The mismatch simulation results of the fully differential charge pump are fitted as shown in Figure 13b. It can be seen very clearly that the fitted plot of the mismatch for the fully differential charge pump is much narrower than the fitted plot of the mismatch for the classical charge pump. It means that σ has been significantly reduced.
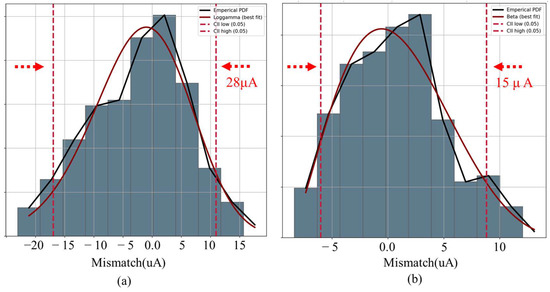
Figure 13.
(a) Simulation results of the classical charge pump. (b) Simulation results of the fully differential charge pump.
5. Discussion
The design of complete phase-locked loops for cryogenic environments is relatively rare [25], and usually separate cryogenic oscillators are more common [8,37,38]; the oscillator in this paper has been improved in different parameters compared to the existing published work, as shown in Table 3. The main thrust of the work in this paper is to design a signal source for a quantum computer that can be used as close as possible to a quantum processor, and therefore not only performance but also other factors such as area, power consumption, etc., are considered, and therefore many performance considerations are weighed. The circuit structure proposed in this paper has not yet reached the stage of production and testing, because the production and testing of chips is a very long process. And in order to verify the correctness of the arguments in this paper, this paper modifies the parameters of the circuit simulator and electromagnetic simulator and the simulation method so that the simulation environment can simulate the circuit operating state as low as 4.2 Kelvin, in order to ensure that the circuit will not be unable to work at low temperatures after the circuit is produced.

Table 3.
Comparison of the performance of cryogenic oscillators proposed in different works.
6. Conclusions
In this paper, in order to meet the demand of quantum computers for high-performance clock sources, the performance requirements of quantum computers for clock sources under low-temperature conditions are analyzed, and a low-power VCO for flicker noise suppression and a fully differential charge pump for mismatch suppression are introduced for this demand. Through theoretical analysis and simulation verification, this paper demonstrates that the structure of the phase-locked loop can meet the requirements of quantum computers under low-temperature conditions. In the future, we will continue to optimize the phase-locked loop structure to achieve a lower-power and higher-performance phase-locked loop structure to meet the needs of larger-scale quantum computers.
Author Contributions
Conceptualization, K.X.; Methodology, K.X.; Software, C.X. and M.L. (Meng Li); Validation, K.X., F.L., K.G., Z.P., C.X., G.Z., W.W. and M.L. (Meng Li); Formal analysis, K.X.; Investigation, K.X.; Resources, M.L. (Mingche Lai) and F.L.; Data curation, K.G., Z.P., G.Z. and W.W.; Writing—original draft, K.X.; Writing—review & editing, K.X.; Visualization, M.L. (Mingche Lai) and F.L.; Project administration, K.X. and M.L. (Mingche Lai); Funding acquisition, M.L. (Mingche Lai) and F.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant number 62204263, the funder is Fangxu Lv.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Montanaro, A. Quantum algorithms: An overview. NPJ Quantum Inf. 2016, 2, 1–8. [Google Scholar] [CrossRef]
- Shor, P.W. Algorithms for quantum computation: Discrete logarithms and factoring. In Proceedings of the 35th Annual Symposium on Foundations of Computer Science, Santa Fe, NM, USA, 20–22 November 1994. [Google Scholar] [CrossRef]
- Grover, L.K. A fast quantum mechanical algorithm for database search. STOC ′96. In Proceedings of the Twenty-Eighth Annual ACM Symposium on Theory of Computing, Philadelphia, PA, USA, 22–24 May 1996; pp. 212–219. [Google Scholar] [CrossRef]
- Feynman, R.P. Simulating physics with computers. Int. J. Theor. Phys. 1982, 21, 467–488. [Google Scholar] [CrossRef]
- Vu, C.; Fay, M. IBM Builds Its Most Powerful Universal Quantum Computing Processors; IBM Research: Armonk, NY, USA, 2017. [Google Scholar]
- Kelly, J.; Barends, R.; Fowler, A.G.; Megrant, A.; Jeffrey, E.; White, T.C.; Sank, D.; Mutus, J.Y.; Campbell, B.; Chen, Y. State preservation by repetitive error detection in a superconducting quantum circuit. Nature 2015, 519, 66–69. [Google Scholar] [CrossRef] [PubMed]
- Monz, T.; Schindler, P.; Barreiro, J.T.; Chwalla, M.; Nigg, D.; Coish, W.A.; Blatt, R. 14-Qubit Entanglement: Creation and Coherence. Phys. Rev. Lett. 2011, 106, 130506. [Google Scholar] [CrossRef]
- Patra, B.; Incandela, R.M.; Van Dijk, J.P.; Homulle, H.A.; Song, L.; Shahmohammadi, M.; Charbon, E. Cryo-CMOS Circuits and Systems for Quantum Computing Applications. IEEE J. Solid-State Circuits 2018, 53, 309–321. [Google Scholar] [CrossRef]
- Van Meter, R.; Horsman, D. A blueprint for building a quantum computer. Commun. ACM 2013, 56, 84–93. [Google Scholar] [CrossRef]
- Vandersypen LM, K.; Bluhm, H.; Clarke, J.S.; Dzurak, A.S.; Ishihara, R.; Morello, A.; Reilly, D.J.; Schreiber, L.R.; Veldhorst, M. Interfacing spin qubits in quantum dots and donors—Hot, dense, and coherent. NPJ Quantum Inf. 2017, 3, 34. [Google Scholar] [CrossRef]
- Mehrpoo, M.; Sebastiano, F.; Charbon, E.; Babaie, M. A Cryogenic CMOS Parametric Amplifier. IEEE Solid-State Circuits Lett. 2019, 3, 5–8. [Google Scholar] [CrossRef]
- Le Guevel, L.; Billiot, G.; Jehl, X.; De Franceschi, S.; Zurita, M.; Thonnart, Y.; Pillonnet, G. 19.2 A 110 mK 295 µW 28 nm FDSOI CMOS Quantum Integrated Circuit with a 2.8 GHz Excitation and nA Current Sensing of an On-Chip Double Quantum Dot. In Proceedings of the 2020 IEEE International Solid- State Circuits Conference—(ISSCC), San Francisco, CA, USA, 16–20 February 2020. [Google Scholar] [CrossRef]
- Vliex, P.; Degenhardt, C.; Grewing, C.; Kruth, A.; Nielinger, D.; Van Waasen, S.; Heinen, S. Bias Voltage DAC Operating at Cryogenic Temperatures for Solid-State Qubit Applications. IEEE Solid-State Circuits Lett. 2020, 3, 218–221. [Google Scholar] [CrossRef]
- Ruffino, A.; Peng, Y.; Sebastiano, F.; Babaie, M.; Charbon, E. A Wideband Low-Power Cryogenic CMOS Circulator for Quantum Applications. IEEE J. Solid-State Circuits 2020, 55, 1224–1238. [Google Scholar] [CrossRef]
- Ball, H.; Oliver, W.D.; Biercuk, M.J. The role of master clock stability in quantum information processing. npj Quantum Inf. 2016, 2, 16033. [Google Scholar] [CrossRef]
- Raftery, J.; Vrajitoarea, A.; Zhang, G.; Leng, Z.; Srinivasan, S.; Houck, A. Direct Synthesis of Microwave Waveforms for Quantum Computing. APS March Meet. Abstr. 2017, 2017, C46-003. [Google Scholar] [CrossRef]
- Green, T.; Uys, H.; Biercuk, M.J. High-Order Noise Filtering in Nontrivial Quantum Logic Gates. Phys. Rev. Lett. 2012, 109, 1224–1238. [Google Scholar] [CrossRef]
- Green, T.J.; Sastrawan, J.; Uys, H.; Biercuk, M.J. Arbitrary quantum control of qubits in the presence of universal noise. New J. Phys. 2013, 15, 095004. [Google Scholar] [CrossRef]
- Reed, M.D.; Maune, B.M.; Andrews, R.W.; Borselli, M.G.; Eng, K.; Jura, M.P.; Kiselev, A.A.; Hunter, A.T. Reduced Sensitivity to Charge Noise in Semiconductor Spin Qubits via Symmetric Operation. Phys. Rev. Lett. 2016, 116, 110402. [Google Scholar] [CrossRef]
- Martins, F.; Malinowski, F.K.; Nissen, P.D.; Barnes, E.; Fallahi, S.; Gardner, G.C.; Manfra, M.J.; Marcus, C.M.; Kuemmeth, F. Noise Suppression Using Symmetric Exchange Gates in Spin Qubits. Phys. Rev. Lett. 2016, 116, 116801. [Google Scholar] [CrossRef]
- Didier, N.; Sete, E.A.; Combes, J.; da Silva, M.P. ac Flux Sweet Spots in Parametrically Modulated Superconducting Qubits. Phys. Rev. Appl. 2019, 12, 054015. [Google Scholar] [CrossRef]
- Anton, S.M.; Müller, C.; Birenbaum, J.S.; O’Kelley, S.R.; Fefferman, A.D.; Golubev, D.S.; Clarke, J. Pure dephasing in flux qubits due to flux noise with spectral density scaling as 1/f α. Phys. Rev. B 2012, 85, 224505. [Google Scholar] [CrossRef]
- Rebentrost, P.; Serban, I.; Schulte-Herbrüggen, T.; Wilhelm, F.K. Optimal Control of a Qubit Coupled to a NonMarkovian Environment. Phys. Rev. Lett. 2009, 102, 090401. [Google Scholar] [CrossRef]
- Nazarov, Y.V. Quantum Noise in Mesoscopic Physics; Springer Science & Business Media: Delft, The Netherlands, 2012; Volume 97. [Google Scholar]
- Gong, J.; Charbon, E.; Sebastiano, F.; Babaie, M. A Cryo-CMOS PLL for Quantum Computing Applications. IEEE J. Solid-State Circuits 2022, 58, 1362–1375. [Google Scholar] [CrossRef]
- Van Dijk, J.P.-G.; Kawakami, E.; Schouten, R.N.; Veldhorts, M.; Vandersypen, L.M.K.; Babaie, M.; Charbon, E.; Sebastiano, F. Impact of Classical Control Electronics on Qubit Fidelity. Phys. Rev. Appl. 2019, 12, 044054. [Google Scholar] [CrossRef]
- Nielsen, M.A. A simple formula for the average gate fidelity of a quantum dynamical operation. Phys. Lett. A 2002, 303, 249–252. [Google Scholar] [CrossRef]
- Pedersen, L.H.; Møller, N.M.; Mølmer, K. Fidelity of quantum operations. Phys. Lett. A 2007, 367, 47–51. [Google Scholar] [CrossRef]
- Croon, J.; Rosmeulen, M.; Decoutere, S.; Sansen, W.; Maes, H. An easy-to-use mismatch model for the MOS transistor. IEEE J. Solid-State Circuits 2002, 37, 1056–1064. [Google Scholar] [CrossRef]
- Pelgrom, M.; Duinmaijer, A.; Welbers, A. Matching properties of MOS transistors. IEEE J. Solid-State Circuits 1989, 24, 1433–1439. [Google Scholar] [CrossRef]
- Shahmohammadi, M.; Babaie, M.; Staszewski, R.B. A 1/f Noise Upconversion Reduction Technique for Voltage-Biased RF CMOS Oscillators. IEEE J. Solid-State Circuits 2016, 51, 2610–2624. [Google Scholar] [CrossRef]
- Hong, F.; Ding, T.; Zhao, D. A 196.5 dBc/Hz FOMT 16.8–21.6-GHz Class-F23 CMOS VCO With Transformer-Based Optimal Q-Factor Tank. IEEE Solid-State Circuits Lett. 2022, 5, 62–65. [Google Scholar] [CrossRef]
- Ming, S.; Zhou, J. A 19 GHz Circular-Geometry Quad-Core Tail-Filtering Class-F VCO with −115 dBc/Hz Phase Noise at 1 MHz Offset in 65-nm CMOS. In Proceedings of the ESSCIRC 2021—IEEE 47th European Solid State Circuits Conference (ESSCIRC), Virtual, 13–22 September 2021. [Google Scholar] [CrossRef]
- Hajimiri, A.; Lee, T. A general theory of phase noise in electrical oscillators. IEEE J. Solid-State Circuits 1998, 33, 179–194. [Google Scholar] [CrossRef]
- Hu, Y.; Siriburanon, T.; Staszewski, R.B. A Low-Flicker-Noise 30-GHz Class-F23 Oscillator in 28-nm CMOS Using Implicit Resonance and Explicit Common-Mode Return Path. IEEE J. Solid-State Circuits 2018, 53, 1977–1987. [Google Scholar] [CrossRef]
- Hu, Y.; Siriburanon, T.; Staszewski, R.B. Oscillator Flicker Phase Noise: A Tutorial. IEEE Trans. Circuits Syst.—II Express Briefs 2021, 68, 538–544. [Google Scholar] [CrossRef]
- Ruffino, A.; Peng, Y.; Yang, T.-Y.; Michniewicz, J.; Gonzalez-Zalba, M.F.; Charbon, E. A fully-integrated 40-nm 5–6.5 GHz cryo-CMOS system-on-chip with I/Q receiver and frequency synthesizer for scalable multiplexed readout of quantum dots. In Proceedings of the 2021 IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 13–22 February 2021; pp. 210–212. [Google Scholar] [CrossRef]
- Peng, Y.; Ruffino, A.; Benserhir, J.; Charbon, E. A cryogenic SiGe BiCMOS hybrid class B/C mode-switching VCO achieving 201 dBc/Hz figure-of-merit and 4.2 GHz frequency tuning range. In Proceedings of the 2022 IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 20–24 February 2022. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).