Abstract
This paper presents the validation of a novel approach for a true-random number generator (TRNG) based on a ring oscillator–physical unclonable function (RO-PUF) for FPGA devices. The proposal takes advantage of the different noise sources that affect the electronic implementation of the RO-PUF to extract the entropy required to guarantee its function as a TRNG, without anything more than minimal changes to the original design. The new RO-PUF/TRNG architecture has been incorporated within a hybrid HW/SW embedded system designed for devices from the Xilinx Zynq-7000 family. The degree of randomness of the generated bit streams was assessed using the NIST 800-22 statistical test suite, while the validation of the RO-PUF proposal as an entropy source was carried out by fulfilling the NIST 800-90b recommendation. The features of the hybrid system were exploited to carry out the evaluation and validation processes proposed by the NIST publications, online and on the same platform. To establish the optimal configuration to generate bit streams with the appropriate entropy level, a statistical study of the degree of randomness was performed for multiple TRNG approaches derived from the different implementation modes and configuration options available on the original RO-PUF design. The results show that the RO-PUF/TRNG design is suitable for secure cryptographic applications, doubling its functionality without compromising the resource–efficiency trade-off already achieved in the design.
1. Introduction
The increase in the connectivity potential that electronic devices currently have in practically any commercial sector requires the development of security strategies that provide more confidence in the management of private data, since security in the exchange of such information has always been a latent concern in society, in addition to being a fundamental right of the citizens. In response to this demand, scientific effort has been largely focused on the study and development of optimal alternatives for one of the most important security primitives: random number generators.
Random numbers are required in multiple scientific fields, such as artificial neural networks [1,2,3], or evolutionary computing [4,5,6], but particularly in the case of cryptography, random numbers are crucial elements since their level of unpredictability can be used to determine the robustness of the security protocols implemented in a given communication system to prevent information from being compromised by attacks from a third party [7,8,9].
Currently, in the study and development of TRNGs, it is possible to group the entropy sources into three main groups: noise [10,11,12], chaos [13,14,15], and jitter [16,17,18]. Within these TRNGs, those based on jitter tend to be easier to integrate and are characterized by being portable implementations, as mentioned in [19].
The jitter phenomena has been investigated as a source of entropy, commonly, by means of the structure of ring oscillators (ROs). ROs take advantage of delays in the logic gates and interconnections of an odd number of closed-loop connected inverters to generate an oscillation at a given frequency. In addition to the variation between different devices caused by variability in the manufacturing process, this frequency is affected by random factors caused by inherent noise sources (jitter), and this random characteristic allows ROs to be exploited as sources of entropy.
Since ROs are based on logic gates, they are ideal candidates to be subjected to study under implementations performed on field programmable gate arrays (FPGAs) [20]. It is increasingly common to see the implementation of TRNGs on FPGAs and other programmable devices since their reconfigurability facilitates the development of solutions in less time compared with devices having a specific purpose (i.e., ASICs), and they are ideal devices for prototyping.
The work presented in [21] reports a TRNG implemented on a Xilinx Virtex-6 FPGA based on the random jitter of a multistage feedback RO (MSFRO). In this proposal, the structure of the traditional RO is modified to add multiple feedback stages with three main objectives: to extend the clock jitter range, to improve the clock sampling frequency, and to increase the randomness level of the entropy source. In [22], the authors present a TRNG approach implemented on a Xilinx Zynq XC7Z020 System-on-Chip (SoC) that takes advantage of the capability of the Xilinx Digital Clock Manager to tune, at run-time, the phase shift between two clock signals, allowing to force the metastability of the flip-flops to generate random numbers. The work cited in [23] uses three D-Latches connected in RO configuration by means of three inverters to exploit the phenomena of metastability and jitter accumulation for random number generation. This proposal has been implemented on a Xilinx Spartan-6 family device, optimizing resource consumption by analyzing in depth the connection structure of the configurable logic blocks (CLBs). In [24], the authors present a TRNG based on ROs and implemented on a Xilinx Spartan-3A FPGA. This variant incorporates programmable delay lines (PDLs) in the oscillator rings with the objective of amplifying the variation in oscillations and introducing larger jitter to the clocks generated by the ROs. The authors highlight that by using PDLs they obtain a better level of randomness since the degree of correlation between several ROs of equal length is reduced. The work cited in [25] presents three types of TRNG based on ROs and implemented in a Zynq-7000 family device. The strength of their proposal lies in the cumulative application of the XOR operation between the outputs of multiple entropy sources to generate numbers with a higher degree of randomness than those that can be obtained by using the same sources individually. In [26], the authors show a TRNG based on nonlinear feedback ROs (NL-FRO) and implemented on an Altera Cyclone IV FPGA device. The incorporation of nonlinear feedback loops increases the chaotic behavior of the RO, and as a consequence, the entropy source is amplified. The work presented in [27] describes a TRNG operating under the on–off uncertainty principle based on a modified RO design implemented in the FPGA of a Virtex 5 development board. This modification consists of adding a controller that allows the ROs to alternate between an even or odd number of inverters through the use of a multiplexer, which is equivalent to controlling the on or off state of the ROs. Periodically alternating between these states allows the degree of randomness to be increased. Some authors have also analyzed the possibility of obtaining random bit sequences through certain types of RO-based physical unclonable functions (PUFs) [28,29,30]. PUFs have become fundamental elements in increasing the security level of systems, as they are used to authenticate electronic devices and generate cryptographic keys, taking advantage of the physical variations that occur naturally during semiconductor manufacturing [31,32,33,34]. The operating principle of a RO-PUF relies on the frequency differences that exist in the oscillation of ROs, even having the same layout, and the intrinsic variations of the device manufacturing process cause each RO to have a characteristic frequency depending on the device in which it is implemented. In practice, this behavior is affected by the presence of different sources of noise in the electronic device, which cause jitter in the oscillating signals and require the use of error correction codes to guarantee correct operation. However, as demonstrated in this work, slight modifications in the RO-PUF design allow the random nature of these phenomena to be exploited as an analog source of entropy and used for the generation of totally random bit streams.
This paper describes the generation of random bit streams by means of a modified version of the RO-PUF design recently proposed in [35]. For this purpose, a strategy has been developed to take advantage of the capacity of the design to generate random bits and increase its versatility by integrating the dual PUF/TRNG functionality, taking full advantage of the resources consumed. The new configurable RO-PUF/TRNG architecture allows selecting Binary or Gray code counters in the RO comparison blocks, which represents two additional alternatives to generate both identifiers and random bit sequences from the intrinsic device characteristics. The placement scheme of the ROs within the RO bank has been updated to follow a snake pattern, to ensure that, when applying the challenge generation mechanism, the relative distance between the CLBs is the same for all RO pair comparisons. The RO-PUF/TRNG design has been encapsulated as an IP module that can be synthesized in characterization or operation mode. The first option allows the extraction of all the output bits of the counters in each comparison, to facilitate the analysis of the behavior of the system with the aim of optimizing its performance or facilitating portability to other devices. Different instances of the IP were incorporated within a hybrid HW/SW test system implemented on a Pynq-Z2 development board for validation and characterization purposes. The processor of this embedded system is used both for accessing the RO-PUF/TRNG through a set of high-level language drivers and to carry out the online evaluation and validation processes of the bit sequences by means of the tests and recommendations proposed by the National Institute of Standards and Technology (NIST).
The main contributions of this work are:
- a novel approach to generate true random numbers based on RO-PUF design for FPGA devices;
- four possible TRNG implementations that can be derived from the configurability of the RO-PUF design to generate random numbers based on the combination of the relative position of the competing ROs and the type of coding of the counters;
- demonstration of random number generation capability of the four possible TRNG implementations, one without the need of any post-processing stage, and by means of the XOR bias corrector in the remaining three configurations;
- assessment and validation of the randomness degree of the TRNG implementations by means of the NIST 800-22 standard and NIST 800-90b recommendation;
- integration of two hardware security primitives in a compact design, optimizing both resource and power consumption.
To guide the reading of this document, Section 2 presents the general background of random number generation and RO-based PUFs and introduces the main features of the RO-PUF in which the TRNG functionality will be integrated. Details of the new RO-PUF/TRNG design, from the entropy collection process to random bit generation, as well as the approach and metrics used to select the most suitable bits for both functionalities, are provided in Section 3. Section 4 describes the execution of an extensive statistical characterization protocol of the random sequences generated, together with a detailed analysis of the results. Finally, Section 5 summarizes the main conclusions reached from the results of this work.
2. Background
2.1. Random Number Generators
Within the literature, two main groups of entropy sources for the generation of random numbers are commonly identified. The first is of digital type and is based on computational procedures (algorithms), and the second one is of analog type, which takes advantage of the intrinsic characteristics of physical phenomena.
The random number generators based on algorithms are characterized by being deterministic; therefore, they can produce an output of periodic sequences using a specific procedure that must be initialized with a “seed” value. However, this fact implies that any person has the possibility to reproduce the random sequence, regardless of its period length, if they have access to the seed value and know beforehand the algorithm that has been used to generate it. Consequently, its applicability for security purposes is hardly recommended. In addition, the continuous development of processors with increasing computational power and the consequent decoding capacity play an important role in this type of entropy source. Since they do not have the ability to generate fully unpredictable outputs, generators based on digital entropy sources are referred to as pseudo-random number generators (PRNG).
In the case of analog entropy sources, random sequences are obtained by means of the exploitation of hardware physical phenomena [36,37,38], which implies that there is no pre-defined process for successive data generation and that an initialization value is not required. Therefore, the independence, non-periodicity, and unpredictability features of the generated outputs are guaranteed. Unlike digital entropy sources, the level of randomness of analog sources does not lie in the software or hardware implementation of the algorithms; hence, this information can be public and, ideally, the robustness of the entropy source is not compromised. Having the ability to generate totally unpredictable outputs, generators based on analog entropy sources are referred to as true-random number generators (TRNG).
The design and validation processes of a TRNG is schematized in the flowchart shown in Figure 1. The design process begins with the identification of a physical phenomenon to which is attributed the capacity to generate random information with a certain level of entropy. Once the source has been identified, this physical phenomenon is exploited by designing a corresponding mechanism that allows its quantification in the binary system, which enables the interpretation of the source behavior from the digital perspective, and allows us to take advantage of it for the generation of bit sequences. Finally, the design stage concludes by providing the digitization mechanism with a strategy to collect all the data generated from the entropy source and structure them in such a way that they are available for processing. Generally, the data collection stage involves the HW/SW interaction to perform the subsequent stages that define the validation process.
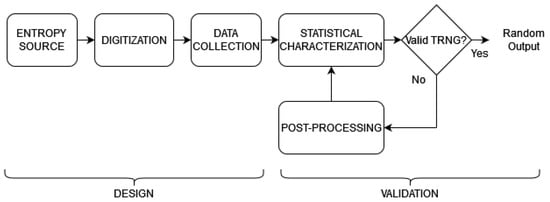
Figure 1.
Flowchart of the design and validation processes of a TRNG.
To assess the degree of randomness of the entropy source digitization, two stages are needed; in the first, a statistical study of the obtained bit sequences is performed with the objective of confirming the unpredictability of the data. Among the strategies available in the literature to assess the degree of randomness, the most common are the analysis of the proportional distribution between ’1’s and ’0’s, and the detection of repetitive patterns within the sequences, both developed from different approaches in different tests. The result of each test indicates whether the entropy source meets the requirements established in it, and it is up to the user to determine the set of tests that allow the validation of the digitization mechanism according to the target application. If the bit streams obtained do not satisfy the set of tests selected for statistical study, there is the alternative of submitting them to one or more post-processing stages to increase their degree of randomness, but this strategy generally compromises the effective length of the bit stream by decreasing it by a significant proportion.
2.2. RO-Based PUFs
As mentioned in the introduction, ring oscillators are ideal candidates for the implementation of TRNGs in FPGAs. ROs are circuits consisting of an odd number of inverting gates connected in series with a feedback path between the output and the input, as shown in Figure 2. Due to the fact that in a physical device the gates do not respond instantaneously to a change in the inputs, the output of each gate within an RO takes a specific duration to invert the value of the input after it has been updated. As a consequence, this arrangement of gates presents a specific oscillation pattern, the period of which depends on the accumulated delays in the feedback loop. Variations in the IC fabrication process cause the frequencies of ROs with identical layouts to be different, and this characteristic is exploited by RO-PUFs to identify a determined device. However, as illustrated in Figure 2b, the RO oscillation frequency exhibits a series of fluctuations over time as a consequence of small changes in the operating conditions and the presence of intrinsic noise sources in the microelectronic device. The random nature of this phenomenon, also known as ’jitter’, presents a drawback in the implementation of a PUF, but can be exploited in the generation of random bit streams, as demonstrated in the next sections of this work.
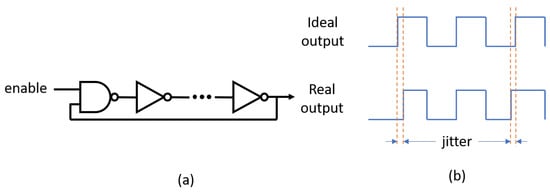
Figure 2.
(a) A generic ring oscillator scheme with the enable stage and (b) its jitter representation.
In general terms, the core of an RO-PUF is described by a bank of n ROs. Each n-th RO can be selected to perform a competition with another RO, both of them selected by means of two multiplexers. To avoid a possible correlation in the generated outputs, a selection strategy for the control signals of the multiplexers is usually defined in such a way that all the ROs of the bank participate in a maximum of two competitions. The frequencies of each selected pair of ROs are compared by using their outputs as the clock signals of two counters in such a way that the difference in the frequencies between them is translated into a difference in speed at which each of them would reach a pre-defined stop criterion for the counters. Once one of the counters reaches the stop criterion condition, the count of the other counter is stopped and its value is used to select the most suitable bits for the PUF output, i.e., those bits that feature appropriate values in the stability, probability and entropy metrics. Stability represents the ability of a PUF to reproduce a given value, while entropy indicates to what extent this value is unpredictable and unique for each PUF. From a PUF perspective, the ideal stability and entropy value of a selectable bit is 1, which would provide reliability and uniqueness for the PUF output. An ideal probability value of 0.5 is also desirable to avoid biases in the output that could make it easier to attack the PUF. From the perspective of TRNG, on the other hand, it is also convenient to select bits with maximum entropy but with stability and probability values close to 0.5, meaning that the output value will not present repeatable and recognizable patterns over time.
It is important to consider that any target application will demand a specific length of bits at the output to create an identifier, obfuscate a key, or generate a random number; therefore, a trade-off must be exhibited in the design of the RO-PUF/TRNG between the resource consumption used for its implementation and the number of bits required to construct the output. In addition to selecting the most suitable bits in each competition, the size of the RO bank must be dimensioned according to the number of bits demanded by a specific application.
Characterizations of the losing counter bits reported in the literature [39,40], along with the data presented later in this work, indicate a decreasing trend in stability and an increasing trend in entropy metrics in the MSB-LSB direction of the counters, making it necessary to establish a trade-off to achieve adequate reliability and uniqueness values for the resulting RO-PUFs. Additionally, these data also reveal that one or more of the LSBs present adequate characteristics to be considered as an entropy source for building TRNGs.
With the idea of corroborating the hypothesis that random variations in RO oscillation frequencies in this type of PUF can be used as a source of entropy for a TRNG, we have designed and encapsulated as an IP an improved version of the RO-PUF described in [35], and have implemented a test system with 10 of these IPs on a device of the Xilinx Zynq-7000 family to facilitate the evaluation of its behavior.
Compared with similar proposals, such as the one described in [29], which also incorporates double PUF/TRNG functionality in the same design, our proposal offers the following novelties: a strategy to double the number of bits generated without increasing the required resources; the possibility of choosing, in each invocation of the module, between different options that determine its functionality and configuration; and its conception as a hybrid HW/SW system that speeds up its online characterization and verification according to NIST guidelines and recommendations.
3. PUF/TRNG Design and Implementation
Based on the RO-PUF block diagram presented in [35], we can draw a parallel between the tasks carried out by each of the PUF components and the functions associated with the design stages of a TRNG presented in Figure 1. As illustrated by the simplified diagram shown in Figure 3, the blocks required for both functionalities are similar. The characteristics of each of these blocks, as well as the input and output signals of the design, are discussed in the following sections.
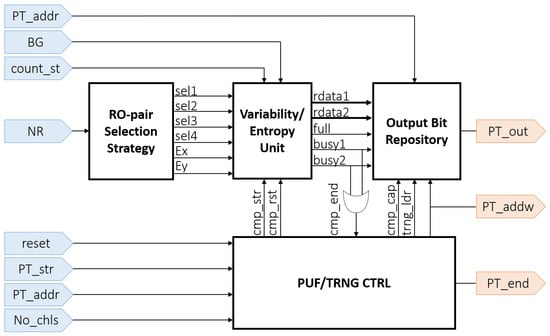
Figure 3.
Simplified block diagram for the RO-PUF/TRNG design.
3.1. Variability/Entropy Unit
Together, the array of ROs, the RO selection stage, and the comparison block constitute the Variability/Entropy Unit presented in Figure 4a. The core of the RO-PUF/TRNG design described in this work is a matrix of Nx columns by Ny rows of CLBs that implement four 4-stages ROs each, as shown in Figure 4b, whose size and position in the programmable device are defined at implementation time. The last three stages of each RO correspond to logic inverters, while the first stage corresponds to an AND gate used both to close the feedback loop of the RO, and to provide the enable signals. The implementation of four four-stage ROs in a CLB, carried out through VHDL placement directives, allows the optimization of the consumption of logic resources for Xilinx Series-7 FPGA and SoC devices, whose CLBs are composed of eight LUTs that individually allow the implementation of two independent Boolean functions of up to five inputs.
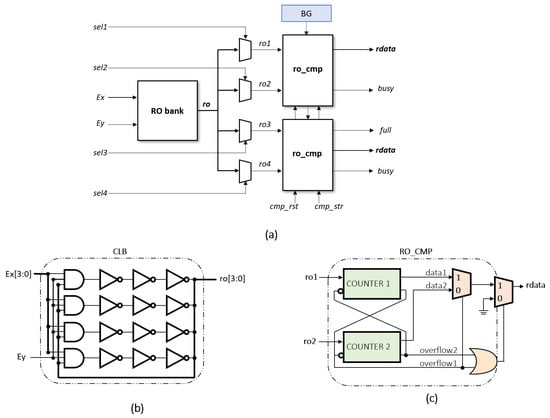
Figure 4.
(a) Variability/Entropy block diagram. (b) Implementation scheme of 4 ROs of 4 stages in a CLB. (c) RO pair comparison module.
One of the main features of this design lies in the realization of two simultaneous competitions, according to two different selection strategies, to optimize the trade-off between bit generation capacity versus resource consumption. Therefore, four ROs are selected from the RO bank by means of a multiplexing stage, and routed to a double instance of the comparison module depicted in Figure 4c.
Each comparison module contains two counters where the oscillating outputs of a pair of ROs are used as clock signals. In this way, the frequencies of each pair of ROs are compared until the faster counter reaches the overflow condition, and triggers a signal to stop the other counter. At the end of both counts, both comparison blocks generate two output signals; a flag indicating that the count has finished (busy) and a signal with the value of the slower counter. One of the comparisons blocks also generates a flag (full) indicating the ‘sign’ of the comparison, i.e., which of the two counters has reached the stop condition first.
Other novel features of this design are the use of internal Gray code counters in the comparison blocks, to avoid errors in the activation of the ’full’ flag that could occur due to glitches caused by the change in multiple bits in the counters, and the inclusion of a new parameter (BG) that allows selecting binary or Gray code values in their outputs.
3.2. RO Pair Selection Strategy
Within the literature, RO-PUF designs have been proposed in which RO frequency comparison is used to generate a single output bit [41] (referred to as “sign bit” in this work) from each comparison, as well as to obtain multiple bits in each comparison from the counter associated with the slowest RO [39]. The results of the study on the effectiveness of these designs carried out in [35] motivated the development of the RO-PUF proposed in [40], where it was shown that the combination of both types of comparison allows the PUF performance to be optimized by increasing the number of output bits. Additionally, the cited study allowed us to establish a relationship between the relative position of competing ROs and the efficiency level of each type of comparison. These results show that comparisons between the ROs implemented in LUTs located in the same position of different CLBs are optimal for providing the “sign bit”, since it satisfies the PUF metrics, while in the case of comparisons between ROs implemented in LUTs located in different positions of the same or a different CLB, it is possible to obtain a greater number of bits from the losing counter, satisfying the same metrics.
Based on these conclusions, our proposal incorporates the two strategies in the execution of the two simultaneous comparisons. To this end, the selection of the quartet of ROs involved in each comparison cycle is performed based on the indices associated with their own positions within the RO bank. To select the first RO of the quartet, we use the output of a counter that is incremented by one each time the system executes the two simultaneous comparisons (sel1); then, the location of the relative positions of the remaining three ROs is obtained by implementing the following equations:
As can be observed in the previous equations, by means of the parameter , it is possible to modify the proximity between the pairs of ROs to be compared, i.e., if = 0, the ROs will be located in the same or contiguous CLBs, but if ≠ 0, the ROs to be compared will be separated by a distance of d CLBs. The proximity of the ROs is parameterized in this design through the NR (Nearby/Farthest) parameter, which is configurable at run time. While this parameter is disabled, is assigned the value ’0’; otherwise, is assigned an internally calculated value that corresponds to the maximum possible distance based on the Nx and Ny parameters of the RO bank.
This design also introduces an improvement in the positioning of the ROs, which consists of placing them within the CLB matrix following a snake pattern and assigning them consecutive labels. This allows going through the matrix while selecting all the rings in a sorted sequence, avoiding abrupt jumps between positions when changing rows or columns of CLBs, and guaranteeing that all comparisons are made between ROs located at the same distance.
In addition to generating the selection signals of the ROs whose oscillation frequencies are to be compared, the RO pair selection strategy block generates two enable signals (Ex and Ey) to exclusively activate the ROs participating in each comparison cycle, as can be seen in Figure 5, thus optimizing power consumption and minimizing switching noise.
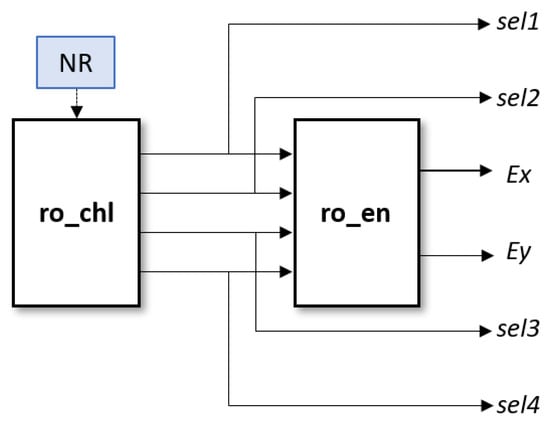
Figure 5.
RO pair selection strategy block diagram.
3.3. Output Bit Repository
The interaction between the RO pair selection strategy block and the Variability/Entropy Unit provides a sequence of data corresponding to the values reached by the two losing counters in each comparison cycle. From these data, the most suitable bits must be selected to constitute the output of the RO-PUF/TRNG module according to the function assigned to it in each invocation.
For this purpose, this design includes as a novelty the possibility of choosing, at implementation time, between two modes of operation that allow the output values to be stored in 32-bit word-length memory. The depth of this memory is established on the basis of the mode of operation and the maximum number of comparisons according to the size of the bank of ROs. When the module is implemented in ’characterization mode’, it stores 32 output bits from the two simultaneous comparisons in successive addresses of the output memory. This mode is especially useful in the early development stages of a design in order to analyze the properties of all the possible output bits to select those most suitable for each functionality (PUF/TRNG). When implemented in the ’operation mode’, the module obtains 4 bits in each comparison cycle and uses a 32-bit shift register to group the results of eight comparison cycles to complete one 32-bit word before storing it in the output memory. According to the results in [35], the bits selected in this case when the design acts as a PUF depend on a series of parameters that can be chosen in each module invocation to define the counter coding scheme, the distance between ROs, and a reliability/uniqueness trade-off.
The characterization mode has been widely used in this work to determine the degree of randomness of the bits obtained in each comparison and to identify that the greatest ability to generate random bits is achieved by using the two least significant bits of each counter. In this way, when the system acts as a TRNG, 4 bits are also collected in each comparison cycle, so that the Output Bit Repository block has the same structure for both PUF and TRNG functionality. Duplicating the design capabilities in this way results in a greater benefit to the resource/performance trade-off.
The test protocol developed to determine the degree of randomness of the bits of each counter and its results are presented in detail in Section 4, which includes the analysis of the effect of the different configuration options that have been described throughout this work (comparison strategy, RO proximity, and counter coding) in order to select the best alternatives to generate truly random bit sequences.
To coordinate the interaction between the RO pair selection strategy, Variability/Entropy Unit, and Output Bit Repository blocks, the PUF/TRNG_ctrl block is implemented, which includes the FSM presented in Figure 6.
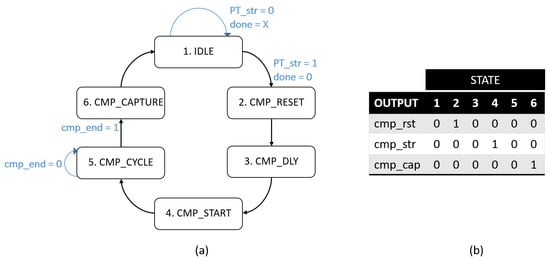
Figure 6.
(a) FSM diagram to coordinate the interaction between the RO pair selection strategy, Variability/Entropy Unit, and Output Bit Repository blocks. (b) Value of the FSM output signals in each state.
The activation of the FSM depends on the input signal PT_str. As long as this signal is deactivated, the FSM is kept in the IDLE state where the output signals are also kept deactivated. When the PT_str signal is activated, the transition to the CMP_RESET state occurs and the counters of the two comparison blocks are initialized to zero by activating the cmp_rst signal. Subsequently, at the next clock cycle, there is a transition to the CMP_DLY state where the cmp_rst signal is deactivated. There, a new transition occurs at the next clock cycle to reach the CMP_START state where the operation of the two comparison blocks is started by activating the cmp_str signal. The next transition is in the CMP_CYCLE state where the cmp_str signal is disabled. The transition to the next state depends on the activation of the input signal cmp_end which indicates when both comparisons are finished. At the end of the comparisons, the CMP_CAPTURE state is reached where the cmp_cap signal is activated to capture the 4 or 32 selected bits to construct the output bit sequence. Once the 4 or 32 bits have been captured, the FSM closes its cycle, returning at the next clock cycle to the IDLE state, waiting for the activation of the PT_str signal to start a new comparison.
As mentioned before, when the system is implemented in ’operation mode’, 4 bits are selected in each comparison cycle and a 32-bit shift register is used to group the results of eight consecutive cycles to complete the word length of the PUF/TRNG memory. For this purpose, using the control signals generated in the FSM, the number of competitions performed is counted with each activation of the cmp_cap signal until a total of eight competitions is reached; at this point the shift register is already filled and the loading of its contents into the memory of the Output Bit Repository block is enabled by means of the PT_ldr signal at the address indicated in the PT_addw signal. This process is repeated until the limit of competitions set by the input signal No_chls is reached. Then, the output signal done is activated to indicate that the PUF/TRNG operation has finished.
3.4. PUF/TRNG IP Integration
In order to ease the use of the PUF/TRNG design and its incorporation as a basic security element in systems on chips (SoCs), it has been encapsulated as a parameterizable IP module provided with an AXI4-lite communication interface. To validate its functionality and characterize its behavior, the IP module has been integrated in a hybrid SW/HW system implemented on a Pynq-Z2 development board. This board includes a Xilinx Zynq-7000 SoC device, which combines an ARM dual-core Cortex-A9 as a processing system (PS) with programmable logic (PL) from the Series-7 Artix family. The communication through the AXI4-lite protocol allows the interaction between the PS and PL components of the device. For this purpose, the four 32-bit memory-mapped registers presented in Table 1 are used, in which the function of the parameters associated with each of them is also detailed.

Table 1.
RO-PUF/TRNG input and output registers.
3.5. Output Bits Characterization
In order to select the most appropriate bits to construct the outputs of the PUF/TRNG functionalities in the operation mode, the characterization mode is used to determine the stability, probability, and entropy of the bits extracted from the output memory as a function of the selection strategy and the parameters used to configure the module. These metrics are evaluated in this work according to the equations provided in [39,40], which are repeated below to facilitate their interpretation:
- Stability (): This provides a measure of the the capacity of the i-th bit of the counters to obtain the same value in response to successive invocations of the PUF/TRNG module, thus determining the level of reproducibility of this value. Its ideal value is 1, and it is calculated through Equation (4) as the average of n RO pair competitions, where the stability of each j-th RO pair is calculated according to Equation (5).where ( = 1) is the probability that bit i-th in the j-th comparison is a ‘1’ after calling the PUF t times, as shown in (6).
- Probability (): This represents the feasibility of obtaining the value ’1’ in the i-th position of the counters in n competitions, which allows the possible bias in the PUF/TRNG output to be analyzed. Its ideal value is 0.5, and it is calculated as the average probability for all the RO pairs and all the comparisons, as shown in Equation (7).The values of these metrics taken into account in our design of the PUF/TRNG correspond to the means calculated on the total number of PUF implementations (m).
- Entropy intra (Hintra): This calculates the uncertainty that exist to obtain the value 0 or 1 in the i-th bit of the counters in n RO pair competitions. It is calculated, through Equations (8)–(10), as an average measurement over the m implementations of the PUF/TRNG (in the same or in different FPGAs), 1 being its ideal value.
- Entropy inter (Hinter): Like Hintra, this metric indicates the measure of the uncertainty to obtain the value 0 or 1 in the i-th bit of the counters, but differs in that it calculates the average over the results of competitions of n RO pairs located in the same position of different FPGAs. Both entropy values are useful for determining the uniqueness property of the bits. Its ideal value is 1, and it is calculated through Equations (11)–(13).
The metrics presented above were evaluated for a set of PUF/TRNG modules implemented on different Pynq-Z2 boards, using the Python Productivity for Zynq (PYNQ) environment, which facilitates high-level hardware–software interaction in a hybrid system by providing a Python framework under an embedded Linux operating system. More specifically, in this work, we used the C API available in [42], which offers an alternative with equivalent functionality but with greater efficiency, as it is based on a compiled language. The set of C routines that make up the API allow the hardware components built into the Zynq-7000 development board to be used through a series of library functions that can be included in application programs and compiled to generate executable code.
Using the above facilities, a test protocol was developed to evaluate the performance of our proposal in a test system implemented on 10 different Pynq-Z2 boards. The test system consists of 10 instances of the PUF/TRNG IP module, where each IP was dimensioned with a RO bank of 15 × 8 CLBs (a total of 480 ROs) and configured in characterization mode. The design was synthesized and implemented using Xilinx’s Vivado Design Suit version 2020.1. Each of the PUFs occupies 545 Slices (4.10% of the resources in the device) where 240 Slices (1.80% ) are used by the matrix of ROs. It also consumes 229 (0.22%) Slice Registers, 260 (0.98%) F7 Muxes, 118 (0.89%) F8 Muxes, and 0.5 (0.36%) BRAMS. Some online configuration options do not make sense in this IP mode, since all counter bits are available in the output for easy characterization. However, the options corresponding to the relative position of the ROs and the coding of the counters influence the system response. Then, by combining these two options, it is possible to obtain four different configurations of the PUF/TRNG design, so the four configurations were considered to characterize their respective output bits.
The values of stability, probability, and entropy were calculated for each bit of the counters from the data obtained in the test systems by executing each PUF 1000 times and performing 480 comparisons (the maximum possible) in each execution. The results obtained for the sign bit and bits 0-13 of the counters in the two comparison blocks for the binary-closest configuration are shown in Figure 7. Data from the other three configurations are very similar, so they are not included. The results indicate that stability and probability present a decreasing trend when analyzed in the MSB-LSB direction, while the entropy values present an increasing trend in the same direction.
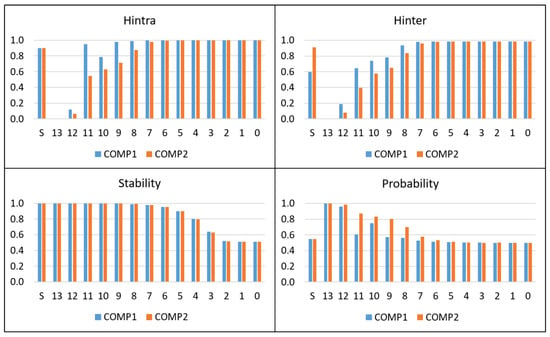
Figure 7.
Stability, probability, and entropy metrics calculated for each bit of the counters under the binary-closest RO-PUF/TRNG configuration.
Since stability and entropy increase in opposite directions, from the perspective of the PUF functionality, it is necessary to establish a compromise to select the bits to use in the operation mode between those whose metrics present the values closest to their respective ideal values. Accordingly, the more appropriate bits to build the PUF output correspond to the sign bit plus one of bits 6–7, for comparisons between ROs implemented in LUTs placed in the same location of different CLBs, and two of bits 6–8, in the other case, confirming the study carried out in [35].
However, from the point of view of TRNG functionality, the entropy increases in the same direction as the stability decreases and the probability approaches its ideal value, so the characterization stage will focus on determining the number of least significant bits that will be selected from each of the comparison blocks and the most suitable configuration(s) of the IP module. Additionally, from the TRNG perspective, the entropy and stability results obtained for the sign bits are less adequate than those of the LSBs of the counters; therefore, these bits will not be considered when the system is implemented in operation mode and used as a TRNG. Considering that the original PUF design extracts 4 bits in each comparison cycle, in this work we decided to characterize the two comparison strategies separately using one, two, and four LSBs to carry out the study presented in the next section.
4. TRNG: Randomness Statistical Assessment and Entropy Source Validation
The proposed RO-PUF/TRNG has a set of design features that allow, when implemented in characterization mode, four selectable configurations at runtime, which intrinsically represent four different possibilities to generate random bits. In order to provide a complete randomness characterization, each of these alternative TRNGs is submitted to a statistical assessment process.
As mentioned earlier, the RO pair relative distance (farthest or closest) and the counter code type (binary or gray) are the options from which four configurations can be derived. If we consider that, in characterization mode, it is possible to extract the LSBs of the two counters independently, this doubles the number of configurations whose randomness must be characterized; if, additionally, considering the results presented in Figure 7, the bits are extracted in groups of one, two, and four LSBs, this triples the number of configurations to characterize, reaching a total of 24 different possibilities to generate random numbers.
To assess the degree of randomness of the RO-PUF/TRNG, every output bit stream that is collected must be submitted to the set of statistical tests defined in the previously mentioned test protocol and executed on the ARM processor available in Xilinx Zynq-7000 devices, in order to ensure that there are no data patterns within that sequence. For every random bit sequence extracted from the 24 configurations, the statistical assessment process is performed following the NIST 800-22 standard and the NIST 800-90b recommendation. The former establishes a set of tests that check whether binary data are uniformly random, ensuring that each bit has the same probability of taking either of the two possible states (0 or 1) and that it is statistically independent from the others, while the latter defines the requirements for the entropy sources used by random bit generators, as well as the tests for the validation of the entropy sources.
4.1. TRNGs Assessment—NIST 800-22 Standard
Table 2 shows the complete set of statistical tests included in the NIST 800-22 standard. As can be seen, each test requires a minimum bitstream length (bl) or a minimum bit-block size (bs) for each data sequence under assessment.

Table 2.
NIST 800-22 Statistical Test Suite.
To characterize the degree of randomness of the 24 possible combinations in such a way that the most robust implementations can be identified, the following strategy has been developed in this work: First, short bit sequences are evaluated by means of the subset of statistical tests with bl ≤ 500 to determine, in a short period of time, a preliminary randomness characterization differentiating the bit sequences according to the number of LSBs collected from the entropy sources, in order to construct them (1, 2, and 4). Subsequently, based on the results of these tests, a more complete statistical characterization of the options that present a higher degree of randomness is carried out, applying the entire set of statistical tests of the standard to the different configurations of TRNGs that arise when considering the other three alternatives (RO pair location, counter coding, and counter from which the bits are taken). Finally, the extracted bit sequences are post-processed using the XOR and von Neumann bit correctors, with the aim to improve the degree of randomness of the proposed TRNG.
4.1.1. First Assessment Stage: Characterization of LSBs
As previously mentioned, the assessment of short bit sequences will allow the identification of the degree of randomness of the LSBs for both selection strategies (the counter data provided by the two comparison blocks). According to the standard [43], no general criterion has been established, defining a minimum or maximum number of tests that must be applied to an entropy source to determine its degree of randomness (including the standard tests themselves). Therefore, considering the optimization of the evaluation process in terms of time, the subset consisting of tests 1, 2, 3 (2 sub-tests), 5, 7, and 8 has been selected, such that their minimum bit sequence lengths required could be fulfilled with the maximum bit sequence length that can be generated in a single run of the system using the full bank of ROs (480 bits). It is important to take into account that the minimum number of bits collected from each entropy source is 1, so the bit sequences constructed from the collection of the 2 and 4 LSBs are limited to 480 bits to establish a fair comparison among their results.
It is also important to ensure that the performance of the circuit is homogeneous for any location where it could be implemented within the programmable logic; hence, with these partial objectives established, the characterization of the degree of randomness is performed by following the next data collection strategy for each implemented test system:
- generate bit sequences of length bl = 480;
- generate 100 bit sequences for each TRNG;
- collect data from 24 candidate TRNGs;
- collect data from the 10 IP modules implemented in a test system.
Submitting the collected data to the selected subset of tests generates the results shown in Table 3, which are organized in columns under the following feature hierarchy: LSBs, RO pair location, counter coding, and counter. For each of the instances, the total number of subset tests that passed successfully by each TRNG is reported, i.e., the maximum expected value to be reported in this table is seven tests. Then, the colored cells within the table indicate that at least one of the tests from the subset has not been passed in the respective feature combination. The darker the shade of the cell, the fewer tests have been passed.

Table 3.
Count of NIST 800-22 subset tests successfully passed by the random bit sequences extracted from the 24 feature combinations derived from the RO-PUF/TRNG design.
According to the results presented in Table 3, the sequences based on four LSBs collected from each counter do not possess a high degree of randomness since, in total, they only pass 96.9% of the test subset considering the 10 IP modules implemented in the test system. In addition, the distribution of the colored cells in each row indicates that these types of sequences do not provide consistent performance regardless of the locations of the IP implementations within the FPGA. On the other hand, random bit sequences based on 1 and 2 LSBs extracted from each losing counter achieve a very high test pass rate of 99.6% and 99.8%, respectively, and do so consistently for any location of the IP implementations within the programmable logic.
Since the possibility to extract as many random bits as possible from the entropy source is profitable, the preliminary characterization of the LSBs allows us to stop considering each of the counters as independent entropy sources, and introduces the possibility of restructuring our approach to propose a set of TRNGs based on the concatenation of the two LSBs extracted from each counter, since they presented the highest level of randomness.
When performing this restructuring, only the influence of the ring pair localization and counter coding is preserved; therefore, it is only possible to derive four TRNG alternatives based on these features. By submitting these four TRNG configurations to the subset of tests, it is observed that the concatenation of LSBs presents positive results in the preliminary characterization with a 100% test pass rate, as reflected in the comparison of results shown in Table 4 against the previous results. Thus, the partial objective of proposing more robust TRNGs based on the LSBs of a higher degree of randomness identified at this stage is fulfilled, while fully exploiting the random bit generation capacity of the system.

Table 4.
Comparison of tests successfully approved by 4 LSBs collected from each entropy source against 4 LSBs concatenated from each counter within the NIST 800-22 subset.
4.1.2. Second Assessment Stage: TRNG Configurations
According to the evaluation strategy proposed in this section, the selection of LSBs leads to the deepening of the study of randomness. For this purpose, the number of tests used in the randomness characterization is extended in this assessment stage to the 15 tests of the standard and, as a consequence, the number of bits to be collected from the entropy source for the four TRNGs proposed must be increased to satisfy the maximum length for the minimum required. Therefore, the data collection strategy is updated as follows:
- generate bit sequences of length bl = 1,000,000;
- generate 100 bit sequences for each TRNG;
- collect data from four candidate TRNGs;
- collect data from the 10 IP modules implemented in a test system.
In this case, the number of tests passed for each RO-PUF/TRNG in all possible configurations is also reported; therefore, the maximum expected value of tests passed for any of the proposed TRNGs is 15.
Analyzing the results shown in Table 5, the assessment shows that the TRNG based on binary counters and RO pairs located in the farthest locations is consistent both in terms of having the best degree of randomness by approving 100% of the statistical test suite, and of showing the same performance in any location of the programmable logic. On the other hand, although the remaining three combinations (Gray/Closest, Gray/Farthest, and Binary/Closest) also have a fairly homogeneous performance all over the FPGA, they have a test pass rate of 64.6%, 78%, and 76%, respectively. The homogeneity of the results for any IP implementation in every configuration can be further corroborated by the color map in Figure 8, where the pass rate of each IP-TEST combination is reflected in the intensity of the cell.

Table 5.
Count of NIST 800-22 subset tests successfully approved by the 4 TRNG configurations.

Figure 8.
Color map of the rate of NIST 800-22 tests passed by each RO-PUF/TRNG implementation (the darker the color, the higher the pass rate) assessing raw data.
These results provide assurance that the base RO-PUF design can be used without further stages as a TRNG if its mode of operation is configured to implement the Binary/Farthest configuration and if the data collection strategy is performed according to the one presented in this subsection, but it is necessary to confirm whether the design’s capability as a TRNG can be enhanced by employing some post-processing strategies.
4.1.3. Third Assessment Stage: Bitstream Post-Processing
The color map in Figure 8 shows that tests 2, 3, 5, and 13 were those for which the lowest pass rates were obtained. As described in [43], the general approach of these four tests lies in analyzing the ratio of zeros and ones of a sequence of random bits, which ideally is 50% for each case.
In other words, the focus of these tests refers to the bias of each sequence; therefore, in order to increase the randomness in the bit generation process of the three configurations with the lowest test pass rate, the collected data are submitted to a post-processing stage to decrease the bias. For this purpose, the von Neumman and XOR correctors are implemented in the software. Both operate using pairs of bits as inputs to generate a single output bit, as shown in Table 6.

Table 6.
Truth table of implemented bit correctors.
The cost of implementing these post-processing strategies lies in the reduction in the number of effective bits of each sequence at the end of the process. Using the von Neumann corrector represents a reduction of approximately 75% in the bits, while the XOR corrector always reduces them to 50%; therefore, in order to adequately compare the degree of randomness between the results of the post-processing strategies and the raw data, the software implementations of these strategies are adjusted such that bit sequences with lengths equal to those indicated by the bit collection strategy in the previous subsection can be constructed.
The data collected considering this post-processing are subjected to the 15 tests of the standard, and their results are presented in Table 7. There it can be observed that for the Gray/Closest, Gray/Farthest, and Binary/Farthest configurations, the results obtained with the von Neumann corrector show test pass rates of 76.7%, 78.7%, and 82.0%, representing an increase of 12.0%, 0.70%, and 6.0%, respectively, while the results obtained with the XOR corrector for the same three configurations achieve a test pass rate of 100.0%, with an increase of 35.3%, 22.0%, and 24.0%, respectively.

Table 7.
Test pass rate obtained using von Neuman and XOR correctors.
Although both strategies present a significant increase in the pass rate of the test, only the post-processing with the XOR corrector allows the maximum degree of randomness of the three evaluated configurations to be reached.
Considering the color maps presented in Figure 9, which correspond to the hit rates obtained for each IP-TEST combination when assessing the post-processed sequences, and comparing them with the color map in Figure 8, we can graphically verify the positive impact on the different tests while maintaining homogeneity in their performance per test.
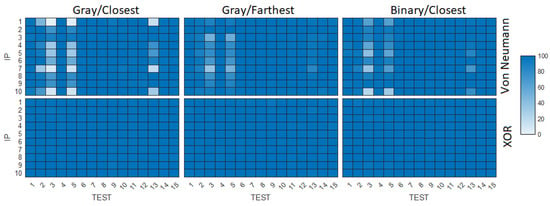
Figure 9.
Color map of the rate of NIST 800-22 tests passed by each RO-PUF/TRNG implementation (the darker the color, the higher the pass rate) assessing data post-processed with von Neumann and Xor bit correctors.
4.1.4. Statistical Assessment Results
According to the NIST 800-22 standard, the minimum pass rate for each statistical test for a sample size of 100 binary sequences, as is the case in this work, is 96. Generally, the evaluation of the Random Excursion Variant test is performed under a different threshold, but in this work the results obtained have been normalized on the same scale to ease their interpretation.
The assessment result of the 4 TRNG configurations that have already been identified as suitable to satisfy the statistical tests of the NIST 800-22 standard are presented in Table 8. In columns 2–5, the test pass rate obtained as the average of 10 IP module implementations can be found. For these results, the overall average pass rate is 98.7, the mode is 99, and the minimum pass rate is 96. Columns 6–14 present the test pass rate obtained in other related works.

Table 8.
Average test pass rate of 4 TRNGs using the NIST 800-22 statistical test suite against related works.
Green cells have been used in this table to highlight those tests where the lowest pass rate obtained among the 4 TRNG configurations of our work exceeds the corresponding reference result(s) when compared to each other. Yellow cells have also been used to indicate those tests where our results equal the test pass rate of the reference.
This color convention allows us to demonstrate that, when comparing the benchmarks using the lower pass rate of our TRNG proposals, there are general improvements in some specific statistics through our design. The most significant of these can be found in test 8, according to which the bitstreams generated by our circuit exceed the appropriate level of oscillation between the zeros and ones that make them up with respect to the works cited in [22,23,29]. In addition, when evaluating the non-periodicity within the bitstreams by searching for specific patterns by means of test 9, it is shown that our results have a greater irregularity than those presented in [29], which represents greater randomness. Likewise, according to the statistical process executed in test 15, when trying to compress a bitstream generated by our TRNG proposals, there is greater robustness against loss of information than that existing in the bitstreams of the proposals reported in [17] and [23]A. Through test 6, the randomness of the bits is evaluated by means of the length of a LFSR, and according to this characteristic, the sequences generated by our circuit present a higher complexity than the two proposals presented in reference [23]. Our results have also surpassed the minimum pass rates in the proposal presented in [17] and the two proposals presented in [29].
In a global comparison, the minimum pass rates of our 4 TRNG proposals equal or exceed more than 40% of the statistical results presented in [24]R, [23]A and [22]. Thus, our design offers a significant variety of options between the TRNG configurations and the statistical results, giving the user the possibility to select the best compromise between them according to the needs of a specific application. These results show that the four TRNG proposals presented in this work are competitive in the state-of-the-art.
Randomness assessment has also been performed, on a preliminary basis, considering temperature fluctuations by exposing the implementation of a TRNG (Binary/Farthest configuration) to five different operating conditions. The results presented in Figure 10 show that all tests successfully matched or exceeded the threshold pass rate of 96 at each operating condition, thus demonstrating that temperature fluctuations do not have a negative impact on the quality of the random numbers.
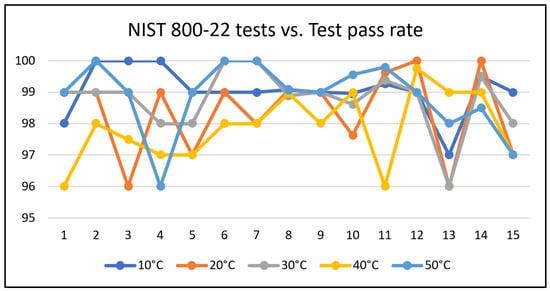
Figure 10.
Test pass rates of a TRNG (Binary/Farthest) using the NIST 800-22 standard when exposed to different temperature conditions.
The four TRNG configurations analyzed were also validated as entropy sources under the NIST 800-90b Recommendation tests listed below in Table 9. The main parameter for this validation is entropy, since a high level of this parameter makes it possible to guarantee that the generated bits are reliable.

Table 9.
Entropy estimation of 4 TRNGs using the NIST 800-90b recommendation.
To perform the validation process, a set of bits obtained from each of the TRNG configurations identified with an appropriate degree of randomness is collected and tested. The NIST Recommendation indicates that this sequence should be collected consecutively, or by concatenating groups of at least 1000 bits. Given the size of the RO bank of our design and the comparison strategies implemented, the maximum number of bits that can be generated by a IP consecutively with a single system run is 1920 (480 × 4); therefore, the bits collected for this test are concatenated after 1000 system runs in groups of 1000.
Additionally, the Repetition Count and Adaptive Test health tests, approved by the same NIST recommendation, are applied with the aim of having a mechanism that detects significant changes in the behavior of the source as a function of entropy. Both tests are approved by selecting the lowest value of estimated entropy, as presented in Table 9.
The entropy results, along with the health check results, indicate that the proposed TRNGs will present no correlation between the bit-streams generated every time the system is restarted, no generated bit-stream will stagnate at a single value, and the ratio of 0 s and 1s will be around 50% as long as the estimated entropy remains relatively constant.
5. Conclusions
The random phenomena inherent to the electronic implementation of a previously proposed RO-PUF are used in this work as a source of entropy for the construction of a configurable TRNG, offering two basic security primitives in the same design. For this purpose, the values of the counters provided in each comparison cycle are analyzed to select the most suitable bits to provide the design with the TRNG functionality. By applying the same methodology used to select the best bits to implement the PUF functionality, we are able to verify that the most suitable bits for the TRNG case correspond to the least significant ones provided by the counters. After characterizing the randomness of the output of the two simultaneous comparisons carried out by the system during its operation, the random bit generation capability of the design is exploited to the maximum by concatenating the two LSBs of each counter and delivering at the output four random bits per pair of competing rings. The configurability of the original system allows four TRNG configurations to be derived based on the relative location of the competing rings (closest or farthest) and the type of counter (binary or Gray code).
The evaluation of the degree of randomness of the four TRNG configurations was performed using the set of statistical tests presented in the NIST-800-22 standard. The four configurations successfully passed all the tests included in the standard, reaching a high entropy rate. It is necessary to highlight that the Binary/Farthest configuration can generate its random bit stream without any post-processing, while the remaining three configurations must be post-processed with the XOR bit corrector to pass the thresholds fixed by the standard, which reduces the number of effective bits of the latter by 50%.
The module was designed for Xilinx 7 series programmable devices and was provided with a standard AXI4-Lite interface to ease interconnection. A test system containing ten instances of the PUF/TRNG design was implemented on the Zynq-7000 SoC available in Pynq-Z2 development boards. Most of the characterization tasks were performed online on the ARM processor system included in the Zynq-7000 device using a set of software applications written in high-level programming languages, developed with the help of the PYNQ environment, which made it possible to simplify and speed up the process.
The presented PUF/TRNG can be exploited to build the Root of Trust of embedded devices in applications intended for fields such as Cyber–Physical Systems or Internet of Things. By incorporating two security primitives and having a compact design, it becomes an ideal component optimized both in resource and power consumption.
Author Contributions
All the authors have actively participated in the research process that led to the realization of this work. Conceptualization, supervision, and writing—review and editing, P.B., M.C.M.-R., L.F.R.-M. and S.S.-S.; methodology, visualization, investigation, and data curation, L.F.R.-M. and S.S.-S.; software and writing—original draft preparation, L.F.R.-M. and S.S.-S.; formal analysis, L.F.R.-M., P.B., M.C.M.-R. and S.S.-S.; resources and project administration, P.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported in part by the SPIRS Project with Grant Agreement No. 952622 under the EU H2020 research and innovation programme and the ARES Project PID2020-116664RB-100 funded by MCIN/AEI/10.13039/501100011033 and the EU NextGeneration EU/PRTR. M.C.M.R. holds a postdoc fellowship from the Andalusia Government with support from PO FSE of EU.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| RO | Ring Oscillator |
| PUF | Physical Unclonable Function |
| FPGA | Field Programmable Gate Array |
| ASIC | Application-Specific Integrated Circuit |
| MSFRO | Multistage Feedback Ring Oscillator |
| PDLs | Programmable Delay Lines |
| NL-FRO | Nonlinear Feedback Ring Oscillator |
| NIST | National Institute of Standards and Technology |
| PRNG | Pseudo-Random Number Generators |
| TRNG | True-Random Number Generators |
| SoC | System on Chip |
| AXI | Advanced eXtensible Interface |
| PL | Programmable Logic |
| PS | Processing System |
| HW | Hardware |
| SW | Software |
| LSB | Least Significant Bit |
| MSB | Most Significatn Bit |
References
- Yang, B.; Li, L.X.; Ji, H.; Xu, J. An early warning system for loan risk assessment using artificial neural networks. Knowl.-Based Syst. 2001, 14, 303–306. [Google Scholar] [CrossRef]
- Alcin, M.; Koyuncu, İ.; Tuna, M.; Varan, M.; Pehlivan, İ. A novel high speed artificial neural network–based chaotic true random number generator on field programmable gate array. Int. J. Circuit Theory Appl. 2019, 47, 365–378. [Google Scholar] [CrossRef]
- Essa, F.; Abd Elaziz, M.; Elsheikh, A.H. An enhanced productivity prediction model of active solar still using artificial neural network and Harris Hawks optimizer. Appl. Therm. Eng. 2020, 170, 115020. [Google Scholar] [CrossRef]
- Mosaad, M.I.; Ramadan, H. Power quality enhancement of grid-connected fuel cell using evolutionary computing techniques. Int. J. Hydrog. Energy 2018, 43, 11568–11582. [Google Scholar] [CrossRef]
- Satrya, G.B.; Shin, S.Y. Evolutionary computing approach to optimize superframe scheduling on industrial wireless sensor networks. J. King Saud-Univ.-Comput. Inf. Sci. 2020, 34, 706–715. [Google Scholar] [CrossRef]
- Liang, S.; Zhu, Y.; Li, H.; Yan, J. Evolutionary Computational Intelligence-Based Multi-Objective Sensor Management for Multi-Target Tracking. Remote Sens. 2022, 14, 3624. [Google Scholar] [CrossRef]
- Manucom, E.M.M.; Gerardo, B.D.; Medina, R.P. Analysis of key randomness in improved one-time pad cryptography. In Proceedings of the 2019 IEEE 13th International Conference on Anti-Counterfeiting, Security, and Identification (ASID), Xiamen, China, 25–27 October 2019; pp. 11–16. [Google Scholar]
- Alibeigi, I.; Amirany, A.; Rajaei, R.; Tabandeh, M.; Shouraki, S.B. A low-cost highly reliable spintronic true random number generator circuit for secure cryptography. In Proceedings of the Spin; World Scientific: Singapore, 2020; Volume 10, p. 2050003. [Google Scholar]
- Saha, R.; Geetha, G.; Kumar, G.; Buchanan, W.J.; Kim, T. A Secure Random Number Generator with Immunity and Propagation Characteristics for Cryptography Functions. Appl. Sci. 2021, 11, 8073. [Google Scholar] [CrossRef]
- Ewert, M. A Random Number Generator Based on Electronic Noise and the Xorshift Algorithm. In Proceedings of the 2018 VII International Conference on Network, Communication and Computing, Taipei City, Taiwan, 14–16 December 2018; pp. 357–362. [Google Scholar]
- Park, B.K.; Park, H.; Kim, Y.S.; Kang, J.S.; Yeom, Y.; Ye, C.; Moon, S.; Han, S.W. Practical true random number generator using CMOS image sensor dark noise. IEEE Access 2019, 7, 91407–91413. [Google Scholar] [CrossRef]
- Matsuoka, S.; Ichikawa, S.; Fujieda, N. A true random number generator that utilizes thermal noise in a programmable system-on-chip (PSoC). Int. J. Circuit Theory Appl. 2021, 49, 3354–3367. [Google Scholar] [CrossRef]
- Gupta, R.; Pandey, A.; Baghel, R.K. FPGA implementation of chaos-based high-speed true random number generator. Int. Numer. Model. Electron. Netw. Devices Fields 2019, 32, e2604. [Google Scholar] [CrossRef]
- Luo, Y.; Wang, W.; Best, S.; Wang, Y.; Xu, X. A high-performance and secure TRNG based on chaotic cellular automata topology. IEEE Trans. Circuits Syst. I Regul. Pap. 2020, 67, 4970–4983. [Google Scholar] [CrossRef]
- Azzaz, M.S.; Fellah, R.; Tanougast, C.; Kaibou, R. Design and FPGA implementation of TRNG based on a new multi-wing attractor in Lorenz chaotic system. Eur. Phys. J. Spec. Top. 2021, 230, 3469–3480. [Google Scholar] [CrossRef]
- Wang, X.; Liang, H.; Wang, Y.; Yao, L.; Guo, Y.; Yi, M.; Huang, Z.; Qi, H.; Lu, Y. High-throughput portable true random number generator based on jitter-latch structure. IEEE Trans. Circuits Syst. I Regul. Pap. 2020, 68, 741–750. [Google Scholar] [CrossRef]
- Cao, Y.; Zhao, X.; Zheng, W.; Zheng, Y.; Chang, C.H. A new energy-efficient and high throughput two-phase multi-bit per cycle ring oscillator-based true random number generator. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 69, 272–283. [Google Scholar] [CrossRef]
- Li, X.; Stanwicks, P.; Provelengios, G.; Tessier, R.; Holcomb, D. Jitter-based Adaptive True Random Number Generation Circuits for FPGAs in the Cloud. In ACM Transactions on Reconfigurable Technology and Systems (TRETS); Association for Computing Machinery: New York, NY, USA, 2022. [Google Scholar]
- Gong, L.; Zhang, J.; Liu, H.; Sang, L.; Wang, Y. True random number generators using electrical noise. IEEE Access 2019, 7, 125796–125805. [Google Scholar] [CrossRef]
- Choi, S.; Shin, Y.; Yoo, H. Analysis of Ring-Oscillator-based True Random Number Generator on FPGAs. In Proceedings of the 2021 International Conference on Electronics, Information, and Communication (ICEIC), Jeju-si, Republic of Korea, 31 January–3 February 2021; pp. 1–3. [Google Scholar]
- Cui, J.; Yi, M.; Cao, D.; Yao, L.; Wang, X.; Liang, H.; Huang, Z.; Qi, H.; Ni, T.; Lu, Y. Design of true random number generator based on multi-stage feedback ring oscillator. IEEE Trans. Circuits Syst. II Express Briefs 2021, 69, 1752–1756. [Google Scholar] [CrossRef]
- Frustaci, F.; Spagnolo, F.; Perri, S.; Corsonello, P. A High-Speed FPGA-based True Random Number Generator using Metastability with Clock Managers. IEEE Trans. Circuits Syst. II Express Briefs 2022. [Google Scholar] [CrossRef]
- Della Sala, R.; Bellizia, D.; Scotti, G. A novel ultra-compact FPGA-compatible TRNG architecture exploiting latched ring oscillators. IEEE Trans. Circuits Syst. II Express Briefs 2021, 69, 1672–1676. [Google Scholar] [CrossRef]
- Anandakumar, N.N.; Sanadhya, S.K.; Hashmi, M.S. FPGA-based true random number generation using programmable delays in oscillator-rings. IEEE Trans. Circuits Syst. II Express Briefs 2019, 67, 570–574. [Google Scholar] [CrossRef]
- Torii, N.; Minagawa, R.; Omae, H.K.; Hayashi, K. Implementation and evaluation of ring oscillator-based true random number generator. In Proceedings of the 2021 Ninth International Symposium on Computing and Networking (CANDAR), Virtual, 23–26 November 2021; pp. 189–195. [Google Scholar]
- Tao, S.; Yu, Y.; Dubrova, E. FPGA based true random number generators using non-linear feedback ring oscillators. In Proceedings of the 2018 16th IEEE International New Circuits and Systems Conference (NEWCAS), Montreal, Canada, 24–28 June 2018; pp. 213–216. [Google Scholar]
- Şarkışla, M.A.; Ergün, S. An area efficient true random number generator based on modified ring oscillators. In Proceedings of the 2018 IEEE Asia Pacific Conference on Circuits and Systems (APCCAS), Chengdu, China, 26–30 October 2018; pp. 274–278. [Google Scholar]
- Maiti, A.; Nagesh, R.; Reddy, A.; Schaumont, P. Physical unclonable function and true random number generator: A compact and scalable implementation. In Proceedings of the 19th ACM Great Lakes Symposium on VLSI, Boston Area, MA, USA, 10–12 May 2009; pp. 425–428. [Google Scholar]
- Buchovecká, S.; Lórencz, R.; Kodýtek, F.; Buček, J. True random number generator based on ring oscillator PUF circuit. Microprocess. Microsystems 2017, 53, 33–41. [Google Scholar] [CrossRef]
- Rai, V.K.; Tripathy, S.; Mathew, J. TRGP: A Low-Cost Re-Configurable TRNG-PUF Architecture for IoT. In Proceedings of the 2021 22nd International Symposium on Quality Electronic Design (ISQED), Santa Clara, CA, USA, 7–9 April 2021; pp. 420–425. [Google Scholar]
- Yan, W.; Jin, C.; Tehranipoor, F.; Chandy, J.A. Phase calibrated ring oscillator PUF design and implementation on FPGAs. In Proceedings of the 2017 27th International Conference on Field Programmable Logic and Applications (FPL), Ghent, Belgium, 4–8 September 2017; pp. 1–8. [Google Scholar]
- Babaei, A.; Schiele, G. Physical unclonable functions in the internet of things: State of the art and open challenges. Sensors 2019, 19, 3208. [Google Scholar] [CrossRef] [PubMed]
- Shamsoshoara, A.; Korenda, A.; Afghah, F.; Zeadally, S. A survey on physical unclonable function (PUF)-based security solutions for Internet of Things. Comput. Netw. 2020, 183, 107593. [Google Scholar] [CrossRef]
- Anandakumar, N.N.; Hashmi, M.S.; Sanadhya, S.K. Design and Analysis of FPGA Based PUFs with Enhanced Performance for Hardware-Oriented Security. ACM J. Emerg. Technol. Comput. Syst. (JETC) 2022, 18, 1–26. [Google Scholar] [CrossRef]
- Martínez-Rodríguez, M.C.; Rojas-Muñoz, L.F.; Camacho-Ruiz, E.; Sánchez-Solano, S.; Brox, P. Efficient RO-PUF for Generation of Identifiers and Keys in Resource-Constrained Embedded Systems. Cryptography 2022, 6, 51. [Google Scholar] [CrossRef]
- Saleem, H.; Afzal, S.; Ahmed, N. Robust entropy harvester for analogue noise sources in TRNG. In Proceedings of the 2018 15th International Bhurban Conference on Applied Sciences and Technology (IBCAST), Islamabad, Pakistan, 9–13 January 2018; pp. 405–414. [Google Scholar]
- Fang, X.; Wetzel, B.; Merolla, J.M.; Dudley, J.M.; Larger, L.; Guyeux, C.; Bahi, J.M. Noise and chaos contributions in fast random bit sequence generated from broadband optoelectronic entropy sources. IEEE Trans. Circuits Syst. I Regul. Pap. 2014, 61, 888–901. [Google Scholar] [CrossRef]
- Lu, Y.; Liang, H.; Yao, L.; Wang, X.; Qi, H.; Yi, M.; Jiang, C.; Huang, Z. Jitter-quantizing-based TRNG robust against PVT variations. IEEE Access 2020, 8, 108482–108490. [Google Scholar] [CrossRef]
- Kodýtek, F.; Lórencz, R. A Design of Ring Oscillator Based PUF on FPGA. In Proceedings of the 2015 IEEE 18th International Symposium on Design and Diagnostics of Electronic Circuits & Systems, Belgrade, Serbia, 22–24 April 2015; pp. 37–42. [Google Scholar] [CrossRef]
- Martínez-Rodríguez, M.C.; Camacho-Ruiz, E.; Brox, P.; Sánchez-Solano, S. A Configurable RO-PUF for Securing Embedded Systems Implemented on Programmable Devices. Electronics 2021, 10, 1957. [Google Scholar] [CrossRef]
- Suh, G.E.; Devadas, S. Physical unclonable functions for device authentication and secret key generation. In Proceedings of the 2007 44th ACM/IEEE Design Automation Conference, San Diego, CA, USA, 4–8 June 2007; pp. 9–14. [Google Scholar]
- Nicholas, B. PYNQ_API : C API Drivers for PYNQ FPGA Board. Available online: https://github.com/mesham/pynq_api (accessed on 16 June 2012).
- Bassham III, L.E.; Rukhin, A.L.; Soto, J.; Nechvatal, J.R.; Smid, M.E.; Barker, E.B.; Leigh, S.D.; Levenson, M.; Vangel, M.; Banks, D.L.; et al. Sp 800-22 rev. 1a. a Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications; National Institute of Standards & Technology: Gaithersburg, MD, USA, 2010. [Google Scholar]
- Acar, B.; Ergün, S. A robust digital random number generator based on transient effect of ring oscillator. In Proceedings of the 2020 IEEE 11th Latin American Symposium on Circuits & Systems (LASCAS), San José, Costa Rica, 25–28 February 2020; pp. 1–4. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).