Designing a Spintronic Based Magnetoresistive Bridge Sensor for Current Measurement and Low Field Sensing
Abstract
1. Introduction
2. Materials and Methods
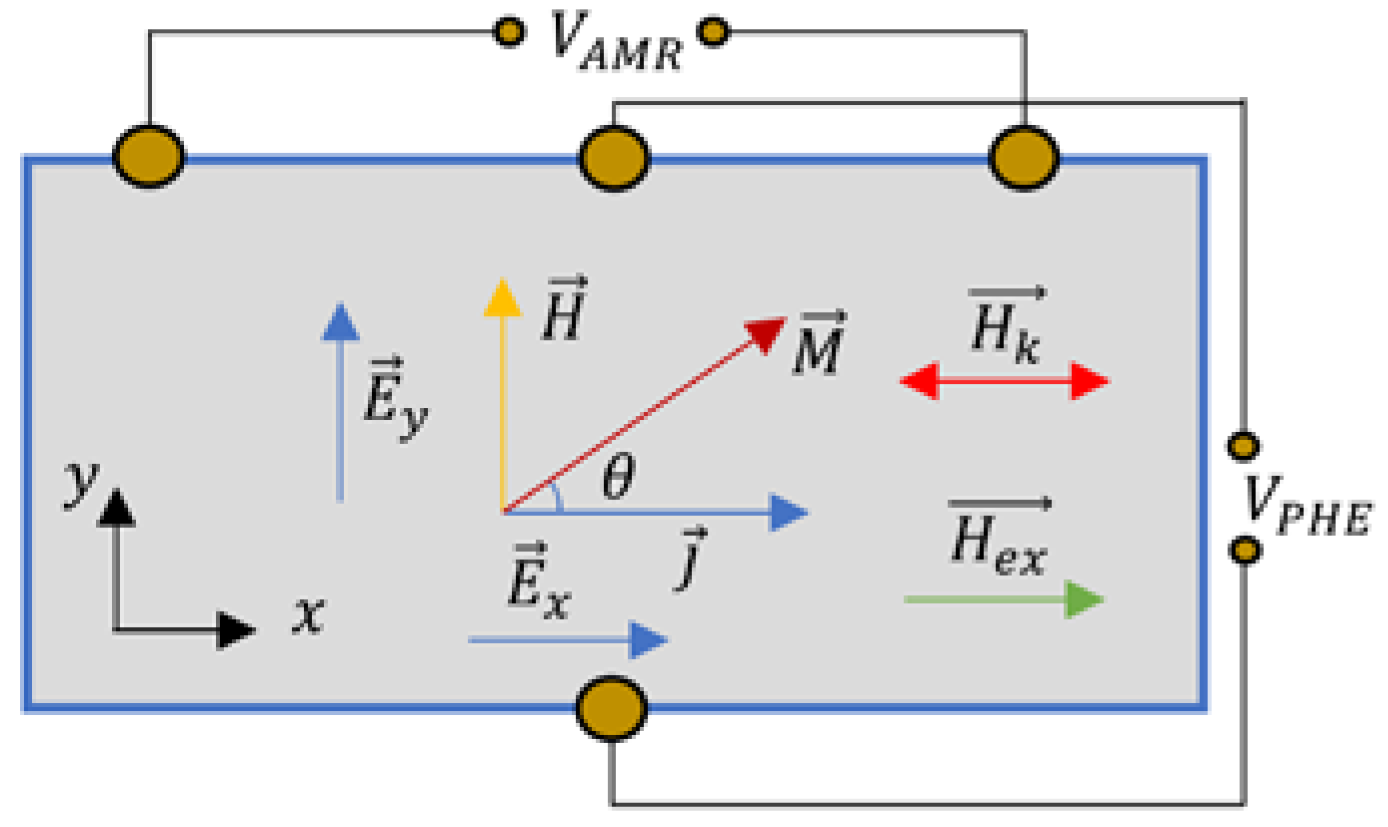
2.1. Principle of Operation–AMR and PHE Effects
2.2. Principle of Operation–GMR Effect
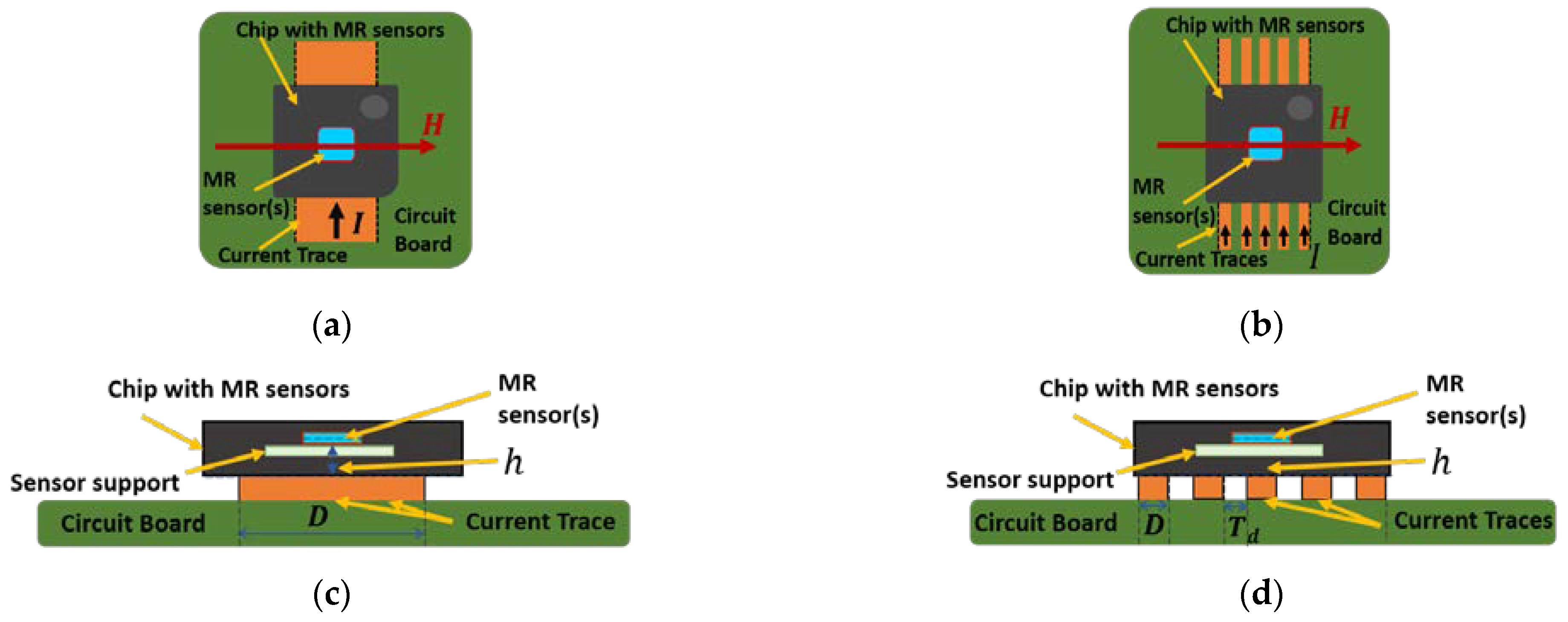
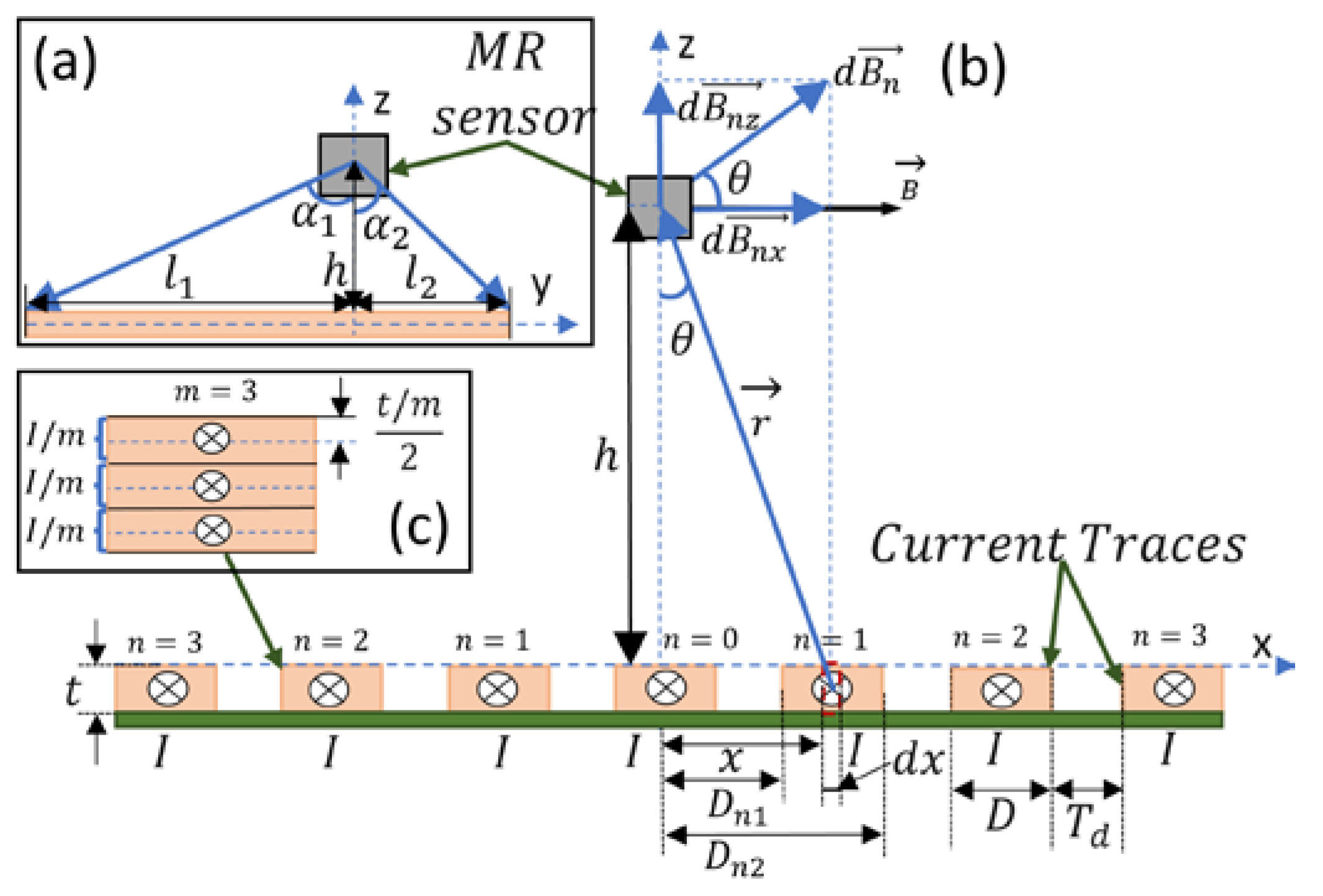
2.3. Design Optimization of the Non-Contacting Current Sensor Based on Analytical Method for Current Stripes
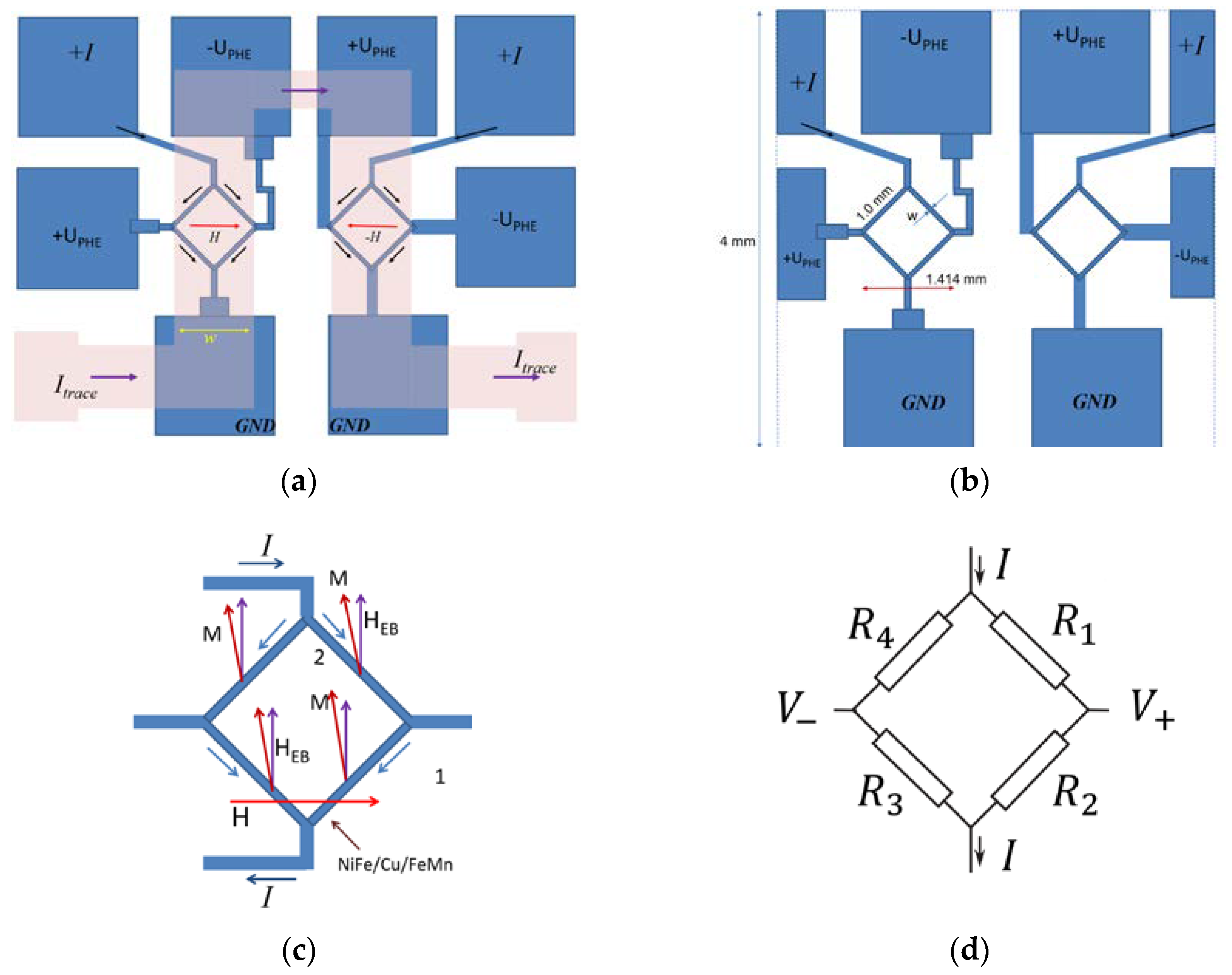
2.4. Principle of Operation of the Exchange Bias AMR Bridge Sensor
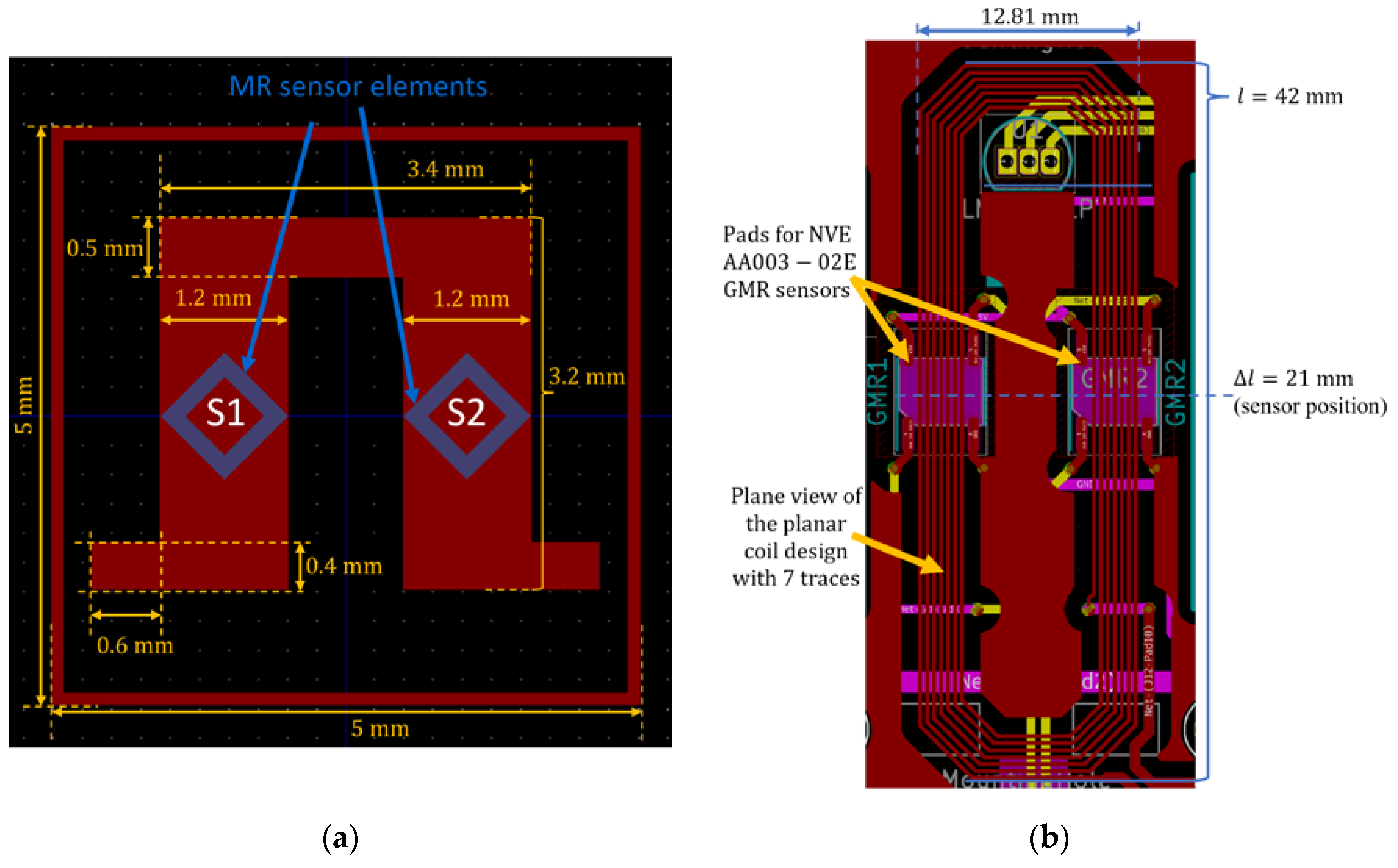
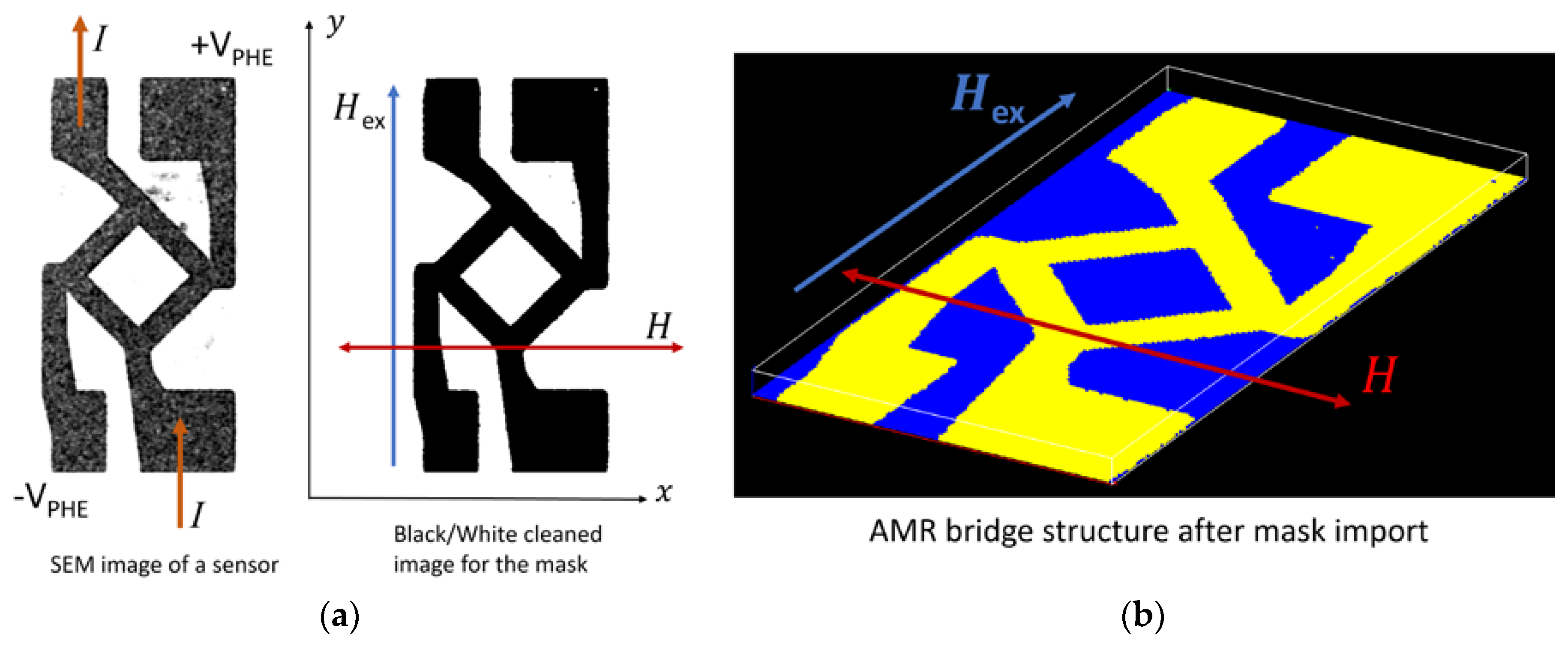
2.5. Fabrication of Exchange Bias AMR Bridge Sensor Demonstrator
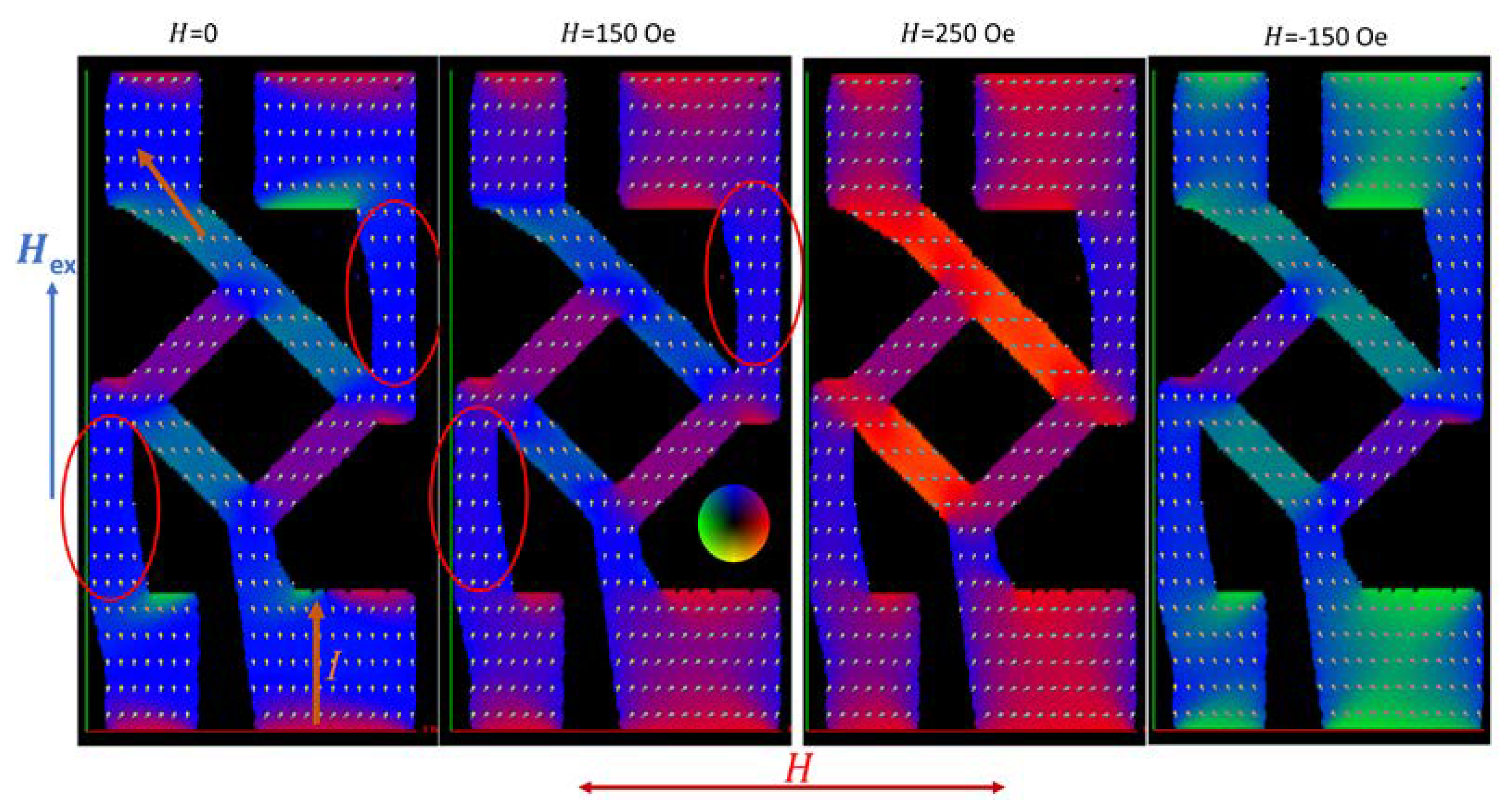
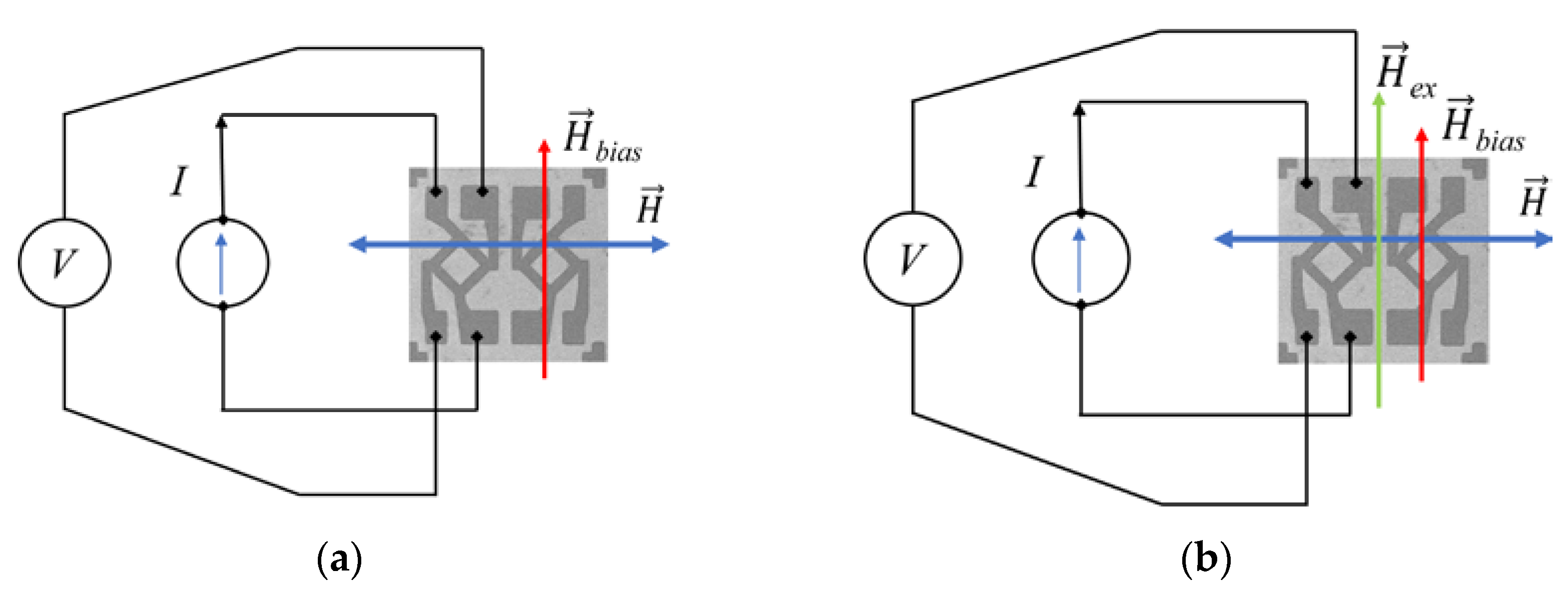
2.6. Galvanomagnetic Characterization of the Exchange-Biased AMR Bridge Sensor
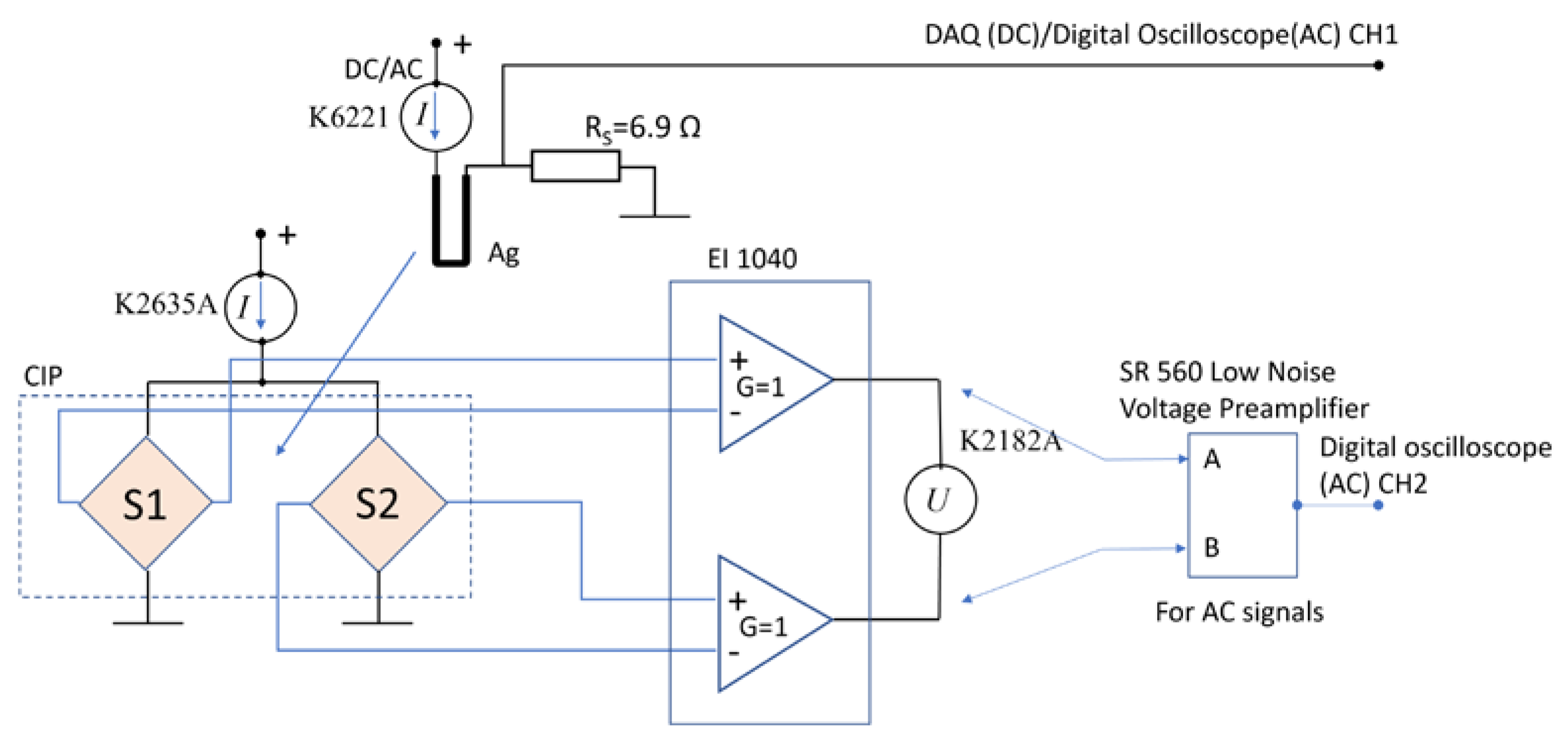
2.6.1. Experimental Setup
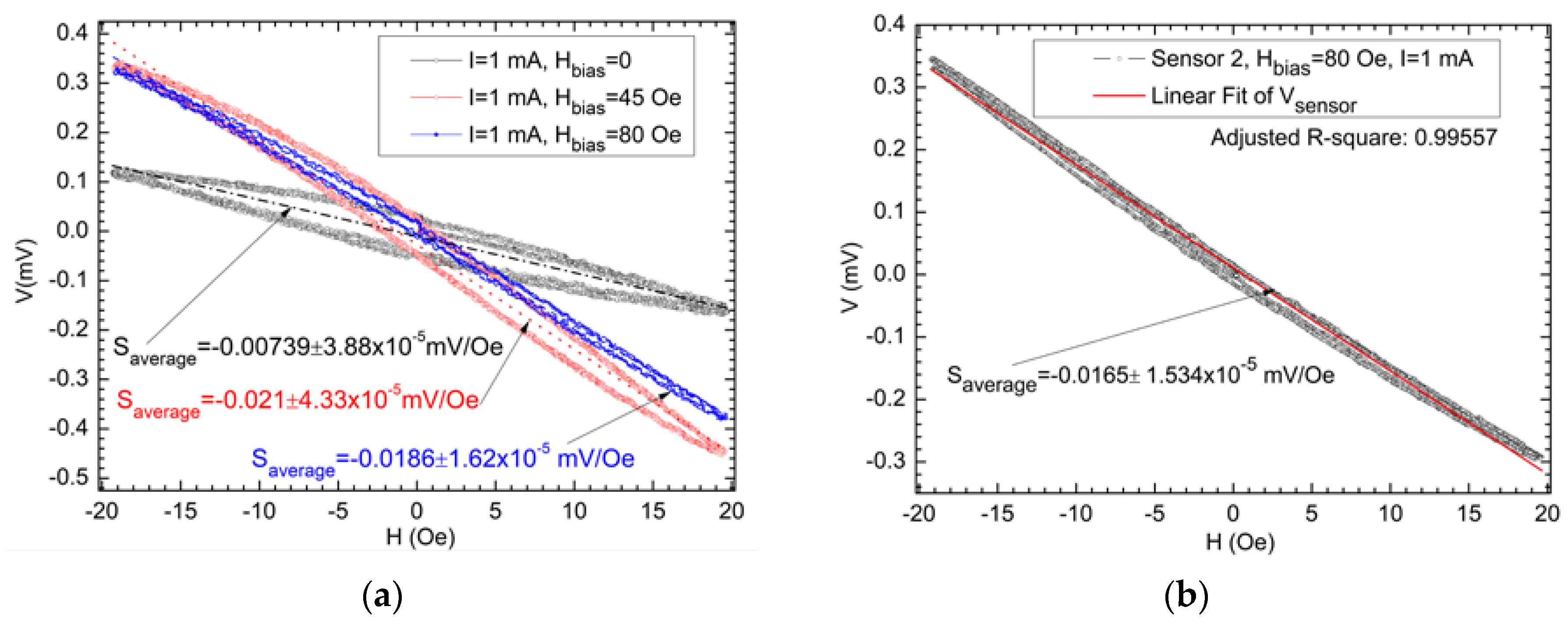
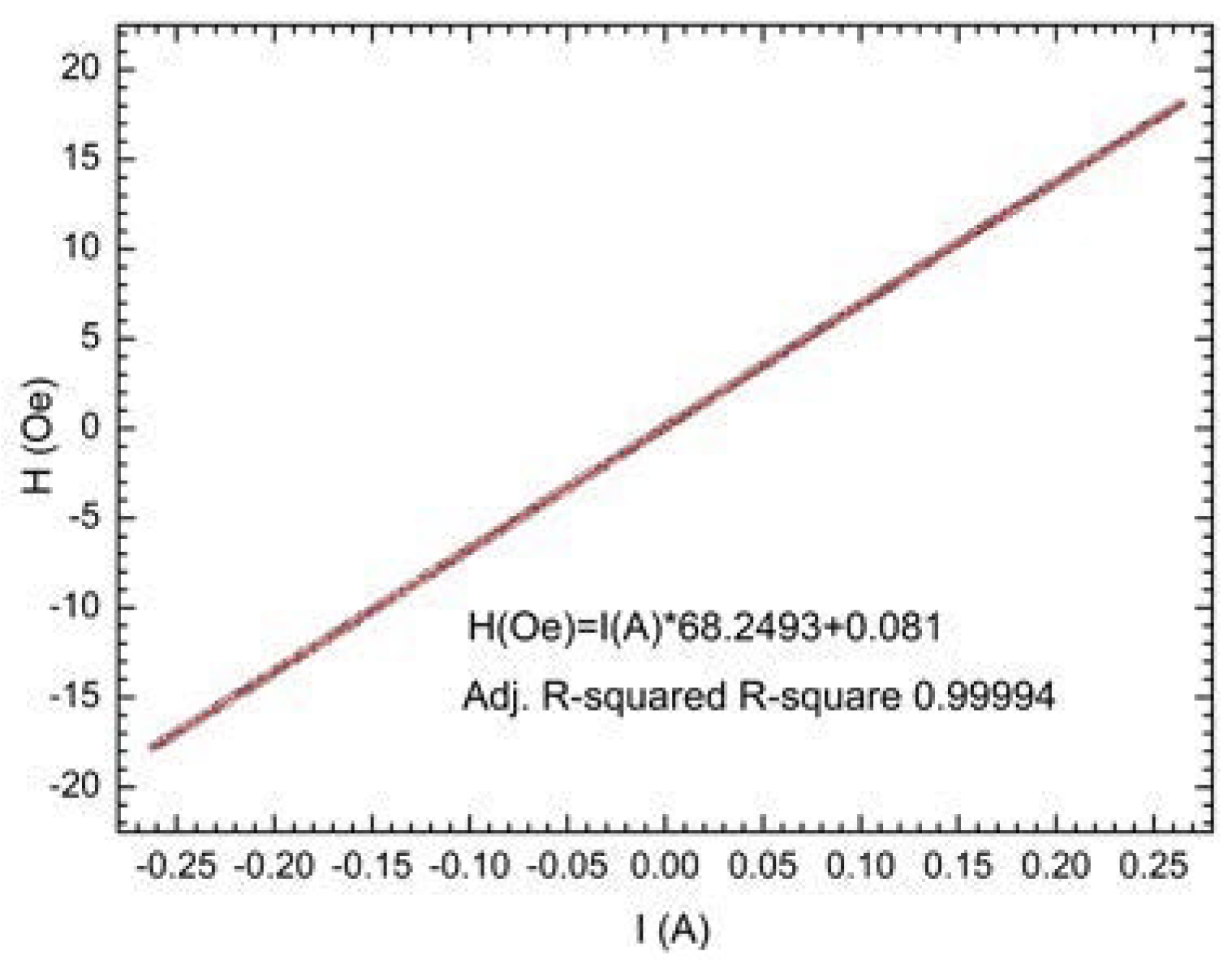
2.6.2. Characterization of the Demonstrator Chip—After Thermal and Magnetic Annealing
3. Results and Discussion
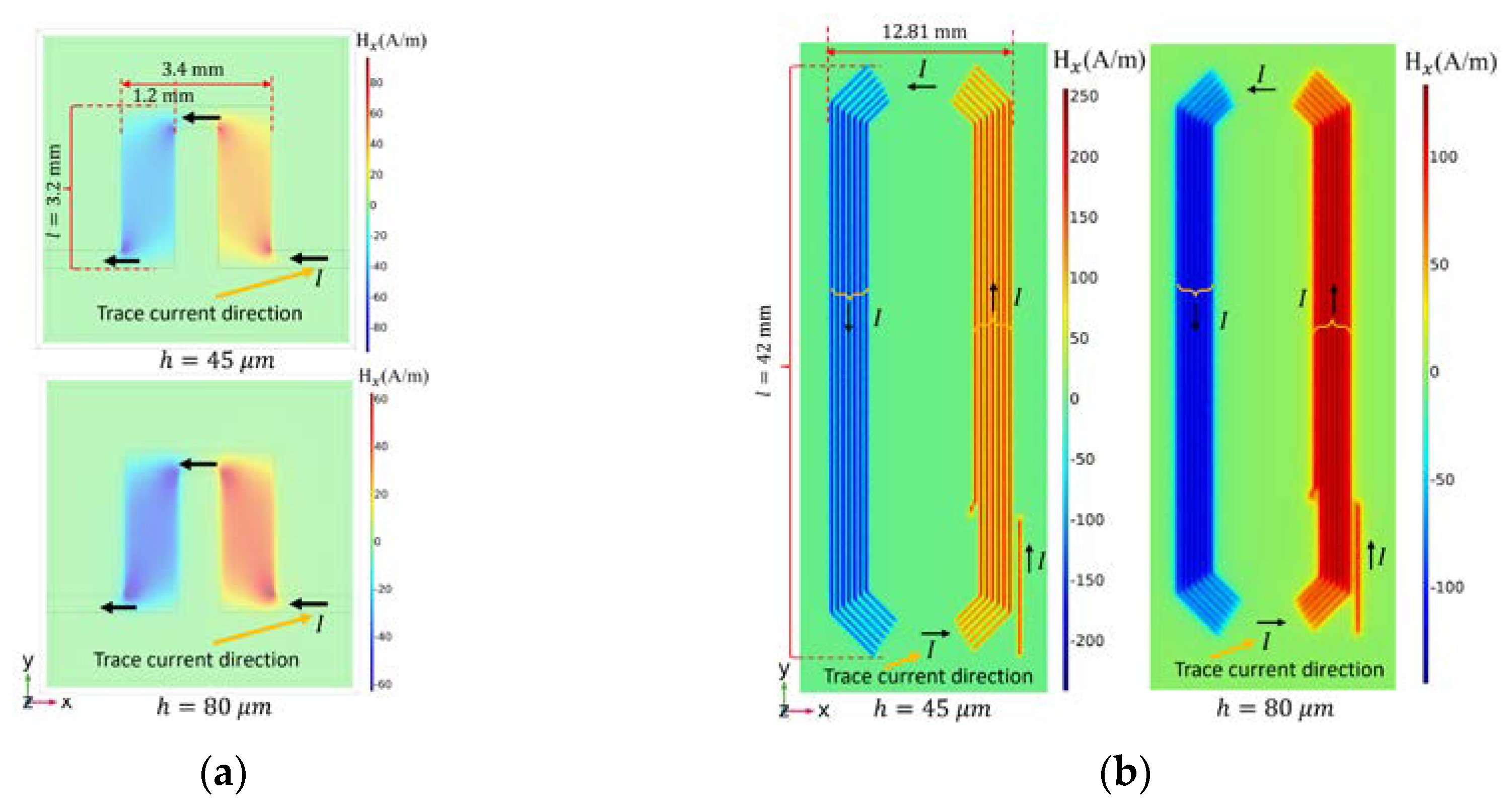
3.1. Case Study Utilizing Analytical Model and Finite Elements Method Simulations for Currrent Stripes Optimization
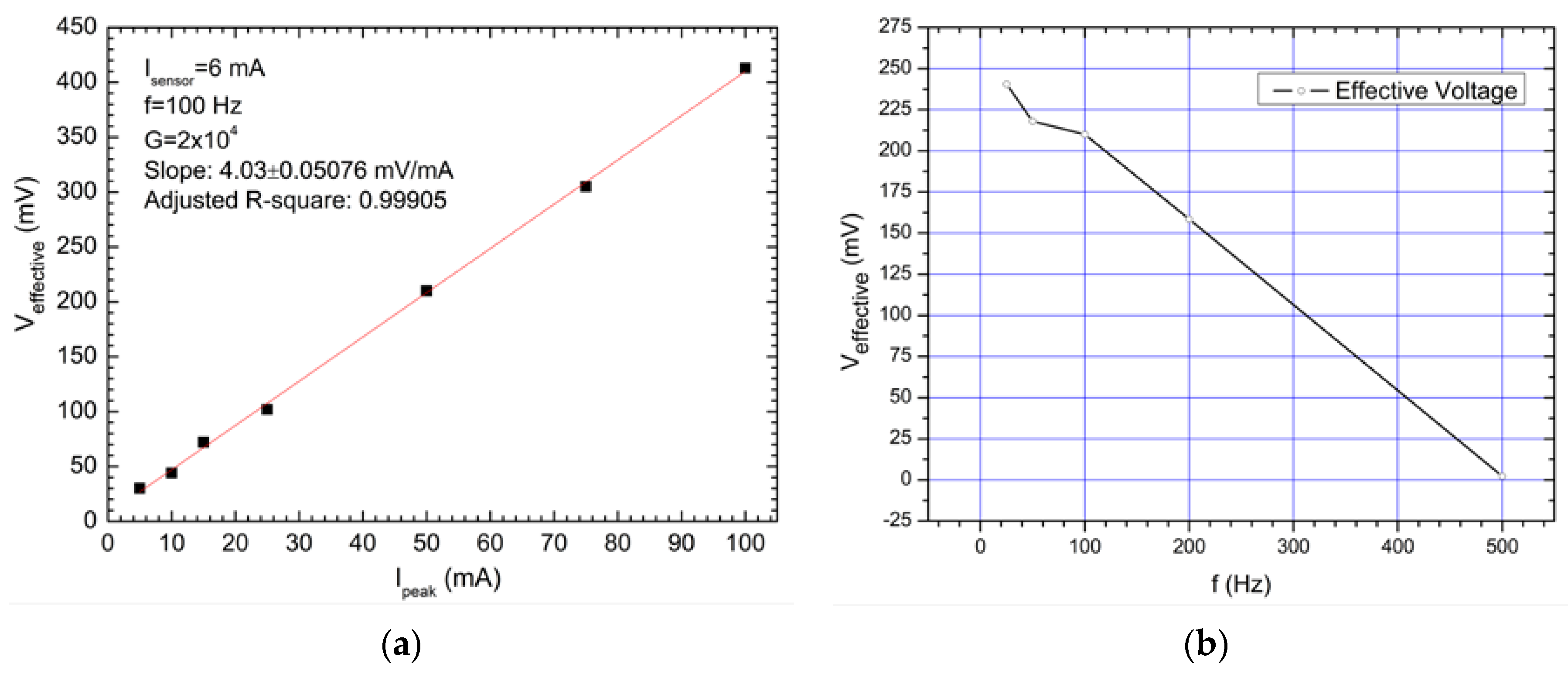
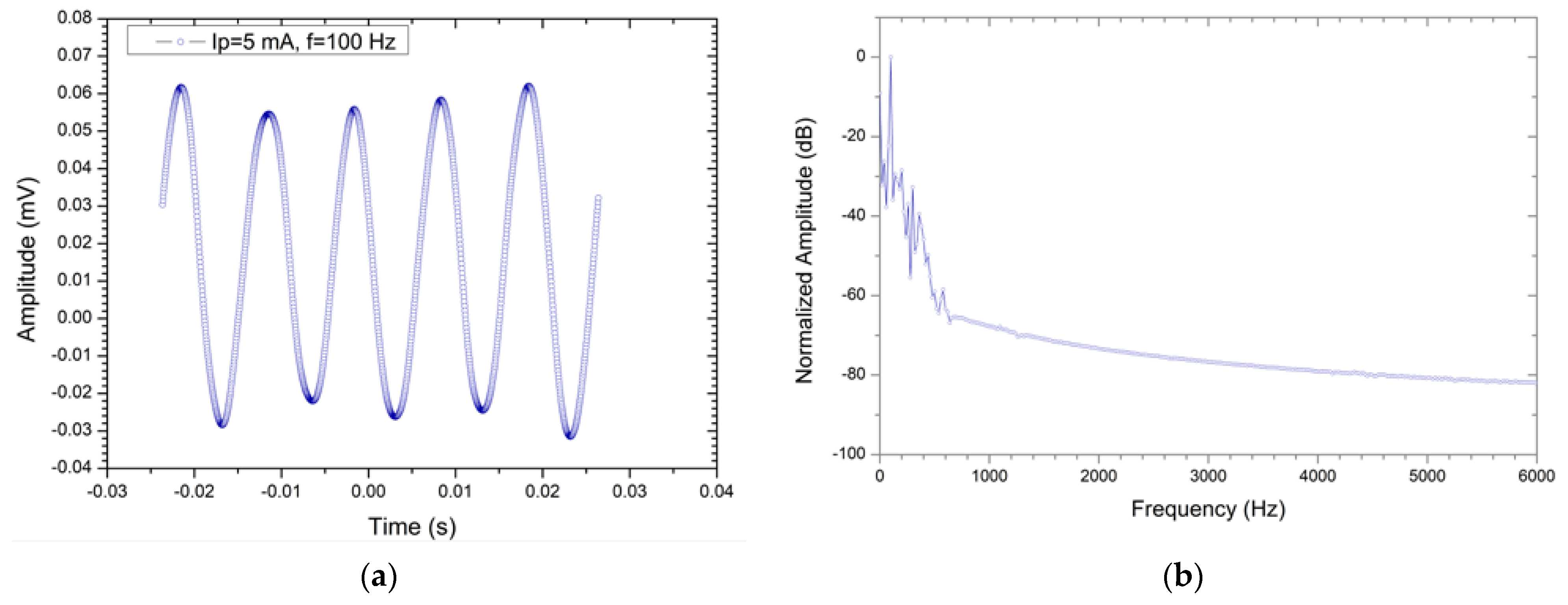
3.2. Demonstrator Chip with AMR Bridge (PHR) Sensors
- The voltage at the terminals of the bridge: 4.399 V;
- The total resistance of the bridge: 0.734 kΩ;
- The power dissipated by the bridge: 13.1 mW.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Patel, A.; Ferdowsi, M. Current Sensing for Automotive Electronics—A Survey. IEEE Trans. Veh. Technol. 2009, 58, 4108–4119. [Google Scholar] [CrossRef]
- Ripka, P.; Mlejnek, P.; Hejda, P.; Chirtsov, A.; Vyhnánek, J. Rectangular Array Electric Current Transducer with Integrated Fluxgate Sensors. Sensors 2019, 19, 4964. [Google Scholar] [CrossRef] [PubMed]
- Snoeij, M.F.; Schaffer, V.; Udayashankar, S.; Ivanov, M.V. Integrated Fluxgate Magnetometer for Use in Isolated Current Sensing. IEEE J. Solid-State Circuits 2016, 51, 1684–1694. [Google Scholar] [CrossRef]
- Weiss, R.; Mattheis, R.; Reiss, G. Advanced giant magnetoresistance technology for measurement applications. Meas. Sci. Technol. 2013, 24, 082001. [Google Scholar] [CrossRef]
- Nhalil, H.; Givon, T.; Das, P.T.; Hasidim, N.; Mor, V.; Schultz, M.; Grosz, A.; Amrusi, S.; Klein, L. Planar Hall effect magnetometer with 5 pT resolution. IEEE Sens. Lett. 2019, 3, 1–4. [Google Scholar] [CrossRef]
- Hung, T.Q.; Oh, S.; Sinha, B.; Jeong, J.R.; Kim, D.Y.; Kim, C. High field-sensitivity planar Hall sensor based on NiFe/Cu/IrMn trilayer structure. J. Appl. Phys. 2010, 107, 9. [Google Scholar] [CrossRef]
- Granell, P.N.; Wang, G.; Cañon Bermudez, G.S.; Kosub, T.; Golmar, F.; Steren, L.; Makarov, D.; Fassbender, J. Highly compliant planar Hall effect sensor with sub 200 nT sensitivity. npj Flex. Electron 2019, 3, 10–1038. [Google Scholar] [CrossRef]
- Du, W.Y. Resistive, Capacitive, Inductive and Magnetic Sensor Technologies; CRC Press: Boca Raton, FL, USA, 2014; pp. 239–253. [Google Scholar]
- Poon, T.Y.; Tse, N.C.F.; Lau, R.W.H. Extending the GMR Current Measurement Range with a Counteracting Magnetic Field. Sensors 2013, 13, 8042–8059. [Google Scholar] [CrossRef]
- Soliman, E.; Hofmann, K.; Reeg, H.; Schwickert, M. Noise study of open-loop direct current-current transformer using magneto-resistance sensors. In Proceedings of the 2016 IEEE Sensors Applications Symposium (SAS), Catania, Italy, 20–22 April 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Li, Z.; Dixon, S. A Closed-Loop Operation to Improve GMR Sensor Accuracy. IEEE Sens. J. 2016, 16, 6003–6007. [Google Scholar] [CrossRef]
- Ziegler, S.; Woodward, R.C.; Iu, H.H.C.; Borle, L.J. Current sensing techniques: A review. IEEE Sens. J. 2009, 9, 354–376. [Google Scholar] [CrossRef]
- Vidal, E.G.; Muñoz, D.R.; Arias, S.I.R.; Moreno, J.S.; Cardoso, S.; Ferreira, R.; Freitas, P. Electronic Energy Meter Based on a Tunnel Magnetoresistive Effect (TMR) Current Sensor. Materials 2017, 10, 1134. [Google Scholar] [CrossRef]
- Mușuroi, C.; Oproiu, M.; Volmer, M.; Firastrau, I. High Sensitivity Differential Giant Magnetoresistance (GMR) Based Sensor for Non-Contacting DC/AC Current Measurement. Sensors 2020, 20, 323. [Google Scholar] [CrossRef] [PubMed]
- Mușuroi, C.; Oproiu, M.; Volmer, M.; Neamtu, J.; Avram, M.; Helerea, E. Low Field Optimization of a Non-Contacting High-Sensitivity GMR-Based DC/AC Current Sensor. Sensors 2021, 21, 2564. [Google Scholar] [CrossRef] [PubMed]
- Ripka, P. Contactless measurement of electric current using magnetic sensors. Tm-Tech. Messen 2019, 86, 586–598. [Google Scholar] [CrossRef]
- Volmer, M.; Neamtu, J. Micromagnetic analysis and development of high sensitivity spin-valve magnetic sensors. J. Phys. Conf. Ser. 2011, 268, 012032. [Google Scholar] [CrossRef]
- Sreevidya, P.V.; Khan, J.; Barshilia, H.C.; Ananda, C.M.; Chowdhury, P. Development of two axes magnetometer for navigation applications. J. Magn. Magn. Mater. 2018, 448, 298–302. [Google Scholar] [CrossRef]
- Hauser, H.; Tondra, M. Magnetoresistors. In Magnetic Sensors and Magnetometers; Ripka, P., Ed.; Artech house: Norwood, MA, USA, 2001; pp. 136–144. [Google Scholar]
- Hansen, M.F.; Rizzi, G. Exchange-biased AMR bridges for magnetic field sensing and biosensing. IEEE Trans. Magn. 2016, 53, 1–11. [Google Scholar] [CrossRef]
- Henriksen, A.D.; Dalslet, B.T.; Skieller, D.H.; Lee, K.H.; Okkels, F.; Hansen, M.F. Planar Hall effect bridge magnetic field sensors. Appl. Phys. Lett. 2010, 97, 013507. [Google Scholar] [CrossRef]
- Elzwawy, A.; Pişkin, H.; Akdoğan, N.; Volmer, M.; Reiss, G.; Marnitz, L.; Schmalhorst, J.M.; Moskaltsova, A.; Gurel, O. Current trends in planar Hall effect sensors: Evolution, optimization, and applications. J. Phys. D Appl. Phys. 2021, 54, 353002. [Google Scholar] [CrossRef]
- McGuire, T.; Potter, R.L. Anisotropic magnetoresistance in ferromagnetic 3d alloys. IEEE Trans. Magn. 1975, 11, 1018–1038. [Google Scholar] [CrossRef]
- Lin, G.; Makarov, D.; Schmidt, O.G. Magnetic sensing platform technologies for biomedical applications. Lab A Chip 2017, 17, 1884–1912. [Google Scholar] [CrossRef] [PubMed]
- West, F.G. Rotating-field technique for galvanomagnetic measurements. J. Appl. Phys. 1963, 34, 1171–1173. [Google Scholar] [CrossRef]
- Tumanski, S. Thin film Magnetoresistance Sensors; CRC Press: Boca Raton, FL, USA, 2001. [Google Scholar]
- Jogschies, L.; Klaas, D.; Kruppe, R.; Rittinger, J.; Taptimthong, P.; Wienecke, A.; Wurz, M.C.; Rissing, L. Recent developments of magnetoresistive sensors for industrial applications. Sensors 2015, 15, 28665–28689. [Google Scholar] [CrossRef] [PubMed]
- Hauser, H.; Stangl, G.; Fallmann, W.; Chabicovsky, R.; Riedling, K. Magnetoresistive Sensors, Preparation, Properties, and Applications of Thin Ferromagnetic Films, June 2000. Available online: http://educypedia.karadimov.info/library/Hauser.pdf (accessed on 23 November 2022).
- Jander, A.; Smith, C.; Schneider, R. Magnetoresistive sensors for nondestructive evaluation. Adv. Sens. Technol. Nondestruct. Eval. Struct. Health Monit. 2005, 5770, 1–13. [Google Scholar] [CrossRef]
- NVE Sensors Catalogue. Available online: https://www.nve.com/Downloads/catalog.pdf (accessed on 23 November 2022).
- Misakian, M. Equations for the magnetic field produced by one or more rectangular loops of wire in the same plane. J. Res. Natl. Inst. Stand. Technol. 2000, 105, 557. [Google Scholar] [CrossRef]
- Nicolaide, A. Electromagnetics. General Theory of the Electromagnetic Field. Classical and Relativistic Approaches, 3rd ed.; Transilvania University Press: Brașov, Romania, 2012; pp. 170–173. [Google Scholar]
- Minnaert, B.; Stevens, N. Evaluation of The Vertical Magnetic Field Generated By A Spiral Planar Coil. In Proceedings of the Nordic Circuits and Systems Conference (NORCAS), Oslo, Norway, 26−28 October 2015; NORCHIP & International Sympo-sium on System-on-Chip (SoC). pp. 1–3. [Google Scholar] [CrossRef]
- Hrabovský, P.; Kravets, O. The Design and Simulation of Spiral Planar Coil in COMSOL Multiphysics. In IEEE International Conference on Modern Electrical and Energy Systems (MEES); IEEE: Piscataway, NJ, USA, 2019; pp. 374–377. [Google Scholar] [CrossRef]
- Gupta, M.; Agarwal, P. To model magnetic field of RF planar coil for portable NMR applications. In Proceedings of the In-ternational Conference on Inventive Computing and Informatics (ICICI), Coimbatore, India, 23−24 November 2017; pp. 490–494. [Google Scholar] [CrossRef]
- NVE ALTxxx-10 TMR Catalogue. Available online: https://www.nve.com/Downloads/ALTxxx-10.pdf (accessed on 23 November 2022).
- Voltera V-One Printer Overview. Available online: https://f.hubspotusercontent30.net/hubfs/5264434/Sales-Docs/Product-Development.pdf (accessed on 23 November 2022).
- Leliaert, J.; Mulkers, J. Tomorrow’s micromagnetic simulations. J. Appl. Phys. 2019, 125, 180901. [Google Scholar] [CrossRef]
- Yin, L.F.; Wei, D.H.; Lei, N.; Zhou, L.H.; Tian, C.S.; Dong, G.S.; Jin, X.F.; Guo, L.P.; Jia, Q.J.; Wu, R.Q. Magnetocrystalline anisotropy in permalloy revisited. Phys. Rev. Lett. 2006, 97, 067203. [Google Scholar] [CrossRef]
- Roshchupkina, O.D.; Strache, T.; McCord, J.; Mücklich, A.; Bähtz, C.; Grenzer, J. Structural modifications of thin magnetic Permalloy films induced by ion implantation and thermal annealing: A comparison. Acta Mater. 2014, 74, 278–284. [Google Scholar] [CrossRef]
- Voltera Flexible Conductor Ink Datasheet. Available online: https://assets.ctfassets.net/e6vf9wdhbae5/2z1lTqP8uRIxYLRCSZ9hCQ/839deb49846f3e75878cea856297f7eb/Voltera-Flexible-Conductive-Ink.pdf (accessed on 23 November 2022).
- LabJack EI1040 Instrumentation Amplifier. Available online: https://labjack.com/products/ei1040-dual-instrumentation-amplifier (accessed on 23 November 2022).
- Mlejnek, P.; Vopalensky, M.; Ripka, P. AMR current measurement device. Sens. Actuators A 2008, 141, 649–653. [Google Scholar] [CrossRef]
- Aceinna Current Sensors Catalogue. Available online: https://www.aceinna.com/current-sensors (accessed on 23 November 2022).
- Sensitec Current Sensors Catalogue. Available online: https://www.sensitec.com/products-solutions/current-measurement/cfs1000 (accessed on 23 November 2022).







| Symbol | Name | Quantity | |
|---|---|---|---|
| D | Trace width | Planar coil with 7 traces: 0.22 mm | |
| U-shaped trace: 1.2 mm | |||
| Td | Distance between traces | Planar coil with 7 traces: 0.19 mm | |
| U-shaped trace: N/A | |||
| I | Current through trace | 0.1 A | |
| h | Distance between sensor and trace | Planar coil with 7 traces: 0.045 [mm] to 3.58 [mm] | |
| U-shaped trace: 0.045 mm to 2.08 mm | |||
| t | Trace thickness | 35 µm | |
| m | Number of layers in which t is divided | 35 (1 μm each layer) | |
| L | Trace length | Planar coil with 7 traces: 42 mm | |
| U-shaped trace: 3.2 mm | |||
| Δl | Sensor position on trace length 1 | Planar coil with 7 traces: 21 mm | |
| U-shaped trace: 1.6 mm | |||
| Vs | Sensor input voltage | U-shaped trace setup: 4.399 V Planar coil setup: 4.096 V | |
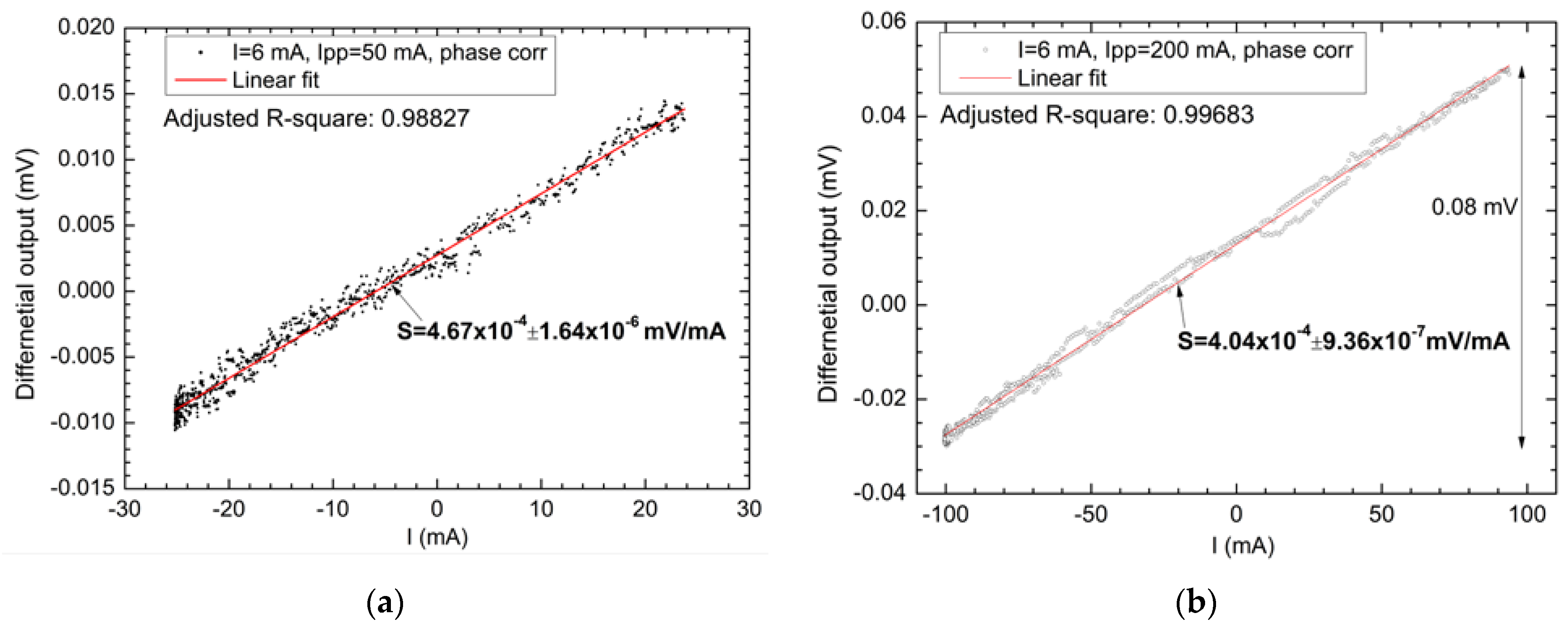
| S | Sensor sensitivity | U-shaped trace sensor setup: | S1: 159 μV/(V × A/m) (0.01268 mV/V-Oe) |
| S2: 188.54 μV/(V × A/m) (0.0150034 mV/V-Oe) | |||
| Sdifferential: 347.94 μV/(V × A/m) (0.0277 mV/V-Oe) | |||
| Planar coil sensor setup: | Sdifferential: 32.67 μV/(V × A/m) | ||
| Trace Type | Validation Case | h 1 [mm] | Hx [A/m] | Vout2 [mV] | Vdifferential 2 [mV] | |
|---|---|---|---|---|---|---|
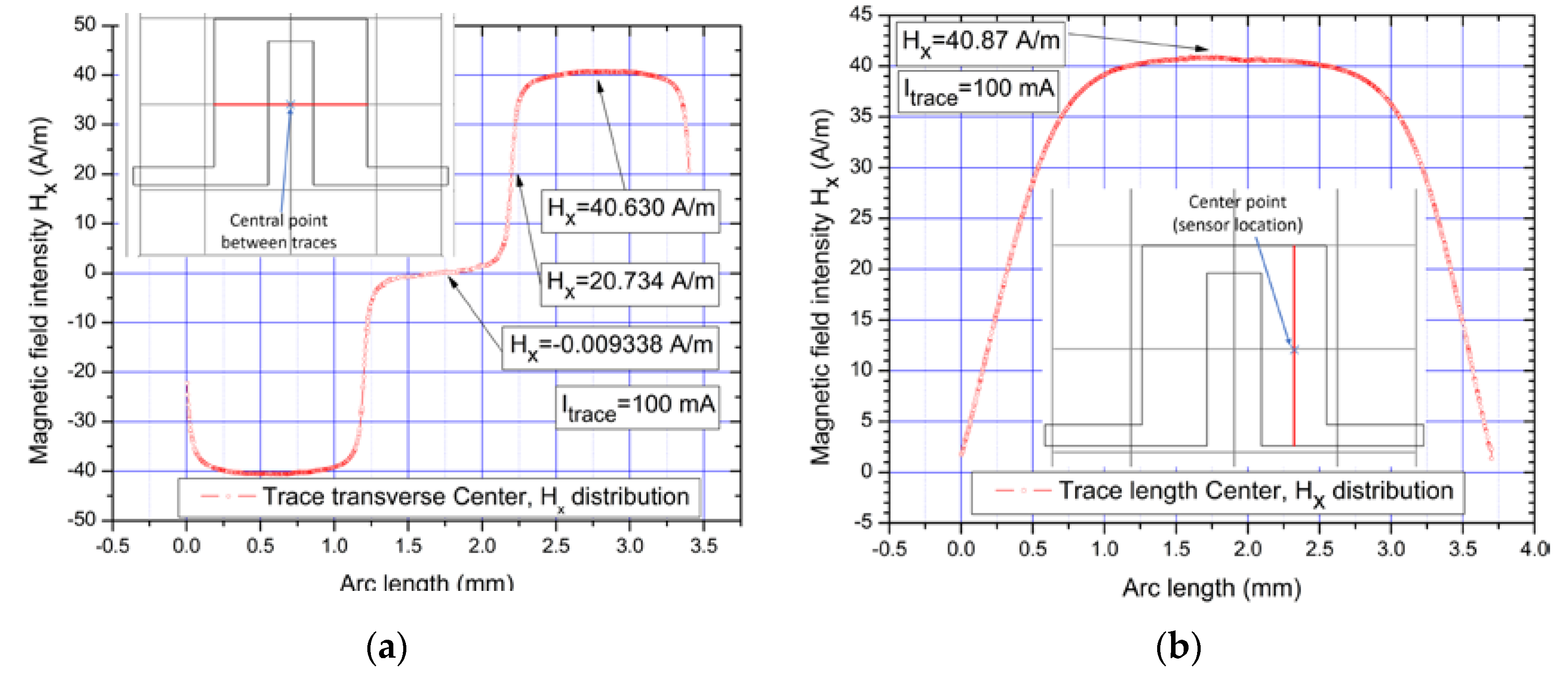
| U-shaped trace (Figure 4a) Itrace = 100 mA Vs = 4.399 V 3 | COMSOL simulations | 0.08 | 39.056 | - | - | |
| 0.045 | 40.630 | - | - | |||
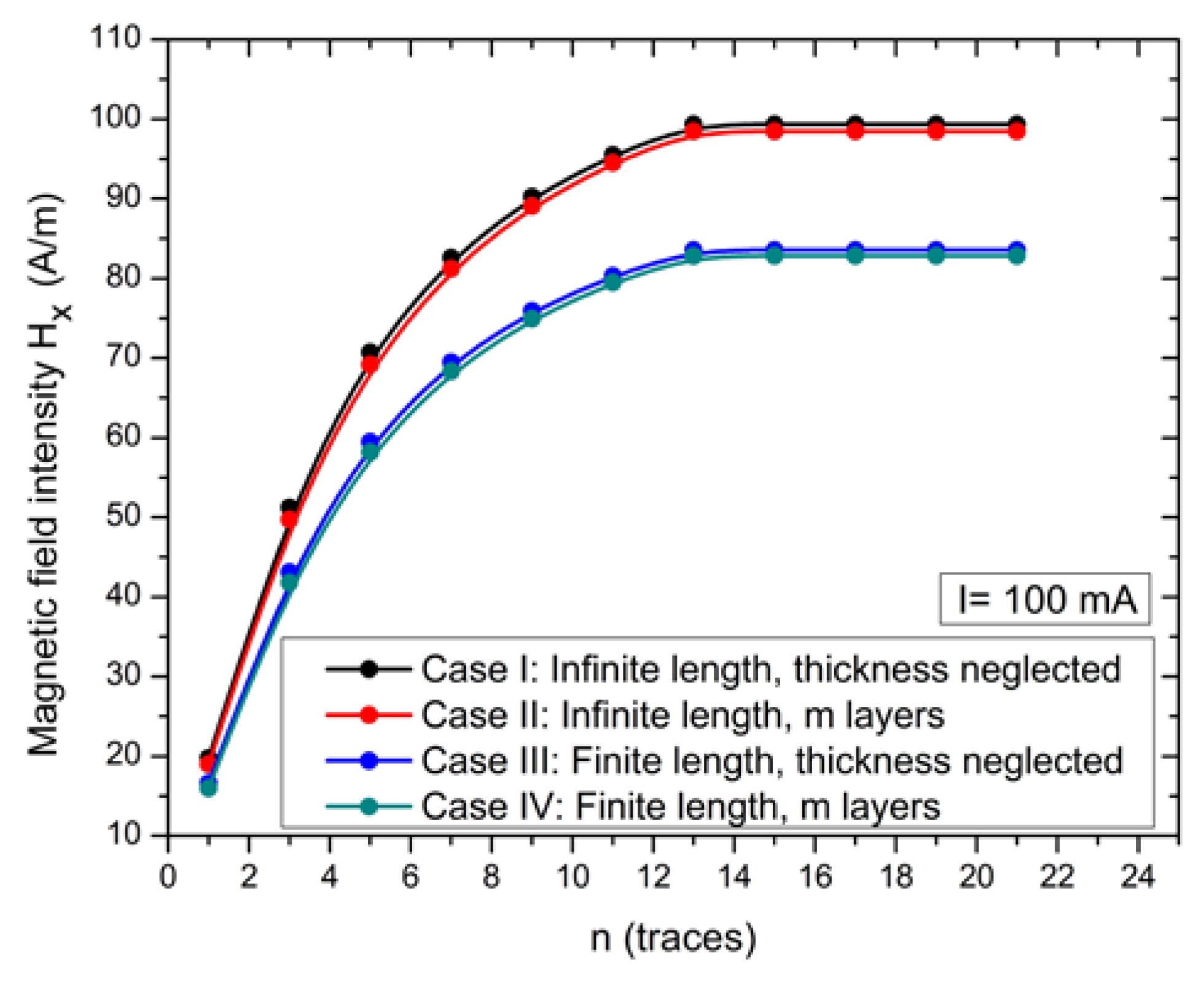
| Analytical method | Case I: Infinite length, t neglected | 0.08 | 38.150 | S1: 0.02675 | 0.05839 | |
| S2: 0.03164 | ||||||
| 0.045 | 39.680 | S1: 0.02782 | 0.06073 | |||
| S2: 0.03291 | ||||||
| Case II: Infinite length, m = 35 layers (1 μm each layer) | 0.08 | 36.7321 | S1: 0.02575 | 0.05622 | ||
| S2: 0.03046 | ||||||
| 0.045 | 38.2408 | S1: 0.02681 | 0.05853 | |||
| S2: 0.03171 | ||||||
| Case III: Finite length, t neglected | 0.08 | 32.0769 | S1: 0.02249 | 0.04910 | ||
| S2: 0.0266 | ||||||
| 0.045 | 33.3818 | S1: 0.02341 | 0.05109 | |||
| S2: 0.02768 | ||||||
| Case IV: Finite length, m = 35 layers (1 μm each layer) | 0.08 | 30.8842 | S1: 0.02165 | 0.04727 | ||
| S2: 0.02561 | ||||||
| 0.045 | 32.1704 | S1: 0.02255 | 0.04924 | |||
| S2: 0.02668 | ||||||
| Experimental results | 0.045 | 31.7423 | S1: 0.0198 | 0.042 | ||
| S2: 0.022 | ||||||
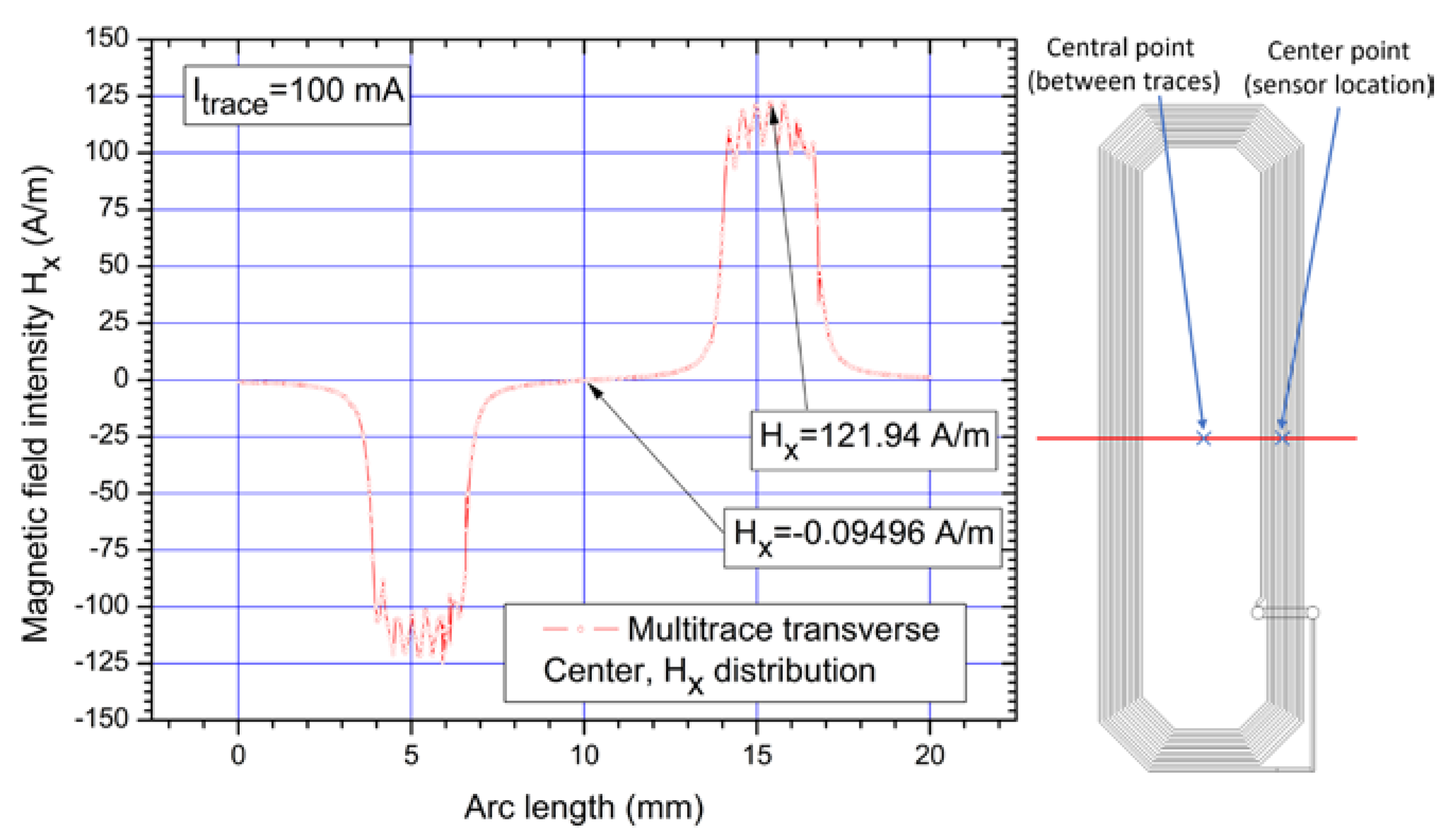
| Planar coil with 7 traces (Figure 4b) Itrace = 100 mA Vs = 4.096 V 3 | COMSOL simulation | 0.8 | 79.780 | - | - | |
| 0.08 | 121.94 | - | - | |||
| Analytical method | Case I: Infinite length, t neglected | 0.8 | 82.5885 | 11.8702 | 23.7404 | |
| 0.08 | 157.422 | 22.6257 | 45.2514 | |||
| Case II: Infinite length, m = 35 layers (1 μm each layer) | 0.8 | 81.2428 | 11.6768 | 23.3536 | ||
| 0.08 | 140.624 | 20.2115 | 40.423 | |||
| Case III: Finite length, t neglected | 0.8 | 67.9498 | 9.9838 | 19.9676 | ||
| 0.08 | 132.465 | 19.0388 | 38.0776 | |||
| Case IV: Finite length, m = 35 layers (1 μm each layer) | 0.8 | 66.8427 | 9.821 | 19.642 | ||
| 0.08 | 118.331 | 17.0073 | 34.0146 | |||
| Experimental results | 0.8 | - | 10.716 | 21.432 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mușuroi, C.; Volmer, M.; Oproiu, M.; Neamtu, J.; Helerea, E. Designing a Spintronic Based Magnetoresistive Bridge Sensor for Current Measurement and Low Field Sensing. Electronics 2022, 11, 3888. https://doi.org/10.3390/electronics11233888
Mușuroi C, Volmer M, Oproiu M, Neamtu J, Helerea E. Designing a Spintronic Based Magnetoresistive Bridge Sensor for Current Measurement and Low Field Sensing. Electronics. 2022; 11(23):3888. https://doi.org/10.3390/electronics11233888
Chicago/Turabian StyleMușuroi, Cristian, Marius Volmer, Mihai Oproiu, Jenica Neamtu, and Elena Helerea. 2022. "Designing a Spintronic Based Magnetoresistive Bridge Sensor for Current Measurement and Low Field Sensing" Electronics 11, no. 23: 3888. https://doi.org/10.3390/electronics11233888
APA StyleMușuroi, C., Volmer, M., Oproiu, M., Neamtu, J., & Helerea, E. (2022). Designing a Spintronic Based Magnetoresistive Bridge Sensor for Current Measurement and Low Field Sensing. Electronics, 11(23), 3888. https://doi.org/10.3390/electronics11233888







