A Multi-Attribute Decision-Making Approach for the Analysis of Vendor Management Using Novel Complex Picture Fuzzy Hamy Mean Operators
Abstract
1. Introduction
2. Preliminaries
- , if and only ifandfor amplitude terms and, andfor phase terms. For all
- If , then .
- If , then .
3. Previous Study
- if .
- if .
- .
- For arithmetic mean operator
- For geometric mean operator
4. Complex Picture Fuzzy Hamy Mean Operators
5. Complex Picture Fuzzy Dual Hamy Mean Operators
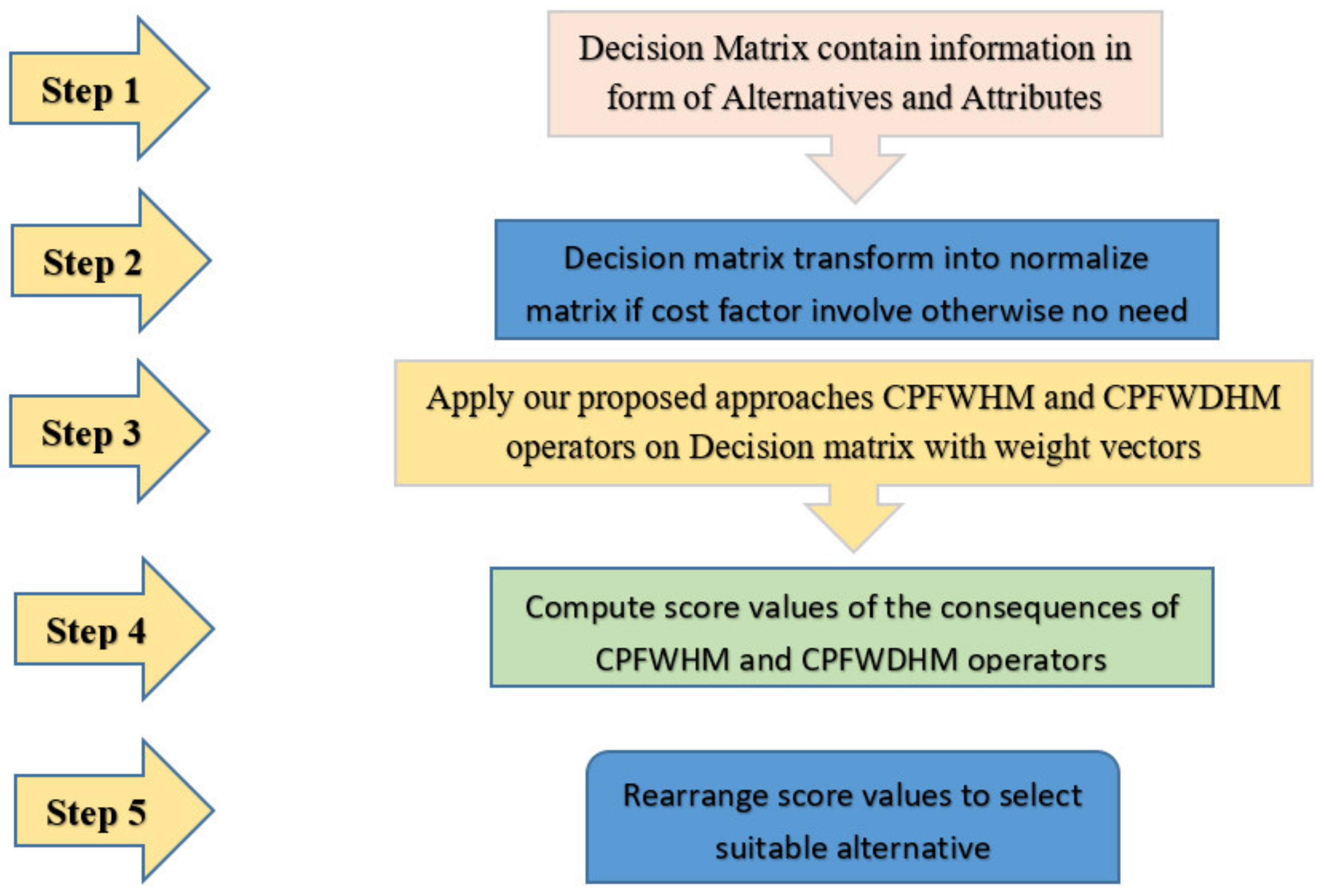
6. MADM Techniques and Its Algorithm
6.1. Application
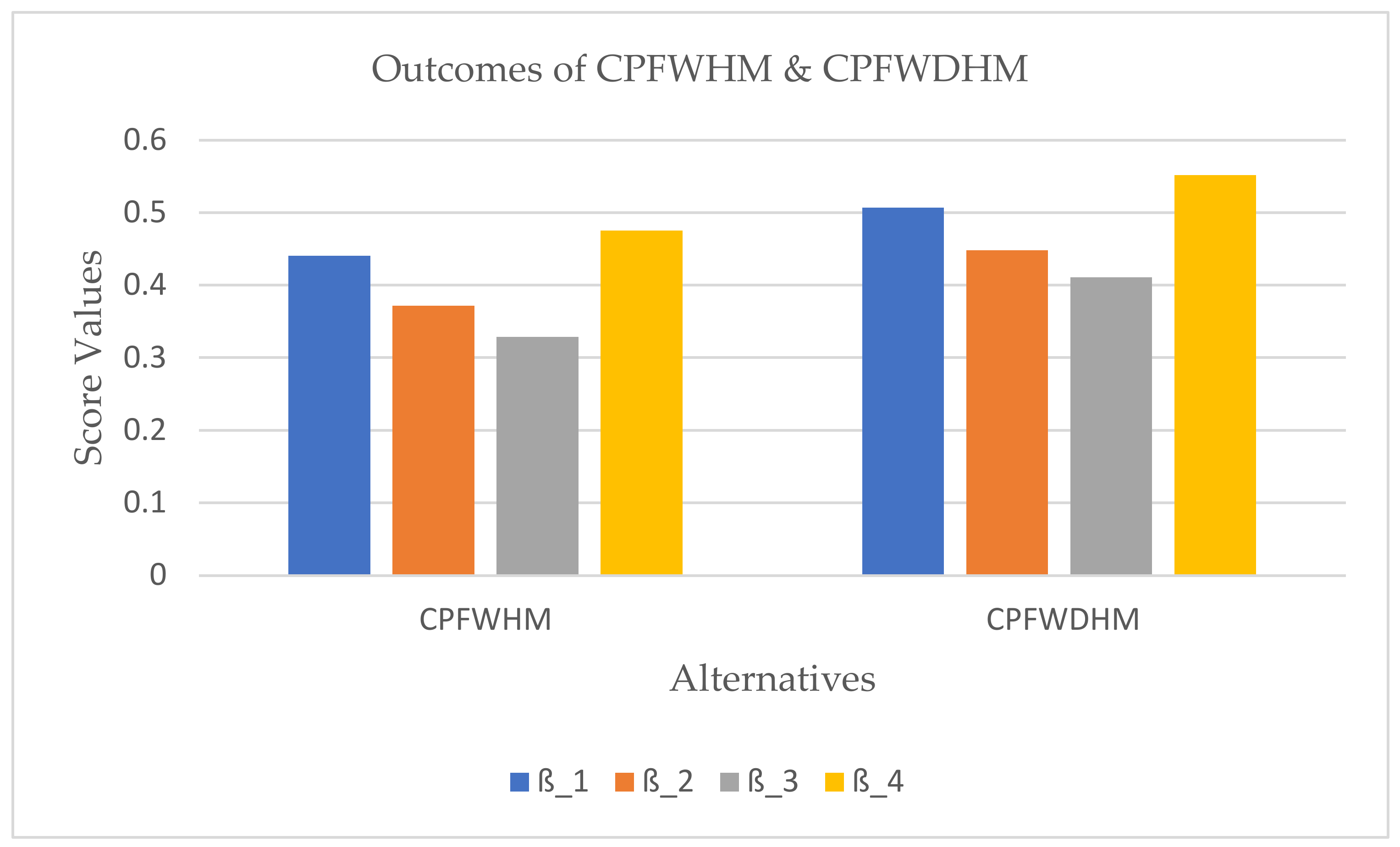
6.2. Numerical Example
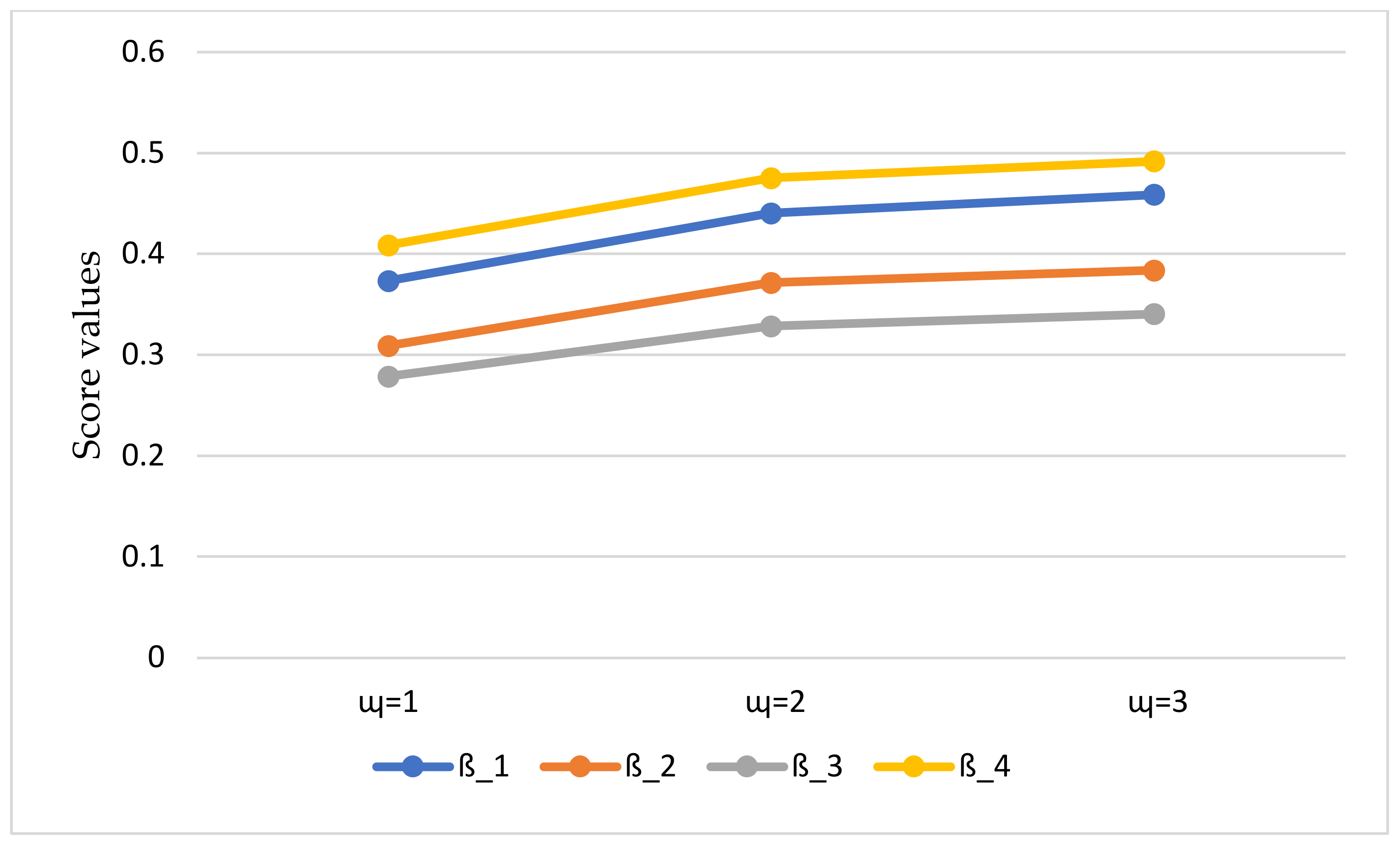
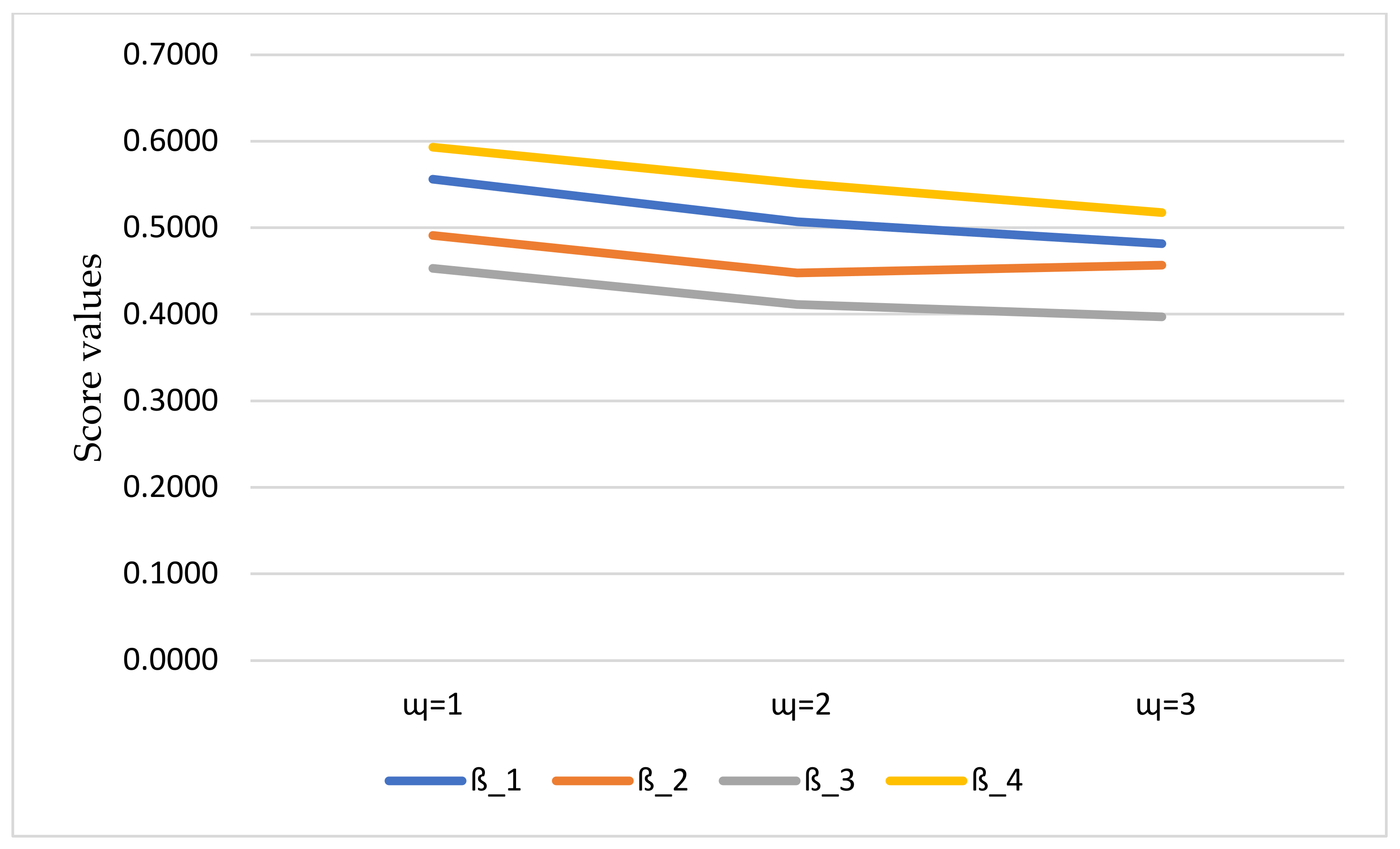
6.3. Influence Study
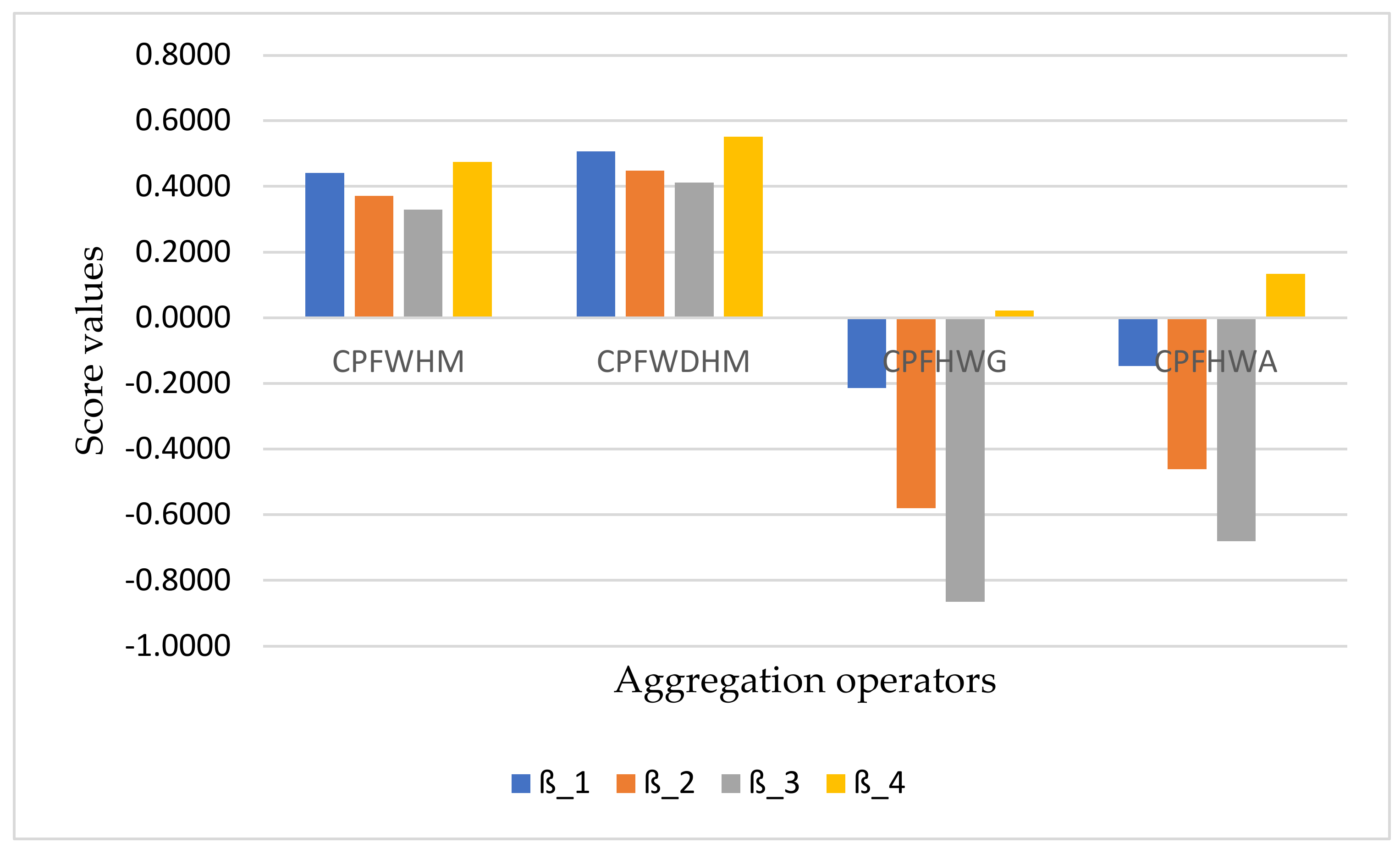
7. Comparative Analysis
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
- (1)
- (2)
- and
- If , and then:
- If and then:
- (1)
- (2)
- and
References
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- El-Bably, M.K.; Abo-Tabl, E.A. A topological reduction for predicting of a lung cancer disease based on generalized rough sets. J. Intell. Fuzzy Syst. 2021, 41, 3045–3060. [Google Scholar] [CrossRef]
- Abu-Gdairi, R.; El-Gayar, M.A.; Al-Shami, T.M.; Nawar, A.S.; El-Bably, M.K. Some Topological Approaches for Generalized Rough Sets and Their Decision-Making Applications. Symmetry 2022, 14, 95. [Google Scholar] [CrossRef]
- El Sayed, M.; El Safty, M.A.; El-Bably, M.K. Topological approach for decision-making of COVID-19 infection via a nano-topology model. AIMS Math. 2021, 6, 7872–7894. [Google Scholar] [CrossRef]
- Atanassov, K. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Yager, R.R. Pythagorean fuzzy subsets. In Proceedings of the 2013 Joint IFSA World Congress and NAFIPS Annual Meeting (IFSA/NAFIPS), Edmonton, AB, Canada, 24–28 June 2013; pp. 57–61. [Google Scholar]
- Yager, R.R. Generalized Orthopair Fuzzy Sets. IEEE Trans. Fuzzy Syst. 2016, 25, 1222–1230. [Google Scholar] [CrossRef]
- Cường, B.C. Picture fuzzy sets. J. Comput. Sci. Cybern. 2015, 30, 409–420. [Google Scholar] [CrossRef]
- Cuong, B.C.; Kreinovich, V. Picture fuzzy sets—A new concept for computational intelligence problems. In Proceedings of the 2013 Third World Congress on Information and Communication Technologies (WICT 2013), Hanoi, Vietnam, 15–18 December 2013; pp. 1–6. [Google Scholar] [CrossRef]
- Lu, H.; Khalil, A.M.; Alharbi, W.; El-Gayar, M.A. A new type of generalized picture fuzzy soft set and its application in decision making. J. Intell. Fuzzy Syst. 2021, 40, 12459–12475. [Google Scholar] [CrossRef]
- Riaz, M.; Athar Farid, H.M. Picture fuzzy aggregation approach with application to third-party logistic provider selection process. Rep. Mech. Eng. 2022, 3, 318–327. [Google Scholar] [CrossRef]
- Rasoulzadeh, M.; Edalatpanah, S.A.; Fallah, M.; Najafi, S.E. A multi-objective approach based on Markowitz and DEA cross-efficiency models for the intuitionistic fuzzy portfolio selection problem. Decis. Mak. Appl. Manag. Eng. 2022, 5, 241–259. [Google Scholar] [CrossRef]
- Limboo, B.; Dutta, P. A q-rung orthopair basic probability assignment and its application in medical diagnosis. Decis. Mak. Appl. Manag. Eng. 2022, 5, 290–308. [Google Scholar] [CrossRef]
- Ashraf, A.; Ullah, K.; Hussain, A.; Bari, M. Interval-Valued Picture Fuzzy Maclaurin Symmetric Mean Operator with application in Multiple Attribute Decision-Making. Rep. Mech. Eng. 2022, 3, 301–317. [Google Scholar] [CrossRef]
- Xu, Z. Intuitionistic Fuzzy Aggregation Operators. IEEE Trans. Fuzzy Syst. 2007, 15, 1179–1187. [Google Scholar]
- Xu, Z.; Xia, M. Induced generalized intuitionistic fuzzy operators. Knowl. Based Syst. 2011, 24, 197–209. [Google Scholar] [CrossRef]
- Biswas, A.; Deb, N. Pythagorean fuzzy Schweizer and Sklar power aggregation operators for solving multi-attribute decision-making problems. Granul. Comput. 2021, 6, 991–1007. [Google Scholar] [CrossRef]
- Garg, H. Generalized Pythagorean fuzzy geometric aggregation operators using Einstein t-norm and t-conorm for multicriteria decision-making process. Int. J. Intell. Syst. 2017, 32, 597–630. [Google Scholar] [CrossRef]
- Mahmood, T.; Ali, Z. Aggregation operators and VIKOR method based on complex q-rung orthopair uncertain linguistic informations and their applications in multi-attribute decision making. Comput. Appl. Math. 2020, 39, 306. [Google Scholar] [CrossRef]
- Riaz, M.; Hashmi, M.R. Linear Diophantine fuzzy set and its applications towards multi-attribute decision-making problems. J. Intell. Fuzzy Syst. 2019, 37, 5417–5439. [Google Scholar] [CrossRef]
- Liu, P. Some Hamacher Aggregation Operators Based on the Interval-Valued Intuitionistic Fuzzy Numbers and Their Application to Group Decision Making. IEEE Trans. Fuzzy Syst. 2013, 22, 83–97. [Google Scholar] [CrossRef]
- Hussain, A.; Ullah, K.; Alshahrani, M.N.; Yang, M.-S.; Pamucar, D. Novel Aczel–Alsina Operators for Pythagorean Fuzzy Sets with Application in Multi-Attribute Decision Making. Symmetry 2022, 14, 940. [Google Scholar] [CrossRef]
- Liu, P.; Munir, M.; Mahmood, T.; Ullah, K. Some Similarity Measures for Interval-Valued Picture Fuzzy Sets and Their Applications in Decision Making. Information 2019, 10, 369. [Google Scholar] [CrossRef]
- Mahmood, T.; Ullah, K.; Khan, Q. Some aggregation operators for bipolar-valued hesitant fuzzy information. J. Eng. Appl. Sci. 2018, 10, 240–245. [Google Scholar]
- Garg, H. Some Picture Fuzzy Aggregation Operators and Their Applications to Multicriteria Decision-Making. Arab. J. Sci. Eng. 2017, 42, 5275–5290. [Google Scholar] [CrossRef]
- Wei, G. Picture Fuzzy Hamacher Aggregation Operators and their Application to Multiple Attribute Decision Making. Fundam. Inform. 2018, 157, 271–320. [Google Scholar] [CrossRef]
- El-Bably, M.K.; El-Sayed, M. Three methods to generalize Pawlak approximations via simply open concepts with economic applications. Soft Comput. 2022, 26, 4685–4700. [Google Scholar] [CrossRef]
- Božanić, D.; Milić, A.; Tešić, D.; Salabun, W.; Pamučar, D. D Numbers–Fucom–Fuzzy Rafsi Model for Selecting The Group Of Construction Machines For Enabling Mobility. Facta Univ. Ser. Mech. Eng. 2021, 19, 447–471. [Google Scholar] [CrossRef]
- Hussain, A.; Ullah, K.; Ahmad, J.; Karamti, H.; Pamucar, D.; Wang, H. Applications of the Multiattribute Decision-Making for the Development of the Tourism Industry Using Complex Intuitionistic Fuzzy Hamy Mean Operators. Comput. Intell. Neurosci. 2022, 2022, 8562390. [Google Scholar] [CrossRef] [PubMed]
- Zhou, B.; Chen, J.; Wu, Q.; Pamucar, D.; Wang, W.; Zhou, L. Risk priority evaluation of power transformer parts based on hybrid FMEA framework under hesitant fuzzy environment. Facta Univ. Ser. Mech. Eng. 2021, 20, 399–420. [Google Scholar] [CrossRef]
- Ramot, D.; Milo, R.; Friedman, M.; Kandel, A. Complex fuzzy sets. IEEE Trans. Fuzzy Syst. 2002, 10, 171–186. [Google Scholar] [CrossRef]
- Ramot, D.; Friedman, M.; Langholz, G.; Kandel, A. Complex fuzzy logic. IEEE Trans. Fuzzy Syst. 2003, 11, 450–461. [Google Scholar] [CrossRef]
- Yazdanbakhsh, O.; Dick, S. Multi-variate timeseries forecasting using complex fuzzy logic. In Proceedings of the 2015 Annual Conference of the North American Fuzzy Information Processing Society (NAFIPS) Held Jointly with 2015 5th World Conference on Soft Computing (WConSC), Redmond, WA, USA, 17–19 August 2015; pp. 1–6. [Google Scholar]
- Alkouri, A.M.D.J.S.; Salleh, A.R. Complex intuitionistic fuzzy sets. In AIP Conference Proceedings; American Institute of Physics: College Park, MD, USA, 2012; Volume 1482, pp. 464–470. [Google Scholar]
- Garg, H.; Rani, D. Some generalized complex intuitionistic fuzzy aggregation operators and their application to multicriteria decision-making process. Arab. J. Sci. Eng. 2019, 44, 2679–2698. [Google Scholar] [CrossRef]
- Ullah, K.; Mahmood, T.; Ali, Z.; Jan, N. On some distance measures of complex Pythagorean fuzzy sets and their applications in pattern recognition. Complex Intell. Syst. 2020, 6, 15–27. [Google Scholar] [CrossRef]
- Liu, P.; Mahmood, T.; Ali, Z. Complex q-rung orthopair fuzzy aggregation operators and their applications in multi-attribute group decision making. Information 2020, 11, 5. [Google Scholar] [CrossRef]
- Rong, Y.; Liu, Y.; Pei, Z. Complex q-rung orthopair fuzzy 2-tuple linguistic Maclaurin symmetric mean operators and its application to emergency program selection. Int. J. Intell. Syst. 2020, 35, 1749–1790. [Google Scholar] [CrossRef]
- Akram, M.; Bashir, A.; Garg, H. Decision-making model under complex picture fuzzy Hamacher aggregation operators. Comput. Appl. Math. 2020, 39, 226. [Google Scholar] [CrossRef]
- Hara, T.; Uchiyama, M.; Takahasi, S.-E. A refinement of various mean inequalities. J. Inequal. Appl. 1998, 1998, 932025. [Google Scholar] [CrossRef]
- Qin, J. Interval type-2 fuzzy Hamy mean operators and their application in multiple criteria decision making. Granul. Comput. 2017, 2, 249–269. [Google Scholar] [CrossRef]
- Wu, L.; Wei, G.; Gao, H.; Wei, Y. Some Interval-Valued Intuitionistic Fuzzy Dombi Hamy Mean Operators and Their Application for Evaluating the Elderly Tourism Service Quality in Tourism Destination. Mathematics 2018, 6, 294. [Google Scholar] [CrossRef]
- Li, Z.; Gao, H.; Wei, G. Methods for Multiple Attribute Group Decision Making Based on Intuitionistic Fuzzy Dombi Hamy Mean Operators. Symmetry 2018, 10, 574. [Google Scholar] [CrossRef]
- Wu, S.; Wang, J.; Wei, G.; Wei, Y. Research on Construction Engineering Project Risk Assessment with Some 2-Tuple Linguistic Neutrosophic Hamy Mean Operators. Sustainability 2018, 10, 1536. [Google Scholar] [CrossRef]
- Li, Z.; Wei, G.; Lu, M. Pythagorean Fuzzy Hamy Mean Operators in Multiple Attribute Group Decision Making and Their Application to Supplier Selection. Symmetry 2018, 10, 505. [Google Scholar] [CrossRef]
- Liu, Z.; Xu, H.; Zhao, X.; Liu, P.; Li, J. Multi-Attribute Group Decision Making Based on Intuitionistic Uncertain Linguistic Hamy Mean Operators with Linguistic Scale Functions and Its Application to Health-Care Waste Treatment Technology Selection. IEEE Access 2019, 7, 20–46. [Google Scholar] [CrossRef]
- Wu, L.; Wang, J.; Gao, H. Models for competiveness evaluation of tourist destination with some interval-valued intuitionistic fuzzy Hamy mean operators. J. Intell. Fuzzy Syst. 2019, 36, 5693–5709. [Google Scholar] [CrossRef]
- Wang, J.; Wei, G.; Lu, J.; Alsaadi, F.E.; Hayat, T.; Wei, C.; Zhang, Y. Some q-rung orthopair fuzzy Hamy mean operators in multiple attribute decision-making and their application to enterprise resource planning systems selection. Int. J. Intell. Syst. 2019, 34, 2429–2458. [Google Scholar] [CrossRef]
- Xing, Y.; Zhang, R.; Wang, J.; Bai, K.; Xue, J. A new multi-criteria group decision-making approach based on q-rung orthopair fuzzy interaction Hamy mean operators. Neural Comput. Appl. 2020, 32, 7465–7488. [Google Scholar] [CrossRef]
- Sinani, F.; Erceg, Z.; Vasiljević, M. An evaluation of a third-party logistics provider: The application of the rough Dombi-Hamy mean operator. Decis. Mak. Appl. Manag. Eng. 2020, 3, 92–107. [Google Scholar] [CrossRef]
- Wei, G.; Wang, J.; Wei, C.; Wei, Y.; Zhang, Y. Dual Hesitant Pythagorean Fuzzy Hamy Mean Operators in Multiple Attribute Decision Making. IEEE Access 2019, 7, 86697–86716. [Google Scholar] [CrossRef]
- Liu, P.; Khan, Q.; Mahmood, T. Application of Interval Neutrosophic Power Hamy Mean Operators in MAGDM. Informatica 2019, 30, 293–325. [Google Scholar] [CrossRef]
- Garg, H.; Sirbiladze, G.; Ali, Z.; Mahmood, T. Hamy Mean Operators Based on Complex q-Rung Orthopair Fuzzy Setting and Their Application in Multi-Attribute Decision Making. Mathematics 2021, 9, 2312. [Google Scholar] [CrossRef]
- Ali, Z.; Mahmood, T.; Pamucar, D.; Wei, C. Complex Interval-Valued q-Rung Orthopair Fuzzy Hamy Mean Operators and Their Application in Decision-Making Strategy. Symmetry 2022, 14, 592. [Google Scholar] [CrossRef]
- Mahmood, T.; Rehman, U.U.; Ahmmad, J. Complex picture fuzzy N-soft sets and their decision-making algorithm. Soft Comput. 2021, 25, 13657–13678. [Google Scholar] [CrossRef]
- ‘Ele-Math—Journal of Mathematical Inequalities: Some Properties of Dual form of the Hamy’s Symmetric Function’. Available online: http://jmi.ele-math.com/01-12/Some-properties-of-dual-form-of-the-Hamy-s-symmetric-function (accessed on 27 September 2022).
- Savasaneril, S.; Erkip, N.K. An analysis of manufacturer benefits under vendor-managed systems. IIE Trans. 2010, 42, 455–477. [Google Scholar] [CrossRef]
- Solyalı, O.; Süral, H. A Relaxation Based Solution Approach for the Inventory Control and Vehicle Routing Problem in Vendor Managed Systems. In Modeling, Computation and Optimization; World Scientific: London, UK, 2009; Volume 6, pp. 171–189. [Google Scholar] [CrossRef]
- Garg, H.; Rani, D. Complex Interval-valued Intuitionistic Fuzzy Sets and their Aggregation Operators. Fundam. Inform. 2019, 164, 61–101. [Google Scholar] [CrossRef]
- Akram, M.; Peng, X.; Sattar, A. A new decision-making model using complex intuitionistic fuzzy Hamacher aggregation operators. Soft Comput. 2021, 25, 7059–7086. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, R.; Huang, H.; Wang, J. Some Picture Fuzzy Dombi Heronian Mean Operators with Their Application to Multi-Attribute Decision-Making. Symmetry 2018, 10, 593. [Google Scholar] [CrossRef]
- Ullah, K. Picture fuzzy maclaurin symmetric mean operators and their applications in solving multiattribute decision-making problems. Math. Probl. Eng. 2021, 2021, 1098631. [Google Scholar] [CrossRef]
- Mahmood, T. A Novel Approach towards Bipolar Soft Sets and Their Applications. J. Math. 2020, 2020, 4690808. [Google Scholar] [CrossRef]
- El-Bably, M.K.; Ali, M.I.; Abo-Tabl, E.-S.A. New Topological Approaches to Generalized Soft Rough Approximations with Medical Applications. J. Math. 2021, 2021, 2559495. [Google Scholar] [CrossRef]
| Symbols | Meanings | Symbols | Meanings |
|---|---|---|---|
| Universal set | Falsity Index of phase term | ||
| Element belonging to Universal set | Score function | ||
| Truth Index/(TI) of amplitude term | Accuracy function | ||
| Abstinence Index /(AI) of amplitude term | Weight vector | ||
| Falsity Index/(FI) of amplitude term | Binomial Coefficient | ||
| CPFS | Unit circle | ||
| Truth Index of phase term | Hesitancy Index | ||
| Abstinence Index of phase term | Complement of CPFV |
| Operators | Ranking and Ordering | ||||
|---|---|---|---|---|---|
| CPFWHM | |||||
| CPFWDHM |
| Operators | Parameters | Ranking and Ordering | ||||
|---|---|---|---|---|---|---|
| CPFWHM | ||||||
| CPFWDHM | ||||||
| Operator | Environment | Results |
|---|---|---|
| CIFWHM operator (current work) | CPFSs | |
| CIFWDHM operator (current work) | CPFSs | |
| CPFHWA Akram et al. [39] | CPFSs | |
| CPFHWG Akram et al. [39] | CPFSs | |
| Akram et al. [60] | CIFSs | Failed |
| Akram et al. [60] | CIFSs | Failed |
| Ullah et al. [36] | CPyFSs | Failed |
| Garg and Rani [59] | CIVIFSs | Failed |
| Zhang et al. [61] | PFSs | Failed |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hussain, A.; Ullah, K.; Pamucar, D.; Vranješ, Đ. A Multi-Attribute Decision-Making Approach for the Analysis of Vendor Management Using Novel Complex Picture Fuzzy Hamy Mean Operators. Electronics 2022, 11, 3841. https://doi.org/10.3390/electronics11233841
Hussain A, Ullah K, Pamucar D, Vranješ Đ. A Multi-Attribute Decision-Making Approach for the Analysis of Vendor Management Using Novel Complex Picture Fuzzy Hamy Mean Operators. Electronics. 2022; 11(23):3841. https://doi.org/10.3390/electronics11233841
Chicago/Turabian StyleHussain, Abrar, Kifayat Ullah, Dragan Pamucar, and Đorđe Vranješ. 2022. "A Multi-Attribute Decision-Making Approach for the Analysis of Vendor Management Using Novel Complex Picture Fuzzy Hamy Mean Operators" Electronics 11, no. 23: 3841. https://doi.org/10.3390/electronics11233841
APA StyleHussain, A., Ullah, K., Pamucar, D., & Vranješ, Đ. (2022). A Multi-Attribute Decision-Making Approach for the Analysis of Vendor Management Using Novel Complex Picture Fuzzy Hamy Mean Operators. Electronics, 11(23), 3841. https://doi.org/10.3390/electronics11233841










