Parity-Check-CRC Concatenated Polar Codes SSCFlip Decoder
Abstract
1. Introduction
- We extend the work of [24] for simplified successive cancellation decoding and propose a PC-CRC-SSCFlip that exploits the role of the distributed parity checks to detect the incorrectly estimated erroneous bit at the early stages in the SSCFlip decoding and corrects that bit. The proposed technique minimizes the average decoding complexity and latency by halting the decoding process with early detection.
- We introduce an error-prone flipping list by incorporating the indices that are more suspected to be in an error [19] and the first bit of each Rate-1 node [11]. The proposed algorithm recalls the parity-bit and narrows down the search space whenever an error is detected. Once an error is detected by a parity bit, the proposed technique considers the bits of FL preceding that parity bit.
- In addition, the proposed PC-CRC-SSCFlip can correct two erroneous bits. It flips the first erroneous decision generated by the initial SC decoding, while the second erroneous decision is flipped in the decoding trajectory determined by the previous flips. This algorithm can be easily employed for more than two erroneous decisions. Although the multi-erroneous decision flipping algorithm improves the BLER performance of SCFlip decoding, it results in high computational complexity. The PC-CRC-SSCFlip immediately terminates the corresponding process with the error detection that minimizing the average decoding complexity and latency of the SCFlip.
2. Preliminaries
2.1. Polar Codes and SC Decoding
2.2. Simplified Successive Cancellation (SSC) Decoding
2.3. Successive Cancellation Flip (SCFlip) Decoding
2.4. Oracle-Assisted Successive Cancellation (OA-SC) Decoding
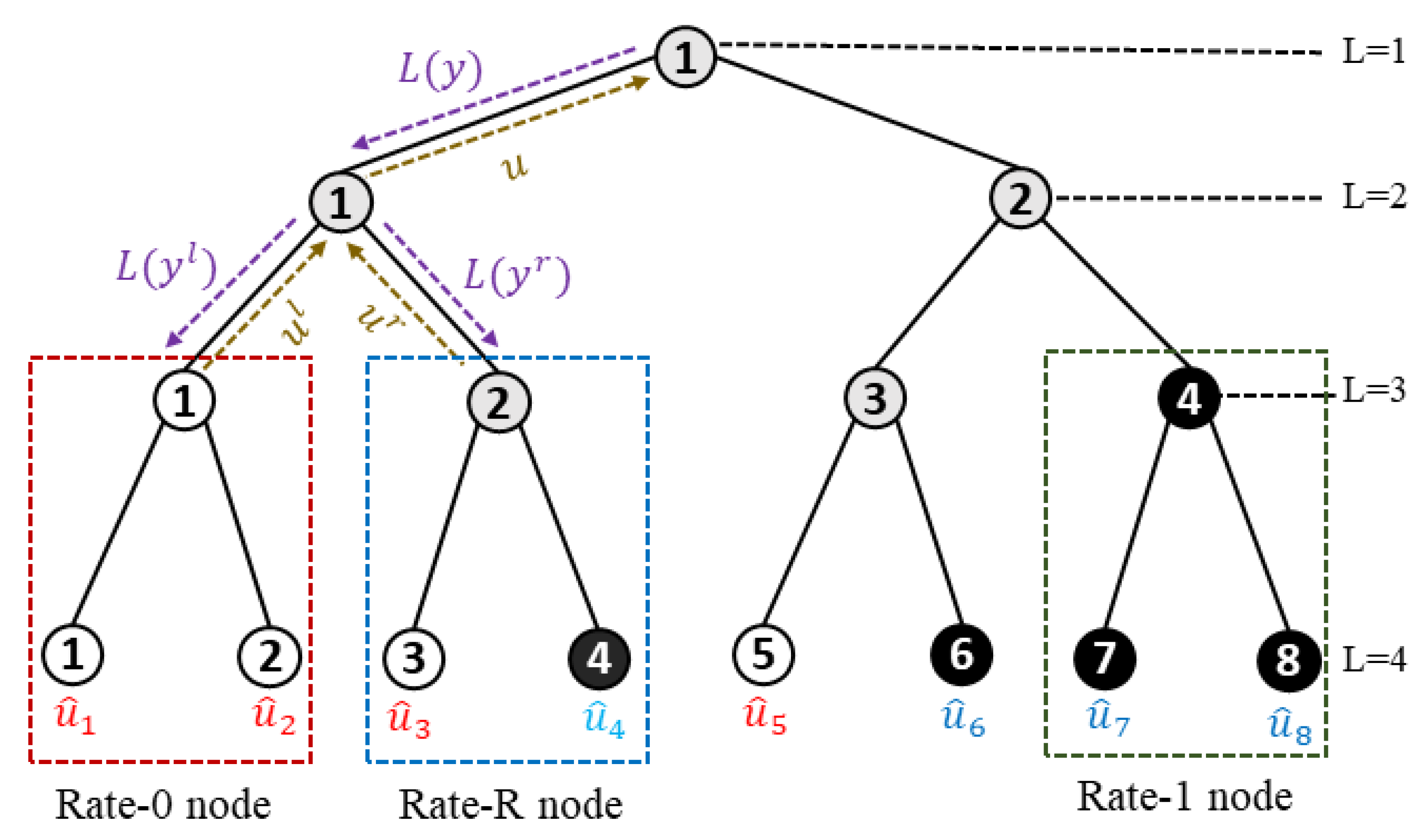
3. Proposed Scheme
3.1. Construction of FL
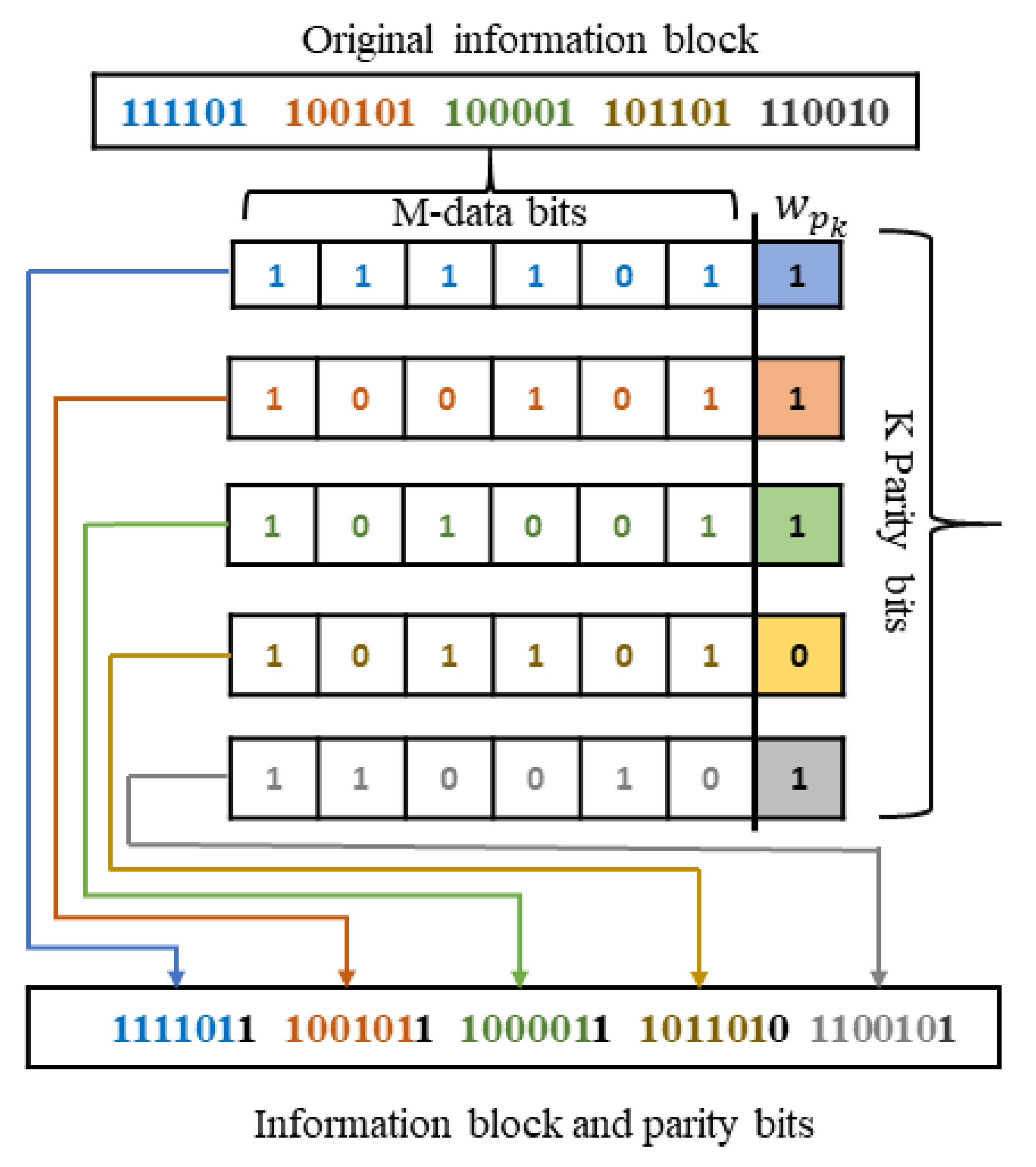
3.2. Parity-Check-CRC-Concatenated Polar Encoder
3.3. Parity-Check-CRC-Aided SSCFlip Decoding
- Initialize the local and global parameters such as the loop control variable (j), information set indices (), parity bit indices (), the maximum number of flipping attempts (), and the number of flips ().
- Algorithm 1 begins decoding with standard SC decoding and obtains the estimated information bits in line 2. Verify the estimated message through the CRC procedure and check the remainder (r) in lines 3 and 4, respectively. If r is zero, break and return . Otherwise, call Algorithm 2 (Calculate_Parity(.)) in line 7.
- (Calculate_Parity(.)) initializes the local parameters and calculates the parity bits in line 4 by iterating through the parity-check vector K. Compare the computed parity with the corresponding in line 5 and set the value. Return the index and value to the calling script.
- Algorithm 1 decides the error-prone bit in line 10 and calls Algorithm 3 (ET_SSCFlip(.)) in line 11 to flip the error-prone bit. The ET_SSCFlip(.) flips and computes the estimated information bit in line 4. The function in Algorithm 3 is used to decide the hard decision through (8).
- The ET_SSCFlip(.) calls Algorithm 2 in line 6 to verify the parity bit. It checks the flag value in line 7 and terminates early once the flag value is zero, and returns to calling script.
- Algorithm 1 checks the returned flag value in line 12. If the flag value is true in line 12, it passes estimated through the CRC procedure and check r in line 14 to verify the estimated message. If r is zero, break. Otherwise, perform the next flipping attempt in lines 9–18.
- Algorithm 4 is used to flip two erroneous decisions. The flipping mechanism for the first incorrectly estimated bit follows the steps of Algorithm 1 in lines 8–17. It further performs the nested i-th () flip in the new trajectory obtained from the previous flips in lines 20–23.where e denotes the error-prone bit.
| Algorithm 1 Single bit flipping PC-CRC-SSCFlip Algorithm |
| Input: , , , , Output:
|
| Algorithm 2 Calculate_Parity() |
|
| Algorithm 3 ET_SSCFlip() |
|
| Algorithm 4 Two bits flipping PC-CRC-SSCFlip Algorithm |
| Input: , , , Output:
|
4. Simulation Results
4.1. Early Stopping Performance and Decoding Latency
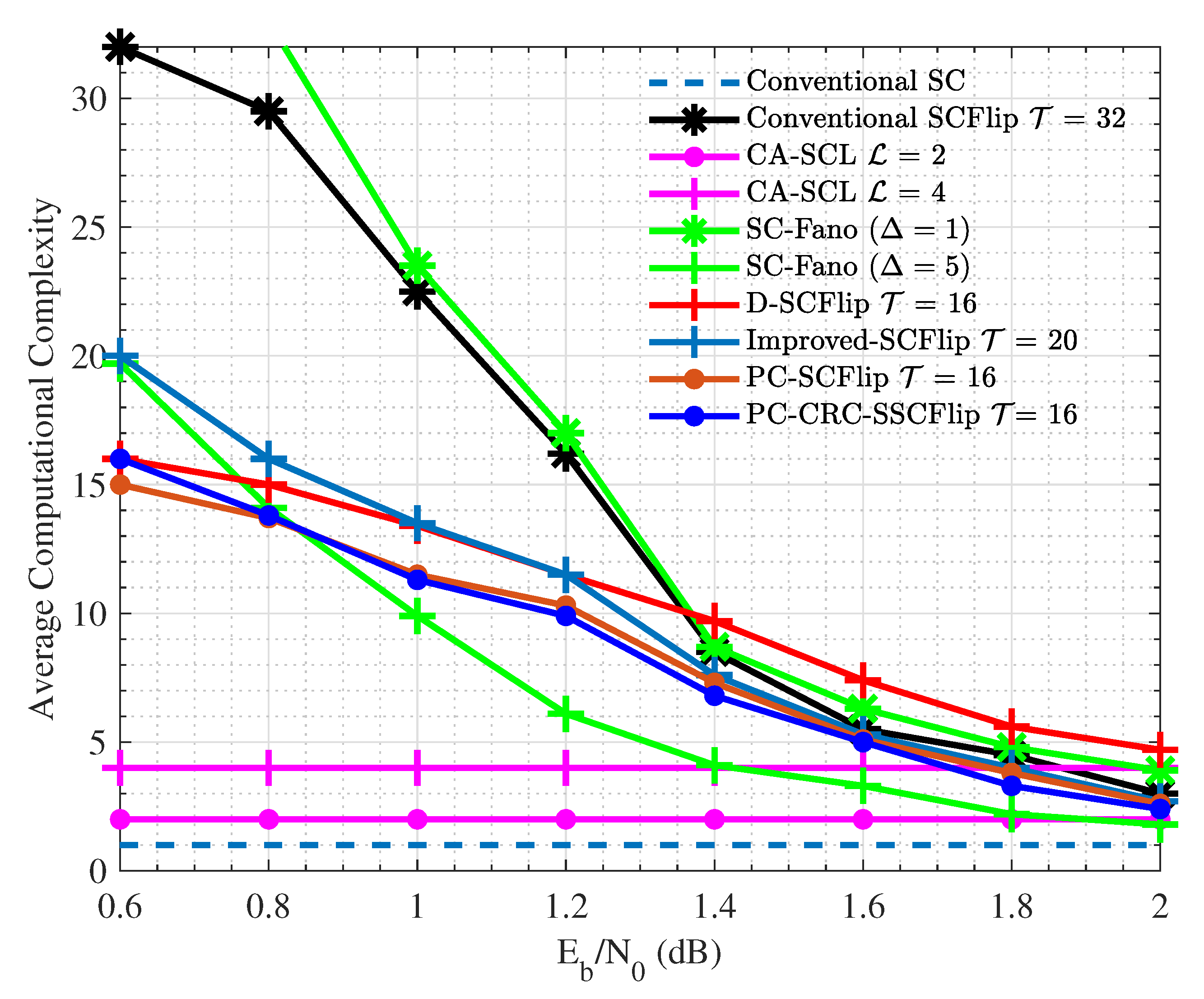
4.2. Average Computational Complexity
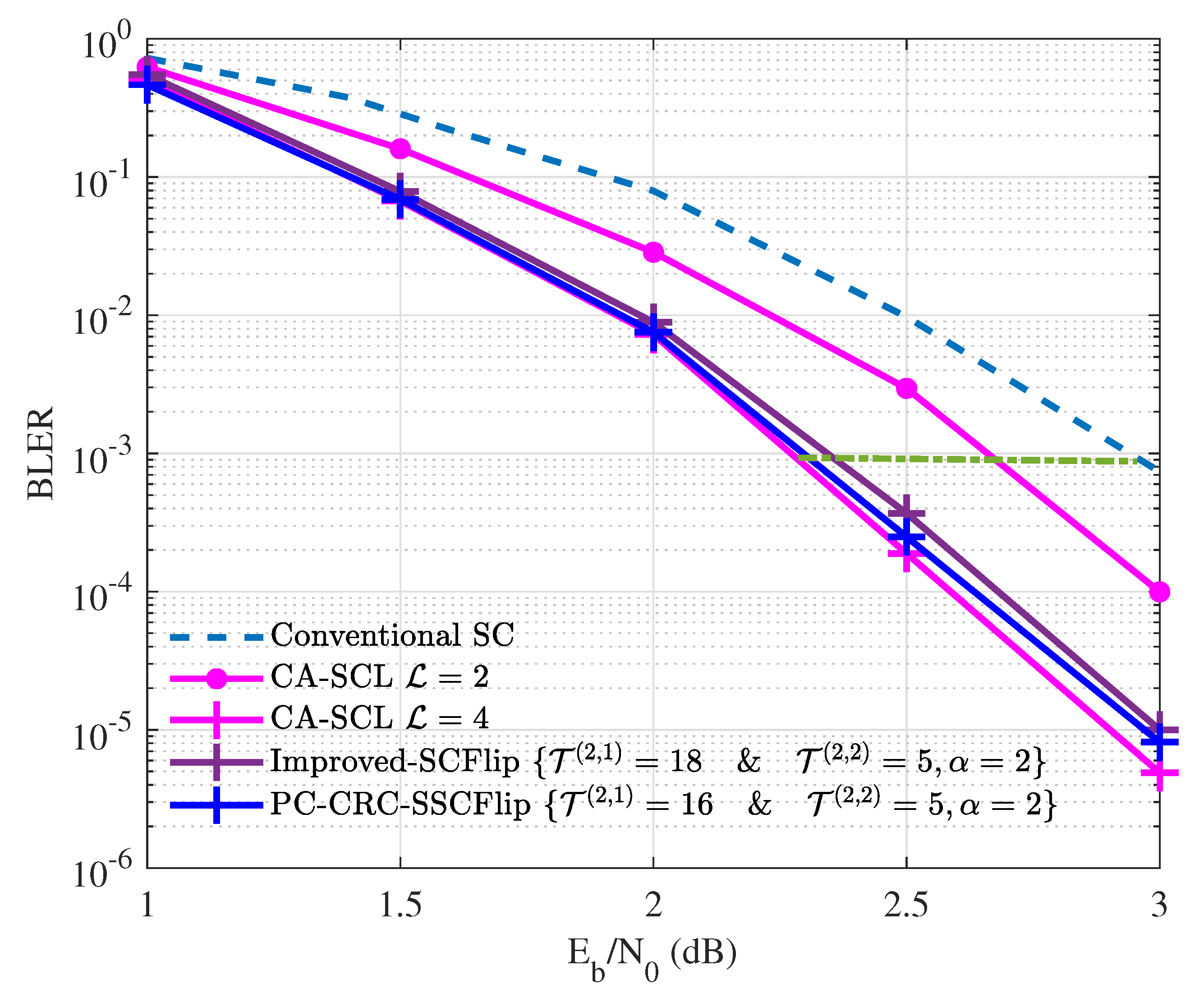
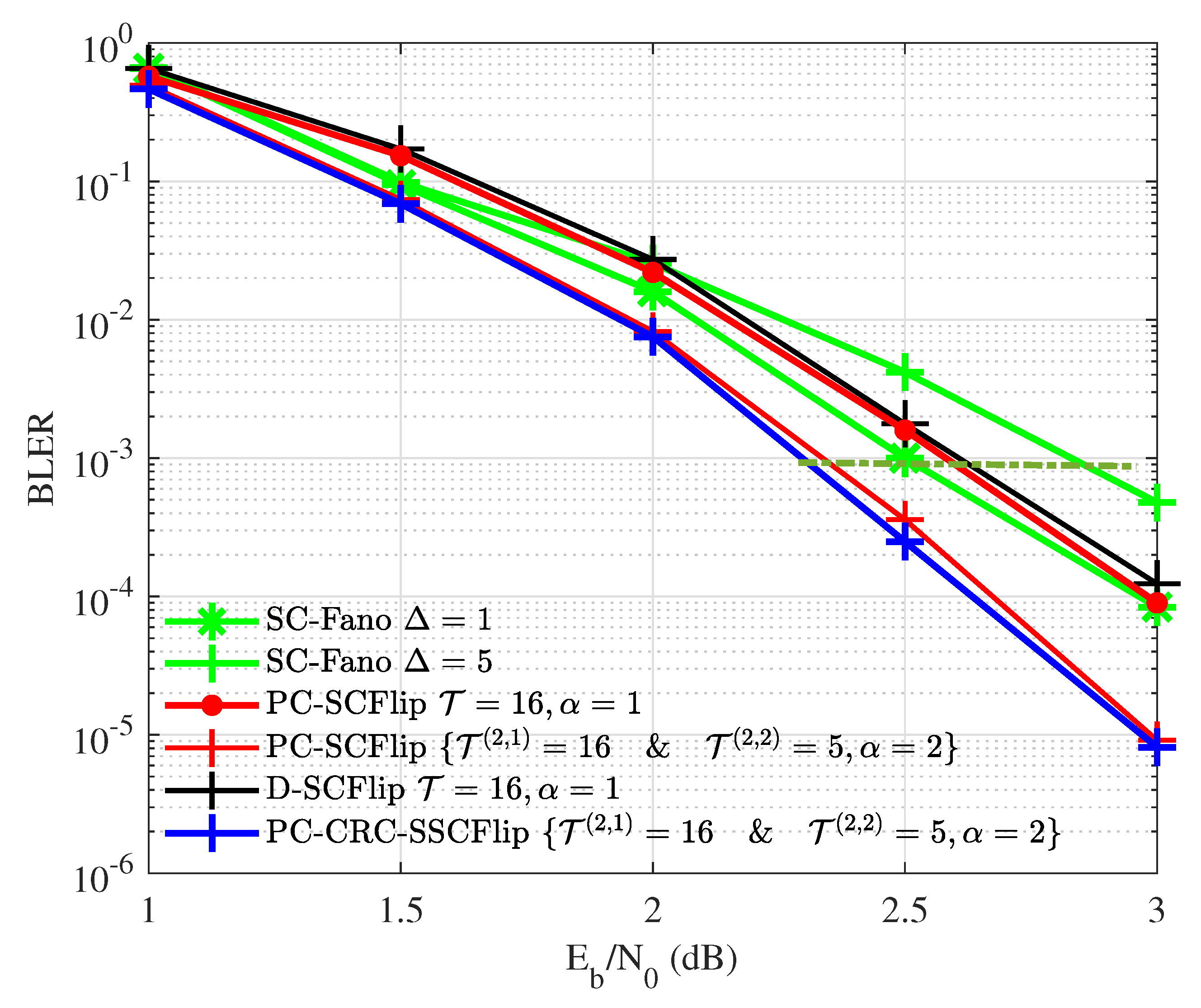
4.3. Block Error Rate (BLER) Performance
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Arikan, E. Channel Polarization: A Method for Constructing Capacity-Achieving Codes for Symmetric Binary-Input Memoryless Channels. IEEE Trans. Inf. Theory 2009, 55, 3051–3073. [Google Scholar] [CrossRef]
- Balatsoukas-Stimming, A.; Giard, P.; Burg, A. Comparison of Polar Decoders with Existing Low-Density Parity-Check and Turbo Decoders. In Proceedings of the 2017 IEEE Wireless Communications and Networking Conference Workshops (WCNCW), San Francisco, CA, USA, 19–22 March 2017; pp. 1–6. [Google Scholar]
- Niu, K.; Chen, K.; Lin, J.; Zhang, Q.T. Polar codes: Primary concepts and practical decoding algorithms. IEEE Commun. Mag. 2014, 52, 192–203. [Google Scholar] [CrossRef]
- Tal, I.; Vardy, A. List decoding of polar codes. In Proceedings of the 2011 IEEE International Symposium on Information Theory Proceedings, St. Petersburg, Russia, 31 July–5 August 2011; pp. 1–5. [Google Scholar]
- Niu, K.; Chen, K. Stack decoding of polar codes. Electron. Lett. 2012, 48, 695–697. [Google Scholar] [CrossRef]
- Niu, K.; Chen, K. CRC-Aided Decoding of Polar Codes. IEEE Commun. Lett. 2012, 16, 1668–1671. [Google Scholar] [CrossRef]
- Tal, I.; Vardy, A. List Decoding of Polar Codes. IEEE Trans. Inf. Theory 2015, 61, 2213–2226. [Google Scholar] [CrossRef]
- Wang, T.; Qu, D.; Jiang, T. Parity-Check-Concatenated Polar Codes. IEEE Commun. Lett. 2016, 20, 2342–2345. [Google Scholar] [CrossRef]
- Afisiadis, O.; Balatsoukas-Stimming, A.; Burg, A. A low-complexity improved successive cancellation decoder for polar codes. In Proceedings of the 2014 48th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 2–5 November 2014; pp. 2116–2120. [Google Scholar]
- Chandesris, L.; Savin, V.; Declercq, D. An Improved SCFlip Decoder for Polar Codes. In Proceedings of the 2016 IEEE Global Communications Conference (GLOBECOM), Washington, DC, USA, 4–8 December 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Zhang, Z.; Qin, K.; Zhang, L.; Zhang, H.; Chen, G.T. Progressive Bit-Flipping Decoding of Polar Codes over Layered Critical Sets. In Proceedings of the GLOBECOM 2017—2017 IEEE Global Communications Conference, Singapore, 4–8 December 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Sarkis, G.; Giard, P.; Vardy, A.; Thibeault, C.; Gross, W.J. Fast Polar Decoders: Algorithm and Implementation. IEEE J. Sel. Areas Commun. 2014, 32, 946–957. [Google Scholar] [CrossRef]
- Giard, P.; Burg, A. Fast-SSC-flip decoding of polar codes. In Proceedings of the 2018 IEEE Wireless Communications and Networking Conference Workshops (WCNCW), Barcelona, Spain, 15–18 April 2018; pp. 73–77. [Google Scholar] [CrossRef]
- Zhou, Y.; Lin, J.; Wang, Z. A New Fast-SSC-Flip Decoding of Polar Codes. In Proceedings of the ICC 2019—2019 IEEE International Conference on Communications (ICC), Shanghai, China, 20–24 May 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Zhou, Y.; Lin, J.; Wang, Z. Improved Fast-SSC-Flip Decoding of Polar Codes. IEEE Commun. Lett. 2019, 23, 950–953. [Google Scholar] [CrossRef]
- Hanif, M.; Ardakani, M. Fast Successive-Cancellation Decoding of Polar Codes: Identification and Decoding of New Nodes. IEEE Commun. Lett. 2017, 21, 2360–2363. [Google Scholar] [CrossRef]
- Ercan, F.; Condo, C.; Hashemi, S.A.; Gross, W.J. Partitioned Successive-Cancellation Flip Decoding of Polar Codes. In Proceedings of the 2018 IEEE International Conference on Communications (ICC), Kansas City, MO, USA, 20–24 May 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Wang, X.; Wang, T.; Li, J.; Zhang, Y. Improved Multiple Bit-Flipping Fast-SSC Decoding of Polar Codes. IEEE Access 2020, 8, 27851–27860. [Google Scholar] [CrossRef]
- Condo, C.; Ercan, F.; Gross, W.J. Improved successive cancellation flip decoding of polar codes based on error distribution. In Proceedings of the 2018 IEEE Wireless Communications and Networking Conference Workshops (WCNCW), Barcelona, Spain, 15–18 April 2018; pp. 19–24. [Google Scholar] [CrossRef]
- Chandesris, L.; Savin, V.; Declercq, D. Dynamic-SCFlip Decoding of Polar Codes. IEEE Trans. Commun. 2018, 66, 2333–2345. [Google Scholar] [CrossRef]
- Ercan, F.; Condo, C.; Gross, W.J. Improved Bit-Flipping Algorithm for Successive Cancellation Decoding of Polar Codes. IEEE Trans. Commun. 2019, 67, 61–72. [Google Scholar] [CrossRef]
- Guo, R.; Chen, K.; Liu, H. Multi-CRC Polar Codes and M-SCFlip-Based Decoding. IEEE Access 2019, 7, 98366–98373. [Google Scholar] [CrossRef]
- Ercan, F.; Tonnellier, T.; Doan, N.; Gross, W.J. Simplified Dynamic SC-Flip Polar Decoding. In Proceedings of the ICASSP 2020—2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020; pp. 1733–1737. [Google Scholar] [CrossRef]
- Dai, B.; Gao, C.; Yan, Z.; Liu, R. Parity Check Aided SC-Flip Decoding Algorithms for Polar Codes. IEEE Trans. Veh. Technol. 2021, 70, 10359–10368. [Google Scholar] [CrossRef]
- Yang, D.; Yang, K. Error-Aware SCFlip Decoding of Polar Codes. IEEE Access 2020, 8, 163758–163768. [Google Scholar] [CrossRef]
- Jan, Q.; Hussain, S.; Zechen, L.; Zhiwen, P.; Nan, L.; Xiaohu, Y. Improved Partitioned Fast-SSC-Flip Decoding for Polar Codes. In Proceedings of the 2022 7th International Conference on Computer and Communication Systems (ICCCS), Wuhan, China, 22–25 April 2022; pp. 382–386. [Google Scholar] [CrossRef]
- Yu, Y.; Pan, Z.; Liu, N.; You, X. Belief Propagation Bit-Flip Decoder for Polar Codes. IEEE Access 2019, 7, 10937–10946. [Google Scholar] [CrossRef]
- Yang, Y.; Yin, C.; Qasim, J.; Hu, Y.; Pan, Z.; Liu, N.; You, X. Noise-Aided Belief Propagation List Bit-Flip Decoder for Polar Codes. In Proceedings of the 2020 International Conference on Wireless Communications and Signal Processing (WCSP), Nanjing, China, 21–23 October 2020; pp. 807–810. [Google Scholar] [CrossRef]
- Jan, Q.; Hussain, S.; Furqan, M.; Pan, Z.; Liu, N.; You, X. A Novel Flip-List-Enabled Belief Propagation Decoder for Polar Codes. Electronics 2021, 10, 2302. [Google Scholar] [CrossRef]
- Alamdar-Yazdi, A.; Kschischang, F.R. A Simplified Successive-Cancellation Decoder for Polar Codes. IEEE Commun. Lett. 2011, 15, 1378–1380. [Google Scholar] [CrossRef]
- Jeong, M.O.; Hong, S.N. SC-Fano Decoding of Polar Codes. IEEE Access 2019, 7, 81682–81690. [Google Scholar] [CrossRef]
- Trifonov, P. Efficient Design and Decoding of Polar Codes. IEEE Trans. Commun. 2012, 60, 3221–3227. [Google Scholar] [CrossRef]
- 3GPP Groups. Final Report of 3GPP TSG RAN WG1 AH1 NR v1.0.0. In Proceedings of the 3GPP TSG RAN WG1 Meeting 88, R1-1701553, Athens, Greece, 13–17 February 2017. [Google Scholar]
- Shukla, S.; Thakur, S.; Hussain, S.; Breslin, J.G.; Jameel, S.M. Identification and authentication in healthcare internet-of-things using integrated fog computing based blockchain model. Internet Things 2021, 15, 100422. [Google Scholar] [CrossRef]
- Hussain, S.; Thakur, S.; Shukla, S.; Breslin, J.G.; Jan, Q.; Khan, F.; Kim, Y.S. A two-layer decentralized charging approach for residential electric vehicles based on fuzzy data fusion. J. King Saud Univ.-Comput. Inf. Sci. 2022, 34, 7391–7405. [Google Scholar] [CrossRef]
- Hussain, S.; Kim, Y.S.; Thakur, S.; Breslin, J.G. Optimization of Waiting Time for Electric Vehicles Using a Fuzzy Inference System. IEEE Trans. Intell. Transp. Syst. 2022, 23, 15396–15407. [Google Scholar] [CrossRef]
- Hussain, S.; Thakur, S.; Shukla, S.; Breslin, J.G.; Jan, Q.; Khan, F.; Ahmad, I.; Marzband, M.; Madden, M.G. A heuristic charging cost optimization algorithm for residential charging of electric vehicles. Energies 2022, 15, 1304. [Google Scholar] [CrossRef]
- Hussain, S.; Ahmed, M.A.; Kim, Y.C. Efficient power management algorithm based on fuzzy logic inference for electric vehicles parking lot. IEEE Access 2019, 7, 65467–65485. [Google Scholar] [CrossRef]
- Hussain, S.; Ahmed, M.A.; Lee, K.B.; Kim, Y.C. Fuzzy logic weight based charging scheme for optimal distribution of charging power among electric vehicles in a parking lot. Energies 2020, 13, 3119. [Google Scholar] [CrossRef]
- Hussain, S.; Lee, K.B.; Ahmed, M.A.; Hayes, B.; Kim, Y.C. Two-stage fuzzy logic inference algorithm for maximizing the quality of performance under the operational constraints of power grid in electric vehicle parking lots. Energies 2020, 13, 4634. [Google Scholar] [CrossRef]

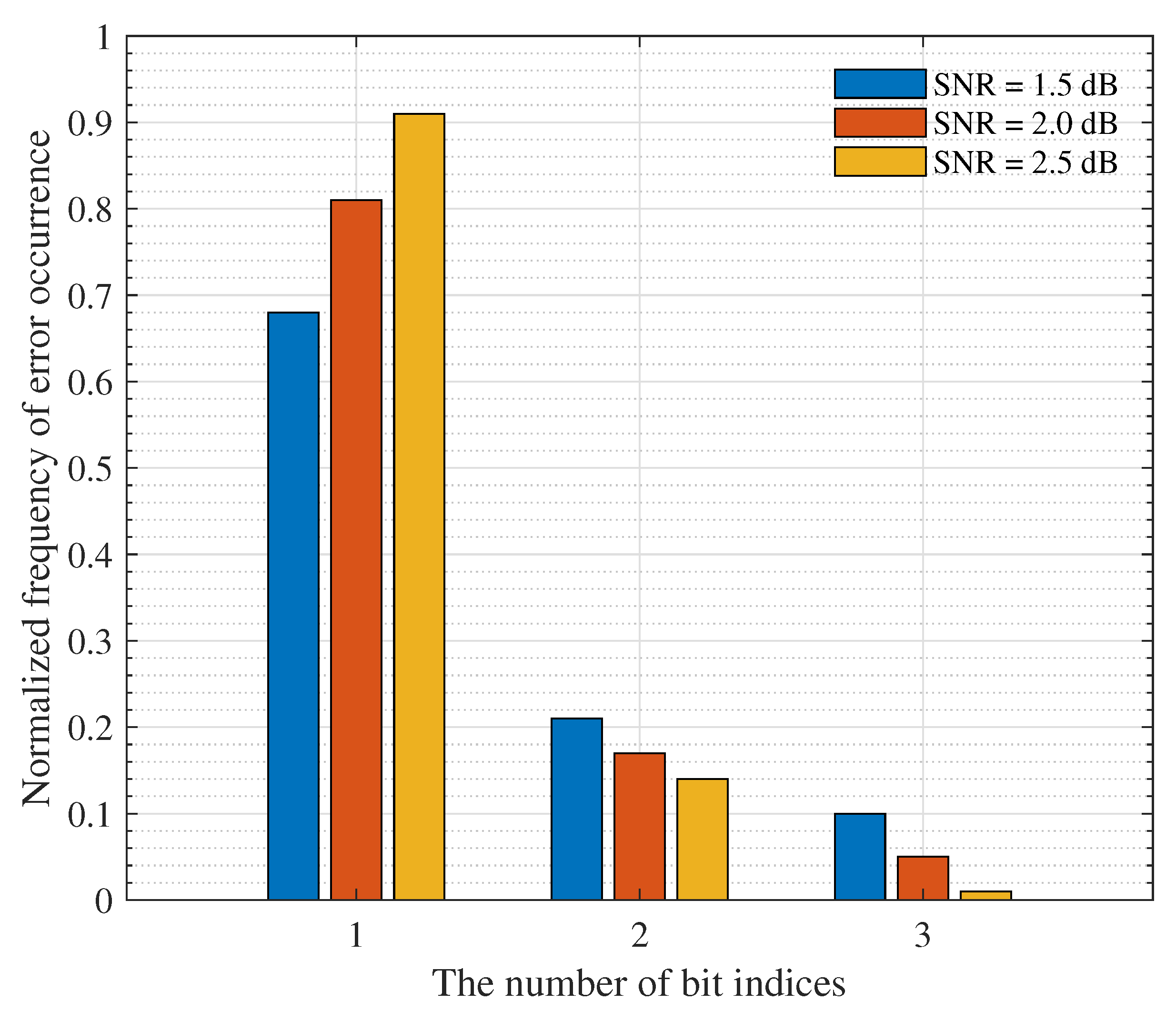


| (dB) | K Parity Bits | |||||||
|---|---|---|---|---|---|---|---|---|
| 1st | 2nd | 3rd | 4th | 5th | 6th | 7th | 8th | |
| 0.2 | 43% | 18% | 16% | 13% | 5% | 1% | 1% | 3% |
| 0.4 | 43% | 16% | 14% | 12% | 6% | 2% | 2% | 5% |
| 0.6 | 41% | 15% | 15% | 10% | 9% | 4% | 1% | 5% |
| 0.8 | 35% | 12% | 14% | 17% | 10% | 4% | 1% | 7% |
| 1 | 35% | 18% | 11% | 13% | 12% | 4% | 1% | 6% |
| 1.2 | 30% | 20% | 16% | 13% | 10% | 5% | 2% | 4% |
| 1.4 | 28% | 17% | 13% | 16% | 12% | 7% | 1% | 6% |
| 1.6 | 24% | 14% | 15% | 16% | 10% | 9% | 1% | 11% |
| 1.8 | 23% | 14% | 11% | 17% | 15% | 8% | 2% | 10% |
| 2 | 20% | 15% | 9% | 17% | 14% | 10% | 2% | 13% |
| Decoding Algorithms | (dB) | |||||
|---|---|---|---|---|---|---|
| 1 | 1.2 | 1.4 | 1.6 | 1.8 | 2 | |
| SCFlip | 46,057 | 33,160 | 17395 | 11,256 | 9210 | 6141 |
| Improved SCFlip | 27,634 | 23,540 | 15,557 | 10,849 | 8188 | 5526 |
| PC-CRC-SCFlip | 9211 | 8410 | 5607 | 4005 | 3043 | 2082 |
| Decoding Methods | SC-Flip [9] | SC-Fano ( = 1) [31] | SC-Fano ( = 5) [31] | Improved SCFlip [10] | D-SCFlip [20] | PC-SCFlip [24] | PC-CRC-SSCFlip | |
|---|---|---|---|---|---|---|---|---|
| Required * (dB) | 2.7 | 2.5 | 2.9 | 2.6 | 2.6 | 2.6 | 2.6 | |
| Complexity () | LLR compute. | 3.072 | 4.096 | 2.048 | 2.8672 | 3.072 | 2.015 | 1.766 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jan, Q.; Hussain, S.; Furqan, M.; Pan, Z.; Liu, N.; You, X. Parity-Check-CRC Concatenated Polar Codes SSCFlip Decoder. Electronics 2022, 11, 3839. https://doi.org/10.3390/electronics11233839
Jan Q, Hussain S, Furqan M, Pan Z, Liu N, You X. Parity-Check-CRC Concatenated Polar Codes SSCFlip Decoder. Electronics. 2022; 11(23):3839. https://doi.org/10.3390/electronics11233839
Chicago/Turabian StyleJan, Qasim, Shahid Hussain, Muhammad Furqan, Zhiwen Pan, Nan Liu, and Xiaohu You. 2022. "Parity-Check-CRC Concatenated Polar Codes SSCFlip Decoder" Electronics 11, no. 23: 3839. https://doi.org/10.3390/electronics11233839
APA StyleJan, Q., Hussain, S., Furqan, M., Pan, Z., Liu, N., & You, X. (2022). Parity-Check-CRC Concatenated Polar Codes SSCFlip Decoder. Electronics, 11(23), 3839. https://doi.org/10.3390/electronics11233839







