Abstract
Energy management is crucial for various activities in the energy sector, such as effective exploitation of energy resources, reliability in supply, energy conservation, and integrated energy systems. In this context, several machine learning and deep learning models have been developed during the last decades focusing on energy demand and renewable energy source (RES) production forecasting. However, most forecasting models are trained using batch learning, ingesting all data to build a model in a static fashion. The main drawback of models trained offline is that they tend to mis-calibrate after launch. In this study, we propose a novel, integrated online (or incremental) learning framework that recognizes the dynamic nature of learning environments in energy-related time-series forecasting problems. The proposed paradigm is applied to the problem of energy forecasting, resulting in the construction of models that dynamically adapt to new patterns of streaming data. The evaluation process is realized using a real use case consisting of an energy demand and a RES production forecasting problem. Experimental results indicate that online learning models outperform offline learning models by 8.6% in the case of energy demand and by 11.9% in the case of RES forecasting in terms of mean absolute error (MAE), highlighting the benefits of incremental learning.
1. Introduction
Forecasting is a key branch for the proper and smooth operation of the energy industry. As a matter of fact, energy forecasting may refer to various quantities in the energy environment, the main ones being grid-level or building-level load forecasting [1], energy production forecasting from renewable energy sources (RES) such as photovoltaic (PV) parks, wind farms and hybrid systems [2], and energy price forecasting [3], among others. The generated forecasts are used by different stakeholders in all segments of the energy sector for planning and operation purposes, both from the aspect of the power system and from the aspect of a business entity [4]. Moreover, the formation of energy communities during the last years also intensifies the need for accurate forecasts, as local energy communities are heavily reliant upon load demand forecasts to schedule energy usage ahead of time in order to achieve higher self-sufficiency levels [5].
On the one hand, forecasting consumption in buildings is very important to maintain an optimal level of energy performance [6]. The immense technological progress in terms of equipment with the evolution of Internet of things (IoT) devices and smart metering sensors has resulted in a digital transformation of buildings, which can be monitored by smart energy management systems and digital twin platforms [7,8]. However, the existence of all this data generated needs to be supported by intelligent algorithms and models offering prescriptive and descriptive and predictive analytics. In this context, many time-series forecasting models have been developed for consumption prediction in buildings, so as to provide continuous monitoring and facilitate the development of data-driven operational strategies.
On the other hand, RES forecasting is vital for several key activities of the energy sector. As the penetration of RES and especially wind and solar energy has increased in the last few years due to decarbonization goals set at the European and global levels [9], solid forecasting models lead to a reliable integration process of RES production [10]. More specifically, solar-based generated power accounted for 3.6% of the electricity mix in 2021, remaining the third largest renewable electricity technology behind hydropower and wind, and this percentage is expected to rapidly increase in the next few years [11]. In this context, forecasting of PV production can be exploited for several purposes and tasks, including energy management of smart grids, ensuring power unit commitment, scheduling and dispatching [12], dynamic pricing, and predictive maintenance [13].
In the case of both RES production forecasting and building consumption forecasting, several studies can be found in the existing literature [14,15]. In general, there are two broad categories of methods: physical methods and data-driven methods. Physical methods rely on weather data, such as surface roughness, temperature, relative humidity, and wind speed, as well as key design parameters of the building or the PV panel, and they use physical equations to generate the forecasts [16]. On the contrary, data-driven methods rely on historical data of time series in order to provide predictions, and they are split into statistical models and machine learning (ML) models, which may be combined with the development of hybrid models to achieve increased accuracy [17].
Although the breakthrough in model development has been rapid and the predictive performance of models is constantly improving, there is a significant gap in the field of ML and DL model development. Most of the studies in the field focus on developing models in a static fashion. This means that models are trained once using a set of training data and they are evaluated on another set of hidden data, which is called test set. This is the most common approach for evaluating the potential of an ML/DL model, but it fails to address the aspect of online re-training of the model to further improve its accuracy. This also creates another gap, as there is not any evidence on how the proposed models would operate as part of a service or application. The process of employing a model in an intelligent service by applying incremental re-training is a fundamental step towards the successful deployment in production.
This study aims to address the above-mentioned gap by assessing the impact of applying incremental (or online) learning to DL models in the energy domain. In this context, an integrated methodological framework is provided describing the whole data life cycle, from connection to the smart-metering equipment to the generation of the forecasts through incrementally trained models in a unified architectural schema. Moreover, the proposed training procedure is applied to a real use case, i.e., a microgrid in Italy composed of a multi-story building and a PV system. One of the most popular DL algorithms, the multilayer perceptron (MLP), is used to develop energy forecasting models for the consumption of the building and the production of the PV system. The online training framework is compared with the traditional training process in order to evaluate the benefits of incremental learning in these time-series forecasting problems.
Apart from this introductory section, the rest of the paper is structured as follows. Section 2 introduces the problems of RES forecasting and building consumption forecasting and provides a short literature review on these topics. Section 3 presents the methodological approach in more detail, presenting the MLP used for developing the models, the basic principles of incremental learning, and the proposed architecture for incremental learning. Section 4 includes the experimental application of incremental learning in PV production and building consumption forecasting. Finally, Section 5 concludes the paper and provides directions for future research.
2. Related Work
2.1. RES Forecasting
Over the last decade the number of forecasting methods that have been proposed to forecast energy generation from RES has significantly increased. This is quite reasonable considering that RES forecasting is a key analytic service for the support of several decisions related to microgrid management, flexibility planning, demand-response mechanisms development, pricing in the energy market, and many others. Most methods have focused on wing and solar power forecasting, as these two sources are the most cost-efficient, resulting in their high degree of penetration.
Focusing on PV production forecasting, many popular regression models have been proposed, including traditional time-series ARIMA models [18], decision-tree-based models [19], support vector machines (SVM) [20], and artificial neural networks (ANNs) [21], among others. Recent studies indicate that DL models result in better forecasting accuracy compared to purely statistical models and simple ML models, but this cannot be generalized for all cases [22]. Moreover, various techniques have also been tested, either with the aim of increasing forecasting accuracy through ensembling [23] or meta-learning [24], or with the aim of addressing data scarcity [25].
In terms of determining the most influencing factors for PV production models, literature has shown that, as expected, global horizontal irradiance (GHI) is the main driver for estimating the energy produced by a solar panel [26]. However, solar radiation is not the only factor exploited for predicting PV production, as other variables such as air temperature, cloud coverage, and humidity also affect the operation of the PV system through complex nonlinear relationships [27,28]. Apart from these, it is evident that for DL models, a significant input feature is historical data from the PV production time series. Finally, another distinction of ML/DL models for PV forecasting is their dependence on numerical weather predictions (NWP). Short-term forecasting models are usually trained and used without NWP, while models with longer forecasting horizons require integration with a weather prediction service [29].
2.2. Building Consumption Forecasting
Buildings account for 40% of the global energy consumption and greenhouse gas (GHG) emissions, giving them a pivotal role in the recent climate crisis and global warming [30,31]. Thus, the ability to predict the electrical consumption of a building or a specific area of the building is extremely useful in the context of the effort made to increase energy efficiency. However, accurately forecasting a building’s energy consumption is not a simplistic task, as there are a great variety of factors that influence the energy needs such as the building’s enclosed structure, the occupancy and energy use patterns of the occupants, and outdoor air temperature and humidity levels [32].
Many studies can be found in the existing literature proposing forecasting methods for short-term and mid-term consumption forecasting [33]. Some recent specialized reviews for electrical energy forecasting in buildings have been provided by Amasyali and El-Gohari [34] and Sun et al. [29]. More specifically, as stated in Section 1, there are two main approaches for predicting a building’s energy consumption: the physical modeling approach and the data-driven approach. On the one hand, physical models apply thermodynamic equations in order to calculate the consumption of an energy subsystem through energy simulations. Such models are implemented in specific energy simulation tools (e.g., EnergyPlus). Although they can be very accurate, they require specific information as input that is not always available to the user. On the other hand, data-driven models do not calculate the consumption via complex equations, but they rely on historical consumption data to extract usage patterns of the building using statistical or ML/DL-based models [35].
Regarding the second category, several models have been evaluated and tested for this problem. For example, in [36], the authors compare SVMs and ANNs to predict a building’s lighting energy consumption, while in [37], the authors compare a purely statistical auto-regressive model and an SVR to forecast building consumption. Literature has not indicated that a specific model outperforms the others as a rule of thumb but, as in most forecasting tasks, DL models are expected to perform better if there are plenty of data available.
2.3. The Need for an Incremental Learning Approach
In the last few years, the amount of generated data has been continuously increasing. The energy sector is not an exception, since the multitude of synchronously installed smart meters generate a large amount of energy consumption data, RES generation data, grid energy flows data, and other energy data [38,39]. Furthermore, according to Sarmas et al. [23], access to open data has been simplified, opening new opportunities for the development of ML models and data-driven approaches. At the same time, however, the generated data from all these heterogeneous IoT devices bring new challenges, as well as opportunities to develop multi-scale systems and data analytics to enhance decision making [40].
A significant dimension of developing intelligent systems is their ability to continuously learn and adapt to new conditions in their environment. According to Bouchachia et al. [41], these systems must incorporate adaptable learning algorithms and continuous adaptation processes, making them capable of responding to new conditions as part of their learning process, just like any intelligent living organism that learns incrementally and dynamically from any changes in its environment [42]. In order to enable the above-mentioned behavior, ML models should be periodically re-trained when new data are available, thus adjusting their behavior when new patterns are detected.
However, although several studies have focused on developing forecasting models for energy-related time-series problems, only few of them have focused on the impact of incremental learning on the forecasting accuracy of the models. One of these studies has developed an incremental learning algorithm called regression enhanced incremental self-organizing neural network (RE-SOINN) in order to predict solar irradiance, finding that the proposed algorithm achieves higher accuracy compared to widely used models such as the persistence model, the exponential smoothing model, and ANNs [43]. Similarly, Qiu et al. [44] used incremental learning to increase accuracy in electrical load forecasting. More specifically, the authors proposed a hybrid incremental learning approach composed of discrete wavelet transform (DWT), empirical mode decomposition (EMD) and random vector functional link networks (RVFL), which demonstrated better forecasting accuracy compared to eight benchmark models.
Summarizing all the above statements, there is a clear gap in evaluating how incremental learning can enhance the accuracy of energy forecasting models, considering both RES production and building load. More specifically, most of the above-mentioned studies have focused on comparing different models and algorithms, on evaluating the influence of different input features, and on testing models on different forecasting horizons. However, they do not assess the possibility of incrementally training the developed models in order to further increase their abilities. Thus, the novelty of this study lies in the evaluation of how continuous periodic re-training boosts ML models for short-term time-series forecasting problems in the energy sector.
3. Methodological Approach
The studies presented in Section 2 pave the way towards further examining the impact of incremental learning in forecasting problems. In this section, the methodological approach is described in detail. Firstly, the MLP model is presented in detail, as it is the basis of the incremental learning approach. Then, the incremental learning approach is analyzed along with the proposed architecture.
3.1. Multi-Layer Perceptron
The multi-layer perceptron (MLP) is a feedforward ANN consisting of a system of interconnected neurons, which are generally referred to as nodes. These nodes are connected by weights and they are activated by a simple non-linear activation function. Since the activation function is non-linear, the MLP is able to provide solutions to non-linear problems. The architecture of the MLP includes an input layer and an output layer, as well as one or more hidden layers. Each node of the MLP is connected to every node in the next layer and the previous layer; thus, it can be considered as a fully connected network [45]. An example of an MLP network with two hidden layers is presented in Figure 1. As a general rule, the output of each hidden and output node is determined by the sum of all the weighted values of the preceding layer’s nodes. Afterwards, the result passes through the activation function [46]. The training of the MLP determines the values for each weight and resolves the network’s modeling. It is based on an algorithm called backpropagation, which computes the gradient of the cost function with respect to the weights of the nodes, aiming to minimize the cost function by adjusting the network’s weights and biases [47].
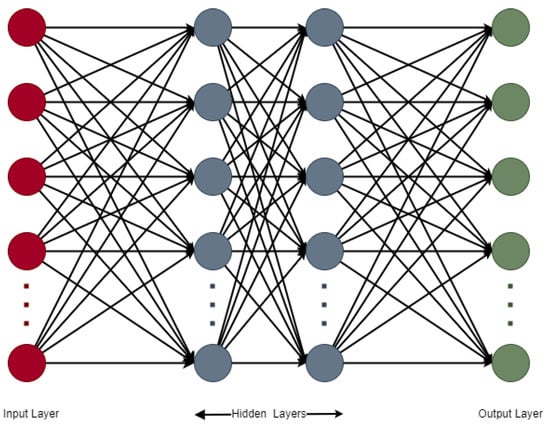
Figure 1.
The architecture of the MLP, which is a fully connected network that includes an input layer, two hidden layers, and an output layer.
The main MLP application goal is to find a function f that associates the input nodes in X to the output vectors in Y(). In that case, , , n is number of training patterns, k the number of input nodes/variables, and j the number of output nodes/variables. During the process of training the model, the function f is optimized. The optimization comes by achieving the lowest possible margin in the output given the input vectors in X to the target values in Y. The function f is based on the adjustable weights of the network’s nodes, and the matrices X,Y represent the training data. The ideas behind the method used for the approximation and prediction are very much alike. The MLP only has one output node, and the dimensions of matrices X and Y in the generic application are and , respectively, since one variable is modeled from the input data. The prediction requires training the model to output the future value of a variable given an input vector containing earlier values [45].
By selecting a suitable set of connecting weights and transfer functions, it has been shown that an MLP is able to estimate all the perceptible functions within the input and output nodes after choosing the appropriate activation/transfer functions and weights [48]. By training the MLP, the network learns the current set of training data, which formulates the input and related output nodes. During this process of training, the MLP is constantly introduced to the training data; by adjusting the weights, the optimal input–output mapping occurs. The training/learning process of a MLP is performed in a supervised approach, and when the desired output is not met during a certain input vector, an error signal is identified as the difference between the desired and real output. During the training process, this error signal is used to establish the adjustable weights in order to reduce the error signal. As a result, the MLP is able to extrapolate to unknown but related input data when trained with the appropriate training data [45].
3.2. Incremental Learning
Most traditional ML and DL methods use offline learning, meaning they ingest training data at once to construct a static model. Incremental learning, or online learning, is a branch of ML that involves processing incoming data from a data stream continuously and in real time. Thus, a model can be trained multiple times and can be iteratively re-adjusted to new data, while still considering older data as well.
Training the model incrementally offers multiple advantages and solves many problems of the traditional training methods. Incremental learning algorithms can be used to solve the problem of shortages in computation power. By providing the data in the form of batches, the model is able to fit to data quickly and efficiently, without the need for a computationally powerful machine. Additionally, at several occasions, the size of training data may be unknown or of very large volume, thus making storage impossible. Exploiting incremental learning, a substantial solution is provided by offering the ability to ingest data in batches and re-train the model. As a result, the whole dataset does not need to be stored and can be gradually stockpiled and used. This method is also beneficial when dealing with streaming data or with data that is provided in small chunks and not in one unified pile. Furthermore, incremental learning helps to implement a system that gradually improves in terms of accuracy whenever new examples emerge, offering an appealing approach to real life problems and actual scenarios, where changes in the data distribution are continuous and real-time monitoring of environments is important [49].
However, incremental learning brings some difficulties that are important to acknowledge. In the process of training and learning new data, one of the main challenges faced by incremental learning algorithms is catastrophic forgetting, which is the tendency of an ANN to completely and abruptly forget previously learned information upon learning new information [50]. For that reason, the behavior of the new obtained values should be monitored closely. Some simple solutions include rehearsal and pseudo-rehearsal methods, i.e., re-training the model on a part of old data when new data is introduced [51]. Another obstacle of online learning is the concept drift. Concept drift means that the properties of the target variable, which the model is trying to predict, change over time in unforeseen ways. This causes problems because the predictions become less accurate as time passes. Concept drift can be avoided by using tracking solutions and updating the set using features of the data in old classes [52].
3.3. Proposed Framework
In this section, we introduce the proposed methodological framework that satisfies the needs for incrementally training the proposed ML models, as well as the methods used to implement it. A high-level representation of the incremental learning framework is presented in Figure 2. Firstly, the framework includes a continuous connection to an MQ telemetry transport (MQTT) broker for collecting data streams in real time, as well as the operations of data pre-processing, cleaning, and analysis. The collected data is aggregated to an hourly format and stored in a database. Thus, data can be loaded from the database once per day in order to periodically re-train the models. The re-training process requires only the most recent data and not the whole dataset, thus offering scalability and reduced training time. The updated models are then stored and can be used directly to produce hourly day-ahead forecasts. More details on the process of online learning are given in the following paragraphs.
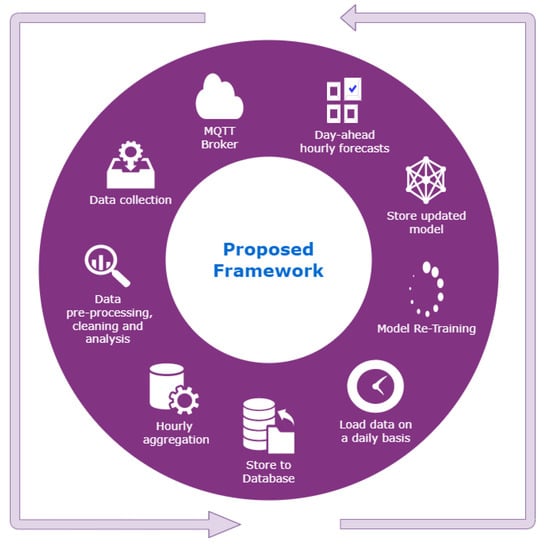
Figure 2.
The proposed framework for incremental learning.
First, as noted above, a connection to a continuous data stream in real time is required, which, in our case is provided via an MQTT broker. The MQTT is a lightweight, publish–subscribe, machine to machine network protocol for message queue/message queuing service. This software component communicates with smart metering equipment and runs on a computing machine on-premises or in the cloud. The broker acts as a post office, since it sends and receives information [53]. Connecting to an MQTT broker is done by using the broker’s address and credentials. In the next step, all collected data are aggregated hourly and pre-processed to detect any unusual details. In this use case, the pre-processing operations focus on missing data and outliers. For instance, when data are missing for a specific hour, missing values are filled by using a special type of linear interpolation averaging past days’ data during the same hour. Additionally, since data originate from a smart meter, some false data may be detected. In order to handle these outliers, a check is performed, replacing negative or unjustifiably high values. This pre-processing routine results in a uniform dataset that can be fed to the ML models.
Consequently, data are stored in a time-series database to allow for easy and direct querying. In this specific use case, a PostgreSQL database is used to store and retrieve the hourly aggregated information. Thus, data can be loaded on a daily basis to re-train ML models. Regarding ML models, the “MLPRegressor” model of the sklearn.neural_network library is used [54]. The proposed framework involves fitting the model to a chunk of already collected data (one year of data), creating a solid baseline model that has learned the patterns of a calendar year. After that period, the baseline model is periodically re-trained once per day using the continuous flow of data previously stored in the time-series database. Stored data is given to the model on a daily basis in mini-batches of 24 values. Consequently, the model is re-trained with the most recent data at the end of the day. As a result of this process, the model keeps adjusting to new data every day and is able to cope with changes in the data distribution in near real time. At the same time, the stored model generates day ahead-forecasts by using the most recent records of the database.
Moving to the core of the incremental learning process, it is noteworthy that in order to perform the training process in an incremental fashion, the function partial_fit() is used instead of the traditional fit() method. The traditional fit method clears the model and provides a different initialization of the weights each time used. On the contrary, the partial_fit method does not completely clear and re-initialize the model, but it updates it with respect to the data provided [55]. The small portion of data (usually a data stream) that is provided as input to the partial_fit method is called a mini-batch. Thus, the ability to learn incrementally from a mini-batch of instances is key to out-of-core learning, as it guarantees that at any given time there will be only a small amount of instances in the main memory [56].
As mentioned above, the algorithm used for evaluating incremental learning is the MLP regressor of Scikit-Learn. The selection of the MLP regressor was made because of its ability to support online learning in mini-batches, as compared to several other ML models. A very important step of the learning process is the selection of optimal model hyper-parameters, as this offers a significant boost to the accuracy of the ML models. The selected hyper-parameters for the case of PV production and electricity consumption are presented in Table 1.

Table 1.
The selected hyper-parameters for the PV production and the electricity consumption forecasting models.
4. Use Case
The incremental learning framework was evaluated on a real case study located in the distribution grid owned by ASM Terni S.p.A. ASM is a public utility owned by the municipality of the city of Terni, in Umbria, Italy, operating in the electrical, gas, water, and waste management sectors. Through its business unit Terni Distributione Elettrica (TDE), it covers the role of distribution system operator (DSO), managing about 65,000 end users, 700 secondary substations, and three primary substations. Every year TDE supplies electric users with about 400 GWh, half of which is produced by RES.
In the context of this study, a portion of Terni’s low-voltage electricity grid is used to test the proposed models, including two secondary substations: a building, namely, the headquarters of ASM, and a PV production plant of 185 kW. The headquarters of ASM comprise a 4050 m three-story office, a 2790 m single-story space, consisting of technical offices, a computer center, an operation control center, and a 1350 m warehouse. The annual building consumption is about 650 MWh, mainly due to lighting, HVAC, and powering computers and data servers.
The infrastructure for data sharing consists of a supervisory control and data acquisition (SCADA) system used by ASM specifically for research and innovation activities. Data are transmitted from the sensors via the MQTT and Modbus protocol to the broker located in ASM’s headquarters. The sensors communicate in near real-time with a time resolution of 1 second. Data are then transmitted, again via the MQTT protocol, to an AVEVA Historian database, which is capable of collecting up to 2 million tags, storing and aggregating the data, guaranteeing the authenticity of the original data, and preventing manipulation of historical data. To access this data, the Microsoft SQL Server interface is used.
4.1. Datasets
Two different dataset were used in the context of this study. The first dataset is a PV production time series, accompanied by weather data for the respective dates, while the second dataset includes the consumption of the investigated building. Although raw PV production and building consumption data comes at irregular time intervals through the MQTT protocol, appropriate aggregations have been applied transforming the data resolution to hourly level. On the other hand, weather data (air temperature, humidity, cloud coverage, and solar radiation) were obtained in hourly resolution from a weather service. Therefore, all the data used are hourly and have a duration of about 2 years and nine months (23,616 h). A visualization of the PV production time series is presented in Figure 3, while the consumption of the building is visualized in Figure 4.
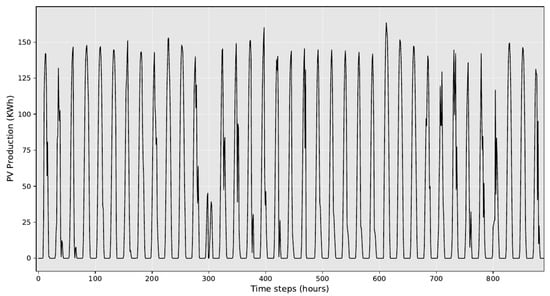
Figure 3.
A visualization of the PV production time series.
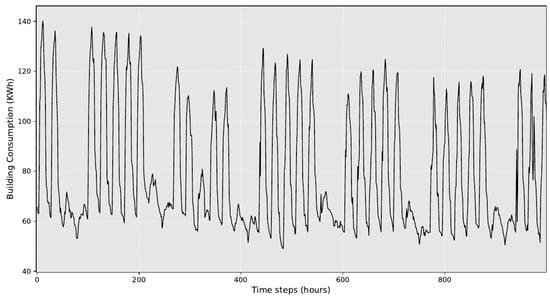
Figure 4.
A visualization of the building consumption time series.
It is obvious that the PV production time series has both daily and yearly patterns due to its dependency on solar radiation. Thus, the position of the sun during the day directly affects the performance of the PV system, and at the same time, seasonal weather differences affect the production at a yearly level, resulting in much more energy production during the summer period compared to winter. On the other hand, as seen in Figure 4, the building consumption time series is more irregular in general, being affected by human factors. An indicative example is the difference observed between weekdays and weekends due to the difference in occupancy levels (during the weekends, the offices are closed and the building is vacant). The same applies for holidays periods.
In general, PV production is stochastic and is mainly influenced by weather conditions. Consequently, the main features driving the performance of the PV forecasting model are seasonal features, such as the hour of the day and the month of the year, as well as weather features, mainly solar radiation. The correlation plots between the PV production and the weather features time series are presented in Figure 5. These plots confirm that PV production is strongly related with solar radiation. On the other hand, the other weather features, namely air temperature, cloud coverage, and relative humidity, are also related with PV production, but to a much weaker extent. Considering all these factors and after experimenting with several combinations of input features, the selected input features for the PV production forecasting model are the following: (a) air temperature, (b) relative humidity, (c) global radiation, (d) month of the year, and (e) hour of the day.
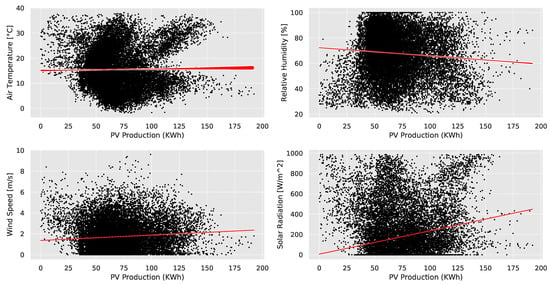
Figure 5.
PV capacity factor (%) compared with solar radiation (), temperature (), cloud coverage, and wind speed (m/s).
On the other hand, the consumption of the building is not strongly affected by weather features. As seen in Figure 4, the consumption time series is more stochastic than the PV production one, as it is influenced mainly by human behavior and use patterns of the building. Thus, consumption patterns vary during the two years and nine months time span. Nevertheless, electricity consumption demonstrates strong seasonality patterns. Figure 6 presents the auto-correlation function (ACF) of the electricity consumption time series across a week (168 h lag). The most interesting insight is that consumption patterns tend to repeat for the same hour of different days. This has led to using past electricity consumption data as input features in the consumption forecasting model. Another useful observation is that similar patterns are detected during weekends and weekdays, highlighting that the day of the week is another useful feature. With respect to the above insights, the selected input features for the electricity consumption forecasting model are the following: (a) hour of the day, (b) day of the week, (c) month of the year. (d) electricity consumption at the same hour last two days, and (e) electricity consumption at the same hour and same day last week.
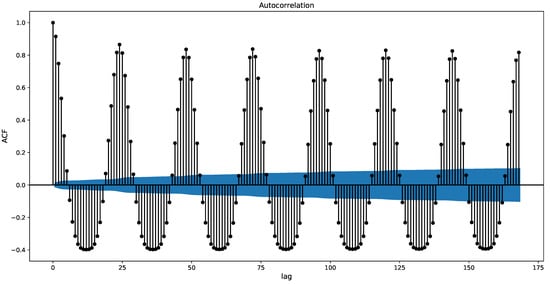
Figure 6.
Auto-correlation function (ACF) of the building’s electricity consumption across the week (168 h lag).
4.2. Evaluation Metrics
Ensuring that the proposed model can achieve accurate forecasts is a prerequisite for evaluating the potential of exploiting incremental learning. In this context, the performance of the MLP models for both PV production and building consumption is evaluated with the following procedure. The dataset is split into a training dataset and an evaluation dataset using a 63–37% split to allow the models to learn the patterns of more than a calendar year (since the month of the year is given as input) and to be evaluated under a whole calendar year as well. Thus, the first 63% of the dataset (14,856 hourly observations or 619 days) is used for the training process and the remaining 37% (8760 hourly observations or 365 days) is used for testing the models.
The accuracy of the models is evaluated by computing the root mean squared error (RMSE) and the mean absolute error (MAE) of the respective forecasts across the evaluation period considered. The mathematical formula for these two metrics is presented as follows:
where is the real value of the PV production or the building consumption time series at hourly interval t of the evaluation period and is the produced forecast of the respective model. Alon with these two evaluation metrics, one additional error metric is considered in order to make the model evaluation process more complete: the normalized root mean squared error (NRMSE). NRMSE is an appropriate metric for comparing models of different scales, connecting the RMSE value with the observed range of the variable [25]. It is calculated as follows:
where is the average of the real values.
4.3. Results and Discussion
In this section, we present the results of the experimental application, comparing the models that were traditionally trained and the ones that were incrementally trained in terms of forecasting accuracy based on the above-mentioned error metrics. Results are presented separately for the case of PV production forecasting and for the case of the building’s electricity consumption forecasting.
A comparative plot of the predictions of the two forecasting models for PV production is presented in Figure 7. It can be observed that the MLP model that was periodically re-trained during the evaluation period is more accurate than the traditionally trained one. This can be attributed to the ability of the first to better adjust to changes in the data distribution or possible trends. If, for example, a PV system has some major performance changes due to anomalies such as PV cell internal damages or cracks in panels, then a traditional model will not be able to adjust to these changes. On the contrary, an incrementally trained model is capable of detecting such patterns in the PV production time series, adjusting and thus accurately forecasting even in these difficult cases.
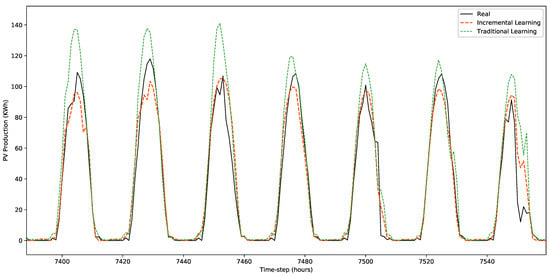
Figure 7.
Comparative plot of the traditional and the online learning frameworks for the PV production forecasting task.
In the case of PV production forecasting, the incrementally trained model demonstrated an MAE index equal to 6.697 KWh, an RMSE index equal to 13.260 KWh and an NRMSE index equal to 0.527. On the contrary, the traditional ML model demonstrated an MAE index equal to 7.273 KWh, an RMSE index equal to 13.340 KWh and an NRMSE index equal to 0.570, as presented in Table 2. Thus, the incrementally trained model outperforms the traditional one by 8.6% in terms of MAE and 8.1% in terms of RMSE, further highlighting the importance of periodical re-training in the predictive task of PV forecasting.

Table 2.
Error metrics for the PV production forecasting models in the cases of traditional and incremental learning.
Considering the case of electricity forecasting in buildings, the impact of re-training the models is even higher. This could be attributed to the fact that electricity consumption is more stochastic in nature compared to the mainly weather-driven PV production forecasting task. This results in a more variant time series influenced by human habits, which, as expected, is more difficult to predict. In this context, incremental re-training allows for the model to adapt in real time to changes in the data distribution. The results of the models for a typical week of the evaluation set are demonstrated in Figure 8.
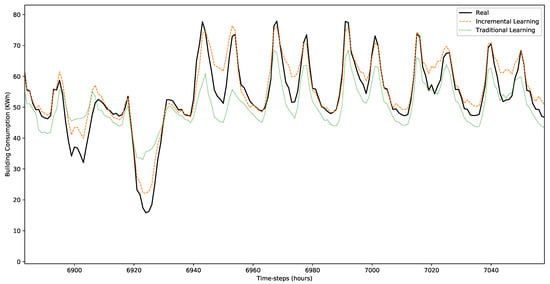
Figure 8.
Comparative plot of the traditional and the online learning framework for the electricity consumption forecasting task.
With regard to accuracy metrics, the incrementally trained MLP model outperforms the traditional MLP, considering both the MAE error index (8.082 KWh for the incremental one against 9.048 KWh for the traditional one) and the RMSE index (12.391 KWh for the incremental one against 13.429 KWh for the traditional one), as presented in Table 3. The respective percentages of improvement are 11.9% for MAE and 8.4% for RMSE.

Table 3.
Error metrics for the electricity consumption forecasting models in the cases of traditional and incremental learning.
It can be observed that the impact of incremental learning is higher on the building electricity consumption task compared to the PV production forecasting task. As expected, this can be attributed to the more stochastic nature of the electricity consumption time series, which is highly influenced by human behavior.
Regarding the benefits in terms of complexity, the incremental learning approach requires over 600 times less memory space than the standard learning process in the examined use case. This can be attributed to the incremental learning architecture, which consumes only a single batch of data each time. In terms of time complexity, the incremental models were trained in significantly less time than the traditional ones, although the training time difference depends on the computational system used.
Consequently, using standard training methods makes storage and manipulation more difficult and time consuming. On the contrary, training a model incrementally offers the option to use batches of data. Thus, the required space is reduced, being equal to the size of a single batch. As for time complexity, incremental training is more efficient and quicker, since the training time required when using a single batch is significantly lower than the respective time when using the whole dataset in standard methods.
5. Conclusions
Progress in measurement devices and data engineering has resulted in an abundance of generated data. In this paper an incremental learning architecture is introduced that is suitable for real-time data streams, recognizing the dynamic nature of learning environments in time-series problems and adjusting to changes in the data distribution. The proposed incremental learning framework was applied on two separate energy forecasting problems with streaming data from a real use case in Italy composed of a PV system and a building. The findings of this study have highlighted the need for incrementally trained ML models, especially for production, as the incrementally trained models have been found to be more robust, showing increased accuracy even when the patterns of incoming data change. Furthermore, except for the increased forecasting accuracy, it should be highlighted that the proposed approach does not require the whole dataset to be held in memory, contrary to offline training procedures. Future research should involve evaluating the proposed framework on other ML and DL models in order to conclude which models are the most suitable for incremental learning processes. Furthermore, it would be beneficial to evaluate the framework with datasets of greater volume in order to gain more insight about the impact of online learning in forecasting accuracy and memory use. Finally, research efforts could also focus on the periodicity with which the re-training process should take place.
Author Contributions
Conceptualization, E.S., H.D. and V.M.; methodology, E.S. and H.D.; software, E.S. and S.S.; validation, M.A.B., F.S. and V.M.; formal analysis, E.S., M.A.B. and S.S.; investigation, E.S, F.S. and S.S.; resources, M.A.B. and F.S.; writing—original draft preparation, E.S., M.A.B. and S.S.; writing—review and editing, V.M., F.S. and H.D.; visualization, E.S. and S.S.; supervision, V.M. and H.D.; project administration, H.D. All authors have read and agreed to the published version of the manuscript.
Funding
The work presented is based on research conducted within the framework of the H2020 European Commission project BD4NRG (grant agreement no. 872613). The content of the paper is the sole responsibility of its author and does not necessary reflect the views of the EC.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| ACF | Auto-Correlation Function |
| ANN | Artificial Neural Network |
| ARIMA | Autoregressive Integrated Moving Average |
| DL | Deep Learning |
| DSO | Distribution System Operator |
| DWT | Discrete Wavelet Transform |
| EMD | Empirical Mode Decomposition |
| GHG | Greenhouse Gas |
| HVAC | Heating, Ventilation, Air-Conditioning |
| IoT | Internet of Things |
| MAE | Mean Absolute Error |
| ML | Machine Learning |
| MLP | Multilayer Perceptron |
| MQTT | MQ Telemetry Transport |
| NRMSE | Normalized Root Mean Squared Error |
| NWP | Numerical Weather Prediction |
| PV | Photovoltaic |
| RE-SOINN | Regression Enhanced Self-organizing Incremental Neural Network |
| RES | Renewable Energy Sources |
| RMSE | Root Mean Squared Error |
| RVFL | Random Vector Functional Link |
| SCADA | Supervisory Control And Data Acquisition |
| SVM | Support Vector Machine |
References
- Marino, D.L.; Amarasinghe, K.; Manic, M. Building energy load forecasting using deep neural networks. In Proceedings of the IECON 2016-42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 23–26 October 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 7046–7051. [Google Scholar]
- Wang, H.; Lei, Z.; Zhang, X.; Zhou, B.; Peng, J. A review of deep learning for renewable energy forecasting. Energy Convers. Manag. 2019, 198, 111799. [Google Scholar] [CrossRef]
- Tang, L.; Wu, Y.; Yu, L. A randomized-algorithm-based decomposition-ensemble learning methodology for energy price forecasting. Energy 2018, 157, 526–538. [Google Scholar] [CrossRef]
- Hong, T.; Pinson, P.; Wang, Y.; Weron, R.; Yang, D.; Zareipour, H. Energy forecasting: A review and outlook. IEEE Open Access J. Power Energy 2020, 7, 376–388. [Google Scholar] [CrossRef]
- Coignard, J.; Janvier, M.; Debusschere, V.; Moreau, G.; Chollet, S.; Caire, R. Evaluating forecasting methods in the context of local energy communities. Int. J. Electr. Power Energy Syst. 2021, 131, 106956. [Google Scholar] [CrossRef]
- Deb, C.; Zhang, F.; Yang, J.; Lee, S.E.; Shah, K.W. A review on time series forecasting techniques for building energy consumption. Renew. Sustain. Energy Rev. 2017, 74, 902–924. [Google Scholar] [CrossRef]
- Henzel, J.; Wróbel, Ł.; Fice, M.; Sikora, M. Energy consumption forecasting for the digital-twin model of the building. Energies 2022, 15, 4318. [Google Scholar] [CrossRef]
- Sarmas, E.; Dimitropoulos, N.; Strompolas, S.; Mylona, Z.; Marinakis, V.; Giannadakis, A.; Romaios, A.; Doukas, H. A web-based Building Automation and Control Service. In Proceedings of the 2022 13th International Conference on Information, Intelligence, Systems & Applications (IISA), Corfu, Greece, 18–20 July 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–6. [Google Scholar]
- Fitch-Roy, O.; Fairbrass, J. Negotiating the EU’s 2030 Climate and Energy Framework; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Sweeney, C.; Bessa, R.J.; Browell, J.; Pinson, P. The future of forecasting for renewable energy. Wiley Interdiscip. Rev. Energy Environ. 2020, 9, e365. [Google Scholar] [CrossRef]
- IEA. Solar PV, Paris. 2022. Available online: https://www.iea.org/reports/solar-pv (accessed on 9 November 2022).
- Das, U.K.; Tey, K.S.; Seyedmahmoudian, M.; Mekhilef, S.; Idris, M.Y.I.; Van Deventer, W.; Horan, B.; Stojcevski, A. Forecasting of photovoltaic power generation and model optimization: A review. Renew. Sustain. Energy Rev. 2018, 81, 912–928. [Google Scholar] [CrossRef]
- Spiliotis, E.; Legaki, N.Z.; Assimakopoulos, V.; Doukas, H.; El Moursi, M.S. Tracking the performance of photovoltaic systems: A tool for minimising the risk of malfunctions and deterioration. IET Renew. Power Gener. 2018, 12, 815–822. [Google Scholar] [CrossRef]
- Ssekulima, E.B.; Anwar, M.B.; Al Hinai, A.; El Moursi, M.S. Wind speed and solar irradiance forecasting techniques for enhanced renewable energy integration with the grid: A review. IET Renew. Power Gener. 2016, 10, 885–989. [Google Scholar] [CrossRef]
- Ahmad, A.S.; Hassan, M.Y.; Abdullah, M.P.; Rahman, H.A.; Hussin, F.; Abdullah, H.; Saidur, R. A review on applications of ANN and SVM for building electrical energy consumption forecasting. Renew. Sustain. Energy Rev. 2014, 33, 102–109. [Google Scholar] [CrossRef]
- Ahmed, R.; Sreeram, V.; Mishra, Y.; Arif, M. A review and evaluation of the state-of-the-art in PV solar power forecasting: Techniques and optimization. Renew. Sustain. Energy Rev. 2020, 124, 109792. [Google Scholar]
- Mayer, M.J. Benefits of physical and machine learning hybridization for photovoltaic power forecasting. Renew. Sustain. Energy Rev. 2022, 168, 112772. [Google Scholar] [CrossRef]
- Fara, L.; Diaconu, A.; Craciunescu, D.; Fara, S. Forecasting of energy production for photovoltaic systems based on ARIMA and ANN advanced models. Int. J. Photoenergy 2021, 2021. [Google Scholar] [CrossRef]
- Hassan, M.A.; Khalil, A.; Kaseb, S.; Kassem, M. Exploring the potential of tree-based ensemble methods in solar radiation modeling. Appl. Energy 2017, 203, 897–916. [Google Scholar] [CrossRef]
- Shi, J.; Lee, W.J.; Liu, Y.; Yang, Y.; Wang, P. Forecasting power output of photovoltaic systems based on weather classification and support vector machines. IEEE Trans. Ind. Appl. 2012, 48, 1064–1069. [Google Scholar] [CrossRef]
- Pazikadin, A.R.; Rifai, D.; Ali, K.; Malik, M.Z.; Abdalla, A.N.; Faraj, M.A. Solar irradiance measurement instrumentation and power solar generation forecasting based on Artificial Neural Networks (ANN): A review of five years research trend. Sci. Total Environ. 2020, 715, 136848. [Google Scholar] [CrossRef]
- Li, P.; Zhou, K.; Lu, X.; Yang, S. A hybrid deep learning model for short-term PV power forecasting. Appl. Energy 2020, 259, 114216. [Google Scholar] [CrossRef]
- Sarmas, E.; Spiliotis, E.; Marinakis, V.; Tzanes, G.; Kaldellis, J.K.; Doukas, H. ML-based energy management of water pumping systems for the application of peak shaving in small-scale islands. Sustain. Cities Soc. 2022, 82, 103873. [Google Scholar] [CrossRef]
- Zang, H.; Cheng, L.; Ding, T.; Cheung, K.W.; Wei, Z.; Sun, G. Day-ahead photovoltaic power forecasting approach based on deep convolutional neural networks and meta learning. Int. J. Electr. Power Energy Syst. 2020, 118, 105790. [Google Scholar] [CrossRef]
- Sarmas, E.; Dimitropoulos, N.; Marinakis, V.; Mylona, Z.; Doukas, H. Transfer learning strategies for solar power forecasting under data scarcity. Sci. Rep. 2022, 12, 1–13. [Google Scholar] [CrossRef] [PubMed]
- De Giorgi, M.G.; Congedo, P.M.; Malvoni, M. Photovoltaic power forecasting using statistical methods: Impact of weather data. IET Sci. Meas. Technol. 2014, 8, 90–97. [Google Scholar] [CrossRef]
- Yu, T.C.; Chang, H.T. The forecast of the electrical energy generated by photovoltaic systems using neural network method. In Proceedings of the 2011 International Conference on Electric Information and Control Engineering, Wuhan, China, 15–17 April 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 2758–2761. [Google Scholar]
- Raza, M.Q.; Nadarajah, M.; Ekanayake, C. On recent advances in PV output power forecast. Sol. Energy 2016, 136, 125–144. [Google Scholar] [CrossRef]
- Sun, X.; Zhang, T. Solar power prediction in smart grid based on NWP data and an improved boosting method. In Proceedings of the 2017 IEEE International Conference on Energy Internet (ICEI), Beijing, China, 17–21 April 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 89–94. [Google Scholar]
- Akeiber, H.; Nejat, P.; Majid, M.Z.A.; Wahid, M.A.; Jomehzadeh, F.; Famileh, I.Z.; Calautit, J.K.; Hughes, B.R.; Zaki, S.A. A review on phase change material (PCM) for sustainable passive cooling in building envelopes. Renew. Sustain. Energy Rev. 2016, 60, 1470–1497. [Google Scholar] [CrossRef]
- Sarmas, E.; Marinakis, V.; Doukas, H. A data-driven multicriteria decision making tool for assessing investments in energy efficiency. Oper. Res. 2022, 22, 5597–5616. [Google Scholar] [CrossRef]
- Kwok, S.S.; Lee, E.W. A study of the importance of occupancy to building cooling load in prediction by intelligent approach. Energy Convers. Manag. 2011, 52, 2555–2564. [Google Scholar] [CrossRef]
- Suganthi, L.; Samuel, A.A. Energy models for demand forecasting—A review. Renew. Sustain. Energy Rev. 2012, 16, 1223–1240. [Google Scholar] [CrossRef]
- Amasyali, K.; El-Gohary, N.M. A review of data-driven building energy consumption prediction studies. Renew. Sustain. Energy Rev. 2018, 81, 1192–1205. [Google Scholar] [CrossRef]
- Li, Q.; Ren, P.; Meng, Q. Prediction model of annual energy consumption of residential buildings. In Proceedings of the 2010 International Conference on Advances in Energy Engineering, Beijing, China, 19–20 June 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 223–226. [Google Scholar]
- Liu, D.; Chen, Q. Prediction of building lighting energy consumption based on support vector regression. In Proceedings of the 2013 9th Asian Control Conference (ASCC), Istanbul, Turkey, 23–26 June 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1–5. [Google Scholar]
- Borges, C.E.; Penya, Y.K.; Fernández, I.; Prieto, J.; Bretos, O. Assessing tolerance-based robust short-term load forecasting in buildings. Energies 2013, 6, 2110–2129. [Google Scholar] [CrossRef]
- Saadi, M.; Noor, M.T.; Imran, A.; Toor, W.T.; Mumtaz, S.; Wuttisittikulkij, L. IoT enabled quality of experience measurement for next generation networks in smart cities. Sustain. Cities Soc. 2020, 60, 102266. [Google Scholar] [CrossRef]
- Sarmas, E.; Spiliotis, E.; Marinakis, V.; Koutselis, T.; Doukas, H. A meta-learning classification model for supporting decisions on energy efficiency investments. Energy Build. 2022, 258, 111836. [Google Scholar] [CrossRef]
- Marinakis, V. Big data for energy management and energy-efficient buildings. Energies 2020, 13, 1555. [Google Scholar] [CrossRef]
- Bouchachia, A.; Gabrys, B.; Sahel, Z. Overview of some incremental learning algorithms. In Proceedings of the 2007 IEEE International Fuzzy Systems Conference, London, UK, 23–26 July 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 1–6. [Google Scholar]
- Ksieniewicz, P.; Zyblewski, P. Stream-learn—Open-source Python library for difficult data stream batch analysis. Neurocomputing 2022, 478, 11–21. [Google Scholar] [CrossRef]
- Puah, B.K.; Chong, L.W.; Wong, Y.W.; Begam, K.; Khan, N.; Juman, M.A.; Rajkumar, R.K. A regression unsupervised incremental learning algorithm for solar irradiance prediction. Renew. Energy 2021, 164, 908–925. [Google Scholar] [CrossRef]
- Qiu, X.; Suganthan, P.N.; Amaratunga, G.A. Ensemble incremental learning random vector functional link network for short-term electric load forecasting. Knowl.-Based Syst. 2018, 145, 182–196. [Google Scholar] [CrossRef]
- Gardner, M.W.; Dorling, S. Artificial neural networks (the multilayer perceptron)—A review of applications in the atmospheric sciences. Atmos. Environ. 1998, 32, 2627–2636. [Google Scholar] [CrossRef]
- Bourlard, H.; Kamp, Y. Auto-association by multilayer perceptrons and singular value decomposition. Biol. Cybern. 1988, 59, 291–294. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Bifet, A.; Gavalda, R.; Holmes, G.; Pfahringer, B. Machine Learning for Data Streams: With Practical Examples in MOA; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Ratcliff, R. Connectionist models of recognition memory: Constraints imposed by learning and forgetting functions. Psychol. Rev. 1990, 97, 285. [Google Scholar] [CrossRef]
- Robins, A. Catastrophic forgetting, rehearsal and pseudorehearsal. Connect. Sci. 1995, 7, 123–146. [Google Scholar] [CrossRef]
- He, J.; Mao, R.; Shao, Z.; Zhu, F. Incremental Learning in Online Scenario. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 16–19 June 2020. [Google Scholar]
- MQTT. Available online: https://docs.oasis-open.org/mqtt/mqtt/v5.0/mqtt-v5.0.html (accessed on 25 November 2022).
- Buitinck, L.; Louppe, G.; Blondel, M.; Pedregosa, F.; Mueller, A.; Grisel, O.; Niculae, V.; Prettenhofer, P.; Gramfort, A.; Grobler, J.; et al. API design for machine learning software: Experiences from the scikit-learn project. In Proceedings of the ECML PKDD Workshop: Languages for Data Mining and Machine Learning, Prague, Czech Republic, 23–27 September 2013; pp. 108–122. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Scitkit-Learn 6. Strategies to Scale Computationally: Bigger Data. Available online: https://scikit-learn.org/0.15/modules/scaling_strategies.html#strategies-to-scale-computationally-bigger-data (accessed on 3 November 2022).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).